Let's see a local CRS for mapping the entire United States. NAD83 / Conus Albers (EPSG:5072) uses an ellipsoid called GRS80 (Geodetic Reference System 1980). It has almost the same properties as WGS84, and they had the same properties back in the time. However, WGS84 underwent some changes (realizations) to give a better fit for GPS systems, and therefore, its flattening became slightly different.
More importantly, NAD83 / Conus Albers uses a local datum--NAD83 (North American Datum 1983). That means, it is not referenced to Earth's center of mass, but to the North American plate. It is still referenced to the same planet, so the question arises--what's the difference? The answer is simple--plate tectonics. The coordinates on global datums are changing constantly due to plate movements. This is a very slow change (a few centimeters every year), however, it still can be an issue for high accuracy surveys and analyses. To avoid the urge for correcting old data, local datums are referenced to local places, and are moving with the plate underneath. This also means that global and local datums are slowly drifting apart. Consider the following diagram:
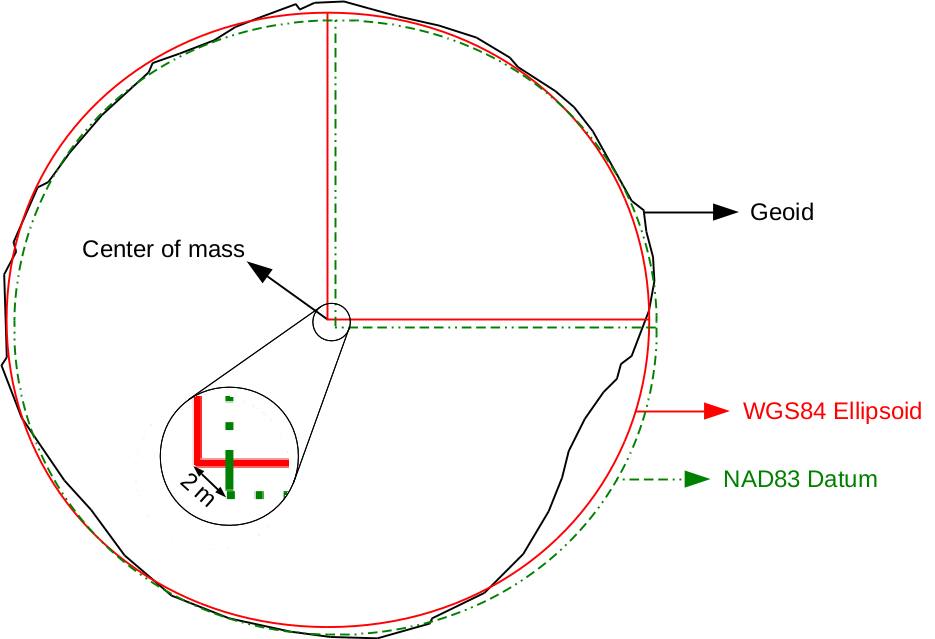
The geoid is the most accurate mathematical model we have for the Earth's shape. Its center is located in the center of Earth's mass. The WGS84 oblate spheroid is a much more general model, whose center is placed at the geoid's center. The difference between the two models is called geoid undulation, which is automatically height-corrected by GPS systems. As the NAD83 datum is referenced to the North American plate, its center slowly drifts apart from the center of the WGS84 ellipsoid.
The NAD83 / Conus Albers (EPSG:5072) uses an Albers projection. It is conic, therefore, the geographic coordinates are projected onto a cone, which, by flattening out, produces a half-circle-shaped map for its whole validity extent. However, there is a catch; it's not perspective. Therefore, the perspective point is meaningless in this concept. Non-perspective projections can only be defined mathematically, we cannot reproduce them with a light source.
