Some of the mechanisms designed for location privacy protection are based on location obfuscation, which is explained in [5] as the means of deliberately degrading the quality of information about an individual's location in order to protect that individual's location privacy.

This is perhaps the simplest way to implement location privacy protection in LBISs because it has barely any impact on the server-side of the application, and is usually easy to implement on the client-side. Another way to implement it would be on the server-side, running periodically over the new data, or as a function applied to every new entry.

The main goal of these techniques is to add random noise to the original location obtained by the cellphone or any other location-aware device, so as to reduce the accuracy of the data. In this case, the user can usually define the maximum and/or minimum amount of noise that they want to add. The higher the noise added, the lower the quality of the service; so it is very important to reasonably set this parameter. For example, if a real-time tracking application receives data altered by 1 km, the information provided to the user may not be relevant to the real location.

Each noise-based location obfuscation technique presents a different way to generate noise:

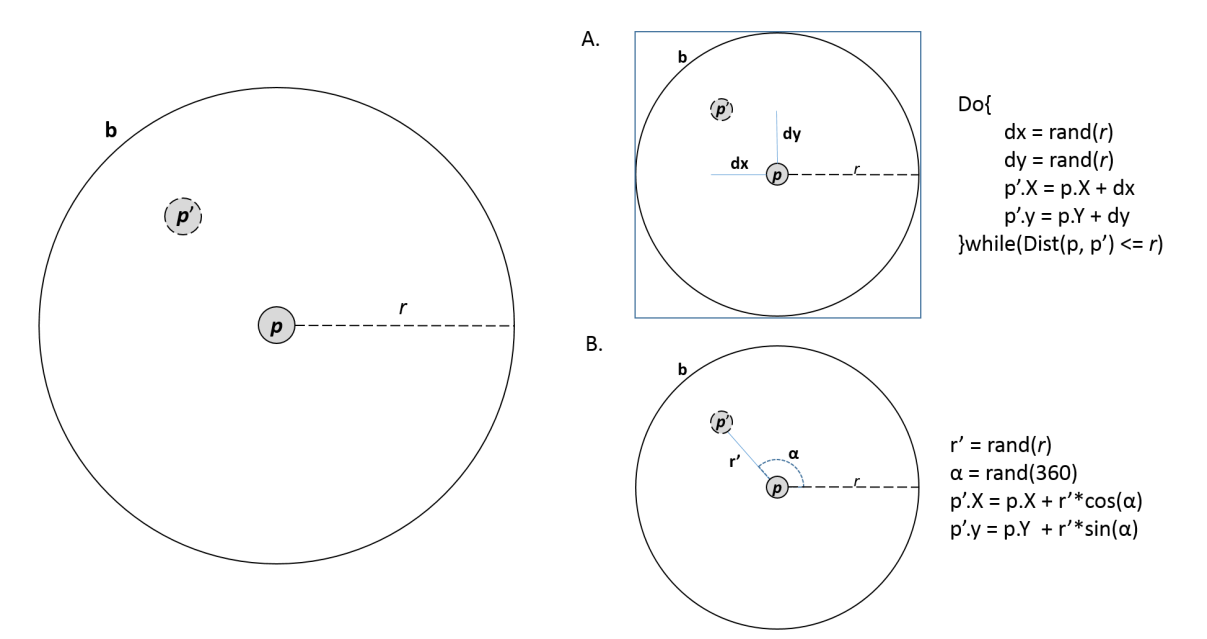
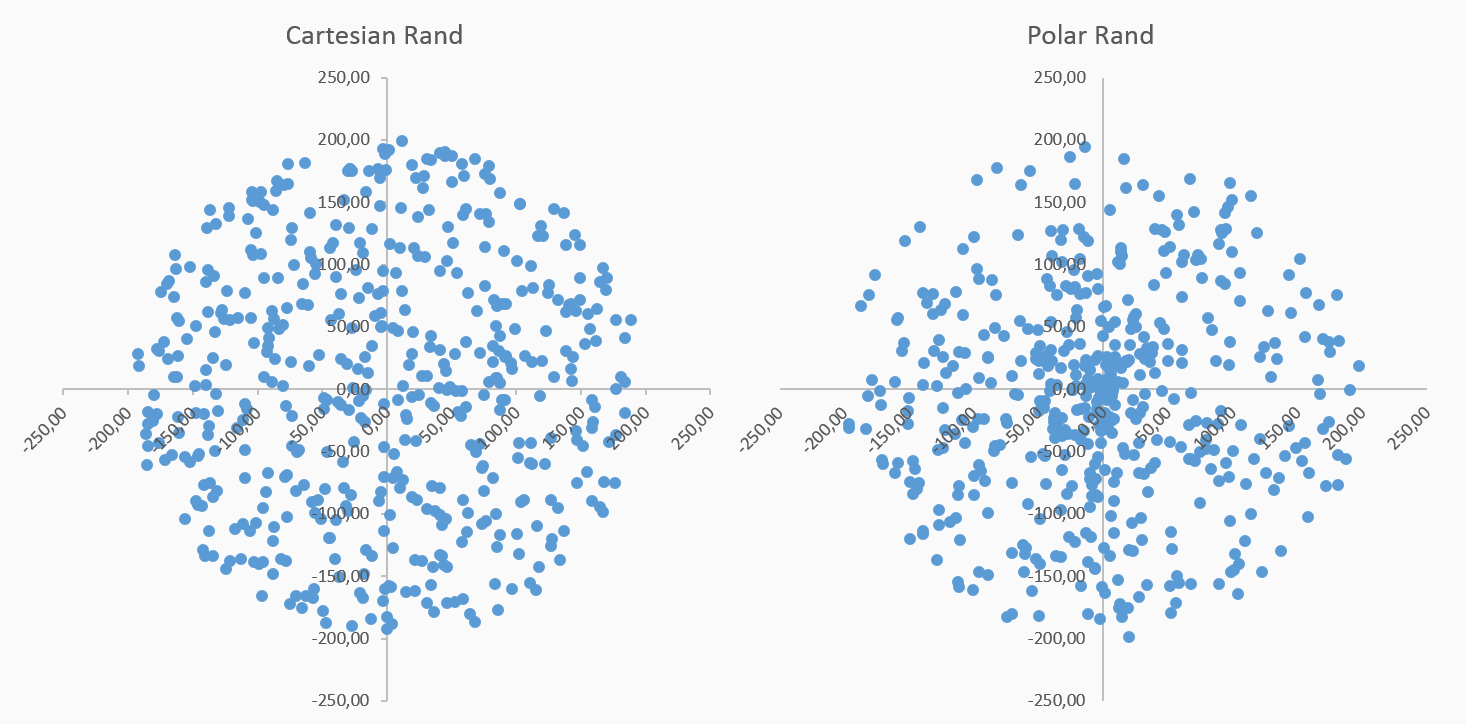
When the noise is generated with polar coordinates, it is more uniformly distributed over a projection of the circular area because both angle and distance follow that distribution. In the case of Cartesian-based noise, points appear to be generated uniformly among the area as a whole, resulting in a lower density of points near the center. The following figure shows the differences in both circular and rectangular projections of 500 random points. In this book, we will work with polar-based random generation:

The following figure illustrates the way the N-RAND [6], θ-RAND [7], and Pinwheel [8] techniques work:

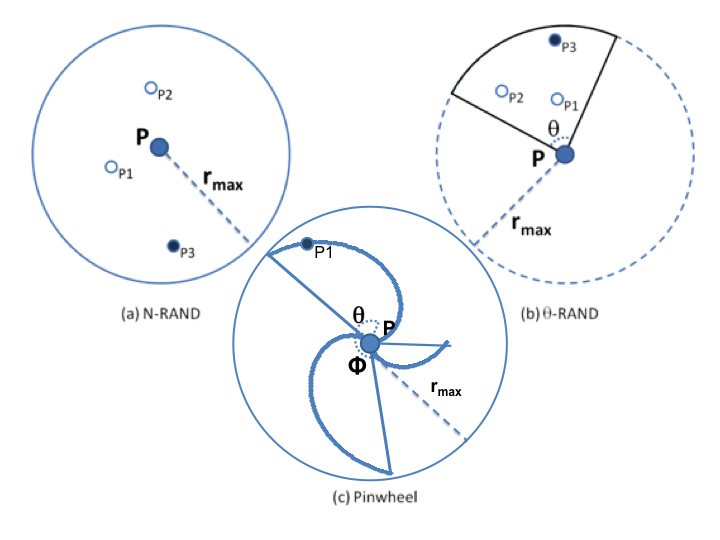
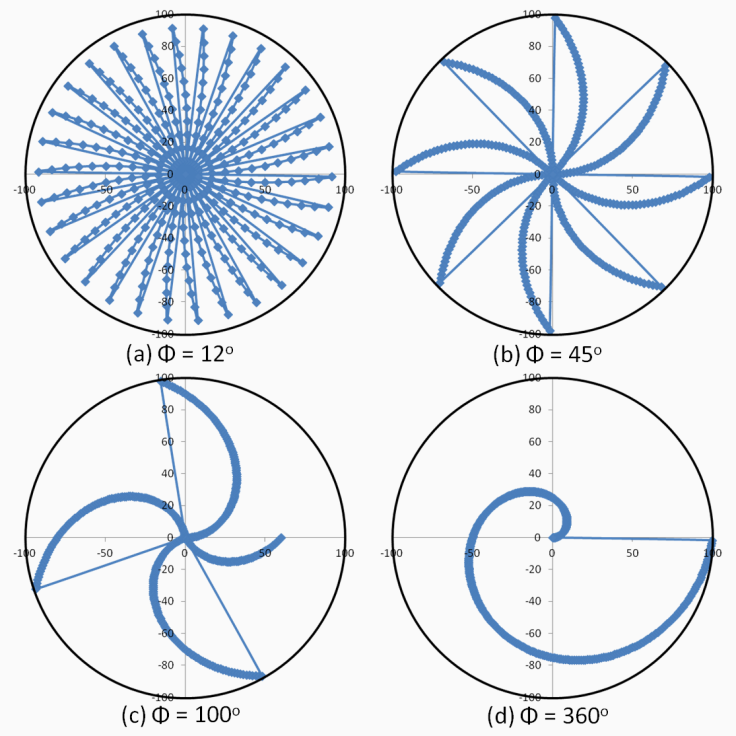
N-RAND generates N points in a given area, and selects the point furthest away from the center. Θ-RAND does the same, but in a specific sector of the circular area. There can be more than just one area to select from. Finally, the Pinwheel mechanism differs from N-RAND and θ-RAND because it does not generate random distances for the points, and instead defines a specific one for each angle in the circumference, making the selection of the radius a more deterministic process when generating random points. In this case, the only random variable in the generation process is the angle α. The formula to calculate the radius for a given angle, α, is presented in (1), as follows:

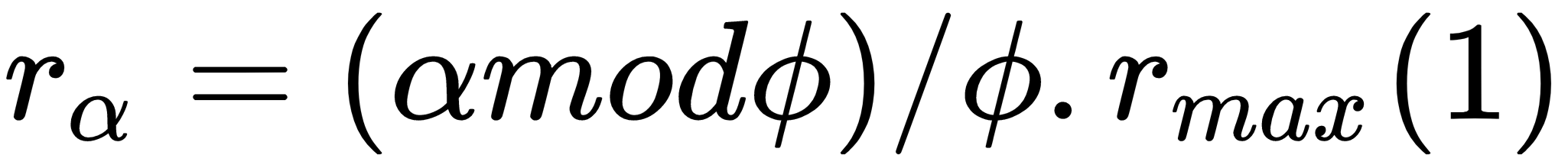
Where φ is a preset parameter defined by the user, it determines the amplitude of the wings of geometry, which resembles a pinwheel.

The lower the value of φ, the more wings the pinwheel will have, but those wings will also be thinner; on the other hand, the higher the value, the fewer the number of wider wings:

Once the locations have been altered, it is very unlikely that you will be able to recover the original information; however, filtering noise techniques are available in the literature that reduce the impact of alterations and allow a better estimation of the location data. One of these mechanisms for noise-filtering is based on an exponential moving average (EMA) called Tis-Bad [9].

There is still an open discussion on how much degradation of the location information is sufficient to provide location privacy to users, and moreover, if the resulting obfuscated information remains useful when accessing a LBS. After all, obtaining relevant responses while performing geospatial analysis is one of the main issues regarding LBS and the study of geo-referenced data.