The steps you need to perform to complete this recipe are as follows:

1. First, use the ST_Distance function to calculate the distances between cities in the USA that have more than 1 million inhabitants using the Spherical Mercator planar projection coordinate system (EPSG:900913, EPSG:3857, or EPSG:3785; all of these SRID representations are equivalent). Use the ST_Transform function as follows to convert the point coordinates from longitude latitude degrees (as the coordinates are originally in EPSG:4326) to a planar metric system if you want the results in meters:

      postgis_cookbook=# SELECT c1.name, c2.name, 
      ST_Distance(ST_Transform(c1.the_geom, 900913), 
      ST_Transform(c2.the_geom, 900913))/1000 AS distance_900913 
      FROM chp03.cities AS c1 
      CROSS JOIN chp03.cities AS c2 
      WHERE c1.pop_2000 > 1000000 AND c2.pop_2000 > 1000000 

      AND c1.name < c2.name 
      ORDER BY distance_900913 DESC; 

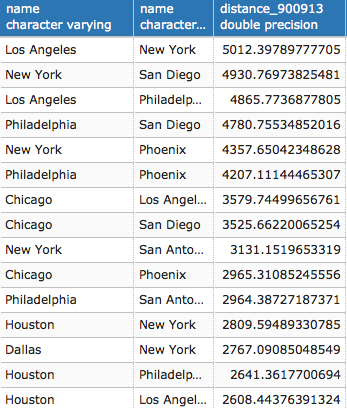
      (36 rows) 

2. Now write the same query as we did in the previous recipe, but in a more compact expression using a PostgreSQL Common Table Expression (CTE):

      WITH cities AS ( 
        SELECT name, the_geom FROM chp03.cities 
        WHERE pop_2000 > 1000000 ) 
      SELECT c1.name, c2.name, 
      ST_Distance(ST_Transform(c1.the_geom, 900913),
      ST_Transform(c2.the_geom, 900913))/1000 AS distance_900913 
      FROM cities c1 CROSS JOIN cities c2 
      where c1.name < c2.name 
      ORDER BY distance_900913 DESC;

3. For large distances such as in this case, it is not correct to use a planar spatial reference system, but you should make the calculations taking into consideration the earth's curvature. For example, the previously used Mercator planar system, while it is very good to use for map outputs, is very bad for measuring distances and areas as it assesses directions. For this purpose, it would be better to use a spatial reference system that is able to measure distance. You can also use the ST_Distance_Sphere or ST_Distance_Spheroid functions (the first being quicker, but less accurate, as it performs calculations on a sphere and not a spheroid). An even better option is converting the geometries to the geography data type, so you can use ST_Distance directly, as it will automatically make the calculations using the spheroid. Note that this is exactly equivalent to using ST_DistanceSpheroid. Try to check the difference between the various approaches, using the same query as before:

      WITH cities AS ( 
        SELECT name, the_geom FROM chp03.cities 
        WHERE pop_2000 > 1000000 ) 
      SELECT c1.name, c2.name, 
      ST_Distance(ST_Transform(c1.the_geom, 900913),
      ST_Transform(c2.the_geom, 900913))/1000 AS d_900913,
      ST_Distance_Sphere(c1.the_geom, c2.the_geom)/1000 AS d_4326_sphere, 
      ST_Distance_Spheroid(c1.the_geom, c2.the_geom,
      'SPHEROID["GRS_1980",6378137,298.257222101]')/1000 
      AS d_4326_spheroid, ST_Distance(geography(c1.the_geom),
      geography(c2.the_geom))/1000 AS d_4326_geography 
      FROM cities c1 CROSS JOIN cities c2 
      where c1.name < c2.name 
      ORDER BY d_900913 DESC;

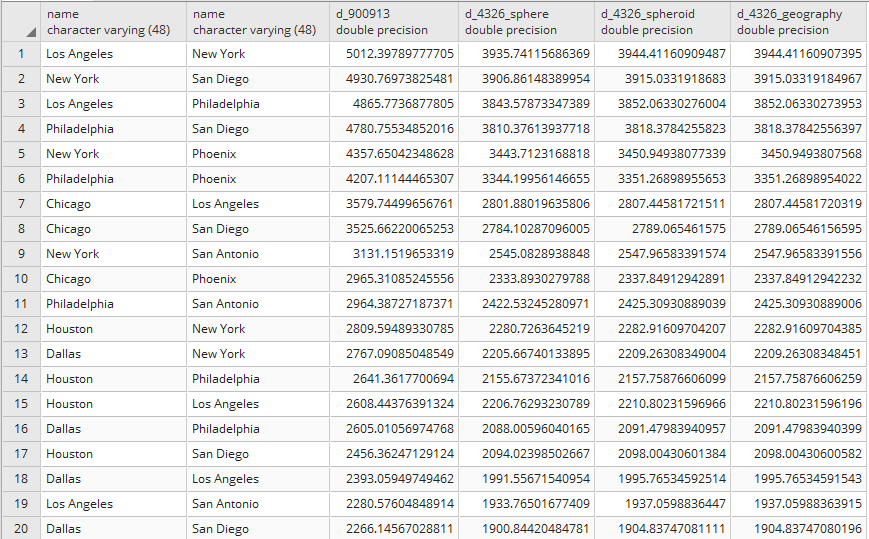
      (36 rows) 

4. You can easily verify from the output that there is a big difference with using the planar system (EPSG:900913, as in the d_900913 column) instead of systems that take into consideration the curvature of the earth.