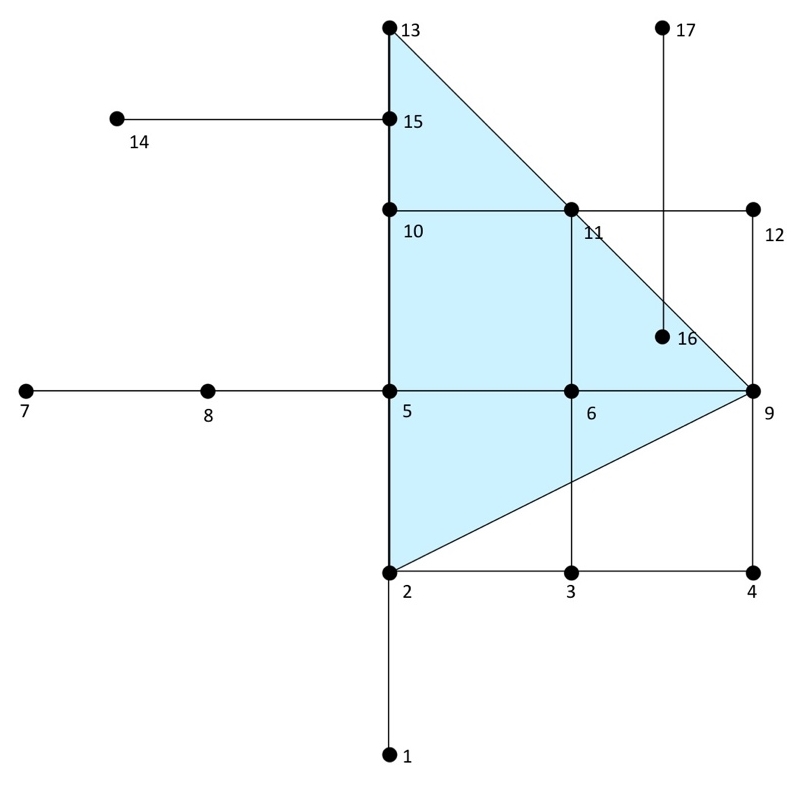
In the following example, we will look at all users within a distance of three units from our starting point—that is, a proposed bike shop at node 2:

SELECT * FROM pgr_drivingDistance(
  'SELECT id, source, target, cost FROM chp06.edge_table',
  2, 3
);

The preceding command gives the following output:

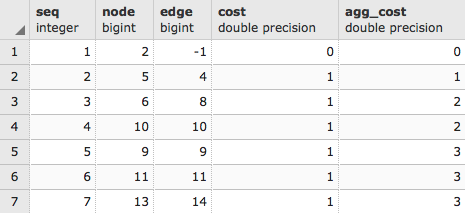
As usual, we just get a list from the pgr_drivingDistance table that, in this case, comprises sequence, node, edge cost, and aggregate cost. PgRouting, like PostGIS, gives us low-level functionality; we need to reconstruct what geometries we need from that low-level functionality. We can use that node ID to extract the geometries of all of our nodes by executing the following script:

WITH DD AS (
  SELECT * FROM pgr_drivingDistance(
    'SELECT id, source, target, cost 
    FROM chp06.edge_table', 2, 3
  )
)
    
SELECT ST_AsText(the_geom)
FROM chp06.edge_table_vertices_pgr w, DD d
WHERE w.id = d.node; 

The preceding command gives the following output:

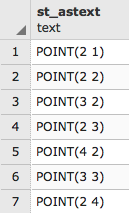
But the output seen is just a cluster of points. Normally, when we think of driving distance, we visualize a polygon. Fortunately, we have the pgr_alphaShape function that provides us that functionality. This function expects id, x, and y values for input, so we will first change our previous query to convert to x and y from the geometries in edge_table_vertices_pgr:

WITH DD AS (
  SELECT * FROM pgr_drivingDistance(
    'SELECT id, source, target, cost FROM chp06.edge_table',
     2, 3
  )
)
SELECT id::integer,  ST_X(the_geom)::float AS x, ST_Y(the_geom)::float AS y 
FROM chp06.edge_table_vertices_pgr w, DD d
WHERE w.id = d.node;

The output is as follows:

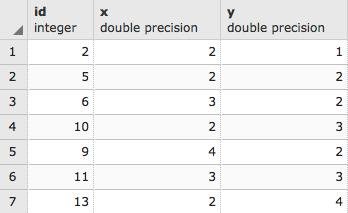
Now we can wrap the preceding script up in the alphashape function:

WITH alphashape AS (
  SELECT pgr_alphaShape('
    WITH DD AS (
      SELECT * FROM pgr_drivingDistance(
        ''SELECT id, source, target, cost 
        FROM chp06.edge_table'', 2, 3
      )
    ),
    dd_points AS(
      SELECT id::integer, ST_X(the_geom)::float AS x, 
      ST_Y(the_geom)::float AS y
      FROM chp06.edge_table_vertices_pgr w, DD d
      WHERE w.id = d.node
    )
    SELECT * FROM dd_points
  ')
),  

So first, we will get our cluster of points. As we did earlier, we will explicitly convert the text to geometric points:

alphapoints AS (
  SELECT ST_MakePoint((pgr_alphashape).x, (pgr_alphashape).y) FROM alphashape
),

Now that we have points, we can create a line by connecting them:

alphaline AS (
  SELECT ST_Makeline(ST_MakePoint) FROM alphapoints
)
SELECT ST_MakePolygon(ST_AddPoint(ST_Makeline, ST_StartPoint(ST_Makeline))) FROM alphaline;

Finally, we construct the line as a polygon using ST_MakePolygon. This requires adding the start point by executing ST_StartPoint in order to properly close the polygon. The complete code is as follows:

WITH alphashape AS (
  SELECT pgr_alphaShape('
    WITH DD AS (
      SELECT * FROM pgr_drivingDistance(
        ''SELECT id, source, target, cost
        FROM chp06.edge_table'', 2, 3
      )
    ),
    dd_points AS(
      SELECT id::integer, ST_X(the_geom)::float AS x,
      ST_Y(the_geom)::float AS y
      FROM chp06.edge_table_vertices_pgr w, DD d
      WHERE w.id = d.node
    )
    SELECT * FROM dd_points
  ')
),
alphapoints AS (
  SELECT ST_MakePoint((pgr_alphashape).x,
  (pgr_alphashape).y)
  FROM alphashape
),
alphaline AS (
  SELECT ST_Makeline(ST_MakePoint) FROM alphapoints
)
SELECT ST_MakePolygon(
  ST_AddPoint(ST_Makeline, ST_StartPoint(ST_Makeline))
)
FROM alphaline;

Our first driving distance calculation can be better understood in the context of the following diagram, where we can reach nodes 9, 11, 13 from node 2 with a driving distance of 3: