KNN is an approach of searching for an arbitrary number of points closest to a given point. Without the right tools, this can be a very slow process that requires testing the distance between the point of interest and all the possible neighbors. The problem with this approach is that the search becomes exponentially slower with a greater number of points. Let's start with this naive approach and then improve on it.

Suppose we were interested in finding the 10 records closest to the geographic location -81.738624, 41.396679. The naive approach would be to transform this value into our local coordinate system and compare the distance to each point in the database from the search point, order those values by distance, and limit the search to the first 10 closest records (it is not recommended that you run the following query as it could run indefinitely):

SELECT ST_Distance(searchpoint.the_geom, addr.the_geom) AS dist, * FROM 
  chp04.knn_addresses addr, 
  (SELECT ST_Transform(ST_SetSRID(ST_MakePoint(-81.738624, 41.396679),
    4326), 3734) AS the_geom) searchpoint 
  ORDER BY ST_Distance(searchpoint.the_geom, addr.the_geom) 
  LIMIT 10; 

This is a fine approach for smaller datasets. This is a logical, simple, fast approach for a relatively small numbers of records; however, this approach scales very poorly, getting exponentially slower with the addition of records (with 500,000 points, this would take a very long time).

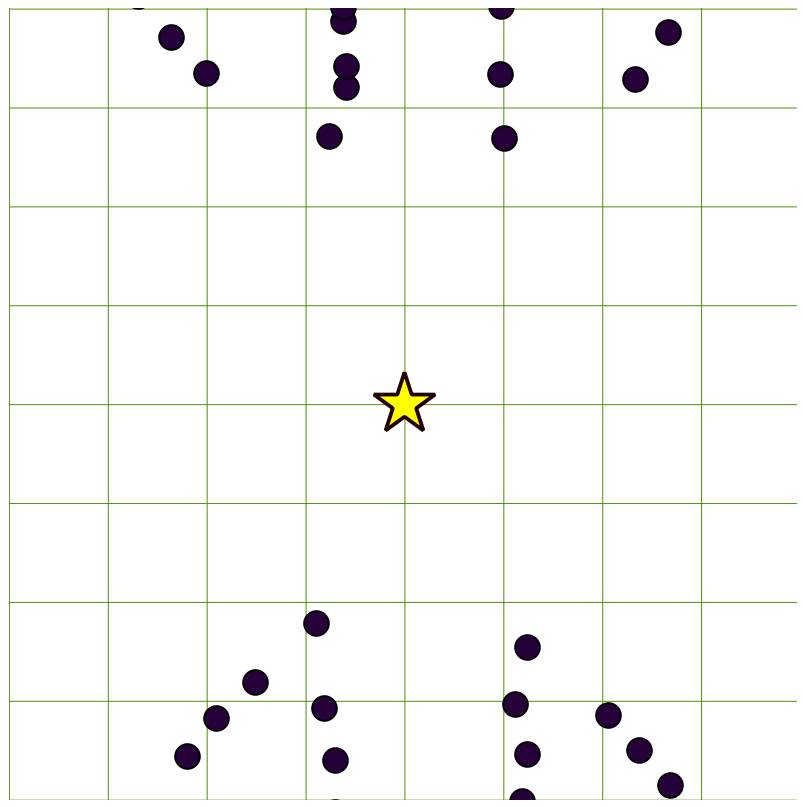
An alternative is to only compare the point of interest to the ones known to be close by setting a search distance. So, for example, in the following diagram, we have a star that represents the current location, and we want to know the 10 closest addresses. The grid in the diagram is 100 feet long, so we can search for the points within 200 feet, then measure the distance to each of these points, and return the closest 10 points:

Thus, our approach to answer this question is to limit the search using the ST_DWithin operator to only search for records within a certain distance. ST_DWithin uses our spatial index, so the initial distance search is fast and the list of returned records should be short enough to do the same pair-wise distance comparison we did earlier in this section. In our case here, we could limit the search to within 200 feet:

SELECT ST_Distance(searchpoint.the_geom, addr.the_geom) AS dist, * FROM 
  chp04.knn_addresses addr, 
  (SELECT ST_Transform(ST_SetSRID(ST_MakePoint(-81.738624, 41.396679), 
    4326), 3734) AS the_geom) searchpoint 
  WHERE ST_DWithin(searchpoint.the_geom, addr.the_geom, 200) 
  ORDER BY ST_Distance(searchpoint.the_geom, addr.the_geom) 
  LIMIT 10; 

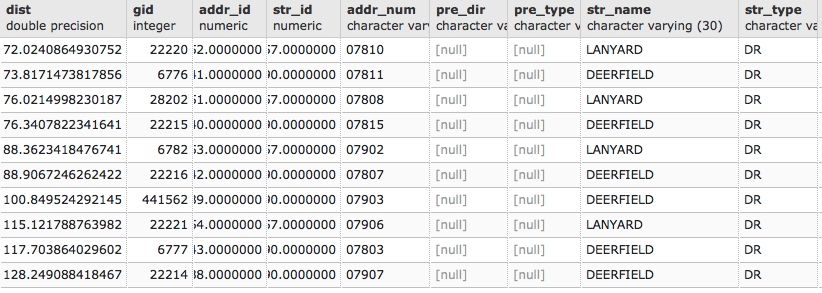
The output for the previous query is as follows:

This approach performs well so long as our search window, ST_DWithin, is the right size for the data. The problem with this approach is that, in order to optimize it, we need to know how to set a search window that is about the right size. Any larger than the right size and the query will run more slowly than we'd like. Any smaller than the right size and we might not get all the points back that we need. Inherently, we don't know this ahead of time, so we can only hope for the best guess.

In this same dataset, if we apply the same query in another location, the output will return no points because the 10 closest points are further than 200 feet away. We can see this in the following diagram:

Fortunately, for PostGIS 2.0+ we can leverage the distance operators (<-> and <#>) to do indexed nearest neighbor searches. This makes for very fast KNN searches that don't require us to guess ahead of time how far away we need to search. Why are the searches fast? The spatial index helps of course, but in the case of the distance operator, we are using the structure of the index itself, which is hierarchical, to very quickly sort our neighbors.

When used in an ORDER BY clause, the distance operator uses the index:

SELECT ST_Distance(searchpoint.the_geom, addr.the_geom) AS dist, * FROM 
  chp04.knn_addresses addr, 
  (SELECT ST_Transform(ST_SetSRID(ST_MakePoint(-81.738624, 41.396679),
    4326), 3734) AS the_geom) searchpoint 
  ORDER BY addr.the_geom <-> searchpoint.the_geom 
  LIMIT 10; 

This approach requires no prior knowledge of how far the nearest neighbors might be. It also scales very well, returning thousands of records in not more than the time it takes to return a few records. It is sometimes slower than using ST_DWithin, depending on how small our search distance is and how large the dataset we are dealing with is. But the trade-off is that we don't need to make a guess of our search distance and for large queries, it can be much faster than the naive approach.