In several recipes in Chapter 4, Working with Vector Data – Advanced Recipes, we explored extracting Voronoi polygons from sets of points. In this recipe, we'll use the Voronoi function employed in the Using external scripts to embed new functionality to calculate Voronoi polygons section to serve as the first step in extracting the centerline of a polygon. One could also use the Using external scripts to embed new functionality to calculate Voronoi polygons—advanced recipe, which would run faster on large datasets. For this recipe, we will use the simpler but slower approach.

One additional dependency is that we will be using the chp02.polygon_to_line(geometry) function from the Normalizing internal overlays recipe in Chapter 2, Structures That Work.

What do we mean by the centerline of a polygon? Imagine a digitized stream flowing between its pair of banks, as shown in the following screenshot:

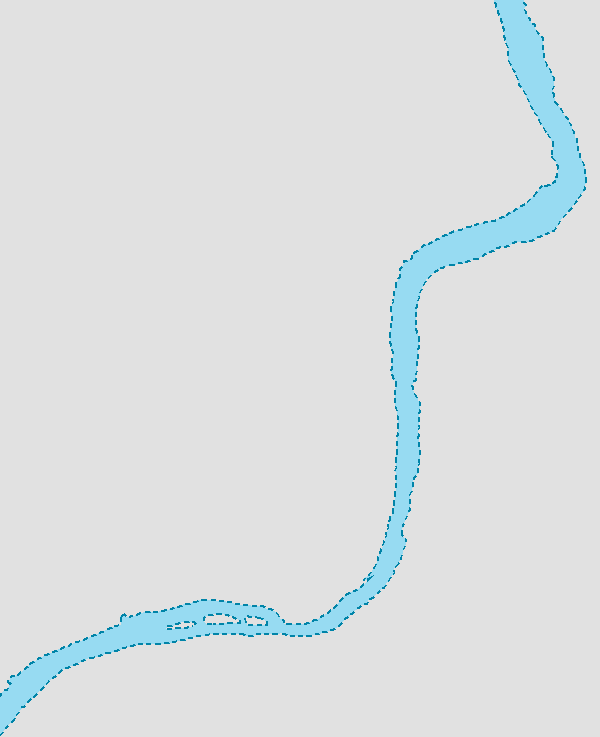
If we wanted to find the center of this in order to model the water flow, we could extract it using a skeletonization approach, as shown in the following screenshot:

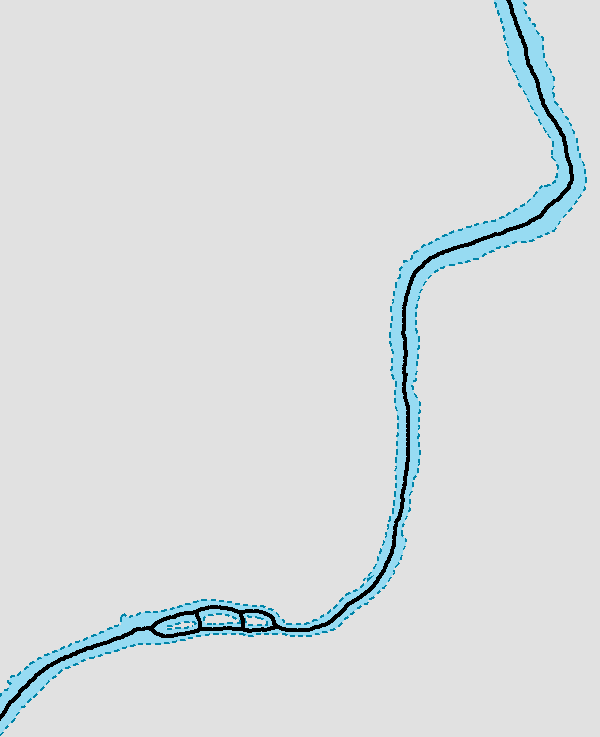
The difficulty with skeletonization approaches, as we'll soon see, is that they are often subject to noise, which is something that natural features such as our stream make plenty of. This means that typical skeletonization, which could be done simply with a Voronoi approach, is therefore inherently inadequate for our purposes.

This brings us to the reason why skeletonization is included in this chapter. Routing is a way for us to simplify skeletons derived from the Voronoi method. It allows us to trace from one end of a major feature to the other and skip all the noise in between.