Raster analysis

Raster data, by organizing the data in uniform grids, is useful to analyze continuous phenomena or find some information at the subobject level. We will use continuous elevation and proximity data in this case, and we will look at the subapplicant object level —at the 30 meter-square cell level. You would choose a cell size depending on the resolution of the data source (for example, from sensors roughly 30 meters apart), the roughness of the analysis (regional versus local), and any hardware limitations.

First, let's make a few notes about raster data:

Nodata refers to the cells that are included with the raster grid because a grid can't have completely undefined cells; however, these cells should really be considered off the layer.
QGIS's raster renderer is more limited than in its proprietary competitors. You will want to use the Identify tool as well as custom styles (Singleband Pseudocolor) to make sense of your outputs.
In this example, we will rely heavily on the GDAL and SAGA libraries that have been wrapped for QGIS. These are available directly through the processing framework with no additional preparation beyond the ordinary raster ETL. For additional functionality, you will want to consider the GRASS libraries. These are wrapped and provided for QGIS but require the additional preparation of a GRASS workspace.

Now that all our data is in the raster format, we can work through how to derive information from these layers and combine this information in order to select the best sites.

Map algebra

Map algebra is a useful concept to work with multiple raster layers and analysis steps, providing arithmetic operations between cells in aligned grids. These produce an output grid with the respective value of the arithmetic solution for each set of cells. We will be using map algebra in this example for additive modeling.

Additive modeling

Now that all our data is in the raster format, we can begin to model for the purpose of site selection. We want to discover which cells are best according to a set of criteria which has either been established for the domain area (for example, the agricultural conservation site selection) by convention or selected at the time of modeling. Additive modeling refers to this process of adding up all the criteria and associated weights to find the best areas, which will have the greatest value.

In this case, we have selected some criteria that are loosely known to affect the agricultural conservation site selection, as shown in the following table:

Layer	Criteria	Rule
`applicants`	Is applicant
`easements`	Proximity	< 2000 m
`landuse (agriculture)`	Land use, proximity	< 100 m
`dem`	Slope	=> 2 and <= 5, average
`landuse (developed)`	Land use, proximity	> 500 m
`roads`	Proximity	> 100m

Proximity

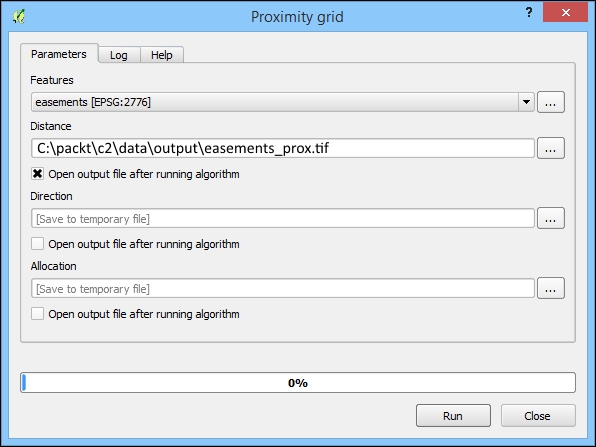
The Proximity grid tool will generate a layer of cells with each cell having a value equal to its distance from the nearest non-nodata cell in another grid. The distance value is given in the CRS units of the other grid. It also generates direction and allocation grids with the direction and ID of the nearest nodata cell.

Creating a proximity to the easements grid

Perform the following steps:

Navigate to Processing Toolbox.
Search for proximity in this toolbox. Ensure that you have the Advanced Interface selected.
Once you've located the Proximity grid tool under SAGA, double-click on it to run it.
Select easements for the Features field.
Specify an output file for Distance at c2/data/output/easements_prox.tif.
Uncheck Open output file after running algorithm for the other two outputs, as shown in the following screenshot:
The resulting grid is of the distance to the closest easement cell.
Repeat these steps to create proximity grids for agriculture, developed, and roads. Finally, you will see the following output: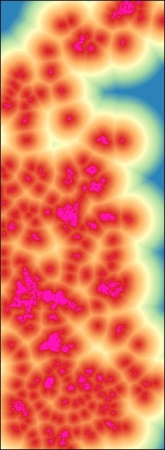

Slope

The Slope command creates a grid where the value of each cell is equal to the upgradient slope in percent terms. In other words, it is equal to how steep the terrain is at the current cell in the percentage of rise in elevation unit per horizontal distance unit. Perform the following steps:

Install and activate the Raster Terrain Analysis plugin if you have not already done so.
Navigate to Raster | Terrain Analysis | Slope.
Select dem, the Digital Elevation Model, for the Elevation layer field.
Save your output in c2/data/output. You can keep the other inputs as default.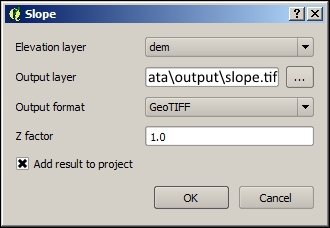
The output will be the steepness of each cell in the percentage of of vertical elevation over horizontal distance ("rise over run").

Combining the criteria with Map Calculator

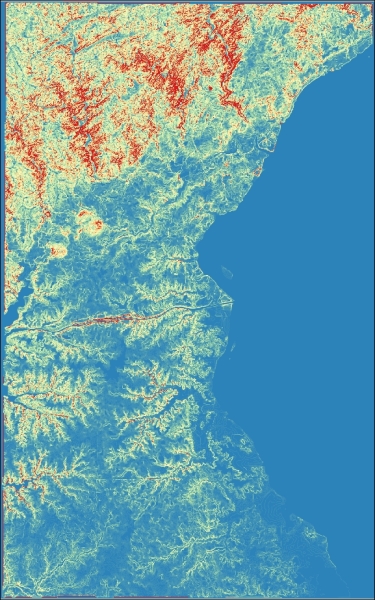
Ensure that all the criteria grids (proximity, agriculture, developed, road, and slope) appear in the Layers panel. If they don't, add them.
Bring up the Raster calculator dialog.
1. Navigate to Raster | Raster calculator
Enter the map algebra expression.
- Add the raster layers by double-clicking on them in the Raster bands selection area
- Add the operators by typing them out or clicking on the buttons in the operators area
- The expression entered should be as follows:
```
("slope@1" < 8) + ("applicants@1" = 1) + ("easement_prox@1"<2000) + ("roads_prox@1">100) + ("developed_prox@1" > 500) + ("agriculture@1" < 100)
```
  Tip
  @1 refers to the first and only band of the raster.
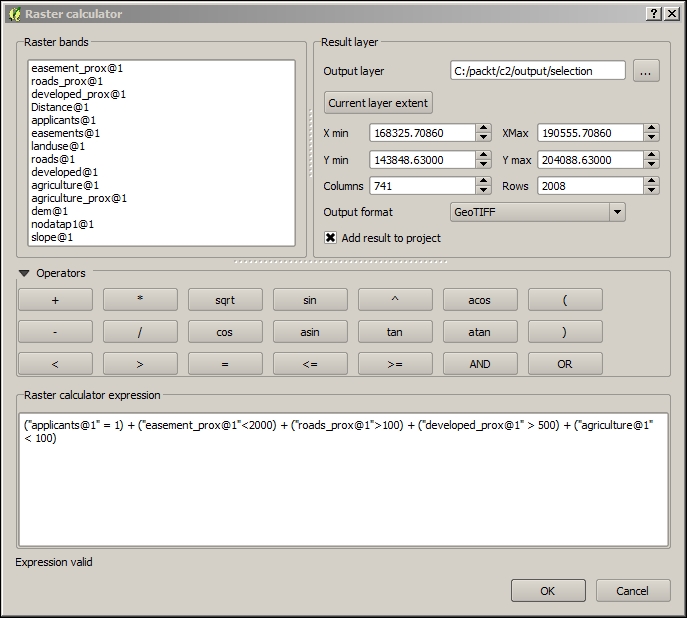
Add a name and path for the output file and hit Enter.
You may need to set a style if it seems like nothing happened. By default, the nonzero value is set to display in white (the same color as our background).

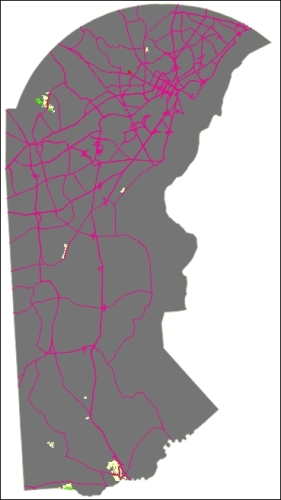
Here's a close up of the preceding map image so that you can see the variability in suitability:

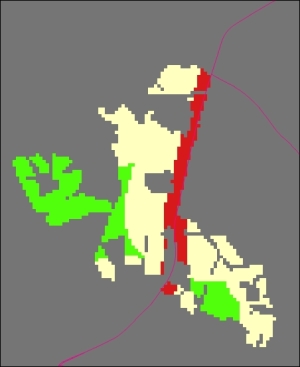
Combining the criteria with Map Calculator

In the preceding screenshot, cells are scored as follows:

Green = 5 (high)
Yellow = 4 (middle)
Red = 3 (low)

Zonal statistics

Zonal statistics are calculated from the cells that fall within polygons. Using zonal statistics, we can get a better idea of what the raster data tells us about a particular cell group, geographic object, or polygon. In this case, zonal statistics will give us an average score for a particular applicant. Perform the following steps:

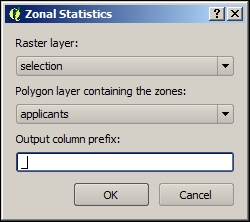
Install and activate the Zonal Statistics plugin.
Navigate to Raster | Zonal Statistics | Zonal statistics, as shown in the following image:
Input a raster layer for the values used to calculate a statistic and a polygon layer that are used to define the boundaries of the cells used. Here, we will use the applicants and land use to count the number of cells in each applicant cell group.
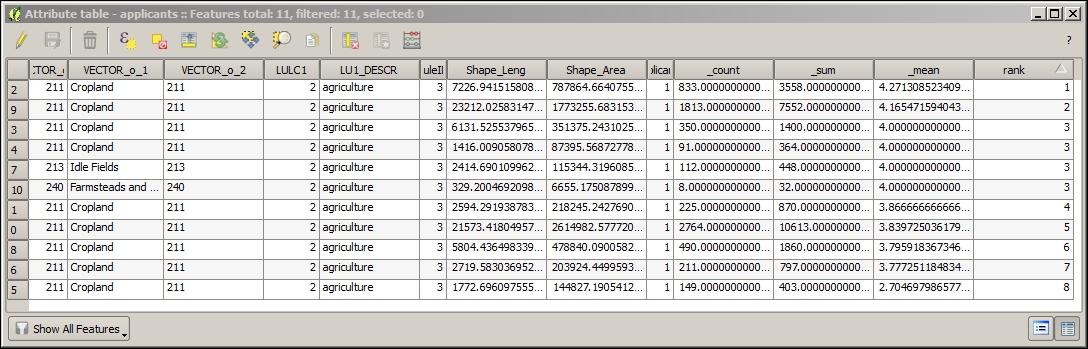
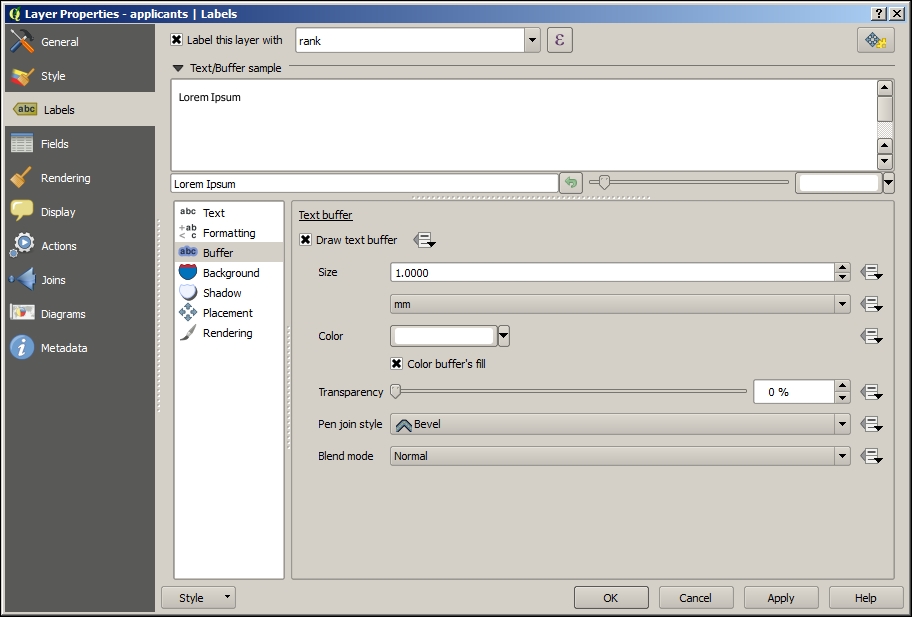
Create a rank field, editing each value manually according to the _mean field created by the zonal statistics step. This is a measure of the mean suitability per cell. We will use this field for a label to communicate the relative suitability to a general audience; so, we want a rank instead of the rough mean value.
Now, label the layer.
1. Under Layer Properties, activate the Labels tab.
2. Choose the rank field as the field to label.
3. Add any other formatting, such as label placement and buffer (halo) using the inner tabs within the label tab dialog, as shown in the following screenshot:
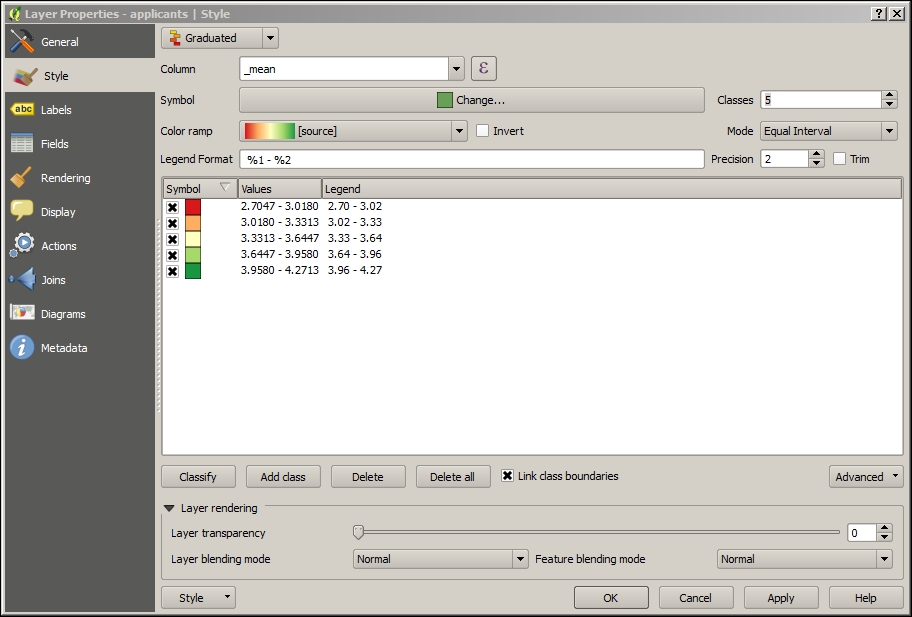
Add a style to the layer.
1. Select the Graduated style.
2. Select a suitable color ramp, number of classes, and classification type.
3. Click on the Classify button, as shown in the following screenshot: