In this section, we are going to create two signals and calculate their error sum:

1. As always, the include statements come first. Then, we declare that we use the std namespace:

      #include <iostream>
      #include <cmath>
      #include <algorithm>
      #include <numeric>

      #include <vector>
      #include <iterator>      

      using namespace std;

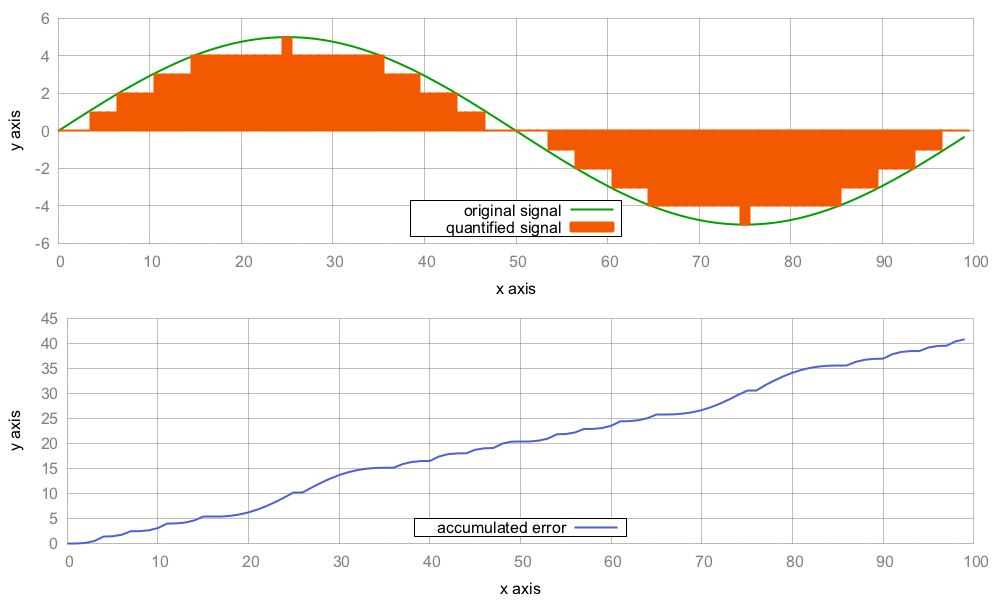
2. We are going to calculate the error sum of two signals. The two signals will be a sine wave and a copy of it, but with a different value type--the original sine wave is saved in a vector of double variables and its copy is saved in a vector of int variables. Because copying a value from a double variable to an int variable cuts its decimal part after the point, we have some loss. Let's name the vector of double values as, which stands for analog signal and the vector of int values ds, which stands for digital signal. The error sum will then later tell us how large the loss actually is:

      int main()
      {
          const size_t sig_len {100};
          vector<double> as (sig_len); // a for analog
          vector<int>    ds (sig_len); // d for digital

3. In order to generate a sine wave signal, we implement a little lambda expression with a mutable counter value n. We can call it as often as we want, and for every call, it will return us the value for the next point in time of a sine wave. The std::generate call fills the signal vector with the generated signal, and the std::copy call copies all the values from the vector of double variables to the vector of int variables afterward:

          auto sin_gen ([n{0}] () mutable { 
              return 5.0 * sin(n++ * 2.0 * M_PI / 100); 
          });
      
          generate(begin(as), end(as), sin_gen);
          copy(begin(as), end(as), begin(ds));

4. Let's first print the signals, as this way, they can be plotted later:

          copy(begin(as), end(as), 
               ostream_iterator<double>{cout, " "});
          cout << 'n';
          copy(begin(ds), end(ds), 
               ostream_iterator<double>{cout, " "});
          cout << 'n';

5. Now to the actual error sum, we use std::inner_product because it can easily be adapted to calculate the difference between every two corresponding elements of our signal vectors. It will iterate through both the ranges, pick items at the same corresponding positions in the ranges, calculate the difference between them, square it, and accumulate the results:

          cout << inner_product(begin(as), end(as), begin(ds), 
                                0.0, std::plus<double>{},
                                [](double a, double b) { 
                                    return pow(a - b, 2); 
                                }) 
               << 'n';
      }

6. Compiling and running the program gives us two long lines of signal output and a third line, which contains a single output value, which is the error between both the signals. The error is 40.889. If we calculate the error in a continuous manner, first for the first pair of items, then for the first two pairs of items, then for the first three pairs of items, and so on, then we get the accumulated error curve, which is visible on the plotted graph as shown: