That was another really complicated-looking lambda expression construct. But as soon as we understand this thoroughly, we will not be confused by any lambda expression anytime soon!

So, let's have a detailed look at it. We should get a mental picture of what needs to happen:

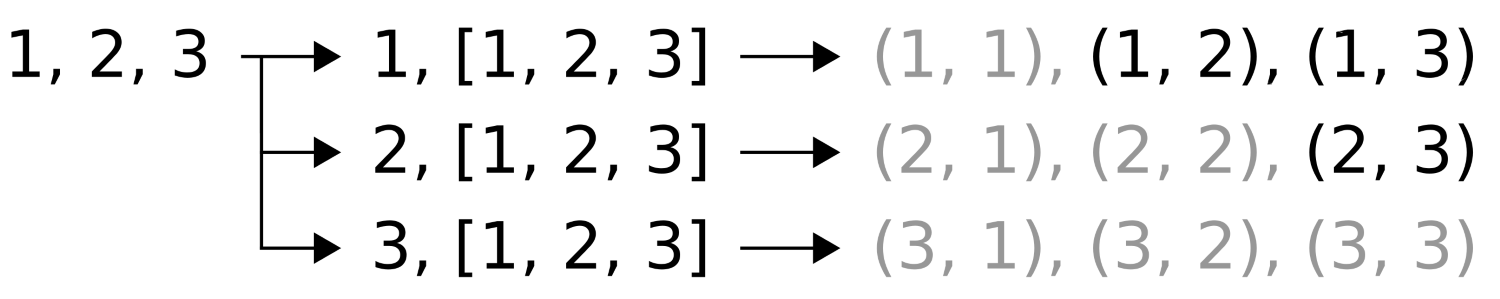
These are three steps:

1. We take our set 1, 2, 3 and compose three new sets from it. The first part of each of these sets is consecutively a single item from the set, and the second part is the whole set itself.
2. We combine the first item with every item from the set and get as many pairs out of it.
3. From these resulting pairs, we only pick the ones that are not redundant (as for example (1, 2) and (2, 1) are redundant) and not same-numbered (as for example (1, 1)).

Now, back to the implementation:

 constexpr auto cartesian ([=](auto ...xs) constexpr {
     return [=](auto f) constexpr {
         (void)std::initializer_list<int>{
             ((void)call_cart(f, xs, xs...), 0)...
         };
     };
 });

The inner expression, call_cart(xs, xs...), exactly represents the separation of (1, 2, 3) into those new sets, such as 1, [1, 2, 3]. The full expression, ((void)call_cart(f, xs, xs...), 0)... with the other ... outside, does this separation for every value of the set, so we also get 2, [1, 2, 3] and 3, [1, 2, 3].

Step 2 and step 3 are done by call_cart:

auto call_cart ([](auto f, auto x, auto ...rest) constexpr {
    (void)std::initializer_list<int>{
        (((x < rest)
            ? (void)f(x, rest)
            : (void)0)
        ,0)...
    };
});

Parameter x always contains the single value picked from the set, and rest contains the whole set again. Let's ignore the (x < rest) conditional at first. Here, the expression f(x, rest), together with the ... parameter pack expansion generates the function calls f(1, 1), f(1, 2), and so on, which results in the pairs being printed. This was step 2.

Step 3 is achieved by filtering out only the pairs where (x < rest) applies.

We made all lambda expressions and the variables holding them constexpr. By doing so, we can now guarantee that the compiler will evaluate their code at compile time and compile a binary that already contains all the number pairs instead of calculating them at runtime. Note that this only happens if all the function arguments we provide to a constexpr function are known at compile time already.