The whole calculation took part during an std::transform call over a one-dimensional array:

vector<int> v (w * h);
iota(begin(v), end(v), 0);
transform(begin(v), end(v), begin(v), to_iteration_count);

So, what exactly happened, and why does it work this way? The to_iteration_count function is basically a call chain from i_to_xy, over scale to mandelbrot_iterations. The following diagram illustrates the transformation steps:

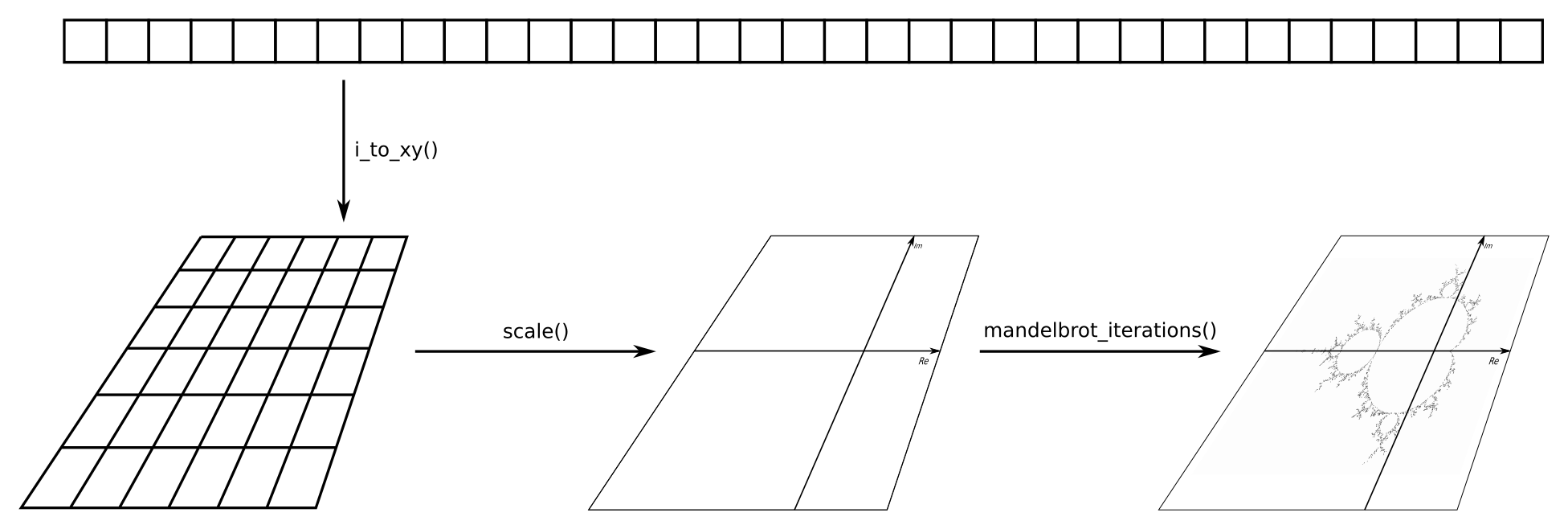
This way, we can use the index of a one-dimensional array as input, and get the number of Mandelbrot formula iterations at the point of the two-dimensional plane, which this array point represents. The good thing is that these three transformations are completely agnostic about each other. Code with such a separation of concerns can be tested very nicely because each component can be tested individually without the others. This way, it is easy to find and fix bugs, or just reason about its correctness.