In this section, we will normalize the values of a vector from an example numeric range to a normalized one in two different ways, one of them using std::minmax_element and one using std::clamp:
- As always, we first need to include the following headers and declare that we use the std namespace:
#include <iostream>
#include <vector>
#include <algorithm>
#include <iterator>
using namespace std;
- We implement a function for later use, which accepts the minimum and maximum values of a range, and a new maximum so that it can project values from the old range to a smaller range that we want to have. The function object takes such values and returns another function object, which does exactly that transformation. For the sake of simplicity, the new minimum is 0, so no matter what offset the old data had, its normalized values will always be relative to 0. For the sake of readability, we ignore the possibility that max and min could be of the same value, which would lead to a division by zero:
static auto norm (int min, int max, int new_max)
{
const double diff (max - min);
return [=] (int val) {
return int((val - min) / diff * new_max);
};
}
- Another function object builder called clampval returns a function object that captures the min and max values and calls std::clamp on values with those values, in order to limit their values to this range:
static auto clampval (int min, int max)
{
return [=] (int val) -> int {
return clamp(val, min, max);
};
}
- The data we are going to normalize is a vector of varying values. This could be, for example, some kind of heat data, landscape height, or stock prices over time:
int main()
{
vector<int> v {0, 1000, 5, 250, 300, 800, 900, 321};
- In order to be able to normalize the data, we need the highest and lowest values. The std::minmax_element function is of a great help here. It returns us a pair of iterators to exactly those two values:
const auto [min_it, max_it] (
minmax_element(begin(v), end(v)));
- We will copy all the values from the first vector to a second one. Let's instantiate the second vector and prepare it to accept as many new items as we have in the first vector:
vector<int> v_norm;
v_norm.reserve(v.size());
- Using std::transform, we copy the values from the first vector to the second. While copying the items, they will be transformed with our normalization helper. The minimum and maximum values of the old vector are 0 and 1000. The minimum and maximum values after normalization are 0 and 255:
transform(begin(v), end(v), back_inserter(v_norm),
norm(*min_it, *max_it, 255));
- Before we implement the other normalization strategy, we print what we have by now:
copy(begin(v_norm), end(v_norm),
ostream_iterator<int>{cout, ", "});
cout << 'n';
- We reuse the same normalized vector with the other helper clampval, which clamps the old range to the range with the minimum of 0 and the maximum of 255:
transform(begin(v), end(v), begin(v_norm),
clampval(0, 255));
- After printing these values too, we're done:
copy(begin(v_norm), end(v_norm),
ostream_iterator<int>{cout, ", "});
cout << 'n';
}
- Let's compile and run the program. Having the values reduced to values from 0 to 255, we could use them as brightness values for RGB color codes, for example:
$ ./reducing_range_in_vector
0, 255, 1, 63, 76, 204, 229, 81,
0, 255, 5, 250, 255, 255, 255, 255,
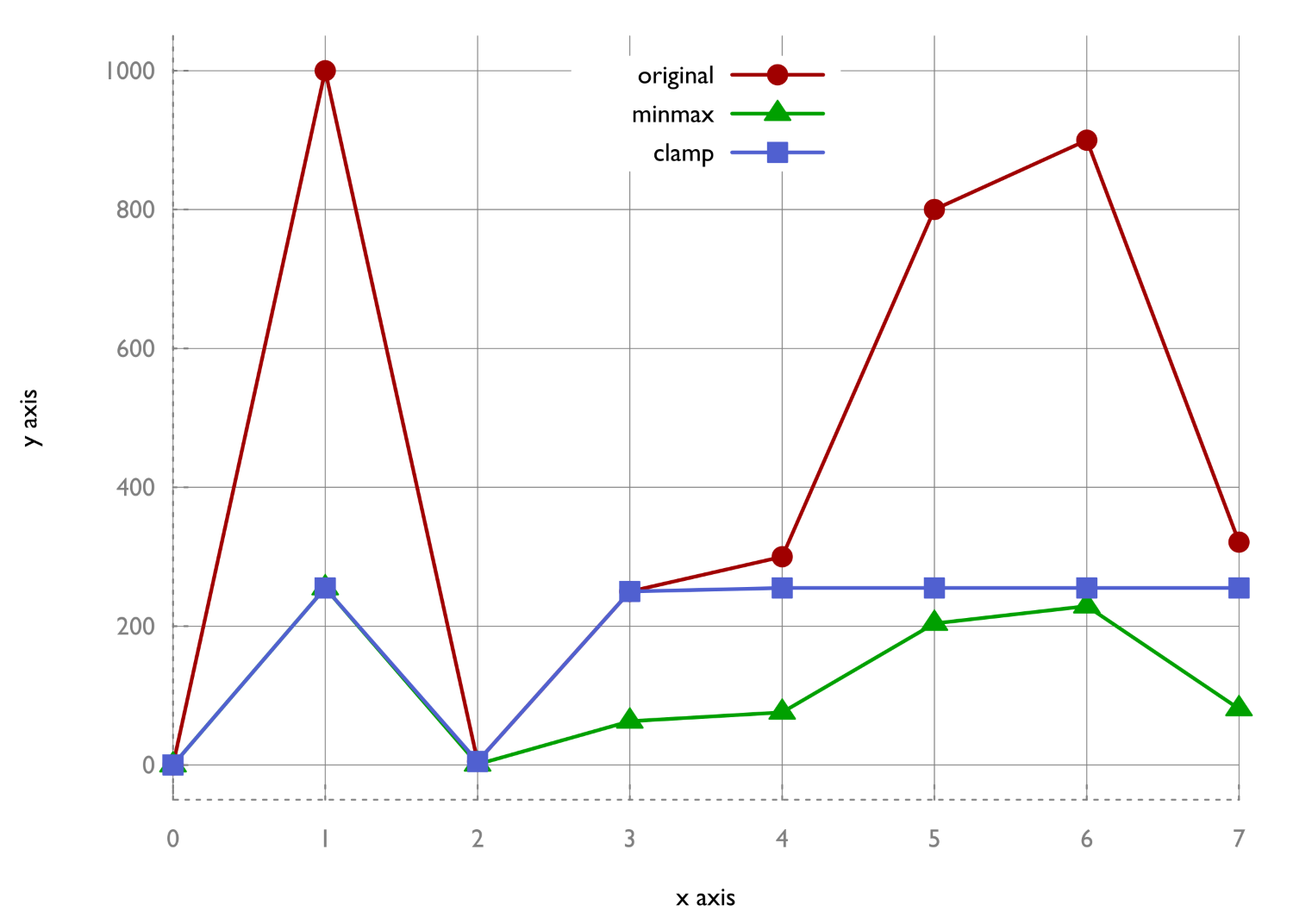
- When we plot the data, we get the following graphs. As we can see, the approach where we divide the values by the difference between the min and max values is a linear transformation of the original data. The clamped graph loses some information. Both variations can be useful in different situations: