When there are very large amounts of numeric data that need to be processed in some situations, it may not be possible to process it all in feasible time. In such situations, the data could be sampled in order to reduce the total amount of data for further processing, which then speeds up the whole program. In other situations, this might be done not to reduce the amount of work for processing but for saving or transferring the data.
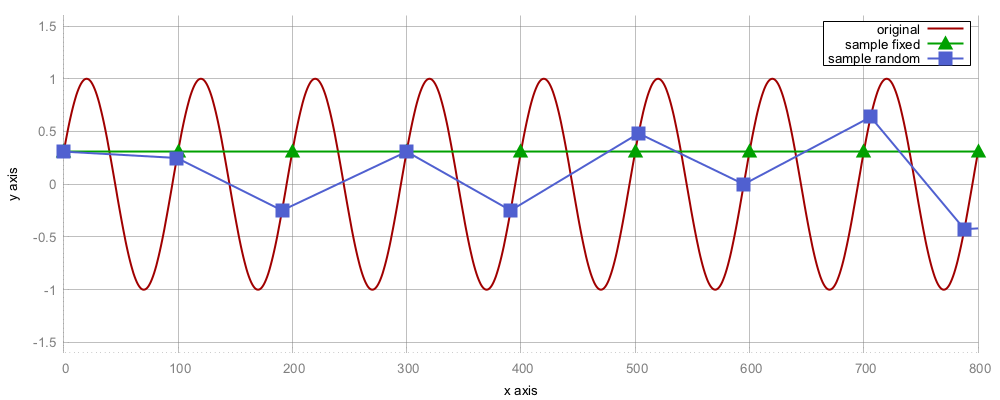
A naive idea of sampling could be to only pick every Nth data point. This might be fine in a lot of cases, but in signal processing, for example, it could lead to a mathematical phenomenon called aliasing. If the distance between every sample is varied by a small random offset, aliasing can be reduced. Have a look at the following diagram, which shows an extreme case just to illustrate the point--while the original signal consists of a sine wave, the triangle points on the graph are sampling points that are sampled at exactly every 100th data point. Unfortunately, the signal has the same y-value at these points! The graph which results from connecting the dots looks like a perfectly straight horizontal line. The square points, however, show what we get when we sample every 100 + random(-15, +15) points. Here, the signal still looks very different from the original signal, but it is at least not completely gone as in the fixed step size sampling case.
The std::sample function does not add random alterations to sample points with fixed offset but chooses completely random points; therefore, it works a bit differently from this example: