The Fourier transformation is a very important and famous formula in signal processing. It was invented nearly 200 years ago, but with computers, the number of use cases for it really skyrocketed. It is used in audio/image/video compression, audio filters, medical imaging devices, cell phone apps that identify music tracks while listening to them on the fly, and so on.

Because of the vastness of general numeric application scenarios (not only because of the Fourier transformation of course), the STL also tries to be useful in the context of numeric computation. The Fourier transformation is only one example among them but a tricky one too. The formula itself looks like the following:

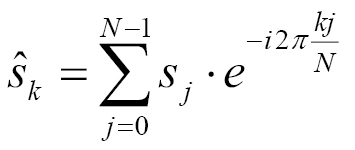
The transformation it describes is basically a sum. Each element of the sum is the multiplication of a data point of the input signal vector, and the expression exp(-2 * i * ...). The maths behind this is a bit scary for everyone who does not know about complex numbers (or who just does not like maths), but it is also not really necessary to completely understand the maths in order to implement it. When having a close look at the formula, it says that the sum symbol loops over every data point of the signal (which is N elements long) using the loop variable j. The variable k is another loop variable because the Fourier transformation is not for calculating a single value, but a vector of values. In this vector, every data point represents the intensity and phase of a certain repetitive wave frequency, which is or is not a part of the original signal. When implementing this with manual loops, we will end up with code similar to the following:

csignal fourier_transform(const csignal &s) { 
    csignal t(s.size()); 
    const double pol {-2.0 * M_PI / s.size()};

    for (size_t k {0}; k < s.size(); ++k) { 
        for (size_t j {0}; j < s.size(); ++j) { 
            t[k] += s[j] * polar(1.0, pol * k * j); 
        }
    } 
    return t; 
}

The csignal type may be an std::vector vector of complex numbers. For complex numbers, there is an std::complex STL class, which helps represent those. The std::polar function basically does the exp(-i * 2 * ...) part.

This works well already, but we are going to implement it using STL tools.