We will sample a very large vector of random data. This random data shows a normal distribution. After sampling it, the resulting points should still show a normal distribution, which we will check:

1. First, we need to include everything we use and declare that we use the std namespace in order to spare us some typing:

       #include <iostream>
       #include <vector>
       #include <random>
       #include <algorithm>
       #include <iterator>
       #include <map>
       #include <iomanip>       

       using namespace std;

2. It is easier to play around with the code if we configure specific characteristics of our algorithm in their own constant variables. These are the size of the large random vector and the number of samples that we are going to take from it:

       int main()
       {
           const size_t data_points   {100000};
           const size_t sample_points {100};

3. The large, randomly filled vector should get numbers from a random number generator, which gives out numbers from a normal distribution. Any normal distribution can be characterized by the mean value and the standard deviation from the mean value:

           const int    mean {10};
           const size_t dev  {3};

4. Now, we set up the random generator. First, we instantiate a random device and call it once to get a seed for the constructor of a random generator. Then, we instantiate a distribution object that applies normal distribution to the random output:

           random_device rd;
           mt19937 gen {rd()};
           normal_distribution<> d {mean, dev};

5. Now, we instantiate a vector of integers and fill it with a lot of random numbers. This is achieved using the std::generate_n algorithm, which will call a generator function object to feed its return value into our vector using a back_inserter iterator. The generator function object just wraps around the d(gen) expression, which gets a random number from the random device and feeds it into the distribution object:

           vector<int> v;
           v.reserve(data_points);
       
           generate_n(back_inserter(v), data_points, 
               [&] { return d(gen); });

6. Now, we instantiate another vector that will contain the much smaller set of samples:

           vector<int> samples;
           v.reserve(sample_points);

7. The std::sample algorithm works similar to std::copy, but it takes two additional parameters: the number of samples, which it shall take from the input range, and a random number generator object, which it will consult to get random sampling positions:

           sample(begin(v), end(v), back_inserter(samples), 
                  sample_points, mt19937{random_device{}()});

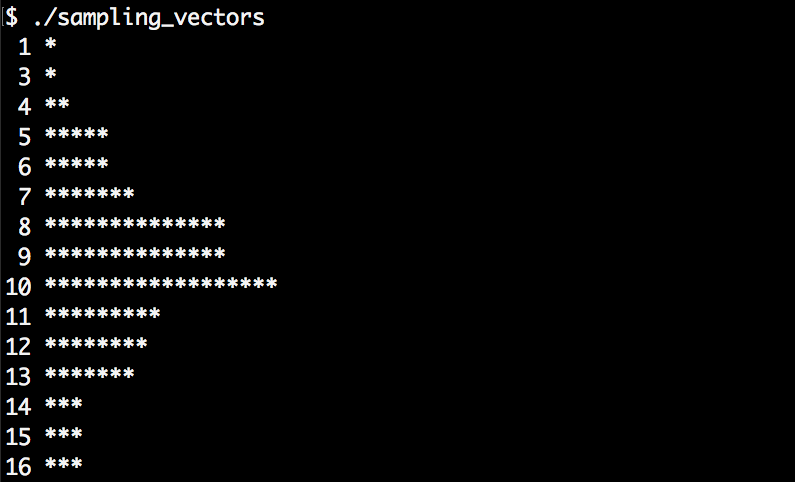
8. We're already done with the sampling. The rest of the code is for displaying purposes. The input data has a normal distribution, and if the sampling algorithm works well, then the sampled vector should show a normal distribution too. To see how much of a normal distribution is left, we will print a histogram of the values:

           map<int, size_t> hist;

           for (int i : samples) { ++hist[i]; }

9. Finally, we loop over all the items in order to print our histogram:

           for (const auto &[value, count] : hist) {
               cout << setw(2) << value << " "
                    << string(count, '*') << 'n';
           }    
       }

10. After compiling and running the program, we see that the sampled vector still roughly shows the characteristics of a normal distribution: