Mastering PostGIS

The last pgRouting algorithm that we are about to have a look at is the traveling sales person algorithm. Its purpose is to answer the following question: Given a list of cities and the distances between each pair of cities, what is the shortest possible route that visits each city exactly once and returns to the origin city?

pgRouting offers two variants of a TSP function:

pgr_eucledianTSP: Takes a set of points and calculates a point order from the internally calculated cost matrix based on the Euclidean distances calculated from point coordinates expressed as Lon/Lat
pgr_TSP: Takes an already calculated distance matrix

Let's calculate the points order for a couple of locations from our Vienna dataset:

select * from pgr_eucledianTSP( 
   'select id, lon::float8 as x, lat::float8 as y from pgr.ways_vertices_pgr where id in (4540,57407,116126,58791,44800,85852,52421,148735)' 
);

The output is as follows:

  seq|  node|               cost|          agg_cost
-----+------+-------------------+------------------
    1|  4540| 0.0272292439764646|                 0
    2|148735| 0.0149659383701813|0.0272292439764646
    3| 57407|0.00798812567815924|0.0421951823466459
    4|116126| 0.0406742028363178|0.0501833080248051
    5| 85852| 0.0422062138944045| 0.090857510861123
    6| 58791| 0.0105530643293782| 0.133063724755527
    7| 44800| 0.0181016168186681| 0.143616789084906
    8| 52421| 0.0106700309212339| 0.161718405903574
    9|  4540|                  0| 0.172388436824808

The preceding output on a map looks as follows:

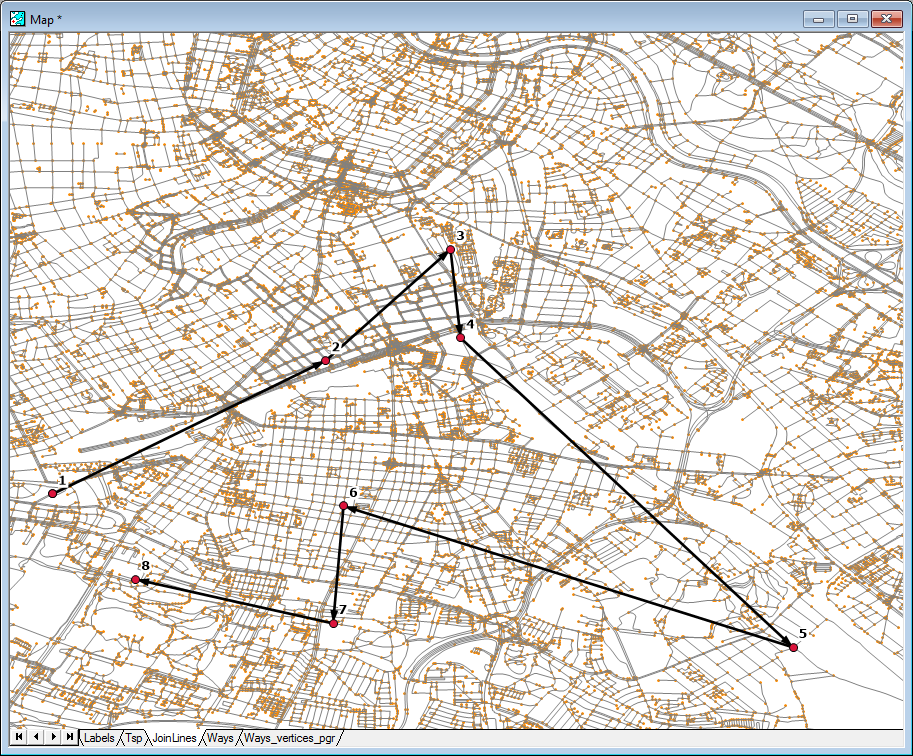
pgRouting 2.2 documentation mentions that using Dijkstra to pre-calculate aggregate costs of the shortest paths between a set of points prior to feeding the data to TSP is not worthy, as solving TSP on a Euclidean plane first and then finding shortest paths in an ordered set of points should give results that are fairly optimal already.

pgRouting 2.3, on the other hand, brings a pgr_dijkstraCostMatrix function, so one should expect that providing data with the distance matrix calculated with real distances is sensible enough to use it. Let's do just that:

select * from pgr_TSP( 
    $$ 
    SELECT * FROM pgr_dijkstraCostMatrix( 
        'SELECT gid as id, source, target, cost, reverse_cost FROM pgr.ways', 
        (select array_agg(id) from pgr.ways_vertices_pgr where id in (4540,57407,116126,58791,44800,85852,52421,148735)), directed := false) 
    $$, 
    start_id := 4540, --if not specified, first in arr would be used 
    randomize := false 
);

Calculating distance matrix with directed networks will likely result in the output matrix being non-symmetric - the cost of traveling from A to B is not the same as the cost of traveling from B to A (cost/reverse cost). This will make the TSP function fail with the following message:
ERROR: A Non symmetric Matrix was given as input

The output is actually the same, although in reversed order:

  seq|  node|               cost|          agg_cost
-----+------+-------------------+------------------
    1|  4540| 0.0156343305442904|                 0
    2| 52421| 0.0255674722245925|0.0156343305442904
    3| 44800| 0.0133600823412494|0.0412018027688828
    4| 58791| 0.0458230476499673|0.0545618851101322
    5| 85852| 0.0475591325608726|   0.1003849327601
    6|116126| 0.0186155727831978| 0.147944065320972
    7| 57407| 0.0272063328584911|  0.16655963810417
    8|148735| 0.0297395689283764| 0.193765970962661
    9|  4540|                  0| 0.223505539891037

Starting with pgRouting 2.3, there are quite a few extra optional parameters that can tweak the way TSP is solved. It is worth doing some further reading on the algorithm implementation though, to fully understand the impact they have on the calculation process.

Table of Contents for
Mastering PostGIS

Traveling sales person

Table of Contents for Mastering PostGIS

Table of Contents for
Mastering PostGIS