In this section, we will turn to some purely mathematical reasoning to judge password strength. We will use tools from scikit-learn to learn and understand password strength by comparing them to past passwords using vector similarities.
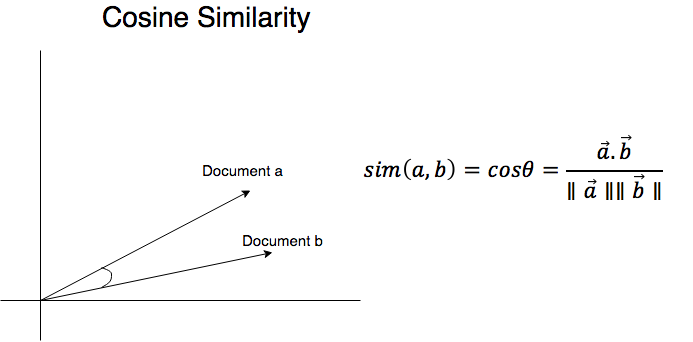
Cosine similarity is a quantitative measure [-1,1] of how similar two vectors are in a Vector Space. The closer they are to each other, the smaller the angle between them. The smaller the angle between them, the larger the cosine of that angle is; for example:
- If two vectors are opposites of each other, their angle is 180, and cos(0) = -1.
- If two vectors are the same, their angle is 0, and cos(0) = 1.
- If two vectors are perpendicular, their angle is 90, and cos(90) = 0. In the text world, we'd say that these documents are unrelated.
The following diagram shows the Cosine Similarity:
The goal now is to build a tool that takes in a password from a user and will spit back an assessment of how powerful that password is. This can be done many ways through various approaches. We will propose one now:
- Vectorize past passwords given to us in our dataset (through some scikit-learn vectorizer).
- Use the cosine similarity to judge the similarity between a given password and past passwords. The closer the given password is to past passwords, the worse we rank the password attempt.
Let's import an implementation of cosine similarity from scikit-learn:
from sklearn.metrics.pairwise import cosine_similarity
# number between -1 and 1 (-1 is dissimilar, 1 is very similar (the same))
We have already built a vectorizer, so let's bring it back. We can then use the cosine_similarity module to see the similarities between different passwords/strings:
five_cv
CountVectorizer(analyzer='char', binary=False, decode_error=u'strict', dtype=<type 'numpy.int64'>, encoding=u'utf-8', input=u'content', lowercase=True, max_df=1.0, max_features=None, min_df=1, ngram_range=(1, 5), preprocessor=None, stop_words=None, strip_accents=None, token_pattern=u'(?u)\\b\\w\\w+\\b', tokenizer=None, vocabulary=None)
# similar phrases
print cosine_similarity(five_cv.transform(["helo there"]), five_cv.transform(["hello there"]))[[0.88873334]]
# not similar phrases
print cosine_similarity(five_cv.transform(["sddgnkjfnsdlkfjnwe4r"]), five_cv.transform(["hello there"]))
[[0.08520286]]
Let's say we want to judge how good the qwerty123 password is. We will first store it as a variable called attempted_password. We will then use our similarity metric on the entire password corpus:
# store a password that we may want to use in a variable
attempted_password="qwerty123"
cosine_similarity(five_cv.transform([attempted_password]), five_char).shape # == (1, 1048485)
# this array holds the cosine similarity of attempted_password and every other password in our corpus. We can use the max method to find the password that is the closest in similarity
# use cosine similarity to find the closest password in our dataset to our attempted password
# qwerty123 is a literal exact password :(
cosine_similarity(five_cv.transform([attempted_password]), five_char).max()
1.0000
It looks like qwerty123 is a password that occurs as in the corpus. So it's probably not a great password to use. We can repeat the process on a slightly longer password, as shown in the following code:
# lets make it harder
attempted_password="qwertyqwerty123456234"
# still pretty similar to other passwords..
cosine_similarity(five_cv.transform([attempted_password]), five_char).max()
0.88648200215
How about using a password that is mostly a random assortment of characters, as shown here:
# fine lets make it even harder
attempted_password="asfkKwrvn#%^&@Gfgg"
# much better!
cosine_similarity(five_cv.transform([attempted_password]), five_char).max()
0.553302871668
Instead of finding the single closest password in our corpus, let's take the top 20 closest passwords and take the average similarity of them. This will give us a more holistic similarity metric.
The following code shows the top 20 most-used similar password mean score:
# use the top 20 most similar password mean score
attempted_password="qwerty123"
raw_vectorization = cosine_similarity(five_cv.transform([attempted_password]), five_char)
raw_vectorization[:,np.argsort(raw_vectorization)[0,-20:]].mean()
0.8968577221
The following code shows the top 20 most-used similar password mean score:
# use the top 20 most similar password mean score with another password
attempted_password="asfkKwrvn#%^&@Gfgg"
raw_vectorization = cosine_similarity(five_cv.transform([attempted_password]), five_char)
raw_vectorization[:,np.argsort(raw_vectorization)[0,-20:]].mean()
0.4220207825
It is easy to see that smaller values imply better passwords, which are not similar to passwords in our training set, and are therefore more unique and harder to guess.
