Chapter 15. Intermezzo: When More Is Different
WHEN DEALING WITH SOME OF THE MORE COMPUTATIONALLY INTENSIVE DATA ANALYSIS OR MINING algorithms, you may encounter an unexpected obstacle: the brick wall. Programs or algorithms that seemed to work just fine turn out not to work once in production. And I don’t mean that they work slower than expected. I mean they do not work at all!
Of course, performance and scalability problems are familiar to most enterprise developers. However, the kinds of problems that arise in data-centric or computationally intensive applications are different, and most enterprise programmers (and, in fact, most computer science graduates) are badly prepared for them.
Let’s try an example: Table 15-1 shows the time required to perform 10 matrix multiplications for square matrices of various size. (The details of matrix multiplication don’t concern us here; suffice it to say that it’s the basic operation in almost all problems involving matrices and is at the heart of operator decomposition problems, including the principal component analysis introduced in Chapter 14.)
Size n | Time [seconds] |
100 | 0.00 |
200 | 0.06 |
500 | 2.12 |
1,000 | 22.44 |
2,000 | 176.22 |
Would you agree that the data in Table 15-1 does not look too threatening? For a 2,000 × 2,000 matrix, the time required is a shade under three minutes. How long might it take to perform the same operation for a 10,000 × 10,000 matrix? Five, maybe ten minutes? Yeah, right. It takes five hours! And if you need to go a little bit bigger still—say, 30,000 × 30,000, the computation will take five days.
What we observe here is typical of many computationally intensive algorithms: they consume disproportionately more time as the problem size becomes larger. Of course, we have all heard about this in school, but our intuition for the reality of this phenomenon is usually not very good. Even if we run a few tests on small data sets, we fail to spot the trouble: sure, the program takes longer as the data sets get larger, but it all seems quite reasonable. Nevertheless, we tend to be unprepared for what appears to be a huge jump in the required time as we increase the data set by a seemingly not very large factor. (Remember: what took us from three minutes to five hours was an increase in the problem size by a factor of 5—not even an order of magnitude!)
The problem is that, unless you have explicitly worked on either a numerical or a combinatorial problem in the past, you probably have never encountered the kind of scaling behavior exhibited by computational or combinatorial problems. This skews our perception.
Where are you most likely to encounter perceptible performance
problems in an enterprise environment? Answer: slow database queries! We
all have encountered the frustration resulting from queries that perform
a full table scan instead of using an indexed lookup (regardless whether
no index is available or the query optimizer fails to use it). Yet a
query that performs a full table scan rather than using an index
exhibits one of the most benign forms of scaling: from
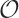 (log n) (meaning that the
response time is largely insensitive to the size of the table) to
(log n) (meaning that the
response time is largely insensitive to the size of the table) to
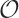 (n) (meaning that doubling
the table size will double the response time).
(n) (meaning that doubling
the table size will double the response time).
In contrast, matrix operations—such as the matrix multiplication
encountered in the earlier example—scale as 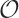 (n3);
this means that if the problem doubles in size, then the time required
grows by a factor of 8 (because
23 = 8). In other words, as you go from a
2,000 × 2,000 matrix to a 4,000 × 4,000 matrix, the problem will take
almost 10 times as long; and if you go to a 10,000 × 10,000 matrix, it
will take 53 = 125 times as long.
Oops.
(n3);
this means that if the problem doubles in size, then the time required
grows by a factor of 8 (because
23 = 8). In other words, as you go from a
2,000 × 2,000 matrix to a 4,000 × 4,000 matrix, the problem will take
almost 10 times as long; and if you go to a 10,000 × 10,000 matrix, it
will take 53 = 125 times as long.
Oops.
And this is the good news. Many combinatorial problems (such as
the Traveling Salesman problem and similar problems) don’t scale
according to a power law (such as 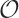 (n3))
but instead scale exponentially (
(n3))
but instead scale exponentially (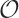 (en)).
In these cases, you will hit the brick wall much
faster and much more brutally. For such problems, an incremental
increase in the size of the problem (i.e., from
n to n + 1) will typically at
least double the runtime. In other words, the last
element to calculate takes as much time as all the previous elements
taken together. System sizes of around
n = 50 are frequently the end of the line. With
extreme effort you might be able to push it to n =
55, but n = 100 will be entirely out of
reach.
(en)).
In these cases, you will hit the brick wall much
faster and much more brutally. For such problems, an incremental
increase in the size of the problem (i.e., from
n to n + 1) will typically at
least double the runtime. In other words, the last
element to calculate takes as much time as all the previous elements
taken together. System sizes of around
n = 50 are frequently the end of the line. With
extreme effort you might be able to push it to n =
55, but n = 100 will be entirely out of
reach.
The reason I stress this kind of problem so much is that in my experience, not only are most enterprise developers unprepared for the reality of it but also that the standard set of software engineering practices and attitudes is entirely inadequate to deal with them. I once heard a programmer say, “It’s all just engineering” in response to challenges about the likely performance problems of a computational system he was working on. Nothing could be further from the truth: no amount of low-level performance tuning will save a program of this nature that is algorithmically hosed—and no amount of faster hardware, either. Moreover, “standard software engineering practices” are either of no help or are even entirely inapplicable (we’ll see an example in a moment).
Most disturbing to me was his casual, almost blissful ignorance—this coming from a guy who definitely should have known better.
A Horror Story
I was once called into a project in its thirteenth hour—they had far exceeded both their budget and their schedule and were about to be shut down for good because they could not make their system work. They had been trying to build an internal tool that was intended to solve what was, essentially, a combinatorial problem. The tool was supposed to be used interactively: the user supplies some inputs and receives an answer within, at most, a few minutes. By the time I got involved, the team had labored for over a year, but the minimum response time achieved by their system exceeded 12 hours—even though it ran on a very expensive (and very expensive to operate) supercomputer.
After a couple of weeks, I came up with an improved algorithm that calculated answers in real time and could run on a laptop.
No amount of “engineering” will be able to deliver that kind of speed-up.
How was this possible? By attacking the problem on many different levels. First of all, we made sure we fully understood the problem domain. The original project team had always been a little vague about what exactly the program was trying to calculate, as a result their “domain model” was not truly logically consistent. Hence the first thing to do was to put the whole problem on sound mathematical footing. Second, we redefined the problem: the original program had attempted to calculate a certain quantity by explicit enumeration of all possible combinations, whereas the new solution calculated an approximation instead. This was warranted because the input data was not known very precisely, anyway, and because we were able to show that the uncertainty introduced by the approximation was less than the uncertainty already present in the data. Third, we treated hot spots differently than the happy case: the new algorithm could calculate the result to higher accuracy, but it did so only when the added accuracy was needed. Fourth, we used efficient data structures and implemented some core pieces ourselves instead of relying on general-purpose libraries; we also judiciously precalculated and cached some frequently used intermediate results.
After putting the whole effort on a conceptually consistent footing, the most important contribution was changing the problem definition: dropping the exact approach, which was unnecessary and infeasible, and adopting an approximate solution that was cheap and all that was required.
Some Suggestions
Computational and combinatorial programming is really different. It runs into different limits and requires different techniques. Most important is the appropriate choice of algorithm at the outset, since no amount of low-level tuning or “engineering” will save a program that is algorithmically flawed.
Here is a list of recommendations in case you find yourself setting out on a project that involves heavy computation or deals with combinatorial complexity issues:
Do your homework. Understand computational complexity, know the complexity of the algorithm you intend to use, and research the different algorithms (and their trade-offs) available for your kind of problem. Read broadly—although the exact problem as specified may turn out to be intractable, you may find that a small change in the requirements may lead to a much simpler problem. It is definitely worth it to renegotiate the problem with the customer or end users than setting out on a project that is infeasible from the outset. (Skiena’s Algorithm Design Manual is a particularly good resource for algorithms grouped by problems.)
Run a few numbers. Do a few tests with small programs and evaluate their scaling performance. Don’t just look at the actual numbers themselves—also consider the scaling behavior as you vary the problem size. If the program does not exhibit the scaling behavior you expect theoretically, it has a bug. If so, fix the bug before proceeding! (In general, algorithms follow the theoretical scaling prediction quite closely for all but the smallest of problem sizes.) Extrapolate to real-sized problems: can you live with the expected runtime predictions?
Forget standard software engineering practices. It is a standard assumption in current software engineering that developer time is the scarcest resource and that programs should be designed and implemented accordingly. Computationally intensive programs are one case where this is not true: if you are likely to max out the machine, then it’s worth having the developer—rather than the computer—go the extra mile. Additional developer time may very well make the difference between an “infeasible” problem and a solved one.
For instance, in situations where you are pressed for space, it
might very well make sense to write your own container implementations
instead of relying on the system-provided hash map. Beware of the trap
of conditioned thinking, though: in one project I worked on, we knew
that we would have a memory size problem and that we therefore had to
keep the size of individual elements small. On the other
hand, it was not clear at first whether the 4-byte Java int data type would be sufficient to
represent all required values or whether we would have to use the
8-bye Java long type. In response,
someone suggested that we wrap the atomic data
type in an object so we could swap out the implementation, in case the
4-byte int turned out to be
insufficient. That’s a fine approach in a standard software
engineering scenario (“encapsulation” and all that), but in this
situation—where space was at a premium—it missed the point entirely:
the space that the Java wrapper would have consumed (in addition to
its data members) would have been larger than the payload!
Remember: standard software engineering practices are typically intended to trade machine resources for developer resources. However, for computationally intensive problems, machine resources (not developer time) are the limiting factor.
Don’t assume that parallelization will be possible. Don’t assume that you’ll be able to partition the problem in such a way that simultaneous execution on multiple machines (i.e., parallelization) will be possible, until you have developed an actual, concrete, implementable algorithm—many computational problems don’t parallelize well. Even if you can come up with a parallel algorithm, performance may be disappointing: hidden costs (such as communication overhead) often lead to performance that is much poorer than predicted; a cluster consisting of twice as many nodes often exhibits a behavior much less than double the original one! Running realistic tests (on realistically sized data sets and on realistically sized clusters) is harder for parallel programs than for single processor implementations—but even more important.
Leave yourself some margin. Assume that the problem size will be larger by a factor of 3 and that hardware will deliver only 50 percent of theoretically predicted performance.
If the results are not wholly reassuring, explore alternatives. Take the results for the expected runtime and memory requirements that you obtained from theoretical predictions and the tests that you have performed seriously. Unless you seem able to meet your required benchmarks comfortably, explore alternatives. Consider better algorithms, research whether the problem can be simplified or whether the problem can be approached in an entirely different manner, and look into approximate or heuristic solutions. If you feel yourself stuck, get help!
If you can’t make it work on paper, STOP. It won’t work in practice, either. It is a surprisingly common anti-pattern to see the warning signs early but to press on regardless with the hopeful optimism that “things will work themselves out during implementation.” This is entirely misguided: nothing will work out better as you proceed with an implementation; everything is always a bit worse than expected.
Unless you can make it work on paper and make it work comfortably, there is no point in proceeding!
The recurring recommendation here is that nobody is helped by a project that ultimately fails, because it was impossible (or at least infeasible) from the get-go. Unless you can demonstrate at least the feasibility of a solution (at an acceptable price point!), there is no use to proceed. And everybody is much better off knowing this ahead of time.
What About Map/Reduce?
Won’t the map/reduce family of techniques make most of these considerations obsolete? The answer, in general, is no.
It is important to understand that map/reduce is not actually a clever algorithm or even an algorithm at all. It is a piece of infrastructure that makes naive algorithms convenient.
That’s a whole different ball game. The map/reduce approach does not speed up any particular algorithm at all. Instead, it makes the parallel execution of many subproblems convenient. For map/reduce to be applicable, therefore, it must be possible to partition the problem in such a way that individual partitions don’t need to talk to each other. Search is such an application that is trivially parallelizable, and many (if not all) successful current applications of map/reduce that I am aware of seem to be related to generalized forms of search.
This is not to say that map/reduce is not a very important advance. (Any device that makes an existing technique orders of magnitudes more convenient is an important innovation!) At the moment, however, we are still in the process of figuring how which problems are most amenable to the map/reduce approach and how best to adapt them. I suspect that the algorithms that will work best on map/reduce will not be straightforward generalizations of serial algorithms but instead will be algorithms that would be entirely unattractive on a serial computer.
It is also worth remembering that parallel computation is not new. What has killed it in the past was the need for different partitions of the problem to communicate with each other: very quickly, the associated communication overhead annihilated the benefit from parallelization. This problem has not gone away, it is merely masked by the current emphasis on search and searchlike problems, which allow trivial parallelization without any need for communication among partitions. I worry that more strictly computational applications (such as the matrix multiplication problem discussed earlier or the simulation of large physical systems) will require so much sharing of information among nodes that the map/reduce approach will appear unattractive.
Finally, amid the excitement currently generated by map/reduce, it should not be forgotten that its total cost of ownership (including the long-term operational cost of maintaining the required clusters as well as the associated network and storage infrastructure) is not yet known. Although map/reduce installations make distributed computing “freely” available to the individual programmer, the required hardware installations and their operations are anything but “free.”
In the end, I expect map/reduce to have an effect similar to the one that compilers had when they came out. The code that they produced was less efficient than handcoded assembler code, but the overall efficiency gain far outweighed this local disadvantage.
But keep in mind that even the best compilers have rendered neither Quicksort nor indexed lookup obsolete.
Workshop: Generating Permutations
Sometimes, you have to see it to believe it. In this spirit,
let’s write a program that calculates all permutations
(i.e., all possible rearrangements) of a set.
(That is, if the set is [1,2,3],
then the program will generate [1,2,3], [1,3,2], [2,1,3], [2,3,1], [3,1,2], [3,2,1].) You can imagine this routine to be
part of a larger program: in order to solve the Traveling Salesman
problem exactly, for example, one needs to generate all possible trips
(i.e., all permutations of the cities to visit)
and evaluate the associated distances.
Of course, we all “know” that the number of permutations grows as n! = 1 · 2 · 3 ··· n, where n is the number of elements in the set and that the factorial function grows “quickly.” Nevertheless, you have to see it to believe it. (Even I was shocked by what I found when developing and running the program below!)
The program that follows reads a positive integer n from the command line and then generates
all permutations of a list of n
elements, using a recursive algorithm. (It successively removes one
element of the list, generates all permutations of the remainder, and
then tacks the removed element back on to the results.) The time
required is measured and printed.
import sys, time
def permutations( v ):
if len(v) == 1: return [ [v[0]] ]
res = []
for i in range( 0, len(v) ):
w = permutations( v[:i] + v[i+1:] )
for k in w:
k.append( v[i] )
res += w
return res
n = int(sys.argv[1])
v = range(n)
t0 = time.clock()
z = permutations( v )
t1 = time.clock();
print n, t1-t0(You may object to the use of recursion here, pointing out that Python does not allow infinite depth of recursion. This is true but is not a factor: we will run into trouble long before that constraint comes into play.)
I highly recommend that you try it. Because we know (or suspect)
that this program might take a while to run when the number of
elements is large, we probably want to start out with three elements.
Or with four. Then maybe we try five, six, or seven. In all cases, the
program finishes almost instantaneously. Then go
ahead and run it with n=10. Just 10
elements. Go ahead, do it. (But I suggest you save all files and clean
up your login session first, so you can reboot without losing too much
work if you have to.)
Go ahead. You have to see it to believe it![26]
Further Reading
The Algorithm Design Manual. Steven S. Skiena. 2nd ed., Springer. 2008.
This is an amazing book, because it presents algorithms not as abstract entities to be studied for their own beauty but as potential solutions to real problems. Its second half consists of a “hitchhiker’s guide to algorithms”: a catalog of different algorithms for common problems. It helps you find an appropriate algorithm by asking detailed questions about your specific problem and provides pointers to existing implementations. In addition, the author’s “war stories” of past successes and failures in the real world provide a vivid reminder that algorithms are real.
[26] Anybody who scoffs that this example is silly, because “you should not store all the intermediate results; use a generator” or because “everyone knows you can’t find all permutations exhaustively; use heuristics” is absolutely correct—and entirely missing the point. I know that this implementation is naive, but—cross your heart—would you really have assumed that the naive implementation would be in trouble for n = 10? Especially, when it didn’t even blink for n = 7?
