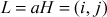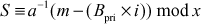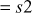Table of Contents for
Cryptography and Network Security

Version ebook / Retour

Cover image for bash Cookbook, 2nd Edition Cryptography and Network Security by S. Bose Published by Pearson Education India, 2016
  1. Cover
  2. Title Page
  3. Engineering Chemistry
  4. Contents
  5. Foreword - 1
  6. Foreword - 2
  7. Preface
  8. Acknowledgements
  9. CHAPTER 1 Cryptography
  10. CHAPTER 2 Mathematics of Modern Cryptography
  11. CHAPTER 3 Classical Encryption Techniques
  12. CHAPTER 4 Data Encryption Standard
  13. Chapter 5 Secure Block Cipher and Stream Cipher Technique
  14. Chapter 6 Advanced Encryption Standard (AES)187
  15. Chapter 7 Public Key Cryptosystem
  16. Chapter 8 Key Management and Key Distribution
  17. Chapter 9 Elliptic Curve Cryptography
  18. Chapter 10 Authentication Techniques
  19. Chapter 11 Digital Signature
  20. Chapter 12 Authentication Applications
  21. Chapter 13 Application Layer Security
  22. Chapter 14 Transport Layer Security
  23. Chapter 15 IP Security
  24. Chapter 16 System Security
  25. Appendix: Frequently Asked University Questions with Solutions
  26. Basic Mechanical Engineering

Chapter 9

Elliptic Curve Cryptography

9.1 Introduction

In 1985, Victor Miller (IBM) and Neil Koblitz (University of Washington) invented elliptic curve ­cryptography (ECC), which comes under public-key cryptosystem. At the time of its invention, the ECC algorithm provided higher potential security than other cryptographic algorithms. However, the ECC also had a limitation that it required an enormous amount of execution time. In order to ­improve its performance, Certicom [1] focused and provided efforts on its implementation part. Later on several years of research, the first commercial toolkit was introduced by Certicom to enhance ECC and created it for practical use in a variety of applications. The ECC is a public-key cryptosystem which is basically derived from the algebraic construction of elliptic curves over finite domains. The ECC has many advantages compared to other cryptographic schemes such as RSA, Elgamal and ­Diffie–Hellman key exchange, etc. One of the major advantages is that it can provide the same degree of protection offered by other cryptography schemes with keys of smaller size. For example, the ­160-bit key used in the ECC provides the same level of security as by the RSA with 1024-bit key. Likewise, the ECC with 224-bit key provides the same degree of protection provided by the RSA with 2048-bit key. Because, a small size key is used for proving high-level security in the ECC, it also takes less computation time for performing encryption and decryption operation. Moreover, it would minimize the storage complexity of processing with smaller size key values.

Similar to other public-key cryptosystem such as RSA and Elgamal, in ECC, each user selects a private key within a finite group from which a public key is computed. For computing the public key from private key, each user selects a base point, which is taken from the elliptic curve. The base point is a point in the curve which is similar to the generator used in other public-key cryptosystems such as Diffie–Hellman key exchange and Elgamal. When this base point is added with the private key, it is necessary to perform point addition and when it is multiplied with the private key it would perform point multiplication. Apart from that, in ECC-based algorithms, it is infeasible to recover the discrete logarithm of a random elliptic curve element from a publicly known base point. This problem is predicted as the ‘elliptic curve discrete log problem’ or ECDLP. The total security of ECC depends on the inability to find the multiplicand value from the given original and product points in a point multiplication.

9.2 ECC Arithmetic

The elliptic curves are described by cubic equations. An elliptic curve is a plane curve and it is defined by the equation as given below:

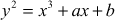
Eqn1.png

where a, b are the elliptic curve coefficients and x and y are the values of real numbers. The main ­characteristics of elliptic curve are summarized as follows:

  1. Elliptic curves obey the abelian group property.

    • Abelian groups: An abelian group is a set, denoted by A, together with an operation denoted by •, any two elements a, b in the set A form another element denoted a • b. The symbol • ­corresponds to the binary operation. The set and operation, (A, •), require to satisfy the ­abelian group axioms:

    – (A1) Closure: If a, b is in A, then the result of a • b is also in A.

    – (A2) Associativity: The equation (a • b) • c = a • (b • c) holds for all a, b, c Eqn5.png A

    – (A3) Identity element: For all elements a in A, there exists an element e in A, such that e • a = a • e = a.

    – (A4) Inverse element: For each a in A, there exists an inverse element a′ in A such that a • a′ = a′ • a = e, where e is the identity element.

    – (A5) Commutativity: a • b = b • a, for all a, b Eqn6.png A.

  2. The point at infinity 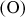Eqn7.png is acting as the identity element.
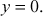
  3. Each elliptic curve is symmetric about Eqn8.png

9.2.1 Elliptic Curve Operations

The main operations involved in the ECC are point addition and point multiplication. In point ­addition, the two adding points that lie on an elliptic curve result in a third point on the curve. From this ­definition, the point addition defines some rules for addition over an elliptic curve.

9.2.2 Geometric Description of Addition

A group can be described based on the set 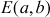Eqn9.png for exact values of a and b in the equation Eqn12.png , which makes the following condition is satisfied:

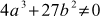
Eqn13.png

To describe the group, an addition operation must be defined which is denoted as +. The above ­equation is satisfied for the values of a and b for the set 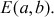Eqn17.png In geometric terms, the following rules are defined for addition over an elliptic curve.

  1. The infinite point (O) can serve as the additive identity. Therefore,Eqn19.png .

    Eqn20.png (Existence of an identity element)

    where L is the point on the elliptic curve.

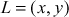  2. If Eqn22.png on the elliptic curve, then the negative of the point is represented as 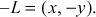Eqn23.png If these two points are connected by a vertical line, then

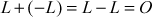    Eqn24.png (Existence of inverses)

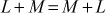  3. Eqn25.png (Commutativity)
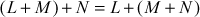  4. Eqn26.png (Associativity)
  5. Point addition: If J and K are the two points with different coordinates on the elliptic curve, then the point addition between the two points can be performed by drawing a straight line between them which touches the third point R on the same elliptic curve. The reflection of R along the x-axis provides the result of 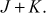Eqn31.png The point addition is illustrated in Figure 9.1.
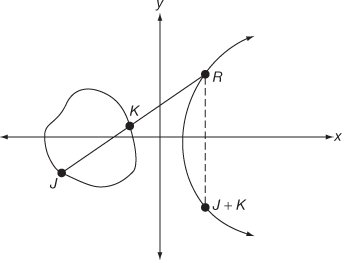
    C09F001.png

    Figure 9.1 Illustration of point addition

  6. Point doubling: In point doubling, a tangent line is drawn to get the other point of intersection 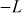Eqn32.png in the same elliptic curve. Point doubling is illustrated in Figure 9.2. Then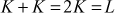 Eqn33.png
C09F002.png

Figure 9.2 Illustration of point doubling

9.2.3 Arithmetic Description of Point Addition

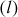Let us consider two distinct points Eqn34.png and Eqn35.png on the elliptic curve. The straight line Eqn36.png between them touches the third point 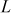Eqn37.png on the same elliptic curve. The reflection of 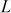Eqn38.png ­denoted as 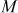Eqn39.png along the x-axis provides the result of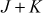Eqn41.png . The slope of the line 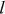Eqn42.png can be calculated as given below:

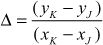
Eqn43.png

Therefore,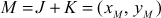Eqn44.png

where,

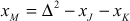
Eqn46.png

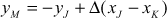
Eqn47.png

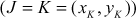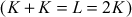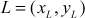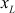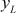If the given two points are same Eqn48.png , then point doubling operation will be ­performed. The addition of two same points is called point doubling. For performing the point doubling ­operation,Eqn49.png , the following equations are used. In the following equations, a new point Eqn50.png is computed based on calculating Eqn51.png and Eqn52.png values.

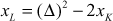
Eqn53.png

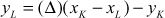
Eqn54.png

where,

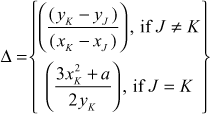
Eqn55.png

9.2.4 Point Multiplication

Point multiplication is performed by using both point addition and point doubling. In point ­addition, two distinct points are added to get a result of another point in the same elliptic curve. In point ­doubling, the same point is added to itself to get a result of another point in the same elliptic curve. In point ­multiplication, a scalar multiplication is performed between a value and a point. Let us consider a scalar value Eqn56.png which is multiplied with the base point Eqn57.png in the elliptic curve to get a new point Eqn58.png on the same curve, i.e. 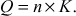to find Eqn59.png

For example, If 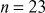Eqn60.png , then 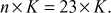Eqn61.png In this case, rather than multiplying the scalar value n with the base point 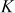Eqn63.png , point doubling and point addition operations are performed. In order to do that, the scalar value 23 is splitted into multiples of 2 to perform point doubling operation as shown below:

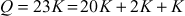
Eqn64.png

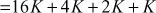
Eqn65.png

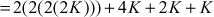
Eqn66.png

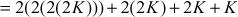
Eqn67.png

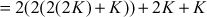
Eqn68.png

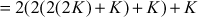
Eqn69.png

In the above example, point addition and point doubling are used to get the result of point multiplication 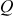Eqn70.png . The ECC is divided into two types, namely, prime curves and binary curves. Prime curves 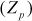Eqn71.png are very much useful for software-oriented applications, because it does not require extended bit-fiddling operation. Binary curves (GF(2n)) are more suitable for hardware application ­because it uses extended bit-fiddling operation. In this book, we have discussed about the prime curves (Zp)-based ECC.

9.2.5 Elliptic Curve Over Zp

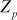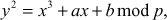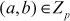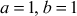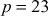In ECC, the variables and coefficients of elliptic curve are limited to a finite fieldEqn75.png . For example, let us assume the elliptic curveEqn76.png whereEqn77.png . In this curve, if Eqn78.png and Eqn79.png .Therefore, the curve becomes 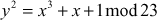Eqn80.png . In order to perform algebraic addition over the given elliptic curve that belongs to 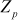Eqn81.png , let us consider two points on the elliptic curve 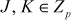Eqn82.png . The algebraic addition rules for elliptic curve over 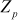Eqn83.png are summarized as follows:

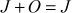
  1. Eqn84.png
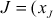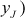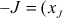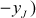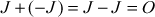
  2. If Eqn85.png , Eqn86.png andEqn87.png , Eqn88.png Then Eqn89.png
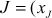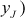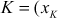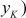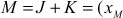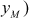  3. If Eqn90.png , Eqn91.png and Eqn92.png , Eqn93.png then Eqn94.png , Eqn95.png can be calculated as

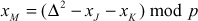
    Eqn96.png

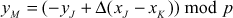
    Eqn97.png

    where

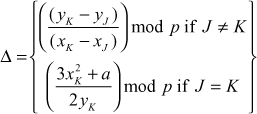
    Eqn98.png

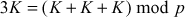  4. Multiplication is done by performing repeated additions and point doubling operations. For example, Eqn100.png .

Example 9.1:

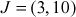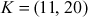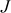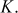
Let consider two different points Eqn102.png and Eqn103.png from the elliptic curve y2 = x3 + x + 1 mod 23. Perform the point addition between the two points Eqn105.png and Eqn106.png

Solution

The slope between the two points can be calculated as

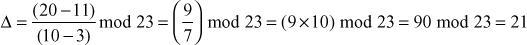
Eqn107.png

Let us consider 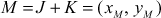Eqn110.png , then

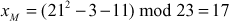
Eqn112.png

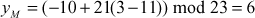
Eqn113.png

Therefore, 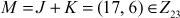Eqn114.png .

Suppose, If 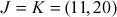Eqn117.png , then Eqn118.png . In this case, point doubling operation as shown below:

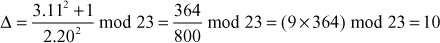
Eqn119.png

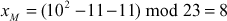
Eqn120.png

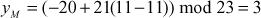
Eqn121.png

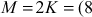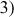
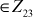Therefore, Eqn122.png , Eqn123.png Eqn124.png .

Example 9.2:

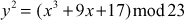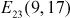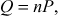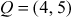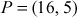Let consider the elliptic curve Eqn125.png . Hence, this is the group which belongs to Eqn126.png . Find the discrete logarithm Eqn127.png for the equation Eqn128.png where Eqn129.png and Eqn130.png .

Solution

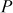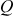Let us assume that the intruder knows the values of Eqn131.png and Eqn132.png . Then, the intruder performs the brute-force method until the value of 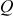Eqn133.png is reached to find the value of Eqn134.png . The point addition and point ­doubling operations are used to perform brute-force method in the following manner.

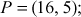
Eqn135.png

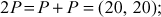
Eqn136.png

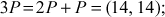
Eqn137.png

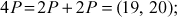
Eqn138.png

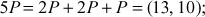
Eqn139.png

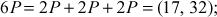
Eqn140.png

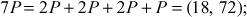
Eqn141.png

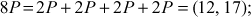
Eqn142.png

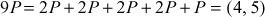
Eqn143.png

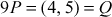Here Eqn144.png . Therefore, the value of the discrete logarithm Eqn145.png is 9. The brute force is ­infeasible to perform, if the value of Eqn146.png is so large.

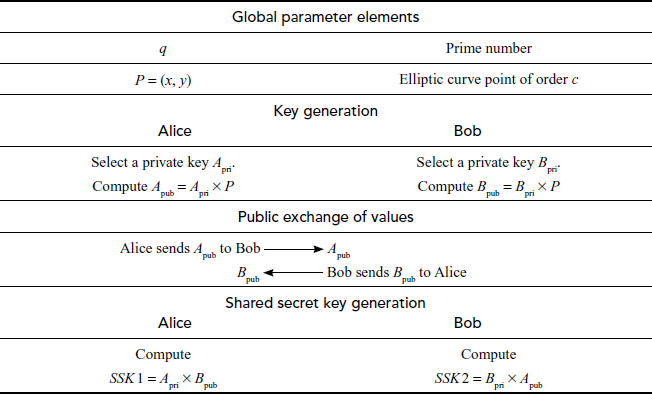
9.3 Diffie–Hellman Key Exchange using Elliptic Curves

The ECC is applied to Diffie–Hellman key exchange to resolve the vulnerability in key exchange problem. The following subsection gives an overall idea about Diffie–Hellman key exchange using elliptic curves.

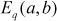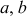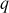Step 1: Initially, Alice and Bob select an elliptic curve Eqn147.png with parameters Eqn148.png for a large prime number Eqn149.png .

Step 2: Alice and Bob also select a base point P = (x, y) on the elliptic curve of order c such that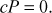Eqn152.png Here, c is the small positive integer. The value of 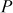Eqn154.png is known to all users in the system.

Step 3: Suppose Alice and Bob want to share a secret key. Alice selects a random integer 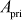Eqn156.png less than c which is considered as Alice’s private key. Alice does not disclose it to anyone. From this private key, Alice computes public key.

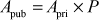
Eqn158.png

Step 4: Similarly, Bob selects a random integer 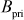Eqn159.png less than c independently which is Bob’s private key and does not disclose to anyone. Based on this, Bob also computes his public key.

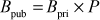
Eqn161.png

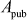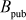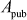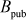Step 5: These computed public key values are exchanged to each other. Alice transmits Eqn162.png to Bob and Bob transmits Eqn163.png to Alice. Notice that the adversary Eve tries to view the values of Eqn164.png and Eqn165.png , since they are exchanged over the insecure communication channel.

Step 6: From the public value (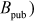Eqn166.png received from Bob, Alice can generate the shared secret key by using the following equation:

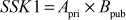
Eqn167.png

Step 7: Bob can also generate the shared secret key from

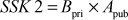
Eqn168.png

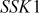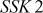The values Eqn169.png and Eqn170.png generated by Alice and Bob are really identical. This can be proved as given below:

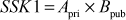
Eqn171.png

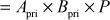
Eqn172.png

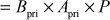
Eqn173.png

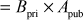Eqn174.png (by the rules of modular arithmetic)

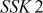
= Eqn175.png

Figure 9.3 shows the diagrammatic representation of ECC-based Diffie–Hellman key exchange. ­Alice wishes to establish a secure communication link with Bob. Then, Alice and Bob choose ­distinct ­one-time private keys 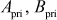Eqn176.png and then calculate 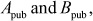Eqn177.png respectively. Alice sends 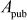Eqn178.png to Bob and Bob sends 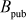Eqn179.png to Alice. Both Alice and Bob can calculate the shared secret key for ­communication. The summary of Diffie–Hellman key exchange using elliptic curves algorithm is shown in Table 9.1.

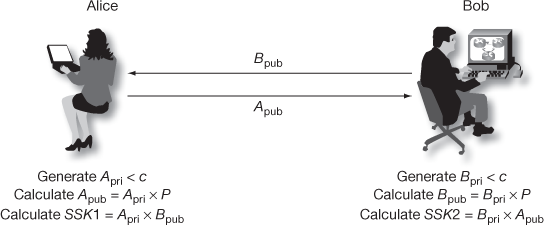
C09F003.png

Figure 9.3 Diffie–Hellman key exchange using elliptic curves

Table 9.1 Summary of Diffie–Hellman key exchange algorithm using elliptic curves

C08F002.png
9.4 Elgamal Cryptosystem using Elliptic Curves

The ECC-based Elgamal cryptosystem was described by Taher Elgamal in 1985. This cryptosystem is developed based on the ECC-based Diffie–Hellman key exchange algorithm. The ECC is applied to Elgamal cryptosystem to make the cryptosystem strong from vulnerabilities. This is consided to be strong because for larger key values it is infeasible to attack. ECC is also effective due to its shorter key length and higher efficiency on encryption and decryption [2]. The following subsection gives an overall idea about Elgamal cryptosystem using elliptic curves.

Step 1: Alice and Bob want to make secure communications with each other. Alice selects a message m to be communicated with Bob.

Step 2: Bob selects an elliptic curve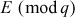Eqn194.png , where 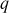Eqn195.png is a large prime number. In addition, Bob selects a base point 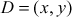Eqn196.png on the elliptic curve and a private key 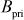Eqn197.png and then ­computes,

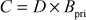
Eqn198.png

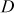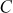Step 3: Bob places Eqn199.png and Eqn200.png in the public directory and keeps the value 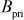Eqn201.png as secret.

Step 4: Now, Alice selects a random integer Eqn202.png and then computes

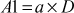
Eqn203.png

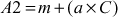
Eqn204.png

Step 5: Now, the pair 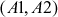Eqn205.png is sent to Bob. Bob decrypts the message 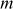Eqn206.png by computing

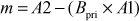
Eqn207.png

Proof of correctness:

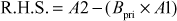
Eqn208.png

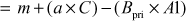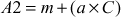Eqn209.png (Since, Eqn210.png )

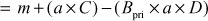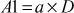Eqn211.png (Since, Eqn212.png )

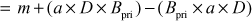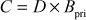Eqn213.png (Since Eqn214.png )

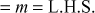
Eqn216.png

The steps involved in Elgamal cryptosystem which is based on the use of elliptic curves are depicted in Figure 9.4.

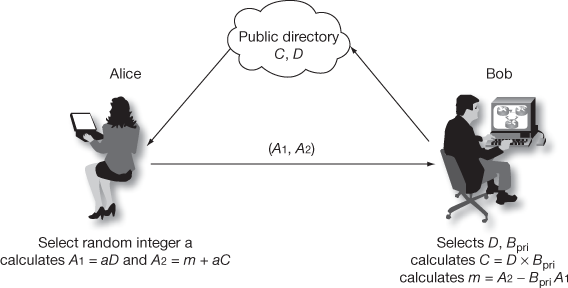
C09F004.png

Figure 9.4 ECC-based Elgamal cryptosystem

Example 9.3:

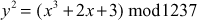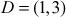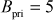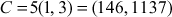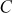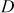Bob chooses an elliptic curve Eqn217.png and Eqn218.png . He also chooses Eqn219.png and then computes Eqn220.png and publishes Eqn221.png and Eqn222.png in the public directory. Alice desires to send the message 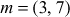Eqn223.png to Bob. Then Alice selects a random integer 3 and computes

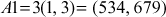
Eqn225.png

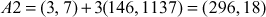
Eqn226.png

Now, the pair 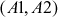Eqn227.png is sent to Bob. Bob decrypts the message m by computing

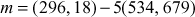
Eqn229.png

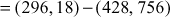
Eqn230.png

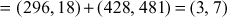
Eqn231.png

9.5 ECC-based Elgamal Digital Signature

The following subsection describes an overall idea about Elgamal digital signature using elliptic curves.

Step 1: Alice and Bob want to make communications with each other. Alice desires to send a message m to Bob and assumes that 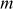Eqn233.png is an integer.

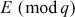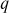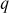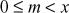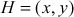Step 2: Alice selects an elliptic curveEqn234.png , where Eqn235.png is a large prime number. If Eqn236.png is not a large prime number, thenEqn237.png , where Eqn238.png is the number of points on the elliptic curve E. Along with that, Alice selects a point Eqn240.png on the elliptic curve and a private key 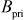Eqn241.png and then computes

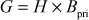
Eqn242.png

Step 3: Alice place G, H, x and the curve E in the public directory and keeps the value 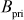Eqn247.png as secret.

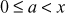
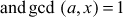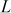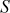Step 4: Now, Alice wants to sign a message m. In order to do that, Alice selects a random integer a such that Eqn250.png Eqn251.png . After that, Alice computes the signature Eqn252.png and Eqn253.png as given below:

  1. Eqn254.png
  2. Eqn255.png

Step 5: Now, the signed message 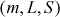Eqn256.png is sent to Bob. Bob verifies the signature S in the ­following way:

  1. Bob first gets the public information of Alice from the public directory.
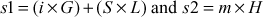
  2. Then, computes Eqn258.png

Proof of correctness:

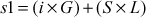
Eqn259.png

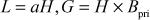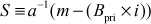
where, Eqn260.png and Eqn261.png

Therefore,

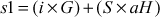
Eqn262.png

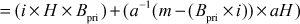
Eqn263.png

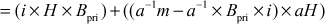
Eqn264.png

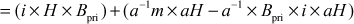
Eqn265.png

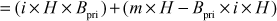
Eqn266.png

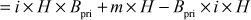
Eqn267.png

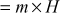
Eqn268.png

Eqn269.png

Since, 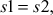Eqn270.png Bob declares the signature as a valid signature.

Key Terms

Abelian group

Elliptic curve cryptography

Elliptic curves

Point addition

Point doubling

Point multiplication

Summary
  • Elliptic curve cryptography (ECC) is a public-key cryptography approach derived from the algebraic construction of elliptic curves over finite domains.
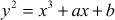  • The elliptic curves are described by cubic equations, Weierstrass equation are in the form of cubic equations for elliptic curves. The elliptic curve with standard form is represented as Eqn271.png .
  • An abelian group is a set, denoted by A, together with an operation denoted by •, any two ­elements a, b in the set A form another element denoted a • b. The symbol • corresponds to the binary ­operation.
  • In point addition, the two adding points that lie on an elliptic curve results in a third point on the curve.
  • Point multiplication is performed by using both point addition and point doubling. In point ­addition, two distinct points are added to get a result of another point in the same elliptic curve.
  • In point doubling the same point is added to itself to get a result of another point in the same ­elliptic curve.
Review Questions
  1. What is meant by elliptic curve cryptography?
  2. Define elliptic curves.
  3. Describe the five axioms of the abelian group.
  4. Explain elliptic curve-based Diffie–Hellman key exchange method in detail.
  5. Explain elliptic curve-based Elgamal cryptosystem in detail.
  6. Explain elliptic curve-based Elgamal digital signature method in detail.
  7. Explain point addition, point doubling, and point multiplication processes in detail.
References
  1. https://www.certicom.com/ecc
  2. Tzer-Long Chen, Yu-Fang Chung, Frank Y.S. Lin (2010), ‘An efficient date-constraint ­hierarchical key management scheme for mobile agents’, Experts Systems with Applications, 37: 7721–7728.