Appendix
Frequently Asked University Questions With Solutions
PART A - Brief Questions
1. What do you mean by cryptanalysis?
Ans: Cryptanalysis: It is a process of attempting to discover the key or plaintext or both Cryptography: It is a science of writing Secret code using mathematical techniques. The many schemes used for enciphering constitute the area of study known as cryptography
2. What is difference between a block cipher and a stream cipher?
Ans: A block cipher processes the input one block of elements at a time, producing an output block for each input block. A stream cipher processes the input elements continuously, producing output one element at a time, as it goes along.
3. What is key distribution center?
Ans: A key distribution center is responsible for distributing keys to pairs of users (hosts, processes, applications) as needed. Each user must share a unique key with the key distribution center for purposes of key distribution. The use of a key distribution center is based on the use of a hierarchy of keys. At a minimum, two levels of keys are used. Communication between end systems is encrypted using a temporary key, often referred to as a session key .
4. Mention the application of public key cryptography.
Ans: Public-key systems are characterized by the use of a cryptographic algorithm with two keys, one held private and one available publicly. Depending on the application, the sender uses either the sender’s private key or the receiver’s public key, or both, to perform some type of cryptographic function. In broad terms, we can classify the use of public-key cryptosystems into three categories:
Encryption/decryption: The sender encrypts a message with the recipient’s public key.
Digital signature: The sender “signs” a message with its private key. Signing is achieved by a cryptographic algorithm applied to the message or to a small block of data that is a function of the message.
Key exchange: Two sides cooperate to exchange a session key. Several different approaches are possible, involving the private key(s) of one or both parties.
5. Specify the requirements for message authentication.
Ans: Authentication Requirements
In the context of communications across a network, the following attacks can be identified:
- Disclosure: Release of message contents to any person or process not possessing the appropriate cryptographic key.
- Traffic analysis: Discovery of the pattern of traffic between parties. In a connection-oriented application, the frequency and duration of connections could be determined. In either a connection-oriented or connectionless environment, the number and length of messages between parties could be determined.
- Masquerade: Insertion of messages into the network from a fraudulent source. This includes the creation of messages by an opponent that are purported to come from an authorized entity. Also included are fraudulent acknowledgments of message receipt or non receipt by someone other than the message recipient.
- Content modification: Changes to the contents of a message, including insertion, deletion, transposition, and modification.
- Sequence modification: Any modification to a sequence of messages between parties, including insertion, deletion, and reordering.
- Timing modification: Delay or replay of messages. In a connection-oriented application, an entire session or sequence of messages could be a replay of some previous valid session, or individual messages in the sequence could be delayed or replayed. In a connectionless application, an individual message (e.g., datagram) could be delayed or replayed.
- Source repudiation: Denial of transmission of message by source.
- Destination repudiation: Denial of receipt of message by destination.
6. What are the two important key issues related to authenticated key exchange?
Ans: Two key issues are confidentiality and timeliness. To prevent masquerade and to prevent compromise of session keys, essential identification and session key information must be communicated in encrypted form. This requires the prior existence of secret or public keys that can be used for this purpose. The second issue, timeliness, is important because of the threat of message replays. Such replays, at worst, could allow an opponent to compromise a session key or successfully impersonate another party. At minimum, a successful replay can disrupt operations by presenting parties with messages that appear genuine but are not.
7. What entities constitute a full-service Kerberos environment?
Ans: If a set of users is provided with dedicated personal computers that have no network connections, then a user’s resources and files can be protected by physically securing each personal computer. When these users instead are served by a centralized time-sharing system, the time-sharing operating system must provide the security. The operating system can enforce access control policies based on user identity and use the logon procedure to identify users.Today, neither of these scenarios is typical. More common is a distributed architecture consisting of dedicated user workstations (clients) and distributed or centralized servers. In this environment, three approaches to security can be envisioned:
- Rely on each individual client workstation to assure the identity of its user or users and rely on each server to enforce a securitypolicy based on user identification (ID).
- Require that client systems authenticate themselves to servers, but trust the client system concerning the identity of its user.
- Require the user to prove his or her identity for each service invoked. Also require that servers prove their identitytoclients.
8. Why does ESP include a padding field?
Ans: The Padding field serves several purposes:
- If an encryption algorithm requires the plaintext to be a multiple of some number of bytes (e.g., the multiple of a single block for a block cipher), the Padding field is used to expand the plaintext (consisting of the Payload Data, Padding, Pad Length, and Next Header fields) to the required length.
- The ESP format requires that the Pad Length and Next Header fields be right aligned within a 32-bit word. Equivalently, the cipher text must be an integer multiple of 32 bits. The Padding field is used to assure this alignment.
- Additional padding may be added to provide partial traffic flow confidentiality by concealing the actual length of the payload.
9. What are the two types of audit records?
Ans:
- Native audit records: Virtually all multiuser operating systems include accounting software that collects information on user activity. The advantage of using this information is that no additional collection software is needed. The disadvantage is that the native audit records may not contain the needed information or may not contain it in a convenient form.
- Detection-specific audit records: A collection facility can be implemented that generates audit records containing only that information required by the intrusion detection system. One advantage of such an approach is that it could be made vendor independent and ported to a variety of systems. The disadvantage is the extra overhead involved in having, in effect, two accounting packages running on a machine.
10. What is an access control matrix? What are its elements?
Ans: The basic elements of the model are as follows:
- Subject: An entity capable of accessing objects. Generally, the concept of subject equates with that of process. Any user or application actually gains access to an object by means of a process that represents that user or application.
- Object: Anything to which access is controlled. Examples include files, portions of files, programs, and segments of memory.
- Access right: The way in which an object is accessed by a subject. Examples are read, write, and execute.
11. Give the types of attack.
Ans:
Passive Attacks
Passive attacks are in the nature of eavesdropping on, or monitoring of, transmissions. The goal of the opponent is to obtain information that is being transmitted. Two types of passive attacks are release of message contents and traffic analysis.
Active Attacks
Active attacks involve some modification of the data stream or the creation of a false stream and can be subdivided into four categories: masquerade, replay, modification of messages, and denial of service.
12. List out the problems of one time pad?
Ans: The one-time pad offers complete security but, in practice, has two fundamental difficulties:
- There is the practical problem of making large quantities of random keys. Any heavily used system might require millions of random characters on a regular basis. Supplying truly random characters in this volume is a significant task.
- Even more daunting is the problem of key distribution and protection. For every message to be sent, a key of equal length is needed by both sender and receiver. Thus, a mammoth key distribution problem exists.
- Because of these difficulties, the one-time pad is of limited utility, and is useful primarily for low-bandwidth channels requiring very high security.
13. Write down the purpose of the S-Boxes in DES?
Ans: The role of the S-boxes in the function F is illustrated as the substitution consists of a set of eight S-boxes, each of which accepts 6 bits as input and produces 4 bits as output. These transformations are interpreted as follows: The first and last bits of the input to box Si form a 2-bit binary number to select one of four substitutions defined by the four rows in the table for Si. The middle four bits select one of the sixteen columns. The decimal value in the cell selected by the row and column is then converted to its 4-bit representation to produce the output. For example, in S1 for input 011001, the row is 01 (row 1) and the column is 1100 (column 12). The value in row 1, column 12 is 9, so the output is 1001.
14. Define : Diffusion.
Ans: Statistical structure of the plaintext is dissipated into long-range statistics of cipher text.
Confusion: Relationship between cipher text and key is made complex.
15. Define: Replay attack.
Ans: An attack in which a service already authorized and completed is forged by another “duplicate request” in an attempt to repeat authorized commands.
- Simple replay: The opponent simply copies a message and replays it later.
- Repetition that can be logged: An opponent can replay a timestamped message within the valid time window.
- Repetition that cannot be detected: This situation could arise because the original message could have been suppressed and thus did not arrive at its destination; only the replay message arrives.
- Backward replay without modification: This is a replay back to the message sender. This attack is possible if symmetric
encryption is used and the sender cannot easily recognize the difference between messages sent and messages received on the basis of content.
16. List out the parameters of AES.
Ans:
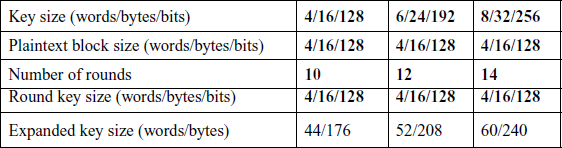
17. Define : Primality test.
Ans:
It is necessary to select one or more very large prime numbers at random. Thus we are faced with the task of determining whether a given large number is prime.
18. State the difference between conventional encryption and public-key encryption.
Ans:

19. Define : Malicious software.
Ans:
Malicious software is software that is intentionally included or inserted in a system for a harmful purpose.
20. Name any two security standards.
Ans: RC4 is used in the SSL/TLS (Secure Sockets Layer/Transport Layer Security) standards that have been defined for communication between Web browsers and servers. SET used by visa Card.
21. Differentiate passive attack from active attack with exzmple.
Ans: Passive attacks are in the nature of eavesdropping on, or monitoring of, transmissions. The goal of the opponent is to obtain information that is being transmitted. Two types of passive attacks are release of message contents and traffic analysis.
Eg: A telephone conversation, an electronic mail message, and a transferred file may contain sensitive or confidential information. We would like to prevent an opponent from learning the contents of these transmissions.
Active attacks involve some modification of the data stream or the creation of a false stream and can be subdivided into four categories: masquerade, replay, modification of messages, and denial of service.
A masquerade takes place when one entity pretends to be a different entity .Masquerade attack usually includes one of the other forms of active attack. For example, authentication sequences can be captured and replayed after a valid authentication sequence has taken place, thus enabling an authorized entity with few privileges to obtain extra privileges by impersonating an entity that has those privileges.
22. What is the use of Fermat’s theorem?
Ans: Fermat’s theorem states the following: If p is prime and a is a positive integer not divisible by p, then
aP-1=1(mod P)
Proof: Consider the set of positive integers less than p:{1,2,..., p 1} and multiply each element bya, modulo p, to get the set X = {a mod p,
2a mod p, . . . (p 1)a mod p}. None of the elements of X is equal to zero because p does not divide a.
23. What are the different modes of operation in DES?
Ans:
- Electronic code Book
- Cipher Block chaining
- Cipher feedback mode
- Output Feedback mode
- Counter
24. Name any two methods for testing prime numbers.
Ans:
- Miller-Rabin Algorithm
- A Deterministic Primality Algorithm
- Chinese Remainder algorithm
25. What is discrete logarithm?
Ans: Discrete logarithms are fundamental to a number of public-key algorithms, including Diffie-Hellman key exchange and the digital signature algorithm (DSA).
Calculation of Discrete Logarithms
Consider the equation
y = gx mod p
Given g, x, and p, it is a straightforward matter to calculate y. At the worst, we must perform x repeated multiplications, and algorithms exist for achieving greater efficiency
26. What do you mean by one-way property in hash function?
Ans: A variation on the message authentication code is the one-way hash function. As with the message authentication code, a hash function accepts a variable-size message M as input and produces a fixed-size output, referred to as a hash code H(M). Unlike a MAC, a hash code does not use a key but is a function only of the input message. The hash code is also referred to as a message digest or hash value. The hash code is a function of all the bits of the message and provides an error-detection capability: A change to any bit or bits in the message results in a change to the hash code.
27. List out the requirements of Kerberos.
Ans: Kerberos listed the following requirements:
- Secure: A network eavesdropper should not be able to obtain the necessary information to impersonate a user. Generally, Kerberos should be strong enough that a potential opponent does not find it to be the weak link.
- Reliable: For all services that rely on Kerberos for access control, lack of availability of the Kerberos service means lack of availability of the supported services. Hence, Kerberos should be highly reliable and should employ a distributed server architecture, with one system able to back up another.
- Transparent: Ideally, the user should not be aware that authentication is taking place, beyond the requirement to enter a password.
- Scalable: The system should be capable of supporting large numbers of clients and servers. This suggests a modular, distributed architecture.
28. Mention four SSL protocols.
Ans:
- SSL Handshake protocol
- SSL change cipher spec protocol
- SSL Alert Protocol
- SSL Record Protocol
29. Define Intruders. Name three different classes of Intruders.
Ans: Threats to security is the intruder (the other is viruses), generally referred to as a hacker or cracker.
- Classes of intruders:
- Masquerader: An individual who is not authorized to use the computer and who penetrates a system’s access controls to exploit a legitimate user’s account
- Misfeasor: A legitimate user who accesses data, programs, or resources for which such access is not authorized, or who is authorized for such access but misuses his or her privileges
Clandestine user: An individual who seizes supervisory control of the system and uses this control to evade auditing and access controls or to suppress audit collection
30. What do you mean by Trojan Horses?
Ans: Trojan horse is a useful, or apparently useful, program or command procedure containing hidden code that, when invoked, performs some unwanted or harmful function.
Example, to gain access to the files of another user on a shared system, a user could create a Trojan horse program that, when executed, changed the invoking user’s file permissions so that the files are readable by any user.
31. Define threads and attacks.
Ans:
Threat: A potential for violation of security, which exists when there is a circumstance, capability, action,or event that could breach security and cause harm.That is, a threat is a possible danger that might exploit a vulnerability.
Attack: An assault on system security that derives from an intelligent threat; that is, an intelligent act that is a deliberate attempt to evade security services and violate the security policy of a system.
32. What are the resources for secure use of conventional encrytion?
Ans: Plaintext,Encryption Algorithm,Secret Key,Ciphertext and Decryption algorithm are the resources for secure use of conventional encrytion.
33. Using Fermat theorem find 3201 mod 11.
Ans:
a=3 ; p=201
ap=a(mod p)
310= 1 (mod 11)
3201=(3)(310)(320)=(3)(310)(320)=(3)(1)20= 3(mod11)n.
34. List the techniques for distribution of public keys.
Ans:
- Public Announcement
- Publicly available directory
- Public Key Authority
- Public Key Certificates
35. What is suppress reply attack.
Ans: The problem occurs when a sender’s clock is ahead of the intended recipient’s clock. In this case, an opponent can intercept a message from the sender and replay it later when the timestamp in the message becomes current at the recipient’s site. This replay could cause unexpected results. This attack is known as suppress replay attack.
36. What is the difference between MD4 and MD5 ?
Ans:
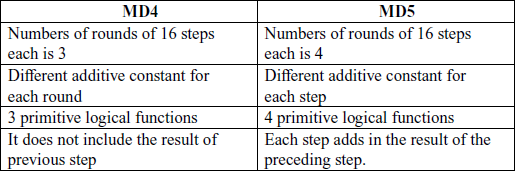
37. What is a realm?
Ans: A kerberos realm is a set of managed nodes that store the same kerberos database. The kerberos database resides on the kerberos master computer.
PART B - Detailed Questions
1. Explain about substitution and transposition techniques with two examples for each.
Ans: Classification of Cryptographic systems:

Substitution Techniques
The two basic building blocks of all encryption techniques are substitution and transposition. A substitution technique is one in which the letters of plaintext are replaced by other letters or by numbers or symbols. If the plaintext is viewed as a sequence of bits, then substitution involves replacing plaintext bit patterns with cipher text bit patterns.
1. Ceaser cipher
2. monoalphabetic cipher
3. Homophonic substitution cipher
4. Polygram Substitution cipher
5. Polyalphabetic cipher
Caesar Cipher
The earliest known use of a substitution cipher, and the simplest, was by Julius Caesar. The Caesar cipher involves replacing each letter of the alphabet with the letter standing three places further down the alphabet.
For example,
plain: meet me after the toga party
cipher: PHHW PH DIWHU WKH WRJD SDUWB
The alphabet is wrapped around, so that the letter following Z is A. We can define the transformation by listing all possibilities, as follows:
plain: a b c d e f g h i j k l m n o p q r s t u v w x y z
cipher: D E F G H I J K L M N O P Q R S T U V W X Y Z A B C
we can also assign a numerical equivalent to each letter:
Monoalphabetic Ciphers
With only 25 possible keys, the Caesar cipher is far from secure. A dramatic increase in the key space can be achieved by allowing an arbitrary substitution. Recall the assignment for the Caesar cipher:
plain: a b c d e f g h i j k l m n o p q r s t u v w x y z
cipher: D E F G H I J K L M N O P Q R S T U V W X Y Z A B C
If, instead, the “cipher” line can be any permutation of the 26 alphabetic characters, then there are 26! or greater than 4 x 10 26 possible keys. This is 10 orders of magnitude greater than the key space for DES and would seem to eliminate brute-force techniques for cryptanalysis. Such an approach is referred to as a monoalphabetic substitution cipher, because a single cipher alphabet (mapping from plain alphabet to cipher alphabet) is used per message.
Playfair Cipher
The best-known multiple-letter encryption cipher is the Playfair, which treats digrams in the plaintext as single units and translates these
M O N A R
C H Y B D
E F G I/J K
L P Q S T
U V W X Z
In this case, the keyword is monarchy. The matrix is constructed by filling in the letters of the keyword (minus duplicates) from left to rightand from top to bottom, and then filling in the remainder of the matrix with the remaining letters in alphabetic order. The letters I and Jount as one letter. Plaintext is encrypted two letters at a time, according to the following rules:
1. Repeating plaintext letters that are in the same pair are separated with a filler letter, such as x, so that balloon would be treated as ba lx lo on.
2. Two plaintext letters that fall in the same row of the matrix are each replaced by the letter to the right, with the first element of the row circularly following the last. For example, ar is encrypted as RM.
3. Two plaintext letters that fall in the same column are each replaced by the letter beneath, with the top element of the column circularly following the last. For example, mu is encrypted as CM.
4. Otherwise, each plaintext letter in a pair is replaced by the letter that lies in its own row and the column occupied by the other plaintext letter. Thus, hs becomes BP and ea becomes IM (or JM, as the encipherer wishes).
Hill Cipher
This cipher is somewhat more difficult to understand than the others in this chapter, but it illustrates an important point about cryptanalysis that will be useful later on. This subsection can be skipped on a first reading.
Another interesting multiletter cipher is the Hill cipher, developed by the mathematician Lester Hill in 1929. The encryption algorithm takes m successive plaintext letters and substitutes for them m ciphertext letters. The substitution is determined by m linear equations in which each character is assigned a numerical value (a = 0, b = 1 ... z = 25). For m = 3, the system can be described as follows:
c3 = (k31P1 + k32P2 + k33P3) mod 26
This can be expressed in term of column vectors and matrices:
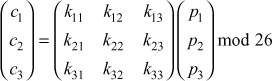
C = KP mod 26
where C and P are column vectors of length 3, representing the plaintext and ciphertext, and K is a 3 x 3 matrix, representing the encryption key. Operations are performed mod 26.
Polyalphabetic Ciphers
Another way to improve on the simple monoalphabetic technique is to use different monoalphabetic substitutions as one proceeds through the plaintext message. The general name for this approach is polyalphabetic substitution cipher. All these techniques have the following features in common:
1. A set of related monoalphabetic substitution rules is used.
2. A key determines which particular rule is chosen for a given transformation.
The best known, and one of the simplest, such algorithm is referred to as the Vigenère cipher. In this scheme, the set of related monoalphabetic substitution rules consists of the 26 Caesar ciphers, with shifts of 0 through 25. Each cipher is denoted by a key letter, which is the ciphertext letter that substitutes for the plaintext letter a.
One-Time Pad
An Army Signal Corp officer, Joseph Mauborgne, proposed an improvement to the Vernam cipher that yields the ultimate in security. Mauborgne suggested using a random key that is as long as the message, so that the key need not be repeated. In addition, the key is to be used to encrypt and decrypt a single message, and then is discarded. Each new message requires a new key of the same length as the new message. Such a scheme, known as a one-time pad, is unbreakable. It produces random output that bears no statistical relationship to the plaintext. Because the ciphertext contains no information whatsoever about the plaintext, there is simply no way to break the code.
Transposition Techniques
- Rail Fence Techniques
- Columnar transposition Techniques
- Book cipher
- Vernam Cipher/one time pad
All the techniques examined so far involve the substitution of a ciphertext symbol for a plaintext symbol. A very different kind of mapping is achieved by performing some sort of permutation on the plaintext letters. This technique is referred to as a transposition cipher. The simplest such cipher is the rail fence technique, in which the plaintext is written down as a sequence of diagonals and then read off as a sequence of rows. For example, to encipher the message “meet me after the toga party” with a rail fence of depth 2, we write the following:
The encrypted message is
MEMATRHTGPRYETEFETEOAAT
This sort of thing would be trivial to cryptanalyze. A more complex scheme is to write the message in a rectangle, row by row, and read the message off, column by column, but permute the order of the columns. The order of the columns then becomes the key to the algorithm. For example,
Key: 4 3 1 2 5 6 7
Plaintext: a t t a c k p
o s t p o n e
d u n t i l t
w o a m x y z
Ciphertext: TTNAAPTMTSUOAODWCOIXKNLYPETZ
A pure transposition cipher is easily recognized because it has the same letter frequencies as the original plaintext. For the type of columnar transposition just shown, cryptanalysis is fairly straightforward and involves laying out the ciphertext in a matrix and playing around with column positions. Digram and trigram frequency tables can be useful. The transposition cipher can be made significantly more secure by performing more than one stage of transposition. The result is a more complex permutation that is not easily reconstructed. Thus, if the foregoing message is reencrypted using the same algorithm,
Key: 4 3 1 2 5 6 7
Input: t t n a a p t
m t s u o a o
d w c o i x k
n l y p e t z
Output: NSCYAUOPTTWLTMDNAOIEPAXTTOKZ
To visualize the result of this double transposition, designate the letters in the original plaintext message by the numbers designating their position. Thus, with 28 letters in the message, the original sequence of letters is
01 02 03 04 05 06 07 08 09 10 11 12 13 14
15 16 17 18 19 20 21 22 23 24 25 26 27 28
Rail Fence techniques:
1. Write down the plain text message as a sequence of diagonals.
2. Read the plaintext written in step 1 as a sequence of rows.
plain text: Come home tomorrow
Cipher text: cmh mt mr ooeoeoorw.
Columnar transposition technique:
1 Writ the plain text message row by row in a rectangle of a predefined size.
2. Read the message column by column .it need not be in the order of the column 1,2,3…
3. The message thus obtained is the cipher text message.
plain text: Come home tomorrow
Let us consider a rectangle with six columns.
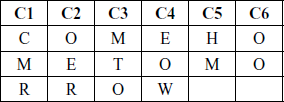
the order of columns chosen in random order say 4,6,1,2,5,3 .Then read the text in order of these columns.
Cipher text: eowoocmroerhmmto
Vernam cipher:
1. Treat each plain text alphabet as a number in an increasing sequence.
2. do the same for each character of the input cipher text.
3. Add each number corresponding to the plaintext alphabet to the corresponding input ciphertext alphabet number.
4. If the sum has produced is greater than 26,subtract 26 from it.
5. translate each number of the sum back to the corresponding alphabet. This gives the cipher test.
2. What is the need for triple DES? Write the disadvantages of double DES and explain triple DES.
Ans: The use of double DES results in a mapping that is not equivalent to a single DES encryption. But there is a way to attack this scheme, one that does not depend on any particular property of DES but that will work against any block encryption cipher.
The algorithm, known as a meet-in-the-middle attack, C = E(K2, E(K1, P))
then (X = E(K1, P) = D(K2, P)
Given a known pair, (P, C), the attack proceeds as follows. First, encrypt P for all 256 possible values of K1 Store these results in a table and then sort the table by the values of X. Next, decrypt C using all 256 possible values of K2. As each decryption is produced, check the result against the table for a match. If a match occurs, then test the two resulting keys against a new known plaintext-ciphertext pair. If the two keys produce the correct ciphertext, accept them as the correct keys.
3. Explain how the elliptic curves are useful for cryptography?
Ans: Several approaches to encryption/decryption using elliptic curves . The first task in this system is to encode the plaintext message m to be sent as an x-y point Pm. It is the point Pm that will be encrypted as a ciphertext and subsequently decrypted. Note that we cannot simply encode the message as the x or y coordinate of a point, because not all such coordinates are in Eq(a, b);. Again, there are several approaches to this encoding, which we will not address here, but suffice it to say that there are relatively straightforward techniques that can be used. As with the key exchange system, an encryption/decryption system requires a point G and an elliptic group Eq(a, b) as parameters. Each user A selects a private key nA and generates a public key PA = nA x G.
To encrypt and send a message Pm to B, A chooses a random positive integer k and produces the ciphertext Cm consisting of the pair of points:
Cm = {kG, Pm + kPB}
Note that A has used B’s public key PB. To decrypt the ciphertext, B multiplies the first point in the pair by B’s secret key and subtracts the result from the second point:
Pm + kPB nB(kG) = Pm + k(nBG) nB(kG) = Pm
A has masked the message Pm by adding kPB to it. Nobody but A knows the value of k, so even though PB is a public key, nobody can remove the mask kPB. However, A also includes a “clue,” which is enough to remove the mask if one knows the private key n B. For an attacker to recover the message, the attacker would have to compute k given G and kG, which is assumed hard. As an example of the encryption process take p = 751; Ep(1, 188), which is equivalent to the curve y2= x3x + 188;and G = (0, 376). Suppose that A wishes to send a message to B that is encoded in the elliptic poinPtm = (562, 201) and that A selects the random number k = 386. B’s public key is PB = (201, 5). We have 386(0, 376) = (676, 558), and (562, 201) + 386(201, 5) = (385, 328). Thus A sends the cipher text {(676, 558), (385, 328)}.
A key exchange between users A and B can be accomplished as follows .A selects an integer nA less than n. This is A’s private key.
1. A then generates a public keyP A = nA x G; the public key is a point in Eq(a, b).
2. B similarly selects a private key nB and computes a public key PB.
3. A generates the secret key K = nA x PB. B generates the secret keyK = nB x PA.

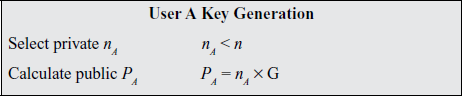
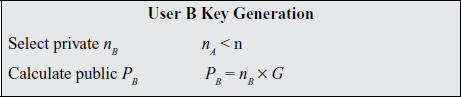


ECC Diffie-Hellman Key Exchange
The two calculations in step 3 produce the same result because
nA x PB = nA x (nB x G) = nB x (nA x G) = nB x PA
To break this scheme, an attacker would need to be able to compute k given G and kG, which is assumed hard.
4. In a public key system using RSA, you intercept the cipher text C = 10 sent to a user whose public key is e=5, n=35. What is the plain text? Explain the above problem with an algorithm description.
Ans: Description of the Algorithm
The scheme developed by Rivest, Shamir, and Adleman makes use of an expression with exponentials. Plaintext is encrypted in blocks, with each block having a binary value less than some number n. That is, the block size must be less than or equal to log2(n); in practice, the block size is i bits, where 2 I ≤ n 2 i+1. Encryption and decryption are of the following form, for some plaintext blockM and ciphertext block C:
C = Memod n
M = Cdmod n = (Me)dmod n = Medmod n
Both sender and receiver must know the value of n. The sender knows the value of e, and only the receiver knows the value of d. Thus, this is a public-key encryption algorithm with a public key of PU = {e, n} and a private key of PU = {d, n}.
For this algorithm to be satisfactory for public-key encryption, the following requirements must be met:
1. It is possible to find values of e, d, n such that M ed mod n = M for all M < n.
2. It is relatively easy to calculate mod Memod n and Cdmod n . for all values of M < n.
3. It is infeasible to determine d given e and n.
To find a relationship of the form Medmod n = M
4. if e and d are multiplicative inverses modulo f(n), where f(n) is the Euler totient function. It is shown in
that for p, q prime, f(pq) = (p- 1)(q-1) The relationship between e and d can be expressed as
1. Select two prime numbers, p = 17 and q = 11.
2. Calculate n = pq = 17 x 11 = 187.
3. Calculate f(n) = (p- 1)(q-1) = 16 x 10 = 160.
4. Select e such that e is relatively prime to f(n) = 160 and less than f(n) we choose e = 7.
Determine d such that de 1 (mod 160) and d < 160. The correct value is d = 23, because 23 x 7 = 161 = 1x 160 + 1; d can be calculated using the extended Euclid’s algorithm.




C=10
e=5
n=35
if n=35 ,p=7,q=5 O(n)=(7-1)(5-1)=24
ed= 1 mod O(n)=5*21=105 mod 24
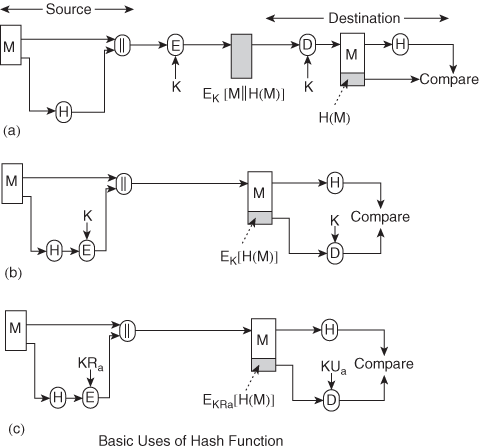
5. Write about the basic uses of MAC and list out the applications.
Ans: An alternative authentication technique involves the use of a secret key to generate a small fixed-size block of data, known as a cryptographic checksum or MAC that is appended to the message. This technique assumes that two communicating parties, say A and B, share a common secret key K. When A has a message to send to B, it calculates the MAC as a function of the message and the key:
MAC= C(K, M), where
M = input message
C = MAC function
K = shared secret key
MAC = message authentication code
The message plus MAC are transmitted to the intended recipient. The recipient performs the same calculation on the received message, using the same secret key, to generate a new MAC. The received MAC is compared to the calculated MAC .If we assume that only the receiver and the sender know the identity of the secret key, and if the received MAC matches the calculated MAC, then
1. The receiver is assured that the message has not been altered. If an attacker alters the message but does not alter the MAC, then the receiver’s calculation of the MAC will differ from the received MAC. Because the attacker is assumed not to know the secret key, the attacker cannot alter the MAC to correspond to the alterations in the message.
2. The receiver is assured that the message is from the alleged sender. Because no one else knows the secret key, no one else could prepare a message with a proper MAC.
3. If the message includes a sequence number (such as is used with HDLC, X.25, and TCP), then the receiver can be assured of the proper sequence because an attacker cannot successfully alter the sequence number.
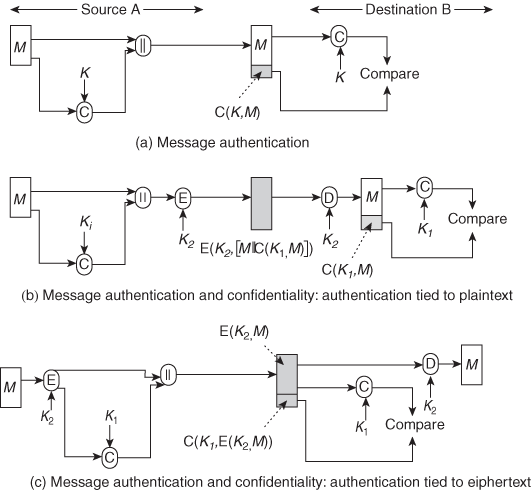
It suggests three situations in which a message authentication code is used:
- There are a number of applications in which the same message is broadcast to a number of destinations. It is cheaper and more reliable to have only one destination responsible for monitoring authenticity. Thus, the message must be broadcast in plaintext with an associated message authentication code. The responsible system has the secret key and performs authentication. If a violation occurs, the other destination systems are alerted by a general alarm.
- An exchange in which one side has a heavy load and cannot afford the time to decrypt all incoming messages. Authentication is carried out on a selective basis, messages being chosen at random for checking.
- Authentication of a computer program in plaintext is an attractive service. The computer program can be executed without having to decrypt it every time, which would be wasteful of processor resources. However, if a message authentication code were attached to the program, it could be checked whenever assurance was required of the integrity of the program.
Three other rationales may be added, as follows:
- For some applications, it may not be of concern to keep messages secret, but it is important to authenticate messages. An example is the Simple Network Management Protocol Version 3 (SNMPv3), which separates the functions of confidentiality and authentication. For this application, it is usually important for a managed system to authenticate incoming SNMP messages, particularly if the message contains a command to change parameters at the managed system. On the other hand, it may not be necessary to conceal the SNMP traffic.
- Separation of authentication and confidentiality functions affords architectural flexibility.
- A user may wish to prolong the period of protection beyond the time of reception and yet allow processing of message contents. With message encryption, the protection is lost when the message is decrypted, so the message is protected against fraudulent modifications only in transit but not within the target system.
- Finally, note that the MAC does not provide a digital signature because both sender and receiver share the same key.
- Provides authentication
Only A and B share K
(a) Message authentication
A B:E(K2, [M||C(K, M)])
B:E(K2, [M||C(K, M)])
Provides authentication
Only A and B share K1
Provides confidentiality
Only A and B share K2
(b) Message authentication and confidentiality: authentication tied to plaintext
A B:E(K2, M)||C(K1, E(K2, M))
B:E(K2, M)||C(K1, E(K2, M))
Provides authentication
Using K1
Provides confidentiality Using K2
(c) Message authentication and confidentiality: authentication tied to ciphertext
6. With a neat sketch, explain signing and verifying functions of DSA.
Ans: Message authentication protects two parties who exchange messages from any third party. However, it does not protect the two parties against each other.
Requirements for a digital signature:
- The signature must be a bit pattern that depends on the message being signed.
- The signature must use some information unique to the sender, to prevent both forgery and denial.
- It must be relatively easy to produce the digital signature.
- It must be relatively easy to recognize and verify the digital signature.
- It must be computationally infeasible to forge a digital signature, either by constructing a new message for an existing digital signature or by constructing a fraudulent digital signature for a given message.
- It must be practical to retain a copy of the digital signature in storage.
A variety of approaches has been proposed for the digital signature function. These approaches fall into two categories: direct and arbitrated.
Direct Digital Signature
- The direct digital signature involves only the communicating parties (source, destination).
- It is assumed that the destination knows the public key of the source.
- A digital signature may be formed by encrypting the entire message with the sender’s private key or by encrypting a hash code of the message with the sender’s private key
- Confidentiality can be provided by further encrypting the entire message plus signature with either the receiver’s public key (public-key encryption) or a shared secret key (symmetric encryption);
- It is important to perform the signature function first and then an outer confidentiality function.
- In case of dispute, some third party must view the message and its signature.
- If the signature is calculated on an encrypted message, then the third party also needs access to the decryption key to read the original message.
- However, if the signature is the inner operation, then the recipient can store the plaintext message and its signature for later use in dispute resolution.
Limitations:
- The validity of the scheme depends on the security of the sender’s private key.
- If a sender later wishes to deny sending a particular message, the sender can claim that the private key was lost or stolen and that someone else forged his or her signature.
- Administrative controls relating to the security of private keys can be employed to thwart or at least weaken this ploy, but the threat is still there, at least to some degree.
- One example is to require every signed message to include a timestamp (date and time) and to require prompt reporting of compromised keys to a central authority.
- Another threat is that some private key might actually be stolen from X at time T. The opponent can then send a message signed with X’s signature and stamped with a time before or equal to T.
Arbitrated Digital Signature
- The problems associated with direct digital signatures can be addressed by using an arbiter.
- Every signed message from a sender X to a receiver Y goes first to an arbiter A, who subjects the message and its signature to a number of tests to check its origin and content.
- The message is then dated and sent to Y with an indication that it has been verified to the satisfaction of the arbiter.
- The presence of A solves the problem faced by direct signature schemes: that X might disown the message.
- The arbiter plays a sensitive and crucial role in this sort of scheme, and all parties must have a great deal of trust that the arbitration mechanism is working properly.
- In the first, symmetric encryption is used. It is assumed that the sender X and the arbiter A share a secret key Kxa and that A and Y share secret key Kay.
- X constructs a message M and computes its hash value H(M).
- Then X transmits the message plus a signature to A.
- The signature consists of an identifier IDX of X plus the hash value, all encrypted using Kxa.
- A decrypts the signature and checks the hash value to validate the message.
- Then A transmits a message to Y, encrypted with Kay. The message includes IDX, the original message from X, the signature, and a timestamp.
- Y can decrypt this to recover the message and the signature.
- The timestamp informs Y that this message is timely and not a replay. Y can store M and the signature.
- In case of dispute, Y, who claims to have received M from X, sends the following message to A:
- The following format is used. A communication step in which P sends a messageM to Q is represented as P Q: M.
- E(Kay, [IDX||M||E(Kxa, [IDX||H(M)])])
Arbitrated Digital Signature Techniques
(a) Conventional Encryption, Arbiter Sees Message
(1) X A: M||E(Kxa,, [IDX||H(M)])
A: M||E(Kxa,, [IDX||H(M)])
(2) A Y: EKay, [IDX||M||E(Kxa,, [IDX||H(M)])||T])
Y: EKay, [IDX||M||E(Kxa,, [IDX||H(M)])||T])
(b) Conventional Encryption, Arbiter Does Not See Message
(1) X A: IDX||E(Kxy, M)||E(Kxa, [IDX||H(E(Kxy, M))])
A: IDX||E(Kxy, M)||E(Kxa, [IDX||H(E(Kxy, M))])
(2) A Y: EKay,[IDX||E(Kxy, M)])||E(Kxa, [IDX||H(E(Kxy, M))||T])
Y: EKay,[IDX||E(Kxy, M)])||E(Kxa, [IDX||H(E(Kxy, M))||T])
(c) Public-Key Encryption, Arbiter Does Not See Message
(1) X A: IDX||E(KRx, [IDX||E(PUy, E(KRx, M))])
A: IDX||E(KRx, [IDX||E(PUy, E(KRx, M))])
(2) A Y: EKRa, [IDX||E(PUy, E(PRx, M))||T])
Y: EKRa, [IDX||E(PUy, E(PRx, M))||T])
Notation:
X = sender
Y = recipient
A = Arbiter
M = message
T = timestamp
The arbiter uses Kay to recover IDX, M, and the signature, and then uses Kxa to decrypt the signature and verify the hash code.
In this scheme, Y cannot directly check X’s signature; the signature is there solely to settle disputes. Y considers the message from X authentic because it comes through A.
In this scenario, both sides must have a high degree of trust in A:
X must trust A not to reveal Kxa and not to generate false signatures of the form E(Kxa, [IDX||H(M)]). Y must trust A to send E(Kay, [IDX||M||E(Kxa, [IDX||H(M)])||T]) only if the hash value is correct and the signature was generated by X. Both sides must trust A to resolve disputes fairly.
If the arbiter does live up to this trust, then X is assured that no one can forge his signature and Y is assured that X cannot disavow his signature.
The preceding scenario also implies that A is able to read messages from X to Y and, indeed, that any eavesdropper is able to do so.
In fig B. shows a scenario that provides the arbitration as before but also assures confidentiality. In this case it is assumed that X and Y share the secret key Kxy. Now, X transmits an identifier, a copy of the message encrypted with K xy, and a signature to A. The signature consists of the identifier plus the hash value of the encrypted message, all encrypted using Kxa. As before, A decrypts the signature and checks the hash value to validate the message. In this case, A is working only with the encrypted version of the message and is prevented from reading it. A then transmits everything that it received from X, plus a timestamp, all encrypted with Kay, to Y.
7. Describe briefly about X.509 authentication procedures. And also list out the drawbacks of X.509 version 2.
Ans: X.509 is based on the use of public-key cryptography and digital signatures. The standard does not dictate the use of a specific algorithm but recommends RSA. The digital signature scheme is assumed to require the use of a hash function. Again, the standard does not dictate a specific hash algorithm.
Certificates
The heart of the X.509 scheme is the public-key certificate associated with each user. These user certificates are assumed to be created by some trusted certification authority (CA) and placed in the directory by the CA or by the user. The directory server itself is not responsible for the creation of public keys or for the certification function; it merely provides an easily accessible location for users to obtain certificates.
It shows the general format of a certificate, which includes the following elements:
Version: Differentiates among successive versions of the certificate format; the default is version 1. If the Issuer Unique Identifier or Subject Unique Identifier are present, the value must be version 2. If one or more extensions are present, the version must be version 3.
Serial number: An integer value, unique within the issuing CA, that is unambiguously associated with this certificate.
Signature algorithm identifier: The algorithm used to sign the certificate, together with any associated parameters. Because this information is repeated in the Signature field at the end of the certificate, this field has little, if any, utility.
Issuer name: X.500 name of the CA that created and signed this certificate.
Period of validity: Consists of two dates: the first and last on which the certificate is valid.
Subject name: The name of the user to whom this certificate refers. That is, this certificate certifies the public key of the subject who holds the corresponding private key.
Subject’s public-key information: The public key of the subject, plus an identifier of the algorithm for which this key is to be used, together with any associated parameters.
Issuer unique identifier: An optional bit string field used to identify uniquely the issuing CA in the event the X.500 name has been reused for different entities.
Subject unique identifier: An optional bit string field used to identify uniquely the subject in the event the X.500 name has been reused for different entities.
Extensions: A set of one or more extension fields. Extensions were added in version 3 .
Signature: Covers all of the other fields of the certificate; it contains the hash code of the other fields, encrypted with the CA’s private key. This field includes the signature algorithm identifier.
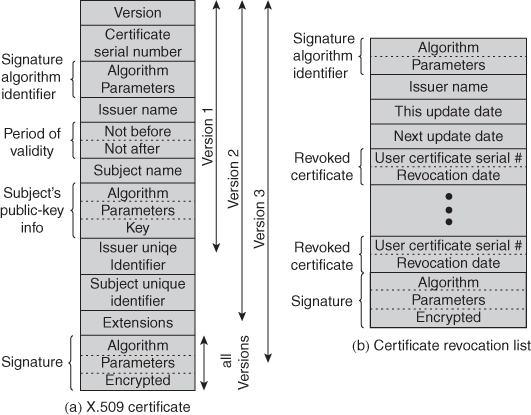
The unique identifier fields were added in version 2 to handle the possible reuse of subject and/or issuer names over time. These fields are rarely used.
The standard uses the following notation to define a certificate:
CA<<A>> = CA {V, SN, AI, CA, TA, A, Ap}
where
Y <<X>> = the certificate of user X issued by certification authority Y
Y {I} = the signing of I by Y. It consists of I with an encrypted hash code appended
The CA signs the certificate with its private key. If the corresponding public key is known to a user, then that user can verify that a certificate signed by the CA is valid.
Obtaining a User’s Certificate
User certificates generated by a CA have the following characteristics:
- Any user with access to the public key of the CA can verify the user public key that was certified.
- No party other than the certification authority can modify the certificate without this being detected.
- Because certificates are unforgeable, they can be placed in a directory without the need for the directory to make special efforts to protect them.
- If all users subscribe to the same CA, then there is a common trust of that CA. All user certificates can be placed in the directory for access by all users. In addition, a user can transmit his or her certificate directly to other users. In either case, once B is in possession of A’s certificate, B has confidence that messages it encrypts with A’s public key will be secure from eavesdropping and that messages signed with A’s private key are unforgeable.
- If there is a large community of users, it may not be practical for all users to subscribe to the same CA. Because it is the CA that signs certificates, each participating user must have a copy of the CA’s own public key to verify signatures. This public key must be provided to each user in an absolutely secure (with respect to integrity and authenticity) way so that the user has confidence in the associated certificates. Thus, with many users, it may be more practical for there to be a number of CAs, each of which securely provides its public key to some fraction of the users.
- Now suppose that A has obtained a certificate from certification authority X1 and B has obtained a certificate from CA X2. If A does not securely know the public key of X2, then B’s certificate, issued by X2, is useless to A. A can read B’s certificate, but A cannot verify the signature. However, if the two CAs have securely exchanged their own public keys, the following procedure will enable A to obtain B’s public key:
A obtains, from the directory, the certificate of X2 signed by X1. Because A securely knows X1’s public key, A can obtain X2’s public key from its certificate and verify it by means of X1’s signature on the certificate.
1. A then goes back to the directory and obtains the certificate of B signed by X2 Because A now has a trusted copy of X2’s public key, A can verify the signature and securely obtain B’s public key.
2. A has used a chain of certificates to obtain B’s public key. In the notation of X.509, this chain is expressed as
X1<<X2>> X2 <<B>>
In the same fashion, B can obtain A’s public key with the reverse chain:
X2<<X1>> X1 <<A>>
This scheme need not be limited to a chain of two certificates. An arbitrarily long path of CAs can be followed to produce a chain. A chain with N elements would be expressed as
X1<<X2>> X2 <<X3>>... XN<<B>>
In this case, each pair of CAs in the chain (Xi, Xi+1) must have created certificates for each other. All these certificates of CAs by CAs need to appear in the directory, and the user needs to know how they are linked to follow a path to another user’s public-key certificate. X.509 suggests that CAs be arranged in a hierarchy so that navigation is straightforward.
CAs; the associated boxes indicate certificates maintained in the directory for each CA entry. The directory entry for each CA includes two types of certificates:
Forward certificates: Certificates of X generated by other CAs
Reverse certificates: Certificates generated by X that are the certificates of other CAs
Revocation of Certificates
Each certificate includes a period of validity, much like a credit card. Typically, a new certificate is issued just before the expiration of the old one. In addition, it may be desirable on occasion to revoke a certificate before it expires, for one of the following reasons:
1. The user’s private key is assumed to be compromised.
2. The user is no longer certified by this CA.
3. The CA’s certificate is assumed to be compromised.
Each CA must maintain a list consisting of all revoked but not expired certificates issued by that CA, including both those issued to users and to other CAs. These lists should also be posted on the directory.
Each certificate revocation list (CRL) posted to the directory is signed by the issuer and includes the issuer’s name, the date the list was created, the date the next CRL is scheduled to be issued, and an entry for each revoked certificate. Each entry consists of the serial number of a certificate and revocation date for that certificate. Because serial numbers are unique within a CA, the serial number is sufficient to identify the certificate.
When a user receives a certificate in a message, the user must determine whether the certificate has been revoked. The user could check the directory each time a certificate is received.
8. Write about SSL and TLS.
Ans: SSL (Secure Socket Layer):
- transport layer security service
- originally developed by Netscape
- version 3 designed with public input
- subsequently became Internet standard known as TLS (Transport Layer Security)
- uses TCP to provide a reliable end-to-end service
- SSL has two layers of protocols
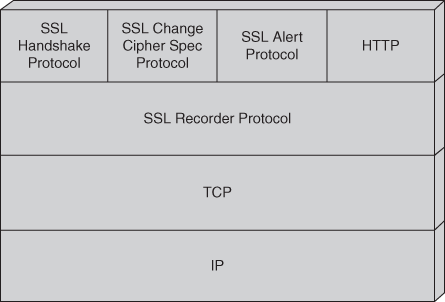
SSL connection
- a transient, peer-to-peer, communications link
- associated with 1 SSL session
SSL session
- an association between client & server
- created by the Handshake Protocol
- define a set of cryptographic parameters
- may be shared by multiple SSL connections
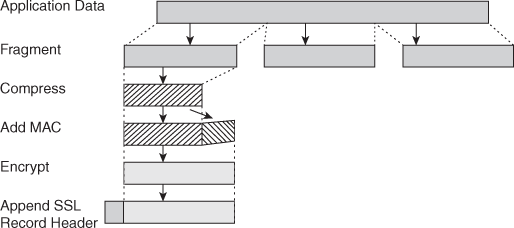
SSL Record Protocol Services:
- message integrity
- using a MAC with shared secret key
- similar to HMAC but with different padding
- confidentiality
- using symmetric encryption with a shared secret key defined by Handshake Protocol
• AES, IDEA, RC2-40, DES-40, DES, 3DES, Fortezza, RC4-40, RC4-128
• message is compressed before encryption
SSL Record Protocol Operation:
SSL Change Cipher Spec Protocol:
- one of 3 SSL specific protocols which use the SSL Record protocol
- a single message
- causes pending state to become current
- hence updating the cipher suite in use
SSL Alert Protocol:
- conveys SSL-related alerts to peer entity
- severity
- warning or fatal
- specific alert
- fatal: unexpected message, bad record mac, decompression failure, handshake failure, illegal parameter
- warning: close notify, no certificate, bad certificate, unsupported certificate, certificate revoked, certificate expired, certificate unknown
- compressed & encrypted like all SSL data
SSL Handshake Protocol:
- allows server & client to:
- authenticate each other
- to negotiate encryption & MAC algorithms
- to negotiate cryptographic keys to be used
- comprises a series of messages in phases
- Establish Security Capabilities
- Server Authentication and Key Exchange
- Client Authentication and Key Exchange
- Finish
Phase 1. Establish Security Capabilities
This phase is used to initiate a logical connection and to establish the security capabilities that will be associated with it. The exchange is initiated by the client, which sends a client_hello message with the following parameters:
Version: The highest SSL version understood by the client.
Random: A client-generated random structure, consisting of a 32-bit timestamp and 28 bytes generated by a secure random number generator. These values serve as nonces and are used during key exchange to prevent replay attacks.
Session ID: A variable-length session identifier. A nonzero value indicates that the client wishes to update the parameters of an existing connection or create a new connection on this session. A zero value indicates that the client wishes to establish a new connection on a new session.
CipherSuite: This is a list that contains the combinations of cryptographic algorithms supported by the client, in decreasing order of preference. Each element of the list (each cipher suite) defines both a key exchange algorithm and a CipherSpec;
Compression Method: This is a list of the compression methods the client supports.
Phase 2. Server Authentication and Key Exchange
The server begins this phase by sending its certificate, if it needs to be authenticated; the message contains one or a chain of X.509 certificates. The certificate message is required for any agreed-on key exchange method except anonymous Diffie-Hellman. If fixed Diffie-Hellman is used, this certificate message functions as the server’s key exchange message because it contains the server’s public Diffie-Hellman parameters. Next, a server_key_exchange message may be sent if it is required. It is not required in two instances:
(1) The server has sent a certificate with fixed Diffie-Hellman parameters, or
(2) RSA key exchange is to be used.
Phase 3. Client Authentication and Key Exchange
Upon receipt of the server_done message, the client should verify that the server provided a valid certificate if required and check that the server_hello parameters are acceptable. If all is satisfactory, the client sends one or more messages back to the server. If the server has requested a certificate, the client begins this phase by sending a certificate message. If no suitable certificate is available, the client sends a no_certificate alert instead. Next is the client_key_exchange message, which must be sent in this phase.
The content of the message depends on the type of key exchange, as follows:
RSA: The client generates a 48-byte pre-master secret and encrypts with the public key from the server’s certificate or temporary RSA key from a server_key_exchange message. Its use to compute a master secret.
Ephemeral or Anonymous Diffie-Hellman: The client’s public Diffie-Hellman parameters are sent.
Fixed Diffie-Hellman: The client’s public Diffie-Hellman parameters were sent in a certificate message, so the content of this message is null.
Fortezza: The client’s Fortezza parameters are sent.
Finally, in this phase, the client may send a certificate_verify message to provide explicit verification of a client certificate. This message is only sent following any client certificate that has signing capability (i.e., all certificates except those containing fixed Diffie-Hellman parameters).
Phase 4. Finish
This phase completes the setting up of a secure connection. The client sends a change_cipher_spec message and copies the pending CipherSpec into the current CipherSpec. Note that this message is not considered part of the Handshake Protocol but is sent using the Change Cipher Spec Protocol. The client then immediately sends the finished message under the new algorithms, keys, and secrets. The finished message verifies that the key exchange and authentication processes were successful.

9. Explain about intrusion detection techniques in detail.
Ans: Intrusion detection system can be broadly classified based on two parameters .
(a) Analysis method used to identify intrusion, which is classified into Misuse IDS and Anomaly IDS.
(b) Source of data that is used in the analysis method, which is classified into Host, based IDS and Network based IDS
2.1. Misuse IDS
Misuse based IDS is a very prominent system and is widely used in industries. Most of the organizations that develop anti-virus solutions base their design methodology on Misuse IDS. The system is constructed based on the signature of all-known attacks. Rules and signatures define abnormal and unsafe behavior. It analyzes the traffic flow over a network and matches against known signatures. Once a known signature is encountered the IDS triggers an alarm. With the advancement in latest technologies, the number of signatures also increase. This demands for constant upgrade and modification of new attack signatures from the vendors and paying more to vendors for their support [6].
- The advantages of this model are easy creation of attack signature databases, faster and easier implementation of IDS and minimal usage of the system resources.
- The main weakness of the traditional and established rule based techniques is that rule based detection is highly dependent on the audit results.
- This one-to-one correspondence between rules and audit records makes the system inflexible. For example, given a particular penetration scenario, the audit results may vary in the sequences of events. This results in variations in the detection outcome.
- This may lead to large number of false positives (Section 3) and in some cases, false negatives too.
- The inability to predict a mishap and take preemptive action. The rule-based technique only helps in prevention of an intrusion when the details and patterns of it are available.
- Rules are framed when a set of administrators are interviewed, different observed penetrations are recorded, rules are set to those penetration scenarios based on the expected outcomes from the analysis of audit records. Therefore, updating of rules is expensive in terms of time and money.
2.2. Anomaly IDS
Anomaly IDS is built by studying the behavior of the system over a period of time in order to construct activity profiles that represent normal use of the system. The anomaly IDS computes the similarity of the traffic in the system with the profiles to detect intrusions. The biggest advantage of this model is that new attacks can be identified by the system as it will be a deviation from normal behavior.
The drawbacks of this model are summarized
(a) There is no defined process or model available to select the threshold value against which the profile is compared.
(b) They are computationally expensive because the profiles have to be constantly updated and compared against.
(c) User behaviors generally vary with time and hence the model must provide a provision to revise and update it.
2.3. Host Based IDS
When the source of data for IDS comes from a single host (System), then it is classified as Host based IDS. They are generally used to monitor user activity and useful to track IDS intrusions caused when an authorized user tries to access confidential information.
2.4. Network Based IDS
The source of data for these type of IDS is obtained by listening to all nodes in a network. Attacks from illegitimate user can be identified using a network based IDS. Commercial IDSs are always a combination of the two types mentioned above. The possible kinds of IDS are host based misuse IDS, network based misuse IDS, host based anomaly IDS and network based anomaly IDS. However, with greater interest and research in this field, new models are being developed such as Network Security monitor.
10. Write about trusted systems in detail.
Ans: One way to enhance the ability of a system to defend against intruders and malicious programs is to implement trusted system technology
Data Access Control
Following successful logon, the user has been granted access to one or a set of hosts and applications. This is generally not sufficient for a system that includes sensitive data in its database. Through the user access control procedure, a user can be identified to the system. Associated with each user, there can be a profile that specifies permissible operations and file accesses. The operating system can then enforce rules based on the user profile. The database management system, however, must control access to specific records or even portions of records. For example, it may be permissible for anyone in administration to obtain a list of company personnel, but only selected individuals may have access to salary information. The issue is more than just one of level of detail. Whereas the operating system may grant a user permission to access a file or use an application, following which there are no further security checks, the database management system must make a decision on each individual access attempt. That decision will depend not only on the user’s identity but also on the specific parts of the data being accessed and even on the information already divulged to the user.
A general model of access control as exercised by a file or database management system is that of an access matrix
The basic elements of the model are as follows:
Subject: An entity capable of accessing objects. Generally, the concept of subject equates with that of process. Any user or application actually gains access to an object by means of a process that represents that user or application.
Object: Anything to which access is controlled. Examples include files, portions of files, programs, and segments of memory.
Access right: The way in which an object is accessed by a subject. Examples are read, write, and execute.
When multiple categories or levels of data are defined, the requirement is referred to as multilevel security. The general statement of the requirement for multilevel security is that a subject at a high level may not convey information to a subject at a lower or noncomparable level unless that flow accurately reflects the will of an authorized user. For implementation purposes, this requirement is in two parts and is simply stated. A multilevel secure system must enforce the following:
No read up: A subject can only read an object of less or equal security level. This is referred to in the literature as th SimpleSecurity Property.
No write down: A subject can only write into an object of greater or equal security level. This is referred to in the literature as the *-Property
[1] The “*” does not stand for anything. No one could think of an appropriate name for the property during the writing of the first report on the model. The asterisk was a dummy character entered in the draft so that a text editor could rapidly find and replace all instances of its use once the property was named. No name was ever devised, and so the report was published with the “*” intact.
These two rules, if properly enforced, provide multilevel security. For a data processing system, the approach that has been taken, and has been the object of much research and development, is based on the reference monitor concept.
The reference monitor is a controlling element in the hardware and operating system of a computer that regulates the access of subjects to objects on the basis of security parameters of the subject and object. The reference monitor has access to a file, known as the security kernel database, that lists the access privileges (security clearance) of each subject and the protection attributes (classification level) of each object. The reference monitor enforces the security rules (no read up, no write down) and has the following properties:
Complete mediation: The security rules are enforced on every access, not just, for example, when a file is opened.
Isolation: The reference monitor and database are protected from unauthorized modification.
Verifiability: The reference monitor’s correctness must be provable. That is, it must be possible to demonstrate mathematically that the reference monitor enforces the security rules and provides complete mediation and isolation.
These are stiff requirements. The requirement for complete mediation means that every access to data within main memory and on disk and tape must be mediated. Pure software implementations impose too high a performance penalty to be practical; the solution must be at least partly in hardware. The requirement for isolation means that it must not be possible for an attacker, no matter how clever, to change the logic of the reference monitor or the contents of the security kernel database. Finally, the requirement for mathematical proof is formidable for something as complex as a general-purpose computer. A system that can provide such verification is referred to as a trusted system.
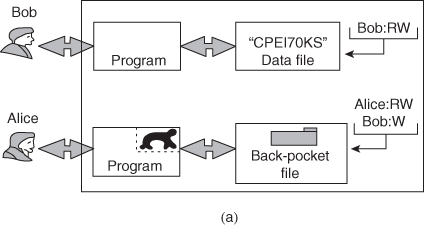
Trojan Horse Defense
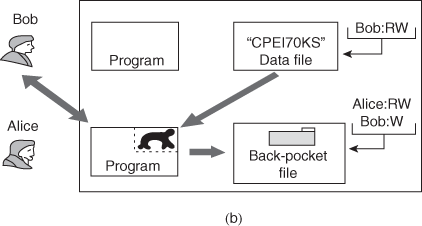
One way to secure against Trojan horse attacks is the use of a secure, trusted operating system. Figure illustrates an example. In this case, a Trojan horse is used to get around the standard security mechanism used by most file management and operating systems: the access control list. In this example, a user named Bob interacts through a program with a data file containing the critically sensitive character string “CPE170KS.” User Bob has created the file with read/write permission provided only to programs executing on his own behalf: that is, only processes that are owned by Bob may access the file.
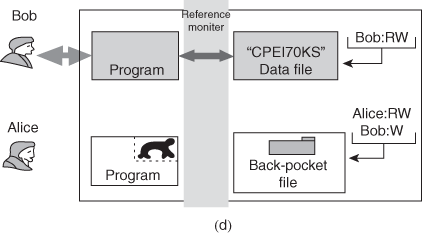
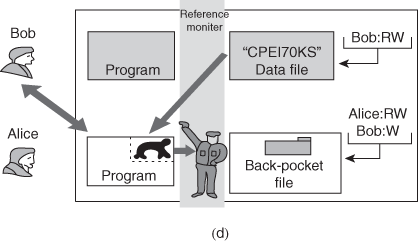
The Trojan horse attack begins when a hostile user, named Alice, gains legitimate access to the system and installs both a Trojan horse program and a private file to be used in the attack as a “back pocket.” Alice givesread/write permission to herself for this file and gives Bob write-only permission .Alice now induces Bob to invoke the Trojan horse program, perhaps by advertising it as a useful utility. When the program detects that it is being executed by Bob, it reads the sensitive character string from Bob’s file and copies it into Alice’s back-pocket file (Figure). Both the read and write operations satisfy the constraints imposed by access control lists. Alice then has only to access Bob’s file at a later time to learn the value of the string. Now consider the use of a secure operating system in this scenario .Security levels are assigned to subjects at logon on the basis of criteria such as the terminal from which the computer is being accessed and the user involved, as identified by password/ID. In this example, there are two security levels, sensitive and public, ordered so that sensitive is higher than public. Processes owned by Bob and Bob’s data file are assigned the security level sensitive. Alice’s file and processes are restricted to public. If Bob invokes the Trojan horse program , that program acquires Bob’s security level. It is therefore able, under the simple security property, to observe the sensitive character string. When the program attempts to store the string in a public file (the back-pocket file), however, the is violated and the attempt is disallowed by the reference monitor. Thus, the attempt to write into the back-pocket file is denied even though the access control list permits it: The security policy takes precedence over the access control list mechanism.
11. Explain the Key Generation, Encryption and Decryption of SDES algorithm in detail.
Ans: Simplified DES
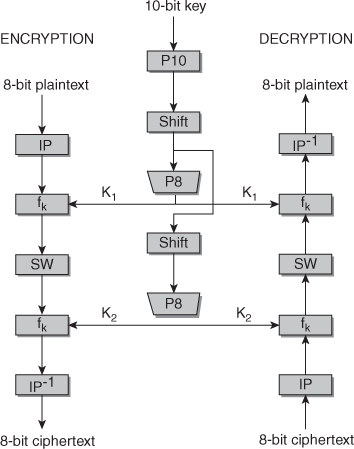
S-DES encryption (decryption) algorithm takes 8-bit block of plaintext (ciphertext) and a 10-bit key, and produces 8-bit ciphertext (plaintext) block. Encryption algorithm involves 5 functions: an initial permutation (IP); a complex function fK, which involves both permutation and substitution and depends on a key input; a simple permutation function that switches (SW) the 2 halves of the data; the function fK again; and finally, a permutation function that is the inverse of the initial permutation (IP-1). Decryption process is similar.
The function fK takes 8-bit key which is obtained from the 10-bit initial one two times. The key is first subjected to a permutation P10. Then a shift operation is performed. The output of the shift operation then passes through a permutation function that produces an 8-bit output (P8) for the first subkey (K1). The output of the shift operation also feeds into another shift and another instance of P8 to produce the 2nd subkey K2.
We can express encryption algorithm as superposition:
Ciphertext= IP-1 (fk2.SW.fk1.IP) or IP-1(fk2 (SW (fk1 (IP(plaintext))))
Where
k1=P8(shift(P10(key)))
k2= P8(shift(shift(P10(key)))
Decryption is the reverse of encryption:
Plaintext= (IP-1(fk1 (SW (fk2 (IP(ciphertext))))
S-DES key generation
Scheme of key generation:
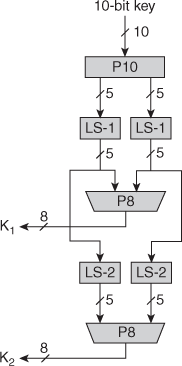
Figure Key Generation for Simplified DES
First, permute the 10-bit key k1,k2,..,k10:
P10(k1,k2,k3,k4,k5,k6,k7,k8,k9,k10)=(k3,k5,k2,k7,k4,k10,k1,k9,k8,k6)
Or it may be represented in such a form

Each position in this table gives the identity of the input bit that produces the output bit in this position. So, the 1st output bit is bit 3 (k3), the 2nd is k5 and so on. For example, the key (1010000010) is permuted to (1000001100).
Next, perform a circular shift (LS-1), or rotation, separately on the 1st 5 bits and the 2nd 5 bits. In our example, the result is (00001 11000)
Next, we apply P8, which picks out and permutes 8 out of 10 bits according to the following rule:

The result is subkey K1. In our example, this yields (10100100)
We then go back to the pair of 5-bit strings produced by the 2 LS-1 functions and perform a circular left shift of 2 bit positions on each string. In our example, the value (00001 11000) becomes (00100 00011). Finally, P8 is applied again to produce K2. In our example, the result is (01000011)
S-DES encryption

Simplified-DES encryption Detail
The input to the algorithm is an 8-bit block of plaintext, which is permuted by IP function:

At the end of the algorithm, the inverse permutation is used:
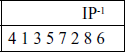
It may be verified, that IP-1(IP(X)) = X.
The most complex component of S-DES is the function fK, which consists of a combination of permutation and substitution functions. The function can be expressed as follows. Let L and R be the leftmost 4 bits and rightmost 4 bits of the 8-bit input to fK, and let F be a mapping (not necessarily one to one) from 4-bit strings to 4-bit strings. Then we let fK(L,R) = (L⊕F(R,SK),R)
where SK is a subkey and ⊕ is the bit-by-bit XOR operation. For example, suppose the output of the IP stage in Fig.3.3 is (1011 1101) and F(1101,SK) = (1110) for some key SK. Then fK(1011 1101) = (0101 1101) because (1011) ⊕ (1110) = (0101).
We now describe the mapping F. The input is a 4-bit number (n1 n2 n3 n4). The 1st operation is an expansion/permutation:
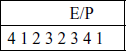
For what follows, it is clearer to depict result in this fashion:
n4|n1 n2|n3
n2|n3 n4|n1
The 8-bit subkey K1 = (k11, k12, k13, k14, k15, k16, k17, k18) is added to this value using XOR:
4+k11|n1+k12 n2+k13|n3+k14
n2+k15|n3+k16 n4+k17|n1+k18
Let us rename these bits:
p00|p01 p02|p03
p10|p11 p12|p13
The 1st 4 bits (1st row of the preceding matrix) are fed into the S-box S0 to produce a 2-bit output, and the remaining 4 bits (2nd row) are fed into S1 to produce another 2-bit output. These 2 boxes are defined as follows:
0 12 3 0 12 3
The S-boxes operate as follows. The 1st and 4th input bits are treated as a 2-bit number that specify a row of the S-box, and the 2nd and 3rd input bits specify a column of the S-box. The entry in that row and column, in base 2, is the 2-bit output. For example, if (p00, p03) = (00) and (p01, p02) = (10), then the output is from row 0, column 2 of S0, which is 3, or (11) in binary. Similarly, (p10, p13) and (p11, p12) are used to index into a row and column of S1 to produce an additional 2 bits.
Next, the 4 bits produced by S0 and S1 undergo a further permutation as follows:

The output of P4 is the output of function F.
The function fK only alters the leftmost 4 bits of input.
The switch function SW interchanges the left and right bits so that the 2nd instance of fK operates on a different 4 bits. In the 2nd instance, the E/P, S0, S1, and P4 functions are the same. The key input is K2.
Analysis of simplified DES
A brute-force attack on S-DES is feasible since with a 10-bit key there are only 1024 possibilities.
What about cryptanalysis? If we know plaintext (p1p2p3p4p5p6p7p8) and respective ciphertext (c1c2c3c4c5c6c7c8), and key (k1k2k3k4k5k6k7k8k9k10) is unknown, then we can express this problem as a system of 8 nonlinear equations with 10 unknowns. The nonlinearity comes from the S-boxes. It is useful to write down equations for these boxes. For clarity, rename (p00,p01,p02,p03)=(a,b,c,d) and (p10,p11,p12,p13)=(w,x,y,z). Then the operation of S0 is defined in the following equations:
q=abcd+ab+ac+b+d
r=abcd+abd+ab+ac+ad+a+c+1
where all additions are made modulo 2. Similar equations define S1.
12. Write the algorithm of RSA and explain with an example.
Ans: Diffie and Hellman introduced a new approach to cryptography and, in effect, challenged cryptologists to come up with a cryptographic algorithm that met the requirements for public-key systems. One of the first of the responses to the challenge was developed in 1977 by Ron Rivest, Adi Shamir, and Len Adleman at MIT .
The RSA scheme is a block cipher in which the plaintext and ciphertext are integers between 0 and n 1 for some n. A typical size for n is 1024 bits, or 309 decimal digits. That is, n is less than 21024.
Description of the Algorithm
The scheme developed by Rivest, Shamir, and Adleman makes use of an expression with exponentials. Plaintext is encrypted in blocks, with each block having a binary value less than some number n. That is, the block size must be less than or equal to log2(n); in practice, the block size is i bits, where 2 I ≤ n 2 i+1. Encryption and decryption are of the following form, for some plaintext block M and ciphertext block C:
C = Memod n
M = Cdmod n = (Me)dmod n = Medmod n
Both sender and receiver must know the value of n. The sender knows the value of e, and only the receiver knows the value of d. Thus, this is a public-key encryption algorithm with a public key of PU = {e, n} and a private key of PU = {d, n}. For this algorithm to be satisfactory for public-key encryption, the following requirements must be met:
1. It is possible to find values of e, d, n such that M ed mod n = M for all M < n.
2. It is relatively easy to calculate mod Memod n and Cdmod n . for all values of M < n.
3. It is infeasible to determine d given e and n. For now, we focus on the first requirement and consider the other questions later. We need to find a relationship of the form Medmod n = M
4. if e and d are multiplicative inverses modulo f(n), where f(n) is the Euler totient function. It is shown in that for p, q prime, f(pq) = (p- 1)(q- 1) The relationship between e and d can be expressed as
1. Select two prime numbers, p = 17 and q = 11.
2. Calculate n = pq = 17 x 11 = 187.
3. Calculate f(n) = (p -1)(q- 1) = 16 x 10 = 160.
4. Select e such that e is relatively prime to f(n) = 160 and less than f(n) we choose e = 7.
Determine d such that de 1 (mod 160) and d < 160. The correct value is d = 23, because 23 x 7 = 161 = 10 x 160 + 1; d can be calculated using the extended Euclid’s algorithm.

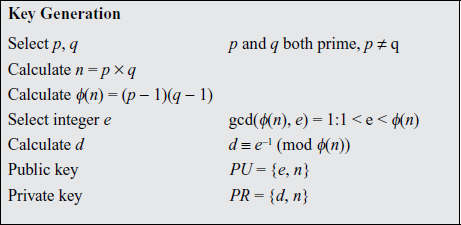


The resulting keys are public key PU = {7,187} and private key PR = {23,187}. The example shows the use of these keys for a plaintext input of M = 88. For encryption, we need to calculate C = 887 mod 187
887 mod 187 = [(884 mod 187) x (88 2 mod 187) x (88 1 mod 187)] mod 187
88 1 mod 187 = 88
88 2mod 187 = 7744 mod 187 = 77
884mod 187 = 59,969,536 mod 187 = 132
887 mod 187 = (88 x 77 x 132) mod 187 = 894,432 mod 187 = 11
For decryption, we calculate M = 1123mod 187:
1123 mod 187 = [(111mod 187) x (112 mod 187) x (114 mod 187) x (118mod 187) x (118mod 187)] mod 187
111mod 187 = 11
112mod 187 = 121
114mod 187 = 14,641 mod 187 = 55
118mod 187 = 214,358,881 mod 187 = 33
1123 mod 187 = (11 x 121 x 55 x 33 x 33) mod 187 = 79,720,245 mod 187 = 88mod 187.
13. Illustrate about the SHA algorithm and explain.
Ans: SHA-1
•SHA was designed by NIST & NSA in 1993, revised 1995 as SHA-1
•US standard for use with DSA signature scheme
o standard is FIPS 180-1 1995, also Internet RFC3174
o note: the algorithm is SHA, the standard is SHS
o produces 160-bit hash values
o now the generally preferred hash algorithm
o based on design of MD4 with key differences
SHA Overview
1. pad message so its length is 448 mod 512
2. append a 64-bit length value to message
3. initialise 5-word (160-bit) buffer (A,B,C,D,E) to (67452301,efcdab89,98badcfe,10325476,c3d2e1f0)
1. process message in 16-word (512-bit) chunks:
•expand 16 words into 80 words by mixing & shifting
•use 4 rounds of 20 bit operations on message block & buffer
•add output to input to form new buffer value
2. output hash value is the final buffer value
3. each round has 20 steps which replaces the 5 buffer words thus:
4. (A,B,C,D,E) <-(E+f(t,B,C,D)+(A<<5)+Wt+Kt),A,(B<<30),C,D)
5. a,b,c,d,e refer to the 5 words of the buffer
6. t is the step number
7. f(t,B,C,D) is nonlinear function for round
8. Wt is derived from the message block
9. Kt is a constant value derived from sin
SHA-1 compression function
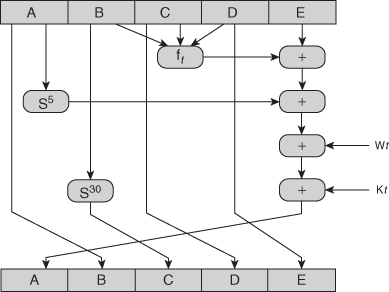
SHA1 vs MD 5
• brute force attack is harder (160 vs 128 bits for MD5)
• not vulnerable to any known attacks (compared to MD4/5)
• a little slower than MD5 (80 vs 64 steps)
• both designed as simple and compact
• optimised for big endian CPU’s (vs MD5 which is optimised for little endian CPU’s)
14. List out the participants of SET system, and explain in detail.
Ans: SET is an open encryption and security specification designed to protect credit card transactions on the internet. SET is not itself payment system.
Services provided are
*Provides secure communication channel among all parties involved in a transaction.
* provided trust by the use of x.509v3 digital certificates.
*Ensures privacy because the information available to parties in a transaction when and where necessary.
Requirements:
- Provide confidentiality of payment and ordering information
- Ensure the integrity of all transmitted data
- Provide authentication that a cardholder is a legitimate user of a credit card account:
- Provide authentication that a merchant can accept credit card transactions through its relationship with a financial institution:
- Ensure the use of the best security practices and system design techniques to protect all legitimate parties in an electronic commerce transaction
- Create a protocol that neither depends on transport security mechanisms nor prevents their use:
- Facilitate and encourage interoperability among software and network providers
Key features of SET:
- Confidentiality of information: Cardholder account and payment information is secured as it travels across the network. An interesting and important feature of SET is that it prevents the merchant from learning the cardholder’s credit card number; this is only provided to the issuing bank. Conventional encryption by DES is used to provide confidentiality.
- Integrity of data: Payment information sent from cardholders to merchants includes order information, personal data, and payment instructions. SET guarantees that these message contents are not altered in transit. RSA digital signatures, using SHA-1 hash codes, provide message integrity. Certain messages are also protected by HMAC using SHA-1.
- Cardholder account authenticationCardholder account authentication: SET enables merchants to verify that a cardholder is a legitimate user of a valid card account number. SET uses X.509v3 digital certificates with RSA signatures for this purpose
Participants of SET system
Merchant authentication: SET enables cardholders to verify that a merchant has a relationship with a financial institution
- Cardholder: In the electronic environment, consumers and corporate purchasers interact with merchants from personal computers over the Internet. A cardholder is an authorized holder of a payment card (e.g., MasterCard, Visa) that has been issued by an issuer.
- Merchant: A merchant is a person or organization that has goods or services to sell to the cardholder. Typically, these goods and services are offered via a Web site or by electronic mail. A merchant that accepts payment cards must have a relationship with an acquirer.
- Issuer: This is a financial institution, such as a bank, that provides the cardholder with the payment card. Typically, accounts are applied for and opened by mail or in person. Ultimately, it is the issuer that is responsible for the payment of the debt of the cardholder.
- Acquirer: This is a financial institution that establishes an account with a merchant and processes payment card authorizations and payments. Merchants will usually accept more than one credit card brand but do not want to deal with multiple bankcard associations or with multiple individual issuers. The acquirer provides authorization to the merchant that a given card account is active and that the proposed purchase does not exceed the credit limit. The acquirer also provides electronic transfer of payments to the merchant’s account. subsequently, the acquirer is reimbursed by the issuer over some sort of payment network for electronic funds transfer.
- Payment gateway: This is a function operated by the acquirer or a designated third party that processes merchant payment messages. The payment gateway interfaces between SET and the existing bankcard payment networks for authorization and payment functions. The merchant exchanges SET messages with the payment gateway over the Internet, while the payment gateway has some direct or network connection to the acquirer’s financial processing system.
- Certification authority (CA): This is an entity that is trusted to issue X.509v3 public-key certificates for cardholders, merchants, and payment gateways. The success of SET will depend on the existence of a CA infrastructure available for this purpose
15. Explain the different types of firewall and its configurations in detail.
Ans: Types of Firewalls
There are three common types of firewalls: packet filters, application-level gateways, and circuit-level gateways

Packet-Filtering Router
A packet-filtering router applies a set of rules to each incoming and outgoing IP packet and then forwards or discards the packet. The router is typically configured to filter packets going in both directions (from and to the internal network). Filtering rules are based on information contained in a network packet:
- Source IP address: The IP address of the system that originated the IP packet (e.g., 192.178.1.1)
- Destination IP address: The IP address of the system the IP packet is trying to reach (e.g., 192.168.1.2)
- Source and destination transport-level address: The transport level (e.g., TCP or UDP) port number, which defines applications such as SNMP or TELNET
- IP protocol field: Defines the transport protocol
- Interface: For a router with three or more ports, which interface of the router the packet came from or which interface of the router the packet is destined for
The packet filter is typically set up as a list of rules based on matches to fields in the IP or TCP header. If there is a match to one of the rules, that rule is invoked to determine whether to forward or discard the packet. If there is no match to any rule, then a default action is taken.
ADVANTAGE:
One advantage of a packet-filtering router is its simplicity. Also, packet filters typically are transparent to users and are very fast.
Weaknesses of packet filter firewalls:
- Because packet filter firewalls do not examine upper-layer data, they cannot prevent attacks that employ application-specific vulnerabilities or functions. For example, a packet filter firewall cannot block specific application commands; if a packet filter firewall allows a given application, all functions available within that application will be permitted.
- Because of the limited information available to the firewall, the logging functionality present in packet filter firewalls is limited.
- Packet filter logs normally contain the same information used to make access control decisions (source address, destination address, and traffic type).
- Most packet filter firewalls do not support advanced user authentication schemes. Once again, this limitation is mostly due to the lack of upper-layer functionality by the firewall.
- They are generally vulnerable to attacks and exploits that take advantage of problems within the TCP/IP specification and protocol stack, such as network layer address spoofing. Many packet filter firewalls cannot detect a network packet in which the OSI Layer 3 addressing information has been altered. Spoofing attacks are generally employed by intruders to bypass the security controls implemented in a firewall platform.
- Finally, due to the small number of variables used in access control decisions, packet filter firewalls are susceptible to security breaches caused by improper configurations. In other words, it is easy to accidentally configure a packet filter firewall to allow traffic types, sources, and destinations that should be denied based on an organization’s information security policy.
- Some of the attacks that can be made on packet-filtering routers and the appropriate countermeasures are the following:
IP address spoofing: The intruder transmits packets from the outside with a source IP address field containing an address of an internal host. The attacker hopes that the use of a spoofed address will allow penetration of systems that employ simple source address security, in which packets from specific trusted internal hosts are accepted. The countermeasure is to discard packets with an inside source address if the packet arrives on an external interface.
Source routing attacks: The source station specifies the route that a packet should take as it crosses the Internet, in the
hopes that this will bypass security measures that do not analyze the source routing information. The countermeasure is to
discard all packets that use this option.
Tiny fragment attacks:
- The intruder uses the IP fragmentation option to create extremely small fragments and force the TCP header information into a separate packet fragment.
- This attack is designed to circumvent filtering rules that depend on TCP header information.
- Typically, a packet filter will make a filtering decision on the first fragment of a packet.
- All subsequent fragments of that packet are filtered out solely on the basis that they are part of the packet whose first fragment was rejected.
- If the first fragment is rejected, the filter can remember the packet and discard all subsequent fragments.
Stateful Inspection Firewalls
- A traditional packet filter makes filtering decisions on an individual packet basis and does not take into consideration any higher layer context.
- For example, for the Simple Mail Transfer Protocol (SMTP), e-mail is transmitted from a client system to a server system.
- The client system generates new e-mail messages, typically from user input. The server system accepts incoming e-mail messages and places them in the appropriate user mailboxes.
- SMTP operates by setting up a TCP connection between client and server, in which the TCP server port number, which identifies the SMTP server application, is 25. T
- The TCP port number for the SMTP client is a number between 1024 and 65535 that is generated by the SMTP client.
- In general, when an application that uses TCP creates a session with a remote host, it creates a TCP connection in which the TCP port number for the remote (server) application is a number less than 1024 and the TCP port number for the local (client) application is a number between 1024 and 65535.
- The numbers less than 1024 are the “well-known” port numbers and are assigned permanently to particular applications (e.g., 25 for server SMTP). T
- The numbers between 1024 and 65535 are generated dynamically and have temporary significance only for the lifetime of a TCP connection.
- A simple packet-filtering firewall must permit inbound network traffic on all these high-numbered ports for TCP-based traffic to occur.
- A stateful inspection packet filter tightens up the rules for TCP traffic by creating a directory of outbound TCP connections.
- There is an entry for each currently established connection.
- The packet filter will now allow incoming traffic to high-numbered ports only for those packets that fit the profile of one of the entries in this directory.
Application-Level Gateway
- An application-level gateway, also called a proxy server, acts as a relay of application-level traffic.
- The user contacts the gateway using a TCP/IP application, such as Telnet or FTP, and the gateway asks the user for the name of the remote host to be accessed.
- When the user responds and provides a valid user ID and authentication information, the gateway contacts the application on the remote host and relays TCP segments containing the application data between the two endpoints.
- If the gateway does not implement the proxy code for a specific application, the service is not supported and cannot be forwarded across the firewall.
- Further, the gateway can be configured to support only specific features of an application that the network administrator considers acceptable while denying all other features.
Advantage
- Application-level gateways tend to be more secure than packet filters.
- Rather than trying to deal with the numerous possible combinations that are to be allowed and forbidden at the TCP and IP level, the application-level gateway need only scrutinize a few allowable applications.
- In addition, it is easy to log and audit all incoming traffic at the application level.
A prime disadvantage
- Additional processing overhead on each connection.
- In effect, there are two spliced connections between the end users, with the gateway at the splice point, and the gateway must examine and forward all traffic in both directions.
Circuit-Level Gateway
- A third type of firewall is the circuit-level gateway.
- This can be a stand-alone system or it can be a specialized function performed by an application-level gateway for certain applications.
- A circuit-level gateway does not permit an end-to-end TCP connection; rather, the gateway sets up two TCP connections, one between itself and a TCP user on an inner host and one between itself and a TCP user on an outside host.
- Once the two connections are established, the gateway typically relays TCP segments from one connection to the other without examining the contents.
- The security function consists of determining which connections will be allowed.
- A typical use of circuit-level gateways is a situation in which the system administrator trusts the internal users.
- The gateway can be configured to support application-level or proxy service on inbound connections and circuit-level functions for outbound connections.
- In this configuration, the gateway can incur the processing overhead of examining incoming application data for forbidden functions but does not incur that overhead on outgoing data.
An example of a circuit-level gateway implementation is the SOCKS package [KOBL92]; version 5 of SOCKS is defined in RFC 1928.
CONFIGURATIONS:
Describe packet filtering router in detail. (8)

In the screened host firewall, single-homed bastion configuration ,the firewall consists of two systems: a packet-filtering router and a bastion host. Typically, the router is configured so that
1. For traffic from the Internet, only IP packets destined for the bastion host are allowed in.
2. For traffic from the internal network, only IP packets from the bastion host are allowed out. The bastion host performs authentication and proxy functions. This configuration has greater security than simply a packet-filtering router
or an application-level gateway alone, for two reasons. First, this configuration implements both packet-level and application-level filtering, allowing for considerable flexibility in defining security policy. Second, an intruder must generally penetrate two separate systems before the security of the internal network is compromised.
This configuration also affords flexibility in providing direct Internet access. For example, the internal network may include a public information server, such as a Web server, for which a high level of security is not required. In that case, the router can be configured to allow direct traffic between the information server and the Internet.
In the single-homed configuration just described, if the packet-filtering router is completely compromised, traffic could flow directly through the router between the Internet and other hosts on the private network. The screened host firewall, dual-homed bastion configuration physically prevents such a security breach .The advantages of dual layers of security that were present in the previous configuration are present here as well. Again, an information server or other hosts can be allowed direct communication with the router if this is in accord with the security policy.
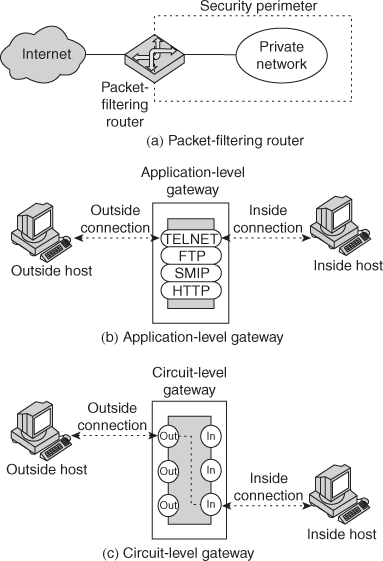
The screened subnet firewall configuration is the most secure of those we have considered. In this configuration, two packet-filtering routers are used, one between the bastion host and the Internet and one between the bastion host and the internal network. This configuration creates an isolated subnetwork, which may consist of simply the bastion host but may also include one or more information servers and modems for dial-in capability.
Typically, both the Internet and the internal network have access to hosts on the screened subnet, but traffic across the screened subnet is blocked. This configuration offers several advantages:
- There are now three levels of defense to thwart intruders.
- The outside router advertises only the existence of the screened subnet to the Internet; therefore, the internal network is invisible to the Internet.
- Similarly, the inside router advertises only the existence of the screened subnet to the internal network; therefore, the systems on the inside network cannot construct direct routes to the Internet
Packet-Filtering Router
A packet-filtering router applies a set of rules to each incoming and outgoing IP packet and then forwards or discards the packet. The router is typically configured to filter packets going in both directions (from and to the internal network). Filtering rules are based on information contained in a network packet:
- Source IP address: The IP address of the system that originated the IP packet (e.g., 192.178.1.1)
- Destination IP address: The IP address of the system the IP packet is trying to reach (e.g., 192.168.1.2)
- Source and destination transport-level address: The transport level (e.g., TCP or UDP) port number, which definesapplications such as SNMP or TELNET
- IP protocol field: Defines the transport protocol
- Interface: For a router with three or more ports, which interface of the router the packet came from or which interface of the router the packet is destined for
- The packet filter is typically set up as a list of rules based on matches to fields in the IP or TCP header. If there is a match to one of the rules, that rule is invoked to determine whether to forward or discard the packet. If there is no match to any rule, then a default action is taken.
Advantage:
One advantage of a packet-filtering router is its simplicity. Also, packet filters typically are transparent to users and are very fast.
Weaknesses of packet filter firewalls:
- Because packet filter firewalls do not examine upper-layer data, they cannot prevent attacks that employ application-specific vulnerabilities or functions. For example, a packet filter firewall cannot block specific application commands; if a packet filter firewall allows a given application, all functions available within that application will be permitted.
- Because of the limited information available to the firewall, the logging functionality present in packet filter firewalls is limited.
- Packet filter logs normally contain the same information used to make access control decisions (source address, destination address, and traffic type).
- Most packet filter firewalls do not support advanced user authentication schemes. Once again, this limitation is mostly due to the lack of upper-layer functionality by the firewall.
- They are generally vulnerable to attacks and exploits that take advantage of problems within the TCP/IP specification and protocol stack, such as network layer address spoofing. Many packet filter firewalls cannot detect a network packet in which the OSI Layer 3 addressing information has been altered. Spoofing attacks are generally employed by intruders to bypass the security controls implemented in a firewall platform.
- Finally, due to the small number of variables used in access control decisions, packet filter firewalls are susceptible to security breaches caused by improper configurations. In other words, it is easy to accidentally configure a packet filter firewall to allow traffic types, sources, and destinations that should be denied based on an organization’s information security policy.
- Some of the attacks that can be made on packet-filtering routers and the appropriate countermeasures are the following:
IP address spoofing: The intruder transmits packets from the outside with a source IP address field containing an address of an internal host. The attacker hopes that the use of a spoofed address will allow penetration of systems that employ simple source address security, in which packets from specific trusted internal hosts are accepted. The countermeasure is to discard packets with an inside source address if the packet arrives on an external interface.
Source routing attacks: The source station specifies the route that a packet should take as it crosses the Internet, in the hopes that this will bypass security measures that do not analyze the source routing information. The countermeasure is to discard all packets that use this option.
Tiny fragment attacks:
- The intruder uses the IP fragmentation option to create extremely small fragments and force the TCP header information into a separate packet fragment.
- This attack is designed to circumvent filtering rules that depend on TCP header information.
- Typically, a packet filter will make a filtering decision on the first fragment of a packet.
- All subsequent fragments of that packet are filtered out solely on the basis that they are part of the packet whose first fragment was rejected.
- If the first fragment is rejected, the filter can remember the packet and discard all subsequent fragments.
Stateful Inspection Firewalls
- A traditional packet filter makes filtering decisions on an individual packet basis and does not take into consideration any higher layer context.
- For example, for the Simple Mail Transfer Protocol (SMTP), e-mail is transmitted from a client system to a server system.
- The client system generates new e-mail messages, typically from user input. The server system accepts incoming e-mail messages and places them in the appropriate user mailboxes.
- SMTP operates by setting up a TCP connection between client and server, in which the TCP server port number, which identifies the SMTP server application, is 25. T
- he TCP port number for the SMTP client is a number between 1024 and 65535 that is generated by the SMTP client.
- In general, when an application that uses TCP creates a session with a remote host, it creates a TCP connection in which the TCP port number for the remote (server) application is a number less than 1024 and the TCP port number for the local (client) application is a number between 1024 and 65535.
- The numbers less than 1024 are the “well-known” port numbers and are assigned permanently to particular applications (e.g., 25 for server SMTP). T
- The numbers between 1024 and 65535 are generated dynamically and have temporary significance only for the lifetime of a TCP connection.
- A simple packet-filtering firewall must permit inbound network traffic on all these high-numbered ports for TCP-based traffic to occur.
- A stateful inspection packet filter tightens up the rules for TCP traffic by creating a directory of outbound TCP connections.
- There is an entry for each currently established connection.
- The packet filter will now allow incoming traffic to high-numbered ports only for those packets that fit the profile of one of the entries in this directory.
Application-Level Gateway
- An application-level gateway, also called a proxy server, acts as a relay of application-level traffic.
- The user contacts the gateway using a TCP/IP application, such as Telnet or FTP, and the gateway asks the user for the name of the remote host to be accessed.
- When the user responds and provides a valid user ID and authentication information, the gateway contacts the application on the remote host and relays TCP segments containing the application data between the two endpoints.
- If the gateway does not implement the proxy code for a specific application, the service is not supported and cannot be forwarded across the firewall.
- Further, the gateway can be configured to support only specific features of an application that the network administrator considers acceptable while denying all other features.
Advantage
- Application-level gateways tend to be more secure than packet filters.
- Rather than trying to deal with the numerous possible combinations that are to be allowed and forbidden at the TCP and IP level, the application-level gateway need only scrutinize a few allowable applications.
- In addition, it is easy to log and audit all incoming traffic at the application level.
A prime disadvantage
- Additional processing overhead on each connection.
- In effect, there are two spliced connections between the end users, with the gateway at the splice point, and the gateway must examine and forward all traffic in both directions.
Circuit-Level Gateway
- A third type of firewall is the circuit-level gateway.
- This can be a stand-alone system or it can be a specialized function performed by an application-level gateway for certain applications.
- A circuit-level gateway does not permit an end-to-end TCP connection; rather, the gateway sets up two TCP connections, one between itself and a TCP user on an inner host and one between itself and a TCP user on an outside host.
- Once the two connections are established, the gateway typically relays TCP segments from one connection to the other without examining the contents.
- The security function consists of determining which connections will be allowed.
- A typical use of circuit-level gateways is a situation in which the system administrator trusts the internal users.
- The gateway can be configured to support application-level or proxy service on inbound connections and circuit-level functions for outbound connections.
- In this configuration, the gateway can incur the processing overhead of examining incoming application data for forbidden functions but does not incur that overhead on outgoing data.
- An example of a circuit-level gateway implementation is the SOCKS package [KOBL92]; version 5 of SOCKS is defined in RFC 1928.
Firewall Configurations:
In the screened host firewall, single-homed bastion configuration, the firewall consists of two systems: a packet-filtering router and a bastion host. Typically, the router is configured so that
1. For traffic from the Internet, only IP packets destined for the bastion host are allowed in.
2. For traffic from the internal network, only IP packets from the bastion host are allowed out. The bastion host performs authentication and proxy functions. This configuration has greater security than simply a packet-filtering router or an application-level gateway alone, for two reasons. First, this configuration implements both packet-level and application-level filtering, allowing for considerable flexibility in defining security policy. Second, an intruder must generally penetrate two separate systems before the security of the internal network is compromised.
This configuration also affords flexibility in providing direct Internet access. For example, the internal network may include a public information server, such as a Web server, for which a high level of security is not required. In that case, the router can be configured to allow direct traffic between the information server and the Internet.
In the single-homed configuration just described, if the packet-filtering router is completely compromised, traffic could flow directly through the router between the Internet and other hosts on the private network. The screened host firewall, dual-homed bastion configuration physically prevents such a security breach .The advantages of dual layers of security that were present in the previous configuration are present here as well. Again, an information server or other hosts can be allowed direct communication with the router if this is in accord with the security policy.
The screened subnet firewall configuration is the most secure of those we have considered. In this configuration, two packet-filtering routers are used, one between the bastion host and the Internet and one between the bastion host and the internal network. This configuration creates an isolated subnetwork, which may consist of simply the bastion host but may also include one or more information servers and modems for dial-in capability.
Typically, both the Internet and the internal network have access to hosts on the screened subnet, but traffic across the screened subnet is blocked. This configuration offers several advantages:
- There are now three levels of defense to thwart intruders.
- The outside router advertises only the existence of the screened subnet to the Internet; therefore, the internal network is invisible to the Internet.
- Similarly, the inside router advertises only the existence of the screened subnet to the internal network; therefore, the systems on the inside network cannot construct direct routes to the Internet
16. Classification of Cryptographic systems:
Ans:

Substitution Techniques
The two basic building blocks of all encryption techniques are substitution and transposition. A substitution technique is one in which the letters of plaintext are replaced by other letters or by numbers or symbols. If the plaintext is viewed as a sequence of bits, then substitution involves replacing plaintext bit patterns with cipher text bit patterns.
1. Ceaser cipher
2. Monoalphabetic cipher
3. Homophonic substitution cipher
4. Polygram Substitution cipher
5. Polyalphabetic cipher
Caesar Cipher
The earliest known use of a substitution cipher, and the simplest, was by Julius Caesar. The Caesar cipher involves replacing each letter of the alphabet with the letter standing three places further down the alphabet.
For example,
plain: meet me after the toga party
cipher: PHHW PH DIWHU WKH WRJD SDUWB
The alphabet is wrapped around, so that the letter following Z is A. We can define the transformation by listing all possibilities, as follows:
plain: a b c d e f g h i j k l m n o p q r s t u v w x y z
cipher: D E F G H I J K L M N O P Q R S T U V W X Y Z A B C
we can also assign a numerical equivalent to each letter:
Monoalphabetic Ciphers
With only 25 possible keys, the Caesar cipher is far from secure. A dramatic increase in the key space can be achieved by allowing an arbitrary substitution. Recall the assignment for the Caesar cipher:
plain: a b c d e f g h i j k l m n o p q r s t u v w x y z
cipher: D E F G H I J K L M N O P Q R S T U V W X Y Z A B C
If, instead, the “cipher” line can be any permutation of the 26 alphabetic characters, then there are 26! or greater than 4 x 10 26 possible keys. This is 10 orders of magnitude greater than the key space for DES and would seem to eliminate brute-force techniques for cryptanalysis. Such an approach is referred to as a monoalphabetic substitution cipher, because a single cipher alphabet (mapping from plain alphabet to cipher alphabet) is used per message.
Playfair Cipher
The best-known multiple-letter encryption cipher is the Playfair, which treats digrams in the plaintext as single units and translates these
M O N A R
C H Y B D
E F G I/J K
L P Q S T
U V W X Z
In this case, the keyword is monarchy. The matrix is constructed by filling in the letters of the keyword (minus duplicates) from left to rightand from top to bottom, and then filling in the remainder of the matrix with the remaining letters in alphabetic order. The letters I and Jount as one letter. Plaintext is encrypted two letters at a time, according to the following rules:
1. Repeating plaintext letters that are in the same pair are separated with a filler letter, such as x, so that balloon would be treated as ba lx lo on.
2. Two plaintext letters that fall in the same row of the matrix are each replaced by the letter to the right, with the first element of the row circularly following the last. For example, ar is encrypted as RM.
3. Two plaintext letters that fall in the same column are each replaced by the letter beneath, with the top element of the column circularly following the last. For example, mu is encrypted as CM.
4. Otherwise, each plaintext letter in a pair is replaced by the letter that lies in its own row and the column occupied by the other plaintext letter. Thus, hs becomes BP and ea becomes IM (or JM, as the encipherer wishes).
Hill Cipher
This cipher is somewhat more difficult to understand than the others in this chapter, but it illustrates an important point about cryptanalysis that will be useful later on. This subsection can be skipped on a first reading.
Another interesting multiletter cipher is the Hill cipher, developed by the mathematician Lester Hill in 1929. The encryption algorithm takes m successive plaintext letters and substitutes for them m ciphertext letters. The substitution is determined by m linear equations in which each character is assigned a numerical value (a = 0, b = 1 ... z = 25). For m = 3, the system can be described as follows:
c3 = (k31P1 + k32P2 + k33P3) mod 26
This can be expressed in term of column vectors and matrices:
or
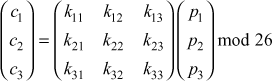
C = KP mod 26
where C and P are column vectors of length 3, representing the plaintext and ciphertext, and K is a 3 x 3 matrix, representing the encryption key. Operations are performed mod 26.
Polyalphabetic Ciphers
Another way to improve on the simple monoalphabetic technique is to use different monoalphabetic substitutions as one proceeds through the plaintext message. The general name for this approach is polyalphabetic substitution cipher. All these techniques have the following features in common:
1. A set of related monoalphabetic substitution rules is used.
2. A key determines which particular rule is chosen for a given transformation.
The best known, and one of the simplest, such algorithm is referred to as the Vigenère cipher. In this scheme, the set of related monoalphabetic substitution rules consists of the 26 Caesar ciphers, with shifts of 0 through 25. Each cipher is denoted by a key letter, which is the ciphertext letter that substitutes for the plaintext letter a.
One-Time Pad
An Army Signal Corp officer, Joseph Mauborgne, proposed an improvement to the Vernam cipher that yields the ultimate in security. Mauborgne suggested using a random key that is as long as the message, so that the key need not be repeated. In addition, the key is to be used to encrypt and decrypt a single message, and then is discarded. Each new message requires a new key of the same length as the new message. Such a scheme, known as a one-time pad, is unbreakable. It produces random output that bears no statistical relationship to the plaintext. Because the ciphertext contains no information whatsoever about the plaintext, there is simply no way to break the code.
Transposition Techniques
- Rail Fence Techniques
- Columnar transposition Techniques
- Book cipher
- Vernam Cipher/one time pad
All the techniques examined so far involve the substitution of a ciphertext symbol for a plaintext symbol. A very different kind of mapping is achieved by performing some sort of permutation on the plaintext letters. This technique is referred to as a transposition cipher. The simplest such cipher is the rail fence technique, in which the plaintext is written down as a sequence of diagonals and then read off as a sequence of rows. For example, to encipher the message “meet me after the toga party” with a rail fence of depth 2, we write the following:
The encrypted message is
MEMATRHTGPRYETEFETEOAAT
This sort of thing would be trivial to cryptanalyze. A more complex scheme is to write the message in a rectangle, row by row, and read the message off, column by column, but permute the order of the columns. The order of the columns then becomes the key to the algorithm. For example,
Key: 4 3 1 2 5 6 7
Plaintext: a t t a c k p
o s t p o n e
d u n t i l t
w o a m x y z
Ciphertext: TTNAAPTMTSUOAODWCOIXKNLYPETZ
A pure transposition cipher is easily recognized because it has the same letter frequencies as the original plaintext. For the type of columnar transposition just shown, cryptanalysis is fairly straightforward and involves laying out the ciphertext in a matrix and playingaround with column positions. Digram and trigram frequency tables can be useful.The transposition cipher can be made significantly more secure by performing more than one stage of transposition. The result is a morecomplex permutation that is not easily reconstructed. Thus, if the foregoing message is reencrypted using the same algorithm,
Key: 4 3 1 2 5 6 7
Input: t t n a a p t
m t s u o a o
d w c o i x k
n l y p e t z
Output: NSCYAUOPTTWLTMDNAOIEPAXTTOKZ
To visualize the result of this double transposition, designate the letters in the original plaintext message by the numbers designating their position. Thus, with 28 letters in the message, the original sequence of letters is
01 02 03 04 05 06 07 08 09 10 11 12 13 14
15 16 17 18 19 20 21 22 23 24 25 26 27 28
Rail Fence techiniques:
1. Write down the plain text message as a sequence of diagonals.
2. Read the plaintext written in step1 as a sequwnce of rows.
plain text: Come home tomorrow
Cipher text: cmh mt mr ooeoeoorw.
Columnar transposition technique:
1. Writ the plain text message row by row in a rectangle of a predefined size.
2. Read the message column by column .it need not be in the order of the column 1,2,3…
3. The message thus obtained is the cipher text message.
plain text: Come home tomorrow
Let us consider a rectangle with six columns.
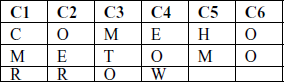
the order of columns chosen in random order say 4,6,1,2,5,3 .Then read the text in order of these columns.
Cipher text: eowoocmroerhmmto
Vernam cipher:
1. Treat each plain text alphabet as a number in an increasing sequence.
2. do the same for each character of the input cipher text.
3. Add each number corresponding to the plaintext alphabet to the corresponding input ciphertext alphabet number.
4. If the sum has produced is greater than 26,subtract 26 from it.
5. translate each number of the sum back to the corresponding alphabet.This gives the cipher test.
17. Euler’s Theorem
Ans:
Euler Totient Function ø(n):
- when doing arithmetic modulo n
- complete set of residues is: 0..n-1
- reduced set of residues is those numbers (residues) which are relatively prime to n
- eg for n=10,
- complete set of residues is {0,1,2,3,4,5,6,7,8,9}
- reduced set of residues is {1,3,7,9}
- number of elements in reduced set of residues is called the Euler Totient Function ø(n)
- to compute ø(n) need to count number of residues to be excluded
- in general need prime factorization, but
- for p (p prime) ø(p) = p-1
- for p.q (p,q prime) ø(pq) =(p-1)x(q-1)
- eg.
ø(37) = 36
ø(21) = (3–1)x(7–1) = 2x6 = 12
Euler’s Theorem:
- a generalisation of Fermat’s Theorem
- aø(n) = 1 (mod n)
- for any a,n where gcd(a,n)=1
- eg.
a=3;n=10; ø(10)=4;
hence 34 = 81 = 1 mod 10
a=2;n=11; ø(11)=10;
hence 210 = 1024 = 1 mod 11
Primality Testing:
- often need to find large prime numbers
- traditionally sieve using trial division
- ie. divide by all numbers (primes) in turn less than the square root of the number
- only works for small numbers
- alternatively can use statistical primality tests based on properties of primes
- for which all primes numbers satisfy property
- but some composite numbers, called pseudo-primes, also satisfy the property
- can use a slower deterministic primality test
Miller Rabin Algorithm:
a test based on Fermat’s Theorem
- algorithm is:
TEST (n) is:
1. Find integers k, q, k > 0, q od’d, so that (n–1)=2kq
2. Select a random integer a, 1<a<n–1
3. ifaqmod n = 1 then return (“maybe prime”);
4. forj = 0 to k – 1 do
5. if (a2jqmod n = n-1)
thenreturn(“ maybe prime “)
5. return (“composite”)
Chinese Remainder Theorem:
- used to speed up modulo computations
- if working modulo a product of numbers
- eg. mod M = m1m2..mk
- Chinese Remainder theorem lets us work in each moduli mi separately
- since computational cost is proportional to size, this is faster than working in the full modulus M
- can implement CRT in several ways
- to compute A(mod M)
- first compute all ai = A mod mi separately
- determine constants ci below, where Mi = M/mi
- then combine results to get answer using:
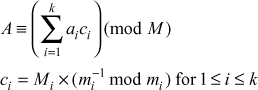
To represent 973 mod 1813 as a pair of numbers mod 37 and 49, define
m1 = 37
m2 = 49
M = 1813
A = 973
We also have M1 = 49 and M2 = 37. Using the extended Euclidean algorithm, we compute = 34 mod m1 and = 4 mod m2. (Note that we only need to compute each Mi and each once.) Taking residues modulo 37 and 49, our representation of 973 is (11, 42), because 973 mod 37 = 11 and 973 mod 49 = 42.
Now suppose we want to add 678 to 973. What do we do to (11, 42)?
1. First we compute (678) (678 mod 37, 678 mod 49) = (12, 41). Then we add the tuples element-wise and reduce (11 + 12 mod 37, 42 + 41 mod 49) = (23, 34).
2. To verify that this has the correct effect, we compute (23,34) a1M1 + a2M2 mod M = [(23)(49)(34) + (34)(37)(4)] mod 1813 = 43350 mod 1813 = 1651 and check that it is equal to (973 + 678) mod 1813 = 1651. Remember that in the above derivation, is the multiplicative inverse of M1 modulo m1, and is the multiplicative inverse of M2 modulo m2. Suppose we want to multiply 1651 (mod 1813) by 73. We multiply (23, 34) by 73 and reduce to get (23 x 73 mod 37, 34 x 73 mod 49) = (14,32). It is easily verified that (32,14) [(14)(49)(34) + (32)(37)(4)] mod 1813 = 865 = 1651 x 73 mod 1813.
18. The algorithm itself is referred to as the Data Encryption Algorithm (DEA). For DES, data are encrypted in 64-bit blocks using a 56-bit key. The algorithm transforms 64-bit input in a series of steps into a 64-bit output. The same steps, with the same key, are used to reverse the encryption.
Ans:
First, the 64-bit plaintext passes through an initial permutation (IP) that rearranges the bits to produce the permuted input. This is followed by a phase consisting of 16 rounds of the same function, which involves both permutation and substitution functions. The output of the last (sixteenth) round consists of 64 bits that are a function of the input plaintext and the key. The left and right halves of the output are swapped to produce the preoutput. Finally, the preoutput is passed through a permutation (IP -1 ) that is the inverse of the initial permutation function, to produce the 64-bit ciphertext.
Initial Permutation:
It is the first step of the data computation . IP reorders the input data bits. It changeeven bits to LH half, odd bits to RH half.
Example:
IP(675a6967 5e5a6b5a) = (ffb2194d 004df6fb)
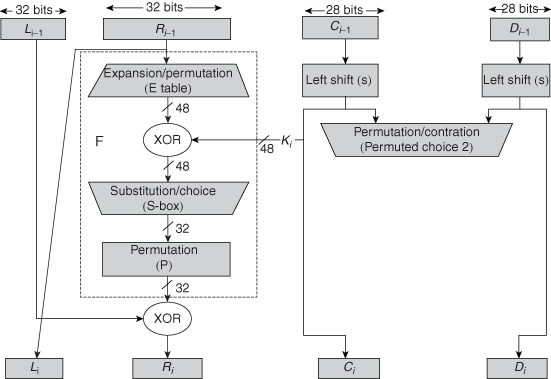
DES Round Structure:
It uses two 32-bit L & R halves as for any Feistel cipher can describe as:
Li = Ri–1
Ri= Li–1 Å F(Ri–1 , Ki)
- F takes 32-bit R half and 48-bit subkey:
- expands R to 48-bits using perm E
- adds to subkey using XOR
- passes through 8 S-boxes to get 32-bit result
- finally permutes using 32-bit perm P
DES Round Structure:
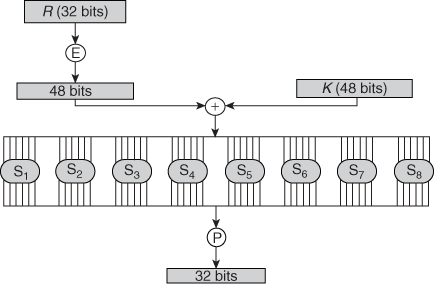
Substitution Boxes S:
DES have eight S-boxes which map Substitution Boxes S:
DES have eight S-boxes which map 6 to 4 bits. Each S-box is actually 4 little 4 bit boxes. Outer bits 1 & 6 (row bits) select one row of 4. Inner bits 2-5 (col bits) are substituted. Result is 8 lots of 4 bits, or 32 bits. Row selection depends on both data & key. Feature known as autoclaving (autokeying).
example:
S(18 09 12 3d 11 17 38 39) = 5fd25e03
DES Key Schedule:
- forms subkeys used in each round
– initial permutation of the key (PC1) which selects 56-bits in two 28-bit halves
– 16 stages consisting of:
- rotating each half separately either 1 or 2 places depending on the key rotation schedule K
- selecting 24-bits from each half & permuting them by PC2 for use in round function F
- note practical use issues in hardwarevs software
DES Decryption:
- decrypt must unwind steps of data computation
- with Feistel design, do encryption steps again using subkeys in reverse order (SK16 … SK1)
- IP undoes final FP step of encryption
- 1st round with SK16 undoes 16th encrypt round
- 16th round with SK1 undoes 1st encrypt round
- then final FP undoes initial encryption IP
- thus recovering original data value
Strength of DES – Analytic Attacks:
- now have several analytic attacks on DES
- these utilise some deep structure of the cipher
- by gathering information about encryptions
- can eventually recover some/all of the sub-key bits
- if necessary then exhaustively search for the rest
- generally these are statistical attacks
- include
- differential cryptanalysis
- linear cryptanalysis
- related key attacks
Detailed explanation:
The round key Ki is 48 bits. The R input is 32 bits. This R input is first expanded to 48 bits by using a table that defines a permutation plus an expansion that involves duplication of 16 of the R bits The resulting 48 bits are XORed with Ki. This 48-bit result passes through a substitution function that produces a 32-bit output, which is permuted .The role of the S-boxes in the function F is illustrated The substitution consists of a set of eight S-boxes, each of which accepts 6 bits as input and produces 4 bits as output. These transformations are defined, which is interpreted as follows:
The first and last bits of the input to box Si form a 2-bit binary number to select one of four substitutions defined by the four rows in the table for Si. The middle four bits select one of the sixteen columns. The decimal value in the cell selected by the row and column is then converted to its 4-bit representation to produce the output. For example, in S1 for input 011001, the row is 01 (row 1) and the column is 1100 (column 12). The value in row 1, column 12 is 9, so the output is 1001.
Each row of an S-box defines a general reversible substitution. Figure 3.1 may be useful in understanding the mapping. The figure shows the substitution for row 0 of box S1. The operation of the S-boxes is worth further comment. Ignore for the moment the contribution of the key (Ki). If you examine the expansion table, you see that the 32 bits of input are split into groups of 4 bits, and then become groups of 6 bits by taking the outer bits from the two adjacent groups.
For example, if part of the input word is
... efgh ijkl mnop ...
this becomes
... defghi hijklm lmnopq ...
The outer two bits of each group select one of four possible substitutions (one row of an S-box). Then a 4-bit output value is substituted for the particular 4-bit input (the middle four input bits). The 32-bit output from the eight S-boxes is then permuted, so that on the next round the output from each S-box immediately affects as many others as possible.
(b) Key Discarding Process:
Differential Cryptanalysis Attack
The differential cryptanalysis attack is complex; provides a complete description. The rationale behind differential cryptanalysis is to observe the behavior of pairs of text blocks evolving along each round of the cipher, instead of observing the evolution of a single text block. Here, we provide a brief overview so that you can get the flavor of the attack.
We begin with a change in notation for DES. Consider the original plaintext block m to consist of two halves m0,m1. Each round of DES maps the right-hand input into the left-hand output and sets the right-hand output to be a function of the left-hand input and the subkey for this round. So, at each round, only one new 32-bit block is created.
mi+1 = mi-1 f(mi, Ki), i = 1, 2, ..., 16
In differential cryptanalysis, we start with two messages, m and m’, with a known XOR difference Dm = m m’, and consider the difference between the intermediate message halves: mi = mi mi’ Then we have:
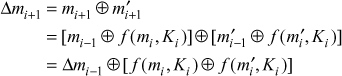
suppose that many pairs of inputs to f with the same difference yield the same output difference if the same subkey is used. To put this more precisely, let us say that X may cause Y with probability p, if for a fraction p of the pairs in which the input XOR is X, the output XOR equals Y. We want to suppose that there are a number of values ofX that have high probability of causing a particular output difference. Therefore, if we know Dmi-1 and Dmi with high probability, then we know Dmi+1 with high probability. Furthermore, if a number of such differences are determined, it is feasible to determine the subkey used in the function f.
The overall strategy of differential cryptanalysis is based on these considerations for a single round. The procedure is to begin with two plaintext messages m and m’ with a given difference and trace through a probable pattern of differences after each round to yield a probable difference for the ciphertext. Actually, there are two probable patterns of differences for the two 32-bit halves: (Dm17||m16). Next, we submit m and m’ for encryption to determine the actual difference under the unknown key and compare the result to the probable difference. If there is a match, E(K, m) E(K, m’) = (Dm17||m16)
Linear Cryptanalysis
This attack is based on finding linear approximations to describe the transformations performed in DES. This method can find a DES key given 2 43 known plaintexts, as compared to 247chosen plaintexts for differential cryptanalysis. Although this is a minor improvement, because it may be easier to acquire known plaintext rather than chosen plaintext, it still leaves linear cryptanalysis infeasible as an attack on DES. So far, little work has been done by other groups to validate the linear cryptanalytic approach.
19. RSA algorithm:
Ans: Diffie and Hellman introduced a new approach to cryptography and, in effect, challenged cryptologists to come up with a cryptographic algorithm that met the requirements for public-key systems. One of the first of the responses to the challenge was developed in 1977 by Ron Rivest, Adi Shamir, and Len Adleman at MIT .
The RSA scheme is a block cipher in which the plaintext and ciphertext are integers between 0 and n 1 for some n. A typical size for n is 1024 bits, or 309 decimal digits. That is, n is less than 21024.
Description of the Algorithm
The scheme developed by Rivest, Shamir, and Adleman makes use of an expression with exponentials. Plaintext is encrypted in blocks, with each block having a binary value less than some number n. That is, the block size must be less than or equal to log2(n); in practice, the block size is i bits, where 2 I ≤n 2 i+1
. Encryption and decryption are of the following form, for some plaintext blockM and ciphertext block C:
C = Memod n
M = Cdmod n = (Me)dmod n = Medmod n
Both sender and receiver must know the value of n. The sender knows the value of e, and only the receiver knows the value of d. Thus, this is a public-key encryption algorithm with a public key of PU = {e, n} and a private key of PU = {d, n}.
For this algorithm to be satisfactory for public-key encryption, the following requirements must be met:
1. It is possible to find values of e, d, n such that M ed mod n = M for all M < n.
2. It is relatively easy to calculate mod Memod n and Cdmod n . for all values of M < n.
3. It is infeasible to determine d given e and n.
To find a relationship of the form Medmod n = M
4. if e and d are multiplicative inverses modulo f(n), where f(n) is the Euler totient function. It is shown in
that for p, q prime, f(pq) = (p- 1)(q-1) The relationship between e and d can be expressed as
1. Select two prime numbers, p = 17 and q = 11.
2. Calculate n = pq = 17 x 11 = 187.
3. Calculate f(n) = (p 1)(q 1) = 16 x 10 = 160.
4. Select e such that e is relatively prime to f(n) = 160 and less than f(n) we choose e = 7.
Determine d such that de 1 (mod 160) and d < 160. The correct value is d = 23, because 23 x 7 = 161 = 10 x 160 + 1; d can be calculated using the extended Euclid’s algorithm.
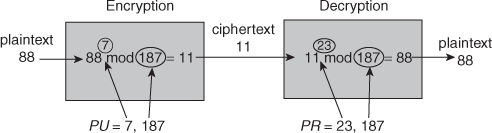
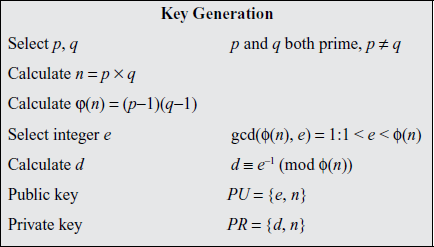


The resulting keys are public key PU = {7,187} and private key PR = {23,187}. The example shows the use of these keys for a plaintext input of M = 88. For encryption, we need to calculate C = 887 mod 187
887 mod 187 = [(884 mod 187) x (88 2 mod 187) x (88 1 mod 187)] mod 187
88 1 mod 187 = 88
88 2mod 187 = 7744 mod 187 = 77
884mod 187 = 59,969,536 mod 187 = 132
887 mod 187 = (88 x 77 x 132) mod 187 = 894,432 mod 187 = 11
For decryption, we calculate M = 1123mod 187:
1123 mod 187 = [(111mod 187) x (112 mod 187) x (114 mod 187) x (118mod 187) x (118mod 187)] mod 187
111mod 187 = 11
112mod 187 = 121
114mod 187 = 14,641 mod 187 = 55
118mod 187 = 214,358,881 mod 187 = 33
1123 mod 187 = (11 x 121 x 55 x 33 x 33) mod 187 = 79,720,245 mod 187 = 88mod 187.
20. Discrete Logarithms: Discrete logarithms are fundamental to a number of public-key algorithms, including Diffie-Hellman key exchange and the digital signature algorithm (DSA).
Ans:
Consider the powers of 7, modulo 19:
71 ≡ 7(mod 19)
72 = 49 = 2 x 19 + 11 ≡ 11(mod 19)
73 = 343 = 18 x 19 + 1 ≡ 1(mod 19)
74 = 2401 = 126 x 19 + 7 ≡ 7(mod 19)
75 = 16807 = 884 x 19 + 11 ≡ 11(mod 19)
There is no point in continuing because the sequence is repeating. This can be proven by noting that 731(mod 19)and therefore 7 3+j ≡ 737j ≡ 7j(mod 19), and hence any two powers of 7 whose exponents differ by 3 (or a multiple of 3) are congruent to each other (mod 19). In other words, the sequence is periodic, and the length of the period is the smallest positive exponent m such that 7 m ≡ 1(mod 19).
The length of the sequence for each base value is indicated by shading. Note the following:
1. All sequences end in 1. This is consistent with the reasoning of the preceding few paragraphs.
2. The length of a sequence divides f(19) = 18. That is, an integral number of sequences occur in each row of the table.
Some of the sequences are of length 18. In this case, it is said that the base integer a generates (via powers) the set of nonzero integers modulo 19. Each such integer is called a primitive root of the modulus 19.
More generally, we can say that the highest possible exponent to which a number can belong (modn ) is f(n). If a number is of this order, it is referred to as a primitive root of n. The importance of this notion is that if a is a primitive root of n, then its powers a, a2,..., a f(n) are distinct (mod n) and are all relatively prime to n. In particular, for a prime number p, if a is a primitive root of p, then a, a2,..., a p1 are distinct (mod p). For the prime number 19, its primitive roots are 2, 3, 10, 13, 14, and 15.
Not all integers have primitive roots. In fact, the only integers with primitive roots are those of the form 2, 4, pa, and 2 pa,, where p is any odd prime and a is a positive integer.
Diffie hellman Key exchange algorithms:
Diffie-Hellman Key Exchange:
- first public-key type scheme proposed
- by Diffie& Hellman in 1976 along with the exposition of public key concepts
- note: now know that Williamson (UK CESG) secretly proposed the concept in 1970
- is a practical method for public exchange of a secret key
- used in a number of commercial products
- a public-key distribution scheme
- cannot be used to exchange an arbitrary message
- rather it can establish a common key
- known only to the two participants
- value of key depends on the participants (and their private and public key information)
- based on exponentiation in a finite (Galois) field (modulo a prime or a polynomial) - easy
- security relies on the difficulty of computing discrete logarithms (similar to factoring) – hard
Diffie-Hellman Setup:
- all users agree on global parameters:
- large prime integer or polynomial q
- a being a primitive root mod q
- each user (eg. A) generates their key
- chooses a secret key (number): xA< q
- compute their public key: yA = axA mod q
- User A selects a random integer X A < q and computes YA = aXA mod q. Similarly, user B independently selects a random integerX A < q and computes YB = a XB mod q. Each side keeps the X value private and makes theY value available publicly to the other side. User A computes the key as
K = (YB)XA mod q and
user B computes the key as K = (YA)XB mod q. These two calculations produce identical results:
K= (YB)XA mod q
= (aXB mod q)XA mod q
(aXB)XA mod q
by the rules of modular arithmetic
= (aXB XA mod q
= (aXA)XB mod q
= (aXA mod q)
= (aXA mod q)XB mod q
= (YA)XB mod q
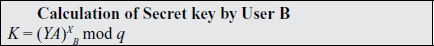
Merits and Demerits:
- Another use of the Diffie-Hellman algorithm, suppose that a group of users (e.g., all users on a LAN) each generate a long-lasting private value Xi (for user i) and calculate a public valueY i. These public values, together with global public values for q and a, are stored in some central directory. At any time, user j can access user i’s public value, calculate a secret key, and use that to send an encrypted message to user A.
- If the central directory is trusted, then this form of communication provides both confidentiality and a degree of authentication. Because only i and j can determine the key, no other user can read the message (confidentiality). Recipient knows that only user j could have created a message using this key (authentication). However, the technique does not protect against replay attacks. It also suffers from man in the middle attack.
21. Explain about MD5 in detail.
Ans:
MD5 algorithm can be used as a digital signature mechanism.
Description of the MD5 Algorithm
- Takes as input a message of arbitrary length and produces as output a 128 bit “fingerprint” or “message digest” of the input.
- It is conjectured that it is computationally infeasible to produce two messages having the same message digest.
- Intended where a large file must be “compressed” in a secure manner before being encrypted with a private key under a public-key cryptosystem such as PGP.explore the technical aspects of the MD5 algorithm.
MD5 Algorithm
- Suppose a b-bit message as input, and that we need to find its message digest.
Step 1 – append padded bits:
– The message is padded so that its length is congruent to 448, modulo 512. • Means extended to just 64 bits shy of being of 512 bits long. – A single “1” bit is appended to the message, and then “0” bits are appended so that the length in bits equals 448 modulo 512
Step 2 – append length:
– A 64 bit representation of b is appended to the result of the previous step. – The resulting message has a length that is an exact multiple of 512 bits.
Step 3 – Initialize MD Buffer
- A four-word buffer (A,B,C,D) is used to compute the message digest. – Here each of A,B,C,D, is a 32 bit register.
These registers are initialized to the following values in hexadecimal:
word A: 01 23 45 67
word B: 89 ab cd ef
word C: fe dc ba 98
word D: 76 54 32 10
Step 4 – Process message in 16-word blocks.– Four auxiliary functions that take as input three 32-bit
words and produce as output one 32-bit word.
F(X,Y,Z) = XY v not(X) Z
G(X,Y,Z) = XZ v Y not(Z)
H(X,Y,Z) = X xor Y xor Z
I(X,Y,Z) = Y xor (X v not(Z))
Process message in 16-word blocks cont.
– if the bits of X, Y, and Z are independent and unbiased, the each bit of F(X,Y,Z), G(X,Y,Z),H(X,Y,Z), and I(X,Y,Z) will be independent and unbiased.
Step 5 – output
– The message digest produced as output is A, B, C, D.
– That is, output begins with the low-order byte of A, and end with the high-order byte of D.
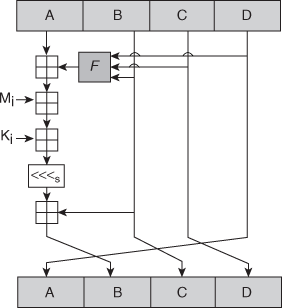
- The MD5 algorithm is simple to implement, and provides a “fingerprint” or message digest of a message of arbitrary length.
- The difficulty of coming up with two messages with the same message digest is on the order of 2^64 operations.
22. Differentiate SSL from SET
Ans:
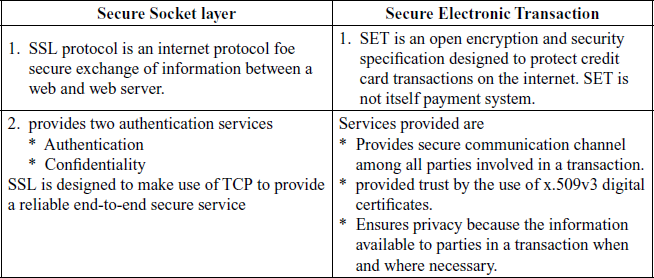
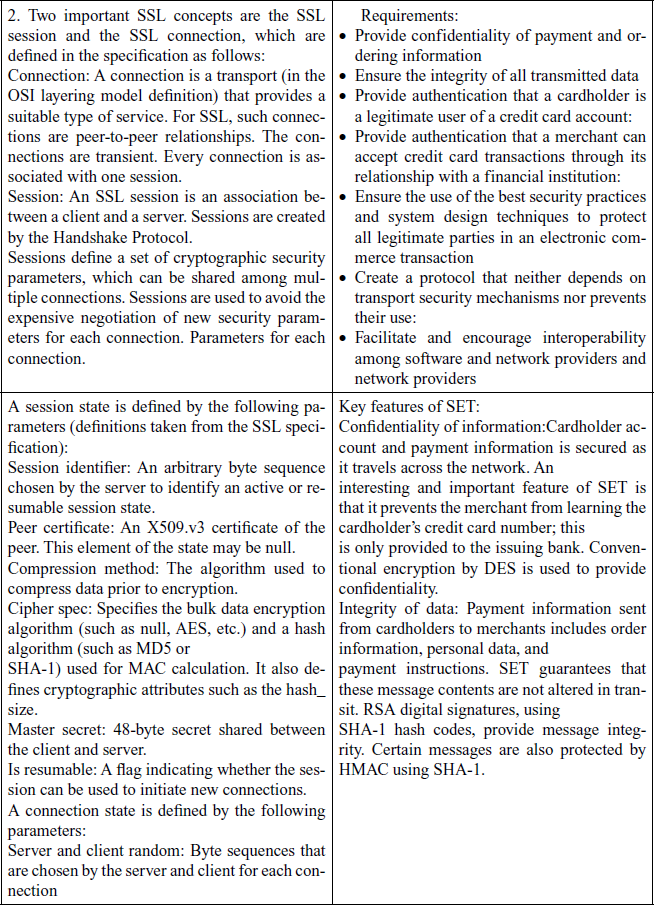

23. Overview of IP Security documents.
Ans: IP Security Documents:
- IP security (IPSec) is a capability that can be added to either current version of the Internet Protocol (IPv4 or IPv6), by means of additional headers.
- IPSec encompasses three functional areas: authentication, confidentiality, and key management.
- Authentication makes use of the HMAC message authentication code. Authentication can be applied to the entire original IP packet ( tunnel mode) or to all of the packet except for the IP header (transport mode).
- Confidentiality is provided by an encryption format known as encapsulating security payload. Both tunnel and transport modes can be accommodated.
- IPSec defines a number of techniques for key management.
IPSec Documents
The IPSec specification consists of numerous documents. The most important of these, issued in November of 1998, are RFCs 2401, 2402, 2406, and 2408:
RFC 2401: An overview of a security architecture
RFC 2402: Description of a packet authentication extension to IPv4 and IPv6
RFC 2406: Description of a packet encryption extension to IPv4 and IPv6
RFC 2408: Specification of key management capabilities
Support for these features is mandatory for IPv6 and optional for IPv4. In both cases, the security features are implemented as extension headers that follow the main IP header. The extension header for authentication is known as the Authentication header; that for encryption is known as the encapsulating Security Payload (ESP) header.
In addition to these four RFCs, a number of additional drafts have been published by the IP Security Protocol Working Group set up by the IETF. The documents are divided into seven groups.
- Architecture: Covers the general concepts, security requirements, definitions, and mechanisms defining IPSec technology.
- Encapsulating Security Payload (ESP): Covers the packet format and general issues related to the use of the ESP for packet encryption and, optionally, authentication.
- Authentication Header (AH): Covers the packet format and general issues related to the use of AH for packet authentication.
- Encryption Algorithm: A set of documents that describe how various encryption algorithms are used for ESP.
- Authentication Algorithm: A set of documents that describe how various authentication algorithms are used for AH and for the authentication option of ESP.
- Key Management: Documents that describe key management schemes.
- Domain of Interpretation (DOI): Contains values needed for the other documents to relate to each other. These include identifiers for approved encryption and authentication algorithms, as well as operational parameters such as key lifetime.
Security Associations
- A key concept that appears in both the authentication and confidentiality mechanisms for IP is the security association (SA).
- An association is a one-way relationship between a sender and a receiver that affords security services to the traffic carried on it. If a peer relationship is needed, for two-way secure exchange, then two security associations are required.
- Security services are afforded to an SA for the use of AH or ESP, but not both.
A security association is uniquely identified by three parameters:
- Security Parameters Index (SPI): A bit string assigned to this SA and having local significance only. The SPI is carried in AH and ESP headers to enable the receiving system to select the SA under which a received packet will be processed.
- IP Destination Address: Currently, only unicast addresses are allowed; this is the address of the destination endpoint of the SA, which may be an end user system or a network system such as a firewall or router.
- Security Protocol Identifier: This indicates whether the association is an AH or ESP security association. Hence, in any IP packet, the security association is uniquely identified by the Destination Address in the IPv4 or IPv6 header and the SPI in the enclosed extension header (AH or ESP).
SA Parameters
In each IPSec implementation, there is a nominal Security Association Database that defines the parameters associated with each SA.
A security association is normally defined by the following parameters:
- Sequence Number Counter: A 32-bit value used to generate the Sequence Number field in AH or ESP headers
- Sequence Counter Overflow: A flag indicating whether overflow of the Sequence Number Counter should generate an auditable event and prevent further transmission of packets on this SA (required for all implementations).
- Anti-Replay Window: Used to determine whether an inbound AH or ESP packet is a replay
- AH Information: Authentication algorithm, keys, key lifetimes, and related parameters being used with AH (required for AH implementations).
- ESP Information: Encryption and authentication algorithm, keys, initialization values, key lifetimes, and related parameters being used with ESP required for ESP implementations).
- Lifetime of This Security Association: A time interval or byte count after which an SA must be replaced with a new SA (and new SPI) or terminated, plus an indication of which of these actions should occur
- IPSec Protocol Mode: Tunnel, transport, or wildcard (required for all implementations).
- Path MTU: Any observed path maximum transmission unit (maximum size of a packet that can be transmitted without fragmentation) and aging variables .
SA Selectors
- IPSec provides the user with considerable flexibility in the way in which IPSec services are applied to IP traffic.
- SAs can be combined in a number of ways to yield the desired user configuration.
- IPSec provides a high degree of granularity in discriminating between traffic that is afforded IPSec protection and traffic that is allowed to bypass IPSec, in the former case relating IP traffic to specific SAs.
- IP traffic is related to specific SAs (or no SA in the case of traffic allowed to bypass IPSec) is the nominal Security Policy Database (SPD).
- In its simplest form, an SPD contains entries, each of which defines a subset of IP traffic and points to an SA for that traffic. In more complex environments, there may be multiple entries that potentially relate to a single SA or multiple SAs associated with a single SPD entry. The reader is referred to the relevant IPSec documents for a full discussion.
* Each SPD entry is defined by a set of IP and upper-layer protocol field values, called selectors.
In effect, these selectors are used to filter outgoing traffic in order to map it into a particular SA. Outbound processing obeys the following general sequence for each IP packet:
1. Compare the values of the appropriate fields in the packet (the selector fields) against the SPD to find a matching SPD entry, which will point to zero or more SAs.
2. Determine the SA if any for this packet and its associated SPI.
3. Do the required IPSec processing (i.e., AH or ESP processing).
The following selectors determine an SPD entry:
- Destination IP Address: This may be a single IP address, an enumerated list or range of addresses, or a wildcard (mask) address. The latter two are required to support more than one destination system sharing the same SA (e.g., behind a firewall).
- Source IP Address: This may be a single IP address, an enumerated list or range of addresses, or a wildcard (mask) address. The latter two are required to support more than one source system sharing the same SA (e.g., behind a firewall).
- UserID: A user identifier from the operating system. This is not a field in the IP or upper-layer headers but is available if IPSec is running on the same operating system as the user.
- Data Sensitivity Level: Used for systems providing information flow security (e.g., Secret or Unclassified).
- Transport Layer Protocol: Obtained from the IPv4 Protocol or IPv6 Next Header field. This may be an individual protocol number, a list of protocol numbers, or a range of protocol numbers.
- Source and Destination Ports: These may be individual TCP or UDP port values, an enumerated list of ports, or a wildcard port.
- Transport and Tunnel Modes
Both AH and ESP support two modes of use: transport and tunnel mode. The operation of these two modes is best understood in the context of a description of AH and ESP.
Transport Mode
- Transport mode provides protection primarily for upper-layer protocols.
- That is, transport mode protection extends to the payload of an IP packet. Examples include a TCP or UDP segment or an ICMP packet, all of which operate directly above IP in a host protocol stack.
- Typically, transport mode is used for end-to-end communication between two hosts (e.g., a client and a server, or two workstations).
- When a host runs AH or ESP over IPv4, the payload is the data that normally follow the IP header.
- ESP in transport mode encrypts and optionally authenticates the IP payload but not the IP header.
- AH in transport mode authenticates the IP payload and selected portions of the IP header.
Tunnel Mode
- Tunnel mode provides protection to the entire IP packet.
- To achieve this, after the AH or ESP fields are added to the IP packet, the entire packet plus security fields is treated as the payload of new “outer” IP packet with a new outer IP header.
- The entire original, or inner, packet travels through a “tunnel” from one point of an IP network to another; no routers along the way are able to examine the inner IP header.
- Because the original packet is encapsulated, the new, larger packet may have totally different source and destination addresses, adding to the security.
- Tunnel mode is used when one or both ends of an SA are a security gateway, such as a firewall or router that implements IPSec.
- With tunnel mode, a number of hosts on networks behind firewalls may engage in secure communications without implementing IPSec.
- The unprotected packets generated by such hosts are tunneled through external networks by tunnel mode SAs set up by the IPSec software in the firewall or secure router at the boundary of the local network.
Authentication Header
- The Authentication Header provides support for data integrity and authentication of IP packets.
- The data integrity feature ensures that undetected modification to a packet’s content in transit is not possible.
- The authentication feature enables an end system or network device to authenticate the user or application and filter traffic accordingly;
- It also prevents the address spoofing attacks observed in today’s Internet.
- The AH also guards against the replay attack .Authentication is based on the use of a message authentication code (MAC), hence the two parties must share a secret key.
The Authentication Header consists of the following fields
- Next Header (8 bits): Identifies the type of header immediately following this header.
- Payload Length (8 bits): Length of Authentication Header in 32-bit words, minus 2. For example, the default length of the authentication data field is 96 bits, or three 32-bit words. With a three-word fixed header, there are a total of six words in the header, and the Payload Length field has a value of 4.
- Reserved (16 bits): For future use.
- Security Parameters Index (32 bits): Identifies a security association.
- Sequence Number (32 bits): A monotonically increasing counter value, discussed later.
- Authentication Data (variable): A variable-length field (must be an integral number of 32-bit words) that contains the Integrity Check Value (ICV), or MAC, for this packet, discussed later.

Anti-Replay Service
- A replay attack is one in which an attacker obtains a copy of an authenticated packet and later transmits it to the intended destination.
- The receipt of duplicate, authenticated IP packets may disrupt service in some way or may have some other undesired consequence.
- The Sequence Number field is designed to thwart such attacks
Encapsulating Security Payload
- The Encapsulating Security Payload provides confidentiality services, including confidentiality of message contents and limited traffic flow confidentiality.
- As an optional feature, ESP can also provide an authentication service.
ESP Format-The format of an ESP packet contains the following fields:
- Security Parameters Index (32 bits): Identifies a security association.
- Sequence Number (32 bits): A monotonically increasing counter value; this provides an anti-replay function, as discussed for AH.
- Payload Data (variable): This is a transport-level segment (transport mode) or IP packet (tunnel mode) that is protected by encryption.
- Padding (0255 bytes.
- Pad Length (8 bits): Indicates the number of pad bytes immediately preceding this field.
- Next Header (8 bits): Identifies the type of data contained in the payload data field by identifying the first header in that payload (for example, an extension header in IPv6, or an upper-layer protocol such as TCP).
- Authentication Data (variable): A variable-length field (must be an integral number of 32-bit words) that contains the Integrity Check Value computed over the ESP packet minus the Authentication Data field.
Encryption and Authentication Algorithms
- The Payload Data, Padding, Pad Length, and Next Header fields are encrypted by the ESP service.
- If the algorithm used to encrypt the payload requires cryptographic synchronization data, such as an initialization vector (IV), then these data may be carried explicitly at the beginning of the Payload Data field.
- If included, an IV is usually not encrypted, although it is often referred to as being part of the ciphertext.
- The current specification dictates that a compliant implementation must support DES in cipher block chaining (CBC) mode ..
- A number of other algorithms have been assigned identifiers in the DOI document and could therefore easily be used for encryption; these include
- Three-key triple DES
- RC5
- IDEA
- Three-key triple IDEA
- CAST
- Blowfish
As with AH, ESP supports the use of a MAC with a default length of 96 bits. Also as with AH, the current specification dictates that a compliant implementation must support HMAC-MD5-96 and HMAC-SHA-1-96.
24. PGP Message generation and reception
Ans:
Phil Zimmermann, PGP provides a confidentiality and authentication service that can be used for electronic mail and file storage applications. In essence, Zimmermann has done the following:
1. Selected the best available cryptographic algorithms as building blocks Integrated these algorithms into a general- purpose application that is independent of operating system and processor and that is based on a small set of easy-to-use commands
2. Made the package and its documentation, including the source code, freely available via the Internet, bulletin boards, and commercial networks such as AOL (America On Line)
3. Entered into an agreement with a company (Viacrypt, now Network Associates) to provide a fully compatible, low-cost commercial version of PGP
4. PGP has grown explosively and is now widely used. A number of reasons can be cited for this growth: It is available free worldwide in versions that run on a variety of platforms, including Windows, UNIX, Macintosh, and many more. In addition, the commercial version satisfies users who want a product that comes with vendor support.
PGP key features
1. It is based on algorithms that have survived extensive public review and are considered extremely secure. Specifically, the package includes RSA, DSS, and Diffie-Hellman for public-key encryption; CAST-128, IDEA, and 3DES for symmetric encryption; and SHA-1 for hash coding.
2. It has a wide range of applicability, from corporations that wish to select and enforce a standardized scheme for encrypting files and messages to individuals who wish to communicate securely with others worldwide over the Internet and other networks.
3. It was not developed by, nor is it controlled by, any governmental or standards organization. For those with an instinctive distrust of “the establishment,” this makes PGP attractive.
4. PGP is now on an Internet standards track (RFC 3156).
Authentication:
The digital signature service provided by PGP. The sequence is as follows:
1. The sender creates a message.
2. SHA-1 is used to generate a 160-bit hash code of the message.
3. The hash code is encrypted with RSA using the sender’s private key, and the result is prepended to the message.
4. The receiver uses RSA with the sender’s public key to decrypt and recover the hash code.
The receiver generates a new hash code for the message and compares it with the decrypted hash code. If the two match, the message is accepted as authentic.
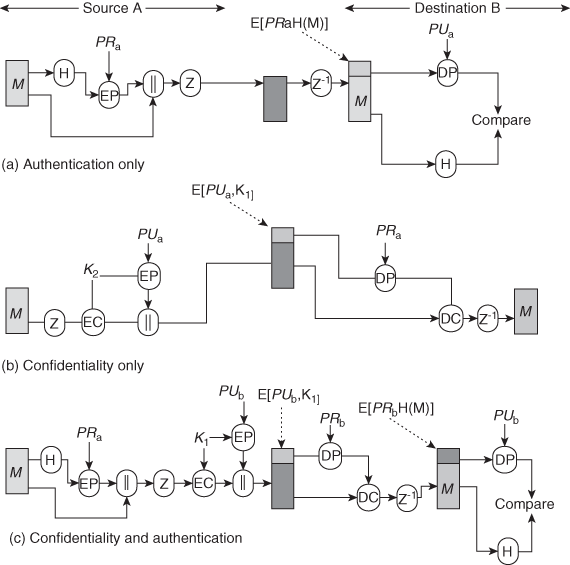
Confidentiality
- Another basic service provided by PGP is confidentiality, which is provided by encrypting messages to be transmitted or to be stored locally as files.
- In both cases, the symmetric encryption algorithm CAST-128 may be used.
- Alternatively, IDEA or 3DES may be used.
- The 64-bit cipher feedback (CFB) mode is used. As always, one must address the problem of key distribution. In PGP, each symmetric key is used only once.
- A new key is generated as a random 128-bit number for each message.
- This is referred as a session key, it is in reality a one-time key.
- Because it is to be used only once, the session key is bound to the message and transmitted with it.
- To protect the key, it is encrypted with the receiver’s public key.
1. The sender generates a message and a random 128-bit number to be used as a session key for this message only.
2. The message is encrypted, using CAST-128 (or IDEA or 3DES) with the session key.
3. The session key is encrypted with RSA, using the recipient’s public key, and is prepended to the message.
4. The receiver uses RSA with its private key to decrypt and recover the session key.
5. The session key is used to decrypt the message.
Confidentiality and authentication:
- Both services may be used for the same message.
- First, a signature is generated for the plaintext message and prepended to the message.
- Then the plaintext message plus signature is encrypted using CAST-128 (or IDEA or 3DES), and the session key is encrypted using RSA (or ElGamal).
- This sequence is preferable to the opposite: encrypting the message and then generating a signature for the encrypted message.
- It is generally more convenient to store a signature with a plaintext version of a message.
- Furthermore, for purposes of third-party verification, if the signature is performed first, a third party need not be concerned with the symmetric key when verifying the signature.
- When both services are used, the sender first signs the message with its own private key, then encrypts the message with a session key, and then encrypts the session key with the recipient’s public key.
Compression
- PGP compresses the message after applying the signature but before encryption.
- This has the benefit of saving space both for e-mail transmission and for file storage.
- The placement of the compression algorithm, indicated by Z for compression and Z-1 for decompression is critical:
The signature is generated before compression for two reasons:
It is preferable to sign an uncompressed message so that one can store only the uncompressed message together with the signature for future verification. If one signed a compressed document, then it would be necessary either to store a compressed version of the message for later verification or to recompress the message when verification is required.
a. Even if one were willing to generate dynamically a recompressed message for verification, PGP’s compression algorithm presents a difficulty. The algorithm is not deterministic; various implementations of the algorithm achieve different tradeoffs in running speed versus compression ratio and, as a result, produce different compressed forms. However, these different compression algorithms are interoperable because any version of the algorithm can correctly decompress the output of any other version. Applying the hash function and signature after compression would constrain all PGP implementations to the same version of the compression algorithm.
b. Message encryption is applied after compression to strengthen cryptographic security. Because the compressed message as less redundancy than the original plaintext, cryptanalysis is more difficult.
2. The compression algorithm used is ZIP,
E-mail Compatibility
- When PGP is used, at least part of the block to be transmitted is encrypted.
- If only the signature service is used, then the message digest is encrypted (with the sender’s private key).
- If the confidentiality service is used, the message plus signature (if present) are encrypted (with a one-time symmetric key). Thus, part or all of the resulting block consists of a stream of arbitrary 8-bit octets.
- However, many electronic mail systems only permit the use of blocks consisting of ASCII text.
- To accommodate this restriction, PGP provides the service of converting the raw 8-bit binary stream to a stream of printable ASCII characters.
Transmission and Reception of PGP Messages
On transmission, if it is required, a signature is generated using a hash code of the uncompressed plaintext. Then the plaintext, plus signature if present, is compressed. Next, if confidentiality is required, the block (compressed plaintext or compressed signature plus plaintext) is encrypted and prepended with the public-key-encrypted symmetric encryption key. Finally, the entire block is converted to radix-64 format.
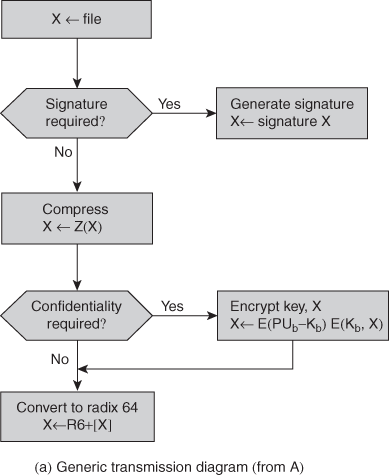
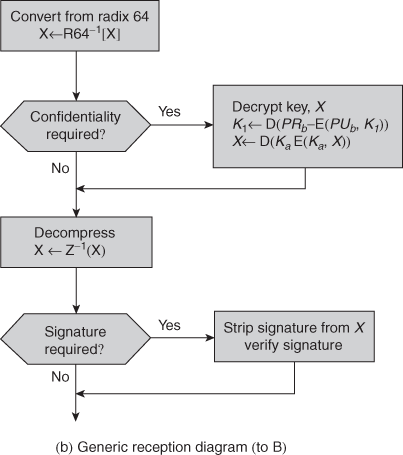
On reception, the incoming block is first converted back from radix-64 format to binary. Then, if the message is encrypted, the recipient recovers the session key and decrypts the message. The resulting block is then decompressed. If the message is signed, the recipient recovers the transmitted hash code and compares it to its own calculation of the hash code.
25. Explain definition, phases, types of virus structures and types of viruses.
Ans: Viruses:
A virus is a piece of software that can “infect” other programs by modifying them; the modification includes a copy of the virus program, which can then go on to infect other programs.
A computer virus carries in its instructional code the recipe for making perfect copies of itself. The typical virus becomes embedded in a program on a computer. Then, whenever the infected computer comes into contact with an uninfected piece of software, a fresh copy of the virus passes into the new program. Thus, the infection can be spread from computer to computer by unsuspecting users who either swap disks or send programs to one another over a network. In a network environment, the ability to access applications and system services on other computers provides a perfect culture for the spread of a virus.
A virus can do anything that other programs do. The only difference is that it attaches itself to another program and executes secretly when the host program is run. Once a virus is executing, it can perform any function, such as erasing files and programs.
During its lifetime, a typical virus goes through the following four phases:
- Dormant phase: The virus is idle. The virus will eventually be activated by some event, such as a date, the presence of another program or file, or the capacity of the disk exceeding some limit. Not all viruses have this stage.
- Propagation phase: The virus places an identical copy of itself into other programs or into certain system areas on the disk. Each infected program will now contain a clone of the virus, which will itself enter a propagation phase.
- Triggering phase: The virus is activated to perform the function for which it was intended. As with the dormant phase, the triggering phase can be caused by a variety of system events, including a count of the number of times that this copy of the virus has made copies of itself.
- Execution phase: The function is performed. The function may be harmless, such as a message on the screen, or damaging, such as the destruction of programs and data files.
Most viruses carry out their work in a manner that is specific to a particular operating system and, in some cases, specific to a particular hardware platform. Thus, they are designed to take advantage of the details and weaknesses of particular systems.
Virus Structure
A virus can be prepended or postpended to an executable program, or it can be embedded in some other fashion. The key to its operation is that the infected program, when invoked, will first execute the virus code and then execute the original code of the program. The virus code, V, is prepended to infected programs, and it is assumed that the entry point to the program, when invoked, is the first line of the program.
A simple virus

An infected program begins with the virus code and works as follows.
- The first line of code is a jump to the main virus program.
- The second line is a special marker that is used by the virus to determine whether or not a potential victim program has already been infected with this virus.
- When the program is invoked, control is immediately transferred to the main virus program. The virus program first seeks out uninfected executable files and infects them.
- Next, the virus may perform some action, usually detrimental to the system. This action could be performed every time the program is invoked, or it could be a logic bomb that triggers only under certain conditions.
- Finally, the virus transfers control to the original program. If the infection phase of the program is reasonably rapid, a user is unlikely to notice any difference between the execution of an infected and uninfected program.
- For each uninfected file P2 that is found, the virus first compresses that file to produce P’ 2, which is shorter than the original program by the size of the virus.
- A copy of the virus is prepended to the compressed program.
- The compressed version of the original infected program, P’1, is uncompressed.
- The uncompressed original program is executed.
Initial Infection
Once a virus has gained entry to a system by infecting a single program, it is in a position to infect some or all other executable files on that system when the infected program executes. Thus, viral infection can be completely prevented by preventing the virus from gaining entry in the first place. Unfortunately, prevention is extraordinarily difficult because a virus can be part of any program outside a system. Thus, unless one is content to take an absolutely bare piece of iron and write all one’s own system and application programs, one is vulnerable.
Types of Viruses
Significant types of viruses:
- Parasitic virus: The traditional and still most common form of virus. A parasitic virus attaches itself to executable files and replicates, when the infected program is executed, by finding other executable files to infect.
- Memory-resident virus: Lodges in main memory as part of a resident system program. From that point on, the virus infects every program that executes.
- Boot sector virus: Infects a master boot record or boot record and spreads when a system is booted from the disk containing the virus.
- Stealth virus: A form of virus explicitly designed to hide itself from detection by antivirus software.
- Polymorphic virus: A virus that mutates with every infection, making detection by the “signature” of the virus impossible.
- Metamorphic virus: As with a polymorphic virus, a metamorphic virus mutates with every infection. The difference is that a metamorphic virus rewrites itself completely at each iteration, increasing the difficulty of detection. Metamorphic viruses my change their behavior as well as their appearance.
One example of a stealth virus that uses compression so that the infected program is exactly the same length as an uninfected version.
For example, a virus can place intercept logic in disk I/O routines, so that when there is an attempt to read suspected portions of the disk using these routines, the virus will present back the original, uninfected program.
A polymorphic virus creates copies during replication that are functionally equivalent but have distinctly different bit patterns. As with a stealth virus, the purpose is to defeat programs that scan for viruses. In this case, the “signature” of the virus will vary with each copy. To achieve this variation, the virus may randomly insert superfluous instructions or interchange the order of independent instructions.
A more effective approach is to use encryption. A portion of the virus, generally called a mutation engine, creates a random encryption key to encrypt the remainder of the virus. The key is stored with the virus, and the mutation engine itself is altered. When an infected program is invoked, the virus uses the stored random key to decrypt the virus. When the virus replicates, a different random key is selected.
Macro Viruses
In the mid-1990s, macro viruses became by far the most prevalent type of virus. Macro viruses are particularly threatening for a number of reasons:
A macro virus is platform independent. Virtually all of the macro viruses infect Microsoft Word documents. Any hardware platform and operating system that supports Word can be infected.
1. Macro viruses infect documents, not executable portions of code. Most of the information introduced onto a computer system is in the form of a document rather than a program.
2. Macro viruses are easily spread. A very common method is by electronic mail.
Macro viruses take advantage of a feature found in Word and other office applications such as Microsoft Excel, namely the macro. In essence, a macro is an executable program embedded in a word processing document or other type of file.
E-mail Viruses
A more recent development in malicious software is the e-mail virus. The first rapidly spreading e-mail viruses, such as Melissa, made use of a Microsoft Word macro embedded in an attachment. If the recipient opens the e-mail attachment, the Word macro is activated. Then
1. The e-mail virus sends itself to everyone on the mailing list in the user’s e-mail package.
2. The virus does local damage.
Worms
A worm is a program that can replicate itself and send copies from computer to computer across network connections. Upon arrival, the worm may be activated to replicate and propagate again. In addition to propagation, the worm usually performs some unwanted function.
An e-mail virus has some of the characteristics of a worm, because it propagates itself from system to system. A worm actively seeks out more machines to infect and each machine that is infected serves as an automated launching pad for attacks on other machines.
Network worm programs use network connections to spread from system to system. Once active within a system, a network worm can behave as a computer virus or bacteria, or it could implant Trojan horse programs or perform any number of disruptive or destructive actions.
To replicate itself, a network worm uses some sort of network vehicle. Examples include the following:
- Electronic mail facility: A worm mails a copy of itself to other systems.
- Remote execution capability: A worm executes a copy of itself on another system.
- Remote login capability: A worm logs onto a remote system as a user and then uses commands to copy itself from one system to the other.
A network worm exhibits the same characteristics as a computer virus: a dormant phase, a propagation phase, a triggering phase, and an execution phase. The propagation phase generally performs the following functions:
1. Search for other systems to infect by examining host tables or similar repositories of remote system addresses.
2. Establish a connection with a remote system.
3. Copy itself to the remote system and cause the copy to be run.
The network worm may also attempt to determine whether a system has previously been infected before copying itself to the system. In a multiprogramming system, it may also disguise its presence by naming itself as a system process or using some other name that may not be noticed by a system operator. As with viruses, network worms are difficult to counter.
The Morris Worm
- The worm released onto the Internet by Robert Morris in 1998.
- The Morris worm was designed to spread on UNIX systems and used a number of different techniques for propagation. When a copy began execution, its first task was to discover other hosts known to this host that would allow entry from this host.
- The worm performed this task by examining a variety of lists and tables, including system tables that declared which other machines were trusted by this host, users’ mail forwarding files, tables by which users gave themselves permission for access to remote accounts, and from a program that reported the status of network connections.
- For each discovered host, the worm tried a number of methods for gaining access:
1. It attempted to log on to a remote host as a legitimate user. In this method, the worm first attempted to crack the local password file, and then used the discovered passwords and corresponding user IDs. The assumption was that many users would use the same password on different systems. To obtain the passwords, the worm ran a password-cracking program that tried
a. Each user’s account name and simple permutations of it
b. A list of 432 built-in passwords that Morris thought to be likely candidates
c. All the words in the local system directory
2. It exploited a bug in the finger protocol, which reports the whereabouts of a remote user.
3. It exploited a trapdoor in the debug option of the remote process that receives and sends mail.
If any of these attacks succeeded, the worm achieved communication with the operating system command interpreter. It then sent this interpreter a short bootstrap program, issued a command to execute that program, and then logged off. The bootstrap program then called back the parent program and downloaded the remainder of the worm. The new worm was then executed.
26. Firewalls:
Ans:
- The firewall is inserted between the premises network and the Internet to establish a controlled link and to erect an outer security wall or perimeter.
- The aim of this perimeter is to protect the premises network from Internet-based attacks and to provide a single choke point where security and audit can be imposed.
- The firewall may be a single computer system or a set of two or more systems that cooperate to perform the firewall function.
Design goals / Characteristics for a firewall:
All traffic from inside to outside, and vice versa, must pass through the firewall. This is achieved by physically blocking all access to the local network except via the firewall.
1. Only authorized traffic, as defined by the local security policy, will be allowed to pass. Various types of firewalls are used, which implement various types of security policies.
2. The firewall itself is immune to penetration. This implies that use of a trusted system with a secure operating system.
- Direction control: Determines the direction in which particular service requests may be initiated and allowed to flow through the firewall.
- User control: Controls access to a service according to which user is attempting to access it. This feature is typically applied to users inside the firewall perimeter (local users). It may also be applied to incoming traffic from external users; the latter requires some form of secure authentication technology, such as is provided in IPSec .
- Behavior control: Controls how particular services are used. For example, the firewall may filter e-mail to eliminate spam, or it may enable external access to only a portion of the information on a local Web server.
3. There are four general techniques that firewalls use to control access and enforce the site’s security policy. Originally, firewalls focused primarily on service control, but they have since evolved to provide all four:
- Service control: Determines the types of Internet services that can be accessed, inbound or outbound. The firewall may filter traffic on the basis of IP address and TCP port number; may provide proxy software that receives and interprets each service request before passing it on; or may host the server software itself, such as a Web or mail service.
Types of Firewalls
There are three common types of firewalls: packet filters, application-level gateways, and circuit-level gateways
Packet-Filtering Router
A packet-filtering router applies a set of rules to each incoming and outgoing IP packet and then forwards or discards the packet. The router is typically configured to filter packets going in both directions (from and to the internal network). Filtering rules are based on information contained in a network packet:
- Source IP address: The IP address of the system that originated the IP packet (e.g., 192.178.1.1)
- Destination IP address: The IP address of the system the IP packet is trying to reach (e.g., 192.168.1.2)
- Source and destination transport-level address: The transport level (e.g., TCP or UDP) port number, which definesapplications such as SNMP or TELNET
- IP protocol field: Defines the transport protocol
- Interface: For a router with three or more ports, which interface of the router the packet came from or which interface of the router the packet is destined for
- The packet filter is typically set up as a list of rules based on matches to fields in the IP or TCP header. If there is a match to one of the rules, that rule is invoked to determine whether to forward or discard the packet. If there is no match to any rule, then a default action is taken.
Advantage:
One advantage of a packet-filtering router is its simplicity. Also, packet filters typically are transparent to users and are very fast.
Weaknesses of packet filter firewalls:
- Because packet filter firewalls do not examine upper-layer data, they cannot prevent attacks that employ application-specific vulnerabilities or functions. For example, a packet filter firewall cannot block specific application commands; if a packet filter firewall allows a given application, all functions available within that application will be permitted.
- Because of the limited information available to the firewall, the logging functionality present in packet filter firewalls is limited.
- Packet filter logs normally contain the same information used to make access control decisions (source address, destination address, and traffic type).
- Most packet filter firewalls do not support advanced user authentication schemes. Once again, this limitation is mostly due to the lack of upper-layer functionality by the firewall.
- They are generally vulnerable to attacks and exploits that take advantage of problems within the TCP/IP specification and protocol stack, such as network layer address spoofing. Many packet filter firewalls cannot detect a network packet in which the OSI Layer 3 addressing information has been altered. Spoofing attacks are generally employed by intruders to bypass the security controls implemented in a firewall platform.
- Finally, due to the small number of variables used in access control decisions, packet filter firewalls are susceptible to security breaches caused by improper configurations. In other words, it is easy to accidentally configure a packet filter firewall to allow traffic types, sources, and destinations that should be denied based on an organization’s information security policy.
- Some of the attacks that can be made on packet-filtering routers and the appropriate countermeasures are the following:
IP address spoofing: The intruder transmits packets from the outside with a source IP address field containing an address of an internal host. The attacker hopes that the use of a spoofed address will allow penetration of systems that employ simple source address security, in which packets from specific trusted internal hosts are accepted. The countermeasure is to discard packets with an inside source address if the packet arrives on an external interface.
Source routing attacks: The source station specifies the route that a packet should take as it crosses the Internet, in the
hopes that this will bypass security measures that do not analyze the source routing information. The countermeasure is to
discard all packets that use this option.
Tiny fragment attacks:
- The intruder uses the IP fragmentation option to create extremely small fragments and force the TCP header information into a separate packet fragment.
- This attack is designed to circumvent filtering rules that depend on TCP header information.
- Typically, a packet filter will make a filtering decision on the first fragment of a packet.
- All subsequent fragments of that packet are filtered out solely on the basis that they are part of the packet whose first fragment was rejected.
- If the first fragment is rejected, the filter can remember the packet and discard all subsequent fragments.
Stateful Inspection Firewalls.
- A traditional packet filter makes filtering decisions on an individual packet basis and does not take into consideration any higher layer context.
- For example, for the Simple Mail Transfer Protocol (SMTP), e-mail is transmitted from a client system to a server system.
- The client system generates new e-mail messages, typically from user input. The server system accepts incoming e-mail messages and places them in the appropriate user mailboxes.
- SMTP operates by setting up a TCP connection between client and server, in which the TCP server port number, which identifies the SMTP server application, is 25. T
- he TCP port number for the SMTP client is a number between 1024 and 65535 that is generated by the SMTP client.
- In general, when an application that uses TCP creates a session with a remote host, it creates a TCP connection in which the TCP port number for the remote (server) application is a number less than 1024 and the TCP port number for the local (client) application is a number between 1024 and 65535.
- The numbers less than 1024 are the “well-known” port numbers and are assigned permanently to particular applications (e.g., 25 for server SMTP). T
- The numbers between 1024 and 65535 are generated dynamically and have temporary significance only for the lifetime of a TCP connection.
- A simple packet-filtering firewall must permit inbound network traffic on all these high-numbered ports for TCP-based traffic to occur.
- A stateful inspection packet filter tightens up the rules for TCP traffic by creating a directory of outbound TCP connections.
- There is an entry for each currently established connection.
- The packet filter will now allow incoming traffic to high-numbered ports only for those packets that fit the profile of one of the entries in this directory.
Application-Level Gateway
- An application-level gateway, also called a proxy server, acts as a relay of application-level traffic.
- The user contacts the gateway using a TCP/IP application, such as Telnet or FTP, and the gateway asks the user for the name of the remote host to be accessed.
- When the user responds and provides a valid user ID and authentication information, the gateway contacts the application on the remote host and relays TCP segments containing the application data between the two endpoints.
- If the gateway does not implement the proxy code for a specific application, the service is not supported and cannot be forwarded across the firewall.
- Further, the gateway can be configured to support only specific features of an application that the network administrator considers acceptable while denying all other features.
Advantage
- Application-level gateways tend to be more secure than packet filters.
- Rather than trying to deal with the numerous possible combinations that are to be allowed and forbidden at the TCP and IP level, the application-level gateway need only scrutinize a few allowable applications.
- In addition, it is easy to log and audit all incoming traffic at the application level.
A prime disadvantage
- Additional processing overhead on each connection.
- In effect, there are two spliced connections between the end users, with the gateway at the splice point, and the gateway must examine and forward all traffic in both directions.
Circuit-Level Gateway
- A third type of firewall is the circuit-level gateway.
- This can be a stand-alone system or it can be a specialized function performed by an application-level gateway for certain applications.
- A circuit-level gateway does not permit an end-to-end TCP connection; rather, the gateway sets up two TCP connections, one between itself and a TCP user on an inner host and one between itself and a TCP user on an outside host.
- Once the two connections are established, the gateway typically relays TCP segments from one connection to the other without examining the contents.
- The security function consists of determining which connections will be allowed.
A typical use of circuit-level gateways is a situation in which the system administrator trusts the internal users.
- The gateway can be configured to support application-level or proxy service on inbound connections and circuit-level functions for outbound connections.
- In this configuration, the gateway can incur the processing overhead of examining incoming application data for forbidden functions but does not incur that overhead on outgoing data.
An example of a circuit-level gateway implementation is the SOCKS package [KOBL92]; version 5 of SOCKS is defined in RFC 1928.
Bastion Host
A bastion host is a system identified by the firewall administrator as a critical strong point in the network’s security. Typically, the bastion host serves as a platform for an application-level or circuit-level gateway. Common characteristics of a bastion host include the following:
1. The bastion host hardware platform executes a secure version of its operating system, making it a trusted system.
2. Only the services that the network administrator considers essential are installed on the bastion host. These include proxy applications such as Telnet, DNS, FTP, SMTP, and user authentication.
3. The bastion host may require additional authentication before a user is allowed access to the proxy services
4. Each proxy is configured to allow access only to specific host systems. This means that the limited command/feature set may be applied only to a subset of systems on the protected network.
5. Each proxy maintains detailed audit information by logging all traffic, each connection, and the duration of each connection. The audit log is an essential tool for discovering and terminating intruder attacks.
6. Each proxy module is a very small software package specifically designed for network security.
7. Each proxy is independent of other proxies on the bastion host. If there is a problem with the operation of any proxy, or if a future vulnerability is discovered, it can be uninstalled without affecting the operation of the other proxy applications. Also, if the user population requires support for a new service, the network administrator can easily install the required proxy on the bastion host.
8. A proxy generally performs no disk access other than to read its initial configuration file. This makes it difficult for an intruder to install Trojan horse sniffers or other dangerous files on the bastion host. Each proxy runs as a nonprivileged user in a private and secured directory on the bastion host.
27. Explain Hill Cipher and encrypt the plain text ‘paymoremoney’ using the ecncryption key
Ans:
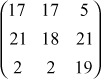
Hill cipher was invented by Lester Hill in 1929. In the encryption algorithm, n successive letters in plaintext are considered as a n-dimension vector P. The algorithm takes a n × n matrix K as a key.The ciphertext C of P is also a n-dimension vector derived by multiplying P by K, modulo 26. That is C = (KP)mod(26). The inverse of the matrix K is used to decrypt the ciphertext. The inverse K−1 of a matrix K is defined by the equation KK−1 = K−1K = I, where I is the identity matrix. In particular, the plaintext P is derived by multiplying ciphertext C by K−1,
i.e., P = (K−1C)mod(26).The cryptographic system of Hill cipher can be summarized as follows.
C = E(K, P) = (KP)mod(26)
P = D(K,C) = (K−1C)mod(26) = K−1KP = P
Consider the plaintext “paymoremoney”, and the key
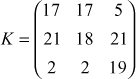
The plaintext is decomposed into 3-letter blocks. For the first block “pay”, its corresponding vector is (15, 0, 24). Then its ciphertext can be derived as
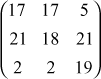 (15 0 24) mod (26) = (375 819 486) mod (26) = (11 13 18) = LNS
(15 0 24) mod (26) = (375 819 486) mod (26) = (11 13 18) = LNS
Applying the same encryption over the rest of 3-letter blocks, we have the ciphertext of the entire plaintext LNSHDLEWMTRW. For decryption, the inverse of key matrix is used.
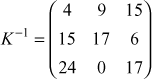
For the first 3-letter block in the ciphertext LNS, its decryption is demonstrated as follows.
 (11 13 18) mod(26) = (431 494 570) mod(26) = (15 0 24) = pay
(11 13 18) mod(26) = (431 494 570) mod(26) = (15 0 24) = pay
The use of a larger n-dimension vector in Hill cipher hides more frequency information, thus provides stronger protection against frequency analysis. Yet Hill cipher is easily broken with a known plaintext attack, because it is completely linear. An opponent who intercepts n2 plaintext/ciphertext character pairs can set up a linear system which can be solved to derive the key matrix.
28. Discuss AES cipher in detail with neat diagram.
Ans: Origins:
- Clear a replacement for DES was needed
- have theoretical attacks that can break it
- have demonstrated exhaustive key search attacks
- Can use Triple-DES – but slow with small blocks
- US NIST issued call for ciphers in 1997
- 15 candidates accepted in Jun 98
- 5 were shortlisted in Aug-99
- Rijndael was selected as the AES in Oct-2000
- Issued as FIPS PUB 197 standard in Nov-2001
AES Requirements:
- private key symmetric block cipher
- 128-bit data, 128/192/256-bit keys
- stronger & faster than Triple-DES
- active life of 20-30 years (+ archival use)
- provide full specification & design details
- both C & Java implementations
- NIST have released all submissions & unclassified analyses
AES Evaluation Criteria:
- Initial criteria:
- security – effort to practically cryptanalyse
- cost – computational
- algorithm & implementation characteristics
- Final criteria
- general security
- software & hardware implementation ease
- implementation attacks
- flexibility (in en/decrypt, keying, other factors)
The AES Cipher – Rijndael:
- designed by Rijmen-Daemen in Belgium
- has 128/192/256 bit keys, 128 bit data
- an iterative rather than feistel cipher
- treats data in 4 groups of 4 bytes
- operates an entire block in every round
- designed to be:
- resistant against known attacks
- speed and code compactness on many CPUs design simplicity
Rijndael:
- processes data as 4 groups of 4 bytes (state)
- has 9/11/13 rounds in which state undergoes:
- byte substitution (1 S-box used on every byte)
- shift rows (permute bytes between groups/columns)
- mix columns (subs using matrix multipy of groups)
- add round key (XOR state with key material)
- initial XOR key material & incomplete last round
- all operations can be combined into XOR and table lookups - hence very fast & efficient
Byte Substitution:
- a simple substitution of each byte
- uses one table of 16x16 bytes containing a permutation of all 256 8-bit values
- each byte of state is replaced by byte in row (left 4-bits) & column (right 4-bits)
- eg. byte {95} is replaced by row 9 col 5 byte
- which is the value {2A}
- S-box is constructed using a defined transformation of the values in GF(28) designed to be resistant to all known attacks
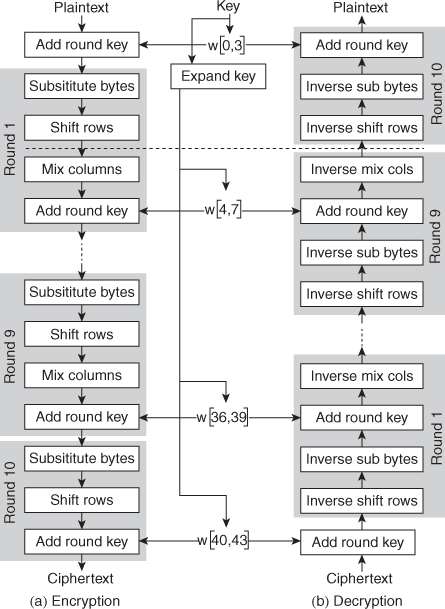
Shift Rows:
- a circular byte shift in each each
- 1st row is unchanged
- 2nd row does 1 byte circular shift to left
- 3rd row does 2 byte circular shift to left
- 4th row does 3 byte circular shift to left
- decrypt does shifts to right
- since state is processed by columns, this step permutes bytes between the columns
Mix Columns:
- each column is processed separately
- each byte is replaced by a value dependent on all 4 bytes in the column effectively a matrix multiplication in GF(28) using prime poly m(x) =x8+x4+x3+x+1

Add Round Key:
- XOR state with 128-bits of the round key
- again processed by column (though effectively a series of byte operations)
- inverse for decryption is identical since XOR is own inverse, just with correct round key
- designed to be as simple as possible
AES Round:

AES Key Expansion:
- takes 128-bit (16-byte) key and expands into array of 44/52/60 32-bit words
- start by copying key into first 4 words
- then loop creating words that depend on values in previous & 4 places back
- in 3 of 4 cases just XOR these together
- every 4th has S-box + rotate + XOR constant of previous before XOR together
- designed to resist known attacks
AES Decryption:
- AES decryption is not identical to encryption since steps done in reverse
- but can define an equivalent inverse cipher with steps as for encryption
- but using inverses of each step
- with a different key schedule
- works since result is unchanged when
- swap byte substitution & shift rows
- swap mix columns & add (tweaked) round key
Implementation Aspects:
- can efficiently implement on 8-bit CPU
- byte substitution works on bytes using a table of 256 entries
- shift rows is simple byte shifting
- add round key works on byte XORs
- mix columns requires matrix multiply in GF(28) which works on byte values, can be simplified to use a table lookup
- can efficiently implement on 32-bit CPU
- redefine steps to use 32-bit words
- can precompute 4 tables of 256-words
- then each column in each round can be computed using 4 table lookups + 4 XORs
- at a cost of 16Kb to store tables
- designers believe this very efficient implementation was a key factor in its selection as the AES cipher
29. Explain in detail about key distribution techniques.
Ans:
Distribution of Public Keys can be considered as using one of:
- public announcement
- publicly available directory
- public-key authority
- public-key certificates
Public Announcement
- users distribute public keys to recipients or broadcast to community at large
- eg. append PGP keys to email messages or post to news groups or email list
- major weakness is forgery
- anyone can create a key claiming to be someone else and broadcast it
- until forgery is discovered can masquerade as claimed user
Publicly Available Directory
- can obtain greater security by registering keys with a public directory
- directory must be trusted with properties:
- contains {name,public-key} entries
- participants register securely with directory
- participants can replace key at any time
- directory is periodically published
- directory can be accessed electronically
- still vulnerable to tampering or forgery
Public-Key Authority
- improve security by tightening control over distribution of keys from directory
- has properties of directory
- and requires users to know public key for the directory
- then users interact with directory to obtain any desired public key securely
- does require real-time access to directory when keys are needed
Public-Key Authority
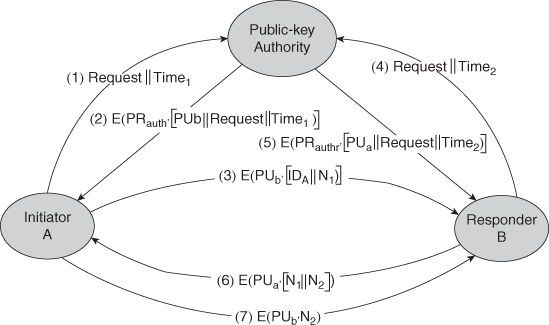
Public-Key Certificates
- certificates allow key exchange without real-time access to public-key authority
- a certificate binds identity to public key
- usually with other info such as period of validity, rights of use etc
- with all contents signed by a trusted Public-Key or Certificate Authority (CA)
- can be verified by anyone who knows the public-key authorities public-key
Public-Key Certificates
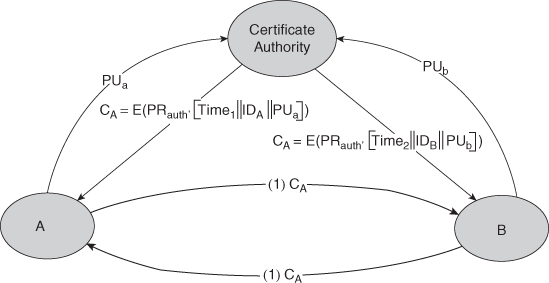
Public-Key Distribution of Secret Keys
- use previous methods to obtain public-key
- can use for secrecy or authentication
- but public-key algorithms are slow
- so usually want to use private-key encryption to protect message contents
- hence need a session key
- have several alternatives for negotiating a suitable session
Simple Secret Key Distribution
- proposed by Merkle in 1979
- A generates a new temporary public key pair
- A sends B the public key and their identity
- B generates a session key K sends it to A encrypted using the supplied public key
- A decrypts the session key and both use
- problem is that an opponent can intercept and impersonate both halves of protocol
Public-Key Distribution of Secret Keys
- if have securely exchanged public-keys:

Hybrid Key Distribution
- retain use of private-key KDC
- shares secret master key with each user
- distributes session key using master key
- public-key used to distribute master keys
- especially useful with widely distributed users
- rationale
- performance
- backward compatibility
30. Perform encryption and decryption using RSA algorithm
P=11 , q=13 , e = 11 and m = 7
Ans: The value of n = p*q = 11*13 = 143
(p-1)*(q-1) = 18*12 = 120
Choose the encryption key e = 11, which is relatively prime to 120 =(p-1)*(q-1).
The decryption key d is the multiplicative inverse of 11 modulo 120.
Run the Extended Euclid algorithm with m = 120 and n = 11.
We find the decryption key d to be also 11 (the multiplicative inverse of 11 in class modulo 120)
The encryption key is (11, 143)
The decryption key is (11, 143)
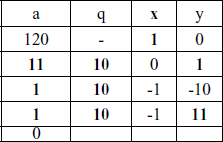
Encryption for Plaintext P = 7
Ciphertext C = Pe mod n = 711 mod 143
71 mod 143 = 7 mod 143 = 7
72 mod 143 = (71 * 71) mod 143 = (7 mod 143 * 7 mod 143) mod 143 = (7 * 7) mod 143 =49 mod 143 = 49
74 mod 143 = (72 * 72) mod 143 = (72 mod 143 * 72 mod 143) mod 143 = (49 * 49) mod 143 = 2401 mod 143 = 113
78 mod 143 = (74 * 74) mod 143 = (74 mod 143 * 74 mod 143) mod 143 = (113 * 113) mod 143 = 12769 mod 143 = 42
711 mod 143 = (78 * 72 * 71) mod 143
= (42 * 49 *7) mod 143
= (((42*49) mod 143) * (7)) mod 143
= ((2058) mod 143) * (7)) mod 143
= ((56) * (7)) mod 143
= (392) mod 143
= 106
Ciphertext is 106
Decryption for Ciphertext C = 106
Plaintext P = Cd mod n = 10611 mod 143
1061 mod 143 = 106 mod 143 = 106
1062 mod 143 = 1061 * 1061) mod 143 = (106 mod 143 * 106 mod 143) mod 143 = (106 * 106) mod 143 = 49 mod 143 = 82
1064 mod 143 = (1062 * 1062) mod 143 = (1062 mod 143 * 1062 mod 143) mod 143 = (82 * 82) mod 143 = 6724 mod 143 = 3
1068 mod 143 = (1064 * 1064) mod 143 = (1064 mod 143* 1064 mod 143) mod 143 = (3 * 3) mod 143 = 9 mod 143 = 9
10611 mod 143 = (1068 * 1062 * 1061) mod 143
= (9 * 82 * 106) mod 143
= (((9 * 82) mod 143) * (106)) mod 143
= (((738) mod 143) * (106)) mod 143
= ((23) * (106)) mod 143
= (2438) mod 143
= 7
Plaintext is 7
31. Write short notes on security of Elliptic Curve Cryptography.
Ans: Relies on elliptic curve logarithm problem
- Fastest method is “Pollard rho method”
- Compared to factoring, can use much smaller key sizes than with RSA etc
- For equivalent key lengths computations are roughly equivalent
- Hence for similar security ECC offers significant computational advantages
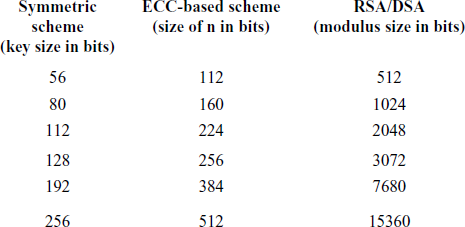
32. Explain Authentication Function in detail.
Ans:
Message authentication or digital signature mechanism can be viewed as having two levels
- At lower level: there must be some sort of functions producing an authenticator – a value to be used to authenticate a message
- This lower level functions is used as primitive in a higher level authentication protocol
- Three classes of functions that may be used to produce an authenticator
- Message encryption
Ciphertext itself serves as authenticator
- Message authentication code (MAC)
A public function of the message and a secret key that produces a fixed-length value that serves as the authenticator
- Hash function
A public function that maps a message of any length into a fixed-length hash value, which serves as the authenticator
Message Encryption
- Conventional encryption can serve as authenticator
- Conventional encryption provides authentication as well as confidentiality
- Requires recognizable plaintext or other structure to distinguish between well-formed legitimate plaintext and meaningless random bits
e.g., ASCII text, an appended checksum, or use of layered protocols
Basic Uses of Message Encryption
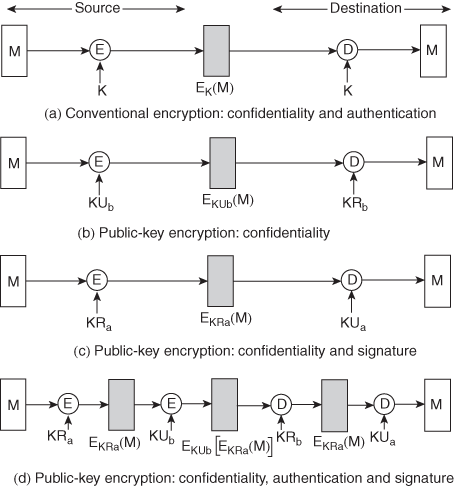
Ways of Providing Structure
- Append an error-detecting code (frame check sequence (FCS)) to each message
Ways of Providing Structure - 2
1. Suppose all the datagrams except the IP header is encrypted.
2. If an opponent substituted some arbitrary bit pattern for the encrypted TCP segment, the resulting plaintext would not include a meaningful header
Confidentiality and Authentication Implications of Message Encryption


Message Authentication Code
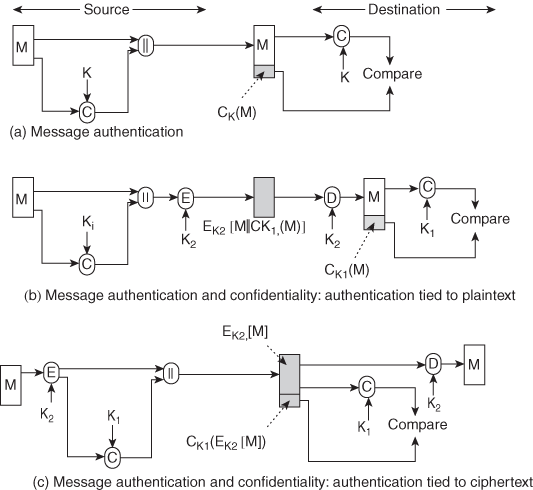
- Uses a shared secret key to generate a fixed-size block of data (known as a cryptographic checksum or MAC) that is appended to the message
- MAC = CK(M)
- Assurances:
- Message has not been altered
- Message is from alleged sender
- Message sequence is unaltered (requires internal sequencing)
- Similar to encryption but MAC algorithm needs not be reversible
Basic Uses of Message Authentication Code C
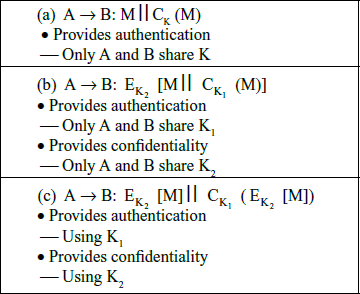
MACs USE
- Cleartext stays clear
- MAC might be cheaper
- Broadcast
- Authentication of executable codes
- Architectural flexibility
- Separation of authentication check from message use
Hash Function
- Converts a variable size message M into fixed size hash code H(M) (Sometimes called a message digest)
- Can be used with encryption for authentication
- E(M || H)
- M || E(H)
- M || signed H
- E( M || signed H ) gives confidentiality
- M || H( M || K )
- E( M || H( M || K ) )
Basic Uses of Hash Function