Table of Contents for

Cryptography and Network Security

Chapter 3

Classical Encryption Techniques

In this chapter, we shall cover some of the basic cryptographic algorithms that were used for providing a secure way of communicating the messages from one person to another person in the olden days. In these cryptographic algorithms, we assign numbers (or) algebraic elements to the given input message to be communicated between two persons. If the assigned numbers (or) algebraic values are in intelligent form, then it is considered as plaintext which is also called clear text. This intelligible plaintext is converted into an unintelligible form called ciphertext. In order to convert the intelligible plaintext into the unintelligible ciphertext, an encryption function is used in the sender side. Similarly, a decryption function is used in the receiver side to find intelligible plaintext from the unintelligible ciphertext. The process of converting the intelligible plaintext into unintelligible ciphertext and back into intelligible plaintext is called cryptography. The cryptographic algorithms are divided into two types, namely secret key cryptography and public key cryptography, which are the two main ideas to perform encryption and decryption. This chapter discusses about secret key cryptography, which is also called symmetric key (single key) cryptography. Public key cryptography will be discussed in Chapter 7. Secret key cryptography is further divided into two types, namely substitution techniques and transposition techniques which are discussed in the later part of this chapter.

3.1 Conventional Encryption

Conventional encryption is a technique in which a single key is used to perform both encryption and decryption operation. The single key used to perform both encryption and decryption operation is called secret key or private key which should be known to both the sender and the receiver. The process of recovering the original, intelligible plaintext from unintelligible ciphertext without using the key value is called cryptanalysis. The combination of cryptography and cryptanalysis is called ­cryptology. Modern encryption protocols will use two keys, namely private key (secret key) and public key. Among the two keys, any one of the keys can be used for performing encryption operation and the other key is used for performing the decryption operation. If the private key is used in the encryption side, then the public key of that private key will be used in the decryption side (vice versa).

3.1.1 The Conventional Encryption Model

In the conventional encryption model, there should be at least two parties to perform secure communication. Let us take the sender name as Alice and the receiver name as Bob. Alice wants to ­communicate a message with Bob in a secure way. In order to do that, the original intelligible message called plaintext is converted into an unintelligible message by Alice and is sent to Bob. To convert the plaintext into ciphertext, the encryption operation takes two parameters as input. They are the original ­intelligible message (P) and a key (K). The key is some bits of information which is generated from a source called key generator. The key is generated independently of the plaintext and is used to convert intelligible message from the original unintelligible message (vice versa). The encryption algorithm uses an encryption function which will produce different ciphertext values for the same plaintext value using different key values. Figure 3.1 shows a conventional encryption model that consists of three components, namely the sender (Alice), the receiver (Bob) and the attacker (Eavesdropper). The main objective of this model is to enable Alice and Bob to communicate over an insecure channel in such a way that the attacker (Eavesdropper) should not understand the original plaintext.

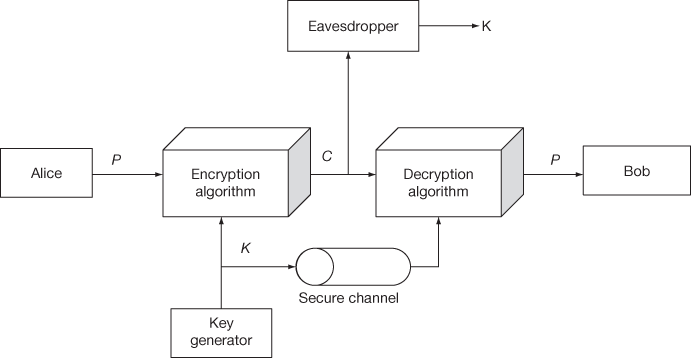
Figure 3.1 Conventional encryption model

Initially, Alice is generating the plaintext P and sends it to the encryption algorithm. The encryption algorithm uses an encryption function to convert the plaintext P into the ciphertext C using a key value K. After computing the ciphertext, Alice transmits it through insecure channel. At the receiver side (Bob), the ciphertext is converted back into the original plaintext using the same key with the help of a decryption algorithm. According to Kerckhoffs principle, the encryption method is assumed to be known to the attacker (Eavesdropper). However, both the sender and receiver keeps the key as secret. As shown in Figure 3.1, the plaintext P and the key K are given as input to the encryption algorithm to produce the ciphertext C and it can be represented as shown below:

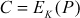
where,

P = plaintext

K = encryption and decryption key

E = encryption algorithm

C = ciphertext

At the receiver side, the ciphertext C and the key K are given as input to the decryption algorithm to produce the plaintext P and it can be represented as shown below:

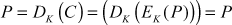
where,

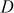= decryption algorithm

During the transmission of the ciphertext, an attacker can capture the ciphertext and tries to perform the following actions:

1. The attacker can find the original plaintext.
2. The attacker can find the key from which he/she can read all messages that are encrypted with the same key in the future.
3. Once the key is found, the attacker can modify the original plaintext into another message in such a way that Bob will believe that the message is coming from Alice.
4. The attacker makes Bob to believe that Bob is communicating with Alice.

3.1.2 Types of Attacks

The attack is a way of breaking the security by finding the key value that depends on the encryption algorithm and some knowledge about the possible structure of the plaintext. The existing methods used for performing an attack depend on whether the ‘attacker’ has ciphertext alone, or pairs of plaintext and ciphertext, or a small amount of information about the plaintext. Based on the information available in the attacker side, an attack is classified into four types, namely, ciphertext-only known attack, known plaintext attack, chosen plaintext attack and chosen ciphertext attack.

3.1.2.1 Ciphertext-only Known Attack

In this attack, an attacker is known with only ciphertext C. From the known ciphertext value, the ­attacker tries to find the key in order to deduce the original plaintext value P. An encryption algorithm is a better algorithm if the algorithm is computationally infeasible to break against ciphertext-only attack.

3.1.2.2 Known Plaintext Attack

In this attack, an attacker is known with small amount of information about the plaintext P. From the known plaintext and ciphertext, the attacker tries to find the key value.

3.1.2.3 Chosen Plaintext Attack

In this attack, an attacker is selecting some known plaintext and ciphertext pairs: (P₁, C₁), (P₂, C₂), …, (P_n, C_n), where P₁, P₂, …, P_n are chosen plaintext values and C₁, C₂, …, C_n are chosen ciphertext values by the attacker. Based on this, when a new ciphertext C arrives, the attacker tries to find the original plaintext P with respect to the ciphertext C. If the original plaintext P is found, it is easy to find the key value.

3.1.2.4 Chosen Ciphertext Attack

In this attack, an attacker is selecting one or more known ciphertexts and sending them into the ­decryption algorithm to obtain the resulting plaintexts. From these pairs of ciphertext and plaintext, the attacker can try to find the key value.

3.2 Substitution Techniques

A substitution technique is a method which replaces (substitutes) each plaintext letter with another alphabetical letter. That is, each of the plaintext letter is substituted (replaced) by another cipher- ­text letter. If the encryption algorithm processes only a single letter at a time to produce the ciphertext letter, it is called a simple substitution encryption algorithm (Caesar cipher). If a cipher operates on a group of plaintext letters, then it is called polyalphabetic substitution algorithm (Vigenere cipher).

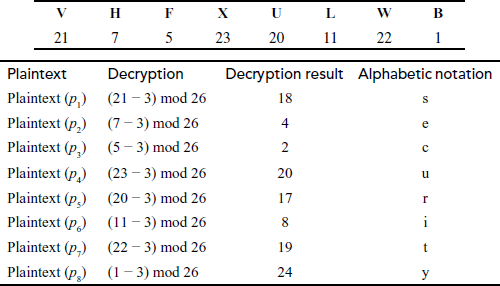
3.2.1 Caesar Cipher (Z⁺_n)

This method was named after Julius Caesar who used it to secretly communicate with his generals. Caesar cipher is the simplest and well-known substitution encryption technique. It is also called shift cipher. Caesar cipher is based on the concept of the additive group (9) and hence it supports addition operation in the encryption function and subtraction operation in the decryption function. Therefore, in this algorithm, the plaintext (p) and key value (K) are selected from (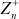 ). Here, each letter of the plaintext is replaced by a letter with some fixed number of positions down the alphabet based on the key value. Therefore, in Caesar cipher, we start at ‘0’ to represent the value of ‘a’ since this shift cipher uses additive group-based encryption function. If any cryptographic algorithm is based on multiplicative group, then ‘a’ value should be considered as 1. If n = 26, then p values are selected from 0 to 25 and K value can be anything from 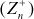. Therefore, p and K values range from 0 to 25 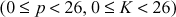. For example, with a shift of three letters ‘a’ would be replaced by ‘D’, ‘b’ would become ‘E’ in such a way that all alphabet are encrypted. Moreover, all the letters are deemed circularly connected. In general, this can be summarized by defining an encryption and decryption functions as shown below.

Encryption function:

C = (p + K) mod 26

Decryption function:

p = (C − K) mod 26

where C is the ciphertext.

p is the plaintext.

K is the key.

p, K, C .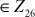

For simplicity, we use lower-case letters to represent plaintext and upper-case letters to represent ciphertext letters in this book. The main advantage of this algorithm is that, it is a simple algorithm and it is widely used one in modern secret-key encryption algorithms. The main limitation of this approach is that, it is easily breakable by brute force attack since it is a simple structure with 26 possible keys. The brute force attack is an attack that tries for all possible keys from 1 to (n − 1), where n is the group size. This algorithm is vulnerable to brute force attack because of the following three reasons. First, the key space is very small since n = 26 in (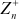 ). Second, we have to assume that the encryption and the decryption algorithms are known to attackers. Finally, the language of the plaintext and ciphertext is known and easily recognizable.

Example 3.1:

Encrypt the plaintext ‘security’ using the Caesar cipher method for the key value K 9 3.

Solution

Encryption:

Plaintext = security Key = 3

plaintext (p):

Ciphertext (C): VHFXULWB

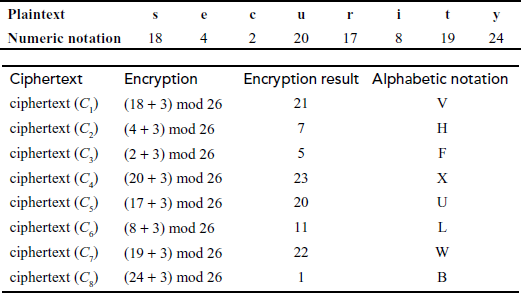
Decryption:

ciphertext (C):

plaintext 9 security

3.2.2 Affine Cipher (Z^*_n)

In Caesar cipher, plaintext messages are encrypted using an additive key. To increase the security level, we can include multiplicative parameter with an additive parameter for encrypting and decrypting the messages. Affine cipher is based on the concept of the multiplicative group (9) and hence it supports multiplication operation in the encryption function and division operation (multiplicative ­inverse) in the decryption function. The readers who are not familiar with multiplicative group shall read ­Section 2.4 prior to this topic for analysis. The affine cipher is a type of substitution cipher, where each letter is encrypted and decrypted using a simple mathematical function. In the affine cipher, the letters of an alphabet of size n are corresponding to the integers of range 0 to (n – 1). Then, this algorithm uses multiplication and multiplicative inverse operations for encrypting and decrypting the messages.

The encryption function can be summarized as shown below:

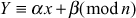
where,

n is the size of the alphabet (group size),

α, β are the key values used in the cipher,

x is the plaintext,

Y is the numerical value of the ciphertext.

The value of x is the numerical value of the given plaintext letter and (α, β ) are the whole numbers between 0 and 25. Note that affine cipher is neither an additive group nor a multiplicative group because the value of n is chosen as 26 which is not a prime number. Therefore, all the values of α cannot produce multiplicative inverse. Because α is multiplied with the plaintext x, there should be a multiplicative inverse element for α in the decryption side. This is not possible here since it is not a multiplicative group when n value is chosen as a composite number (n = 26). Therefore, we have to make it as an Euler group in such a way that all the values of α should produce a multiplicative inverse. In order to satisfy this condition, the value of α must be chosen such that α and n are co-primes and α is relatively prime to 26.

The decryption function used in the receiver side is summarized as shown below:

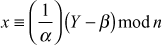
In the decryption function, 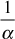is the multiplicative inverse of α with respect to n = 26. The multiplicative inverse of α exists if and only if α and n are co-primes. Hence, without the restriction on α, the decryption is not be possible. α and n are relatively prime if gcd(α, n) = 1. Some of the important conditions to be followed in affine cipher are given below:

1. gcd(α, 26) = 1
2. β = {0, 1, 2, …, 25}
3. α = {1, 3, 5, 7, 9, 11, 15, 17, 19, 21, 23, 25}

Thus, from the above three conditions, it can be concluded that the affine cipher’s key size is 312 (because 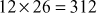). The value 12 represents that only 12 numbers (α) are relatively prime to n as shown in step 3 and 26 represents all the 26 numbers can be used as β. The main advantage of this algorithm is the increase in key size when compared to Caesar cipher since affine cipher involves multiplication as an extra operation along addition operation. But the limitation is that it involves matching of frequently occurred ciphertext letters with frequently occurred plaintext letters. In addition to this, brute force attack is also possible to perform in affine cipher since the key size is only 312.

Example 3.2:

Encrypt the plaintext firewall using Affine cipher method for α = 9 and β = 2.

Solution

Encryption:

plaintext = firewall.

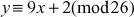
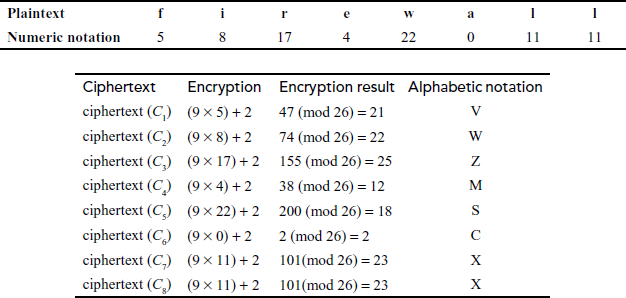
ciphertext: VWZMSCXX

Decryption:

ciphertext = VWZMSCXX

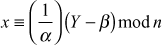
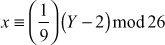
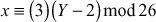
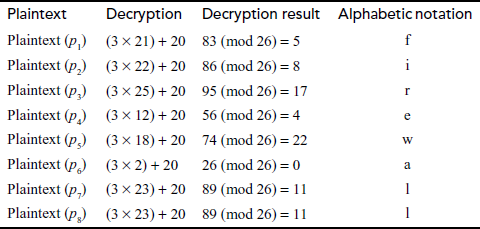
Plaintext: firewall

3.2.3 Playfair Cipher

Playfair cipher was invented by Charles Wheatstone in 1854, which was named after his friend Baron Playfair. This was widely used for many years in the US and the British military during the First World War. Playfair cipher is a polyalphabetic substitution algorithm. In playfair cipher, a pair of ­letters known as digrams is encrypted into another digrams of ciphertext using a 5 × 5 matrix. First, the matrix is filled with letters of the keyword in a rowwise starting from left to right and top to ­bottom. ­After that, remaining cells are filled with the rest of alphabet in their natural order. Usually ‘i’ and ‘j’ are filled within the same cell in order to place all alphabet in their respective cells (within 5 × 5 ­matrix). The reason is 5 × 5 matrix can have a maximum of 25 cells, which cannot store all the ­alphabet since we have 26 alphabetical letters. If the letters ‘i’ and ‘j’ are already available in the key word, then any other two letters will be placed in one cell. For example, if the keyword is ‘Hijack’, then it is necessary to place any two letters other than ‘i’ and ‘j’ in one cell in order to place all the 26 alphabet in a 5 × 5 matrix. Note that, in Playfair cipher, the matrix is deemed circularly connected.

3.2.3.1 Encryption

The following steps are executed in performing the encryption operation in Playfair cipher.

1. If a letter is a repeated in a digram, insert a filler letter like ‘x’ in order to make no repetitions in the digram. For example, if the plaintext is ‘dollar’, it has to be converted into digram ‘do ll ar’. In this case, the letter ‘ll’ repeats in a digram which needs to be segregated by introducing a filler letter ‘x’. After introducing it, the digram would appear like ‘do lx la rx’ for which encryption operation is to be performed.
2. If both letters lie in the same row, then substitute each letter with the letter located to the right (wrapping back to start from the end). For example, if the input digram to the encryption algorithm is ‘ar’, then it will be encrypted as ‘RM’ as shown in Table 3.1.
3. If both letters lie in the same column, then substitute each letter with the letter underneath it (again wrapping to top from bottom). For example, ‘mu’ is encrypted as ‘CM’ as shown in Table 3.1.
4. Otherwise, each letter is replaced by the one lying in its own row and the column of the other letter of the pair. For example, ‘hs’ is encrypted as ‘BP’, and ‘ea’ is encrypted ‘IM’ or ‘JM’ (as desired).

3.2.3.2 Decryption

The following steps are executed in performing the decryption operation in Playfair cipher.

1. If both letters fall in the same row, then substitute each with the letter located to its left (wrapping back to start from the end). For example, if the input digram to decryption algorithm is ‘RM’, then it will be decrypted as ‘ar’ as shown in Table 3.1.
2. If both letters fall in the same column, then substitute each with the letter on top of it (again wrapping to top from bottom). For example, ‘CM’ is decrypted as ‘mu’.
3. Otherwise, each letter is replaced by the letter lying in its own row and the column of the other letter of the pair. For example, ‘BP’ is decrypted as ‘hs’.
4. After completing the decryption operation, remove the filler letter ‘x’ introduced during the encryption operation in order to produce the digram with repetition of letters.

The advantage of this algorithm is that, it has 26 × 26 = 676 diagrams for which it would need 676 combinations to analyse.

3.2.3.3 Cryptanalysis of the Playfair

The Playfair cipher is vulnerable to known plaintext and known ciphertext attack. If the plaintext and ciphertext both are known, then it is easy to find the key. In some cases, ciphertext alone is known to a hacker. In that case, brute force attack can be performed by searching through the key space for matches between the standard frequency of occurrence of digrams and the known frequency of occurrence of digrams in the original plaintext message. For example, the frequently used digrams in the English language are TH, HE, AN can be compared with the frequency of occurrence of digrams in the original plaintext message.

Example 3.3:

Encrypt and Decrypt the plaintext daddy using Playfair cipher for the key value monarchy.

Solution

Initially construct a 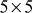matrix and fill it using the letters of the key monarchy. After filling it, fill the rest of the matrix with other alphabet in their natural order.

Table 3.1 Playfair key matrix

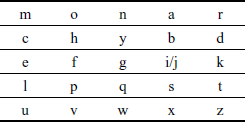
The plaintext (daddy) needs to be converted into digrams. Hence, we should introduce the filler ­letter ‘x’ between ‘d’ in the second digram since there is a repetition. Therefore, the digrams of the given plaintext are ‘da dx dy’.

Encryption of the first digram (da) is = BR (because ‘da’ falls in different row and different column).

Encryption of the second digram (dx) is = BZ (because ‘dx’ falls in different row and different column).

Encryption of the third digram (dy) is = CB (because ‘dy’ falls in the same row).

dadxdy

BRBZCB

Decryption is performed in the reverse order.

Decryption of the first digram (BR) is = da (because ‘BR’ falls in different row and different column).

Decryption of the second digram (BZ) is = dx (because ‘BZ’ falls in different row and different column).

Decryption of the third digram (CB) is = dy (because ‘CB’ falls in the same row).

3.2.4 Vigenere Cipher

The Vigenere cipher was developed by Blaise de Vigenere in the year 1596. Vigenere cipher is an ­example of a polyalphabetic cipher. In this cipher, each plaintext letter is replaced by a ciphertext ­letter from any one of many ciphertext alphabet. Since any letter may be replaced by any other letter of the alphabet, the frequency distribution is diffused here. Therefore, this cipher is suitable for lengthy ­message and this cipher was regarded as unbreakable. Vigenere cipher uses a 26 × 26 table of alphabet as shown in Table 3.2 to which a plaintext letter is used to select a column and a key letter is used to select a row.

Table 3.2 Encryption using Vigenere tableau

Vigenere cipher selects a keyword of arbitrary length. This keyword is used as key to encrypt the plaintext. If the key is smaller than the plaintext, then the key is repeated to fill the whole length of the plaintext. Each ciphertext letter corresponds to the cell at the intersection of the plaintext of a ­column and keyword of a particular row.

Example 3.4:

Encrypt and Decrypt the plaintext tobeornottobe using the Vigenere cipher for the key value Now.

Solution

Repeat the key till the end of the plaintext to cover the whole length of the plaintext since key size is smaller than plaintext size. After that, this can be encrypted using the principle of the Caesar cipher.

3.2.4.1 Encryption

The first character of the plaintext, t is encrypted by the character corresponding to the first character of the key, N. This means that the plaintext, t is encrypted using the key value 14 since the key letter is N by the Caesar cipher method. Hence, the ciphertext is computed by C = (p + K) mod 26 as used in the Caesar cipher method. Therefore, the first ciphertext letter is G (because, C = (19 + 14) = 33 mod 26 = 7). The first ciphertext letter can also be computed by taking the intersection of two letters t and G as shown in Table 3.2. Similarly, other ciphertext letters are computed and the final result would ­appear as shown below:

3.2.4.2 Decryption

In the decryption side, key letter is used to locate the row. After locating the row, the plaintext value is obtained by locating a column value which is indicated by the ciphertext letter available in that particular row. The plaintext letter is at the top of that column. For example, in the key row ‘N’ and for the ciphertext letter ‘G’, the plaintext letter ‘t’ is located at the top. Similarly, other plaintext letters are computed and the final result is shown below:

3.2.4.3 Cryptanalysis of the Vigenere Cipher

The power of this cipher is that there are various ciphertext letters for every plaintext letter. Thus, the frequency distribution is obscured. However, this approach can also be broken by finding the length of the key. In Example 3.4, we have chosen a key, which is smaller than the plaintext. In that case, initially, an opponent considers that the ciphertext was encrypted using monoalphabetic substitution or Vigenere cipher technique. If monoalphabetic substitution is used, then the frequency distribution method can be applied. If the Vigenere cipher method is suspected, then determine the length of the key. In order to find the length of the key, it is necessary to find identical sequences in the ciphertext. If two matching sequences of plaintext letters occur at some distance, then they generate identical ciphertext letter. From this, it is easy to find the length of the key. For example, the plaintext letters ‘tobe’ and ‘tobe’ are separated by nine character positions. In both the cases, the plaintext letter ‘t’ is encrypted with the ciphertext letter ‘G’, ‘o’ is encrypted with the ciphertext letter ‘C’, ‘b’ by ‘X’ and so on. Thus, in both the cases, the ciphertext letters are ‘GCXR’ for the plaintext letters ‘tobe’. So, the distance between the two ciphertext letter sequence ‘GCXR’ is nine which makes the assumption that the key is either nine or three letters in length.

If the key length is N, then the Vigenere cipher consists of N monoaplbabetic substitution ciphers. Thus, we can use the frequency distribution method to attack each of the monoaplbhabetic ciphers separately. If the key length is three as used in Example 3.4, then it will perform the encryption operation as we do in the Caesar ciphers using three key values over and over again. If the key length is one, then the Vigenere cipher will be identical to just using the Caesar cipher. Therefore, the security of the Vigenere cipher depends on the length of the key.

Example 3.5:

Encrypt the plaintext welcome to anna university using the Vigenere cipher for the key value security.

Solution

3.2.5 Vernam One-Time Pad Cipher

First described by Frank Miller in 1882, the one-time pad was re-invented by Gilbert Vernam in 1917 and it was later improved by the US army Major Joseph Mauborgne. This cipher is made as secure by ­using a random sequence of characters as the key value and hence it is unbreakable. This is also called one-time pad since the key is used only once for encrypting a message. This algorithm is unbreakable and more secure algorithm because the key is a random sequence of 0’s and 1’s of the same length as the message. The key used for performing encryption operation is used only once and it is destroyed immediately after sending the message. Therefore, different keys are used for different messages in this method. The encryption is performed by adding the key to the plaintext message mod 2. Hence, it is a bit-by-bit operation which is equal to XOR operation. During the decryption operation, the key is XOR’ed with the ciphertext value to produce the plaintext. The main advantage of this approach is that the encryption method is completely unbreakable for a ciphertext-only known attack. In addition to this, in most cases, a chosen plaintext or chosen ciphertext attack is also not possible.

The main limitations of this approach are given below:

1. Generation of a truly random sequence of 0’s and 1’s is a difficult task.
2. It requires a very long key. It is a computationally complex task to produce a long key and it would take more communication complexity to transmit it to the receiver side.
3. Hence, it is only in limited use.

Example 3.6:

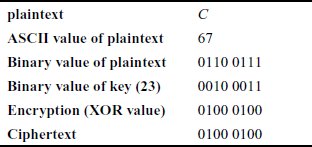
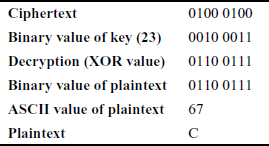
Encrypt and decrypt the plaintext C using the Vernam one-time pad cipher for the key value 23.

Solution

Initially, convert the plaintext into ASCII value in turn convert the ASCII value into binary values.

Encryption:

The plaintext is: C

ASCII value of C: 67

Binary value of 67: 0110 0111

Binary value of the key (23): 0010 0011

Encryption (XOR value): 0100 0100

The ciphertext is 0100 0100 = 44

Decryption:

During the decryption operation, it uses the same key to XOR the key with the ciphertext.

ciphertext 0100 0100 = 44

3.2.6 Hill Cipher (Z^*_n)

The Hill cipher was developed by Lester S. Hill in 1929. The Hill cipher was the first cipher which was purely based on the concept of linear algebra. The Hill cipher makes use of the multiplicative group (9)-based linear algebra and hence it supports matrix multiplication operation in the encryption side and inverse matrix multiplication in the decryption side. The Hill cipher is a polygraphic substitution cipher where a group of plaintext letters is converted into a group of ciphertext letters. For ­converting a group of plaintext letters into a group of ciphertext letters, a key matrix is used. The size of the key matrix is (n × n), where n is number of plaintext letters in a group. If the plaintext letters are divided into 2-gram (digram) group, then the value of n = 2. Hence, a (2 × 2) matrix will be generated as a key matrix. If the plaintext letters are divided into 3-gram (trigram), then a (3 × 3) matrix will be generated as a key matrix. In general, if the plaintext letters are divided into n-gram, then (n × n) ­matrix will be generated. For representing the plaintext letters a–z, the plaintext letters are assigned with decimal values from the range of 0–25.

3.2.6.1 Encryption

The encryption algorithm takes plaintext letters in a group and generates for them ciphertext letters. For generating ciphertext letters, linear equations are generated using the 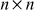key value matrix and plaintext letters. If the plaintext letters are divided into 3-gram (trigram), then 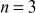. In that case, the cipher can generate three linear equations using the formula shown below:

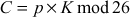
where,

C represents a group of ciphertext letters.

p represents a group of plaintext letters.

K is a key matrix.

.

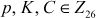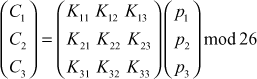
This can be expressed in terms of column vectors and matrices for the n plaintext letters where n = 3 as shown below:

9

3.2.6.2 Decryption

To perform the decryption operation, n ciphertext letters in a group are converted into n plaintext ­letters by multiplying the inverse key matrix with n ciphertext letters. Hence, the inverse key matrix is needed to compute the plaintext letters during decryption operation. In order to compute the inverse matrix, determinant value is computed for the key matrix.

Let K be the key matrix. Let d be the determinant of K. We wish to find the inverse of K(K^–1), such that 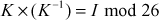, where I is the identity matrix. The following formula is used to find (K^–1) for the key matrix K.

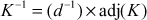
where 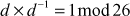and 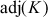is adjoint or adjugate of the key matrix.

Not that all square matrices have inverses and if a square matrix has an inverse, then it is called an invertible or a non-singular matrix. If a square matrix does not have an inverse matrix, then it is called a non-invertible or a singular matrix. This subsection explains the method to find the inverse of a given matrix which may be useful for the readers to understand the working principles of the Hill cipher.

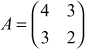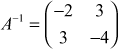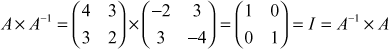Let the given matrix be . The inverse of this matrix is since . There are many ways to find the inverse of a given matrix. In this book, we have only explained a simplest way of finding the inverse matrix. If the input matrix is 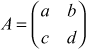, then the inverse of this matrix can be found using the formula, .

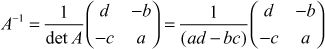For example, compute the inverse matrix of the given matrix 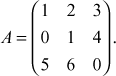In order to find the inverse matrix, first compute the determinant of A. the determinant of A is det A = 1(0 – 24) –2(0 – 20) + 3 (0 – 5) = 1(−24) + 40 − 15 = −39 + 40 = 1. Second, find the transpose of the given input matrix. The transpose of the matrix is 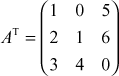. Finally, find the determinant of each of the 2 × 2 minor matrices. The determinants of each of the 2 × 2 minor matrices are given below:

, ,

, ,

, ,

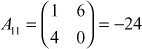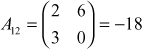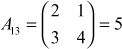
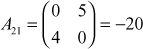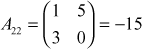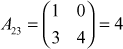
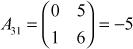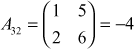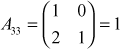
Place the results in to the transpose matrix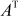 and multiply it with the corresponding symbols available in the matrix 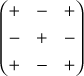. From this, it is easy to find the inverse matrix using the formula,

= .

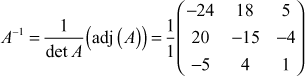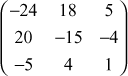Similar to this process, the inverse matrix is computed in the decryption side of the Hill cipher. Once the inverse matrix is found in the decryption side, the receiver can complete the decryption operation using the formula shown below:

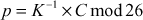
where,

C represents a group of ciphertext letters.

p represents a group of plaintext letters.

K^–1 is the inverse key matrix and .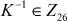

3.2.6.3 Cryptanalysis of Hill Cipher

The Hill cipher hides 1-gram, 2-gram, …, n − 1-gram frequencies. Hence, it is strong against ciphertext only known attacks. However, it can be broken with a known plaintext attack by knowing n-pairs of plaintext vector with ciphertext vectors. From this, it is easy to form a 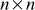matrix as shown below:

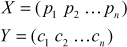
Once the plaintext and ciphertext values are known and it is placed in a vector format, from which, we can find the key value using the following relations:

Y = X × K mod 26

K = X^–1 × Y mod 26

Thus, the key matrix can be computed using known plaintext attack.

Example 3.7

Encrypt and decrypt the plaintext cryptography using the Hill cipher for the key value 9

Solution

plaintext = cryptography

Key =

Encryption:

It is performed using the following formula:

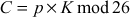
c → 2, r → 17, y → 24, p → 15, t → 19, o → 14, g → 6, r → 17, a → 0, p → 15, h → 7, y → 24.

Consider, for example, the encryption algorithm process trigrams of plaintext letters at a time. Hence, process the first three plaintext letters ‘cry’:

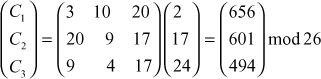
C₁ = 656 mod 26 = 6 = G

C₂ = 601 mod 26 = 3 = D

C₃ = 494 mod 26 = 0 = A

Next process the second trigram ‘pto’:

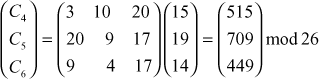
C₄ = 515 mod 26 = 21 = V

C₅ = 709 mod 26 = 7 = H

C₆ = 449 mod 26 = 7 = H

Next process the third trigram ‘gra’:

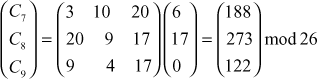
C₇ = 188 mod 26 = 6 = G

C₈ = 273 mod 26 = 13 = N

C₉ = 122 mod 26 = 18 = S

Next process the fourth trigram ‘phy’:

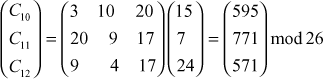
C₁₀ = 595 mod 26 = 23 = X

C₁₁ = 771 mod 26 = 17 = R

C₁₂ = 571 mod 26 = 25 = Z

ciphertext = ‘GDAVHHGNSXRZ’

Decryption:

It is performed using the following formula:

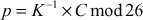
G → 6, D → 3, A → 0, V → 21, H → 7, H → 7, G → 6, N → 13, S → 18, X → 23, R → 17, Z → 25.

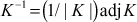
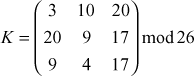
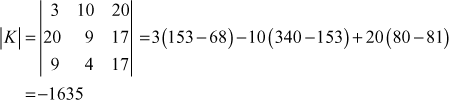
adj K =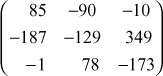

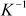= 1/−1635 =

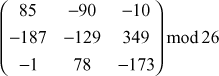Now, decryption can be performed using the inverse matrix computed above. First, decrypt the first ciphertext trigram ‘GDA’.

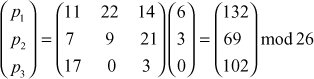
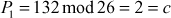
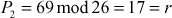
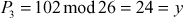
Next, decrypt the second ciphertext trigram ‘VHH’:

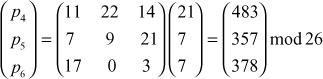
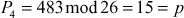
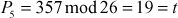
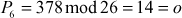
Next, decrypt the third ciphertext trigram ‘GNS’:

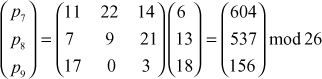
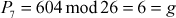
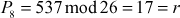
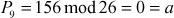
Next, decrypt the fourth ciphertext trigram ‘XRZ’:

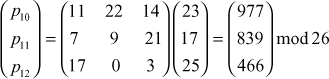
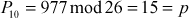
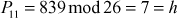
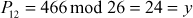
plaintext = ‘cryptography’.

3.3 Transposition Techniques

Transposition techniques are permutation techniques where the plaintext letters are rearranged or permuted according to some given key sequence. Transposition techniques are insecure techniques and are limited in practical use. Transposition techniques are mainly divided into two types, namely, rail fence cipher and column transposition.

3.3.1 Rail Fence Cipher

The rail fence cipher is a type of the transposition techniques in which the plaintext letters are written in the alternating rows and then the message is read off in rows form during the encryption process. This technique is named as rail fence, because the plaintext is written downwards on successive ‘rails’ of a pretend ‘fence’. For example, the plaintext ‘cryptography’ can be written using two ‘rails’ as shown below:

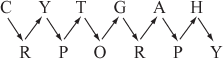
After writing the plaintext letter in a rail fence format, the plaintext letters are read off in rowwise from the first row to the last row. The rails (row) may be taken off in either order to produce the ciphertext. However, in this book, we take the first row first. Therefore, the ciphertext is ‘CYTGAHRPORPY’. The key used to perform encryption and decryption is the number of rails and the order in which they are taken off (two rails are used in the above example). During the decryption process, the ciphertext letters are written in alternate rows. Since, there are 12 letters available in the given example, the first 6 letters are written in the first row and the remaining letters are written in the second row as shown below.

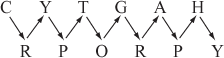
The plaintext can be obtained by reading the letters in rail format.

3.3.2 Column Transposition

Column transposition is a technique in which the message is written in the form of a matrix, row-­ by-row procedure from top to bottom and left to right. After that, the message is read out again column by column depending on the given key value during the encryption process. The row and column size are fixed based on the number of letters available in the plaintext. For example, if there are 49 letters in the plaintext message, then a 7 × 7 matrix is to be declared to place all the 49 letters of the plaintext.

After placing the plaintext letters in a matrix, it is also necessary to select a keyword consists of numbers that should have a length equal to the number of columns. In many cases, the plaintext message can exactly fit in the rectangular matrix. If the message does not completely occupy the square matrix, then filler letter say ‘x’ can be introduced to fill the remaining cells of the matrix. Otherwise, a non-square matrix can be fixed to fill the letters of the plaintext. In the decryption process, the ciphertext is obtained by placing the ciphertext pairs in the correct column according to the key value specified and reading the letters in a row-by-row method. In this way, the plaintext letters are obtained in the receiver side.

Example 3.8:

Encrypt and decrypt the plaintext ‘cryptography’ using the column transposition method for the key value ‘3124’.

Solution

Plaintext is ‘cryptography’ that contains 12 letters. Key = 3124.

Initially, construct a non-square matrix since the plaintext contains 12 letters and fill the plaintext letters top to bottom and left to right in a row-by-row procedure.

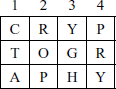
During the encryption process, read off the plaintext letter in column-by-column method according to the order specified by the key value. Therefore, column value is read first, 1^st column value is read next and so on.

Ciphertext = YGHCTAPRYROP

During the decryption process, divide the length of ciphertext by the length of the key to get the plaintext size.

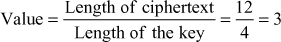
Because, the value is 3, divide the ciphertext letters in a group of three letters. Therefore, the ciphertext = YGH CTA PRY ROP. After that, place the ciphertext group in the right column specified by the key value. For example, first ciphertext pair ‘YGH’ is placed in the third column because first key value is 3. Next, place the second ciphertext pair ‘CTA’ in the first column since second key value is 1. This process is continued by placing all the ciphertext groups in various columns to get the same matrix as used in the encryption side. After completing this process, read off the letters in row-by-row procedure to get the entire plaintext letters. Hence, the plaintext value ‘cryptography’ is obtained.

3.4 Steganography

Steganography is derived from the two Greek words ‘Steganos’ and ‘Graphie’ which mean ‘covered’ and ‘writing’, respectively. The steganography is a data hiding technique in which the content of an original message is being hidden in a carrier such that the variations that take place in the carrier are not visible. In steganography, the feasible carriers are text, image, audio, video and some other digitally representing codes which are used to hold the hidden information. In the case of cryptography, the sender encrypts the message using encryption key and transforms the data into a different form. Then, the encrypted data can be transformed to its original form only by the person who knows the decryption key. The main drawback of cryptography is that the existence of data is not hidden. Even though the encrypted message is unreadable, the attacker can decrypt the message in an infeasible amount of time. This drawback in cryptography is overcome by steganography in which the existence of hidden message is not detectable. The main advantage of steganography is that the transmission of messages from the sender to receiver is very difficult to discover by the attacker. The hidden information may be plaintext, ciphertext, image or anything that can be embedded in a bit stream. The carrier and the embedded message are being combined to produce a stegano-carrier. In order to hide the information into the carrier, there is a need of a key termed as stegano key which is also secret information such as a password. For example, when secret information is hidden within a carrier image, the resulting product is a stegano-image. A feasible formula for the steganography process may be represented as:

carrier image + embedded plaintext + stegano key = stegano-image.

Figure 3.2 shows a steganography system in which the embedding function is represented as Em to which the embedded plaintext, the carrier image and the stegano key are given as inputs. The embedding function hides the plaintext message into the carrier image using stegano key. Thus, the stegano-image (carrier image with the hidden message) is generated by the embedded function and then transferred to the receiver. The receiver receives the stegano-image from which it extracts the embedded plaintext using extraction function represented as Ex in Figure 3.2. The extraction function uses the incoming stegano-image and the steagano key as inputs to obtain the embedded plaintext from the carrier image

.

3.4.1 Modern Steganography Techniques

Some of the modern steganographic techinques are discussed as follows.

• Masking and filtering: It is a technique in which the secret data are masked over the original data by changing the luminance of particular areas. In this technique, the message is embedded within the significant bits of the carrier image and also the carrier image manipulation does not affect the secret message.
• Algorithms and transformations: In this technique, the messages are hidden within the ­mathematical functions. This technique is frequently used in compression algorithms.
• Least significant bit (LSB) insertion: In this technique, the messages are hidden inside LSB of a picture’s pixel information. This technique is good when the carrier image file is bigger than the message file and also the carrier image should be in a grey scale.

3.4.2 Attacks on Steganography

Similar to cryptography, steganography algorithms can also be attacked by attackers using various attacks. There are different kinds of possible attacks in steganography, namely, compression attack, random tweaking attack, reformat attack.

• Compression attack: It is the simplest attack. In this attack, the attackers try to compress the file. The attackers use compression algorithms to remove the extraneous information from a carrier image.
• Random tweaking attack: In this attack, an attacker could simply make fine adjustments (tweaks) on the carrier image to make some modification in the original message in order to confuse the legitimated receiver.
• Reformat attack: In this attack, an attacker can change the format of the file (BMP, GIF, JPEG). Using these different file formats, the attacker can make the legitimated receiver to deny the transmission since there is a change in the file format.

3.4.3 Applications

Some of the applications of steganography are listed as follows.

• It is used to hide military secrets in a carrier source during transmission, because it is impossible to prove the existence of the military secrets inside the carrier.
• Steganography is used to secure the plaintext during secret communication where strong cryptography is impossible.
• In steganography, the existence of confidential data is hidden from an adversary.
• It is very difficult to detect the hidden data by the attacker.

3.5 Linear Feedback Shift Registers

Linear feedback shift register (LFSR) is a shift register which is based on linear operation where the input bit is a linear function of its premature state. Exclusive-OR (XOR) function is the most commonly used linear function in LFSR. For n bit input, the LFSR typically has 2ⁿ – 1 states (a primitive form) which can be made to have 2ⁿ states by providing extended sequence logic. LFSR consists of fewer numbers of flip-flops to store bits and XOR gates to perform linear operation. Each flip-flop has a capability of storing one bit of information. Therefore, if a 4-bit LFSR is to be designed, then four flip-flops are required. Generally LFSR is divided into two types. The first type is external feedback LFSR and the second type is internal feedback LFSR. Both the internal and external feedback LFSR are better than counters because it requires few gates and has a higher clock frequency. LFSRs are used in many applications such as pseudo-noise sequences, generating pseudo-random numbers, fast digital counters and whitening sequences. Due to the repeating sequence of states, the LFSRs can also be used as clock dividers.

Figure 3.3 shows the typical example of external feedback LFSR which consists of three boxes and each box represents a flip-flop in which a bit of information is stored. The bits stored in each flip-flop are denoted as S_{M + i}, where 0 ≤ i ≤ 2ⁿ – 2 and n is the number of bits. The first bit is denoted as S_M in which M = 1 and second and third bits are denoted as S_{M + 1} and S_{M + 2}, respectively. In this case, if the given input is of n-bits, then the external feedback LFSR can execute maximum of 2ⁿ – 1 clock cycles to produce various output bits. For each increment of a clock cycle, the bit in each flip-flop is shifted to the right side of flip-flop which is indicated using the arrow direction. After that, the shifted bit is XORed with previous bit value to produce the new output and it is denoted as ⊕ in Figure 3.3. In this example, this XOR operation is represented by a recurrence relation S_{M + 3} ≡ S_{M + 1} + S_M (mod2). Hence, if the initial values (S₁, S₂ and S₃) are given, then the external feedback LFSR produces the subsequent bits in an effective manner.

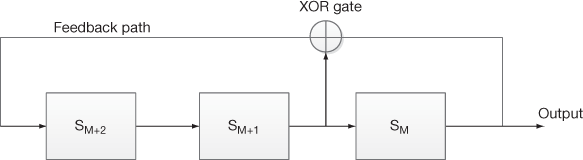
Figure 3.3 External feedback LFSR

Figure 3.4 shows the typical example of internal LFSR. The operation of both external and internal feedback LFSR is same. But the main differences between these two types are that the internal feedback LFSR has a higher clock frequency compared to external feedback LFSR. In both kinds of LFSR, the output of the feedback path is given to the input of first flip-flop. For performing XOR operation in both LFSR, one input is taken from the output of a flip-flop and the other input is taken from the feedback path. The most commonly used flip-flops in LFSR are D-flip-flops. In order to implement more complicated recurrences, it requires more registers and more XORs.

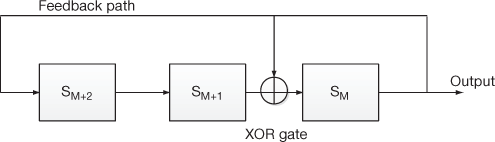
Figure 3.4 Internal feedback LFSR

3.5.1 Linear Recurrence Relation

The linear recurrence relation of length M can be written as

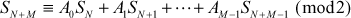
In the linear recurrence relation, if the initial values S₁, S₂, …, S_M are specified, then the subsequent values of S_N can be generated from the initial sequence using recurrence relation. The coefficients A₀, A₁, …, A_M–1 values can be either 1 or 0. If the coefficient is 0, then there is no connection from flip-flop output to an XOR gate for that particular coefficient. Connection is established for the coefficients whose values are 1. Consider, for example, the initial input sequence 11011 can be implemented using D-flip-flops as shown in Figure 3.5.

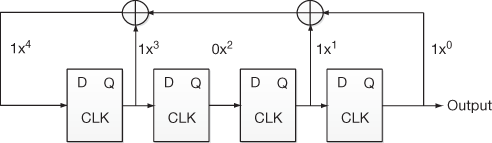
Figure 3.5 Implementation of input sequence 11011 in LFSR

For the given input sequence 11011, the LFSR is designed for, which four flip-flops are required in order to store the first four initial bits (1101) and the last one bit is the output bit which is given to the input of the feedback path. The XOR gates are used to make the linear operations and hence the characteristic polynomial is defined by XOR operations. The characteristic polynomial p(x) = x⁴ + x³ + x¹ + 1 is constructed from the input sequence 11011 in which the coefficient of x² term is 0. Since the coefficient is 0 for x², there is no connection established with the feedback path from the output of the second flip-flop.

3.5.2 LFSR Operation

The LFSR operation is briefly explained in this section by using the characteristic polynomial p(x) = xⁿ + x^n–1 + … + x¹ + 1 in which n represents the degree of polynomial. When it is represented in polynomial, an LFSR must start in a non-zero state. Because it does not produce any pattern and it gets jammed when all are 0’s in that state. The characteristic polynomial of an LFSR that generates a maximum-length sequence is called a primitive polynomial.

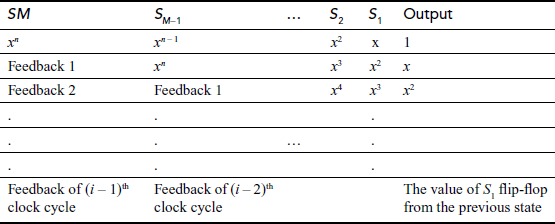
LFSR operation is depicted in Figure 3.6 in which S_M, S_M–1 … S₁ are represented as flip-flops. Initially, the coefficient of xⁿ is stored in the flip-flop S_M. Similarly, the coefficient of x^n–1 is stored in S_M–1 and the coefficients of this polynomial are stored in corresponding flip-flops. Thus, the LFSR produces various states in the shift registers as shown in Table 3.3. In Table 3.3, Feedback 1 represents the feedback generated from the first clock cycle and Feedback 2 represents the second clock cycle. Similarly, (n – 1) clock cycles are generated for a polynomial whose degree is n.

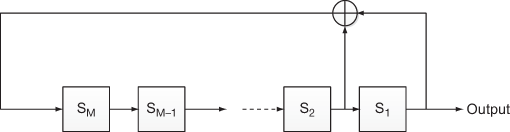
Figure 3.6 LFSR operation

Table 3.3 Various states generated for the polynomial of degree n

Example 3.9:

Construct a LFSR corresponding to the input sequence S₁S₂S₃S₄ = 1100.

Solution

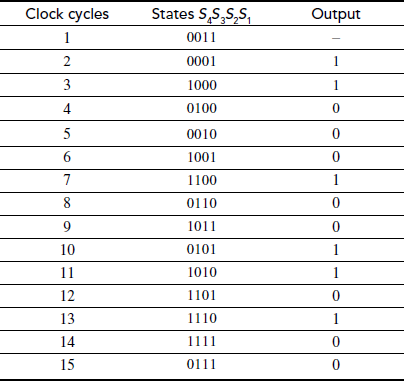
In this example, n = 4 and so the maximum required number of states without generating the repeated sequence is 2⁴ − 1 = 15. In this case, the feedback for each cycle is equal to S₂ ⊕ S_1. In the first clock cycle, the initial value is available in the four flip-flops as shown in Figure 3.7. Then, in the second clock cycle, the XOR operation is being performed between the bits in flip-flops S₂ and S₁. After that, the output of the XOR operation is given to the input of flip-flop S₄ and the values in S₄, S₃ and S₂ are shifted towards right to S₃, S₂ and S₁ as shown in Table 3.4. Thus, the value in the flip-flop S₁ is shifted towards the output. This process is repeated up to 15 clock cycles. After that, the same sequences are repeated from the initial input sequence. Table 3.4 shows the subsequences generated from the initial sequence 1100. The third column output that consists of 1’s and 0’s are taken as the key for encrypting the plaintext to produce the ciphertext.

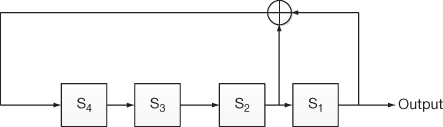
Figure 3.7 LFSR based on the sequence 1100

Table 3.4 The subsequences generated from the initial sequence 1100

Explanation:

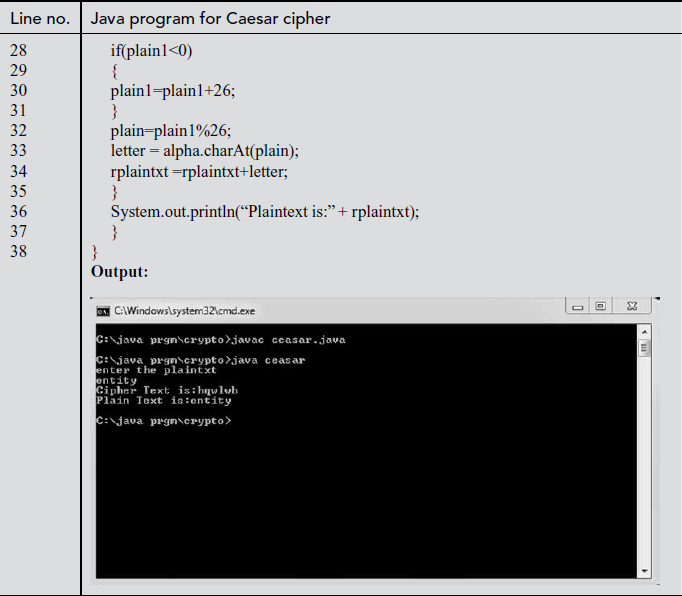
In the above program, the input (plaintext) is given by the user using scanner class which is specified in line number 7. Line number 10 denotes the key value as ‘3’ which is subjected to change. In line number 13, ‘alpha’ is declared as a string variable that contains 26 alphabet. Line numbers between 15 and 21 are used for encryption. In the encryption block, index of each letter in plaintext is stored into ‘num’ variable with respect to alpha. Key value (3) and ‘num’ values are added and the result is stored in ‘cipher1’ variable. The ‘cipher1’ value is taken mod with 26 and the resultant value is stored in ‘cipher’ variable. In line number 19, corresponding character value for ‘cipher’ is stored in the variable ‘letter’. Finally, all ‘letter’ variables are concatenated to form a ciphertext. Line numbers between 24 and 35 are used for decryption. The index of each letter in ciphertext is again stored in ‘num’ variable. Line number 27 is used to subtract the key value (3) from ‘num’ value and the value is assigned to ‘plain1’ variable. In line number 30, ‘plain1’ and ‘26’ are added and the result is stored in ‘plain1’ if and only if the value of plain1 is negative. In line number 32, modulus operation is performed for ‘plain1’ variable with respect to 26 and the resultant value is stored in ‘plain’ variable. In line number 33, corresponding character value of ‘plain’ is stored in ‘letter’ variable. Finally, all ‘letter’ variables are concatenated to form the plaintext given by the user.

Explanation:

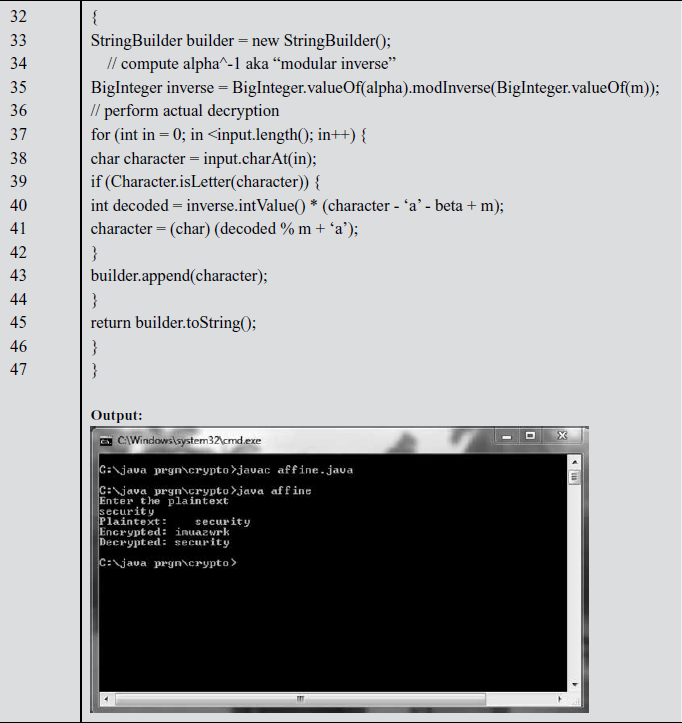
In the above program, line numbers 5, 6 and 7 are used to assign the values for ‘alpha’, ‘beta’ and ‘m’, respectively. Line number 11 is used to get the plaintext from the user. Line numbers between 19 and 26 are used for encrypting the plaintext. In line number 25, ‘alpha’ and input character values are multiplied and added to ‘beta’. In the resultant value of encryption, if the value exceeds 26, then the modulus operation with respect to 26 is performed. Line numbers between 32 and 42 define decryption block. In line number 40, inverse value for alpha with respect to 26 is taken and it is multiplied with the difference of ciphertext and beta to obtain the plaintext given by the user.

Explanation:

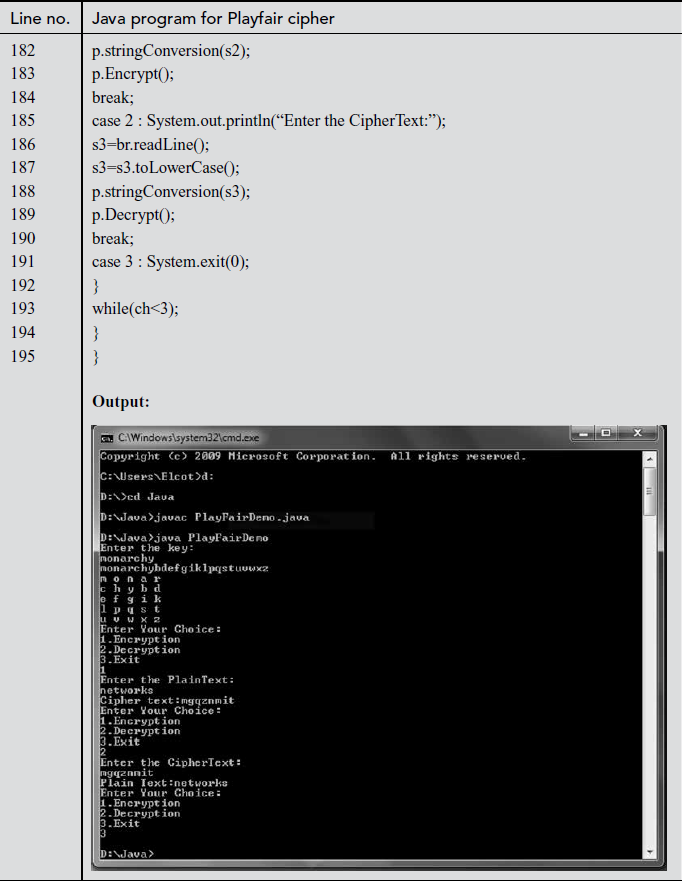
In the above program, Line numbers between 4 and 6 are used for declaring string variables which are used in the program. Line numbers from 8 to 24 are used for setting the key value using the matrix builder function. In line number 47, the key value is displayed. Line numbers between 177 and 194 make use of switch case where ‘encrypt’ and ‘decrypt’ functions are called when choices are selected as 1 and 2, respectively. Line numbers between 76 and 118 are used for encryption. In line number 117, encrypted text is displayed. Line numbers between 120 and 162 are used for decrypting the ciphertext. In line number 161, plaintext for respective ciphertext is displayed.

Explanation:

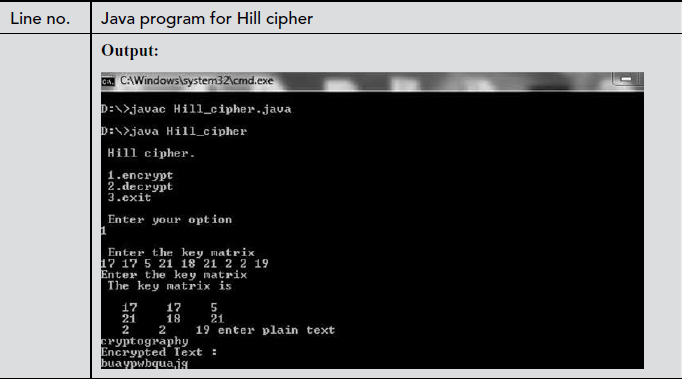
In the above program, line number 10 denotes the object created for Hill cipher class. This object is mainly used to call the encryption and decryption functions. In line number 11, double array variable key[][] is declared which is used to get the key values in a matrix format. Line numbers between 12 and 32 make use of do while loop where encryption and decryption functions are called based on the choice selected by the user. Line numbers between 43 and 51 display the key matrix received from the user. Line number 73 denotes the result of encryption obtained by multiplying key matrix and plaintext. Line numbers between 90 and 131 display the determinant value and the inverse of key matrix entered by the user. Line number 147 denotes the ciphertext for the respective plaintext. Line numbers between 155 and 166 denote the multiplication operation performed between inverse matrix and ­ciphertext. Line number 169 displays the plaintext for corresponding ciphertext.

Explanation:

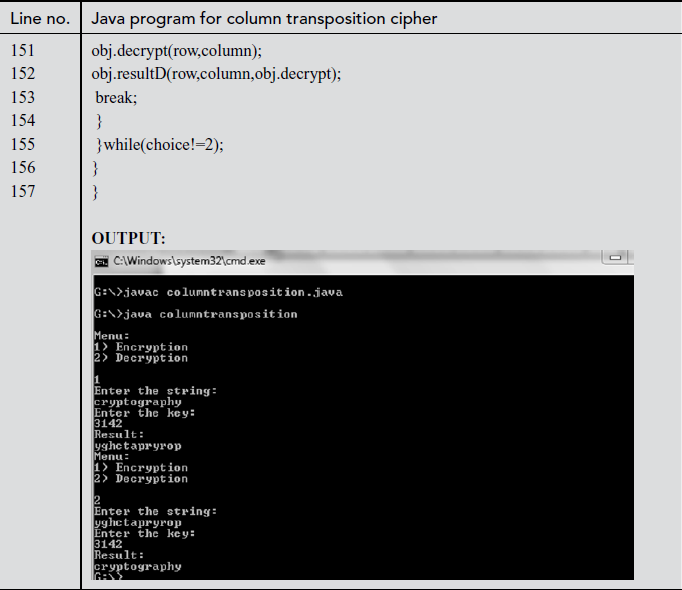
In the above program, line number 4 is used for declaring character array variables such as arr, encrypt, decrypt, keya, keytemp. Line number 128 represents column transposition class created with an object ‘obj’. Line numbers between 133 and 135 take input text and key received from the user and their corresponding values are assigned to s value and key variables. In line number 136, input text length is divided by key length and its value is stored in row variable. In line number 139, key length value is assigned to the column variable. In line number 140, if the choice is 1, then case 1 gets invoked. In line number 143, creatematrixE is called by passing the arguments, namely s, key, row, column. The s value is stored in an array variable arr[][] in matrix format. In line number 144, createkey function is called by passing the arguments, namely, key, column. In line number 145, the encrypt function is called by passing variables of rows and columns. In line number 146, resultE function is called and the encrypted text is printed. In line number 151, ‘decrypt’ function is called and the decrypted value is stored in decrypt[][] array variable. Finally, line number 152 prints the decrypted value using result D function.

Key Terms

Affine cipher

Arbitrary length

ASCII value

Caesar cipher

Ciphertext

Column transposition

Compression algorithms

Confidential data

Cryptanalysis

Cryptography

D-Flip-flops

Decryption

Determinant

Embedding function

Encryption

External feedback LFSR

Extraction function

Extraneous information

Feedback path

Filler letter

Flip-flop

Hidden message

Higher clock frequency

Hill cipher

Identity matrix

Image manipulation

Internal feedback LFSR

Inverse matrix

Key

Key cryptosystem

Key matrix

Keyword

Linear-feedback shift register

Linear algebra

Linear recurrence relation

Luminance

Monoalphabetic substitution

Multiplicative inverse

Non-singular matrix

Plaintext

Playfair cipher

Polygraphic substitution

Polygraphic substitution

Premature state

Primitive polynomial

Public key cryptography

Rail fence cipher

Rectangular matrix

Security

Square matrices

Standard frequency distribution

Stegano-image

Steganography

Substitution techniques

Symmetric key cryptography

Transposition techniques

Two rails

Vigenere cipher

Summary

• The process of converting the intelligible plaintext into unintelligible cipher text and back into intelligible plaintext is called cryptography.
• The process of recovering the original, intelligible plaintext from unintelligible cipher text without using the key value is called cryptanalysis.
• The combination of cryptography and cryptanalysis is called cryptology.
• The key is some bits of information which is generated from a source called key generator.
• A substitution technique is a method which replaces (substitutes) each plaintext letter with another alphabetical letter.
• Caesar cipher is based on the concept of the additive group (Z⁺_n) and hence it supports addition operation in the encryption function and subtraction operation in the decryption function.
• Affine cipher is based on the concept of the multiplicative group (Z^*_n ) and hence it supports ­multiplication operation in the encryption function and division operation (multiplicative inverse) in the decryption function.
• In Playfair cipher, a pair of letters known as digrams is encrypted into another digrams of cipher text using a 5 × 5 matrix.
• Vigenere cipher is an example of a polyalphabetic cipher. In this cipher, each plaintext letter is replaced by a cipher text letter from any one of many cipher text alphabet.
• Vernam one-time pad cipher is used only once for encrypting a message. This algorithm is an unbreakable and a more secure algorithm because the key is a random sequence of 0’s and 1’s of the same length as the message.
• The Hill cipher makes use of the multiplicative group (Z^*_n)-based linear algebra and hence it supports matrix multiplication operation in the encryption side and inverse matrix multiplication in the decryption side.
• The steganography is a data hiding technique in which the content of an original message is being hidden in a carrier such that the variations that take place in the carrier are not visible.
• Steganography algorithms can also be attacked by attackers using various attacks. There are different kinds of possible attacks in steganography, namely, compression attack, random tweaking attack, reformat attack.
• Linear-feedback shift register (LFSR) is a shift register which is based on linear operation where the input bit is a linear function of its premature state.
• In the linear recurrence relation, if the initial values S₁, S₂, …, S_M are specified, then the subsequent values of S_N can be generated from the initial sequence using recurrence relation.
• LFSR operation can be explained using the characteristic polynomial. When it is represented in a polynomial, an LFSR must start in a non-zero state.

Review Questions

1. Encrypt and decrypt the plaintext networks using the Caesar cipher method for the key value K = 7.
2. Perform cryptanalysis over the given cipher text ‘LFDPHLVDZFRQTXHUHG’.
3. Encrypt and decrypt the plaintext computer using Affine cipher method for α = 5 and b = 13.
4. Suppose that K = (a, b) = (α, β) = (7, 3), encrypt and decrypt the word ‘HOT’ using affine cipher.
5. Encrypt and decrypt the plaintext firewall using Playfair cipher for the key value ‘monarchy’.
6. Perform encryption and decryption in the plaintext = balloon, key = MONARCHY using Playfair cipher.
7. Encrypt and decrypt the plaintext tobeornottobe using the Vigenere cipher for the key value ‘Can’.
8. Encrypt and decrypt the plaintext V using the Vernam one-time pad cipher for the key value ‘18’.
9. Encrypt and decrypt the plaintext cipher using the Hill cipher for the key value
10. Break the following cipher. The plaintext is taken from a popular computer textbook, so ‘computer’ is a probable word. The plaintext consists entirely of letters (no spaces). The cipher text is broken up into blocks of five characters, for readability.

    aauan cvlre rurnn dltme aeepb ytust

    iceat npmey iicgo gorch srsoc

    nntii imiha oofpa gsivt tpsit lbolr otoex.

11. Construct a LFSR corresponding to the input sequence S₁S₂S₃S₄ = 1001.