Chapter 7
Public Key Cryptosystem
7.1 Introduction to Public-Key Cryptosystem
All the encryption techniques are purely classified based on the concept of a key. A key is the foundation for transmitting a message into an unintelligible message. Forty years before, only one key was used for performing both the encryption and decryption operations and it is called symmetric/private key cryptosystem [1]. After that, public-key cryptosystem was developed. The public-key cryptosystem uses a pair of keys. Each pair consists of two keys, namely private key and public key. The pair is mathematically related to each other. The private key is kept as secret in the user’s storage space. The public key is publicly announced to all the users. The public-key cryptosystem is also called asymmetric encryption technique, because the same key is not used to encrypt and decrypt the message. Instead, encryption and decryption operations are performed using different keys.
Initially, each user generates a private key from which a public key is computed. After computing the public key, each user stores their public key in a public directory which is called as Certification Authority (CA). This process eliminates the need for sharing the secret key in advance as used in a secret key cryptosystem [2–3]. If any user wants to send a message to any other user, then the user has to download the intended recipient’s public key from the public directory. Then the sending user has to use this public key to encrypt the message and the encrypted message is sent to the recipient. When the recipient gets the message, he/she decrypt it with the recipient’s private key. In a public-key cryptosystem, both the keys can be used for performing encryption and decryption. If a message is encrypted with the recipient’s public key, then it must be decrypted with the recipient’s private key. This provides the cryptographic service, named as confidentiality. If a message is encrypted with the sender’s private key, then it must be decrypted with the sender’s public key. This provides the cryptographic service named as authentication.
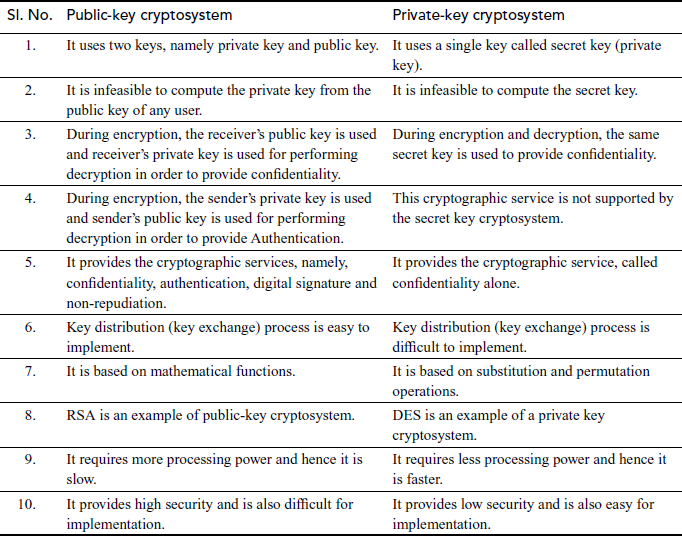
Figure 7.1 shows the way in which the public-key cryptosystem is used for providing cryptographic service called confidentiality. In this figure, Alice (sender) creates a plaintext and encrypts it using the public key 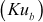 of Bob. This can be decrypted only by using the private key
of Bob. This can be decrypted only by using the private key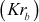 of Bob. Since Bob has his private key
of Bob. Since Bob has his private key 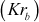 in his computer, no one can decrypt it other than Bob. Figure 7.2 shows the way in which the public-key cryptosystem is used for providing cryptographic service called authentication. In this figure, Alice (sender) creates a plaintext and encrypts it using the private key
in his computer, no one can decrypt it other than Bob. Figure 7.2 shows the way in which the public-key cryptosystem is used for providing cryptographic service called authentication. In this figure, Alice (sender) creates a plaintext and encrypts it using the private key 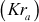 of Alice. This can be decrypted only by using the public key
of Alice. This can be decrypted only by using the public key 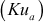 of Alice. In this case, everyone can decrypt it because the public key of Alice is known to all. Hence, this method does not provide confidentiality, but it provides authentication. This method also provides digital signature since the message is encrypted using the sender’s private key. Here, Alice is digitally signing over a message to indicate that the message has come from Alice.
of Alice. In this case, everyone can decrypt it because the public key of Alice is known to all. Hence, this method does not provide confidentiality, but it provides authentication. This method also provides digital signature since the message is encrypted using the sender’s private key. Here, Alice is digitally signing over a message to indicate that the message has come from Alice.
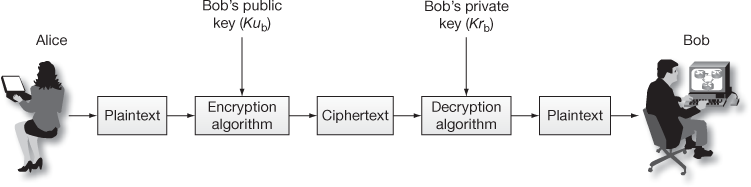
Figure 7.1 Public-key cryptosystem with confidentiality
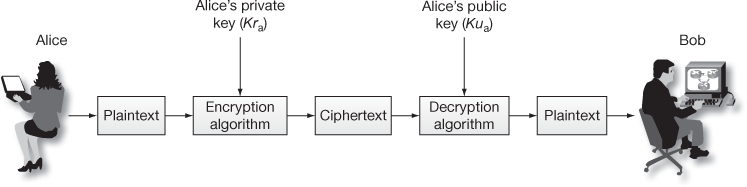
Figure 7.2 Public-key cryptosystem with authentication
In some applications, the sender and receiver expect both the cryptographic services confidentiality and authentication. In such kind of applications, two encryption operations are performed on the sender side and two decryption operations are performed on the receiver side. Figure 7.3 shows an example of this case. In this figure, initially Alice is encrypting the plaintext using the private key 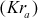 of Alice. This provides authentication. The output of this encryption is denoted as ciphertext 1. The ciphertext 1 is given as input to the second encryption that makes use of the public key
of Alice. This provides authentication. The output of this encryption is denoted as ciphertext 1. The ciphertext 1 is given as input to the second encryption that makes use of the public key 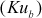 of Bob. This provides confidentiality. In the receiver (Bob) side, Bob has to decrypt using the private key
of Bob. This provides confidentiality. In the receiver (Bob) side, Bob has to decrypt using the private key 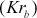 of Bob to get ciphertext 1. The ciphertext 1 can be decrypted using public key
of Bob to get ciphertext 1. The ciphertext 1 can be decrypted using public key 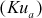 of Alice. The main advantage of this method is that both confidentiality and authentication are provided. The main limitation of this approach is that computation complexity is increased because, double time encryption is performed in the sender and double time decryption is performed in the receiver.
of Alice. The main advantage of this method is that both confidentiality and authentication are provided. The main limitation of this approach is that computation complexity is increased because, double time encryption is performed in the sender and double time decryption is performed in the receiver.
The public-key cryptosystem is used to provide secure electronic communication over the Internet. Since the Internet is an open network, it is susceptible to a variety of security problems such as IP-spoofing, denial of service and man-in-the-middle attacks. In such an open network, when sending a message from one place to another in a secure way, the message should not be known to anyone other than the sender and receiver. This would provide confidentiality of the communication. Moreover, the message should not be modified during transmission in order to provide message integrity. In addition to these two cryptographic services, the public-key cryptosystem also provides the cryptography services such as digital signature and non-repudiation. Table 7.1 gives the difference between public-key cryptosystem and private-key cryptosystem.
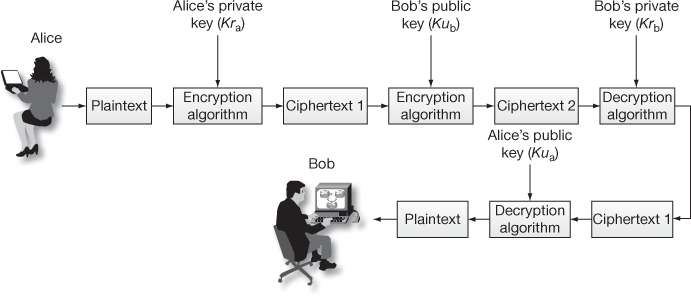
Figure 7.3 Public-key cryptosystem with confidentiality authentication
Table 7.1 Difference between public and private-key cryptosystem
From Table 7.1, it is clear to understand that public-key cryptosystem is a computationally expensive one. But it provides more security. In order to increase the security level, large-size key values are used. For example, 512 bits or 1024 bits is used in RSA and Elgamal public-key cryptosystem. However, the private key cryptosystem is less computationally expensive and hence it provides low security. Therefore, it is advised to combine the public and private-key cryptosystem together to form a new cryptosystem which is called hybrid cryptosystem. This hybrid cryptosystem is efficient in terms of speed and security. In the hybrid cryptosystem, a key-exchange algorithm is used to exchange a secret key using the public-key cryptosystem. After exchanging the key successfully, a private key (symmetric key) cryptosystem can be used for exchanging the messages securely. The hybrid cryptosystem is used in many places such as PGP and the SSL/TLS. It is also used in all the secure multimedia multicast applications such as video on demand, video broadcasting, Pay-TV, etc.
7.2 RSA Algorithm
Rivest, Shamir and Adleman [4] were a perfect team in developing a new public-key cryptosystem. Rivest is a computer scientist who has innovated new ideas in new places. Shamir was also a computer scientist who has an ability to focus on the core of a problem. Rivest and Shamir generated ideas for the one-way function that could be used in any of the public-key cryptosystems. Adleman was responsible for finding the flaws within the ideas of Rivest and Shamir, and he ensured that they were proceeding in the right direction. Rivest, Shamir and Adleman joined together and proposed RSA algorithm at MIT in the year 1977. Hence, RSA stands for Rivest, Shamir and Adleman. It was published as one of the first public-key cryptosystems in 1978. Since it is a public-key cryptosystem, the sender can use receivers public key for encrypting the message and the receiver can use receivers private key for decrypting the message.
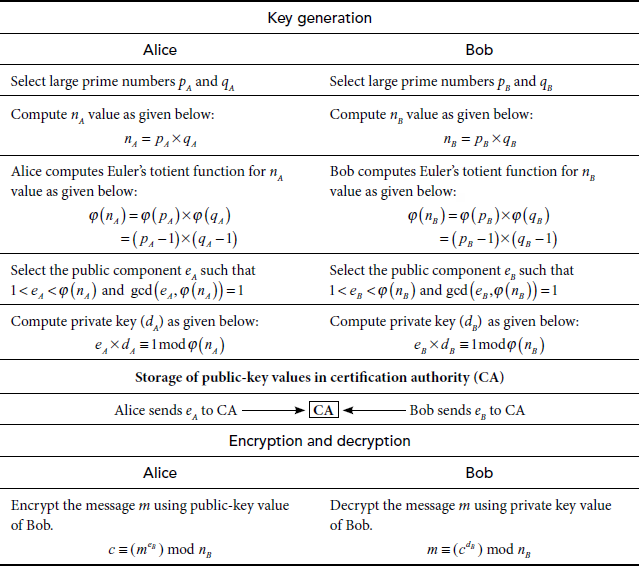
The RSA is a best known and widely used public-key scheme that uses large integers (1024 bits) as key values. It is a block cipher and hence it can encrypt and decrypt a block of letters at a time. It also provides high security since it relies on the difficulty to factor the large integers. The RSA algorithm consists of three phases, namely, key generation, encryption and decryption. In key generation phase, each user selects their public key from which they compute their corresponding private key. The public key is stored in a CA and private key is kept as secret. During the encryption phase, a block of plaintext letters is encrypted to produce ciphertext value, where each plaintext letter is converted into a suitable sequence of integers such that a = 1 and z = 26. Significant steps of key generation phase are briefly explained as follows:
Step 1: Initialization
The sender (Alice) and the receiver (Bob) select two large prime numbers. Alice selects the prime numbers as 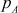 and
and 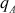 . Bob selects prime numbers as
. Bob selects prime numbers as  and
and 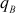 .
.
Step 2: Computation of 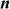 value
value
After that, both the sender and the receiver compute 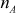 and
and 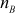 values as given below:
values as given below:
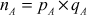
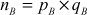
Here, 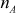 and
and 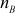 are used as the modulus for both the public and private keys.
are used as the modulus for both the public and private keys.
Step 3: Computes Euler’s totient function
Next, Alice and Bob compute Euler’s totient function of 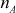 and
and 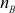 values as given below:
values as given below:
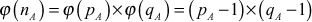
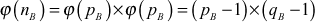
Since 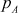 ,
, 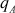 ,
, 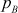 and
and 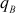 are prime numbers, Euler’s totient function of these values is obtained by subtracting the respective prime numbers from one as shown above.
are prime numbers, Euler’s totient function of these values is obtained by subtracting the respective prime numbers from one as shown above.
Step 4: Generation of Public keys
After computing these values, Alice and Bob generate their own public-key values 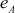 and
and 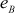 . When they generate the pubic key value, they should check two conditions given below:
. When they generate the pubic key value, they should check two conditions given below:
- 1.
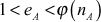
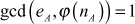 .
.
The value 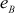 should also satisfy the above two conditions.
should also satisfy the above two conditions.
Step 5: Generation of Private keys
After computing the public key, Alice and Bob compute their corresponding private key (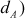 and
and 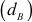 as given below:
as given below:
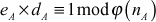
Similarly, 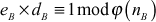
Step 6: Publish the public keys
After computing the private and public-key values, both the users publish their public-key values 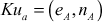 and
and 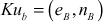 in a public directory.
in a public directory.
Step 7: Make private key as secret
After publishing the public keys, each user keeps their own private key values 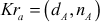 and
and 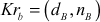 as secret.
as secret.
Encryption and Decryption
To send a message in a secure way from Alice to Bob, intially Alice has to download the public-key value of Bob from the public directory. After getting the public key, she can encrypt the plaintext 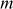 by using the public-key value of Bob to produce a ciphertext. The encryption process is done as given below.
by using the public-key value of Bob to produce a ciphertext. The encryption process is done as given below.
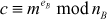
This cipher text value is sent to Bob. Bob can decrypt the ciphertext using his own secret key value dB. The decryption is done as given below.
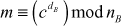
Thus, the plaintext 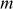 is obtained.
is obtained.
Proof of correctness:
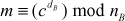
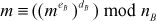
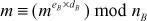
(Since, 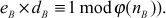 This can be written as
This can be written as 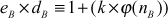
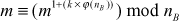
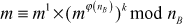
(using Fermat–Euler’s totient theorem 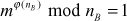 )
)
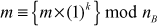

Figure 7.4 shows the diagrammatic representation of an RSA public-key cryptosystem. In this figure, Alice and Bob initially generate two prime numbers and compute a public and private key from those two prime numbers. After that, both the users store their public-key value in the CA. If Alice wants to send a message to Bob in a secure way, the public key of Bob is to be downloaded from the CA. Using the public key, Alice can encrypt the message and the encrypted message can be sent to Bob. Bob can decrypt it using his own private key as shown in Figure 7.4. Table 7.2 gives the overall summary of RSA public-key cryptosystem. In this table, we have considered Alice as sender and Bob as receiver.
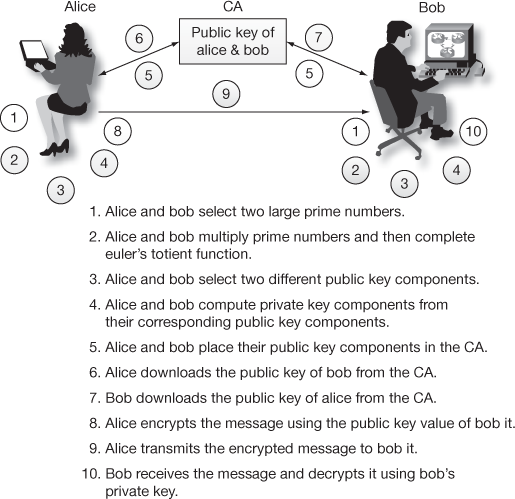
Figure 7.4 RSA public-key cryptosystem with confidentiality
Table 7.2 Summary of RSA algorithm
Example 7.1:
Encrypt the plaintext ‘security’ using the RSA algorithm for the values 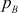 = 7,
= 7, 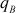 = 11 and
= 11 and 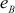 = 13.
= 13.
Solution
Encryption:
Plaintext = security
plaintext (p) :
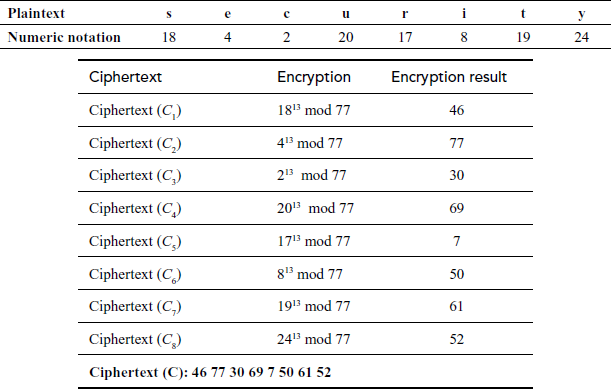
Decryption:
Ciphertext (C): 46 77 30 69 7 50 61 52
Key generation in Bob side:
-
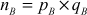 = 7 × 11 = 77
= 7 × 11 = 77 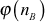 =
= 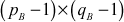 = (7 - 1) × (11 - 1) = 6 × 10 = 60
= (7 - 1) × (11 - 1) = 6 × 10 = 60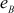 = 13
= 13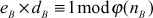
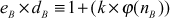
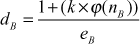
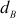 = ((
= ((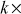 60) + 1)/13
60) + 1)/13If
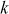 = 1,
= 1, 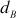 = 61/13 = 4.69
= 61/13 = 4.69If
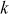 = 2,
= 2, 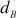 = 121/13 = 9.30
= 121/13 = 9.30If
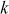 = 3,
= 3, 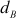 = 181/13 = 13.92
= 181/13 = 13.92If
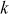 = 4,
= 4, 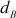 = 241/13 = 18.53
= 241/13 = 18.53If
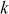 = 5,
= 5, 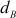 = 301/13 = 23.15
= 301/13 = 23.15If k = 6, dB = 361/13 = 27.76
If k = 7, dB = 421/13 = 32.38
If k = 8, dB = ((8 × 60) + 1)/13 = 481/13 = 37
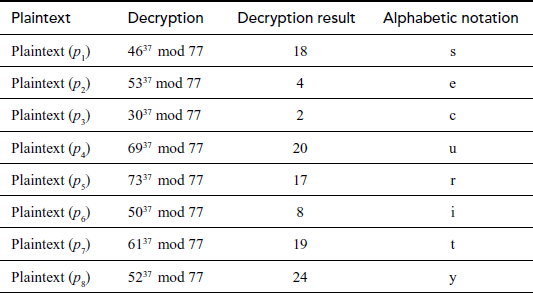
plaintext = security
7.3 Attacks on RSA
There are three kinds of attacks that can be performed on the RSA algorithm. The three well-known attacks are brute-force attack, mathematical attack and timing attack [5].
7.3.1 Brute-Force Attack
It is a trial-and-error method. In this attack, an intruder tries for all possible trials to find the private key of the receiver and to decrypt the ciphertext. If the size of private key (dB) is w bits, then the attacker has to use 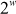 total number of trials. The time taken to derive dB can be increased by choosing the large dB for each user’s private key. In this algorithm, the size of dB must be 512 bits or 1024 bits. Therefore, when large-size pB and
total number of trials. The time taken to derive dB can be increased by choosing the large dB for each user’s private key. In this algorithm, the size of dB must be 512 bits or 1024 bits. Therefore, when large-size pB and 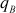 are used, it is not possible to find the value of dB. One of the limitations of choosing large size key is that computation complexity of RSA would increase.
are used, it is not possible to find the value of dB. One of the limitations of choosing large size key is that computation complexity of RSA would increase.
7.3.2 Mathematical Attack
This is an attack in which an intruder focuses on factoring the product of two prime numbers from which, the intruder will try to find the value of dB. This attack can be performed by computing the Euler’s totient value of nB or factoring nB into two prime numbers 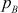 and
and 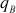 to compute
to compute 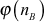 .
.
Let 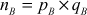 , where
, where 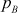 and
and 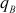 are distinct odd primes and let
are distinct odd primes and let 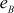 be an integer which is relatively prime to
be an integer which is relatively prime to 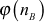 . Let
. Let 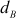 satisfy
satisfy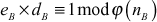 and
and 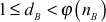 . In this equation, the intruder knows the value of eB and the intruder can compute
. In this equation, the intruder knows the value of eB and the intruder can compute 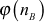 from nB since nB is a public value. If these two values are known, then the attacker can compute dB by substituting eB and
from nB since nB is a public value. If these two values are known, then the attacker can compute dB by substituting eB and 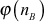 in
in 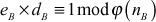 .
.
7.3.3 Timing Attack
Timing attacks resemble to side channel attacks that utilize some vital information regarding time, power and sound, etc. This attack was introduced by Paul Kocher. It mainly depends on the running time of the decryption operation used in the RSA decryption algorithm. Here, the attacker infers the time for decryption by the receiver and thereby essential ingredients of the private key of the receiver can be easily known by the attacker. Moreover, sometimes the original private key can also be known using this attack. Timing attack mainly depends on the size of data that is intended for decryption by the receiver. Timing attack creates a greater impact by destroying the security of the entire system since the private key of the receiver is being exposed. Many public-key cryptographic algorithms can also be attacked using this timing attack. There are three possible countermeasures for this timing attack that are listed below:
- Constant exponentiation time
- Random delay
- Blinding.
Among these three countermeasures, blinding is an effective method by which disclosure of the private key can be avoided. All these three countermeasures are briefly explained below:
Constant exponentiation time: In this countermeasure, the time taken for exponentiation calculation in the decryption side of the receiver is taken as a constant. On taking exponentiation calculation time as a constant value, the actual time for decryption would not be revealed to the attacker and thereby timing attack is prevented. But this countermeasure is not much efficient because of the reason that, the constant exponentiation calculation time can also be revealed to the attackers after a prolonged inspection on the decryption process and hence this becomes inefficient.
Random delay: In this countermeasure, a random delay is introduced while sending the message to the receiver. By introducing this random delay, the time predicted by the attacker during decryption would go wrong and hence an incorrect value would be resulted as a private key by the attackers. However, this countermeasure too has a drawback. The drawback is that, a series of random delays introduced by the senders is composed by the attackers based on which the time for decrypting the actual message becomes certain by the attackers.
Blinding: This is more efficient than all other countermeasures to avoid timing attack. In this countermeasure, before performing the exponentiation operation, the message is multiplied with a constant and the result is corrected by multiplying with another constant. Thus, introducing two constants makes it much difficult for the attackers to guess the actual time of decryption and hence this countermeasure blinds the attackers. In addition to that, this countermeasure gives an uncertain inference to attackers in choosing the two constants in the analysis of timing attack.
7.4 JAVA Implementation of RSA


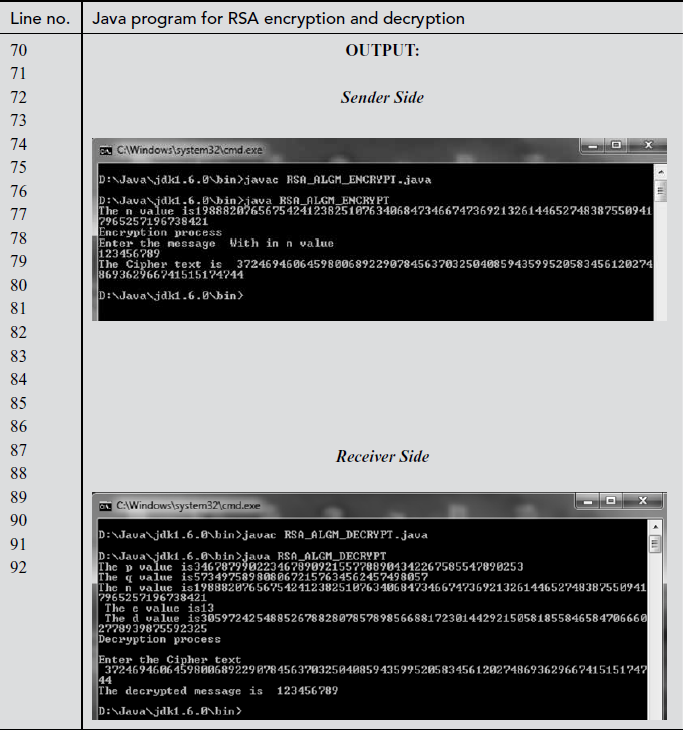
In the above program, there are two modules that can be used in the sender and receiver side. In line number 11 of the sender module, the public component n is defined. In the same module, the public value (e) of the receiver is copied in line number 13. Line numbers between 19 to 26 are used for performing the encryption operation in the sender side. Line numbers between 37 to 41 in the receiver side are used for initializing the large prime numbers p, q and the public-key value e. Line number 43 is used for computing the private key d to be used in the decryption operation. Line number 53 is used for performing the decryption operation in the receiver side.
7.5 Knapsack Cryptosystem
It is a public-key cryptosystem and hence it requires two keys for encryption and decryption purposes. Among the two keys, one key is made as a public key which can be used to encrypt the message and another key is a private key which is kept secret and is used for decrypting the message. Therefore, the person who knows the private key can decrypt the message. Merkle–Hellman published the knapsack public-key cryptosystem in the year 1978. Subsequently, in 1982, the basic Merkle–Hellman knapsack cryptosystem was broken by Shamir’s attack on single-iteration knapsack cryptosystem and hence it is not a secure algorithm.
7.5.1 Definition
Let us consider a predefined set of positive integers which is termed as knapsack 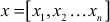 that is an n-tuple. The plaintext
that is an n-tuple. The plaintext 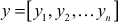 is also an n-tuple that consists of values 0 and 1. Based on the values of the plaintext, we can define the elements of x that are discharged from the knapsack. For the given knapsack and the plaintext, the ciphertext S can be generated in the knapsack cryptosystem using the following equation.
is also an n-tuple that consists of values 0 and 1. Based on the values of the plaintext, we can define the elements of x that are discharged from the knapsack. For the given knapsack and the plaintext, the ciphertext S can be generated in the knapsack cryptosystem using the following equation.
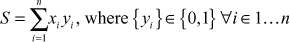
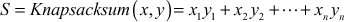
From the above equation, it is easy to obtain the value of S if the values of x and y are given. But it is not possible to obtain the value of y even if the values of S and x are known. That is, 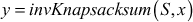 is difficult to find from S and x. Hence, it is distinctly shown that Knapsacksum is a one-way function if x is a common n-tuple. The common n-tuple is the one that does not satisfy superincreasing knapsack.
is difficult to find from S and x. Hence, it is distinctly shown that Knapsacksum is a one-way function if x is a common n-tuple. The common n-tuple is the one that does not satisfy superincreasing knapsack.
7.5.2 Superincreasing Knapsack
Let us consider a knapsack tuple 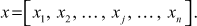 This tuple is said to be superincreasing knapsack, if and only if
This tuple is said to be superincreasing knapsack, if and only if 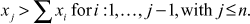 If x is a superincreasing knapsack tuple, it is easy to calculate the value of y provided the values of S and x are known. In superincreasing knapsack tuple, each value is greater than or equal to the sum of its previous values except the first value. The following example shows the way of finding superincreasing knapsack tuple.
If x is a superincreasing knapsack tuple, it is easy to calculate the value of y provided the values of S and x are known. In superincreasing knapsack tuple, each value is greater than or equal to the sum of its previous values except the first value. The following example shows the way of finding superincreasing knapsack tuple.
Example 7.2:
Check whether the given tuples [2, 4, 10, 13] and [1, 2, 4, 8] are superincreasing or not.
Solution
In the first tuple, compare the second value 4 with the first value 2. In such a comparison, the current value 4 is greater than the previous value 2. Then, add the value 4 with 2 and compare the sum 6 with 10. This also satisfies the superincreasing principle. Again add the values 2, 4, 10 and then compare the sum 16 with the next value 13 in the tuple. In this case, it is not greater than the sum 16 (13 ≮ 2 + 4 + 10) and hence it does not satisfy the superincreasing principle. Hence, it is not a superincreasing tuple. Similarly, in the second tuple, compare the second value 2 with the first value 1. Since 2 is greater than the previous value 1, it satisfies the superincreasing principle. Then, add the value 2 with 1 and compare the sum 3 with 4. This also satisfies the superincreasing principle. Finally, add the values 1, 2, 4 and then compare the sum 7 with the next value 8. In this case, the result is greater than the sum 7 (8 > 1 + 2 + 4) and hence it satisfies the superincreasing principle. Hence, it is an example for superincreasing tuple.
Example 7.3:
Encrypt the plaintext 10011110100101100000 using the knapsack [1 2 8 15 26].
Solution
In this example, the given knapsack has five values. Therefore, the given plaintext sequence is decomposed into subsequences each has 5 bits length. The ciphertext is generated from the plaintext and the knapsack using the equation 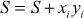 . Let us consider the first subsequence 10011 and knapsack [1 2 8 15 26] from which the ciphertext S can be generated as S = 1 × 1 + 0 × 2 + 0 × 8 + 1 × 15 + 1 × 26 = 42. Similarly the ciphertext can be generated from other subsequences.
. Let us consider the first subsequence 10011 and knapsack [1 2 8 15 26] from which the ciphertext S can be generated as S = 1 × 1 + 0 × 2 + 0 × 8 + 1 × 15 + 1 × 26 = 42. Similarly the ciphertext can be generated from other subsequences.

7.5.3 Encryption and Decryption Algorithm for Knapsack Cryptosystem


7.5.4 Secret Communication using Knapsack
This part explains the way of transferring a message from sender to receiver in a secure way using knapsack cryptosystem. To exchange the message in a secure way, three phases are involved, namely key generation phase, encryption phase and decryption phase.
7.5.4.1 Key Generation Phase
The following steps are involved in the key generation process to generate encryption and decryption keys.
- Take a superincreasing sequence
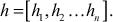
- Decide a modulus number p which should be greater than the sum of all the numbers in the sequence
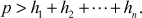
- Then, choose a multiplier q which is relatively prime to p and
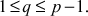
- Then, choose another tuple
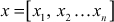 of same size n in which
of same size n in which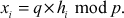
- Therefore, the tuple x is assigned as a public key.
- So, the private key is h.
7.5.4.2 Encryption Phase
- Let us consider the plaintext
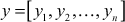 .
. - Then, the sender generates the ciphertext
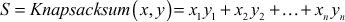 and sends this ciphertext to the receiver side.
and sends this ciphertext to the receiver side.
7.5.4.3 Decryption Phase
- The person who wants to decrypt the ciphertext must know the two numbers
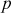 and
and 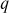 chosen by the sender.
chosen by the sender. - Find the multiplicative inverse of
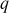 denoted as
denoted as 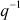 .
. - The receiver calculates
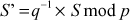
- Find the plaintext
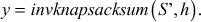
Example 7.4:
This example shows how the message is transferred from sender to receiver in a secure way using Knapsack cryptosystem.
Key generation process
The following steps are involved in the key generation process for encryption and decryption by the sender and the receiver, respectively.
- Take a superincreasing sequence
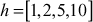 .
. - Decide a modulus number 110, which should be greater than the sum of all the numbers in the sequence 110 > 1 + 2 + 5 + 10.
- Then choose a multiplier 31, which is relatively prime with 110 and 1 ≤ 31 ≤ 109.
- The knapsack sequence would be:
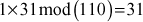
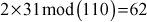
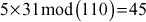
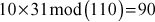
- So, the public key is
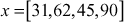 and the private key is
and the private key is 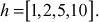
Encryption by the sender
- Let us consider the plaintext
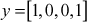
- Then the sender generates the ciphertext
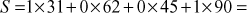 121 and sends this ciphertext to the receiver.
121 and sends this ciphertext to the receiver.
Decryption by the receiver
- The person who decrypts the ciphertext must know the two numbers the modulus 110 and the multiplier 31.
- Find the multiplicative inverse of 31 which is 71.
- The receiver calculates
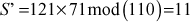 .
. - Then, calculate the plaintext
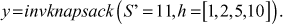
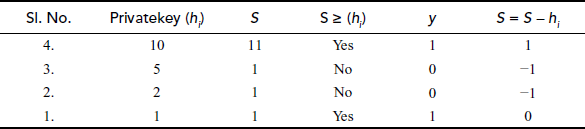
- According to the decryption algorithm for invknapsacksum, the results are obtained as shown in Table 7.3.
Table 7.3 The result of decryption operation
- Hence, the plaintext
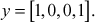
Key Terms
Authentication
Brute-force attack
Confidentiality
Constant exponentiation time
Digital signature
Euler’s totient function
Knapsack cryptosystem
Knapsacksum
Mathematical attack
Multiplicative inverse
n-Tuple
Non-repudiation
Private key
Public-key cryptosystem
Public key
Random delay
RSA Algorithm
Superincreasing knapsack
Timing attack
Summary
- All the encryption techniques are purely classified based on the concept of a key.
- The public-key cryptosystem uses a pair of keys. Each pair consists of two keys, namely private key and public key.
- The public-key cryptosystem is used to provide secure electronic communication over an the Internet.
- This hybrid cryptosystem is efficient in terms of speed.
- The hybrid cryptosystem is used in many places such as PGP and the SSL/TLS.
- The RSA is a best known and widely used public-key scheme that uses large integers (1024 bits) as key values.
- There are three kinds of attacks that can be performed on the RSA algorithm. The three well-known attacks are brute-force attack, mathematical attack and timing attack.
- Brute-force attack is a trial-and-error method where the intruder tries for all possible trials.
- In mathematical attack, the intruder focuses on factoring the product of two prime numbers.
- Timing attacks resemble to side channel attacks that utilize some vital information regarding time, power and sound, etc.
- There are three possible countermeasures for this timing attack are constant exponentiation time, random delay and blinding.
- knapsack cryptosystem is a public-key cryptosystem and hence it requires two keys for encryption and decryption purposes.
- Knapsacksum is a one-way function if
 is a common n-tuple. The common n-tuple is the one that does not satisfy superincreasing knapsack.
is a common n-tuple. The common n-tuple is the one that does not satisfy superincreasing knapsack. - In superincreasing knapsack tuple, each value is greater than or equal to the sum of its previous values except the first value.
- To exchange the message in a secure way, three phases are involved, namely key generation phase, encryption phase and decryption phase.
Review Questions
- Diffirentiate private key cryptography and public-key cryptography with 10 significant points.
- How confidentiality is achieved in public-key cryptography?
- How authentication is achieved in public-key cryptography?
- How both confidentiality and authentication are achieved in public-key cryptography?
- Expalin in detail about RSA algorithm.
- Encrypt and decrypt the word ‘HELLO’ in a block cipher manner using RSA algorithm for the value
 = 12347,
= 12347, 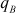 = 181 and
= 181 and 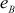 = 13.
= 13. - Encrypt and decrypt the word ‘HELLO’ by processing individual letters of the given word using RSA algorithm for the value
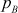 = 12347,
= 12347, 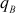 = 181 and
= 181 and 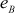 = 13.
= 13. - Explain briefly about the attacks performed on RSA.
- Explain about knapsack cryptosystem with a suitable example.
References
- http://publib.boulder.ibm.com/infocenter/wsdoc400/v6r0/index.jsp?topic=/com.ibm.websphere.iseries.doc/info/ae/ae/csec_pubki.html
- http://nrich.maths.org/2200
- https://developer.mozilla.org/en/docs/Introduction_to_Public-Key_Cryptography
- http://homepages.math.uic.edu/~leon/mcs425-s08/handouts/RSA.pdf
- http://www.cs.sjsu.edu/faculty/stamp/students/article.html
