Table of Contents for

Cryptography and Network Security

Chapter 10

Authentication Techniques

System security depends upon the proper design of a system, and its management. Network security monitors authorized access and it prevents misuse of network resources. Authentication is a process that verifies the identity of the user who accesses the particular system. It is one of the pillars for ­information assurance. The authentication involves with single-level factor (user name) or multilevel factors (user name, password, finger print). The authentication function generates Message Authentication Code (MAC) that is derived from message and secrete key. Hash function is an important element of message authentication technique. It gets various size input and produces fixed size hash value. Hash function uses compression function repetitively to generate n-bit output. In digital signature procedure, the hash value uses private and public keys for processing. This chapter discusses about the importance of authentication and some authentication algorithms. It specifies the properties of hash function and further discusses about the evolution of hash algorithms and includes comparative study among them. Working style of some important hash functions is explained with block structure.

10.1 MESSAGE AUTHENTICATION

Message authentication deals the protection of message with integrity. It checks the identity of the message sender and non-repudiation of the origin. It checks whether the received messages are originated from the original sender. It ensures that content of the message is not modified or altered. It also verifies the sequence and timing of the messages. Digital signature is an authentication technique that is used to check the repudiation from the sender side or from the receiver side. The authentication of digital signature is done in two levels. The sender sends signed message to receiver. The receiver compares the computed hash codes with the hash code he got. If both hashes match, he/she can view the message. To generate an authenticated message, any one of the following functions can be used.

1. Message encryption: The message is scrambled into unreadable form called the cipher text whereas the cipher text can be readable only by the intended user. The actual message is encrypted and converted into cipher text and the cipher text itself is treated as the authenticator.
2. Message Authentication Code (MAC): This is a special function with secret keys. Both the sender and receiver have secret keys. The message digest has fixed length and this is treated as an authenticator. The authentication algorithm conform the sender, receiver and message integrity.
3. Hash functions: It is the public function that maps the message to a fixed size hash value and this will be served as the authenticator for the message and for the sender. In general, the MAC and the hash functions use the cryptographic keys but the hash code does not need secret or cryptographic keys.

10.1.1 Message Authentication Requirements

During transformation time, some attempts make the message unavailable. These attacks interrupt the communication. Some important message authentication requirements are specified in this section. Attacks conclude for several security requirements in order to prevent the misuse of data. Knowledge of these attacks helps for the effective and efficient design the security system.

• Disclosure: In this type, the original data during transmission is opened by unintended users. The content of the data or the message is read by the attackers and takes a copy of it. This happens if the cryptographic keys are not used for encryption of the message or due to weak cryptographic keys.
• Traffic analysis: The pattern of data communication between two parties are observed by the attacker to determine whether the traffic is connection oriented or connectionless. According to this constraint, the attacker can guess the communication between the users and guess the data and the type.
• Masquerade: It functions like insertion of messages to the traffic from unintended users. This makes the way to the receivers to be got from the legitimate sender or from authorized one. Also the fake acknowledgement may be sent by the attackers to the receivers pretends to be the acknowledgement comes from the original sender or sometimes the acknowledgement may be trapped by the attacker.
• Content modification: Attackers can do some additions, modifications and change of contents to the original message. The intended users may not know the data which are modified by the ­attackers. The change may be insertion, deletion, transposition or modification function.
• Sequence modification: In addition with the content change of the message, the attackers even change the order of the message delivery by changing the sequence of the messages. The entire meaning of the data gets modified when the order changes.

  Example:

  Message sequence: 10 20 30 40 50 60

  Modified sequence: 10 30 50 20 40 60

• Timing modification: In connection-oriented communication, the messages are going in ­sequence and timely based as some live relay contents will be played. Here, the attackers do some programs to delay the connection-oriented packets sent and make it meaningless.
• Repudiation: Receipt of the message is denied or the message is denied by the source.

10.1.2 Message Authentication Functions

There are several message authentication functions that exist for integrity checking and encryption. They are hash functions, MAC, MD5, SHA, etc. All these cryptographic authentication functions provide message integrity and authentication. Some functions are used to compute the actual ­message if the data or the message is modified. The authentication functions provide the mechanism to find the message modification and also the origin of the message. The sender of the message is also verified using the authentication functions. The following section discusses about the authentication ­functions.

10.2 HASH FUNCTIONS

For message authentication, some functions are used to generate a hash value. A hash function is ­generally having some set of functions that compresses the input. It means generally the output ­produced is unique for any of the input. This function takes the input in a random manner and produces the hash value output of fixed length, commonly 160 bits.

h = H(M)

where M is the variable length message

H is the hash function

h is the fixed length hash value

10.2.1 Requirements of Hash Functions

The main use of hash function is generating the fingerprint of a message a file or the block of data. The hash function properties are the requirements needed for the hash function to show the message authentication and given as

1. H is applied to the data or the message or the block of data of variable size.
2. Then H generates a fixed length or fixed size message digest.
3. H(x) can be easily calculated for the given x in terms of both hardware and software implications.
4. The code h is basically very complicated and infeasible to calculate and find x for H(x) = h.
5. For the given x, it is not possible to find the value y equal to x and otherwise it is called a weak collision property also its hard to find (x, y) in which H(x) = H(y) called strong collision property.

One-way property in which the code can be generated using a message but it is not possible to generate a message using the code. This property is mandatory if some secret keys are used in this technique. The secret key will not be sent in communication but if the property is not one way then it easily give way for the attackers to compute and find the secret key. These properties are discussed further in ­Section 10.4.2.

If the attacker attacks and gets the massage M and the hash code C = H(S||M) then after getting this information the attackers may try to go for inverse function. It applies to the function with the ­message and the secret key S||M = H inverse (C). Even though the attacker has M and S||M it is ­difficult to Recover S. The fifth property states that doing another copy of message hashing to the same value the original message will not be find and this avoids the illegitimacy when an encrypted hash code is used. A hash function if it satisfies the first properties is called the weak hash functions and if H(x) = H(y) property is satisfied, then it is called strong hash function. This function prevents the birthday attack.

10.2.2 Security of Hash Functions

Cryptographic hash functions have two types. The first depends on mathematical operations and ­functions. It has security proof based on mathematical models complexity theory and formal ­reduction. These are called provably secure cryptographic hash functions. This can be broken, moreover it is very hard to develop and it has limitations in practical use.

The second type is also based on mathematical functions in which hash is produced by the mixing of text bits. It is assumed to be hard to break the function. Most of the hash algorithms fall under these two categories in which the broken algorithms are dropped from usage.

10.3 MESSAGE AUTHENTICATION CODE

In cryptography, a MAC is the simple one and the length is very less among any other method to authenticate the message. It also provides a better integrity check value to the message and assures integrity. Integrity of the message concludes any other changes and the modifications of the message where authenticity represents the message originality and the origin of the sender.

The only possible chance to generate MAC code is by the available cryptographic hash function and so it is called keyed method. These algorithms get a secret key as input and produce a lengthy arbitrary message as the authentication called MAC. The MAC checks for the integrity of the message and authentication. The authenticity is confirmed by checking or computing the MAC value using the secret keys hold by the users and checks for any message misuse for the change of contents.

10.3.1 Requirements of MAC

Message authentication is concerned with some requirements which are as follows. The requirements mention the data is not altered or modified. The sender and receiver are authenticated. Truthfulness of the message is not denied in any circumstance.

1. Protecting the integrity of the message
2. Validating the identity of the originator
3. Non-repudiation of origin

10.3.2 Security of MAC

MAC functions are like cryptographic hash functions, and the security requirements are different. The MAC must withstand for plain text attack. A plain text attack is the attacker guesses at least the minimum-level contents. It should not be vulnerable for attacks even though the attacker has the secret key. It should maintain the infeasibility condition to mathematical computation.

There are the differences between the MACs and digital signatures. But both uses same secret key for verification as the sender and the receiver uses same key values for message transmission like symmetric encryption. MACs are not based on non-repudiation property in a network-based key ­communication, whereas digital signature is based on public key cryptography in which it uses private key for authentication. This method is best as the private key. It is only used by the holder and it is easy for the user to check the message authenticity whether the message is misused by the attackers or not as the holder only permitted to access the key. These mechanisms are widely used in banking and finance institutions.

10.4 AUTHENTICATION ALGORITHMS

There are several authentication algorithms are there to deal with the security parameters like maintain integrity, confidentiality, secrecy, authenticity. Every authentication algorithms has different ­properties, methods and working mechanisms depending upon the input criteria. Several types and keys and ­different length of messages give unique output whereas the original message will be encrypted into unreadable form. The strength of integrity is verified by different authentication algorithms and are discussed as follows.

10.4.1 MD5

Figure 10.1 shows the overall working architecture of MD5 algorithm. There are two levels of message digest that take place in a continuous sequence for ensuring multiple-level security policy. This however reduces the way of targeting to break the security by brute-force attacks. In the first level, the message digest is produced by two level inputs. The data is subdivided into a number of blocks and each block is given as input with 432-bit words. Applying the message digest function, first level of encrypted message digest is produced with a length of 432-bit words. Now, this generated message digest is given as input to the other set of 512-byte data block. Applying the message digest function again produces a new message digest of length 432-bit words.

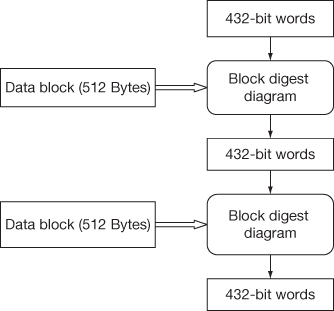
Figure 10.1 Architecture of MD5

10.4.1.1 Message Compression Function

This MD5 algorithm works in a safer level. It takes the input from the message and converts it into a message digest as the output of 128-bit length. The hash value is unique and the message digests are not same. It is not possible to compute such a lengthy message digest of another. Figure 10.2 shows compression function of MD5. Consider an input is given like a bit and the message digest is calculated as follows.

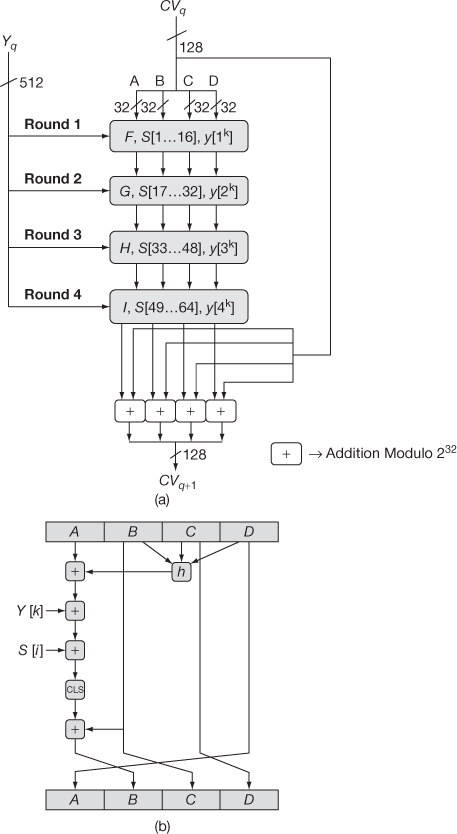
Figure 10.2 (a) Overall processing of MD5; (b) Compression function of MD5

• Step 1: The given message is padded and made the length congruent to 448 modulo 512. In other way, it means extending the message to 64 bit and being of 512-bits long. Then the single 1 bit is added to the message and also some 0 bits are added with the message input so as to produce the length in bits equal to 448 modulo 512 bit.
• Step 2: Adding the length. For the given input A, the corresponding 64-bit representation is ­computed and the value is appended with the result of the previous step and the resultant message got will be the multiple of 512 bits.
• Step 3: In this step, buffer for the message digest is initialized and the message digest is calculated using a four-word buffer (A, B, C, D) and all these are 32-bit register and the values of these ­registers will be assigned in terms of hexadecimal codes.

  Word A: 01 23 45 67

  Word B: 78 ce ae de

  Word C: ba fe cd 98

  Word D: 10 32 54 76

• Step 4: Now the given input will be processed as ‘w’ 16-word blocks. For each block, the inputs are Y_q and CV_q, where Y_q is the q^th input block, CV_q is chaining variable, the value of q ranges from 0 to w − 1. Initially, CV has words A, B, C and D. The output of each block is considered as value for next block’s CV. The compression function is shown in Figure 10.2. Each block goes through four rounds and each round composed of 16 steps.

  For each round, the auxiliary function h takes three 32-bit words and then throws out the output of a single 32-bit word, where h can be expressed as follows:

  Round 1: h(B, C, D) = (B ^ C) ∨ (¬B ^ D)

  Round 2: h(B, C, D) = (B ^ D) ∨ (C ^ ¬D)

  Round 3: h(B, C, D) = B ⊕ C ⊕ d

  Round 4: h(B, C, D) = C ⊕ (B ∨ ¬D)

  The given message is processed like 16 word blocks. If the bits of A, B, C and D are ­independent and unbiased each bit of F(A, B, C, D), G(A, B, C, D), H(A, B, C, D) and I(A, B, C, D) are ­independent and unbiased.

  Y[k] – Message Word

  S[i] – Round Constant

  CLS – Circular Left Shift

• Step 5: The output A, B, C and D is now produced as output with the starting word as the ­lower-order byte. The ending word is the higher-order byte.

Thus the MD algorithm is very simple to implement and produces the message digest with the length corresponding with the input size. It is very complicated to produce the same message digest for ­different inputs.

10.4.2 Secure Hash Algorithms

Secure Hash Algorithms (SHAs) are cryptographic algorithms that provide data integrity and ­authentication. They are published by the National Institute of Standards and Technology (NIST). TLS, SSL, SSH and PGP applications use SHA. It is a deterministic function that takes arbitrary length block of data (message) and performs randomness process and returns a fixed size string called as hash value. A hash algorithm generates a condensed representation of message. It takes message of any length less than 2¹²⁸ bit as input and results message digest as output ranges from 160 to 512 bit. Any change in the message causes different message digest with a very high probability. The success of hash code against brute-force attacks and cryptanalysis requires 160 bits. The hash functions are affected by collisions and attacks.

The feasible computer knowledge cannot be used to regenerate the original message. Secure hash algorithms are often used in combination with cryptographic algorithms like keyed hash MACs or random number generation and digital signature algorithms to authenticate messages, including digital signatures.

Some network routers and firewalls implement SHA directly in their hardware. Many SHA ­softwares also exist and it includes many open source implementations. It makes data packets to be authenticated with limited impact on throughput. The US NIST and the canadian Communications Security Establishment (CSE) jointly establish the Cryptographic Module Verification Program (CMVP). This official program validates cryptographic modules to Federal Information Processing Standards (FIPS) 140-1 and certifies the correct operation of secure hash algorithm implementations for sensitive applications.

10.4.2.1 Properties of SHA

A cryptographic hash function must have some properties to withstand for cryptanalytic attacks and to be useful for authentication. It is applied to a block of variable size. SHA should go easy with software and hardware implementations. In addition to this, it should have some important properties and they are given below and Figure 10.3 shows the properties.

1. Pre-image resistance (one-way): Take h as hash value. Find any message M that hashes to that value. Find data mapping for the specific hash value. Computationally it is infeasible. The one-way property is defined as ‘It is infeasible to find any data mapping between message and message digest and to find any message M that hashes to that value’.
2. Second – Pre-image resistance: (Weak collision-resistant): Take any input x, and find another input y such a way that x and y hashes to the same value, where x and y are different. The weak collision-resistant property is defined as ‘It should be difficult to find another input y for an input x such a way that they both hash to the same value h(y) = h(x), where x ≠ y’.
3. Collision resistance: Find two inputs x and y where they have the same hash values. The collision-free property is defined as ‘It is computationally infeasible to find two inputs x and y in such a way that h(y) = h(x).’

Figure 10.3 SHA properties

10.4.2.2 Applications of Cryptographic Hashes

The main application of secure hashes is message integrity. It provides message integrity by comparing message digest before and after transmission or during any other event. Most of the digital signature algorithms provide authentication with signed messages. Cryptographic hashes are commonly used in digital signatures and MACs. They are also used to index data in hash tables, to detect duplicate data and data corruption.

10.4.2.3 Digital Signature Algorithms

A message is transmitted with its hash allowing the receiver to hash the message and compare the ­outputs. The message with sender’s key conforms the message is not misused. Execution of the ­algorithm ­produces hash value. The integrity of the data is checked by comparing the hash values in the ­receiver end.

Example

Secure electronic transaction in E-Commerce.

10.4.2.4 Storage of Passwords

Cryptographic hashes are useful in password storage. Instead of storing user’s password directly, it stores hash of password. When the system gets password from user, the hash is computed and ­compared with stored hash. Collision-resistance property compares both hashes and informs about password match.

Example

For an input ‘test’, SHA-1 outputs ‘a94a8fe5ccb19ba61c4c0873d391e987982fbbd3’. After that when system gets ‘test’ SHA-1 always get ‘a94a8fe5ccb19ba61c4c0873d391e987982fbbd3’. If anyone finds ‘a94a8fe5ccb19ba61c4c0873d391e987982fbbd3’ comes from the SHA-1, and it is infeasible to find what was entered to get ‘a94a8fe5ccb19ba61c4c0873d391e987982fbbd3’ from the hash function.

The computer passwords are stored in this way. When a password is fed into the system, it stores it after hashing. In case, if anyone traces this hashed figure, it is impossible to trace out the original password because of the one-way property. The computer never stores the actual text. It stores only the fingerprint of it.

10.4.2.5 Integrity Checking

The sender can hash a file like message before sending to the receiver. The receiver hashes the received file and checks hash match. This is used to store files with out corruption or modification.

10.4.2.6 Comparative Study of SHA Family

The SHA algorithms differ mostly in security strengths. It also differs in block size, word size. They are believed to have good randomized features. Table 10.1 shows the comparative study of SHA family.

1. SHA-0: This is the first incarnation of SHA that is published in 1993 and withdrawn so early because of undisclosed significant flaw.
2. SHA-1: This is the second version of SHA. It was released in 1994. It is considered as ­successor of MD5 but slower than MD5. It results 160-bit hash value. The standard was not approved for most of the applications after 2010. It is commonly used in many security protocols and applications.

   Table 10.1 Comparative study of SHA family

   
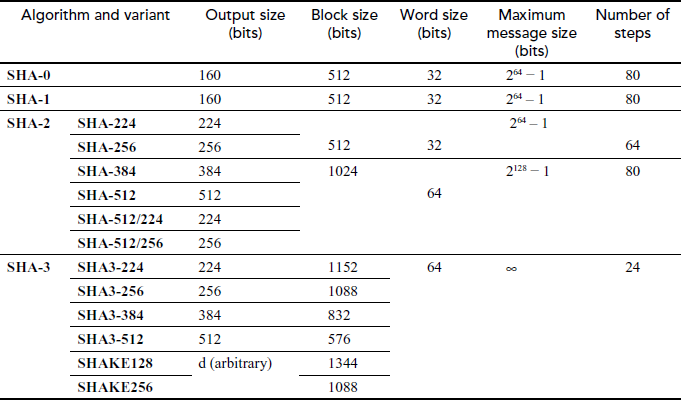
3. SHA-2: This is a family of two hash functions SHA-256 and SHA-512 with different block size. SHA-256 uses 32-bit words and SHA-512 uses 64-bit words. Security of SHA-2 is still unsure.
4. SHA-3: This is a hash function is also called as Keccak. It works like other SHA family and it shows significant change in its internal structure.

The SHA algorithms specify that it is not possible to find the message from hash value. It also ensures that two different messages do not produce the same hash value.

10.4.2.7 Functionality of SHA

The hash algorithms have the following two stages.

1. Pre-processing: It handles padding of message. It breaks the padded message as m-bit blocks and initializes the values for hash process. Hash computation generates message schedule from padded message. This message schedule is used with functions and word operations to generate a series of hash values iteratively.
2. Hash computation: The compression function outputs fixed length value. The hash function applies compression function repeatedly to get message digest. This process breaks the ­message into blocks depending upon the compression function involved. Padding is also involved to make the size of the message as multiple of block size. The blocks are processed consecutively to generate hash value for the message.

SHA-512 algorithm takes a message as input with a maximum length of 2¹²⁸ bit. It results in 512-bit message digest as output. SHA breaks the message into blocks of certain length with compression function and makes the message as multiple of block size. Each block is of size 1024 bit. The block diagram of message digest creation is specified in Figure 10.4 and message digest creation in SHA-512 consists of four steps.

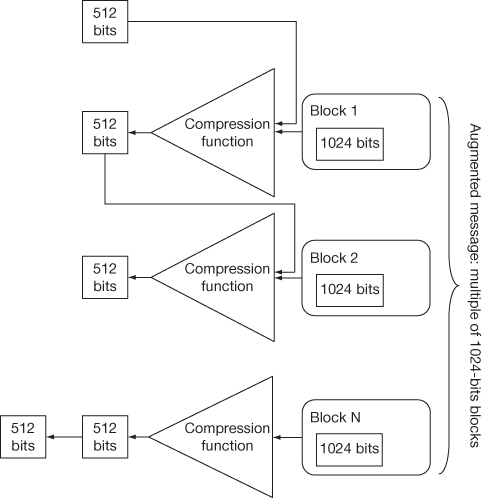
Figure 10.4 Message digest creation SHA-512

1. Append padding bits
2. Append length
3. Initialize hash buffer
4. Process message as 1024-bit blocks

SHA processes message in fixed length block. The padding scheme appends predictable data to make the final block as fixed length block. The message length becomes congruent to 896 modulo 1024. SHA appends a block of 128-bit unsigned integer to the message. This block maintains the length of original message before padding. A 512-bit buffer holds the intermediate and final results of hash function. The buffer consists of 8 registers and each register can store 64-bit value. They are represented as a, b, c, d, e, f, g, h. To generate message digest, the registers are initialized with 64-bit ­hexadecimal values. The algorithm consists of 80 rounds. Each round takes 64-bit values from the 8 blocks. The ­64-bit values are represented as W_t and they are obtained from the 1024-bit block (M_i), which is being processed. Each round t updates the intermediate hash value, Hi-1. The completion of the 80^th round outputs ­512-bit message digest.

The block diagram of SHA-512 compression function is given in Figure 10.5. It processes message in 1024-bit blocks and returns 512-bit message as output. The 1024 bits are considered as 16 words. Each word consists of 64 bits. It consists of 80 rounds. It takes a message of length less than 2¹²⁸ as initial value and 512 bits as message digest. It derives W_t the expanded message word of round t from current message block.

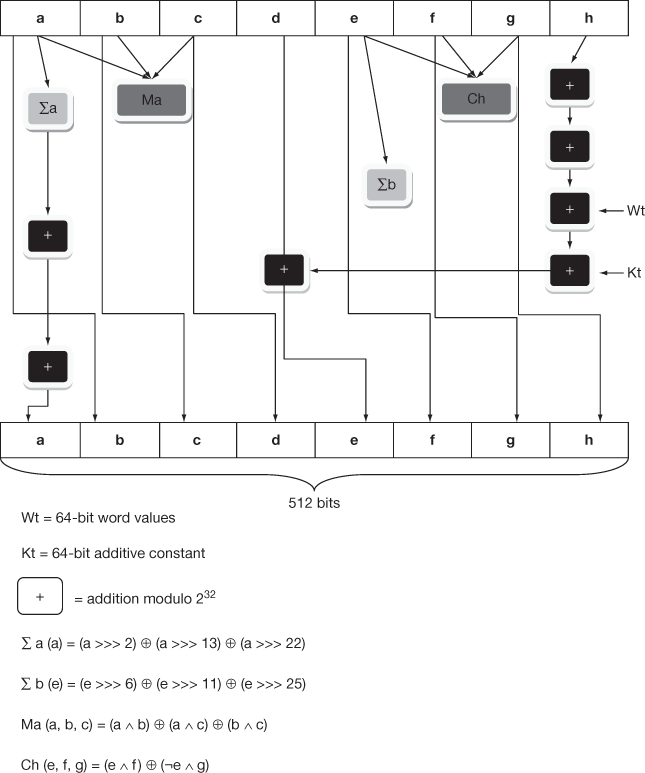
Figure 10.5 Working of SHA-512 compression function

Example 10.1:

The length of the original message is 2590 bits. What is the number of padding bits?

Solution

The number of padding bits |p| = (−2590 − 28) mod 1024 = −2618 mod 1024 = 354

The padding consists of one 1 followed by 353 0’s.

Example 10.2:

The length of the original message is already a multiple of 1024 bits. Mention does the message need padding?

Solution

Yes the message needs padding because it needs to add the length field. Padding makes the new block as a multiple of 1024 bits. So, it is needed.

Example 10.3:

Mention the minimum and maximum number of padding bits that can be added to a message and explain how.

Solution

1. (a) The minimum length of padding can be 0. This situation happens when (−M −128) mod 1024 becomes 0. It means |M| = −128 mod 1024 = 896 mod 1024 bits. Otherwise, the last block in the original message is 896 bits. A 128-bit length field is added to make the block complete.
2. (b) The maximum length of padding can be 1023. This case occurs when (−|M| −128) = 1023 mod 1024. It means that the length of the original message is |M| = (−128 −1023) mod 1024 or the length is |M| = 897 mod 1024. In this scenario, padding cannot be done easily because the length of the last block exceeds 1 bit more than 1024. To complete the block, it is needed to add 897 bits.

10.4.3 Birthday Attacks

The birthday problem works like a probability problem. It states the probability of at least one pair of people in a group of n people that share the same birthday. A birthday attack is used to refer to a class of brute-force attacks. The probability of finding two people in a group of 23 with same birthday is greater than 0.5.

The birthday problem can be defined as ‘given a random variable that is an integer with uniform distribution between 1 and n and a selection of k instances (k ≤n) of the random variable. What is the probability P(n, k), that there is at least one duplicate?’. The probability of the complement helps to solve the problem. By subtracting the probability from the value 1, the probability of at least one pair having the same birthday may be finding. For example, the probability of 40 people with at least one of the same birthdays goes as follows:

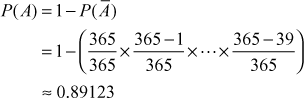
The collisions of hash functions are identified using birthday attack. Birthday problem is useful to solve birthday attack and brute-force attack. One-way hash function, a collision-free hash function, a trapdoor one-way hash functions are some hash functions. Consider a function that returns one of a k equally like values with random input. The repeated evaluation of the function with different inputs is expected to get the same output after 1.2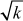 evaluations. Ideal cryptographic hash functions are easy to compute a hash value for a message, infeasible to create a message with a given hash, infeasible to modify a message without changing the hash, and infeasible to find different messages with the same hash.

Example 10.4:

What is the probability that two people in a class of 25 have the same birthday? (Disregard leap years.)

Solution

Use complement to calculate answer. It is very simple to calculate 1 − P (no matches) = the probability of minimum one pair of people has the same birthday.

What is the probability of no matches?

Denominator: how many sets of 25 birthdays are there?

With replacement (order matters)

365 power 25

Numerator: How many ways 365 birthdays can be distributed to 25 people without replacement?

Order matters, without replacement:

10.4.4 RIPEMD-160

RACE Integrity Primitives Evaluation Message Digest (RIPEMD) is a fast cryptographic hash function that is tuned in 32-bit architectures. It is designed by Hans Dobbertin, Antoon Bosselaers and Bart Preneel. It is mainly based on the design principles of MD4. It works like SHA-1. RIPEMD-160 is commonly used improved version of RIPEMD. RIPEMD-128, RIPEMD-256, and RIPEMD-320 ­versions also exist, and RIPEMD-160 is the popular version of this family. It is aimed for the replace­ment of 128-bit hash function because it offers less security. RIPEMD-256 and RIPEMD-320-bit ­versions minimize the chance of accidental collision. They do not provide higher level of security against pre-image attacks when compared with RIPEMD-128 and RIPEMD-160.

In 1995, Hans Dobbertin found that RIPEMD is restricted to some level. He also found collisions of MD4 in the same year. Ron Rivest developed MD4 and MD5 for RSA data security and he recommended that MD4 shows poor performance due to collision. It is also found that MD5 should not be used for future applications that require the hash function to be collision-resistant.

Later, Xiaoyun Wang, Dengguo Feng, Xuejia Lai and Hongbo Yu found collisions for MD4, MD5, RIPEMD, and the 128-bit version of HAVAL. RIPEMD-160 is the strengthened version in its family. It outputs 160-bit hash value.

RIPEMD-160 consists of 16 steps and 5 rounds. They are left rotation of words, bitwise Boolean operations (AND, NOT, OR, exclusive – OR) and two’s complement modulo 2³² addition of words. It uses 2 parallel lines. It outputs 160-bit message digest. It is slower than SHA, but more secure. RIPEMD-160 divides the input into blocks of 512 bits. The compression function works on ­512-bit message block. It uses chaining variable CV of 160-bit length. The 512-bit block is divided into 16 strings of 32-bit word. In MD-SHA family, SHA-2 and RIPEMD-160 are most secure compression functions. Recent analysis says the compression function in RIPEMD-128 is not collision-resistant.

10.4.4.1 Characteristics of RIPEMD-160

It uses 2 parallel lines of 5 rounds with increased complexity

1. The 2 parallel lines are very similar.
2. Step operations are very close to MD5.
3. Permutation varies in parts of the message.
4. Circular shifts are designed for the best result.

10.4.4.2 RIPEMD-160 Algorithm Steps

Input: a message of arbitrary length, processed in 512-bit block

Output: 160-bit message digest

Logic:

Step 1: append padding bits

The message is padded. Its length is congruent to 448 mod 512

Padding is always added (1 to 512 bits)

The padding pattern is 100…0

Step 2: append length

A 64-bit length value is appended with original message

Step 3: initialize MD buffer

A 160-bit buffer holds intermediate and final results of the hash function.

The buffer is represented as five registers. They are A, B, C, D, E and they can store 32-bit value. These five registers are initialized as follows.

A = 67452301

B = EFCDAB89

C = 98BADCFE

D = 10325476

E = C3D2E1F0

The values are stored in such a way that the least significant byte of a word in the low-address position:

word A = 01 23 45 67

word B = 89 AB CD EF

word C = FE DC BA 98

word D = 76 54 32 10

word E = F0 E1 D2 C3

Step 4: process message in 512-bit blocks

A module is executed 10 rounds with 16 steps each. The 10 rounds are organized with 2 ­parallel lines of 5 rounds each. The output of the last round becomes input for the first round.

Step 5: output

The L-th stage generates 160-bit message digest.

10.4.4.3 Working of RIPEMD-160

Figure 10.6 shows the working of RIPEMD-160 compression function. It starts with padding scheme which helps to prevent length extension attack. Padding is done at the end of the message. The bytes are then adjusted in such a way that the low end comes first. The length of the message is then added second to the last element.

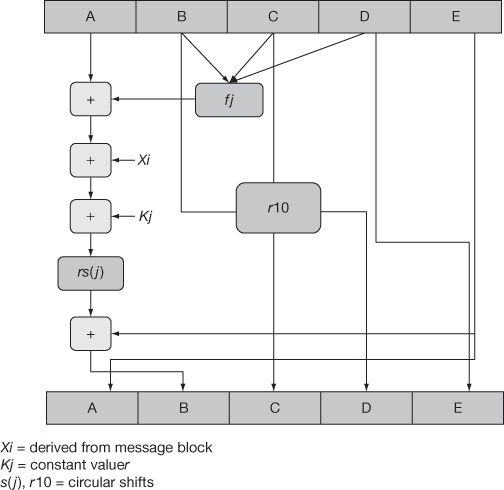
Figure 10.6 Working of RIPEMD-160 compression function

Compression function consists of two parallel streams. It processes this message block by block. It initializes the chaining variable with 32-bit fixed value to hash the first message block. It also initializes intermediate hash value for the following message blocks. Compression function updates the state variables in each stream. This update depends on expanded message word wi. The state variables are combined with initial value IV. The compression function works with 16 words of 32-bit length.

The working of RIPEMD-160 can be explained with two stages message expansion and state update transformation. The message expansion of RIPEMD-160 is iteration with permutation of the message words. Each iteration step uses different left and right streams. State update transformation begins with initial value IV of A, B, C, D, E registers and expanded message word wi. This transformation works as 5 rounds and each round has 16 steps. The function fj is used in the jth round in the left stream ad f6-j is used in the right stream. A step constant is added in each step and it is different for each round and stream. The value sj represents rotation value and it is used in each step of both streams. The last step combines the value of right and left streams and results the out of single iteration. Iteration adds the permutations of initial value with the output of left and right stream.

The working of RIPEMD-160 compression function is illustrated in Figure 10.6. The critical path has addition stages and a multiplexer. The values are fed and received via multiplexer for the operation block. The rounds in the working of RIPEMD-160 works in a similar way but each round performs with different operation for the inputs of A,B, C, D, E registers. The data is processed 16 times in each transformation.

10.4.5 Hash Message Authentication Code

Keyed Hash Message Authentication Code (HMAC) is a MAC. It is calculated by a cryptographic hash function with secret key. Normally the data passes through insecure communication channel. The checksum for this data is called as MAC. In MAC during transmission, the sender and receiver share the secret key for authentication. Hash-based MAC is called as HMAC. HMAC verifies both data ­integrity and authentication simultaneously like other MAC. HMAC works on message and secret key with any cryptographic hash functions like MD5 and SHA-1. The strength of HMAC depends upon the strength of cryptographic function used, size and quality of the key and the size of the resultant hash output. It addresses several cryptographic schemes and various problems in it and solves them with arbitrary keyed hash constructions.

10.4.5.1 Design Objectives

Hash function codes are freely available in the Internet. HMAC applies hash function as a black box. Existing implementation of hash function can be applied as individual module in implementing HMAC. The HMAC code is readily available and it can be used without modification. The following are design objectives of HMAC.

• Use existing hash functions without correction.
• Replace existing hash function with embedded hash function for the need of more secure hash functions.
• Maintain the level of performance of the hash function without modifying its significance.
• Use and handle keys in flexible way.
• Preserve a well-understood cryptographic analysis and authentication mechanism with reasonable assumptions in the embedded hash function.

The first two objectives are important for the acceptability of HMAC. The last objective makes HMAC more popular over other proposed hash-based algorithms as the embedded hash function has some reasonable cryptographic strength.

10.4.5.2 Definition of HMAC

HMAC is defined with a cryptographic hash function H, and a secret key K. Authentication key K can be of any length up to the byte-length of each block B. The cryptographic hash function H iterates the basic compression function. The byte-length of hash output is represented as L. Hash function H hashes the keys longer than B bytes. Then the resultant L byte string is used as the actual key in HMAC. Usually the minimal recommended length for the authentication key is the byte length of hash output L.

The secret key of HMAC can be of any length. HMAC hashes the keys more than the block length are hashed first. It accepts keys more than hash output length because the extra length will not improve the strength of the hash function. When the randomness of the key becomes weak, the length of the secret key is increased.

Keys need to be generated randomly or with a pseudo random generator and it should be refreshed periodically. Current cryptographic attacks do not specify about the frequency of key change because detection of these attacks are infeasible. However, the periodic refreshment of the security key controls the potential weakness of the function and the limits any damages of the current secret key.

HMAC generates a MAC using the following formula.

HMAC (M) = H[(K+opad) & H[(k+ipad) & M]]

where

M = Message

H[] = Underlying Hash function

K = Shared Secret Key

opad = 36hex, repeated as needed

ipad = 5Chex, repeated as needed (the ‘i’ and ‘o’ are mnemonics for inner and outer)

& = concatenation operation

+ = XOR operation

The HMAC(M) message is then sent as any typical MAC(M) message in message transaction over insecure channels. HMAC is quite faster than block ciphers such as DES and AES. HMAC is freely available, and is not subjected to the export restriction rules of the USA and other countries. HMAC is authenticated as the sender and receiver generates an exactly same HMAC output.

Steps

1. Append zeros to the end of shared secret key K. It creates block of bytes B
2. Apply XOR (bitwise exclusive-OR) operation on block byte string B with ipad. The value of B is derived from step 1.
3. Append the stream of data ‘text’ to the result of step (2)
4. Apply H to the value obtained from step (3)
5. Apply XOR (bitwise exclusive-OR) operation on block byte string B with opad. B is obtained from step (1)
6. Append the H result from step (4) to the result from step (5)
7. Apply H to the value generated in step (6)
8. Output the resultant hash value

The exclusive OR (XOR) operation is applied on block byte string B with ipad. It results in flipping one-half of the bits of secret key K. Following this, the exclusive OR (XOR) operation is applied on block byte string B with opad. It also results flipping in one-half of the bits of K in other set of bits. HMAC applies three executions of the hash compression function. Passing the two flipped messages Si and So through the compression function of the hash algorithm results pseudo randomly generated two keys from K. HMAC uses the same execution time for embedded hash function for long messages also. The block diagram for working of HMAC is given in Figure 10.7.

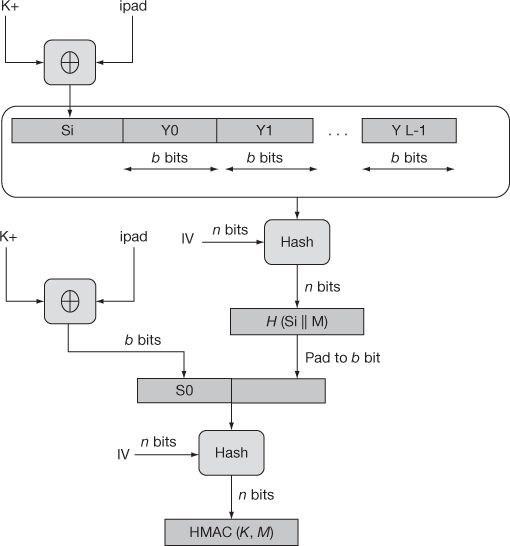
Figure 10.7 Block diagram for working of HMAC

H Embedded hash function

IV initial value

M Message input for HMAC (includes padding specified in the embedded hash function)

Y_i is the ith block of M, where 0 ≤i ≤L − 1

L Number of blocks in Message M

B number of bits in a block

n length of hash code produced by embedded hash function

K Secret key

K+ padded secrete key with zeros in left

ipad 00110110 (36 in hexadecimal) repeated b/8 times

opad 01011100 (5C in hexadecimal) repeated b/8 times

If secret key length K is more than bits in a block, the key is given to the hash function to generate n-bit key. Secret key is recommended to have length more than n.

Message input and secret key are functionally two distinct parameters of HMAC. The secret key is known only by the sender and receiver. HMAC does not work like a cipher. It works as mechanism that handles signing of packet by sender with secret key and verification of the signature in receiver side using the same secret key. HMAC insists that it is impossible to generate packet without the knowledge of secret key.

10.4.5.3 HMAC Security

The strength of any MAC function depends on the strength of cryptographic hash function. The security of the hash function is expressed as the probability of successful forgery. It depends on the amount of time spent by the forger and the number of messages generated with same secrete key the attacker can forge the HMAC function in any one of the following two ways.

1. The attacker can find the collisions in hash function.

   The attack on the hash function can be a brute-force attack on the key or a birthday attack.

2. The attacker may try to compute the output of the compression function.

   The attacker may try to look for two messages x and y which produces the same hash value H(x) = H(y). It needs 2^n/2 level of effort for hash length of n. The attackers need to observe sequence of messages generated by HMAC with the same secret key.

   For example, consider the hash code with length 128 bits. The attacker needs to observe 2⁶⁴ sequences of messages generated by HMAC with same secret key.

HMAC provide data integrity since attackers cannot generate the actual input or hashed message ­offline because attackers do not know the secrete key.

10.4.6 Whirlpool

Whirlpool is developed by Paulo S.L.M. Barreto and Vincent Rijmen. It is a one-way hash function. The one-way hashing function says it is computationally infeasible to find data mapping to specific hash. Whirlpool was submitted to NESSIE (New European Schemes for Signatures, Integrity and Encryption) project. Then it is accepted by the international organization for standardization (ISO) and the international electrotechnical commission (IEC) as part of the joint ISO/IEC 10118-3 international standard. The first version of Whirlpool is called as Whirlpool-T and latest version is referred as Whirlpool. The original Whirlpool is called as Whirlpool-0. The working flow is shown in Figure 10.6.

10.4.6.1 Features and Goals of Whirlpool

Whirlpool is based on 512-bit block cipher. Its structure is similar to Rijndael (AES). It takes a ­message of any length less than 2²⁵⁶ bits and returns a 512-bit message digest. Whirlpool has the following ­features:

1. The hash code length of Whirlpool is 512 bits. This length is similar to the hash length of SHA.
2. The entire structure of the Whirlpool hash function is resistant to the usual attacks. The hash function of Whirlpool is based on block cipher.
3. The 512-bit block cipher in Whirlpool is based on AES. It is flexibly designed by considering important features like compactness and performance. It can be used in both software and hardware implementations.
4. The security goals of Whirlpool are as follows.
5. The required quantity of workload to generate collision should be the order of 2^n/2 executions.
6. For a given n-bit input value, the required workload to find a message that hashes to the input value should be the order of 2ⁿ executions.
7. For a given input message, the output n-bit hash value is measured. The required workload to find other input message that hashes to the same output should be of the order of 2ⁿ executions.
8. It should not be feasible to find any relation between the combinations of input and combinations of hash value. It should not be possible to find the bits of value which predict the hash result when input is flipped.
9. Whirlpool should be resistant against different cryptographic attacks.

The algorithm designers trust about these claims that met considerable safety margin. However, the formal proof of these claims has not been achieved.

10.4.6.2 Whirlpool Hash Structure

Consider the given a message consists of a sequence of blocks m₁, m₂ ... m_t. The Whirlpool hash ­function is represented as

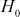= initial valu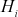e

= E(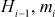 ) ⊕ 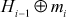= intermediate value

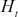= hash code value

Each iteration i gets 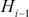value as input from previous iteration. The current message block m_i is the plain text from Message. The ith iteration results intermediate value 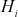that consists of bitwise XOR of the current message block and intermediate hash value from previous iteration 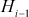, and the output from block cipher W. The algorithm considers a message with a maximum length of less than 2²⁵⁶ bits as input and produces 512-bit as hash value. Whirlpool processes input as 512-bit blocks. Figure 10.8 depicts the overall processing of a message to produce a digest.

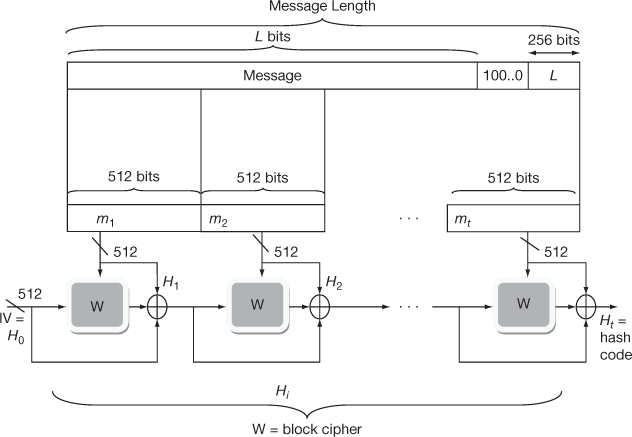
Figure 10.8 Working of whirlpool

The complete message digest is generated in four steps.

1. Append padding bits: Message is padded to odd multiple of 256 bits. Padding is done, even if the message is already of the desired length. Sometimes the unpadded message may be of the required length. In this case, the message is padded with maximum padding length 512 bits (2 × 256). Minimum padding length is 1 bit.

   For example, the length of the message is 768 bit. It is padded with maximum length. Now the message length is 1280 bits. Padding bit ranges from 1 to 512. Padding involves single 1 bit followed by required number of 0 bits.

2. Append length: A block of 256 bits is appended to the input message. This block is considered as an unsigned 256-bit integer. It consists of the length in bits of the actual message. Now the message length is n × 512 bits, where n = 1, 2 ….

   The above two steps convert the message length as a multiple of 512 bits. In the figure the ­message is denoted as expanded message m₁, m₂, … m_t. The total length of expanded message is t × 512 bits. These blocks are treated as arrays of bytes with 8-bit chunks.

3. 3. Initialize hash matrix: The results of the intermediate and final hash functions 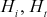are stored in an 8 × 8 matrix. Each element of the matrix is 8-bit message. The hash matrix holds 512 bits in total. 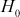is initialized with 0000 0000.
4. Block Cipher: The block cipher handles the message as 512-bit blocks. Whirlpool hash function is specially designed to use a block cipher. The whirlpool block cipher maintains the security and efficiency of AES but its hash length is similar to SHA-512.

   The structure and basic functions of block cipher W looks like AES. But it is not an extension of it. The block cipher W uses 512-bit keys and 512-bit blocks. The block length of AES is 128 and key length may be 128 or 192 or 256. The block cipher is faster since it operates with 8 × 8 byte matrices.

10.4.6.3 Overall Structure

The Whirlpool encryption algorithm functions with 512-bit plaintext block. It takes 512-bit key as ­input and produces 512 bit as message digest. The Whirlpool algorithm handles four different functions or transformations. They are Add Keys (AK), Substitute Bytes (SB), Shift Columns (SC), and Mix Rows (MR). Overall structure of Whirlpool cipher W is shown in Figure 10.9.

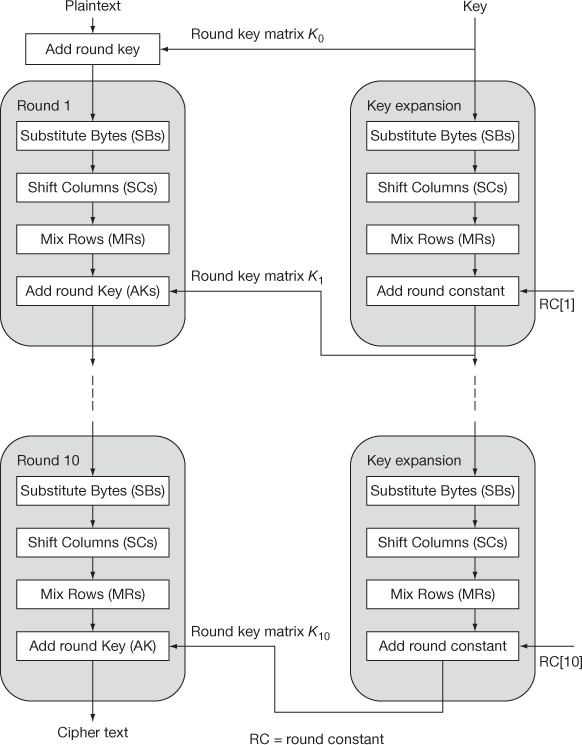
Figure 10.9 Whirlpool cipher W

The block cipher W consists of one AK followed by 10 rounds. These rounds involve SBs, SCs, MRs and add round key (AK) operations.

The following equation specifies how one round is expressed as round function RF.

RF(K_r) = AK(K_r) 6 MR 6 SC 6 SB

where K_r is the round key matrix for round r.

The overall algorithm, with key input K, can be defined as

W(K) = (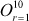 RF(K_r)) 6 AK(K₀)

Large circle indicates the iteration of composition function.

Index r ranges from 1 to 10. The plaintext input to W is a single 512-bit block. This block is treated as an 8 × 8 square matrix of bytes and represented as CState. The first row of CState is formed by first eight bytes of 512-bit plaintext. The second row of CState is formed by second eight bytes and so on.

Whirlpool uses KState which is a 512-bit key. Like CState, KState is also a 8 × 8 matrix. Key is used as input to initial AK function. The successive rounds take the hash value from previous round and uses as key.

10.4.6.4 The Non-linear Layer SB

In Whirlpool, the substitution box is denoted as S-box. It is a 16 × 16 table which has all possible 8-bit values. These values are called as 256 permutations. S-box helps for nonlinear mapping. Each byte in CState is mapped with a new byte. The row indicator for S-Box is represented with four leftmost bits from CState. The four right most bit is used as a column index.

Mathematically the non-linear layer SB function can be expressed as

B = SB(A)

b_{i, j} = S[a_{i, j}]

where B is the output, A is the CState.

b_{i, j} is the value of S-box

a_{i, j} is the individual byte of CState.

Indices i and j range from 0 to 7.

S is the process of S-box mapping.

10.4.6.5 The Permutation Layer SC

The permutation layer shifts each column of CState downwards. This shift is a circular shift except for the first column. One byte shift is performed for the second column. Two-byte shift is performed on the third column and so on.

The SC function for input matrix A and Output matrix B is expressed as

B = SC(A) ⇔ b_{i, j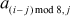} = 0 ≤i, j ≤ 7.

The shift column transformation gets significant attention because CState is an 8 × 8 matrix. The first 8 bytes of plaintext is copied in the first row, and so on. The transformation insists that the 8 bytes of one row are spread out for eight different rows.

10.4.6.6 The Diffusion Layer MR

The diffusion layer (mix rows) achieves diffusion individually within each row. Each byte of a row is mapped into a new value. This new value is a function of all eight bytes in that row. In diffusion ­function, the output bit is affected by many input bits.

The transformation is represented by the matrix multiplication.

B = AC,

where A is the input matrix, B is the output matrix, and C is the transformation matrix.

The sum of products of figures of one row and one column is denoted as figures in product matrix. Each row of transformation matrix is built with a circular right shift of the previous row. The transformation matrix C is designed as maximum distance separable (MDS) matrix which provides a high degree of diffusion.

10.4.6.7 The Add Key Layer AK

Add key layer applies XOR operations on 512 bits of CState with 512 bits of round key bitwise.

AK can be expressed as

B = AK[K_i] (A) ⇔ b_{i, j}= a_{i, j} ⊕ K_{i, j} 0 ≤i, j ≤7.

where A is the input matrix, B is the output matrix and K_i is a round key.

The key expansion for the block cipher W is achieved with the round key. The round constant for row r is represented as a matrix RC[r] in which only the first row is non-zero and others can be defined as

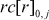= S[8(r − 1) + j], 0 ≤j ≤7, 1 ≤r ≤10.

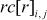= 0, 1 ≤i ≤7, 0 ≤j ≤7, 1 ≤r ≤10.

S refers to S-box.

The key schedule expands 512 bit cipher key K with set of round keys K₀, K₁, … K₁₀.

K₀ = K

K_r = RF [RC [r]](K_r-1)

where RF is the round function. RF(K_r) = AK(K_r) ○ MR ○ SC ○ SB

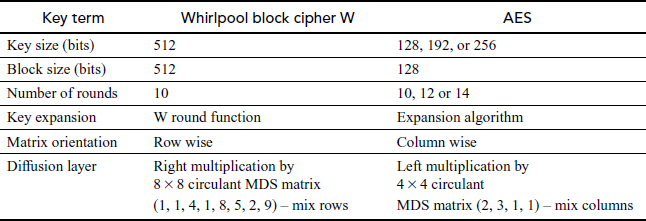
10.4.6.8 Comparison of Whirlpool Block Cipher W with AES

Advanced Encryption Standard (AES) is one of the cryptographic symmetric key standards. It is ­designed to overcome DES. Whirlpool building blocks are similar to AES. Table 10.2 depicts some differences among them.

Table 10.2 Comparison of Whirlpool block cipher W with AES

Key Terms

Birthday attack

Block cipher

Compression function

Hash value

HMAC

MAC

MD5

RIPEMD-160

SHA

Whirlpool

Summary

• MAC is generated with cryptographic hash function and secrete key. The design of hash functions is started with MD4 followed by MD5. The next hash function is SHA. SHA represents the message with multiple of 512-bit length. SHA makes any file or input with different size as 160-bit ­digest. SHA construction is similar to MD4 and MD5 hash functions. SHA prevents the attacker to find hash collisions. The birthday problem is an interesting model which shows the probability of collisions of 365 days in a year. Different variations of the original problem help to solve other related problems. The birthday attack shows the expected number of attempted values before finding a collision. Birthday attack is sometimes computationally intensive strategy to break ­encrypted message and it shows poor performance when the hash length is increased. RIPEMD-160 is an iterative hash function that processes 512-bit input message blocks with compression function and produces 160-bit hash value. RIPEMD-160 shows resistance against brute-force collision search attack. It is widely used in several banking applications. It is currently in consideration for standardization under ISO/IEC JTC1/SC27. HMAC looks like a special construction mechanism to calculate MAC. MD5 or SHA-1 can be used in HMAC. The resulting MAC algorithms are denoted as HMAC-MD5 and HMAC-SHA-1, respectively. HMAC applies hash function in a block box way. HMAC codes are readily available. The strength of HMAC depends upon the quality of secret key and its size. Whirlpool is a block cipher-based secure hash function. The NIST evaluation of Rijndael says that Whirlpool better performance in execution speed in different hardware and software. It works well during low memory requirements. Whirlpool hash function shows good resistant to the usual attacks on block-cipher-based hash codes. Whirlpool needs only 10 clock cycles to transform each block. RIPEMD-160 needs 80 clock cycles and MD5 needs 64 block cycles.

Review Questions

1. What is message authentication code (MAC)? Mention the requirement of MAC.
2. What is SHA? Mention its applications.
3. Mention the properties and applications of SHA.
4. Write a note on SHA family.
5. How does SHA work?
6. State birthday problem.
7. How can you relate birthday problem with data security?
8. What are the operations of RIPEMD-160?
9. What are the characteristics of RIPEMD-160?
10. Mention the steps of RIPEMD-160.
11. Briefly explain the operational block of RIPEMD-160.
12. What is HMAC?
13. Mention the design objective of HMAC.
14. Briefly explain HMAC algorithm step and its working block.
15. Mention the features of Whirlpool.
16. Mention the security goals of Whirlpool.
17. Mention the hash function expression in Whirlpool.
18. Briefly explain the steps of message digest generation in Whirlpool with a block diagram.
19. How the diffusion layer differs in Whirlpool block cipher W and AES?
20. Mention any four differences between Whirlpool block cipher W and AES.
21. Write a short note on Whirlpool cipher W.