Table of Contents for
Cryptography and Network Security

Version ebook / Retour

Cover image for bash Cookbook, 2nd Edition Cryptography and Network Security by S. Bose Published by Pearson Education India, 2016
  1. Cover
  2. Title Page
  3. Engineering Chemistry
  4. Contents
  5. Foreword - 1
  6. Foreword - 2
  7. Preface
  8. Acknowledgements
  9. CHAPTER 1 Cryptography
  10. CHAPTER 2 Mathematics of Modern Cryptography
  11. CHAPTER 3 Classical Encryption Techniques
  12. CHAPTER 4 Data Encryption Standard
  13. Chapter 5 Secure Block Cipher and Stream Cipher Technique
  14. Chapter 6 Advanced Encryption Standard (AES)187
  15. Chapter 7 Public Key Cryptosystem
  16. Chapter 8 Key Management and Key Distribution
  17. Chapter 9 Elliptic Curve Cryptography
  18. Chapter 10 Authentication Techniques
  19. Chapter 11 Digital Signature
  20. Chapter 12 Authentication Applications
  21. Chapter 13 Application Layer Security
  22. Chapter 14 Transport Layer Security
  23. Chapter 15 IP Security
  24. Chapter 16 System Security
  25. Appendix: Frequently Asked University Questions with Solutions
  26. Basic Mechanical Engineering

Chapter 6

Advanced Encryption Standard (AES)

6.1 AES Introduction (GF(2n))

All the symmetric encryption algorithms that we have studied so far have some problems with respect to security and efficiency, because some of the earlier encryption algorithms such as S-DES and DES can be broken easily using modern computers. The DES algorithm was broken in 4.5 months using distributed search in January 1997. Subsequently, it was broken in 15 days in 1998 using a high end system that costs about $250,000 [1]. In January 1999, it was broken in 22 hours and 15 minutes using a distributed search. Moreover, it was also not an efficient encryption algorithm since it was very slow to use it in various softwares as it was developed for old softwares and hardwares. To improve the security of DES algorithm, Triple DES algorithm was developed and it was used to provide secure data transmission in banking systems. However, triple DES also takes more computational complexity, since it performs three-time encryption operation on the sender side and three-time decryption operation on the receiver side. Therefore, it was required to develop a new secure and efficient encryption algorithm.

In order to do that, the national institute of standards and technology (NIST) issued a call for proposal for designing a new cipher in January 1997. Many groups had submitted various ciphers. After several rounds of review, 15 ciphers were accepted in the first round of the review. This was narrowed down to 5 ciphers in the second round and these five selected ciphers are given in Table 6.1. These five ciphers were tested for speed and security and NIST has finally chosen an algorithm known as Rijndael. Rijndael was named because it was developed by two Belgian cryptographers Dr Joan Daemen and Dr Vincent Rijmen at the Electrical Engineering Department of Katholieke University in Leuven.

Table 6.1 Five selected ciphers for the call for proposal by the NIST

alg1.png

Rijndael was selected as advanced encryption standard (AES) in October 2000 because, Rijndael was the best algorithm in terms of security, cost, flexibility and simplicity of the algorithm. In November 2001, AES became a FIPS (Federal Information Processing Standards) standard. AES is making use of arithmetic operations based on Galois Filed that was discussed in Chapter 2. Those who are not familiar with Galois Filed, we advise them to read Chapter 2 before reading the AES algorithm. The AES algorithm is making use of GF(2n) structure in which n = 8.

6.2 Working principle of the AES

AES is a symmetric cipher that uses the same key for both encryption and decryption process. However, AES differs from DES in a number of ways. First, AES is a block cipher process that can process a 128-bit block of plaintext at a time. But DES can process only 56 bits of plaintext. Second, AES uses a large 128-bit key size to perform encryption and decryption process. AES increases the key size to 128 bits, 192 bits and 256 bits. Depending on the three types of keys, three versions are used in AES. The three versions are AES-128, AES-192 and AES-256. However, DES uses only a 56-bit key to perform encryption and decryption processes. Third, AES cipher uses 10 rounds of operation for performing encryption and decryption processes. In each round, AES performs substitution and permutation operations. The number of rounds used in three versions of AES can differ. For example, AES-128 uses 10 rounds, AES-192 uses 12 rounds and AES-256 uses 14 rounds of operations. However, DES supports 16 rounds of operations which would slow down the speed of encryption and decryption processes. Fourth, AES is not using Feistel structure and hence entire data block is processed in a parallel way during each round. In contrast to this, DES uses Feistel structure. Therefore, the left-hand side of half of the plaintext block is used to modify the right-hand side of the plaintext block. Similarly, right-hand side of half of the plaintext block is used to modify the left-hand side of the plaintext block. Finally, in AES, all the transformations that are used in the encryption process will have the inverse transformations that are used in the decryption process. In DES, only the keys are in reverse order during the decryption process.

6.3 AES Encryption and Decryption

The AES is a symmetric cipher that encrypts a 128-bit block of plaintext using a 128-bit key value to produce a 128-bit ciphertext. To encrypt a 128-bit plaintext, AES uses 10 rounds of operations. The plaintext and ciphertext size are fixed to 128 bits. However, the key size can be changed to 192 bits or 256 bits. Accordingly, the number of rounds is increased to 12 rounds or 14 rounds. In each round, it performs four transformations, namely SubBytes(), ShiftRows(), MixColumns() and ­AddRoundKey(). Among the four transformations, SubBytes() and MixColumns() are used to perform simple substitution operations. The ShiftRows() transformation is used to perform the permutation operation. These three transformations are used to provide confusion, diffusion and non-linearity during the encryption process. The AddRoundKey() transformation is used to perform the XOR operation in the encryption and decryption process. Similar to the substitution and transposition transformations performed in the encryption process, there are inverse transformations in the decryption process. The inverse transformations are InvSubBytes(), InvShiftRows() and InvMixColumns(). These three inverse transformations are the inverse of the SubBytes(), ShiftRows() and MixColumns() transformations. Therefore, in AES, each transformation used in the encryption process is easily reversible in the decryption process. The AddRoundKey() transformation used in the encryption process is also a reversible transformation in the decryption side if the key is known. For example, the ciphertext C is obtained by XOR-ing the plaintext block with key K. This can be written as 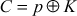Eqn5.png . This operation is a reversible operation on the decryption side if the key K is known Eqn7.png . Table 6.2 shows the various transformations and symbols that are used in this algorithm.

Table 6.2 Transformations and symbols used in AES

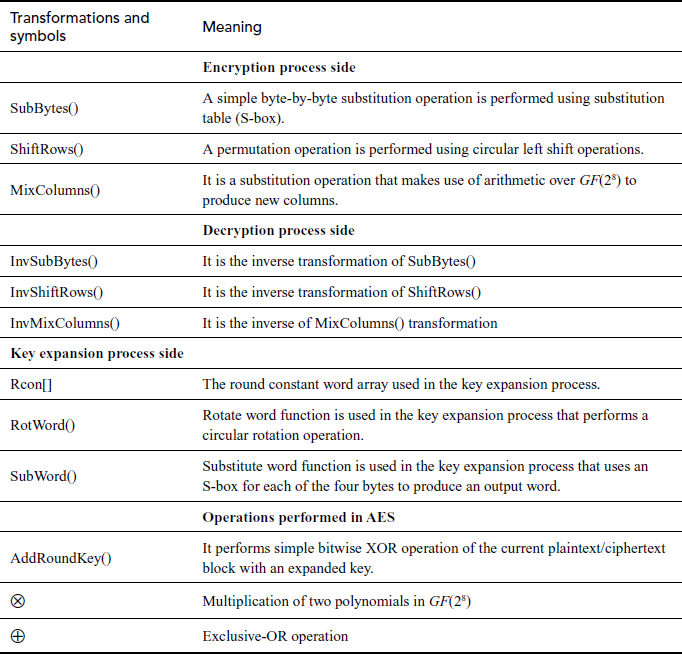
alg1.png

Figure 6.1 shows the overall structure of the AES cipher that comprises three parts. The first part (left-hand side) shows the encryption process, second part (middle one) shows the key expansion process and third part (right-hand side) shows the decryption process. The input to the encryption and decryption process is a single 128-bit block which is represented as a (4 × 4) square matrix that consists of 16 cells. In each cell, one byte of the plaintext/ciphertext is placed. When the plaintext/ciphertext is placed in the square matrix, the first four bytes are placed in the first column and the second four bytes are placed in the second column and so on. So, bytes are placed in column-by-column method. At each transformation of the encryption and decryption process, this square matrix is processed by copying the values into the state array.

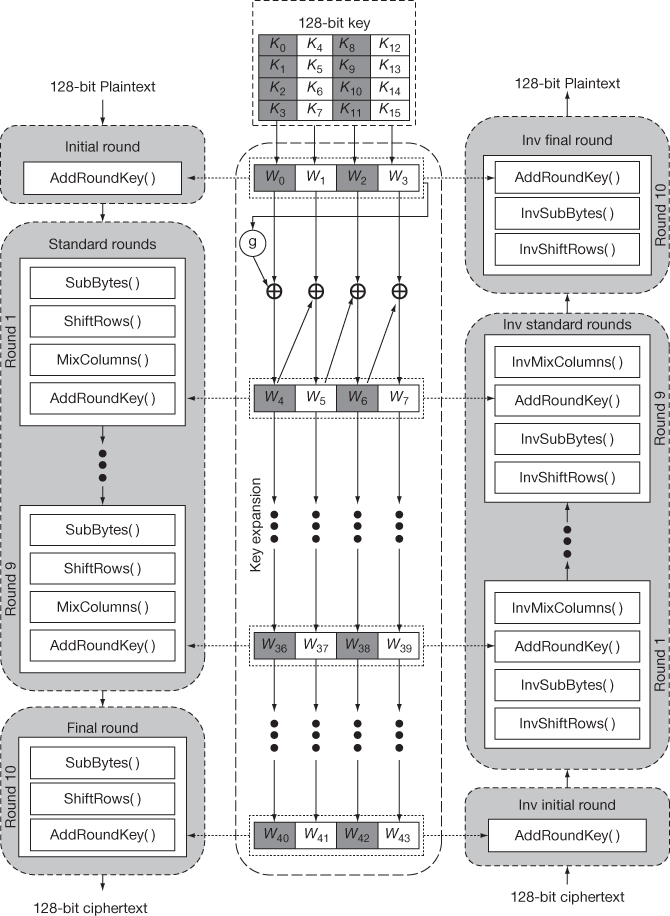
C06F001.png

Figure 6.1 Overall structure of the AES cipher

This process is shown in Figure 6.2. This state array value is modified in each transformation and state array is copied into an output matrix after the final transformation (Add round key). Similar to this, the 128-bit key is also as a represented as a (4 × 4) square matrix to fill the key value as bytes in the square matrix. From the initial matrix, four words are generated in each round and hence 44 words are generated in total for all the 11 rounds (1 initial round + 10 standard rounds). Each word Wi size is 4 bytes (1 word = 4 bytes = 32 bits). To generate four words (128 bits) for each round of encryption and decryption process, a key expansion process is used. These four words are used as a subkey for each round to perform the encryption process. During the decryption process, the keys are used in reverse order as shown in the third part of Figure 6.1.

C06F002.png

Figure 6.2 State array input and output

SubBytes() and InvSubBytes() Transformations

The SubBytes() transformation is a byte substitution that operates on each byte of the state array using a substitution box (S-box). The AES defines a 16 × 16 matrix for representing the S-box that consists of all the 256-byte values. Figure 6.3 shows the S-box and inverse S-box used for performing encryption and decryption process. The S-box and inverse S-box used in the SubBytes() and InvsubBytes() transformations are presented in hexadecimal format. Each input byte given to the S-box is mapped into a new byte in the following way: The leftmost 4 bits are used for selecting one of the row values from the S-box and the rightmost 4 bits are used for selecting a column value. These row and column values serve as indices to the S-box for selecting a unique byte value from the S-box. For example, if the input to the S-box is 75, then it will select the value which is located in the 7th row and 5th column which contains the value 9D. During the decryption process, the hexadecimal value 9D is used to select the value 75 from the inverse S-box defined for decryption process. The S-box is used to make the AES algorithm resistant against the differential and linear cryptanalysis and attacks. The following shows an example for SubBytes() transformation using S-box.

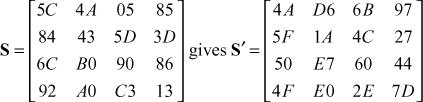
Eqn12.png

In this example, initially, the number 5C is given as input to SubBytes() transformation. So, the value located in 5th row and Cth column position is 4A. Similarly, the substitution is performed for all the remaining bytes.

C06F003a.png
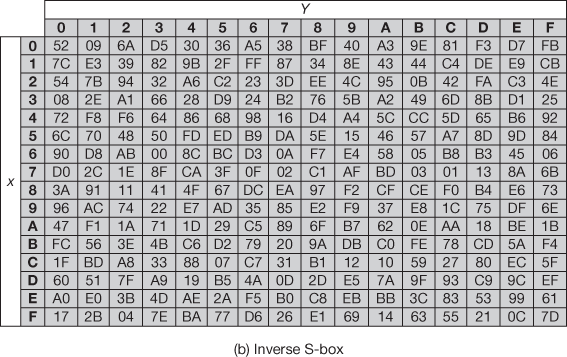
C06F003b.png

Figure 6.3 S-box and inverse S-box

ShiftRows() and InvShiftRows() Transformations

In ShiftRows() transformation, rows in the state array are circularly left shifted with different offsets. Row 1 is not shifted. Row 2 is shifted by 1 byte, row 3 is shifted by 2 bytes, and row 4 is shifted by 3 bytes. In InvShiftRows() transformation, rows in the state array are circularly right shifted. Figure 6.4 shows ShiftRows() transformation. The following shows an example for ShiftRows() transformation using S-box.

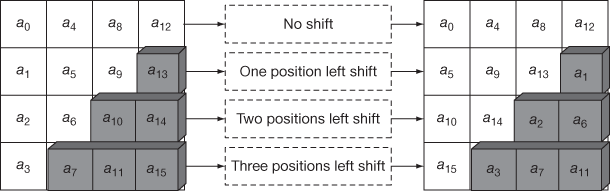
C06F004.png

Figure 6.4 ShiftRows() transformation

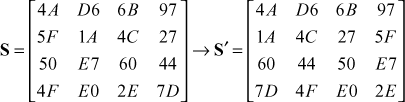
Eqn16.png

MixColumns() and InvMixColumns() Transformation()

The Mixcolumns() transformation is basically a substitution that makes use of arithmetic operations over 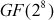Eqn17.png with an irreducible polynomial 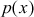Eqn18.png . There are 30 irreducible polynomials available for the algebraic structure 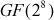Eqn19.png as shown in Table 6.3. All these 30 irreducible polynomials can be used for different time intervals for sending different messages to improve the security level. 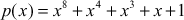The irreducible polynomial that is used for the AES algorithm isEqn20.png .

Table 6.3 Irreducible polynomials that can be used for AES

alg1.png

Each column is operated on individually in the Mixcolumns() transformation. While doing Mixcolumns() transformation, each byte of the state array value is modified into a new value. The transformation can be determined by performing a matrix multiplication based on 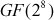Eqn22.png with respect to a matrix defined for Mixcolumns() transformation. Each element of the product matrix is the sum of products of elements of one row and one column. In this case, the individual additions are ­performed as XOR operation since operations are based on 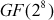Eqn23.png . The multiplication operation is performed in GF(28). The following matrix is defined for performing Mixcolumns() transformation in the ­encryption process.

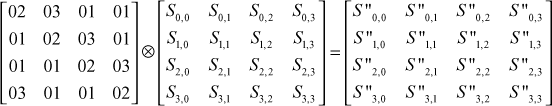
Eqn25.png

The following matrix is defined for performing InvMixcolumns() transformation in the decryption process. This matrix is the inverse of the matrix defined for Mixcolumns() transformation.

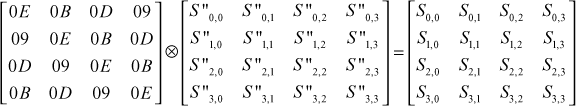
Eqn26.png

This matrix is the inverse of the matrix defined for Mixcolumns() transformation. One of the important conditions to be satisfied by this matrix is that the multiplication of this matrix and the matrix used in the Mixcolumns() transformation is an identity matrix I as shown below.

Eqn28.png

Addroundkey()

In Addroundkey() transformation, the output produced by the mixcolumn() transformation is XOR-ed with the subkey value produced by the key expansion algorithm. For performing the XOR operation, first column of the output of the mixcolumn() transformation is XOR-ed with first column of subkey value. Similarly, a column-by-column XOR operation is performed. This can be represented as shown below:

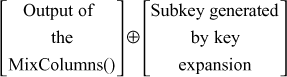
Eqn29.png

6.4 AES Key Expansion Algorithm

The AES encryption and decryption uses a RoundKey in each round from the given 128-bit key value. For a 128-bit key value, totally 11 round keys are generated. Among the 11 keys, one key is used for the initial round, 9 for standard rounds and 1 for the final round. For generating 11 keys, initially the input key is copied into a (4 × 4) square matrix. In this matrix, the first four bytes are copied into first column and next four bytes are copied into next column as shown below:

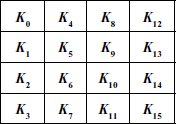
alg1.png

From this matrix, four words (128 bits) are generated for each round and hence 44 words are ­generated in total. Each word w[i] depends on the immediately preceding word, w[i − 1], and the word located four positions previous (w[i − 4]) to w[i]. Figure 6.5 shows AES key expansion algorithm.

C06F005.png

Figure 6.5 Key expansion algorithm

As shown in the key expansion algorithm, first four words w[i] (0 ≤ i ≤ 3) are generated from the initial matrix. For the remaining words w[i] (4 ≤ i ≤ 43), the key expansion algorithm is ­followed. For generating the words 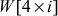Eqn30.png (1 ≤ i ≤ 10), two transformations and an XOR operation are used. The two transformations are ShiftRows() and SubBytes(). In ShiftRows() transformation, one-byte circular left shift on a word is performed. In SubBytes() transformation, a simple substitution transformation is performed using S-box. This result is XOR-ed with a round constant defined for each 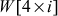Eqn31.png . This round constant is 01 for 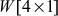Eqn32.png , and it is 02 for 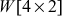Eqn33.png and so on. For ­generating the round constant for 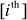Eqn34.png word, the value 02 is multiplied with its previous round constant value. This multiplication is performed on 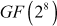Eqn35.png . 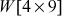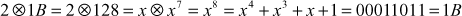For example, the round constant for Eqn36.png is Eqn37.png . Table 6.4 shows round constant for all the 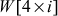Eqn38.png values.

Table 6.4 Round constants

alg1.png

Consider an example of generating the word 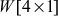Eqn39.png . Initially, w[i − 1] is copied into the temporary variable (temp = w[i − 1] = w[3]). If the value stored in temp = [X1, X2, X3, X4], then it will be supplied into rotateword() transformation which will rotate only one byte in the input as [X2, X3, X4, X1]. Then, a SubBytes() transformation is performed using S-box. 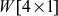Finally, the result will be XOR-ed with [01, 0, 0, 0] because round constant is 01 for Eqn40.png .

6.5 AES Exercises Based on GF (28)

The following shows an example for MixColumns() transformation for the input matrix

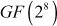Eqn41.png using Eqn42.png .

Eqn43.png

First, multiply the first row of the MixColumns() matrix with the first column of the input matrix and perform an XOR operation to find the first byte in the resultant matrix. This is obtained as given below:

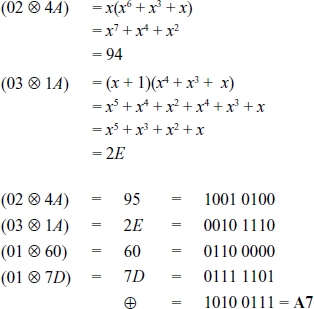
alg1.png

Next, multiply the first row of the MixColumns() matrix with the second column of the input matrix and perform an XOR operation.

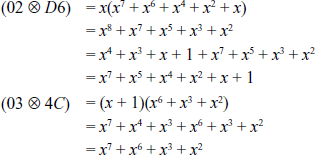
alg1.png

XOR-Operation of the resultant values:

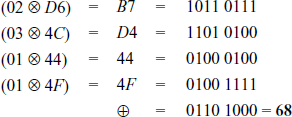
alg1.png

Next, multiply the first row of the MixColumns() matrix with the third column of the input matrix to find the third value in the first row of the resulting matrix.

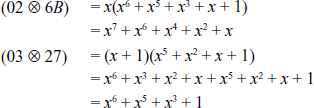
alg1.png

XOR-Operation of the resultant values:

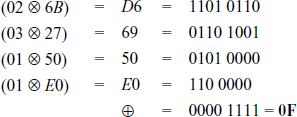
alg1.png

Next, multiply the first row of the MixColumns() matrix with the fourth column of the input matrix to find the fourth value in the first row of the resulting matrix.

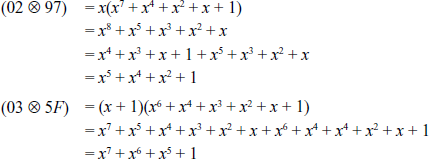
alg1.png

XOR-Operation of the resultant values:

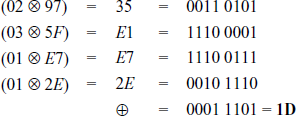
alg1.png

Similarly, this process is followed for the multiplication of the second row of the MixColumns() matrix with all the four columns of the given input matrix.

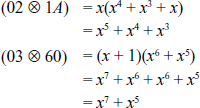
alg1.png

XOR-Operation of the resultant values:

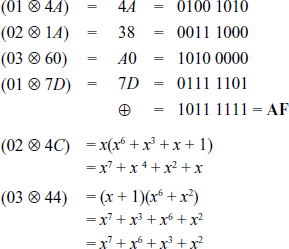
alg1.png

XOR-Operation of the resultant values:

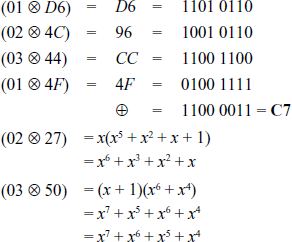
alg1.png

XOR-Operation of the resultant values:

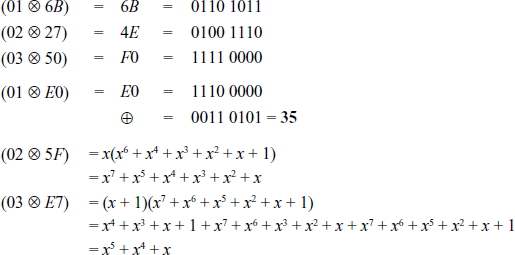
alg1.png

XOR-Operation of the resultant values:

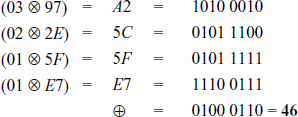
alg1.png

XOR-Operation of the resultant values:

alg1.png
alg1.png

OR-Operation of the resultant values:

alg1.png
Key Terms

10 rounds of operation

AddRoundKey()

Advanced Encryption Standard (AES)

Circular left shift

FIPS (Federal Information Processing Standards)

Galois filed

InvMixColumns()

InvShiftRows()

InvSub-Bytes()

Irreducible polynomial

Key expansion

MixColumns()

Rcon[]

Rijndael

Rotateword()

RotWord()

ShiftRows()

Standard Rounds

Sub-Bytes()

SubWord()

Summary
  • AES is making use of arithmetic operations based on Galois Filed GF(2n) structure in which n = 8.
  • AES is a symmetric cipher that uses the same key for both encryption and decryption process.
  • AES is a symmetric cipher that encrypts a 128-bit block of plaintext using a 128-bit key value to produce a 128-bit cipher text. To encrypt a 128-bit plaintext, AES uses 10 rounds of operations.
  • AES performs four transformations, namely SubBytes(), ShiftRows(), MixColumns() and AddRoundKey() in each round of the encryption process.
  • AES uses the inverse transformations InvSubBytes(), InvShiftRows() and InvMixColumns() in the decryption process.
  • Therefore, in AES, each transformation used in the encryption process is easily reversible in the decryption process.
  • The input to the encryption and decryption process is a single 128-bit block which is represented as a (4 × 4) square matrix that consists of 16 cells.
  • Similar to this, the 128-bit key is also as a represented as a (4 × 4) square matrix to fill the key value as bytes in the square matrix. From the initial matrix, four words are generated in each round and hence 44 words are generated in total for all the 11 rounds (1 initial round + 10 standard rounds).
  • These row and column values serve as indices to the S-box for selecting a unique byte value from the S-box.
  • In ShiftRows() transformation, rows in the state array are circularly left shifted with different offsets.
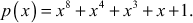
  • The irreducible polynomial that is used for the AES algorithm isEqn46.png
  • In Addroundkey() transformation, the output produced by the mixcolumn() transformation is XOR-ed with the subkey value produced by the key expansion algorithm.
  • For generating the round constant for[ith] word, the value 02 is multiplied with its previous round constant value. This multiplication is performed on Eqn48.png .
Review Questions
  1. Why NIST has selected Rijndael as the AES?
  2. What are the other four algorithms that were not selected?
  3. Write short description about ShiftRows() transformation that constitutes the second transformation in each round of AES.
  4. Write short description about MixColumns() transformation that constitutes the third transformation in each round of AES. Explain with an example.
  5. How many words of the key metrics are used for key expansion algorithm and how many words are generated from it in total?
  6. Let us consider the first four words of the key schedule are w0, w1, w2, w3. From this, how do we need to obtain the next four words w4, w5, w6, w7?
  7. Explain about AES encryption process with a neat diagram in detail.
  8. Explain about AES key expansion process.
References
  1. http://cs.ucsb.edu/~koc/cs178/docx/w04x-des.pdf
  2. http://csrc.nist.gov/archive/aes/rijndael/Rijndael-ammended.pdf