Table of Contents for

Cryptography and Network Security

Chapter 11

Digital Signature

Cryptosystem is the field of study about techniques for achieving and maintaining secure state. In cryptosystem, only authorized users are allowed to use the information contained within the system. In this chapter, different techniques such as digital signature, attacks on digital signature, RSA-based Digital Signature Algorithm (DSA) and java implementation for batch DSA are discussed in detail.

11.1 INTRODUCTION TO DIGITAL SIGNATURE

Digital signature is one of the most important inventions in modern cryptography. The necessity behind the invention of digital signature is a user, who has to sign a message such that intended addressee alone can verify the digital signature. Digital signature of each user should be verifiable by other users but digital signing on behalf of other users should be prohibited. Digital signature is different from a handwritten signature. Digital signature of a message is associated with the message, which is different for each message. But the handwritten signature is adjoined to the message, which always looks the same. Some salient features of digital signature are enumerated as follows:

1. It depends on the message signed.
2. It must use information which is unique to sender for prevention of both forgery and repudiation.
3. It must be relatively easy to generate and verify.

A digital signature should be computationally infeasible to regenerate by adversaries to avoid fraudulent digital signature.

11.1.1 Uses of Digital Signature

Digital signatures are mainly used for authentication purpose. It is used to convince communicating parties with each other’s identity and exchange their session keys. It is an electronic format of signature that can be used by a person to authenticate the identity of message’s sender or identity of document’s signer. It ensures that the original content of message or document sent is intact.

Digital signatures are transportable. It cannot be imitated by someone else. It can be automatically time-stamped. It ensures that the original signed message reached, so that sender cannot easily repudiate it later. A digital signature can be used for any form of message. The receiver can be sure of sender’s identity and that the message arrived is intact with the help of digital signature.

11.1.2 Comparison of Digital Signature with Digital Certificate

A digital certificate has digital signature of certificate-issuing authority, which can be used by a person to verify that the certificate is real. Digital signature and digital certificate are security measures, which are different in their usage and generation aspects.

Digital certificates are used for verification of website’s trustworthiness, while digital signatures are used to verify information authentication. In case of digital certificates, an organization can ensure the website’s security if and only if digital certificates are issued by organization itself or by a trusted certification source, like Verisign Inc. Although the website has certificated from trusted source, it can be insecure because hacker can infiltrate this website to modify its content.

Digital signature generates checksum for information that has to be sent, which can be verified by recipient that information is unaltered. For example, a person has to send a signed Microsoft Word as an attachment in an e-mail. The e-mail attachment in transit can be obtained by a hacker using man-in-the-middle attack and can insert malicious piece of code with this attachment. The checksum of altered attachment will be different from checksum of sent attachment. Hence the recipient is alerted that the content was modified in some way from the original with the aid of checksum.

Nowadays business dealings are done over the internet. For example, online trading as well as transactions is done in an untrusted environment like the internet where any website has digital certificate whose trustworthiness has to be scrutinized. Here any content available for transfer was digitally signed to ensure it was unaltered. This is depicted in Figure 11.1.

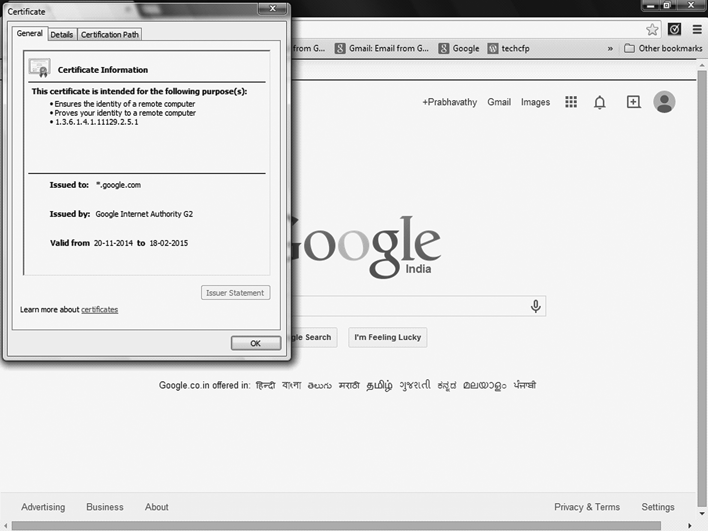
Figure 11.1 Website using a trusted digital certificate

11.1.3 Digital Signature Standard

Digital Signature Standard (DSS) was developed by the U.S. National Security Agency (NSA) for the generation of digital signature to authenticate electronic documents. In 1994, DSS was put forth by the National Institute of Standards and Technology (NIST). The US government standard for authentication of electronic documents is DSS, which is specified in Federal Information Processing Standard (FIPS) 186.

DSA is a pair of large numbers that are computed according to the specified algorithm within parameters that enable the authentication of the signatory. As a consequence, the integrity of the data attached is ensured. Digital signatures are generated through DSA, as well as verified. Using the private key, signatures are generated. Public key corresponding to it is used for verification. Each signatory has their own paired public and private keys. Hence signature can be generated only by an authorized person using their private key, whereas anyone can use the corresponding public key to verify the signature. Message digest is the checksum, which depicts summary of the information is created using a hash function called the Secure Hash Standard (SHS). SHS is specified in FIPS 180. The message digest along with the DSA algorithm is used to create the digital signature, which has to be sent along with the message. Signature verification involves the use of the same hash function.

A digital signature system consists of the following:

1. Ptxt: space for possible plaintexts
2. Sign: space for possible signatures
3. K: space for possible keys
4. V: space for verification

For each k ∈ K there is a signing algorithm sig_k ∈ Sign and a corresponding verification algorithm ver_k ∈ V such that

1. sig_k: Ptxt → Sign
2. ver_k: Ptxt ⊗ Sign → {true, false}, where ⊗ is the verification algorithm.
3. ver_k (w, s): true, if s = sig (w); false, otherwise

Algorithms sig_k and ver_k have to be computable in polynomial time. Verification algorithm can be publically known whereas signing algorithm has to keep only its key as secret.

11.2 DIGITAL SIGNATURE SCHEMES

In this section, various signature schemes available for digital signing purpose are discussed. They are ElGamal signature scheme, DSA signature scheme, RSA signature scheme, Fiat–Shamir signature scheme, Lamport signature scheme, Chaum–Antwerpen undeniable signature scheme, Chaum’s blind signature scheme, Ong–Schnorr–Shamir subliminal channel signature scheme, Heyst–Pedersen signature scheme and probabilistic signature scheme.

11.2.1 ElGamal Signature Scheme

ElGamal signature scheme is based on computing difficulty of discrete logarithms. In 1984, a person named Taher ElGamal described this scheme. Hence this scheme is named after Taher ElGamal as ElGamal signature scheme.

11.2.1.1 Design

Choose: prime p, integers 1 ≤ q ≤ x ≤ p, q be a primitive element of Z_p*, where x is the private key of the signer.

Compute: y = q^x mod p

key K = (p, q, x, y)

Publish the public key (p, q, y) and keep private key (x) as secret.

11.2.1.2 Signature

Let w be the message and r ∈ Z_p−1* be randomly selected secret number, where 1 < r < p−1 and gcd(r, p − 1) = 1.

sig(w, r) = (a, b), where a = q^r mod p and b = (w − xa)r ⁻¹ (mod p – 1).

11.2.1.3 Verification

Accept the signature (a, b) of w as valid if

y^aa^b ≡ q^w (mod p) (Indeed: y^aa^b ≡ q^axq^rb ≡ q^{ax + w – ax} ≡ q^w (mod p))

Example 11.1

Assume Anto considers p = 467; q = 2; x = 127 and calculates y = q^x mod p = 2¹²⁷ mod 467 = 132. So, Anto’s key pair is (127, 132).

Anto takes message, w = 100 and assumes r = 213 for the signature of the message. Notice that gcd(213, 466) = 1 and 1 < 213 < 126.

Anto calculates signature as a and b as follows.

a = q^r mod p = 2²¹³ mod 467 = 29.

b = (w − xa)r⁻¹ (mod p –1)

= (100 − 127 * 29) * 213⁻¹ mod 466

= (100 − 127 * 29) * 431 (mod 466) = 51.

Therefore, sig(w, r) = (a, b) = (29, 51).

Anto sends the message with the signature to Brad. Brad verifies Anto’s signature to accept the message.

Brad calculates y^aa^b ≡ q^w (mod p).

132²⁹ * 29⁵¹ mod 467 = 2¹⁰⁰ mod 467.

189 = 189.

Thus, Brad verifies Anto’s signature and accepts the message.

11.2.2 DSA Signature Scheme

The Federal Information Processing Standard for digital signatures gives DSA. The NIST proposed DSA in August 1991, adopted as FIPS 186 in 1993. DSA is a different form of ElGamal Signature Scheme.

DSA uses public key and private key for generation and verification of digital signatures. DSA key pair is based on two large prime numbers, p and q, where (p – 1) mod q = 0. DSA cannot be used to encrypt messages.

11.2.2.1 Design

The following global public key components are chosen in the key generation process:

p is a random l-bit prime, 512 ≤ l ≤ 1024, l = 64t, where t = 8,…,16.

q is a random 160-bit prime dividing p − 1.

r = h ^{(p – 1)/q} mod p, where h is random primitive element of Z_p, such that r > 1

User’s private key components are:

x is a private key which is a random integer, 0 < x < q

y = r^x mod p.

Therefore, the Key = (p, q, r, x, y)

After computing the key, Anto publish the public key (p, q, r, y) in the public directory.

11.2.2.2 Signature

Signing of a 160-bit plaintext w to be sent.

Choose a random number k, where 0 < k < q such that gcd(k, q) = 1

Compute a = (r^k mod p) mod q

Compute b = k⁻¹(w + xa) mod q, where kk⁻¹ ≡ 1 (mod q)

Signature: sig(w, k) = (a, b)

11.2.2.3 Verification

Verification of signature (a, b)

Compute z = b⁻¹ mod q

Compute u₁ = wz mod q, u₂ = az mod q

Verification: ver_k(w, a, b) = true <=> (r^u1y^u2 mod p) mod q = a

Proof:

(r ^u1y ^u2 mod p) mod q = ((r ^wz mod q)(y^az mod q) mod p) mod q

= ((r ^wz mod q) ((r ^xaz mod p) mod q) mod p) mod q

= ((r (^{w + xa})^z) mod p) mod q

= ((r ^bkz) mod p) mod q

= ((r ^bkb - 1) mod p) mod q

= (r ^k mod p) mod q

= a

Example 11.2

Anto chooses prime number p = 11 and q = 5, w = 54, h = 2 and x = 3.

Calculate r = h ^{(p –1)/q} mod p = 2^{(11 – 1)/5} mod 11 = 4.

y = r ^x mod p = 4³ mod 11 = 9.

Anto publish the public key (11, 5, 4, 9).

Anto signs the message w as sig(w, k) = (a, b)

Anto assumes k = 3 such that gcd(3, 5) = 1.

Anto computes a = (r^k mod p) mod q = (4³ mod 11) mod 5 = 4.

b = k-¹(w + xa) mod q = 3⁻¹ (54 + 3 * 4) mod 5 = 2.

Anto sends the message with the signature to Brad.

Brad verifies Anto’s signature as follows:

Compute z = b⁻¹ mod q = 2⁻¹ mod 5 = 3.

u₁ = wz mod q = 54 * 3 mod 5 = 2.

u₂ = az mod q = 4 * 3 mod 5 = 2.

(r^u1y^u2 mod p) mod q = (4² * 9² mod 11) mod 5 = 4 = a.

Signature has been checked and verified successfully.

Example 11.3

Anto chooses choose prime number p = 48731 and q = 443, w = 343, h = 7 and x = 242.

Calculate r = h^(p - ^1)/q mod p = 7⁽⁴⁸⁷³¹ - ^1)/443 mod 48731 = 5260.

y = r^x mod p = 5260²⁴² mod 48731 = 3438.

Anto publish the public key (48731, 443, 5260, 3438).

Anto signs the message w as sig(w, k) = (a, b)

Anto assumes k = 427 such that gcd(427, 443) = 1.

Anto computes a = (r ^k mod p) mod q = (5260⁴²⁷ mod 48731) mod 443 = 59.

b = k⁻¹(w + xa) mod q = 427⁻¹ (343 + 242 * 59) mod 443 = 166.

Anto sends the message with the signature to Brad.

Brad verifies Anto’s signature as follows:

Compute z = b⁻¹ mod q = 166⁻¹ mod 443 = 435.

u₁ = wz mod q = 343 * 435 mod 443 = 357.

u₂ = az mod q = 59 * 435 mod 443 = 414.

(r^u1y^u2 mod p) mod q = (5260³⁵⁷ * 3438⁴¹⁴ mod 48731) mod 443 = 59 = a.

Signature has been checked and verified successfully.

11.2.3 RSA Signature Scheme

The abbreviation for RSA is the last name of three person named Ron Rivest, Adi Shamir and Leonard Adleman, who first publicly described this algorithm in 1977. This can be used for encryption as well as signature generation and verification.

11.2.3.1 Design

The key components of RSA include p, q. Select p and q such that both are large prime numbers and p ≠ q.

Calculate n = p * q and ϕ (n) = (p − 1) * (q − 1).

Select an integer e such that gcd(ϕ (n), e) = 1 and 1 < e < ϕ (n).

Calculate d ≡ e⁻¹ mod (ϕ (n)).

The public and private keys are (e, n) and (d, n), respectively.

11.2.3.2 Signature

Consider a message w such that w < n.

Signature of w is sign(w, s), where s = w ^d mod n

11.2.3.3 Verification

Verification of a signature is verify(w, s)

To verify, calculate s ^e mod n, which is equal to w that is w = s^e mod n

Example 11.4

Ando selects p = 7, q = 13.

Calculate n = p * q = 7 * 13 = 91

f (n) = (p − 1) * (q − 1) = 6 * 12 = 72.

Choose e = 5 such that gcd(5, 72) = 1.

Calculate d ≡ e⁻¹ mod (f (n)) = 5⁻¹ mod 72 = 29.

Public Key (5, 91) and Private Key (29, 91).

Anto signs the message w = 35.

Calculate s = w ^d mod n = 35²⁹ mod 91 = 42

Anto sends the signature, sign(w, s) = sign(35, 42) to Brad.

Brad verifies the received message by calculating w from s as

w = s ^d mod n = 42⁵ mod 91 = 35.

11.2.4 Fiat–Shamir Signature Scheme

Fiat–Shamir is the person who first proposed the use of zero-knowledge interactive proofs for authentication. Their trick for generation of digital signatures is widely used. Paradigm for changing identification scheme into signature scheme has been popular from its introduction because it gives efficient signatures.

11.2.4.1 Design

One-time set-up:

Trusted centre (T ) selects RSA-like modulus n = pq, where n is public, p and q are secret. Choose s as co-prime to n, such that 1 ≤ s ≤ n – 1,

Compute v = s² mod n and registers v with T, where v is public and s is secret.

11.2.4.2 Signature

1. Sender chooses random commitment r, such that 1 ≤ r ≤ n – 1
2. Sender sends to Receiver x = r² mod n
3. Receiver sends to Sender a random value e, such that e = 0 or e = 1
4. Sender sends to Receiver y = r * s^e mod n

11.2.4.3 Verification

1. Verification done by Receiver involves computation of y²
2. 2. If y² ≡ x * v^e mod n, then Receiver accepts else rejects it.

Example 11.5

Let p = 683, q = 811.

Trusted centre (T ) selects RSA-like modulus n = pq = 683 * 811 = 553913.

Anto selects s = 43215 which is coprime to n and 1 ≤ s ≤ n – 1.

Compute v = s² mod n = 43215² mod 553913 = 295502.

Anto registers v with T, where v is public and s is kept secret.

This is one time set-up.

Then Anto chooses random r = 16785, where ≤ r ≤ n – 1.

Anto sends x = r² mod n = 16785² mod 553913 = 348421 to Brad.

Brad sends random e = 1.

Anto sends to Brad y = r * s^e mod n = 16785 * 43215 mod 553913 = 291658.

Brad checks by computing y² ≡ x * v ^e mod n

291658² mod 553913 = 348421 * 295502 mod 553913

523467 = 523467

Hence, verified and accepted.

11.2.5 Lamport Signature Scheme

In 1979, person named Leslie Lamport invented a signature cryptosystem. It is named after the inventor as Lamport signature. It is a method used to generate a digital signature which can be built from any cryptographically secure one-way function. Lamport signatures with large hash functions would still be secure, even in the presence of quantum computers.

11.2.5.1 Design

To construct a signature scheme for one-time use from any one-way function.

Let k be a positive integer and let P = {0, 1}^k be the set of messages.

Let f: Y → Z be a one-way function and let Y be the set of ‘signatures’

For 1 ≤ i ≤ k, j = 0, 1 let y_ij ∈ Y be chosen randomly and z_ij = f (y_ij ). The key K consists of 2k y’s and z’s. y’s are secret, z’s are public.

11.2.5.2 Signature

Message x = x₁… x_k ∈{0, 1}^k

Sign the message x as sig(x₁… x_k) = (y_{1, x1},…, y_{k, xk}) = (a₁,…, a_k)

sig(x₁… x_k) denotes signature of message x.

(y_{1, x1},…, y_{k, xk}) denotes the output of the signature which can be simply represented as (a₁,…, a_k)

11.2.5.3 Verification

ver_k(x₁… x_k, a₁,…, a_k) = true <=> f(a_i) = z_{i, xi}, 1 ≤ i ≤ k

Anyone cannot forge a signature because it is unable to invert one-way functions.

Example 11.6

Assume 7879 which is prime and 3 is primitive element in Z₇₈₇₉^*

f(x) = 3^x mod 7879. Suppose k = 3, Anto chooses 6 random and secret numbers

Y_1,0 = 5831 Y_1,1 = 735 Y_2,0 = 803 Y_2,1 = 2467

Y_3,0 = 4285 Y_3,1 = 6449

Then Anto computes images of these 6 Y ’s under the function f :

Z_1,0 = 2009 Z_1,1 = 3810 Z_2,0 = 4672 Z_2,1 = 4721

Z_3,0 = 268 Z_3,1 = 5731. These Z’s are published.

Suppose Anto wants to sign message x = (1, 1, 0), then signature of x is (Y_1,1, Y_2,1, Y_3,0) = (735, 2467, 4285).

Brad verifies this signature by using the following computation:

3⁷³⁵ mod 7879 = 3810

3²⁴⁶⁷ mod 7879 = 4721

3⁴²⁸⁵ mod 7879 = 268

Hence, signature is verified.

11.2.6 Chaum–Antwerpen Undeniable Signature Scheme

This signature scheme was found by Chaum and Antwerpen in 1989. Undeniable signatures are signatures that have the following properties: Any signature can be verified only at the cooperation of the signer with aid of a challenge-and-response protocol. Signer cannot deny a correct signature. This scheme forces signer to ensure non-repudiation by obeying a disavowal protocol. It makes possible to prove the invalidity of a signature and to show that it is a forgery.

11.2.6.1 Design

Similar to Schnorr scheme, but the value of p = 2q + 1. Let α ε Z_p* and its order is q.

α = g(^p - 1)^/q = g2, g is a generator for Z_p*.

K = {(p, q, α, a, β):β= α ^a mod p}, only a is private such that 1 ≤ a ≤ q - 1.

q = (p - 1)/2. α = g² mod p.

11.2.6.2 Signature

Signature: y = sig_k(x) = x^a mod p.

Receiver received y = sig_k(x) = x^a mod p supposedly signed/sent from Sender.

y can be a forgery or a valid signature.

Hence Receiver issues a challenge to Sender for a response to either verify y is valid signature or y is indeed a forgery.

11.2.6.3 Verification

Receiver chooses e₁, e₂ randomly from Z_q*.

Receiver computes c = y^e1 β^e2 mod p and send to Sender.

Sender computes d = c^z mod p, z = a-¹ mod q.

Receiver accepts y, whenever d = x^e1 α^e2 mod p.

Example 11.7

Let p = 467, g = 2.

Calculate α = g² mod p = 2² mod 467 = 4.

Calculate q = (p − 1)/2 = (467 − 1)/2 = 233.

Anto chooses a = 101 and computes β = a ^a mod p = 4¹⁰¹ mod 467 = 449.

Anto assumes x = 119 and computes y = x^a mod p = 119¹⁰¹ mod 467= 129.

Now Brad verifies as follows:

Assumes e₁ = 38, e₂ = 397 and computes c = y ^e1 β ^e2 mod p = 129³⁸ * 449³⁹⁷ mod 467 = 13.

Brad sends c to Anto.

Now Anto computes z = a⁻¹ mod q = 101⁻¹ mod 233 = 30 and d = c^z mod p = 13³⁰ mod 467 = 9.

Brad accepts y whenever d = x^e1 α ^e2 mod p = 119³⁸ * 4³⁹⁷ mod 467 = 9.

Hence verified and accepted.

11.2.7 Chaum’s Blind Signature Scheme

Cryptographic protocol used to get a valid signature for a message from a signer is called blind signature scheme. Here signer’s view of protocol cannot be linked to resulting message and signature pair. This signature scheme uses RSA cryptosystem. The security of the given scheme depends upon the strength of RSA algorithm.

11.2.7.1 Design

It combines RSA with blinding and unblinding features.

Receiver’s RSA public key is (num, encrypt) and his private key is (num, decrypt).

Let m be a message, 0 < m < num,

11.2.7.2 Signature

1. 1. Sender chooses a random 0 < k < num with gcd(num,k) = 1. Sender computes m^* = mk^e (mod num) and sends it to Receiver (this way Sender blinds the message). Here e is the public key.
2. Receiver computes s^* = (m^*)^d(mod num) and sends s^* to Sender (Receiver signs the blinded message m^*). Here d is the private key.
3. Sender computes s = k-1s^*(mod num) to obtain Receiver’s signature m^d of m (Sender performs unblinding of m^*).

Example 11.8

Anto chooses a random number k = 5 and num = 11 such that gcd(5,11) = 1.

Let m = 13 and e = 17.

Anto calculates m^* = mk ^e (mod num) = 13 * 5¹⁷ mod 11 = 6

Let d = 19

s^* = (m^*)^d(mod num) = 6¹⁹ mod 11 = 2

Calculate s = k⁻¹s^*(mod num) = 5⁻¹ * 6 mod 11 = 7

Calculate m^d(mod num) = 13¹⁹ mod 11 = 6.

Hence, verified.

11.2.8 Ong–Schnorr–Shamir Subliminal Channel Signature Scheme

Covert channels can be used for secret communication. They seem to be normal looking communication over an insecure channel, which is normal and unencrypted. Secret information to be passed will be hidden in the channel. Such channels are called as subliminal channels.

11.2.8.1 Design

Assume Anto sends a secret message to Brad through Dev. They choose a large number n and an integer k such that gcd(n, k) = 1. The common key k is shared between Anto and Brad but n is public. Anto’s intention is to send a message to Brad through Dev. Though Dev is having the message the meaning of the message is not revealed to Dev.

Let w and w’ be the original and fake messages.

11.2.8.2 Signature

Anto calculates two signatures S₁ and S₂.

Signature: (S₁, S₂)

S₁ = (1/2) * ((w’/w) + w) mod n

S₂ = (1/2) * ((w’/w) − w) mod n

Anto sends (w’, S₁, S₂) to Brad through Dev.

Dev reads w’ and assumes w’ as the original message.

11.2.8.3 Verification

Brad recovers the original message as w = [w’/(S₁ + k⁻¹S₂)] mod n and verifies the signature S₁² − S₂²/k² ≡ w’(mod n).

11.2.9 Heyst–Pedersen Signature Scheme

Signature schemes using a trusted authority for providing ways to prove that a powerful adversary is around who could break the signature scheme and therefore its use should be stopped. It is maintained by a trusted authority, which will choose a secret key for each signer. The private key is kept secret, even from the signers and announces only the related public key.

11.2.9.1 Design

They are many signature schemes that use a trusted authority. It provides many ways to prove that a powerful enough trusted third party adversary is around who could break the signature scheme. Scheme is maintained by a trusted third party authority, it chooses a secret key for each signer.

11.2.9.2 Signature and Verification

A significant idea is that signing and verification algorithms are enhanced by the so-called proof of forgery algorithm. When the signer looks into a forged signature, then it is able to compute the secret key. The key is submitted to the trusted authority to prove the existence of a forgery. This achieves that any further use of the signature scheme is used.

11.2.10 Probabilistic Signature Scheme

It was designed by Bellare and Rogaway. It is a signature scheme provably well secured against chosen message attack. It uses random oracle model, which is secured equivalently to RSA cryptosystem.

11.2.10.1 Design

Let us have a trapdoor permutation

Pseudorandom bit generator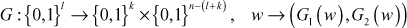

and a hash function h: {0,1}* → {0,1}^l

This scheme is applicable to messages of arbitrary length.

11.2.10.2 Signature

Message w ∈ {0,1}*.

1. Choose random r ∈ {0,1}^k and compute m = h (w || r).
2. Compute G(m) = (G₁(m), G₂(m)) and y = m || (G₁(m) ⊕ r) || G₂(m).
3. Signature of w is s = f ⁻¹(y).

11.2.10.3 Verification

Message (w, s).

1. Compute f(s) and decompose f(s) = m || t || u, where |m| = l, |t| = k and |u| = n − (k + l).
2. Compute r = t ⊕ G₁(m).
3. Accept signature s if h(w || r) = m and G₂(m) = u; otherwise reject it.

11.3 BATCH DIGITAL SIGNATURE ALGORITHM

In 1991, DSS is proposed by the US government. It is one of the ElGamal-type signature schemes which are based on the discrete logarithm problem. Since verifying each its type signature requires at least two modular exponentiations and modular exponentiation is a computational-intensive operation, it becomes very desirable to use special-purpose hardware or an efficient software algorithm to speed up the signature verification process.

Hence efficient and secure algorithms are essential to verify multiple digital signatures based on the discrete logarithm. Verifying multiple signatures simultaneously instead of single signature verification saves time and effort. Batch verification algorithm can maintain constant verification time as to verify a single signature. Naccache et al. had an interactive DSA batch verification protocol in which signer generates t signatures through interactions with the verifier and verifier validates these t signatures at once based on batch verification criterion. Lim and Lee specified that the interactive DSA batch protocol is insecure. Harn gave a DSA-type secure interactive batch verification protocol.

11.3.1 Naccache et al. Batch Verification Algorithm

An example is used to illustrate Naccache et al. batch verification algorithm. Assume that there are three messages m₁, m₂, m₃ needed to be signed by the signer. The signer interacts with the verifier and generates three individual signatures {r₁, s₁}, {r₂, s₂}, {r₃, s₃} of messages m₁, m₂, m₃, respectively, based on the DSA algorithm. The verifier checks these signatures based on the following batch verification criterion as r₁r₂r₃ = (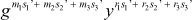 mod p) mod q.

11.3.2 Lim and Lee’s Attack

Here, fake signatures can assure the batch verification without the knowledge of the secret key. First, the attacker randomly selects {u_i, v_i} and computes r_i = g ^ui y ^vi mod p, for i = 1, 2, 3. The attacker then computes s₁’ that satisfies v₁ = r₁s₁’ mod q. Now, the attacker can solve s₂’ and s₃’ from the following two equations:

u₁+ u₂+ u₃= m₁s₁’+ m₂s₂’+ m₃s₃’ mod q.

v₁+ v₂+ v₃ = r₁s₁’+ r₂s₂’+ r₃s₃’ mod q.

The issue in Naccache et al. approach is DSA is an insecure algorithm for the batch verification criterion, which is used to verify multiple signatures.

Even the Lim and Lee’s attack does not work properly. In their attack, the attacker can randomly select all r_i first. Then the attacker can solve s_i accordingly. However, in secure DSA algorithms, r_i cannot be randomly selected at the first place. Signature algorithm used to sign each individual signature is so secure.

11.4 ATTACKS ON DIGITAL SIGNATURE

Key issues in digital signature are confidentiality in protecting session keys and timeliness to prevent replay attacks. Replay attacks are done by copying valid signed message and resending later on. Countermeasures include sequence number usage, timestamps and challenge/response protocol.

There are many ways to produce signature using ElGamal signature scheme. A valid forged signature can be done using this scheme. It will not allow an opponent to forge signatures on messages of their preference. For example, if 0 ≤ i, j ≤ p − 2 and gcd( j, p − 1) = 1, then for a = qⁱ y^j mod p; b = −aj⁻¹ mod ( p − 1); w = −aij⁻¹ mod ( p − 1); the pair(a, b) is a valid signature of the message w. It is proven by the verification condition. If ElGamal signature is not used carefully enough, then it can be easily broken. For example, any random number r used in signature must be kept secret, otherwise the system can be broken and signatures forged. If r is known, then x can be computed by x = (w − rb) a⁻¹ mod ( p − 1). A hacker who knows value of x can forge signatures at their own choice. If same value of r is chosen to sign two messages, then x can be computed to break the security of system.

The attack works on RSA digital signature with public exponent e = 3 and PCKS-1 padding. A PKCS-1 digital signature is computed on a hash value H(M) that is padded as: 00 01 FF FF …FF 00 || ASN.1 || H(M), where 00 01 FF FF …FF 00 is a padding value, ASN.1 is used to provide information about the hash function (basically, the length of the hash value), and H(M) is the hash value. Note that the hash value H(M) is supposed to be right-justified.

The padded message is obtained by decrypting the digital signature using the public exponent e = 3. H(M) is the hash value which can be extracted by searching past the padding and the ASN.1 values to select the appropriate number of bytes that follow. To verify the signature, compare extracted value of H(M) with separately computed hash value on received message M. The digital signature is considered valid if and only if the comparison is true. In ANS X9.31, the hash value is followed by a 2 byte trailer with a fixed value instead of being right-justified. If SHA-1 is used, then padded hash value is 6B BB BB ...BB BA || H(M) || 33 CC.

11.4.1 Problem

In certain cases, hash value is obtained by getting bits from the padding relative location thereby unpredicted data coming after the hash value is left out. In case of PKCS-1, the padding end and the ASN.1 value is selected for the hash value. In case of ANS X9.31, the end of the padding is selected for hash value, without checking that only two bytes with expected values follow the hash value in padded hash string.

11.4.2 Attacks

If PKCS-1 padding method is used, then any message M″ with hash value H(M″) can be easily found using cubic root of string like 00 01 FF …FF 00 || ASN.1 || H(M″) || garbage where number of occurrences of FF in padding is reduced. Garbage can be cleverly selected to make the modified string into a cube of other value. If ANS X9.31 padding method is used, then padded hash could be changed as follows by reducing number of occurrences of BB in padding 6B BB BB ...BB BA || H(M) || garbage, where last two bytes of garbage are trailer. Modified padded hash string has a cubic root. For example, this attack is presented with e = 3. For both padding methods, if small value of e is used, then eth root of a string can be found leading to the attack. If e is large, then determining an eth root modulo n is hard.

To prevent the attack when PKCS-1 is used:

1. Use any value except 3 as public exponent for RSA signatures.
2. 2. When its padding is used to find the hash value, verify that any data doesn’t exist on the right of hash value.

To prevent the attack when ANS X9.31 is used:

1. Use any value except 2 and 3 as public exponent for digital signatures.
2. 2. When its padding is used to point the hash value, verify that only two bytes having expected value of trailer is preceded by the hash value.

Another possible attack is an attacker can compute a signature sig on a random fingerprint z. The value of x can be computed from z = h(x). In such a case (x, sig) is a valid signature. A hash function h is collision-free, if it is computationally infeasible to find messages w and w’ such that h(w) = h(w’). To prevent the above attack, it is necessary that signatures have to use one-way hash functions.

Digital signing algorithm can be compromised in many ways. For example, if an attacker determines the secret key of receiver, then forging signatures on any sender’s message is possible. If this happens, then authenticity of all messages signed by sender before attacker got the secret key is to be questioned. The key issue is that there is no way to find when a message was signed. Hence time stamping should be provided as proof for a message signed at a certain time. For example, stock-market data is denoted as stk, which is publically known and could not be predicted before the day of the signature. Timestamping by Person A of a signature on a message w is done as follows:

Person A computes z = h(w); computes z′ = h(z || stk); computes y = sig(z’). It publishes (z, stk, y) in following days’ newspaper. It is now clear that signature could not be done after triple (x, stk, y) was published, but also not before date stk was known.

11.4.2.1 Man-in-the-middle Attack

Consider the following protocol in the data communication; Anto and Brad are sender and receiver, respectively. Mike is the man in the middle of communication performing the attack.

1. Anto sends Brad the pair (encrypt_B(encrypt_B(w)A), B) to B.
2. Brad uses decrypt_B to get A and w, and acknowledges by sending the pair (encrypt_A(encrypt_A(w)B), A) to Anto.
3. Mike can learn (encrypt_A(encrypt_A(w) B), A) and therefore encrypt_A(w’), w ‘ = encrypt_A(w)B.
4. Mike can now send to Anto the pair (encrypt_A(encrypt_A(w ‘) C), A).
5. Anto, thinking that this is the step 1 of the protocol, acknowledges by sending the pair (encrypt_C(encrypt_C(w ‘) A), C) to Mike.
6. Mike is now able to learn w ‘ and therefore also encrypt_A(w).
7. Mike now sends to Anto the pair (encrypt_A(encrypt_A(w) C), A).
8. Anto acknowledges by sending the pair (encrypt_C(encrypt_C(w) A), C).
9. Mike (attacker) is now able to learn w.

11.4.2.2 Solution to Man-in-the-middle Attack

Authenticated Diffie–Hellman key exchange.

Let each user U have a signature function sign_U and a verification algorithm verify_U. The following protocol allows Anto and Brad to establish a key K, which is used with an encryption function encrypt_K to avoid the man-in-the-middle attack.

1. Anto and Brad choose large prime p and a generator q ∈ Z_p*.
2. Anto chooses a random x and Brad chooses a random y.
3. Anto computes q^x mod p, and Brad computes q^y mod p.
4. Anto sends q^x to Brad.
5. Brad computes K = q^xy mod p.
6. Brad sends q^y and encrypt_K (s_B (q^y, q^x)) to Anto.
7. Anto computes K = q^xy mod p.
8. Anto decrypts encrypt_K (s_B (q^y, q^x)) to obtain s_B (q^y, q^x), where s_B is signing algorithm of Brad.
9. Anto verifies, using an authority, that v_B is Brad’s verification algorithm.
10. Anto uses v_B to verify Brad’s signature.
11. Anto sends encrypt_K (s_A (q^x, q^y)) to Brad, where s_A is signing algorithm of Anto.
12. Brad decrypts, verifies v_A, and verifies Anto’s signature.

An enhanced version of the above protocol is known as station-to-station protocol.

11.4.2.3 Chosen Message Attack

Process giving signature to a message of its choice using an input of verification key is called chosen message attack. It is successful, if it can output a valid signature for a message in which no request for a signature is done during the attack. It is said that any signature scheme is secure if and only if every feasible chosen message attack does not succeed with at least negligible probability.

11.5 MERITS AND DEMERITS OF DIGITAL SIGNATURE SCHEMES

Signature schemes discussed in the aforesaid topics allow for signing only ‘short’ messages. For example, sign 160-bit messages with 320-bit signatures. Let us assume message as msg of arbitrary length. Hence message digest, md = h(msg) (160 bits) signature, sg = sign(md) (320 bits) a naive solution is to break long message into a sequence of short messages, where each block has to be signed separately.

Signing consumes more time and for long signatures, integrity is not protected. The solution is to use fast public hash functions h, which can map a message of arbitrary length to a fixed length fingerprint. The fingerprint is then signed.

11.6 JAVA IMPLEMENTATION OF DSA

Many researchers have attempted to make public key algorithms that directly support batch signing and batch verification, which was formalized by M. Bellare. With Batch RSA, several messages can be combined together and signed in one exponentiation if they are to be verified with different public exponents. Optimizations for DSA signing have also been proposed. Other approaches for increasing the throughput of public key algorithms include algorithms that can do parallel exponentiations of a constant g to random exponents by caching g^x1…g^xn [25] for a 42–85% improvement. Exponents can also be selected that offer efficient batch exponentiation.

11.6.1 History

In 1989, batch cryptography was introduced by Fiat. It is a variant of RSA. Later, in 1994, Naccache, Vaudenay and Raphaeli gave their first and an efficient batch verifier for DSA signatures. In 1995, Laih and Yen gave a method for batch verification of both DSA and RSA signatures. In the year 1998, Bellare, Garay and Rabin took their first systematic look at batch verification and presented three generic methods for batching modular exponentiations, called

1. the random subset test;
2. the small exponents test; and
3. the bucket test

These methods are applied to batch verification of DSA signatures. A weaker form of batch verification called screening is introduced. Later, Cheon and Lee had given two methods, namely sparse exponents test and complex exponent test. These are about twice as fast as the small exponents test. Boyd and Pavlovski gave few attacks against different batch verification schemes based on the small exponents test and related tests. A small exponent test is often used in a wrong way is depicted by these attacks.

Yoon, Cheon and Kim gave an ID-based signature scheme with batch verification. Their security proof is for aggregation of signatures. Hence, it does not meet the definition of batch verification by M. Bellare. Methods for identifying invalid signatures in RSA-type batch signatures are proven flawed. Practical application of batch verification is done by using modified version of Fiat’s batch verifier for RSA. It improves the efficiency of SSL handshakes on a busy server.

DSA implementation using java, java cryptographic algorithms and batch processing is given below.

11.6.2 DSA Implementation using JCA

In Java, a framework called Java Cryptography Architecture (JCA) helps to exploit and design cryptographic solutions. A JCA provider implements the cryptographic functionalities like Digital Signatures and Message Digests. The default JCA provider in JDK 1.4.2 is SUN.

11.6.3 Security Considerations while Implementing Digital Signature

When implementing digital signatures, two main security considerations have to be taken into account. They are listed as follows:

1. Sign the message and then encrypt the signed message
2. Sign the hash of the message instead of the entire message

Note:

Execute the KeyGenerator program for creating private and public key files. Use the private-key. bin in JCA Sign program as keyFile and public-key.bin in JcaVerify program execution.

11.6.4 Simple Batch Processing of DSA

Note:

This program requires a folder named ‘sample’ containing batch of files for digital signature and verification. For this output, three files are included in sample folder.

Key Terms

Batch DSA

Chaum–Antwerpen Undeniable Signature Scheme

Chosen message attack

Chaum’s blind signature

Digital certificate

Digital signature

DSA signature

Elgamal signature

Fiat–Shamir signature

Heyst–Pedersen signature

JCA

Lamport signature

Man-in-the-middle attack

Ong–Schnorr–Shamir subliminal channel

Probabilistic signature

RSA attack

Summary

• Digital signatures are used for integrity purpose of security. It is one among other techniques that lead to advancement in cryptosystem. Digital certificates are issued by trusted third parties for non-repudiation purpose. The differentiation between handwritten signature, digital signature and digital certificate is clearly stated in this chapter.
• Key generation, signing and verification of DSA are illustrated in this chapter. Various possible attacks on digital signatures are provided with corresponding solutions. Various digital signing and verification schemes are discussed in this chapter.
• RSA-based digital signature with its variants, interoperability and working principle are discussed. ElGamal digital signature generation and verification are discussed with its correctness of operation. DSA and batch processing of digital signatures are discussed in detail along with its merits and demerits. The implementation of digital signing and verification is provided as a simple Java program, as a Java program using JCA as well as Java program performing batch processing.

Review Questions

1. What is a digital signature?
2. Differentiate digital certificate with digital signature.
3. What are the uses of digital signature?
4. Give a short note on DSS.
5. List down a few attacks on digital signature.
6. How ElGamal signatures are generated and verified?
7. Write short note on Fiat–Shamir signature.
8. What is Ong–Schnorr–Shamir subliminal channel signature scheme?
9. Give short note on Lamport signature scheme.
10. Write short note on Chaum–Antwerpen Undeniable Signature Scheme.
11. Explain the generation and verification of Chaum’s blind signature.
12. What is a Heyst–Pedersen signature?
13. Differentiate probabilistic signature with Chaum–Antwerpen Undeniable Signature Scheme.
14. Why batch processing of DSA is necessary?
15. Write down the merits and drawbacks of digital signature.