Python can do multiplication and division–and a contented multiplication and division of arbitrarily large integers with complete precision:

If we have 1001 and then we calculate 1001 squared, we get the right answer, of course; and even if we take a number like 10**100 + 1, it correctly gets that number a hundred places with a 1 at each end. Now, if we square that number, it again gets it correct, all the way to the one at each end.

So, for simple integer operations, Python's precision is unlimited. However, if we want to square root, we need to import a math library:

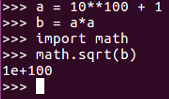
The math library does not keep any arbitrary number of places, as you can see in the preceding code. If we take 10 **100 + 1 and square it, then take the square root, we don't get 10 **100 + 1. We get 10 ** 100, which means it rounded off to some number of places less than 100, and that's fine for many purposes. However, it's not fine for what we want to do here, which is factor large integers.

In order to do that, you use the decimal library, and we will import it as shown:

As you can see, we have imported the decimal library and set value to a as 10 **100+ 1. Here b equals to a squared, and then instead of calculating the square root of b with the math library, you calculate the decimal value of b with the decimal library. Use the square root method of that and this gives you again the wrong answer, because by default, the decimal library rounds things off. But if you set the precision to be higher, you get exactly the right answer, and that's why the decimal library is better for our purposes. This getcontext().prec command lets us set it to keep enough places to be as precise as we want.

All right, so, you wouldn't be able to factor a large number in the general case, and that's what makes RSA secure. But, if a mistake is made by using numbers and can be predictable in some way, then RSA can be cracked:

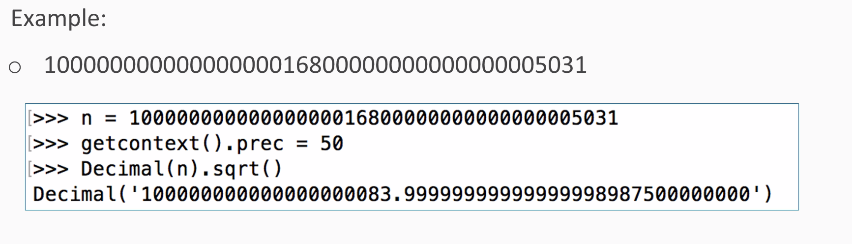
Here the mistake is using two prime factors that are close together instead of choosing independent random numbers for the two prime factors. So, this large number is the product of two prime factors, and so you can factor it. So, if we put that number in a value called n, we set the precision to 50 places and calculate the square root. We find that the square root is 1 followed by many zeros, and that is ended at 83 +a fraction.

Now, if the number is the product of two prime numbers, and the two prime numbers are close together, one number must be less than the square root and the other number must be larger than the square root.

So, if we simply start at the square root and try numbers close to the square root by jumping back by two every time, we will eventually find the prime factor, and we do:

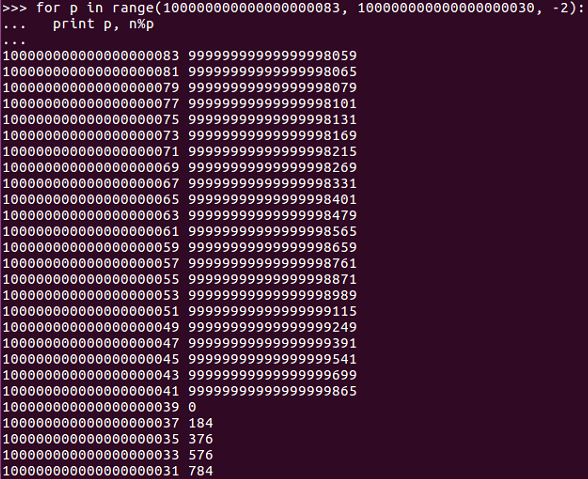
Of course, we can jump back by twos because even numbers are certainly not prime, so we don't need to test the even numbers.

And, as we can see, now we've found a number where the modulus of n modulus the number is zero, so this is a prime factor.

We can get the other prime factor by just dividing n by the first one:

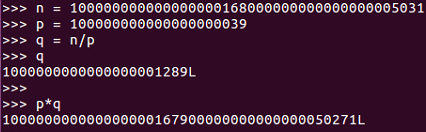
So, here's the original number, n, which is the product of two primes, and we have one of the primes; q is n over p which you can see. To test it, if we calculate p*q, we get the original number again. So, we have factored a large number into p and q, and that is enough information to crack RSA.

So, let's try that in Python. Go to the Terminal and run python:

So, we have n equal to the large number shown. We import this number to the decimal library and set the position to 50 places. Now, if we take the square root, we get 1 followed by many zeros, and then 83, and then a fraction. Then, we copy the integer part of the square root:

Now we set p in range of that number followed by the number, as shown here:

>>> for p in range(100000000000000000083, 100000000000000000030, -2):

This begins a loop, and all we have to do is print:

...  print p, n%p
...

It will calculate n modulus p, which will be zero. If that's an integral multiple, pressing Enter twice runs the loop:

So, we can see this number is p:

100000000000000000039 0

If we copy that number, we can set p equal to that and can set q equal to n over p:

>>> p = 100000000000000000039
>>> q = n/p

If we print, we will get the following:

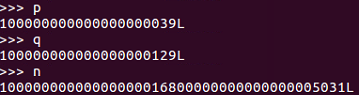
You can see n matches with p*q. So, we've now factored that long number into its complement primes.

Here's the first challenge:

Here's the second challenge:

In both cases, you will be able to factor them.