CHAPTER 9
Adding TLS 1.2 Support to Your TLS Library
TLS 1.2 was formally specified in 2008 after several years of debate. It represents a significant change to its predecessor TLS 1.1 — mostly in terms of increased security options and additional cipher suite choices. This chapter details the changes that you need to make to the TLS 1.0 implementation of the previous three chapters to make it compliant with TLS 1.2.
The next two sections detail the message-format level changes that TLS 1.2 introduced. I move quickly here, assuming a good familiarity with the material in the previous three chapters — if you don't remember what the PRF is or what messages are involved in the TLS handshake, you may want to jump back and briefly review at least Chapter 6. Alternatively, if you're more interested in what TLS 1.2 does, rather than how it does it, you can skip ahead to the section in the chapter on AEAD encryption.
Supporting TLS 1.2 When You Use RSA for the Key Exchange
This section covers changes sufficient enough to support TLS 1.2 in the most straightforward case: when RSA is used directly for key exchange. To do so, you would follow these basic steps.
- Obviously, you should change the version number declared in the header file from 3.1 to 3.3 as shown in Listing 9-1.
- After this, you need to make the code TLS 1.1 compliant. If you recall from Chapter 6, the most significant difference between TLS 1.0 and TLS 1.1 is that, for CBC-based block ciphers, TLS 1.1 prepends the IV to each block rather than computing it from the master secret. TLS 1.2 does this as well.
- You can go ahead and remove the IV calculation from the calculate_keys routine if you're so inclined. However, it's not really important that you do; for TLS 1.1+, computing an unused set of IVs just becomes a few wasted clock cycles.
- You do, however, have to modify send_message and tls_decrypt to prepend the IVs and recognize them, respectively.
The necessary changes to send_message are shown in Listing 9-2.
Listing 9-2: "tls.c" send_message with explicit IVs
// Finally, write the whole thing out as a single packet. if ( active_suite->bulk_encrypt ) { unsigned char *encrypted_buffer = malloc( send_buffer_size + active_suite->IV_size ); int plaintext_len; // TODO make this random memset( parameters->IV, '\0', active_suite->IV_size ); // The first 5 bytes (the header) and the IV aren't encrypted memcpy( encrypted_buffer, send_buffer, 5 ); memcpy( encrypted_buffer + 5, parameters->IV, active_suite->IV_size ); plaintext_len = 5 + active_suite->IV_size; active_suite->bulk_encrypt( send_buffer + 5, send_buffer_size - 5, encrypted_buffer + plaintext_len, parameters->IV, parameters->key ); free( send_buffer ); send_buffer = encrypted_buffer; send_buffer_size += active_suite->IV_size;As you can see, there's not much to change, here; just make sure to overwrite the IV with random bytes before encrypting, and put the IV in between the send buffer header and the encrypted data. You may wonder why you should keep the IV pointer in parameters at all given that the IV is being generated randomly each time a message is sent. Well, don't forget that the IV parameter was used as a generic state area for stream ciphers such as RC4 and needs to be kept intact, because RC4 looks just the same in TLS 1.1+ as it does in TLS 1.0.
- Listing 9-3 details the converse changes that you must make to tls_decrypt to properly decode buffers that are written this way.
Listing 9-3: "tls.c" tls_decrypt with explicit IVs
CipherSuite *active_suite = &( suites[ parameters->suite ] ); encrypted_length -= active_suite->IV_size; *decrypted_message = ( unsigned char * ) malloc( encrypted_length ); if ( active_suite->bulk_decrypt ) { if ( active_suite->IV_size ) { memcpy( parameters->IV, encrypted_message, active_suite->IV_size ); } active_suite->bulk_decrypt( encrypted_message + active_suite->IV_size, encrypted_length, *decrypted_message, parameters->IV, parameters->key );To decrypt, it's even easier; just check to see if the cipher suite calls for an IV, and, if so, copy the first IV_size bytes of the message into the parameters->IV.
If you change the TLS_MINOR_VERSION to 2, you actually now have a TLS 1.1-compliant implementation. You can probably easily see how this code could have been structured to allow the same function to service TLS 1.1 and TLS 1.0 with a handful of if statements. You might even want to try to do this as an exercise.
NOTE Note that this code makes no attempt at checking versions. If a client asks for version 3.1, it gets version 3.3, which is actually an error. To be properly compliant, the server should either negotiate the version requested by the client, or the highest version it supports. It can never negotiate a version higher than was requested.
TLS 1.2 Modifications to the PRF
The code in the previous section is still not TLS 1.2 compliant. TLS 1.2 made two significant structural changes to the message formats. The first was a change in the PRF.
Remember from Listing 6-33 that the TLS PRF defined a P_hash function that took as input a label and a seed, and securely generated an arbitrary number of bytes based on a hash function. In TLS 1.1 and earlier, this P_hash function was called twice; once with the hash function MD5, and once with the hash function SHA-1. The two calls each got half of the secret, and the outputs were XORed together to create the final output. Getting the PRF right is by far the most difficult part of implementing TLS.
If you're cringing in terror at what new horrors might await you with the complexity of TLS 1.2's modifications to the PRF, you'll be pleasantly surprised that TLS 1.2 actually simplifies the PRF. The P_hash function stays the same, but it's no longer a combination of two separate hash functions. You just call P_hash one time, give it the whole secret, and return the results directly as the output.
You may be wondering, of course, which hash function you should use if you're calling P_hash just one time. MD5 or SHA-1? Actually, TLS 1.2 makes this configurable; there's a new client hello extension that enables the client to suggest a hash function that should be used. If the client doesn't suggest one, though, both sides should default to SHA-256. Modify the PRF function from Listing 6-29 as shown in Listing 9-4.
Listing 9-4: "prf.c" PRF2
void PRF( const unsigned char *secret,
int secret_len,
const unsigned char *label,
int label_len,
const unsigned char *seed,
int seed_len,
unsigned char *output,
int out_len )
{
unsigned char *concat = ( unsigned char * ) malloc( label_len + seed_len );
memcpy( concat, label, label_len );
memcpy( concat + label_len, seed, seed_len );
P_hash( secret, secret_len, concat, label_len + seed_len, output,
out_len, new_sha256_digest );
free( concat );
}
As you can see, you almost don't need a PRF function anymore; you could just as easily change the callers to directly invoke P_hash because PRF isn't really adding any value anymore. Leaving it in place minimizes the changes to other code, though; everything else can stay just as it is.
TLS 1.2 Modifications to the Finished Messages Verify Data
You may recall from Listing 6-53 that there was one other data value that depended on the combination of an MD5 and an SHA-1 hash: the verify data in the finished message. And yes, sure enough, this changes in TLS 1.2 as well. Rather than tracking the MD5 and SHA-1 hashes of the handshake messages and then running those hashes through the PRF to generate the finished message, TLS 1.2 instead tracks a single hash; the same one that the PRF uses (the one negotiated in the client hello or the default SHA-256). It still hashes all handshake messages, and does so in the same way as TLS 1.1.
To support the TLS 1.2 finished message, follow these steps:
- Modify TLSParameters as shown in Listing 9-5 to keep track of an SHA-256 digest.
- Of course, the two digest updates in send_handshake_message and receive_tls_msg must be changed to update this digest as shown in Listing 9-6.
Listing 9-6: "tls.c" SHA-256 digest update
int send_handshake_message( int connection, int msg_type, const unsigned char *message, int message_len, TLSParameters *parameters ) { ... memcpy( send_buffer + 1, &record.length, 3 ); memcpy( send_buffer + 4, message, message_len ); update_digest( ¶meters->sha256_handshake_digest, send_buffer, send_buffer_size ); response = send_message( connection, content_handshake, send_buffer, send_buffer_size, ¶meters->active_send_parameters ); ... static int receive_tls_msg( int connection, char *buffer, - Finally, tls_resume and tls_connect must both be changed to initialize this digest rather than the two parallel digests that they initialized in Chapters 6 and 8. Listing 9-7 demonstrates.
Listing 9-7: "tls.c" TLS 1.2 handshake digest initialization
int tls_resume( int connection, int session_id_length, const unsigned char *session_id, const unsigned char *master_secret, TLSParameters *parameters ) { init_parameters( parameters, 0 ); parameters->connection_end = connection_end_client; parameters->session_id_length = session_id_length; memcpy( ¶meters->session_id, session_id, session_id_length ); new_sha256_digest( ¶meters->sha256_handshake_digest ); ... int tls_connect( int connection, TLSParameters *parameters, int renegotiate ) { init_parameters( parameters, renegotiate ); parameters->connection_end = connection_end_client; new_sha256_digest( ¶meters->sha256_handshake_digest ); ... int tls_accept( int connection, TLSParameters *parameters ) { init_parameters( parameters, 0 ); parameters->connection_end = connection_end_server; new_sha256_digest( ¶meters->sha256_handshake_digest ); ...
Of course, if you want to implement this code to support TLS 1.0 through TLS 1.2 concurrently, you'd have some conditional logic to initialize the handshake digests depending on the version of TLS.
Impact to Diffie-Hellman Key Exchange
As mentioned previously, the changes in the previous section are sufficient to support TLS 1.2 in the most straightforward case: when RSA is used directly for key exchange. However, there's one other significant structural change that was introduced by TLS 1.2 that impacts ephemeral Diffie-Hellman (DHE) key exchange suites. Recall that when DHE is used for key exchange the server must sign the DH parameters g, p, and Ys with the private key corresponding to the public key in the server's certificate. Prior to TLS 1.2, the type of signature was implied. If the server certificate included an RSA key, the client knew that the signature was an RSA signature. If the certificate was a DSA key, the client knew to perform a DSA signature check.
This works, but in the long-term is a bit of a burden on the implementer. It would be nice if each signature included an indicator of what type it is; this is exactly what TLS 1.2 added to the inline signatures. Additionally, recall from Listing 8-21 that RSA signatures were RSA-encrypted concatenations of the MD5 hash followed by the SHA-1 hash. TLS 1.2 changes this here, just as it does in the PRF; an RSA signature is an encrypted representation of a single hash — SHA-256 unless a client hello extension has negotiated a different hash. The hash algorithm is also identified in the encrypted data, just like an X.509 signature is. This is redundant; the signature first declares the hash algorithm, and then the signature itself redeclares it. Why was it done this way? DSA has no provision for including a declaration of a hash algorithm, so TLS 1.2 adds it before the signature as well.
Parsing Signature Types
To parse these new signature types, modify the verify_signature code from Listing 8-21 as shown in Listing 9-8 to first read off the hash and signature algorithm and then to ASN.1-decode the decrypted RSA signature value to locate the actual signed hash code. (DSS validation stays the same, as it must.)
Listing 9-8: "tls.c" TLS 1.2 signature verification
int verify_signature( unsigned char *message,
int message_len,
unsigned char *signature,
int signature_len,
TLSParameters *parameters )
{
...
digest_ctx sha_digest;
new_sha256_digest( &sha_digest );
... if ( parameters->server_public_key.algorithm == rsa ) { unsigned char *decrypted_signature; int decrypted_signature_length; struct asn1struct rsa_signature; decrypted_signature_length = rsa_decrypt( signature, signature_len, &decrypted_signature, ¶meters->server_public_key.rsa_public_key ); // TLS 1.2; no longer includes MD-5, just SHA-256, // but the RSA signature also includes the signature scheme, // so must be DER-decoded asn1parse( decrypted_signature, decrypted_signature_length, &rsa_signature ); if ( memcmp( sha_digest.hash, rsa_signature.children->next->data, SHA256_BYTE_SIZE ) ) { asn1free( &rsa_signature ); free( decrypted_signature ); return 0; } asn1free( &rsa_signature ); free( decrypted_signature ); }
Notice that the MD5 computation has been removed here; it's no longer needed. The implementation in Listing 9-8 also completely ignores the declared hash algorithm; it's included as an OID as the first child of the top-level structure. The implementation ought to verify that the declared hash algorithm is SHA-256 and, in theory, compute a separate hash if it isn't. Because no other hash algorithms are supported here, this check is omitted. If the server gives back, say, SHA-384, the hashes don't match and an alert is thrown.
The signature structures also prepend the signature and hash algorithms, but they don't do so as full-blown X.509 OIDs (fortunately). Instead, an enumeration of supported algorithms is declared as shown in Listing 9-9.
Listing 9-9: "tls.h" signature and hash algorithms
typedef enum
{
none = 0,
md5 = 1,
sha1 = 2,
sha224 = 3,
sha256 = 4,
sha384 = 5,
sha512 = 6
} HashAlgorithm; typedef enum { anonymous = 0, sig_rsa = 1, sig_dsa = 2, sig_ecdsa = 3 } SignatureAlgorithm;
This is less extensible, but significantly easier to code, than the X.509 OID structure.
Modify parse_server_key_exchange from Listing 8-19 as shown in Listing 9-10 to read the hash and signature algorithm from the beginning of the packet. Note that this implementation reads, but completely ignores, the declared signature and hash algorithms; a proper, robust implementation verifies that the algorithm is one that has a public key to verify with and, if the hash algorithm is not SHA-256, the implementation computes that hash or throws an alert indicating that it can't.
Listing 9-10: "tls.c" parse_server_key_exchange with signature and hash algorithm declaration
static char *parse_server_key_exchange( unsigned char *read_pos,
TLSParameters *parameters )
{
short length;
int i;
unsigned char *dh_params = read_pos;
HashAlgorithm hash_alg;
SignatureAlgorithm sig_alg;
// TLS 1.2 read off the signature and hash algorithm
hash_alg = read_pos[ 0 ];
sig_alg = read_pos[ 1 ];
read_pos += 2;
for ( i = 0; i < 4; i++ )
These changes are necessary to support ephemeral key exchange algorithms. Because the structure of the message itself changes, you must be ready to at least look in a different place for the key exchange parameters.
Finally, remember that if the server wants a client certificate, the client must also send back a certificate verify message with its own signature. To save the client the trouble of sending a certificate whose public key the server cannot use to verify a signature, the certificate request message was changed in TLS 1.2 to include a list of supported signature and hash algorithms. The enumerations from Listing 9-9 are reused here. To properly parse the certificate request, modify the parse_certificate_request routine from Listing 8-29 as shown in Listing 9-11:
Listing 9-11: "tls.c" parse_certificate_request with TLS 1.2 support
#define MAX_CERTIFICATE_TYPES 4
typedef enum
{
rsa_signed = 1,
dss_signed = 2,
rsa_fixed_dh = 3,
dss_fixed_dh = 4
}
certificate_type;
#define MAX_SIGNATURE_ALGORITHMS 28
typedef struct
{
HashAlgorithm hash;
SignatureAlgorithm signature;
}
SignatureAndHashAlgorithm;
typedef struct
{
unsigned char certificate_types_count;
certificate_type supported_certificate_types[ MAX_CERTIFICATE_TYPES ];
unsigned char signature_algorithms_length;
SignatureAndHashAlgorithm
supported_signature_algorithms[ MAX_SIGNATURE_ALGORITHMS ];
}
CertificateRequest;
static unsigned char *parse_certificate_request( unsigned char *read_pos,
TLSParameters *parameters )
{
...
read_pos = read_buffer(
( void * ) &request.supported_certificate_types[ i ], read_pos, 1 );
}
read_pos = read_buffer( &request.signature_algorithms_length, read_pos, 2 );
for ( i = 0; i < request.signature_algorithms_length; i++ )
{
read_pos = read_buffer( ( void * )
&request.supported_signature_algorithms[ i ].hash, read_pos, 1 );
read_pos = read_buffer( ( void * ) &request.supported_signature_algorithms[ i ].signature, read_pos, 1 ); } read_pos = read_buffer( ( void * ) &trusted_roots_length, read_pos, 2 );
The supported signature/hash algorithms list occurs between the list of supported certificate types and the list of trusted root authorities. The length of the list is declared as being two bytes, even though there are only 7 × 4 = 28 possible combinations of signature and hash algorithms; the length is declared to be this long for future extensibility. In a full-featured implementation, the signature and hash algorithms are used to select an appropriate certificate, end the handshake prematurely, or just decline to supply a certificate and see what happens.
Now, it may occur to you that it's not very fair for the server to list its supported signature and hash algorithms while the client is left at the mercy of whatever the server supports, and you'd be right. RFC 5246 also standardizes a new client hello extension that enables the client to list its supported signature and hash algorithms; this extension takes the same form as the list of signature and hash algorithms in the certificate request (see Listing 8-29). This new extension is extension number 13 and is documented in section 7.4.1.4.1 of the TLS 1.2 specification.
To summarize, TLS 1.2 differs from TLS 1.0, at the message-format level, in the following ways:
- Initialization vectors are explicitly declared at the start of each message for block ciphers.
- The client can negotiate, by way of a new hello extension, a stronger hash algorithm to be used whenever the algorithm itself calls for one.
- The PRF is based on a single hash, rather than a combination of MD-5 and SHA-1. If no stronger hash algorithm is negotiated, the default is SHA-256.
- The finished message's verify data is also based on SHA-256 instead of MD-5 and SHA-1.
- Signatures computed over handshake messages such as the server key exchange and certificate verify declare their hash and signature algorithms explicitly.
The changes described in this section are, at a minimum, what you need to change in order to support TLS 1.2. Of course, there's no significant benefit to making these changes just to upgrade to TLS 1.2 if you don't take advantage of the cool new features that it includes. The following two sections examine the most significant cryptographic advances introduced by TLS 1.2: Authenticated Encryption with Associated Data (AEAD) ciphers and Elliptic-Curve Cryptography (ECC) support.
Adding Support for AEAD Mode Ciphers
TLS 1.0 defined two cipher modes: block and stream. The primary reason for the distinction is that block ciphers need an IV and padding whereas block ciphers don't. TLS 1.2 describes a third cipher mode — Authenticated Encryption with Associated Data (AEAD) — that is often described as combining the authentication with the encryption in one fell swoop. I find this description somewhat misleading; AEAD ciphers encrypt the data and then MAC it, just like block and stream ciphers do. However, the main difference is that an AEAD cipher describes both a protection and an authentication method that must be used as an inseparable unit.
Maximizing Throughput with Counter Mode
Recall from Chapter 2 that the simplest way to apply a block cipher is the electronic code book (ECB) mode: chop the input into blocks and process each one according to the block cipher itself. This mode has some problems, though, because identical input blocks become identical output blocks. Because most block ciphers operate on relatively short block sizes, an attacker can spot a lot of similarities in a large block of plaintext encrypted with a single key. Cipher block chaining (CBC), the preferred mode of SSL and TLS, combats this by XORing each block, before encryption, with the encrypted prior block. Yet another mode, output feedback (OFB), inverts CBC and, rather than encrypting the plaintext and then XORing it with the initialization vector, encrypts the initialization vector over and over again, XORing it with the plaintext and turning a block cipher into a stream cipher.
STREAM CIPHERS VERSUS BLOCK CIPHERS
Stream ciphers have some advantages in some contexts. With stream ciphers, there's no padding, so the ciphertext length is the same as the plaintext length. On the other hand, this can be a vulnerability as well. If the ciphertext is as long as the plaintext, a passive eavesdropper can determine the length of the plaintext, which is a problem in many contexts. In HTTPS, for instance, the browser usually sends a fixed-length block of header and preamble, with the only variable-length part of the request being the page being requested. If an eavesdropper knows the length of the plaintext, he can likely narrow down the actual requested page to a short list. Block ciphers have an advantage because the padding doesn't necessarily have to be the minimum amount that makes a full block; if you need three bytes of padding to satisfy an eight-byte block, you can choose to provide 3, 11, 19, 27, and so on up to 251 blocks of padding to frustrate such an attack.
You could, of course, define a stream cipher that allows optional padding, but that sort of defeats the purpose. The principal benefit of a stream cipher is that you can transmit data as soon as it becomes available and not wait for an entire block.
Counter (CTR) mode, illustrated in Figure 9-1, is similar to OFB, but instead of encrypting an initialization vector over and over again, it encrypts a monotonically increasing sequence called a nonce and XOR's that with the plaintext to produce the ciphertext. This approach has an advantage over CBC and OFB because it's infinitely parallelizable. If you have 10 dedicated AES chips that can encrypt a block in a single clock cycle, you can encrypt 10 blocks in a single clock cycle with CTR mode; this is not the case with CBC and OFB because the final output of each block depends on all of the blocks that preceded it. Additionally, if you lose one block somewhere in the middle, you can't recover the following block if you're using CBC and OFB, but you can recover it with CTR mode.
Figure 9-1: Counter mode encryption
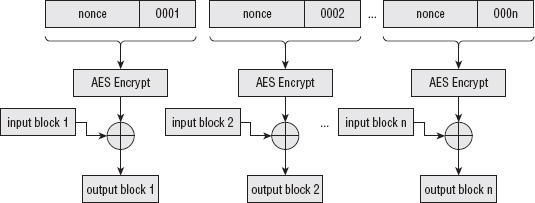
Listing 9-12 illustrates how to modify the AES-CBC sample from Listing 2-42 to work in CTR mode.
Listing 9-12: AES-CTR mode
void aes_ctr_encrypt( const unsigned char *input,
int input_len,
unsigned char *output,
void *iv,
const unsigned char *key )
{
unsigned char *nonce = ( unsigned char * ) iv;
unsigned char input_block[ AES_BLOCK_SIZE ]; unsigned int next_nonce; int block_size; while ( input_len ) { block_size = ( input_len < AES_BLOCK_SIZE ) ? input_len : AES_BLOCK_SIZE; aes_block_encrypt( nonce, input_block, key, 16 ); xor( input_block, input, block_size ); // implement CTR memcpy( ( void * ) output, ( void * ) input_block, block_size ); memcpy( ( void * ) &next_nonce, ( void * ) ( nonce + 12 ), sizeof( unsigned int ) ); // Have to preserve byte ordering to be NIST compliant next_nonce = ntohl( next_nonce ); next_nonce++; next_nonce = htonl( next_nonce ); memcpy( ( void * ) ( nonce + 12 ), ( void * ) &next_nonce, sizeof( unsigned int ) ); input += block_size; output += block_size; input_len -= block_size; } }
If you compare Listing 9-12 with Listing 2-42, you notice a few key differences:
- Of course, the IV is referred to as a nonce to fit the terminology used in the CTR-mode specification.
- The input itself is never encrypted; only the nonce is. The input is XORed with the encrypted nonce output.
This function expects to be passed in a 16-byte value, the first 12 bytes of which should be randomly chosen, but not necessarily kept secret, and the last 4 bytes of which should be all zeros. Each block computation is followed by an increment of the nonce; the last 4 bytes are treated as a four-byte integer, incremented, and updated in-place.
Also notice that the input does not need to be block-aligned. CTR mode turns a block cipher into a stream cipher. Because the nonce is the only thing that's encrypted, it's the only thing that has to be an even multiple of the block size. This implementation is hard-coded to use the 128-bit AES encryption algorithm; of course, you can modify this or make it configurable if you are so inclined.
One particularly interesting point about the CTR mode is that the exact same routine is used to decrypt. Recall from Chapter 2 that AES isn't a reversible cipher like DES is, but when you use AES in CTR mode, AES doesn't need to be reversible. Because the counter is what's encrypted at each step, re-creating it and encrypting it again, XORing each such encrypted block with the ciphertext recovers the plaintext. In fact, if you try to use aes_decrypt here, you end up getting the wrong answer.
Nonce selection is crucial with CTR mode, though. You can never, ever reuse a nonce with the same key. In CBC mode, reusing an initialization vector was sort of bad. With CTR mode, it's catastrophic. Consider the CTR-mode encryption of the ASCII string "Hello, World!!" (0x68656c6c6f20776f726c642121) with the key 0x404142434445464748494a4b4c4d4e4f and a nonce of 0x10111213141516. This encrypts, in CTR mode, to 0xfb35f1556ac63f6f226935cd57. So far, so good; an attacker can't determine anything about the plaintext from the ciphertext.
Later, though, you encrypt the plaintext "Known Plaintxt" (0x4b6e6f776e20506c616e747874), which the attacker knows. Using the same key and the same nonce (starting from counter 0), this encrypts to 0xd83ef24e6bc6186c316b259402. Unfortunately, if the attacker now XOR's the first cipher text block with the second, and then XOR's this with the known input, he recovers p1. This attack is illustrated in Table 9-1. This vulnerability has nothing to do with the strength of the cipher or the choice of the key; it's a fixed property of CTR mode itself. As long as you keep incrementing the counter, you're safe. As soon as the counter is reset (or wraps) back to 0, you must change the nonce.
Table 9-1: Recovering unknown plaintext from known plaintext when a nonce is reused
| PURPOSE | VALUE |
| cipher text block 2 (c1) | 0xfb35f1556ac63f6f226935cd57 |
| cipher text block 1 (c2) | 0xd83ef24e6bc6186c316b259402 |
| c1⊕c2 | 0x230b031b010027031302105955 |
| plain text 2 (p2) | 0x4b6e6f776e20506c616e747874 |
| p2⊕c1⊕c2 | 0x68656c6c6f20776f726c642121 |
As usual, the implementation presented by this book completely disregards this critical security advice and reuses the same hardcoded nonce over and over again for the sake of illustration. However, at least you can get around this security hole by making sure never to reuse a nonce. There's another problem with CTR mode that you can't solve, at least not within CTR mode.
Consider the plaintext 0xAB and the CTR-mode key stream byte 0x34. XORed together, they become the cipher text 0xB2. So far, so good; the attacker can't recover the plaintext 0xAB without the keystream byte 0x34 and can't learn anything about the plaintext from the ciphertext. But say that the attacker does know that the first nibble is "A", and he wants to change it to a "C" (pretend this is a really simple protocol where C is an identifier representing the attacker and B is a value indicating that A or C should get a million dollars). Because "A" XOR "C" is "2", he can XOR the first nibble of the cipher text with 2 to produce 0x82. When the recipient decrypts it, he applies the keystream byte 0x34 and reveals 0xCB.
This is called a bit-flipping attack, and CTR mode is particularly vulnerable to it. If the attacker knows part of the plaintext, he can change it to anything he wants by XORing the known plaintext with the desired plaintext and then XORing that with the ciphertext. Of course, you can probably guess the solution: a MAC. This is why AEAD ciphers are so named; they use a cipher mode that must be combined with a MAC function.
Reusing Existing Functionality for Secure Hashes with CBC-MAC
Chapter 4 focuses on HMAC to provide Message Authentication Codes; HMAC is a widely used, intensively scrutinized MAC algorithm. It isn't, however, the only way to generate a secure MAC. Recall from Chapter 4 what sort of qualities you should look for in a good MAC algorithm. It should be impossible:
- To reverse-engineer. Knowing the input and the MAC should not make it any easier to discover the shared MAC key.
- For somebody without the shared key to generate a valid MAC.
- To deliberately construct a message such that it shares a MAC with another message.
- To engineer two separate messages that share a MAC.
Of course, to be cryptographically correct, you must replace the word "impossible" with "computationally infeasible" in the requirements, but this is the essence of a keyed-MAC construction. The second two requirements are met by the use of secure hash algorithms; the first two come from the HMAC construct itself.
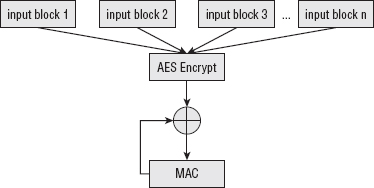
Similar to the concept of using OFB or CTR mode to convert a block cipher into a stream cipher, CBC-MAC converts a block cipher into a secure keyed-MAC construction. The construct itself is simple; you can probably guess how it works. Encrypt the input using the block cipher in CBC mode — start with an IV of all zeros. Throw away all output blocks except the last; this is your MAC. Notice that a secure hash of the input is not computed or required with CBC-MAC. You can actually implement this using the aes_encrypt function from Listing 2-42 directly, but to be a bit more memory efficient, you should write a separate function that only uses a single block of output, as shown in Listing 9-13.
Listing 9-13: aes_cbc_mac
#define MAC_LENGTH 8 void aes_cbc_mac( const unsigned char *key, int key_length, const unsigned char *text, int text_length, unsigned char *mac ) { unsigned char input_block[ AES_BLOCK_SIZE ]; unsigned char mac_block[ AES_BLOCK_SIZE ]; memset( mac_block, '\0', AES_BLOCK_SIZE ); while ( text_length >= AES_BLOCK_SIZE ) { memcpy( input_block, text, AES_BLOCK_SIZE ); xor( input_block, mac_block, AES_BLOCK_SIZE ); aes_block_encrypt( input_block, mac_block, key, key_length ); text += AES_BLOCK_SIZE; text_length -= AES_BLOCK_SIZE; } memcpy( mac, mac_block, MAC_LENGTH ); }
If you compare Listing 9-13 to Listing 2-42, you see that the only difference here — besides different variable names — is that the output is copied to the same mac_block over and over again. The mac output pointer can't be used for this purpose because it's not guaranteed to be the same length as an AES block; if you need fewer bytes of MAC, you discard the least-significant bytes of the final AES block. Of course, if you need a longer MAC, you must use a different MAC function; the output of the CBC-MAC is bounded by the block size of the underlying block cipher. The process is illustrated in Figure 9-2.
However, CBC-MAC fails to provide all of the requirements for a secure MAC.
- It satisfies the first and second requirements. You cannot discover the key from the output, and somebody without the key cannot generate a valid MAC.
- It fails to satisfy the last two requirements; it is possible to deliberately engineer collisions this way.
Therefore, CBC-MAC must be used with an encryption algorithm; the MAC itself must be protected by a cipher.
Combining CTR and CBC-MAC into AES-CCM
AES-CCM uses AES in CTR mode to achieve encryption and the same algorithm in CBC-MAC mode to achieve authentication (CCM just stands for Counter with CBC-MAC). AES-CCM is specified by the U.S. government's NIST at http://csrc.nist.gov/publications/nistpubs/800-38C/SP800-38C.pdf. Both encryption and MAC are used with the same key to provide a simultaneously encrypted and authenticated block. The length of the output is the same as that of the input, plus the chosen length of the MAC.
The length of the MAC is variable; as noted previously, you can make it any length you want, up to the length of an AES block. However, both sides must agree, before exchanging any data, what this length is; although the MAC length affects the output, it's not recoverable from the ciphertext. Therefore, the length must generally be fixed at implementation time, or exchanged out of band. To keep things relatively simple, you fix it at eight bytes.
Conceptually, AES-CCM is simple — CTR mode and CBC-MAC are both fairly easy to understand. However, as they say, "the devil is in the details." Actually implementing AES-CCM according to the standard is fairly complex, because everything has to be just-so to achieve proper interoperability. Most of the complexity in CCM surrounds the MAC. Remember from Chapter 4 that a good MAC function must include the length of the input somehow; MD5 and SHA both append a padding block terminated with the length of the input, in bits. This ensures that a single 0 bit MAC's to something different than, say, two 0 bits. CCM uses CBC-MAC with such a length, but the length is prepended rather than appended.
In fact, the first input block to the MAC function is an entire 16-byte block of header information. This header information is never encrypted, but is just used to initialize the MAC. The first byte of this header information declares both the length of the MAC and the number of bytes that encode the length of the input. In other words, if the length of the input is encoded in a four-byte integer, then the first byte of the header block declares "4". (This also means that the length of the input must be known before encryption begins. AES-CCM does not lend itself to "running" computations.)
The remaining 15 bytes of the header block are split between the nonce and the actual length of the input. Therefore, if the number of bytes that encode the length of the input is 4, then the nonce is 11 bytes. The encoding of the first byte is particularly complex, to keep things packed tightly; to simplify, just hardcode the value 0x1F, which declares — in a very roundabout way — that the MAC is 8 bytes long, and the length of the length is also 8 bytes long. This implies that the nonce is 7 bytes long.
Therefore, if the nonce is 0x01020304050607 and the input length is 500 bytes, the header block looks like this:
0x1F 0x01020304050607 0x00000000000001F4
This should be fed into the CBC-MAC function to initialize it. After this initialization is complete, the CBC-MAC function operates on the input exactly as shown in Listing 9-13.
The first "input-length" bytes of output are the CTR-mode encryption of the input itself. The only stipulation that CCM places on the CTR mode is that the first byte of each nonce must be a declaration of the number of bytes that encode the length that was described in the header, followed by the nonce as was declared in the header, followed by an incrementing sequence that starts at 1 (not 0!).
Finally, the last "mac-length" bytes of output are, of course, the MAC, but before the MAC is output, it's counter-mode encrypted itself. It's encrypted with the counter at 0. The whole process is illustrated in Figure 9-3.
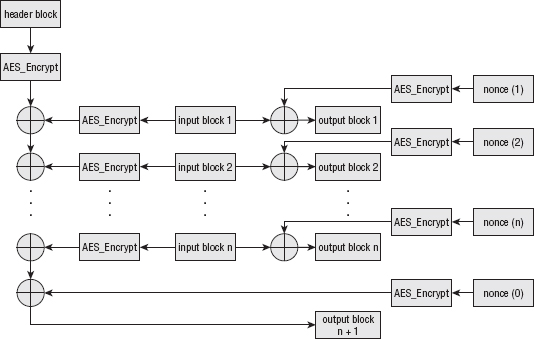
If this is not quite clear, the code in Listing 9-14 should clarify.
Listing 9-14: "aes.c" aes_ccm_encrypt
#define MAC_LENGTH 8
/**
* This implements 128-bit AES-CCM.
* The IV is the nonce; it should be seven bytes long.
* output must be the input_len + MAC_LENGTH
* bytes, since CCM adds a block-length header
*/
int aes_ccm_encrypt( const unsigned char *input,
int input_len,
unsigned char *output,
void *iv,
const unsigned char *key )
{
unsigned char nonce[ AES_BLOCK_SIZE ];
unsigned char input_block[ AES_BLOCK_SIZE ];
unsigned char mac_block[ AES_BLOCK_SIZE ];
unsigned int next_nonce;
int block_size;
unsigned int header_length_declaration;
// The first input block is a (complicated) standardized header
// This is just for the MAC; not output
memset( input_block, '\0', AES_BLOCK_SIZE );
input_block[ 0 ] = 0x1F; // t = mac_length = 8 bytes, q = 8 bytes (so n = 7)
header_length_declaration = htonl( input_len );
memcpy( ( void * ) ( input_block + ( AES_BLOCK_SIZE - sizeof( int ) ) ),
&header_length_declaration, sizeof( unsigned int ) );
memcpy( ( void * ) ( input_block + 1 ), iv, 8 );
// update the CBC-MAC
memset( mac_block, '\0', AES_BLOCK_SIZE );
xor( input_block, mac_block, AES_BLOCK_SIZE );
aes_block_encrypt( input_block, mac_block, key, 16 );
// Prepare the first nonce
memset( nonce, '\0', AES_BLOCK_SIZE );
nonce[ 0 ] = 0x07; // q hardcode to 8 bytes, so n = 7
memcpy( ( nonce + 1 ), iv, 8 );
while ( input_len )
{
// Increment counter
memcpy( ( void * ) &next_nonce, ( void * ) ( nonce + 12 ),
sizeof( unsigned int ) );
// Preserve byte ordering, although not strictly necessary
next_nonce = ntohl( next_nonce );
next_nonce++;
next_nonce = htonl( next_nonce ); memcpy( ( void * ) ( nonce + 12 ), ( void * ) &next_nonce, sizeof( unsigned int ) ); // encrypt the nonce block_size = ( input_len < AES_BLOCK_SIZE ) ? input_len : AES_BLOCK_SIZE; aes_block_encrypt( nonce, input_block, key, 16 ); xor( input_block, input, block_size ); // implement CTR memcpy( output, input_block, block_size ); // update the CBC-MAC memset( input_block, '\0', AES_BLOCK_SIZE ); memcpy( input_block, input, block_size ); xor( input_block, mac_block, AES_BLOCK_SIZE ); aes_block_encrypt( input_block, mac_block, key, 16 ); // advance to next block input += block_size; output += block_size; input_len -= block_size; } // Regenerate the first nonce memset( nonce, '\0', AES_BLOCK_SIZE ); nonce[ 0 ] = 0x07; // q hardcode to 8 bytes memcpy( ( nonce + 1 ), iv, 8 ); // encrypt the header and output it aes_block_encrypt( nonce, input_block, key, AES_BLOCK_SIZE ); // MAC is the CBC-mac XOR'ed with S0 xor( mac_block, input_block, MAC_LENGTH ); memcpy( output, mac_block, MAC_LENGTH ); return 0; }
The first section builds the CCM mode header in the input_block:
memset( input_block, '\0', AES_BLOCK_SIZE ); input_block[ 0 ] = 0x1F; // t = mac_length = 8 bytes, q = 8 bytes (so n = 7) header_length_declaration = htonl( input_len ); memcpy( ( void * ) ( input_block + ( AES_BLOCK_SIZE - sizeof( int ) ) ), &header_length_declaration, sizeof( unsigned int ) ); memcpy( ( void * ) ( input_block + 1 ), iv, 8 );
As always, the length of the length must be put in network byte order.
The next section updates the CBC-MAC with this header:
memset( mac_block, '\0', AES_BLOCK_SIZE ); xor( input_block, mac_block, AES_BLOCK_SIZE ); aes_block_encrypt( input_block, mac_block, key, 16 );
This is followed by a single loop through the input data that simultaneously performs the CTR-mode encryption and updates the CBC-MAC. This enables the encrypt-and-authenticate process to pass over the data only one time. Because CTR mode encryption encrypts the counter, and CBC-MAC encrypts the input itself, it's necessary to invoke aes_block_encrypt twice inside the loop. If you want to be hyper-efficient, you can modify aes_block_encrypt to accept two inputs and generate two outputs; you can then reuse the key schedule computation.
The order of things in the main loop of Listing 9-14 is only slightly different than those of Listings 9-12 and 9-13 (you may want to compare them before continuing). Because AES-CCM wants the first counter block to have the value of 1, the counter is initialized outside the loop and then incremented at the top instead of after encryption.
Finally, the MAC itself is encrypted in CTR mode with the 0 counter and output:
// Regenerate the first nonce memset( nonce, '\0', AES_BLOCK_SIZE ); nonce[ 0 ] = 0x07; // q hardcode to 8 bytes memcpy( ( nonce + 1 ), iv, 8 ); // encrypt the header and output it aes_block_encrypt( nonce, input_block, key, AES_BLOCK_SIZE ); // MAC is the CBC-mac XOR'ed with S0 xor( mac_block, input_block, MAC_LENGTH ); memcpy( output, mac_block, MAC_LENGTH );
Although counter-mode makes a reversible cipher from any block cipher, you do still need a special decrypt routine for AES-CCM. The encryption routine generates the output and appends a MAC, so the decryption routine must be aware of the MAC and not output it. For robustness, the decryption routine should probably verify the MAC as well. However, the bulk of the routine is the same as the encryption routine, so it makes sense to combine them into one common routine and just pass in a flag indicating which operation is taking place: encrypt or decrypt.
Rename aes_ccm_encrypt to aes_ccm_process and add a decrypt flag to it as shown in Listing 9-15.
Listing 9-15: "aes.c" aes_ccm_process common routine for encrypt and decrypt
int aes_ccm_process( const unsigned char *input,
int input_len,
unsigned char *output,
void *iv,
const unsigned char *key,
int decrypt )
{
...
unsigned int next_nonce; int process_len; int block_size; ... input_block[ 0 ] = 0x1F; // t = mac_length = 8 bytes, q = 8 bytes (so n = 7) process_len = input_len - ( decrypt ? MAC_LENGTH : 0 ); header_length_declaration = htonl( process_len ); ... while ( process_len ) { // Increment counter memcpy( ( void * ) &next_nonce, ( void * ) ( nonce + 12 ), sizeof( unsigned int ) ); ... block_size = ( process_len < AES_BLOCK_SIZE ) ? process_len : AES_BLOCK_SIZE; ... // update the CBC-MAC memset( input_block, '\0', AES_BLOCK_SIZE ); memcpy( input_block, decrypt ? output : input, block_size ); xor( input_block, mac_block, AES_BLOCK_SIZE ); ... output += block_size; process_len -= block_size; } ... if ( !decrypt ) { xor( mac_block, input_block, MAC_LENGTH ); memcpy( output, mac_block, MAC_LENGTH ); return 1; } else { xor( input_block, input, MAC_LENGTH ); if ( memcmp( mac_block, input_block, MAC_LENGTH ) ) { return 0; } return 1; } int aes_ccm_encrypt( const unsigned char *input, int input_len, unsigned char *output, void *iv, const unsigned char *key ) { return aes_ccm_process( input, input_len, output, iv, key, 0 ); }
int aes_ccm_decrypt( const unsigned char *input, int input_len, unsigned char *output, void *iv, const unsigned char *key ) { return aes_ccm_process( input, input_len, output, iv, key, 1 ); }
As you can see, most of the changes involve making sure to process only the ciphertext in decrypt mode. The big change is at the end; in decrypt mode, rather than outputting the MAC, you decrypt it and then compare the computed MAC with the one that was received. If they don't match, return false.
Note that there's nothing AES-specific about this routine; for optimum flexibility, you could pass a pointer to a block encrypt function and invoke that for each block. However, CCM with AES has been extensively studied and is believed to be secure; if you swap AES with some arbitrary block cipher function, you may not be so lucky. Your best bet for now is to only use CCM with AES.
Maximizing MAC Throughput with Galois-Field Authentication
CBC-MAC has some theoretical problems, which are not serious enough to discount using it (AES-CCM is actually becoming pretty popular), but the problems are significant enough that professional cryptanalysts have spent effort trying to find improvements. Additionally, recall that one of the benefits of CTR mode is that it's infinitely parallelizable. Unfortunately, CBC-MAC has the same throughput problems that CBC encryption has, so CCM loses one of the main advantages of using CTR mode in the first place.
An alternative that avoids the problems with CBC-MAC is the GHASH authentication routine. GHASH is based on Galois-Field (GF) multiplication; i.e. multiplication in a finite field. The idea behind GHASH is to XOR each block with the previous block, but compute the GF(2128) multiplication in the fixed polynomial field x128 + x7 + x2 + x + 1. This may sound somewhat familiar — it's actually the same thing that you did to code the AES matrix multiplication, only it's relative to a different polynomial. The code to perform this multiplication is similar to the dot/xtime computation from Listing 2-36. The only real difference here, other than the new polynomial, is that GHASH computation is done over 128-bit fields rather than only 8.
If all of that doesn't mean much to you, don't worry; you can treat the GHASH function as a black box in the same way you treated the MD5 and SHA functions. It creates a probabilistically unique, impossible-to-reverse output from its input. How it does so is not as important as the fact that it does. Listing 9-16 shows the gf_multiply function.
Listing 9-16: "aes.c" gf_multiply
/** * "Multiply" X by Y (in a GF-128 field) and return the result in Z. * X, Y, and Z are all AES_BLOCK_SIZE in length. */ static void gf_multiply( const unsigned char *X, const unsigned char *Y, unsigned char *Z ) { unsigned char V[ AES_BLOCK_SIZE ]; unsigned char R[ AES_BLOCK_SIZE ]; unsigned char mask; int i, j; int lsb; memset( Z, '\0', AES_BLOCK_SIZE ); memset( R, '\0', AES_BLOCK_SIZE ); R[ 0 ] = 0xE1; memcpy( V, X, AES_BLOCK_SIZE ); for ( i = 0; i < 16; i++ ) { for ( mask = 0x80; mask; mask >>= 1 ) { if ( Y[ i ] & mask ) { xor( Z, V, AES_BLOCK_SIZE ); } lsb = ( V[ AES_BLOCK_SIZE - 1 ] & 0x01 ); for ( j = AES_BLOCK_SIZE - 1; j; j-- ) { V[ j ] = ( V[ j ] >> 1 ) | ( ( V[ j - 1 ] & 0x01 ) << 7 ); } V[ 0 ] >>= 1; if ( lsb ) { xor( V, R, AES_BLOCK_SIZE ); } } } }
This is just another variant of the same double-and-add multiplication routine that has come up over and over again throughout this book — the counter variables i and mask iterate over the bits of the input Y and add X to the Z computation whenever the input bit is 1 (you may want to refer to Listing 3-9 for a more detailed look at this format). The only big difference is that X — which is copied into the temporary variable V at the start of the routine — is right-shifted at each step and, if the least-significant bit of X is a 1, X is additionally XORed with the field polynomial 0xE1 × 2120. The value of this polynomial is significant, in the number-theoretic sense, but you can just treat it as a magic constant that you must use to maintain compatibility with other implementations.
The GHASH routine, illustrated in Figure 9-4, takes as input a key that the specification calls H. It computes a variable-length MAC from its input by GF-multiplying each input block by H and XORing all of the resulting blocks to each other. If the last block is not block-length aligned, it's padded with 0's, and there's a single "pseudo-block" trailer that includes the 64-bit length of the input itself.
Figure 9-4: GHASH MAC algorithm
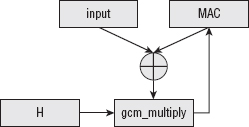
A standalone GHASH implementation is shown in Listing 9-17.
Listing 9-17: "aes.c" ghash
static void ghash( unsigned char *H,
unsigned char *X,
int X_len,
unsigned char *Y ) // Y is the output value
{
unsigned char X_block[ AES_BLOCK_SIZE ];
unsigned int input_len;
int process_len;
memset( Y, '\0', AES_BLOCK_SIZE );
input_len = htonl( X_len << 3 ); // remember this for final block
while ( X_len )
{
process_len = ( X_len < AES_BLOCK_SIZE ) ? X_len : AES_BLOCK_SIZE;
memset( X_block, '\0', AES_BLOCK_SIZE );
memcpy( X_block, X, process_len );
xor( X_block, Y, AES_BLOCK_SIZE );
gf_multiply( X_block, H, Y );
X += process_len;
X_len -= process_len;
}
// Hash the length of the ciphertext as well memset( X_block, '\0', AES_BLOCK_SIZE ); memcpy( X_block + 12, ( void * ) &input_len, sizeof( unsigned int ) ); xor( X_block, Y, AES_BLOCK_SIZE ); gf_multiply( X_block, H, Y ); }
As you can see, it's not too complex after you've gotten gf_multiply working. The input is gf_multiply'ed, one block at a time, and each resulting block is XOR'ed with the last. Here, the block size is hardcoded as AES_BLOCK_SIZE because this is used in the context of AES. The terse variable names presented here match the specification so you can easily compare what this code is doing with what the specification declares.
Combining CTR and Galois-Field Authentication with AES-GCM
AES-GCM is specified by http://csrc.nist.gov/publications/nistpubs/800-38D/SP-800-38D.pdf and in more detail in http://www.csrc.nist.gov/groups/ST/toolkit/BCM/documents/proposedmodes/gcm/gcm-revised-spec.pdf. It's a lot like AES-CCM, but it uses GHASH instead of CBC-MAC. It also MAC's the encrypted values rather than the plaintext, so although you can, in theory, try to write one über-routine that encapsulated both, you'd end up with such a mess of special cases it wouldn't really be worth it. AES-GCM also does away with AES-CCM's special header block and starts the encryption on counter block 2, rather than counter block 1; the MAC is encrypted with counter block 1 rather than counter block 0.
Listing 9-18 illustrates a combined CTR/GHASH implementation of AES-GCM. There are a lot of similarities between this and the AES-CCM implementation in Listing 9-14, but not quite enough to make it worth trying to combine them into a single common routine.
Listing 9-18: "aes.c" aes_gcm_encrypt
/**
* This implements 128-bit AES-GCM.
* IV must be exactly 12 bytes long and must consist of
* 12 bytes of random, unique data. The last four bytes will
* be overwritten.
* output must be exactly 16 bytes longer than input.
*/
int aes_gcm_encrypt( const unsigned char *input,
int input_len,
unsigned char *output,
void *iv,
const unsigned char *key ) { unsigned char nonce[ AES_BLOCK_SIZE ]; unsigned char input_block[ AES_BLOCK_SIZE ]; unsigned char zeros[ AES_BLOCK_SIZE ]; unsigned char H[ AES_BLOCK_SIZE ]; unsigned char mac_block[ AES_BLOCK_SIZE ]; unsigned int next_nonce; int original_input_len; int block_size; memset( zeros, '\0', AES_BLOCK_SIZE ); aes_block_encrypt( zeros, H, key, 16 ); memcpy( nonce, iv, 12 ); memset( nonce + 12, '\0', sizeof( unsigned int ) ); // MAC initialization memset( mac_block, '\0', AES_BLOCK_SIZE ); original_input_len = htonl( input_len << 3 ); // remember this for final block next_nonce = htonl( 1 ); while ( input_len ) { next_nonce = ntohl( next_nonce ); next_nonce++; next_nonce = htonl( next_nonce ); memcpy( ( void * ) ( nonce + 12 ), ( void * ) &next_nonce, sizeof( unsigned int ) ); block_size = ( input_len < AES_BLOCK_SIZE ) ? input_len : AES_BLOCK_SIZE; aes_block_encrypt( nonce, input_block, key, 16 ); xor( input_block, input, block_size ); // implement CTR memcpy( ( void * ) output, ( void * ) input_block, block_size ); // Update the MAC; input_block contains encrypted value memset( ( input_block + AES_BLOCK_SIZE ) - ( AES_BLOCK_SIZE - block_size ), '\0', AES_BLOCK_SIZE - block_size ); xor( input_block, mac_block, AES_BLOCK_SIZE ); gf_multiply( input_block, H, mac_block ); input += block_size; output += block_size; input_len -= block_size; } memset( input_block, '\0', AES_BLOCK_SIZE ); memcpy( input_block + 12, ( void * ) &original_input_len, sizeof( unsigned int ) ); xor( input_block, mac_block, AES_BLOCK_SIZE ); gf_multiply( input_block, H, output );
// Now encrypt the MAC block and output it memset( nonce + 12, '\0', sizeof( unsigned int ) ); nonce[ 15 ] = 0x01; aes_block_encrypt( nonce, input_block, key, 16 ); xor( output, input_block, AES_BLOCK_SIZE ); return 0; }
As you can see, the H parameter that GHASH requires is a block of all zeros, AES-encrypted with the shared key.
memset( zeros, '\0', AES_BLOCK_SIZE ); aes_block_encrypt( zeros, H, key, 16 ); memset( nonce + 12, '\0', sizeof( unsigned int ) );
The CTR-mode computation is identical to that of AES-CCM; the only difference is that the nonce counter starts at 2, rather than at 1. However, the MAC is different: AES-GCM MACs the encrypted output, instead of the plaintext as AES-CCM does. The only potentially confusing line of Listing 9-18, then, is this one:
memset( ( input_block + AES_BLOCK_SIZE ) -
( AES_BLOCK_SIZE - block_size ), '\0',
AES_BLOCK_SIZE - block_size );
Because the MAC is computed over the encrypted output, and input_block currently contains the encrypted output (it was memcpy'd into output on the previous line), you can feed this block into the MAC computation. However, the GHASH MAC requires that a non-aligned block be zero-padded, whereas the CTR mode just drops any unused output. This complex line, then, zero pads the final block, if needed. Otherwise, this looks just like the GHASH computation in Listing 9-17, with somewhat more meaningful variable names.
Finally, the trailer is appended to the MAC:
memset( input_block, '\0', AES_BLOCK_SIZE ); memcpy( input_block + 12, ( void * ) &original_input_len, sizeof( unsigned int ) ); xor( input_block, mac_block, AES_BLOCK_SIZE ); gf_multiply( input_block, H, output );
Note that original_input_len is given in bits, not bytes — hence the << 3 at the start of the function.
Finally, the whole MAC is CTR-mode encrypted with nonce 1 (not nonce 0, as it was with AES-CCM), and output as the final block:
memset( nonce + 12, '\0', sizeof( unsigned int ) ); nonce[ 15 ] = 0x01; aes_block_encrypt( nonce, input_block, key, 16 ); xor( output, input_block, AES_BLOCK_SIZE );
Of course, it's not particularly useful to write an encryption routine without a decryption routine. As with AES-CCM, decrypting is pretty much the same as encrypting, you just have to remember to authenticate the last block rather than decrypting and outputting it. In fact, the changes to support decryption in aes_gcm_process in Listing 9-19 are nearly identical to those to apply the same change to aes_ccm_process in Listing 9-15.
Listing 9-19: "aes.c" aes_gcm_process with encrypt and decrypt support
int aes_gcm_process( const unsigned char *input,
int input_len,
unsigned char *output,
void *iv,
const unsigned char *key,
int decrypt )
{
...
int original_input_len;
int process_len;
int block_size;
...
memset( nonce + 12, '\0', sizeof( unsigned int ) );
process_len = input_len - ( decrypt ? AES_BLOCK_SIZE : 0 );
// MAC initialization
memset( mac_block, '\0', AES_BLOCK_SIZE );
original_input_len = htonl( process_len,, 3 );
...
while ( process_len )
{
...
block_size = ( process_len < AES_BLOCK_SIZE ) ? process_len : AES_BLOCK_SIZE;
aes_block_encrypt( nonce, input_block, key, 16 );
xor( input_block, input, block_size ); // implement CTR
memcpy( ( void * ) output, ( void * ) input_block, block_size );
if ( decrypt )
{
// When decrypting, put the input – e.g. the ciphertext -
// back into the input block for the MAC computation below
memcpy( input_block, input, block_size );
}
// Update the MAC; input_block contains encrypted value
memset( ( input_block + AES_BLOCK_SIZE ) -
...
process_len -= block_size;
}
... memset( nonce + 12, '\0', sizeof( unsigned int ) ); nonce[ 15 ] = 0x01; if ( !decrypt ) { gf_multiply( input_block, H, output ); // Now encrypt the MAC block and output it aes_block_encrypt( nonce, input_block, key, 16 ); xor( output, input_block, AES_BLOCK_SIZE ); } else { gf_multiply( input_block, H, mac_block ); // Now decrypt the final (MAC) block and compare it aes_block_encrypt( nonce, input_block, key, 16 ); xor( input_block, input, AES_BLOCK_SIZE ); if ( memcmp( mac_block, input_block, AES_BLOCK_SIZE ) ) { return 1; } } return 0; } int aes_gcm_encrypt( const unsigned char *input, int input_len, unsigned char *output, void *iv, const unsigned char *key ) { return aes_gcm_process( input, input_len, output, iv, key, 0 ); } int aes_gcm_decrypt( const unsigned char *input, int input_len, unsigned char *output, void *iv, const unsigned char *key ) { return aes_gcm_process( input, input_len, output, iv, key, 1 ); }
AES-CCM and AES-GCM are fairly simple to understand, but not necessarily simple to implement, due to the required precision surrounding their associated MACs. Fortunately, once you get the details all worked out, you can treat the functions as black boxes — plaintext goes in, ciphertext comes out. As long as you're careful to ensure that nonces are never reused with a single key, you can be confident that the encrypted data is safely protected.
Authentication with Associated Data
By now you may be wondering, "If AEAD stands for Authenticated Encryption with Associated Data, what's the associated data part?" The Associated Data is data that should be authenticated along with the encrypted data, but not itself encrypted. If you remember the use of the MAC in TLS 1.0, it MAC'ed one additional piece of data that was not transmitted — the sequence number — and some that were transmitted but not encrypted. Because the main upside of AEAD is to incorporate the authentication into the encryption, you need to replicate the authentication of the original TLS 1.0 MAC.
The associated data, if present, is MAC'ed before the rest of the data stream, but in the case of CCM, after the header block. In order to process associated data during AES-CCM or AES-GCM, make the changes shown in Listing 9-20 to the encrypt and decrypt routines.
Listing 9-20: "aes.h" AES-CCM and AES-GCM with associated data support
int aes_ccm_encrypt( const unsigned char *input,
const int input_len,
const unsigned char *addldata,
const int addldata_len,
unsigned char output[],
void *iv,
const unsigned char *key )
{
return aes_ccm_process( input, input_len, addldata, addldata_len,
output, iv, key, 0 );
}
int aes_ccm_decrypt( const unsigned char *input,
const int input_len,
const unsigned char *addldata,
const int addldata_len,
unsigned char output[],
void *iv,
const unsigned char *key )
{
return aes_ccm_process( input, input_len, addldata, addldata_len,
output, iv, key, 1 );
}
int aes_gcm_encrypt( const unsigned char *plaintext,
const int input_len,
const unsigned char *addldata, const int addldata_len, unsigned char output[], void *iv, const unsigned char *key ) { return aes_gcm_process( input, input_len, addldata, addldata_len, output, iv, key, 0 ); } int aes_gcm_decrypt( const unsigned char *input, const int input_len, const unsigned char *addldata, const int addldata_len, unsigned char output[], void *iv, const unsigned char *key ) { return aes_gcm_process( input, input_len, addldata, addldata_len, output, iv, key, 1 ); }
Now modify aes_ccm_process and aes_gcm_process to accept and authenticate the associated data. This is not too terribly complex; you just run the associated data through the MAC computation before beginning the encrypt/MAC process. The only complicating factor for CCM is that the first two bytes of the first block of associated data must include the length of the additional data. Remember that every time you MAC anything, you must include the length of what you're MAC'ing in the processing somehow to ensure that two inputs of differing lengths whose trailing bytes are all zeros MAC to different values (if the reason for this isn't clear, you might want to jump back and briefly review Chapter 4). AES-CCM with additional data support is shown in Listing 9-21.
Listing 9-21: "aes.c" aes_ccm_process with associated data
int aes_ccm_process( const unsigned char *input,
int input_len,
const unsigned char *addldata,
unsigned short addldata_len,
unsigned char *output,
void *iv,
const unsigned char *key,
int decrypt )
{
...
memset( input_block, '\0', AES_BLOCK_SIZE );
input_block[ 0 ] = 0x1F; // t = mac_length = 8 bytes, q = 8 bytes (so n = 7)
input_block[ 0 ] |= addldata_len ? 0x40 : 0x00; ... xor( input_block, mac_block, AES_BLOCK_SIZE ); aes_block_encrypt( input_block, mac_block, key, 16 ); if ( addldata_len ) { int addldata_len_declare; int addldata_block_len; // First two bytes of addl data are the length in network order addldata_len_declare = ntohs( addldata_len ); memset( input_block, '\0', AES_BLOCK_SIZE ); memcpy( input_block, ( void * ) &addldata_len_declare, sizeof( unsigned short ) ); addldata_block_len = AES_BLOCK_SIZE - sizeof( unsigned short ); do { block_size = ( addldata_len < addldata_block_len ) ? addldata_len : addldata_block_len; memcpy( input_block + ( AES_BLOCK_SIZE - addldata_block_len ), addldata, block_size ); xor( input_block, mac_block, AES_BLOCK_SIZE ); aes_block_encrypt( input_block, mac_block, key, 16 ); addldata_len -= block_size; addldata += block_size; addldata_block_len = AES_BLOCK_SIZE; memset( input_block, '\0', addldata_block_len ); } while ( addldata_len ); } // Prepare the first nonce memset( nonce, '\0', AES_BLOCK_SIZE );
Remember that, in CCM, there was a header that was MAC'ed before the data, and that the first byte of this header was a byte of flags. One of these flags indicates whether to expect associated data. The first change in Listing 9-21 sets the adata flag in the header that indicates that there is associated data in the first place; the remainder of the changes are contained in the if block. This if block just cycles through the additional data supplied (if any) and computes it into the MAC; the only thing that makes this a bit complex is that the first two bytes of the first block must be the length of the additional data, in network byte order.
To see this in action, go ahead and modify the AES test main routine to call aes_ccm_encrypt instead of aes_128_encrypt when the key size is 16 bytes, and add a provision to optionally pass in some additional data as shown in Listing 9-22.
Listing 9-22: "aes.c" main routine modified to accept associated data
#ifdef TEST_AES
int main( int argc, char *argv[ ] )
{
unsigned char *key;
unsigned char *input;
unsigned char *iv;
unsigned char *addl_data;
int key_len;
int input_len;
int iv_len;
int addldata_len;
if ( argc < 5 )
{
fprintf( stderr, "Usage: %s [-e|-d] <key> <iv> <input> [<addl data>]\n",
argv[ 0 ] );
exit( 0 );
}
key_len = hex_decode( argv[ 2 ], &key );
iv_len = hex_decode( argv[ 3 ], &iv );
input_len = hex_decode( argv[ 4 ], &input );
if ( argc > 5 )
{
addldata_len = hex_decode( argv[ 5 ], &addl_data );
}
else
{
addldata_len = 0;
addl_data = NULL;
}
if ( !strcmp( argv[ 1 ], "-e" ) )
{
unsigned char *ciphertext = ( unsigned char * )
malloc( input_len + MAC_LENGTH );
if ( key_len == 16 )
{
aes_ccm_encrypt( input, input_len, addl_data, addldata_len, ciphertext,
( void * ) iv, key );
}
...
else if ( !strcmp( argv[ 1 ], "-d" ) )
{ unsigned char *plaintext = ( unsigned char * ) malloc( input_len – MAC_LENGTH ); if ( key_len == 16 ) { if ( aes_ccm_decrypt( input, input_len, addl_data, addldata_len, plaintext, ( void * ) iv, key ) ) { fprintf( stderr, "Error, MAC mismatch.\n" ); } } ... show_hex( plaintext, input_len - MAC_LENGTH ); free( plaintext ); ... free( iv ); free( key ); free( input ); free( addl_data ); return 0; } #endif
Now, you can see an AES-CCM encryption in action:
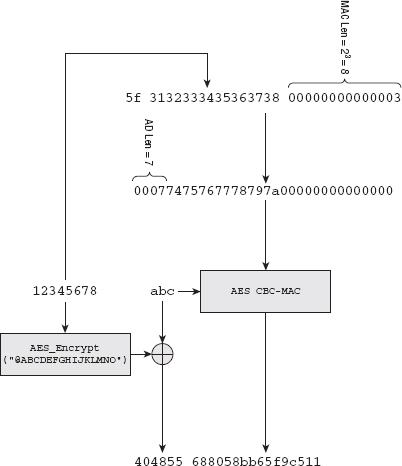
[jdavies@localhost ssl]$ ./aes -e "@ABCDEFGHIJKLMNO" "12345678" "tuvwxyz" "abc" 404855688058bb65f9c511
Here, "@ABCDEFGHIJKLMNO" is the key, "12345678" is the nonce, "tuvwxyz" is the associated data, and "abc" is the data to encrypt. The encrypted output — the CTR-mode part — is the three bytes 0x404855. The remainder of the output is the eight-byte MAC 0x688058bb65f9c511. This MAC is computed over first the header block 0x5f313233343536373800000000000003. 0x5F is the declaration that there is associated data, the MAC size is eight bytes, and that the declaration of the length of the input takes up seven bytes. This is followed by the nonce itself and the length of the input — in this case, three bytes. The associated data is then added to the MAC — this is 0x00077475767778797a00000000000000. Notice that the first two bytes are the length of the associated data, followed by the zero-padded associated data itself. Finally, the plaintext input "abc" is added to the MAC (again, zero-padded). This final MAC block is AES-counter-mode encrypted with nonce 0: 0x31323334353637380000000000000000.
This entire operation is illustrated in Figure 9-5.
Figure 9-5: AES-CCM encryption example
Decrypting gives you back the original input:
[jdavies@localhost ssl]$ ./aes -d "@ABCDEFGHIJKLMNO" "123456789012" "tuvwxyz" \ 0x404855688058bb65f9c511 616263
If the MAC is wrong, though, you just get back nothing:
[jdavies@localhost ssl]$ ./aes -d "@ABCDEFGHIJKLMNO" "123456789012" "tuvwxyz" \ 0x404855688058bb65f9c5112 Error, MAC mismatch.
Technically, though, there's nothing stopping you, if you have the key, from writing a CTR-mode decryption routine and decrypting the first three bytes anyway. If you know the MAC is eight bytes, you know the input was three. You can decrypt, but not authenticate, the ciphertext even if you don't know what the additional data was; it's just used in the MAC computation.
AES-GCM with associated data is even easier; there's no length to prepend to the associated data, so you can just incorporate the associated data processing into the MAC just before encryption starts, as shown in Listing 9-23:
Listing 9-23: "aes.c" aes_gcm_process with associated data support
int aes_gcm_process( const unsigned char *input,
int input_len,
const unsigned char *addl_data,
unsigned short addldata_len,
unsigned char *output,
void *iv,
const unsigned char *key,
int decrypt )
{
...
original_input_len = htonl( process_len << 3 ); // remember this for final block
while ( addldata_len )
{
block_size = ( addldata_len < AES_BLOCK_SIZE ) ?
addldata_len : AES_BLOCK_SIZE;
memset( input_block, '\0', AES_BLOCK_SIZE );
memcpy( input_block, addl_data, block_size );
xor( input_block, mac_block, AES_BLOCK_SIZE );
gf_multiply( input_block, H, mac_block );
addl_data += block_size;
addldata_len -= block_size;
}
next_nonce = htonl( 1 );
...
However, remember from the previous section that the GCM MAC itself included a trailer block whose last eight bytes was the length, in bits, of the MAC'ed data. If you start including additional data in the MAC, you must declare that length as well. Because the trailer block is 16 bytes long, and the last 8 bytes are the length of the ciphertext, you can probably guess that the first 8 bytes are the length of the additional data. Modify aes_gcm_process as shown in Listing 9-24 to account for this.
Listing 9-24: "aes.c" aes_gcm_process with associated data length declaration
int original_input_len, original_addl_len; ... original_input_len = htonl( process_len << 3 ); // remember this for final blockt
original_addl_len = htonl( addldata_len << 3 ); // remember this for final block ... memset( input_block, '\0', AES_BLOCK_SIZE ); memcpy( input_block + 4, ( void * ) &original_addl_len, sizeof( unsigned int ) ); memcpy( input_block + 12, ( void * ) &original_input_len, sizeof( unsigned int ) );
You can see this in action, as well, if you modify the main routine to invoke aes_gcm_encrypt or aes_gcm_decrypt instead of aes_ccm:
[jdavies@localhost ssl]$ ./aes -e "@ABCDEFGHIJKLMNO" "12345678" "tuvwxyz" "abc" 87fd0515d242cf110c77b98055c3ad3196aec6 [jdavies@localhost ssl]$ ./aes -d "@ABCDEFGHIJKLMNO" "12345678" "tuvwxyz" \ 0x87fd0515d242cf110c77b98055c3ad3196aec6 616263
Notice that the AES-GCM output for the same input is 8 bytes longer than the AES-CCM output because the AES-GCM routine included a 16-byte MAC, but AES-CCM's was just 8. There's no particular reason why it must be this way. This is the way they're shown in their relative specifications, so they were coded this way here. The MAC-length is variable, but remember that because the length itself is not included anywhere in the output, both sides must agree on what it must be before transmitting any data.
Incorporating AEAD Ciphers into TLS 1.2
AEAD ciphers such as AES-CCM and AES-GCM are just different enough than block and stream ciphers, from the perspective of TLS 1.2, to warrant their own format. Both ciphers examined here are stream ciphers with a MAC, which is just like RC4 with SHA-1. However, AEAD ciphers must also transmit their nonce. Block ciphers do something similar with their IVs; they incorporate padding, but in theory you could implement an AEAD cipher by treating it as a block-ciphered structure with a 0-length input block.
In fact, you could get away with this for AES-CCM. If you declared the cipher as aes_ctr_(en/de)crypt, you could make the MAC function variable and replace the default HMAC operation with a CBC-MAC. This would actually work with the block ciphered encryption structure coded in Listing 6-64. However, this would fail for AES-GCM. AES-GCM computes a MAC over the ciphertext, rather than the plaintext. Although you could probably write code to maintain this as a special case, AEAD ciphers are designed to be treated as a black-box. You give it the plaintext and the key, and it gives you back an arbitrarily sized chunk of data that it promises to decrypt and authenticate, with the key, at a later date. To properly support AEAD, you must treat AEAD ciphers as yet another sort of cipher.
To this end, modify the CipherSuite structure declaration to include a section for AEAD ciphers as shown in Listing 9-25.
Listing 9-25: "tls.h" CipherSuite declaration with AEAD support
typedef struct
{
...
void (*new_digest)( digest_ctx *context );
int (*aead_encrypt)( const unsigned char *plaintext,
const int plaintext_len,
const unsigned char *addldata,
const int addldata_len,
unsigned char ciphertext[],
void *iv,
const unsigned char *key );
int (*aead_decrypt)( const unsigned char *ciphertext,
const int ciphertext_len,
const unsigned char *addldata,
const int addldata_len,
unsigned char plaintext[],
void *iv,
const unsigned char *key );
}
CipherSuite;
Now, to add support for the standardized AES_GCM cipher mode, you must just add another element to the list of cipher suites declared in Listing 6-10. Unfortunately, RFC 5288 assigns the cipher suite ID 0x9C to AES-GCM. Remember that the suites array is positional; if you skip an element, you have to insert a NULL placeholder. Cipher suite ID 0x9C works out to element 156. Prior to this chapter, the last element in this array was 58. To keep up with this method of inserting new ciphers, you'd have to include 98 empty elements in this array. Instead, just expand the list as shown in Listing 9-26.
Listing 9-26: "tls.h" aes-gcm cipher suite
typedef enum
{
...
TLS_DH_anon_WITH_AES_256_CBC_SHA = 0x003A,
TLS_RSA_WITH_AES_128_GCM_SHA256 = 0x009C,
MAX_SUPPORTED_CIPHER_SUITE = 0x009D
} CipherSuiteIdentifier
Now, rather than explicitly declaring this new cipher suite in the array initializer, add it to the init_tls call as shown in Listing 9-27.
Listing 9-27: "tls.c" init_tls with AES-GCM cipher suite
void init_tls() { ... // Extra cipher suites not previously declared suites[ TLS_RSA_WITH_AES_128_GCM_SHA256 ].id = TLS_RSA_WITH_AES_128_GCM_ SHA256; suites[ TLS_RSA_WITH_AES_128_GCM_SHA256 ].block_size = 0; suites[ TLS_RSA_WITH_AES_128_GCM_SHA256 ].IV_size = 12; suites[ TLS_RSA_WITH_AES_128_GCM_SHA256 ].key_size = 16; suites[ TLS_RSA_WITH_AES_128_GCM_SHA256 ].hash_size = 16; suites[ TLS_RSA_WITH_AES_128_GCM_SHA256 ].bulk_encrypt = NULL; suites[ TLS_RSA_WITH_AES_128_GCM_SHA256 ].bulk_decrypt = NULL; suites[ TLS_RSA_WITH_AES_128_GCM_SHA256 ].new_digest = NULL; suites[ TLS_RSA_WITH_AES_128_GCM_SHA256 ].aead_encrypt = aes_gcm_encrypt; suites[ TLS_RSA_WITH_AES_128_GCM_SHA256 ].aead_decrypt = aes_gcm_decrypt; }
This declares the new cipher suite TLS_RSA_WITH_AES_128_GCM_SHA256. "But wait," you may be saying, "what is this 'SHA256'? Doesn't AES-GCM declare its own MAC?" It does, in fact; RFC 5288 indicates that the SHA-256 should be used to control the PRF. This is in response to section 5 of RFC 5246, which states
At this point, all that's left to do is invoke the AEAD cipher when such a suite becomes active. This happens in the functions send_message, originally defined in Listing 6-64, and tls_decrypt, originally defined in Listing 6-68. You might want to peek back to their final definitions before continuing. After the digest routines, these are the two most complex functions in this book.
If you recall, send_message first computed a MAC over the data to be sent, prepended with a 64-bit sequence number. It then applies padding as necessary, prepends the IV in the case of a block cipher (TLS 1.1+), and encrypts the plaintext and the MAC before sending. AES-GCM is not much different, but a single call computes the ciphertext and the MAC, and the associated data is the sequence number and the header. The CipherSuite declaration from Listing 9-27 lists the new_digest as NULL, but the hash_size as 16. You can rewrite send_ message to take advantage of this by calculating the associated data whenever the hash_size is non-zero as shown in Listing 9-28.
Listing 9-28: "tls.c" send_message with associated data support
int send_message( int connection,
int content_type,
const unsigned char *content,
short content_len, ProtectionParameters *parameters ) { ... unsigned char *mac = NULL; unsigned char mac_header[ 13 ]; digest_ctx digest; ... active_suite = &suites[ parameters->suite ]; // Compute the MAC header always, since this will be used // for AEAD or other ciphers // Allocate enough space for the 8-byte sequence number, the 5-byte pseudo // header, and the content. // These will be overwritten below if ( active_suite->hash_size ) { int sequence_num; memset( mac_header, '\0', 8 ); sequence_num = htonl( parameters->seq_num ); memcpy( mac_header + 4, &sequence_num, sizeof( int ) ); header.type = content_type; header.version.major = TLS_VERSION_MAJOR; header.version.minor = TLS_VERSION_MINOR; header.length = htons( content_len ); mac_header[ 8 ] = header.type; mac_header[ 9 ] = header.version.major; mac_header[ 10 ] = header.version.minor; memcpy( mac_header + 11, &header.length, sizeof( short ) ); } if ( active_suite->new_digest ) { unsigned char *mac_buffer = malloc( 13 + content_len ); mac = ( unsigned char * ) malloc( active_suite->hash_size ); active_suite->new_digest( &digest ); memcpy( mac_buffer, mac_header, 13 ); memcpy( mac_buffer + 13, content, content_len ); ...
This change just creates a new mac_header buffer and pulls its computation out of the MAC computation so that it's accessible to the AEAD encryption function.
Of course, you must also do the encryption itself. This is a tad complex just because you're indexing into various places in various buffers but ultimately boils down to a call to AEAD encrypt with the plaintext, associated data, nonce, and key previously negotiated. This is shown in Listing 9-29.
Listing 9-29: "tls.c" send_message with AEAD encryption support
...
if ( active_suite->bulk_encrypt || active_suite->aead_encrypt )
{
unsigned char *encrypted_buffer = malloc( send_buffer_size +
active_suite->IV_size +
( active_suite->aead_encrypt ? active_suite->hash_size : 0 ) );
int plaintext_len;
// TODO make this random
memset( parameters->IV, '\0', active_suite->IV_size );
// The first 5 bytes (the header) and the IV aren't encrypted
memcpy( encrypted_buffer, send_buffer, 5 );
memcpy( encrypted_buffer + 5, parameters->IV, active_suite->IV_size );
plaintext_len = 5 + active_suite->IV_size;
if ( active_suite->bulk_encrypt )
{
active_suite->bulk_encrypt( send_buffer + 5,
send_buffer_size - 5, encrypted_buffer + plaintext_len,
parameters->IV, parameters->key );
}
else if ( active_suite->aead_encrypt )
{
active_suite->aead_encrypt( send_buffer + 5,
send_buffer_size - 5 - active_suite->hash_size,
mac_header, 13, ( encrypted_buffer + active_suite->IV_size + 5 ),
parameters->IV, parameters->key );
}
free( send_buffer );
send_buffer = encrypted_buffer;
send_buffer_size += active_suite->IV_size;
}
...
As you can see, other than allocating enough space in the target encryption buffer for the MAC, this isn't that much different than ordinary block cipher encryption.
Decrypting with AEAD cipher support is about the same. First, declare a mac_header independent of the MAC buffer and precompute it. However, remember that the length declared in the MAC header was the length of the data before padding or the MAC was added. For this reason, it's impossible, in the block cipher case, to precompute the MAC header before decrypting the data; you need to know how much padding was added, and you can't do that without decrypting. All this means is that a bit of code — the MAC header computation — must be duplicated in tls_decrypt as shown in Listing 9-30 whereas it was reused in send_message.
Listing 9-30: "tls.c" tls_decrypt with AEAD decryption
int tls_decrypt( const unsigned char *header, // need this for MAC verification unsigned char *encrypted_message, short encrypted_length, unsigned char **decrypted_message, ProtectionParameters *parameters ) { ... unsigned char *mac_buffer; unsigned char mac_header[ 13 ]; int sequence_number; ... if ( active_suite->bulk_decrypt ) { ... } else if ( active_suite->aead_decrypt ) { if ( active_suite->IV_size ) { memcpy( parameters->IV, encrypted_message, active_suite->IV_size ); } decrypted_length = encrypted_length - active_suite->hash_size; // Compute the MAC header, which is the AD part. This // has to be done separately here, since the length computation // is slightly different than in the block cipher case memset( mac_header, 0x0, 13 ); sequence_number = htonl( parameters->seq_num ); memcpy( mac_header + 4, &sequence_number, sizeof( int ) ); memcpy( mac_header + 8, header, 3 ); length = htons( decrypted_length ); memcpy( mac_header + 11, &length, 2 ); if ( active_suite->aead_decrypt( encrypted_message + active_suite->IV_size, encrypted_length, mac_header, 13, *decrypted_message, parameters->IV, parameters->key ) ) { // MAC verification failed return −3; } }
Notice that if aead_decrypt returns a non-zero response, indicating a MAC failure, this routine returns −3, which triggers a "bad mac" error to be returned to the caller.
This implementation of AEAD is crucially flawed, though. It does exactly what I warned you earlier to never ever do, which is to reuse a nonce. There's no provision here to ever change the IV; because each call to aead_encrypt starts the nonce counter back over at 0, every record is encrypted with the same set of input. You can't let the counter run over from one record to the next, either. The other end fails to decrypt the message because the receiving code expects to start over from 2 (or 1, or whatever) at decryption time. However, the 12 bytes of nonce are controlled entirely by the sender. There's nothing stopping you from making the last four bytes of the nonce itself another counter, whose values do persist from one aead_encrypt to the next. In fact, you could go ahead and safely use the MAC sequence_num for exactly this purpose.
AES-CCM has not yet been assigned a cipher suite identifier in the TLS space; when and if such an identifier is assigned, its use would be exactly like the AES-GCM example shown here.
In actual practice, AEAD ciphers don't offer much benefit over block ciphers with strong MAC functions when implemented in software. Most of the interest in these ciphers surrounds dedicated hardware. AES-GCM can be parallelized to encrypt 10Gbps, which is more than enough to encrypt an HDMI video stream in real time. Intel's newest processors include a PCLMULQDQ instruction that is explicitly stated as being an optimization to support AES-GCM. Expect AEAD ciphers to be of great interest to embedded hardware implementers.
Working ECC Extensions into the TLS Library
Strictly speaking, ECC is not unique to TLS 1.2; AEAD is, but ECC is not. Although TLS 1.2 is the first version of TLS to mention ECC specifically, RFC 4492, which defines the ECC extensions to TLS, was written with TLS 1.1 in mind. In fact, OpenSSL version 1.0, which was released in March of 2010, supports RFC 4492 ECC extensions but does not support TLS 1.1. Make sure that you have a good grasp of the ECC concepts presented in Chapters 3 and 4 before reading this section.
Recall that ECC is mostly of interest for public-key operations; ECC operations are used to exchange a symmetric key and validate signatures, but plain-old AES usually takes over from there. Key exchange is done via elliptic-curve Diffie-Hellman (ECDH), and signatures are verified using elliptic-curve DSA (ECDSA).
ECDH is analogous to integer Diffie-Hellman. Integer Diffie-Hellman has both sides agree on a starting point — an integer — and each side raises it to an arbitrary (secret) power, exchanging the results with one another. Each side then raises the result by the secret. The distributivity of exponentiation guarantees that each side arrives at the same answer; the difficulty of the discrete logarithm problem thwarts an attacker's attempt to look at the starting point and the result to try to work backward and discover one of the secret numbers.
ECDH works the same way; both sides agree to a starting point, in this case a point on an elliptic curve whose parameters are negotiated in the clear. Each side then multiplies that point by a secret number, shares the resulting point with the other, and completes the shared multiplication with its own secret number. Because ECC point multiplication is distributive, they both arrive at the same shared point, and because ECC division is a difficult problem to which no efficient solution is known, an attacker can't work backward to uncover the secret number.
As discussed in Chapter 8, this is actually good enough for a key exchange in plain view of a passive eavesdropper. However, in order to guard against man-in-the-middle attacks, at least one side must authenticate the other, and the key exchange parameters must be digitally signed. Digital signatures imply public keys, and public keys imply certificates. Therefore, a complete ECC key exchange solution additionally involves the exchange of a certificate bearing an ECDSA public key, which is then used to sign the ECDH parameters verifiably. As long as the client trusts the signer of the certificate (or the signer of the signer, and so on), the key exchange is authentic.
ECDSA is, of course, analogous to DSA. A DSA public/private keypair is just two numbers x and y, along with a set of parameters p, g, and q. The signature is computed over a hash of the message and produces two numbers r and s — the verifier takes p, g, q, and y and verifies that r is correct for s according to y.
An ECDSA public key is a point, and the private key is an integer. Of course, everything is relative to a curve that is defined in terms of two numbers a and b, and a starting point G. The signer computes an r and s pair from the private key point; the verifier checks to see if r and s match according to the public key point. So, to support ECC, you must implement ECDH for key exchange and ECDSA for signature verification.
Note that there's no reason at all why you must use ECDH and ECDSA together. It's perfectly permissible — and even preferable, in some cases — for a server to present an RSA certificate and use the RSA key to sign a set of parameters for ECDH key exchange. Just like using an RSA key to sign a set of DH keys, this enables you to present an RSA certificate but still achieve perfect forward secrecy.
Most of the heavy lifting surrounding the ECC implementation is done in Chapter 4. However, to actually put it in practice, there are a couple of practical considerations. The first is the elliptic curve itself. Chapter 4 glossed over the selection of the a and b parameters that defined the curve, the generator point G, the prime field p, and the order n. As it turns out, it's not easy to create a correct set, and it's even harder to do so securely. Fortunately, you don't have to. The NIST has created a set of "named curves" that you can use. There's no particular danger in letting everybody share the same set of curves as long as everyone randomly chooses the secret parameters.
The Standards for Efficient Cryptography Group (SECG) lists the named curves and their values at http://www.secg.org/download/aid-784/sec2-v2.pdf. The names the groups gives to the curves are along the lines of secp192r1, which indicates that it's an SEC (Standards for Efficient Cryptography) prime-field curve, 192 bits long, and that it is randomly generated. You also might see sectnnn curves that identify characteristic 2 finite-field curves and secpnnnk curves that identify Koblitz curves. The distinction isn't particularly important here; this book focuses on the "secp" curves.
Some of the SECP curves come from an older NIST standard, which referred to the curves as simply primennnvx where nnn was the length of the parameters and x was just a version. prime192v1 is identical to secp192r1, and prime256v1 is identical to secp256r1.
Named curve support is straightforward, if slightly tedious. A 256-bit named curve such as secp256r1 is described by a list of six 256-bit (32-byte) numeric values. To support a little bit of diversity, go ahead and implement two named curves — prime192v1/secp192r1 and prime256v1/secp256r1 — as shown in Listing 9-31.
Listing 9-31: "ecc.c" get_named_curve
unsigned char prime192v1_P[] = {
0xFF, 0xFF, 0xFF, 0xFF, 0xFF, 0xFF, 0xFF, 0xFF,
0xFF, 0xFF, 0xFF, 0xFF, 0xFF, 0xFF, 0xFF, 0xFF,
0xFF, 0xFF, 0xFF, 0xFF, 0xFF, 0xFF, 0xFF, 0xFF
};
unsigned char prime192v1_A[] = {
0xFF, 0xFF, 0xFF, 0xFF, 0xFF, 0xFF, 0xFF, 0xFF,
0xFF, 0xFF, 0xFF, 0xFF, 0xFF, 0xFF, 0xFF, 0xFF,
0xFF, 0xFF, 0xFF, 0xFF, 0xFF, 0xFF, 0xFF, 0xFC
};
unsigned char prime192v1_B[] = {
0x64, 0x21, 0x05, 0x19, 0xE5, 0x9C, 0x80, 0xE7,
0x0F, 0xA7, 0xE9, 0xAB, 0x72, 0x24, 0x30, 0x49,
0xFE, 0xB8, 0xDE, 0xEC, 0xC1, 0x46, 0xB9, 0xB1
};
unsigned char prime192v1_Gx[] = {
0x18, 0x8D, 0xA8, 0x0E, 0xB0, 0x30, 0x90, 0xF6,
0x7C, 0xBF, 0x20, 0xEB, 0x43, 0xA1, 0x88, 0x00,
0xF4, 0xFF, 0x0A, 0xFD, 0x82, 0xFF, 0x10, 0x12
};
unsigned char prime192v1_Gy[] = {
0x07, 0x19, 0x2B, 0x95, 0xFF, 0xC8, 0xDA, 0x78,
0x63, 0x10, 0x11, 0xED, 0x6B, 0x24, 0xCD, 0xD5,
0x73, 0xF9, 0x77, 0xA1, 0x1E, 0x79, 0x48, 0x11
};
unsigned char prime192v1_N[] = {
0xFF, 0xFF, 0xFF, 0xFF, 0xFF, 0xFF, 0xFF, 0xFF,
0xFF, 0xFF, 0xFF, 0xFF, 0x99, 0xDE, 0xF8, 0x36, 0x14, 0x6B, 0xC9, 0xB1, 0xB4, 0xD2, 0x28, 0x31 }; unsigned char prime256v1_P[] = { 0xFF, 0xFF, 0xFF, 0xFF, 0x00, 0x00, 0x00, 0x01, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0xFF, 0xFF, 0xFF, 0xFF, 0xFF, 0xFF, 0xFF, 0xFF, 0xFF, 0xFF, 0xFF, 0xFF }; unsigned char prime256v1_A[] = { 0xFF, 0xFF, 0xFF, 0xFF, 0x00, 0x00, 0x00, 0x01, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0xFF, 0xFF, 0xFF, 0xFF, 0xFF, 0xFF, 0xFF, 0xFF, 0xFF, 0xFF, 0xFF, 0xFC }; unsigned char prime256v1_B[] = { 0x5A, 0xC6, 0x35, 0xD8, 0xAA, 0x3A, 0x93, 0xE7, 0xB3, 0xEB, 0xBD, 0x55, 0x76, 0x98, 0x86, 0xBC, 0x65, 0x1D, 0x06, 0xB0, 0xCC, 0x53, 0xB0, 0xF6, 0x3B, 0xCE, 0x3C, 0x3E, 0x27, 0xD2, 0x60, 0x4B }; unsigned char prime256v1_Gx[] = { 0x6B, 0x17, 0xD1, 0xF2, 0xE1, 0x2C, 0x42, 0x47, 0xF8, 0xBC, 0xE6, 0xE5, 0x63, 0xA4, 0x40, 0xF2, 0x77, 0x03, 0x7D, 0x81, 0x2D, 0xEB, 0x33, 0xA0, 0xF4, 0xA1, 0x39, 0x45, 0xD8, 0x98, 0xC2, 0x96 }; unsigned char prime256v1_Gy[] = { 0x4F, 0xE3, 0x42, 0xE2, 0xFE, 0x1A, 0x7F, 0x9B, 0x8E, 0xE7, 0xEB, 0x4A, 0x7C, 0x0F, 0x9E, 0x16, 0x2B, 0xCE, 0x33, 0x57, 0x6B, 0x31, 0x5E, 0xCE, 0xCB, 0xB6, 0x40, 0x68, 0x37, 0xBF, 0x51, 0xF5 }; unsigned char prime256v1_N[] = { 0xFF, 0xFF, 0xFF, 0xFF, 0x00, 0x00, 0x00, 0x00, 0xFF, 0xFF, 0xFF, 0xFF, 0xFF, 0xFF, 0xFF, 0xFF, 0xBC, 0xE6, 0xFA, 0xAD, 0xA7, 0x17, 0x9E, 0x84, 0xF3, 0xB9, 0xCA, 0xC2, 0xFC, 0x63, 0x25, 0x51 }; int get_named_curve( const char *curve_name, elliptic_curve *target ) { if ( !strcmp( "prime192v1", curve_name ) || !strcmp( "secp192r1", curve_name ) ) { load_huge( &target->p, prime192v1_P, sizeof( prime192v1_P ) ); load_huge( &target->a, prime192v1_A, sizeof( prime192v1_A ) ); load_huge( &target->b, prime192v1_B, sizeof( prime192v1_B ) );
load_huge( &target->G.x, prime192v1_Gx, sizeof( prime192v1_Gx ) ); load_huge( &target->G.y, prime192v1_Gy, sizeof( prime192v1_Gy ) ); load_huge( &target->n, prime192v1_N, sizeof( prime192v1_N ) ); return 0; } else if ( !strcmp( "prime256v1", curve_name ) || !strcmp( "secp256r1", curve_name ) ) { load_huge( &target->p, prime256v1_P, sizeof( prime256v1_P ) ); load_huge( &target->a, prime256v1_A, sizeof( prime256v1_A ) ); load_huge( &target->b, prime256v1_B, sizeof( prime256v1_B ) ); load_huge( &target->G.x, prime256v1_Gx, sizeof( prime256v1_Gx ) ); load_huge( &target->G.y, prime256v1_Gy, sizeof( prime256v1_Gy ) ); load_huge( &target->n, prime256v1_N, sizeof( prime256v1_N ) ); return 0; } // Unsupported named curve return 1; }
Of course, there's no rule that you must use a named curve. Everywhere that TLS calls for an elliptic curve, a provision is made to enable either side to declare a curve explicitly by providing the p, a, b, G, and n values. However, named curves are far more common, so explicit curves aren't examined here.
ECDSA Certificate Parsing
The first step in adding ECC support is parsing an ECDSA certificate — that is, an X.509 certificate whose public key info includes an ECDSA public key and a description of a curve to which the public key (a point on the curve) is relative. Recall from Chapter 5 that a certificate consists of eight elements: the version, the serial number, the signature algorithm, the issuer, the validity period, the subject, the subject's public key, and an optional set of extensions. Of these, only two are dependent on the public key algorithm: the signature algorithm and the public key itself.
First, add ECDSA as a valid algorithm identifier as shown in Listing 9-32 and then modify parse_algorithm_identifier from Listing 5-16 to accept SHA-256 with ECDSA as shown in Listing 9-33.
Listing 9-32: "x509.h" ecdsa algorithm identifier
typedef enum { md5WithRSAEncryption, shaWithRSAEncryption, shaWithDSA, sha256WithECDSA } signatureAlgorithmIdentifier;
Listing 9-33: "x509.c" parse_algorithm_identifier with ECDSA support
static const unsigned char OID_md5WithRSA[] =
{ 0x2A, 0x86, 0x48, 0x86, 0xF7, 0x0D, 0x01, 0x01, 0x04 };
static const unsigned char OID_sha1WithRSA[] =
{ 0x2A, 0x86, 0x48, 0x86, 0xF7, 0x0D, 0x01, 0x01, 0x05 };
static const unsigned char OID_sha1WithDSA[] =
{ 0x2A, 0x86, 0x48, 0xCE, 0x38, 0x04, 0x03 };
static const unsigned char OID_sha256WithECDSA[] =
{ 0x2A, 0x86, 0x48, 0xCE, 0x3D, 0x04, 0x03, 0x02 };
static int parse_algorithm_identifier( signatureAlgorithmIdentifier *target,
struct asn1struct *source )
{
struct asn1struct *oid = ( struct asn1struct * ) source->children;
...
else if ( !memcmp( oid->data, OID_sha256WithECDSA, oid->length ) )
{
*target = sha256WithECDSA;
}
As you can see, there's nothing particularly complex or surprising here; you just recognize a new OID.
Although parsing the public key is not necessarily complex, it's odd in the context of ASN.1. An RSA public key is a bit-string representation of two numbers n and e, both given in an ASN.1 structure, and both properly ASN.1 encoded with a tag and a length. A DSA public key is similarly encoded as a bit string representation of ASN.1 encoded data. An ECDSA key, however, is not. Although the public key is an ASN.1 bit string, it's not an ASN.1 encoded structure, but a different, incompatible ASNI X9.62 encoded structure. This was probably done for compatibility with existing software, or perhaps it was done in the IETF's ongoing quest to ensure that every specification ever written for any purpose is somehow relevant to TLS.
Fortunately, the X9.62 structure — at least in the context of an ECDSA public key — isn't too hard to parse. The first byte is an identifier whose value is either 3, meaning compressed, or 4, meaning uncompressed. An uncompressed ECC point lists the x and y values back-to-back with no delimiter or length declaration. The parser must split the data in half and recognize that the first half is x and the last half is y.
What about the compressed format? Well, if you think about it, it's somewhat redundant to provide the y value. After all, an elliptic curve is defined by an algebraic formula that describes y in terms of x. Technically speaking, all you really need to know is the x value, along with the curve parameters themselves, and you can compute the y value. The only wrinkle here is that there are two possible y values for a given x — one positive and one negative — because the formula is y2 = x3 + ax + b. A compressed point, then, is just the x value with a single extra bit indicating whether the y value is the positive or the negative one; the implementation must multiply out the elliptic curve to recover y. This book only deals with uncompressed points.
Modify the algorithm identifier as shown in Listing 9-34 to recognize the new public key algorithm type, and modify parse_public_key_info from Listing 5-19 as shown in Listing 9-35 to properly parse ECDSA public keys.
Listing 9-34: "x509.h" ECDSA algorithm identifier
typedef enum
{
rsa,
dsa,
dh,
ecdsa
}
algorithmIdentifier;
typedef struct
{
algorithmIdentifier algorithm;
...
elliptic_curve ecdsa_curve;
point ecdsa_public_key;
}
public_key_info;
Listing 9-35: "x509.c" parse_public_key_info with ECDSA support
static const unsigned char OID_RSA[] =
{ 0x2A, 0x86, 0x48, 0x86, 0xF7, 0x0D, 0x01, 0x01, 0x01 };
static const unsigned char OID_DSA[] =
{ 0x2A, 0x86, 0x48, 0xCE, 0x38, 0x04, 0x01 };
static const unsigned char OID_DH[] =
{ 0x2A, 0x86, 0x48, 0xCE, 0x3E, 0x02, 0x01 };
static const unsigned char OID_ECDSA[] =
{ 0x2A, 0x86, 0x48, 0xCE, 0x3D, 0x02, 0x01 };
// A.K.A. secp192R1, AKA NIST P-192 static const unsigned char OID_PRIME192V1[] = { 0x2A, 0x86, 0x48, 0xCE, 0x3D, 0x03, 0x01, 0x01 }; static int parse_public_key_info( public_key_info *target, struct asn1struct *source ) { ... public_key = source->children->next; if ( !memcmp( oid->data, &OID_ECDSA, sizeof( OID_ECDSA ) ) ) { // TODO this only supports named curves (actually, only one specific // curve). struct asn1struct *curve = oid->next; target->algorithm = ecdsa; if ( !memcmp( curve->data, &OID_PRIME192V1, sizeof( OID_PRIME192V1 ) ) ) { // TODO generate a mapping of OIDs to curve names if ( get_named_curve( "prime192v1", &target->ecdsa_curve ) ) { return 1; } } else { fprintf( stderr, "Error, unsupported named curve in ECDSA certificate\n" ); return 1; } load_huge( &target->ecdsa_public_key.x, public_key->data + 2, ( public_key->length - 2 ) / 2 ); load_huge( &target->ecdsa_public_key.y, ( public_key->data + 2 ) + ( ( public_key->length - 2 ) / 2 ), ( public_key->length - 2 ) / 2 ); return 0; } ...
As you can see, the certificate doesn't refer to curve names by their actual names; it uses another alias in OID form. The named curve OID is inserted after the public key OID — if the OID is recognized, it's converted into a string curve name and the curve is populated into the ecdsa_curve parameter of the supplied public_key_info instance.
Now, if you go back and look at Listing 5-19 that parses the RSA public key info or Listing 5-32 that parses the DSA public key info, you see that the next step in both cases is to ASN.1 parse the bit string that contains the public key info. ECDSA keys are not ASN.1 encoded. They're instead encoded as shown in Figure 9-6.
Figure 9-6: X9.62 ECC point encoding

The end of Listing 9-35 illustrates this parsing. Because every byte-aligned ASN.1 bit string must begin with a leading 0 byte as discussed in Chapter 5, the parsing must skip over this 0 byte and the "compressed/uncompressed" declaration. The remainder is split down the middle and the first half becomes the x point and the second half the y point.
Recall that the function parse_x509_chain, introduced in Listing 6-29, is responsible for parsing a certificate and copying its public key info into that of the TLSParameters structure. This must be modified as shown in Listing 9-36 to recognize the case of ECDSA.
Listing 9-36: "x509.c" parse_x509_chain with ECDSA support
char *parse_x509_chain( unsigned char *buffer,
int pdu_length,
public_key_info *server_public_key )
{
...
switch ( server_public_key->algorithm )
{
...
case ecdsa:
set_huge( &server_public_key->ecdsa_curve.a, 0 );
set_huge( &server_public_key->ecdsa_curve.b, 0 );
set_huge( &server_public_key->ecdsa_curve.G.x, 0 );
set_huge( &server_public_key->ecdsa_curve.G.y, 0 );
set_huge( &server_public_key->ecdsa_curve.p, 0 );
set_huge( &server_public_key->ecdsa_curve.n, 0 );
set_huge( &server_public_key->ecdsa_public_key.x, 0 );
set_huge( &server_public_key->ecdsa_public_key.y, 0 );
copy_huge( &server_public_key->ecdsa_curve.a,
&certificate.tbsCertificate.subjectPublicKeyInfo.ecdsa_curve.a );
copy_huge( &server_public_key->ecdsa_curve.b,
&certificate.tbsCertificate.subjectPublicKeyInfo.ecdsa_curve.b );
copy_huge( &server_public_key->ecdsa_curve.G.x,
&certificate.tbsCertificate.subjectPublicKeyInfo.ecdsa_curve.G.x );
copy_huge( &server_public_key->ecdsa_curve.G.y,
&certificate.tbsCertificate.subjectPublicKeyInfo.ecdsa_curve.G.y );
copy_huge( &server_public_key->ecdsa_curve.p,
&certificate.tbsCertificate.subjectPublicKeyInfo.ecdsa_curve.p );
copy_huge( &server_public_key->ecdsa_curve.n, &certificate.tbsCertificate.subjectPublicKeyInfo.ecdsa_curve.n ); copy_huge( &server_public_key->ecdsa_public_key.x, &certificate.tbsCertificate.subjectPublicKeyInfo.ecdsa_public_key.x ); copy_huge( &server_public_key->ecdsa_public_key.y, &certificate.tbsCertificate.subjectPublicKeyInfo.ecdsa_public_key.y ); break; ...
What about the ECDSA signature itself? Actually, there's no special handling there; an ECDSA signature is two numbers, r and s, just like a DSA signature. There's no need for a special handler. Modify parse_x509_certificate to recognize this case as shown in Listing 9-37.
Listing 9-37: "x509.c" parse_x509_certificate with ECDSA signatures
int parse_x509_certificate( const unsigned char *buffer,
const unsigned int certificate_length,
signed_x509_certificate *parsed_certificate )
{
...
switch ( parsed_certificate->algorithm )
{
case md5WithRSAEncryption:
case shaWithRSAEncryption:
if ( parse_rsa_signature_value( parsed_certificate, signatureValue ) )
{
return 42;
}
break;
case shaWithDSA:
case sha256WithECDSA:
if ( parse_dsa_signature_value( parsed_certificate, signatureValue ) )
{
return 42;
}
break;
...
switch ( parsed_certificate->algorithm )
{
...
case sha256WithECDSA:
new_sha256_digest( &digest );
break;
Remember that there's no particular reason that a certificate containing an ECDSA public key must be signed using ECDSA. In fact, it's likely that a commercially signed certificate is going to be signed using RSA because that's all that commercial CAs currently support.
You're unlikely to be able to find a server that presents an ECDSA certificate. However, as of version 1.0.0, OpenSSL enables you to create a self-signed ECDSA, certificate. First, generate a set of parameters; in other words, select a named curve:
[jdavies@localhost ssl]$ openssl ecparam -name prime192v1 -out ecprime192v1.pem
As you can see from the ASN.1 output, there's nothing in there except the OID of the named curve:
[jdavies@localhost ssl]$ ./asn1 -pem ecprime192v1.pem 0000: OBJECT IDENTIFIER (6:8) 2a 86 48 ce 3d 03 01 01
However, you can use this as input to the req command to generate a new ECDSA certificate:
[jdavies@localhost ssl]$ openssl req -x509 -newkey ec:ecprime192v1.pem \ -keyout ecdsa_key.pem -out ecdsa_cert.pem -sha256
ECDHE Support in TLS
To actually make use of this new certificate, you should extend the TLS implementation to support the ECDHE_ECDSA cipher suites. Not every cipher algorithm is supported with ECDHE_ECDSA key exchange (nor ECDH_RSA). In fact, the only algorithms standardized by RFC 4492 are RC4, 3DES, AES-128, and AES-256. These suites are given the identifiers 0xC007–0xC00A. Because these are large numbers, you should instantiate them in the init_tls function just like the AEAD ciphers from Listing 9-27. The initialization of TLS_ECDHE_ECDSA_WITH_AES_128_CBC_SHA is shown in Listing 9-38.
Listing 9-38: "tls.c" init_tls with ECDHE_ECDSA support
void init_tls()
{
...
suites[ TLS_ECDHE_ECDSA_WITH_AES_128_CBC_SHA ].id =
TLS_ECDHE_ECDSA_WITH_AES_128_CBC_SHA;
suites[ TLS_ECDHE_ECDSA_WITH_AES_128_CBC_SHA ].block_size = 16;
suites[ TLS_ECDHE_ECDSA_WITH_AES_128_CBC_SHA ].IV_size = 16;
suites[ TLS_ECDHE_ECDSA_WITH_AES_128_CBC_SHA ].key_size = 16;
suites[ TLS_ECDHE_ECDSA_WITH_AES_128_CBC_SHA ].hash_size = SHA1_BYTE_SIZE;
suites[ TLS_ECDHE_ECDSA_WITH_AES_128_CBC_SHA ].bulk_encrypt = aes_128_encrypt;
suites[ TLS_ECDHE_ECDSA_WITH_AES_128_CBC_SHA ].bulk_decrypt = aes_128_decrypt;
suites[ TLS_ECDHE_ECDSA_WITH_AES_128_CBC_SHA ].new_digest = new_sha1_digest;
suites[ TLS_ECDHE_ECDSA_WITH_AES_128_CBC_SHA ].aead_encrypt = NULL;
suites[ TLS_ECDHE_ECDSA_WITH_AES_128_CBC_SHA ].aead_decrypt = NULL;
}
You should have no problem filling in the remaining cipher suites; they all use SHA-1 MACs, so the only change is the bulk_encrypt and bulk_decrypt function pointers. There are no currently defined cipher suites that use both AEAD encryption and ECC key exchange.
If you look at the typical SSL handshake shown in Figure 6-1, you can see that the key exchange portion affects three messages: the certificate, which was addressed earlier, the client key exchange, and, optionally, the server key exchange. (It also affects the client certificate and client certificate verify, if client authentication is being used). Because the cipher suites being examined here are ECDHE cipher suites, the server is sending a key exchange message.
To complete its side of the ECDHE key exchange, the server must select a curve, choose a random number b, multiply the curve's generator point by b, and send the resulting point on to the client. It must also, of course, hang on to b so that it can multiply the client's response point by this amount. Therefore, the server key exchange must consist of a curve — either explicitly or by name — and a point. Note that the selected curve does not have to be the same as the curve in the certificate. As always, the whole server key exchange is signed according to the previously exchanged certificate, unless an anonymous cipher suite is being used.
To support ECDH, you need a place to put the ephemeral key parameters:
- Modify the TLSParameters, as shown in Listing 9-39.
- Modify the parse_server_key_exchange function from Listing 8-19 to read and populate these new parameters as shown in Listing 9-40.
Listing 9-40: "tls.c" parse_server_key_exchange with ECDH support
typedef enum
{
secp192r1 = 19,
secp256r1 = 23
}
named_curve;
typedef enum
{
explicit_prime = 1, explicit_char2 = 2, named = 3 } ec_curve_type; typedef enum { compressed = 3, uncompressed = 4 } ec_point_type; static char *parse_server_key_exchange( unsigned char *read_pos, TLSParameters *parameters ) { short length; int i; unsigned char *dh_params = read_pos; HashAlgorithm hash_alg; SignatureAlgorithm sig_alg; hash_alg = read_pos[ 0 ]; sig_alg = read_pos[ 1 ]; read_pos += 2; switch ( parameters->pending_send_parameters.suite ) { case TLS_ECDHE_ECDSA_WITH_AES_128_CBC_SHA: { unsigned char curve_type; unsigned char curve; unsigned char public_key_length; unsigned char point_type; read_pos = read_buffer( ( void * ) &curve_type, read_pos, 1 ); switch ( curve_type ) { case named: // named curve takes up two bytes, but only one is populated read_pos += 1; read_pos = read_buffer( ( void * ) &curve, read_pos, 1 ); switch ( curve ) { case secp256r1: get_named_curve( "prime256v1", ¶meters->server_ecdh_params ); break; default: fprintf( stderr, "error, unsupported named curve %d\n", curve );
return NULL; } break; default: fprintf( stderr, "Error, unsupported curve type %d.\n", curve_type ); return NULL; } // Followed by a length-delimited (opaque) public key. read_pos = read_buffer( ( void * ) &public_key_length, read_pos, 1 ); read_pos = read_buffer( ( void * ) &point_type, read_pos, 1 ); if ( point_type == uncompressed ) { load_huge( ¶meters->server_ecdh_key.x, read_pos, ( public_key_length - 1 ) / 2 ); load_huge( ¶meters->server_ecdh_key.y, ( read_pos + ( ( public_key_length - 1 ) / 2 ) ), ( ( public_key_length - 1 ) / 2 ) ); read_pos += ( public_key_length - 1 ); // Read and verify the signature memcpy( &length, read_pos, 2 ); length = ntohs( length ); read_pos += 2; if ( !verify_signature( dh_params, ( read_pos - 2 - dh_params ), read_pos, length, parameters ) ) { return NULL; } read_pos += length; } else { printf( "point type %d\n", point_type ); fprintf( stderr, "Error, compressed ECDH public keys not supported.\n" ); return NULL; } break; default: // XXX assume DHE if not ECDHE for ( i = 0; i < 4; i++ ) {
Most of the logic here surrounds erroring out if any of the unsupported options are presented. This code handles the simplest case, when the server uses a named curve and presents the public key in uncompressed format. The first part of this is pretty similar to the public key parsing in Listing 9-35, which is unsurprising because both functions are parsing an ECC public key. Although they are both for different algorithms — one for ECDSA, and the other for ECDH — the key itself is the same in both cases; a curve followed by a point on that curve. Both functions only accept named curves, although an option is defined in the specification to accept explicit curves. Of course, the public key parsing routine in the certificate code is looking for an OID. TLS has a simpler means of naming curves — each one is assigned a unique two-byte identifier. At present, only 25 are defined, but expect more to be defined over time.
The curve itself, whether presented by name or explicitly, is followed by the point that identifies the public key. This is encoded in the exact same ANSI X9.62 format that the certificate is coded in — one byte compressed/uncompressed marker, with the remaining bytes split in half between x and y.
Finally, the whole parameter list — the curve specification and the public key point — are signed using the certificate's private key, and the signature follows the server key exchange parameters. This whole thing is passed into verify_signature. In the case of ECDSA, just like DSA, the signature is two values r and s, encoded in ASN.1 DER format. Because an ECDSA signature looks just like a DSA signature, you can reuse a lot of the code from Listing 8-26 to verify an ECDSA signature, as shown in Listing 9-41.
Listing 9-41: "tls.c" verify_signature with ECDSA support
int verify_signature( unsigned char *message,
int message_len,
unsigned char *signature,
int signature_len,
TLSParameters *parameters )
{
...
else if ( ( parameters->server_public_key.algorithm == dsa ) ||
( parameters->server_public_key.algorithm == ecdsa ) )
{
int verified;
...
asn1free( &decoded_signature );
if ( parameters->server_public_key.algorithm == dsa )
{
verified = dsa_verify( ¶meters->server_public_key.dsa_parameters,
¶meters->server_public_key.dsa_public_key,
( unsigned char * ) sha_digest.hash,
SHA1_BYTE_SIZE,
&received_signature );
}
else
{
digest_ctx sha256_digest;
new_sha256_digest( &sha256_digest ); update_digest( &sha256_digest, parameters->client_random, RANDOM_LENGTH ); update_digest( &sha256_digest, parameters->server_random, RANDOM_LENGTH ); update_digest( &sha256_digest, message, message_len ); finalize_digest( &sha256_digest ); verified = ecdsa_verify( ¶meters->server_public_key.ecdsa_curve, ¶meters->server_public_key.ecdsa_public_key, sha256_digest.hash, SHA256_BYTE_SIZE, &received_signature ); } if ( !verified ) { free_huge( &received_signature.r ); free_huge( &received_signature.s ); return 0; }
NOTE The ECDSA verification routine itself was shown in Listing 4-40.
To support ECDHE on the client side, in the most common case of server-only authentication, the only thing left is to actually perform the key exchange. Modify send_client_key_exchange from Listing 6-33 to recognize ECDHE as an option, as shown in Listing 9-42.
Listing 9-42: "tls.c" send_client_key_exchange with ECDHE support
static int send_client_key_exchange( int connection, TLSParameters *parameters )
{
...
switch ( parameters->pending_send_parameters.suite ) {
case TLS_NULL_WITH_NULL_NULL:
...
case TLS_ECDHE_ECDSA_WITH_AES_128_CBC_SHA:
premaster_secret_len = parameters->server_ecdh_params.p.size;
premaster_secret = malloc( premaster_secret_len );
key_exchange_message_len = ecdh_key_exchange(
¶meters->server_ecdh_key, ¶meters->server_ecdh_params,
premaster_secret, &key_exchange_message );
break;
default:
break;
}
The rest of send_client_key_exchange doesn't change in the case of ECDH; the key exchange function itself populates the handshake message and the premaster secret. All that's left is to implement the ECDH key exchange itself using the curve and the point specified by the server in the server key exchange, which is shown in Listing 9-43.
Listing 9-43: "tls.c" ecdh_key_exchange
int ecdh_key_exchange( point *server_ecdh_key,
elliptic_curve *curve,
unsigned char *premaster_secret,
unsigned char **key_exchange_message )
{
ecc_key A;
point K;
set_huge( &A.d, 4 ); // TODO this should be random, and larger
set_huge( &A.Q.x, 0 );
set_huge( &A.Q.y, 0 );
copy_huge( &A.Q.x, &curve->G.x );
copy_huge( &A.Q.y, &curve->G.y );
multiply_point( &A.Q, &A.d, &curve->a, &curve->p );
// Response is now A.Q; put that into "key_exchange_message" as an
// explicit point
// XXX x & y must both be the same size for the encoding to work.
*key_exchange_message = ( unsigned char * ) malloc( A.Q.x.size +
A.Q.y.size + 2 );
(*key_exchange_message)[ 0 ] = A.Q.x.size + A.Q.y.size + 1;
(*key_exchange_message)[ 1 ] = 0x04;
memcpy( (*key_exchange_message) + 2, A.Q.x.rep, A.Q.x.size );
memcpy( (*key_exchange_message) + 2 + A.Q.x.size, A.Q.y.rep, A.Q.y.size );
// Now compute the premaster secret from the server's point
set_huge( &K.x, 0 );
set_huge( &K.y, 0 );
copy_huge( &K.x, &server_ecdh_key->x );
copy_huge( &K.y, &server_ecdh_key->y );
multiply_point( &K, &A.d, &curve->a, &curve->p );
// The premaster secret is in K.x
memcpy( premaster_secret, K.x.rep, curve->p.size );
free_huge( &K.x );
free_huge( &K.y );
free_huge( &A.d );
free_huge( &A.Q.x );
free_huge( &A.Q.y );
return A.Q.x.size + A.Q.y.size + 3;
}
The client responsibility in an ECDH key exchange — just as in an integer DH key exchange — is lighter than the server's; the client must just respond with a point. The implementation presented here is hardcoded to return the generator point * 4. A proper, secure implementation would naturally choose much larger numbers, and choose them randomly. The resulting point is encoded in ANSI X9.62 format; this is the handshake message itself. This same "secret" value 4 is then multiplied by the server's point; this is the shared, premaster secret. You may want to compare this to dh_key_exchange in Listing 6-43. In effect, the mod_pow calls are replaced by point multiplication calls, and the shared secret is retrieved from the x-coordinate of the shared point. Otherwise, these routines are very similar.
ECC Client Hello Extensions
As you might imagine, it would be a shame if the client and the server went to all the trouble to try to perform an ECC key exchange only to find out that the server wanted to use a named curve that the client didn't support. It would be even worse to find out that the client and the server do share a named curve, but the server keeps picking the wrong one because it doesn't know which one the client supports.
To address this, RFC 4492 defines a new client hello extension, extension 10, which enables the client to list the named curves it supports. It uses the same two-byte characters for the curves that the server key exchange uses. The special values 0xFF01 and 0xFF02 denote explicit prime curves and explicit characteristic 2 curves, respectively. If either of these two values appears in the supported curves extension, this indicates that the client can accept explicit curves. The specification is silent on what the server should do if the client presents an elliptic-curve cipher suite, but does not indicate which named curves it supports. OpenSSL currently just defaults to secp256r1 in this case.
In addition, RFC 4492 defines a second client hello extension, extension 11, that enables the client to indicate what point formats it supports — compressed, uncompressed, or both. It would be strange for a client to support compressed but not uncompressed, and the specification states that all implementations must support uncompressed points, so it's somewhat redundant for the client to inform the server that it can support uncompressed points, but you can do so if you like.
The Current State of TLS 1.2
One thing you may have noticed about this chapter was the conspicuous lack of examples. TLS 1.2 is still very new and hasn't found its way into very many TLS implementations yet. OpenSSL doesn't yet support it, although all the pieces are in place. GnuTLS does support TLS 1.2, but it's not enabled by default. To run a TLS 1.2-aware server:
[jdavies@localhost ssl]$ gnutls-serv -p 8443 --x509fmtder --x509certfile cert.der \ --x509keyfile key.der --protocols TLS1.2
GnuTLS doesn't have an option to supply a password-protected key file, so you have to remove password protection from the key file if you've enabled it as is shown in Chapter 7. At the time of this writing, version 2.8.6 is also not quite RFC 5246 compliant, either; it's compliant to an earlier, draft specification. The most glaring difference is that it uses SHA-1 instead of SHA-256 to compute the PRF and the finalize data. This may be corrected by the time you read this, so you may want to double-check and see if this has been addressed yet. Even with TLS 1.2 support, it doesn't yet support any AEAD or ECC cipher suites.
OpenSSL 1.0.0 does support ECC, but only in the context of TLS 1.0. It doesn't yet even support TLS 1.1. To run an ECDHE-ECDSA-capable OpenSSL server, you must have an ECDSA certificate as discussed previously, and then run:
[jdavies@localhost openssl-1.0.0]$ apps/openssl s_server -tls1 -cipher \ ECDHE-ECDSA-AES128-SHA -cert ecdsacert.pem -key ecdsakey.pem -accept 8443
If you want to test the code in the previous section against this server, though, you need to first ensure that everything else is TLS 1.0 compliant.
