CHAPTER 4

Authenticating Communications Using Digital Signatures

In Chapter 3, you examined public key cryptography in detail. Public key cryptography involves generating two mathematically related keys, one of which can be used to encrypt a value and the other of which can be used to decrypt a value previously encrypted with the other. One important point to note is that it technically doesn't matter which key you use to perform the encryption, as long as the other one is available to perform the decryption. The RSA algorithm defines a public key that is used to encrypt, and a private key that is used to decrypt. However, the algorithm works if you reverse the keys — if you encrypt something with the private key, it can be decrypted with — and only with — the public key.

At first glance, this doesn't sound very useful. The public key, after all, is public. It's freely shared with anybody and everybody. Therefore, if a value is encrypted with the private key, it can be decrypted by anybody and everybody as well. However, the nature of public/private keypairs is such that it's also impossible — or, to be technically precise, mathematically infeasible — for anybody except the holder of the private key to generate something that can be decrypted using the public key. After all, the encryptor must find a number c such that c^e%n = m for some arbitrary m. By definition, c = m^d satisfies this condition and it is believed to be computationally infeasible to find another such number c.

As a result, the private key can also be used to prove identity. The holder of the private key generates a message m, and sends it to the receiver (unencrypted). Then the holder of the private key encrypts m using the private key (d,n) and sends the resulting c to the receiver. The receiver uses the public key (e,n) to "decrypt" c. If the decrypted value is exactly equal to m, the message is verified. The receiver is confident that it was truly sent by somebody with access to the private key. Note that, in this scenario, anybody can read m — it is sent in cleartext. In this case, you're just proving identity. Of course, this sort of digital signature can be easily combined with encryption. The sender could encrypt the request, sign the encrypted value, and send that on for the receiver to verify. An eavesdropper could, of course, decrypt the signature, but all he would get is the encrypted string, which he can't decrypt without the key.

There's another benefit to this approach as well. If anything changed in transit — due to a transmission error or a malicious hacker — the decrypted value won't match the signature. This guarantees not only that the holder of the private key sent it, but that what was received is exactly what was sent.

There's one problem with this approach to digital signatures, though. You've essentially doubled, at least, the length of each message. And, as you recall from the previous chapter, public key cryptography is too slow for large blocks of information. In general, you use public key operations to encode a symmetric key for subsequent cryptography operations. Obviously, you can't do this for digital signatures; you're trying to prove that somebody with access to the private key generated the message. What you need is a shortened representation of the message that can be computed by both sides. Then the sender can encrypt that using the private key, and the receiver can compute the same shortened representation, decrypt it using the public key and verify that they're identical.

Using Message Digests to Create Secure Document Surrogates

Such a shortened representation of a message is referred to as a message digest. The simplest form of a message digest is a checksum. Given a byte array of arbitrary length, add up the integer value of each byte (allowing the sum to overflow), and return the total, for example, Listing 4-1.

Listing 4-1: checksum

int checksum( char *msg )
{
 int sum = 0;
 int i;

 for ( i = 0; i < strlen( msg ); i++ )
 {
   sum += msg[ i ];
 }

return sum;
}

Here, the message "abc" sums to 294 because, in ASCII, a = 97, b = 98 and c = 99; "abd" sums to 295. Because you just ignore overflow, you can compute a digest of any arbitrarily sized message.

The problem with this approach is that it can be easily reversed. Consider the following scenario: I want to send a message that says, "Please transfer $100 to account 123," to my bank. My bank wants to ensure that this message came from me, so I digitally sign it. First I compute the checksum of this message: 2,970. I then use my private key to compute the signature. Using the mini-key pair e = 79, d = 1019, n = 3337 from Chapter 3, this encodes (without any padding) to 2970¹⁰¹⁹ % 3337 = 2552. The bank receives the message, computes the same checksum, decodes 2552 using the public key and computes 2552⁷⁹ % 3337 = 2970. Because the computed checksum matches the encrypted checksum, the message can be accepted as authentic because nobody else can solve x⁷⁹ % 3337 = 2970.

However, there's a problem with this simple checksum digest routine. Although an attacker who might want to submit, "Please transfer $1,000,000 to account 3789," which sums to 3171, is not able to solve x⁷⁹ % 3337 = 3171, he can instead look for ways to change the message itself so that it sums to 2970. Remember that the signature itself is public, transmitted over a clear channel. If the attacker can do this, he can reuse my original signature of 2552. As it turns out, it's not hard to work backward from 2970 to engineer a collision by changing the message to "Transfer $1,000,000 to account 3789 now!" (Notice that I dropped the "please" from the beginning and inserted "now!") A bank employee might consider this rude, but the signature matches. You may have to play tricks with null terminators and backspace characters to get the messages to collide this way, but for $1,000,000, an attacker would consider it well worth the effort. Note that this would have been a vulnerability even if you had encoded the whole message rather than the output of the digest algorithm.

Therefore, for cryptographic security, you need a more secure message digest algorithm. Although it may seem that cryptography would be the hardest category of secure algorithms to get right, message digests actually are. The history of secure message digest algorithms is littered with proposals that were later found to be insecure — that is, not properly collision resistant.

Implementing the MD5 Digest Algorithm

One of the earliest secure message digest algorithms in the literature is MD2 (MD1 appears never to have been released). It was followed by MD4 (rather than MD3), which was finally followed by MD5 and is the last of the MD series of message digest algorithms. All were created by Dr. Ron Rivest, who was also one-third of the RSA team.

Understanding MD5

The goal of MD5, specified in RFC 1321, or any secure hashing algorithm, is to reduce an arbitrarily sized input into an n-bit hash in such a way that it is very unlikely that two messages, regardless of length or content, produce identical hashes — that is, collide — and that it is impossible to specifically reverse engineer such a collision. For MD5, n = 128 bits. This means that there are 2¹²⁸ possible MD5 hashes. Although the input space is vastly larger than this, 2¹²⁸ makes it highly unlikely that two messages will share the same MD5 hash. More importantly, it should be impossible, assuming that MD5 hashes are evenly, randomly distributed, for an attacker to compute a useful message that collides with another by way of brute force.

MD5 operates on 512-bit (64-byte) blocks of input. Each block is reduced to a 128-bit (16-byte) hash. Obviously, with such a 4:1 ratio of input blocks to output blocks, there will be at least a one in four chance of a collision. The challenge that MD5's designer faced is making it difficult or impossible to work backward to find one.

If the message to be hashed is greater than 512 bits, each 512-bit block is hashed independently and the hashes are added together, being allowed to overflow, and the result is the final sum. This obviously creates more potential for collisions.

Unlike cryptographic algorithms, though, message digests do not have to be reversible — in fact, this irreversibility is the whole point. Therefore, algorithm designers do not have to be nearly as cautious with the number and type of operations they apply to the input. The more operations, in fact, the better; this is because operations make it more difficult for an attacker to work backward from a hash to a message. MD5 applies 64 transformations to each input block. It first splits the input into 16 32-bit chunks, and the current hash into four 32-bit chunks referred to tersely as A, B, C, and D in the specification. Most of the operations are done on A, B, C, and D, which are subsequently added to the input. The 64 operations themselves consist of 16 repetitions of the four bit flipping functions F, G, H, and I as shown in Listing 4-2.

Listing 4-2: "md5.c" bit manipulation routines

unsigned int F( unsigned int x, unsigned int y, unsigned int z )
{
 return ( x & y ) | ( ~x & z );
}

unsigned int G( unsigned int x, unsigned int y, unsigned int z )
{
 return ( x & z ) | ( y & ~z );
}

unsigned int H( unsigned int x, unsigned int y, unsigned int z )
{
 return ( x ^ y ^ z );
}

unsigned int I( unsigned int x, unsigned int y, unsigned int z )
{
 return y ^ ( x | ~z );
}

The purpose of these functions is simply to shuffle bits in an unpredictable way; don't look for any deep meaning here.

Notice that this is implemented using unsigned integers. As it turns out, MD5, unlike any of the other cryptographic algorithms in this book, operates on little-endian numbers, which makes implementation a tad easier on an Intel-based machine — although MD5 has an odd concept of "little endian" in places.

The function F is invoked 16 times — once for each input block — and then G is invoked 16 times, and then H, and then I. So, what are the inputs to F, G, H, and I? They're actually permutations of A, B, C, and D — remember that the hash was referred to as A, B, C, and D. The results of F, G, H, and I are added to A, B, C, and D along with each of the input blocks, as well as a set of constants, shifted, and added again. In all cases, adds are performed modulo 32 — that is, they're allowed to silently overflow in a 32-bit register. After all 64 operations, the final values of A, B, C, and D are concatenated together to become the hash of a 512-bit input block.

More specifically, each of the 64 transformations on A, B, C, and D involve applying one of the four functions F, G, H, or I to some permutation of A, B, C, or D, adding it to the other, adding the value of input block (i % 4), adding the value of 4294967296 * abs(sin(i)), rotating by a per-round amount, and adding the whole mess to yet one more of the A, B, C, or D hash blocks.

A Secure Hashing Example

If this is all making your head spin, it's supposed to. Secure hashing algorithms are necessarily complex. In general, they derive their security from their complexity:

1. Define a ROUND macro that will be expanded 64 times, as shown in Listing 4-3.

   Listing 4-3: "md5.c" ROUND macro

   #define BASE_T 4294967296.0
   
   #define ROUND( F, a, b, c, d, k, s, i ) \
   a = ( a + F( b, c, d ) + x[ k ] + \

   ( unsigned int ) ( BASE_T * fabs( sin( ( double ) i ) ) ) ); \
   a = ( a << s ) | ( a >> ( 32 - s ) ); \
   a += b;

   This macro takes as input the function to be performed, a, b, c and d; a value k which is an offset into the input; a value s which is an amount to rotate; and a value i which is the operation number. Notice that i is used to compute the value of 4294967296 * abs(sin(i)) on each invocation. Technically speaking, these values ought to be precomputed because they'll never change.

2. Using this macro, the MD5 block operation function is straightforward, if a bit tedious, to code, as in Listing 4-4:

   Listing 4-4: "md5.c" md5_block_operate function

   // Size of MD5 hash in ints (128 bits)
   #define MD5_RESULT_SIZE 4
   
   void md5_block_operate( const unsigned char *input,
                  unsigned int hash[ MD5_RESULT_SIZE ] )
   {
    unsigned int a, b, c, d;
    int j;
    unsigned int x[ 16 ];
   
    a = hash[ 0 ];
    b = hash[ 1 ];
    c = hash[ 2 ];
    d = hash[ 3 ];
   
    for ( j = 0; j < 16; j++ )
    {
       x[ j ] = input[ ( j * 4 ) + 3 ] << 24 |
                          input[ ( j * 4 ) + 2 ] << 16 |
                          input[ ( j * 4 ) + 1 ] << 8 |
                          input[ ( j * 4 ) ];
    }
   
    // Round 1
    ROUND( F, a, b, c, d, 0, 7, 1 );
    ROUND( F, d, a, b, c, 1, 12, 2 );
    ROUND( F, c, d, a, b, 2, 17, 3 );
    ROUND( F, b, c, d, a, 3, 22, 4 );
    ROUND( F, a, b, c, d, 4, 7, 5 );
    ROUND( F, d, a, b, c, 5, 12, 6 );
    ROUND( F, c, d, a, b, 6, 17, 7 );
    ROUND( F, b, c, d, a, 7, 22, 8 );
    ROUND( F, a, b, c, d, 8, 7, 9 );
    ROUND( F, d, a, b, c, 9, 12, 10 );

   ROUND( F, c, d, a, b, 10, 17, 11 );
    ROUND( F, b, c, d, a, 11, 22, 12 );
    ROUND( F, a, b, c, d, 12, 7, 13 );
    ROUND( F, d, a, b, c, 13, 12, 14 );
    ROUND( F, c, d, a, b, 14, 17, 15 );
    ROUND( F, b, c, d, a, 15, 22, 16 );
   
    // Round 2
    ROUND( G, a, b, c, d, 1, 5, 17 );
    ROUND( G, d, a, b, c, 6, 9, 18 );
    ROUND( G, c, d, a, b, 11, 14, 19 );
    ROUND( G, b, c, d, a, 0, 20, 20 );
    ROUND( G, a, b, c, d, 5, 5, 21 );
    ROUND( G, d, a, b, c, 10, 9, 22 );
    ROUND( G, c, d, a, b, 15, 14, 23 );
    ROUND( G, b, c, d, a, 4, 20, 24 );
    ROUND( G, a, b, c, d, 9, 5, 25 );
    ROUND( G, d, a, b, c, 14, 9, 26 );
    ROUND( G, c, d, a, b, 3, 14, 27 );
    ROUND( G, b, c, d, a, 8, 20, 28 );
    ROUND( G, a, b, c, d, 13, 5, 29 );
    ROUND( G, d, a, b, c, 2, 9, 30 );
    ROUND( G, c, d, a, b, 7, 14, 31 );
    ROUND( G, b, c, d, a, 12, 20, 32 );
   
    // Round 3
    ROUND( H, a, b, c, d, 5, 4, 33 );
    ROUND( H, d, a, b, c, 8, 11, 34 );
    ROUND( H, c, d, a, b, 11, 16, 35 );
    ROUND( H, b, c, d, a, 14, 23, 36 );
    ROUND( H, a, b, c, d, 1, 4, 37 );
    ROUND( H, d, a, b, c, 4, 11, 38 );
    ROUND( H, c, d, a, b, 7, 16, 39 );
    ROUND( H, b, c, d, a, 10, 23, 40 );
    ROUND( H, a, b, c, d, 13, 4, 41 );
    ROUND( H, d, a, b, c, 0, 11, 42 );
    ROUND( H, c, d, a, b, 3, 16, 43 );
    ROUND( H, b, c, d, a, 6, 23, 44 );
    ROUND( H, a, b, c, d, 9, 4, 45 );
    ROUND( H, d, a, b, c, 12, 11, 46 );
    ROUND( H, c, d, a, b, 15, 16, 47 );
    ROUND( H, b, c, d, a, 2, 23, 48 );
   
    // Round 4
    ROUND( I, a, b, c, d, 0, 6, 49 );
    ROUND( I, d, a, b, c, 7, 10, 50 );
    ROUND( I, c, d, a, b, 14, 15, 51 );
    ROUND( I, b, c, d, a, 5, 21, 52 );
    ROUND( I, a, b, c, d, 12, 6, 53 );
    ROUND( I, d, a, b, c, 3, 10, 54 );

   ROUND( I, c, d, a, b, 10, 15, 55 );
    ROUND( I, b, c, d, a, 1, 21, 56 );
    ROUND( I, a, b, c, d, 8, 6, 57 );
    ROUND( I, d, a, b, c, 15, 10, 58 );
    ROUND( I, c, d, a, b, 6, 15, 59 );
    ROUND( I, b, c, d, a, 13, 21, 60 );
    ROUND( I, a, b, c, d, 4, 6, 61 );
    ROUND( I, d, a, b, c, 11, 10, 62 );
    ROUND( I, c, d, a, b, 2, 15, 63 );
    ROUND( I, b, c, d, a, 9, 21, 64 );
   
    hash[ 0 ] += a;
    hash[ 1 ] += b;
    hash[ 2 ] += c;
    hash[ 3 ] += d;
   }

3. Create a work area to hold the a, b, c, and d values from the current hash. You see in just a minute how this is initialized — this is important. Then, split the input, which is required to be exactly 512 bits, into 16 integers. Notice that you convert to integers using little-endian conventions, rather than the big-endian conventions you've been following thus far:

   for ( j = 0; j < 16; j++ )
    {
       x[ j ] = input[ ( j * 4 ) + 3 ] << 24 |
            input[ ( j * 4 ) + 2 ] << 16 |
            input[ ( j * 4 ) + 1 ] << 8 |
            input[ ( j * 4 ) ];
    }

Technically speaking, because you know you're compiling to a 32-bit little-endian architecture, you could actually memcpy into x — or even forgo it completely if you are willing to be fast and loose with your typecasting. The rest of the function consists of 64 expansions of the ROUND macro. You can probably see how, if you just index hash directly, rather than using the work area variables a, b, c, and d, you can change this from a macro expansion to a loop. In fact, if you want to get a bit tricky, you could follow the pattern in the k's and s's and code the whole thing in a terse loop. You can replace md5_block_operate with the shorter, but more divergent — in terms of the specification — function shown in Listing 4-5.

Listing 4-5: Alternate md5_block_operate implementation

static int s[ 4 ][ 4 ] = {
 { 7, 12, 17, 22 },
 { 5, 9, 14, 20 },
 { 4, 11, 16, 23 },
 { 6, 10, 15, 21 }
};

void md5_block_operate( const unsigned char *input,
               unsigned int hash[ MD5_RESULT_SIZE ] )
{
 int a, b, c, d, x_i, s_i;
 int i, j;
 unsigned int x[ 16 ];
 unsigned int tmp_hash[ MD5_RESULT_SIZE ];

 memcpy( tmp_hash, hash, MD5_RESULT_SIZE * sizeof( unsigned int ) );

 for ( j = 0; j < 16; j++ )
 {
    x[ j ] = input[ ( j * 4 ) + 3 ] << 24 |
        input[ ( j * 4 ) + 2 ] << 16 |
        input[ ( j * 4 ) + 1 ] << 8 |
        input[ ( j * 4 ) ];
 }

 for ( i = 0; i < 64; i++ )
 {
   a = 3 - ( ( i + 3 ) % 4 );
   b = 3 - ( ( i + 2 ) % 4 );
   c = 3 - ( ( i + 1 ) % 4 );
   d = 3 - ( i % 4 );

   if ( i < 16 )
   {
      tmp_hash[ a ] += F( tmp_hash[ b ], tmp_hash[ c ], tmp_hash[ d ] );
      x_i = i;
   }
   else if ( i < 32 )
   {
      tmp_hash[ a ] += G( tmp_hash[ b ], tmp_hash[ c ], tmp_hash[ d ] );
      x_i = ( 1 + ( ( i - 16 ) * 5 ) ) % 16;
   }
   else if ( i < 48 )
   {
      tmp_hash[ a ] += H( tmp_hash[ b ], tmp_hash[ c ], tmp_hash[ d ] );
      x_i = ( 5 + ( ( i - 32 ) * 3 ) ) % 16;
   }
   else
   {
      tmp_hash[ a ] += I( tmp_hash[ b ], tmp_hash[ c ], tmp_hash[ d ] );
      x_i = ( ( i - 48 ) * 7 ) % 16;
   }
   s_i = s[ i / 16 ][ i % 4 ];
   tmp_hash[ a ] += x[ x_i ] + ( unsigned int )
  ( BASE_T * fabs( sin( ( double ) i + 1 ) ) );
   tmp_hash[ a ] = ( tmp_hash[ a ] << s_i ) | ( tmp_hash[ a ] >> ( 32 - s_i ) );

tmp_hash[ a ] += tmp_hash[ b ];
 }

 hash[ 0 ] += tmp_hash[ 0 ];
 hash[ 1 ] += tmp_hash[ 1 ];
 hash[ 2 ] += tmp_hash[ 2 ];
 hash[ 3 ] += tmp_hash[ 3 ];
}

The longer implementation in Listing 4-5 follows the specification more closely; the shorter implementation is a bit difficult to read, but it yields the same results.

This produces a 128-bit hash on a 512-bit block. If the input is greater than 512 bits, just call the function again, this time passing the output of the previous call as the initializer. If this is the first call, initialize the hash code to the cryptographically meaningless initializer in Listing 4-6.

Listing 4-6: "md5.c" md5 initial hash

unsigned int md5_initial_hash[ ] = {
 0x67452301,
 0xefcdab89,
 0x98badcfe,
 0x10325476
};

Notice that this initializer doesn't have any quasi-mystical cryptographic security properties; it's just the byte sequence 0123456789abcdef (in little-endian form), followed by the same thing backward. It doesn't much matter what you initialize the hash to — although 0's would be a bad choice — as long as every implementation agrees on the starting value.

Securely Hashing Multiple Blocks of Data

If you need to encrypt less than 512 bits, or a bit string that's not an even multiple of 512 bits, you pad the last block. However, you can't just pad with 0's or just with 1's. Remember, 512 0's is a legitimate input to MD5. So is one 0. You need some way to ensure that 512 0's hashes to a different value than one 0. Therefore, MD5 requires that the last eight bytes of the input be set to the length, in bits (remember that you may want to hash a value that's not an even multiple of eight bits) of the input preceding it. This means that MD5 is essentially undefined for lengths greater than 2⁶⁴ bits, and that if the input happens to be between 448 (512 – 64) and 512 bits, you need to add an extra 512-bit block of padding just to store the length. A sole "1" bit follows the last bit of input, followed by enough 0's to pad up to 448 bits, followed by the length of the message itself in bits.

Now, the MD5 specification has a strange formulation for the length. Rather than just being a little-endian 64-bit integer, it's instead stored as "low-order 32 bits" and "high-order 32 bits."

The code to process an arbitrarily sized input into an MD5 hash, including padding and iteration over multiple blocks, is shown in Listing 4-7.

Listing 4-7: "md5.c" md5 hash algorithm

#define MD5_BLOCK_SIZE 64
#define MD5_INPUT_BLOCK_SIZE 56
#define MD5_RESULT_SIZE 4

int md5_hash( const unsigned char *input,
      int len,
      unsigned int hash[ MD5_RESULT_SIZE ] )
{
 unsigned char padded_block[ MD5_BLOCK_SIZE ];
 int length_in_bits = len * 8;

 // XXX should verify that len < 2^64, but since len is only 32 bits, this won't
 // be a problem.

 hash[ 0 ] = md5_initial_hash[ 0 ];
 hash[ 1 ] = md5_initial_hash[ 1 ];
 hash[ 2 ] = md5_initial_hash[ 2 ];
 hash[ 3 ] = md5_initial_hash[ 3 ];

 while ( len >= MD5_INPUT_BLOCK_SIZE )
 {
   // Special handling for blocks between 56 and 64 bytes
   // (not enough room for the 8 bytes of length, but also
   // not enough to fill up a block)
   if ( len < MD5_BLOCK_SIZE )
   {
     memset( padded_block, 0, sizeof( padded_block ) );
     memcpy( padded_block, input, len );
     padded_block[ len ] = 0x80;
     md5_block_operate( padded_block, hash );

     input += len;
     len = −1;

}
  else
  {
     md5_block_operate( input, hash );

     input += MD5_BLOCK_SIZE;
     len -= MD5_BLOCK_SIZE;
   }
 }

 // There's always at least one padded block at the end, which includes
 // the length of the message
 memset( padded_block, 0, sizeof( padded_block ) );
 if ( len >= 0 )
 {
   memcpy( padded_block, input, len );
   padded_block[ len ] = 0x80;
 }

 // Only append the length for the very last block
 // Technically, this allows for 64 bits of length, but since we can only
 // process 32 bits worth, we leave the upper four bytes empty
 // This is sort of a bizarre concept of "little endian"...
 padded_block[ MD5_BLOCK_SIZE - 5 ] = ( length_in_bits & 0xFF000000 ) >> 24;
 padded_block[ MD5_BLOCK_SIZE - 6 ] = ( length_in_bits & 0x00FF0000 ) >> 16;
 padded_block[ MD5_BLOCK_SIZE - 7 ] = ( length_in_bits & 0x0000FF00 ) >> 8;
 padded_block[ MD5_BLOCK_SIZE - 8 ] = ( length_in_bits & 0x000000FF );

 md5_block_operate( padded_block, hash );

 return 0;
}

Now, follow these steps:

1. Initialize the hash response to the standard starting value defined earlier.
2. Iterate through 512-bit blocks, calling md5_block_operate until you come to the last, or next-to-last block depending on whether the last block aligns on less than 448 bits or not.
3. If the last block is between 448 and 512 bits (56 and 64 bytes), pad by adding a "1" bit, which is always hex 0x80 because this implementation never accepts non-byte-aligned input, and fill the rest of the buffer with 0's.
4. The length is appended to the next block. Set len = –1 as a reminder for the next section not to append another "1" bit.

   // Special handling for blocks between 56 and 64 bytes
    // (not enough room for the 8 bytes of length, but also
    // not enough to fill up a block)
    if ( len < MD5_BLOCK_SIZE )
    {
      memset( padded_block, 0, sizeof( padded_block ) );
      memcpy( padded_block, input, len );
      padded_block[ len ] = 0x80;
      md5_block_operate( padded_block, hash );
   
      input += len;
      len = −1;
    }

5. Append the length, the padding bits and a trailing "1" bit — if it hasn't already been added — and operate on the final block. There will be 448 – l. These are l bits of padding, where l is the length of the input in bits. Note that this always happens, even if the input is 1 bit long.

   // There's always at least one padded block at the end, which includes
    // the length of the message
    memset( padded_block, 0, sizeof( padded_block ) );
    if ( len >= 0 )
    {
      memcpy( padded_block, input, len );
      padded_block[ len ] = 0x80;
    }
   
    // Only append the length for the very last block
    // Technically, this allows for 64 bits of length, but since we can only
    // process 32 bits worth, we leave the upper four bytes empty
    // This is sort of a odd concept of "little endian"...
    padded_block[ MD5_BLOCK_SIZE - 5 ] = ( length_in_bits & 0xFF000000 ) >> 24;
    padded_block[ MD5_BLOCK_SIZE - 6 ] = ( length_in_bits & 0x00FF0000 ) >> 16;
    padded_block[ MD5_BLOCK_SIZE - 7 ] = ( length_in_bits & 0x0000FF00 ) >> 8;
    padded_block[ MD5_BLOCK_SIZE - 8 ] = ( length_in_bits & 0x000000FF );
   
    md5_block_operate( padded_block, hash );

6. Because input greater than 2³² isn't allowed in this implementation, leave the last four bytes empty (0) in all cases.

And you now have a 128-bit output that is essentially unique to the input.

MD5 Vulnerabilities

If you gathered 366 people in a room, there's a 100 percent chance that two of them will share the same birthday. There are only 365 birthdays to go around, so with 366 people at least two must have the same birthday (367 if you want to count Feb. 29 and Mar. 1 as two distinct birthdays). This is clear. Here's a question for you, though: How many people would you have to gather in a room to have a 50 percent chance that two of them share the same birthday? You might hazard a guess that it would take about 183 — half the people, half the chance.

As it turns out, the answer is stunningly lower. If 23 people are gathered together in a room, there's a 50 percent chance that two of them share the same birthday. To resolve this seeming paradox, consider this: If there are n people in a room, there are 365ⁿ possible birthdays. The first person can have any of 365 birthdays; the second can have any of 365 birthdays; and so on. However, there are only 365*364 ways that two people can have unique birthdays. The first person has "used up" one of the available birthdays. Three people can only have 365*364*363 unique birthday combinations. In general, n people can have 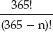unique combinations of birthdays. So, there are 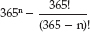ways that at least two people share a birthday — that is, that the birthday combinations are not unique. The math is complex, but clear: With n possibilities, you need n + 1 instances to guarantee a repeat, but you need 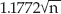to have a 50% chance of a repeat. This surprising result is often referred to as the birthday paradox.

This doesn't bode well for MD5. MD5 produces 128 bits for each input. 2¹²⁸ is a mind-bogglingly large number. In decimal, it works out to approximately 340 million trillion trillion. However, 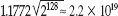. That's still a lot, but quite a few less than 2¹²⁸. Remember that the purpose of using MD5 rather than a simple checksum digest was that it ought to be impossible for an attacker to engineer a collision. If I deliberately go looking for a collision with a published hash, I have to compute for a long time. However, if I go looking for two documents that share a hash, I need to look for a much shorter time, albeit still for a long time. And, as you saw with DES, this brute-force birthday attack is infinitely parallelizable; the more computers I can add to the attack, the faster I can get an answer.

This vulnerability to a birthday attack is a problem that all digest algorithms have; the only solution is to make the output longer and longer until a birthday attack is infeasible in terms of computing power. As you saw with symmetric cryptography, this is a never-ending arms race as computers get faster and faster and protocol designers struggle to keep up. However, MD5 is even worse off than this. Researchers have found cracks in the protocol's fundamental design.

In 2005, security researchers Xiaoyan Wang and Hongbo Yu presented their paper "How to break MD5 and other hash functions" (http://merlot.usc.edu/csac-s06/papers/Wang05a.pdf), which detailed an exploit capable of producing targeted MD5 collisions in 15 minutes to an hour using commodity hardware. This is not a theoretical exploit; Magnus Daum and Stefaun Lucks illustrate an actual real-world MD-5 collision in their paper http://th.informatik.uni-mannheim.de/people/lucks/HashCollisions/.

In spite of this, MD5 is fairly popular; TLS mandates its use! Fortunately for the TLS-using public, it does so in a reasonably secure way — or, at least, a not terribly insecure way — so that the TLS protocol itself is not weakened by the inclusion of MD5.

Increasing Collision Resistance with the SHA-1 Digest Algorithm

Secure Hash Algorithm (SHA-1) is similar to MD5. The only principal difference is in the block operation itself. The other two superficial differences are that SHA-1 produces a 160-bit (20-byte) hash rather than a 128-bit (16-byte) hash, and SHA-1 deals with big-endian rather than little-endian numbers. Like MD5, SHA-1 operates on 512-bit blocks, and the final output is the sum (modulo 32) of the results of all of the blocks. The operation itself is slightly simpler; you start by breaking the 512-bit input into 16 4-byte values x. You then compute 80 four-byte W values from the original input where the following is rotated left once: W[0<t<16] = x[t], and W[17<7<80] = W[ t – 3 ] xor W[ t – 8 ] xor W[ t – 14 ] xor W[ t – 16 ]

This W array serves the same purpose as the 4294967296 * abs(sin(i)) computation in MD5, but is a bit easier to compute and is also based on the input.

After that, the hash is split up into five four-byte values a, b, c, d, and e, which are operated on in a series of 80 rounds, similar to the operation in MD5 — although in this case, somewhat easier to implement in a loop. At each stage, a rotation, an addition of another hash integer, an addition of an indexed constant, an addition of the W array, and an addition of a function whose operation depends on the round number is applied to the active hash value, and then the hash values are cycled so that a new one becomes the active one.

Understanding SHA-1 Block Computation

If you understood the MD5 computation in Listing 4-4, you should have no trouble making sense of the SHA-1 block computation in Listing 4-8.

Listing 4-8: "sha.c" bit manipulation, initialization and block operation

static const int k[] = {
 0x5a827999, // 0 <= t <= 19
 0x6ed9eba1, // 20 <= t <= 39
 0x8f1bbcdc, // 40 <= t <= 59
 0xca62c1d6 // 60 <= t <= 79
};

// ch is functions 0 - 19
unsigned int ch( unsigned int x, unsigned int y, unsigned int z )

{
 return ( x & y ) ^ ( ~x & z );
}

// parity is functions 20 - 39 & 60 - 79
unsigned int parity( unsigned int x, unsigned int y, unsigned int z )
{
 return x ^ y ^ z;
}

// maj is functions 40 - 59
unsigned int maj( unsigned int x, unsigned int y, unsigned int z )
{
 return ( x & y ) ^ ( x & z ) ^ ( y & z );
}

#define SHA1_RESULT_SIZE 5

void sha1_block_operate( const unsigned char *block,
unsigned int hash[ SHA1_RESULT_SIZE ] )
{
 unsigned int W[ 80 ];
 unsigned int t = 0;
 unsigned int a, b, c, d, e, T;

 // First 16 blocks of W are the original 16 blocks of the input
 for ( t = 0; t < 80; t++ )
 {
   if ( t < 16 )
   {
     W[ t ] = ( block[ ( t * 4 ) ] << 24 ) |
            ( block[ ( t * 4 ) + 1 ] << 16 ) |
            ( block[ ( t * 4 ) + 2 ] << 8 ) |
            ( block[ ( t * 4 ) + 3 ] );
   }
   else
   {
     W[ t ] = W[ t - 3 ] ^
            W[ t - 8 ] ^
            W[ t - 14 ] ^
            W[ t - 16 ];
     // Rotate left operation, simulated in C
     W[ t ] = ( W[ t ] << 1 ) | ( ( W[ t ] & 0x80000000 ) >> 31 );
   }
 }

 a = hash[ 0 ];
 b = hash[ 1 ];
 c = hash[ 2 ];
 d = hash[ 3 ];
 e = hash[ 4 ];

for ( t = 0; t < 80; t++ )
 {
   T = ( ( a << 5 ) | ( a >> 27 ) ) + e + k[ ( t / 20 ) ] + W[ t ];

   if ( t <= 19 )
   {
     T += ch( b, c, d );
   }
   else if ( t <= 39 )
   {
     T += parity( b, c, d );
   }
   else if ( t <= 59 )
   {
     T += maj( b, c, d );
   }
   else
   {
     T += parity( b, c, d );
   }

   e = d;
   d = c;
   c = ( ( b << 30 ) | ( b >> 2 ) );
   b = a;
   a = T;
 }

 hash[ 0 ] += a;
 hash[ 1 ] += b;
 hash[ 2 ] += c;
 hash[ 3 ] += d;
 hash[ 4 ] += e;
}

Regarding Listing 4-8:

1. The constants k are defined — one for each set of 20 rounds.
2. The functions ch, maj, and parity are defined: ch for rounds 0 – 19, maj for rounds 40–59, and parity for the remaining rounds. Like MD5's F, G, H, and I, these four functions just shuffle the bits of their input randomly.
3. The block operation function computes the W array. Notice that you're using unsigned ints here, rather than four-byte blocks, so you have to be careful to account for endian-ness as usual. The benefit is that you only have to keep track of this transformation once, at the beginning of the computation, and from that point you can use native operations on a 32-bit architecture.
4. After W has been computed, the individual five hash integers are copied into a, b, c, d, and e for computation; at each round, a new T value is computed according to

   T = ( ( a << 5 ) | ( a >> 27 ) ) + e + k[ ( t / 20 ) ] + W[ t ] +
     ch/parity/maj(b,c,d);

5. a, b, c, d, and e are then rotated through each other, just as in MD5, and, for good measure, c is rotated left 30 positions as well. Although the mechanics are slightly different, this is very similar to what was done with MD5.

You don't really have to try to make sense of the mechanics of this. It's supposed to be impossible to do so. As long as the details are correct, you can safely think of the block operation function as a true black-box function.

Understanding the SHA-1 Input Processing Function

The input processing function of SHA-1 is almost identical to that of MD5. The length is appended, in bits, at the very end of the last block, each block is 512 bits, the hash must be initialized to a standard value before input begins, and the hash computations of each block are added to one another, modulo 32, to produce the final result. The function in Listing 4-9, which computes SHA-1 hashes of a given input block, differs from md5_hash in only a few places, which are highlighted in bold.

Listing 4-9: "sha.c" SHA-1 hash algorithm

#define SHA1_INPUT_BLOCK_SIZE 56
#define SHA1_BLOCK_SIZE 64

unsigned int sha1_initial_hash[ ] = {
 0x67452301,
 0xefcdab89,
 0x98badcfe,
 0x10325476,
 0xc3d2e1f0
};

int sha1_hash( unsigned char *input, int len,
       unsigned int hash[ SHA1_RESULT_SIZE ] )
{
 unsigned char padded_block[ SHA1_BLOCK_SIZE ];
 int length_in_bits = len * 8;


 hash[ 0 ] = sha1_initial_hash[ 0 ];
 hash[ 1 ] = sha1_initial_hash[ 1 ];

hash[ 2 ] = sha1_initial_hash[ 2 ];
 hash[ 3 ] = sha1_initial_hash[ 3 ];
 hash[ 4 ] = sha1_initial_hash[ 4 ];

 while ( len >= SHA1_INPUT_BLOCK_SIZE )
 {
   if ( len < SHA1_BLOCK_SIZE )
   {
     memset( padded_block, 0, sizeof( padded_block ) );
     memcpy( padded_block, input, len );
     padded_block[ len ] = 0x80;
     sha1_block_operate( padded_block, hash );

     input += len;
     len = −1;
  }
  else
  {
     sha1_block_operate( input, hash );

     input += SHA1_BLOCK_SIZE;
     len -= SHA1_BLOCK_SIZE;
  }
 }

 memset( padded_block, 0, sizeof( padded_block ) );
 if ( len >= 0 )
 {
   memcpy( padded_block, input, len );
   padded_block[ len ] = 0x80;
 }

 padded_block[ SHA1_BLOCK_SIZE - 4 ] = ( length_in_bits & 0xFF000000 ) >> 24;
 padded_block[ SHA1_BLOCK_SIZE - 3 ] = ( length_in_bits & 0x00FF0000 ) >> 16;
 padded_block[ SHA1_BLOCK_SIZE - 2 ] = ( length_in_bits & 0x0000FF00 ) >> 8;
 padded_block[ SHA1_BLOCK_SIZE - 1 ] = ( length_in_bits & 0x000000FF );

 sha1_block_operate( padded_block, hash );

 return 0;
}

In fact, sha1_hash and md5_hash are so similar it's almost painful not to just go ahead and consolidate them into a common function. Go ahead and do so.

Because md5_block_operate and sha1_block_operate have identical method signatures (what a coincidence!), you can just pass the block_operate function in as a function pointer as in Listing 4-10.

Listing 4-10: "digest.h" digest_hash function prototype

int digest_hash( unsigned char *input,
        int len,
        unsigned int *hash,
        void (*block_operate)(const unsigned char *input, unsigned int hash[] ));

Because SHA1_BLOCK_SIZE and MD5_BLOCK_SIZE are actually identical, there's not much benefit in using two different constants. You could pass the block size in as a parameter to increase flexibility, but there are already quite a few parameters, and you don't need this flexibility — at least not yet. The initialization is different because SHA has one extra four-byte integer, but you can just initialize outside of the function to take care of that.

Understanding SHA-1 Finalization

The only remaining difference is the finalization. Remember that MD5 had sort of an odd formulation to append the length to the end of the block in little-endian format. SHA doesn't; it sticks with the standard big endian. You could probably code your way around this, but a better approach is to just refactor this into another function in Listing 4-11 and Listing 4-12.

Listing 4-11: "md5.c" md5_finalize

void md5_finalize( unsigned char *padded_block, int length_in_bits )
{
 padded_block[ MD5_BLOCK_SIZE - 5 ] = ( length_in_bits & 0xFF000000 ) >> 24;
 padded_block[ MD5_BLOCK_SIZE - 6 ] = ( length_in_bits & 0x00FF0000 ) >> 16;
 padded_block[ MD5_BLOCK_SIZE - 7 ] = ( length_in_bits & 0x0000FF00 ) >> 8;
 padded_block[ MD5_BLOCK_SIZE - 8 ] = ( length_in_bits & 0x000000FF );
}

Listing 4-12: "sha.c" sha1_finalize

void sha1_finalize( unsigned char *padded_block, int length_in_bits )
{
 padded_block[ SHA1_BLOCK_SIZE - 4 ] = ( length_in_bits & 0xFF000000 ) >> 24;
 padded_block[ SHA1_BLOCK_SIZE - 3 ] = ( length_in_bits & 0x00FF0000 ) >> 16;
 padded_block[ SHA1_BLOCK_SIZE - 2 ] = ( length_in_bits & 0x0000FF00 ) >> 8;
 padded_block[ SHA1_BLOCK_SIZE - 1 ] = ( length_in_bits & 0x000000FF );
}

So the final "digest" function looks like Listing 4-13, with two function parameters.

Listing 4-13: "digest.c" digest_hash

#define DIGEST_BLOCK_SIZE 64
#define INPUT_BLOCK_SIZE 56

/**
 * Generic digest hash computation. The hash should be set to its initial
 * value *before* calling this function.
 */
int digest_hash( unsigned char *input,
                     int len,
                                      unsigned int *hash,
                     void (*block_operate)(const unsigned char *input,
                                     unsigned int hash[] ),
                     void (*block_finalize)(unsigned char *block, int length ) )
{
 unsigned char padded_block[ DIGEST_BLOCK_SIZE ];
 int length_in_bits = len * 8;

 while ( len >= INPUT_BLOCK_SIZE )
 {
   // Special handling for blocks between 56 and 64 bytes
   // (not enough room for the 8 bytes of length, but also
   // not enough to fill up a block)
   if ( len < DIGEST_BLOCK_SIZE )
   {
    memset( padded_block, 0, sizeof( padded_block ) );
    memcpy( padded_block, input, len );
    padded_block[ len ] = 0x80;
    block_operate( padded_block, hash );

    input += len;
    len = −1;
  }
  else
  {
    block_operate( input, hash );

    input += DIGEST_BLOCK_SIZE;
    len -= DIGEST_BLOCK_SIZE;
  }
 }

 memset( padded_block, 0, sizeof( padded_block ) );
 if ( len >= 0 )
 {
   memcpy( padded_block, input, len );
   padded_block[ len ] = 0x80;
 }

 block_finalize( padded_block, length_in_bits );

 block_operate( padded_block, hash );

 return 0;
}

This single function is now responsible for computing both MD5 and SHA-1 hashes. To compute an MD5 hash, call

unsigned int hash[ 4 ];
 memcpy( hash, md5_initial_hash, 4 * sizeof( unsigned int ) );
 digest_hash( argv[ 2 ], strlen( argv[ 2 ] ), hash, 4, md5_block_operate,
  md5_finalize );

and to compute an SHA-1 hash, call

unsigned int hash[ 5 ];
 memcpy( hash, sha1_initial_hash, 5 * sizeof( unsigned int ) );
 digest_hash( argv[ 2 ], strlen( argv[ 2 ] ), hash, 5, sha1_block_operate,
  sha1_finalize );

If you were paying close attention, you may have also noticed that the first four integers of the sha1_initial_hash array are the same as the first four integers of the md5_initial_hash array. Technically you could even use one initial_hash array and share it between the two operations.

There's one final problem you run into when trying to use digest as in Listing 4-13. The output of md5 is given in big-endian format, whereas the output of SHA-1 is given in little-endian format. In and of itself, this isn't really a problem, but you want to be able to treat digest as a black box and not care which algorithm it encloses. As a result, you need to decide which format you want to follow. Arbitrarily, pick the MD5 format, and reverse the SHA-1 computations at each stage. The changes to sha.c are detailed in Listing 4-14.

Listing 4-14: "sha.c" SHA-1 in little-endian format

unsigned int sha1_initial_hash[ ] = {
 0x01234567,
 0x89abcdef,
 0xfedcba98,
 0x76543210,
 0xf0e1d2c3
};

...

void sha1_block_operate( const unsigned char *block, unsigned int hash[ 5 ] )
{
...
   W[ t ] = ( W[ t ] << 1 ) | ( ( W[ t ] & 0x80000000 ) >> 31 );
 }
}

 hash[ 0 ] = ntohl( hash[ 0 ] );
 hash[ 1 ] = ntohl( hash[ 1 ] );
 hash[ 2 ] = ntohl( hash[ 2 ] );
 hash[ 3 ] = ntohl( hash[ 3 ] );
 hash[ 4 ] = ntohl( hash[ 4 ] );

a = hash[ 0 ];
 b = hash[ 1 ];
 c = hash[ 2 ];
 d = hash[ 3 ];
...
 hash[ 3 ] += d;
 hash[ 4 ] += e;

 hash[ 0 ] = htonl( hash[ 0 ] );
 hash[ 1 ] = htonl( hash[ 1 ] );
 hash[ 2 ] = htonl( hash[ 2 ] );
 hash[ 3 ] = htonl( hash[ 3 ] );
 hash[ 4 ] = htonl( hash[ 4 ] );
}

Notice that all this does is reverse the hash values prior to each sha1_block_operate call so that you can use the native arithmetic operators to work on the block. It then re-reverses them on the way out. Of course, you also have to reverse sha1_initial_hash.

Now you can call digest and treat the hash results uniformly, whether the hash algorithm is MD5 or SHA-1. Go ahead and build a test main routine and see some results as shown in Listing 4-15.

Listing 4-15: "digest.c" main routine

#ifdef TEST_DIGEST
int main( int argc, char *argv[ ] )
{
 unsigned int *hash;
 int hash_len;
 int i;
 unsigned char *decoded_input;
 int decoded_len;

 if ( argc < 3 )
 {
   fprintf( stderr, "Usage: %s [-md5|-sha] [0x]<input>\n", argv[ 0 ] );
   exit( 0 );
 }

 decoded_len = hex_decode( argv[ 2 ], &decoded_input );

 if ( !( strcmp( argv[ 1 ], "-md5" ) ) )
 {
   hash = malloc( sizeof( int ) * MD5_RESULT_SIZE );
   memcpy( hash, md5_initial_hash, sizeof( int ) * MD5_RESULT_SIZE );
   hash_len = MD5_RESULT_SIZE;
   digest_hash( decoded_input, decoded_len, hash,
     md5_block_operate, md5_finalize );
 }

else if ( !( strcmp( argv[ 1 ], "-sha1" ) ) )
 {
   hash = malloc( sizeof( int ) * SHA1_RESULT_SIZE );
   memcpy( hash, sha1_initial_hash, sizeof( int ) * SHA1_RESULT_SIZE );
   hash_len = SHA1_RESULT_SIZE;
   digest_hash( decoded_input, decoded_len, hash,
     sha1_block_operate, sha1_finalize );
 }
 else
 {
   fprintf( stderr, "unsupported digest algorithm '%s'\n", argv[ 1 ] );
   exit( 0 );
 }

 {
   unsigned char *display_hash = ( unsigned char * ) hash;

   for ( i = 0; i < ( hash_len * 4 ); i++ )
   {
     printf( "%.02x", display_hash[ i ] );
   }
    printf( "\n" );
 }

 free( hash );
 free( decoded_input );

 return 0;
}
#endif

Compile and run this to see it in action:

jdavies@localhost$ digest -md5 abc
900150983cd24fb0d6963f7d28e17f72

jdavies@localhost$ digest -sha1 abc
a9993e364706816aba3e25717850c26c9cd0d89d

Notice that the SHA-1 output is a bit longer than the MD5 output; MD5 gives you 128 bits, and SHA-1 gives you 160.

Even More Collision Resistance with the SHA-256 Digest Algorithm

Even SHA, with its 160 bits of output, is no longer considered sufficient to effectively guard against hash collisions. There have been three new standardized SHA extensions named SHA-256, SHA-384 and SHA-512. In general, the SHA-n algorithm produces n bits of output. You don't examine them all here, but go ahead and add support for SHA-256 because it's rapidly becoming the minimum required standard where secure hashing is concerned (you'll also need it later in this chapter, to support elliptic-curve cryptography). At the time of this writing, the NIST is evaluating proposals for a new SHA standard, which will almost certainly have an even longer output.

Everything about SHA-256 is identical to SHA-1 except for the block processing itself and the output length. The block size, padding, and so on are all the same. You can reuse the digest_hash function from Listing 4-13 verbatim, if you just change the block_operate function pointer.

SHA-256's block operation is similar; ch and maj reappear, but the parity function disappears and four new functions, which are identified in the specification as Σ¹, Σ⁰, σ¹ and σ⁰are introduced:

This choice of nomenclature doesn't translate very well into code, so call S sigma_rot (because the last operation is a rotr — "rotate right") and s sigma_shr (because the last operation is a shr — "shift right"). In code, this looks like Listing 4-16.

Listing 4-16: "sha.c" SHA-256 sigma functions

unsigned int rotr( unsigned int x, unsigned int n )
{
 return ( x >> n ) | ( ( x ) << ( 32 - n ) );
}

unsigned int shr( unsigned int x, unsigned int n )
{
 return x >> n;
}

unsigned int sigma_rot( unsigned int x, int i )
{
 return rotr( x, i ? 6 : 2 ) ^ rotr( x, i ? 11 : 13 ) ^ rotr( x, i ? 25 : 22 );
}

unsigned int sigma_shr( unsigned int x, int i )
{
 return rotr( x, i ? 17 : 7 ) ^ rotr( x, i ? 19 : 18 ) ^ shr( x, i ? 10 : 3 );
}

The block operation itself should look familiar; instead of just a, b, c, d and e, you have a-h because there are eight 32-bit integers in the output now. There's a 64-int (instead of an 80-int) W that is precomputed, and a static k block. There's also a 64-iteration round that's applied to a-h where they shift positions each round and whichever input is at the head is subject to a complex computation. The code should be more or less self-explanatory; even if you can't see why this works, you should be more than convinced that the output is a random permutation of the input, which is what you want from a hash function. This is shown in Listing 4-17.

Listing 4-17: "sha.c" SHA-256 block operate

void sha256_block_operate( const unsigned char *block,
                          unsigned int hash[ 8 ] )
{
 unsigned int W[ 64 ];
 unsigned int a, b, c, d, e, f, g, h;
 unsigned int T1, T2;
 int t, i;

 /**
  * The first 32 bits of the fractional parts of the cube roots
  * of the first sixty-four prime numbers.
  */
 static const unsigned int k[] =
 {
   0x428a2f98, 0x71374491, 0xb5c0fbcf, 0xe9b5dba5, 0x3956c25b, 0x59f111f1,
   0x923f82a4, 0xab1c5ed5, 0xd807aa98, 0x12835b01, 0x243185be, 0x550c7dc3,
   0x72be5d74, 0x80deb1fe, 0x9bdc06a7, 0xc19bf174, 0xe49b69c1, 0xefbe4786,
   0x0fc19dc6, 0x240ca1cc, 0x2de92c6f, 0x4a7484aa, 0x5cb0a9dc, 0x76f988da,
   0x983e5152, 0xa831c66d, 0xb00327c8, 0xbf597fc7, 0xc6e00bf3, 0xd5a79147,
   0x06ca6351, 0x14292967, 0x27b70a85, 0x2e1b2138, 0x4d2c6dfc, 0x53380d13,
   0x650a7354, 0x766a0abb, 0x81c2c92e, 0x92722c85, 0xa2bfe8a1, 0xa81a664b,
   0xc24b8b70, 0xc76c51a3, 0xd192e819, 0xd6990624, 0xf40e3585, 0x106aa070,
   0x19a4c116, 0x1e376c08, 0x2748774c, 0x34b0bcb5, 0x391c0cb3, 0x4ed8aa4a,
   0x5b9cca4f, 0x682e6ff3, 0x748f82ee, 0x78a5636f, 0x84c87814, 0x8cc70208,
   0x90befffa, 0xa4506ceb, 0xbef9a3f7, 0xc67178f2
 };

 // deal with little-endian-ness
 for ( i = 0; i < 8; i++ )
 {
   hash[ i ] = ntohl( hash[ i ] );
 }

 for ( t = 0; t < 64; t++ )
 {
   if ( t <= 15 )
   {
     W[ t ] = ( block[ ( t * 4 ) ] << 24 ) |
              ( block[ ( t * 4 ) + 1 ] << 16 ) |

( block[ ( t * 4 ) + 2 ] << 8 ) |
              ( block[ ( t * 4 ) + 3 ] );
   }
   else
   {
     W[ t ] = sigma_shr( W[ t - 2 ], 1 ) +
              W[ t - 7 ] +
              sigma_shr( W[ t - 15 ], 0 ) +
              W[ t - 16 ];
   }
 }

 a = hash[ 0 ];
 b = hash[ 1 ];
 c = hash[ 2 ];
 d = hash[ 3 ];
 e = hash[ 4 ];
 f = hash[ 5 ];
 g = hash[ 6 ];
 h = hash[ 7 ];

 for ( t = 0; t < 64; t++ )
 {
   T1 = h + sigma_rot( e, 1 ) + ch( e, f, g ) + k[ t ] + W[ t ];
   T2 = sigma_rot( a, 0 ) + maj( a, b, c );
   h = g;
   g = f;
   f = e;
   e = d + T1;
   d = c;
   c = b;
   b = a;
   a = T1 + T2;
 }

 hash[ 0 ] = a + hash[ 0 ];
 hash[ 1 ] = b + hash[ 1 ];
 hash[ 2 ] = c + hash[ 2 ];
 hash[ 3 ] = d + hash[ 3 ];
 hash[ 4 ] = e + hash[ 4 ];
 hash[ 5 ] = f + hash[ 5 ];
 hash[ 6 ] = g + hash[ 6 ];
 hash[ 7 ] = h + hash[ 7 ];

 // deal with little-endian-ness
 for ( i = 0; i < 8; i++ )
 {
   hash[ i ] = htonl( hash[ i ] );
 }
}

Notice that there are quite a few more k values for SHA-256 than for SHA-1, and that σ shows up only in the computation of W and Σ in the main loop. You also have to have an initial hash in Listing 4-18.

Listing 4-18: "sha.c" SHA-256 initial hash

static const unsigned int sha256_initial_hash[] =
{
 0x67e6096a,
 0x85ae67bb,
 0x72f36e3c,
 0x3af54fa5,
 0x7f520e51,
 0x8c68059b,
 0xabd9831f,
 0x19cde05b
};

These are presented here backward (that is, in little-endian format) with respect to the specification. If you want to invoke this, you need to call the same digest_hash function developed earlier:

unsigned int hash[ 8 ];
 memcpy( hash, sha256_initial_hash, 8 * sizeof( unsigned int ) );
 digest_hash( argv[ 2 ], strlen( argv[ 2 ] ), hash, 8, sha256_block_operate,
  sha1_finalize );

Notice that the finalize pointer points to sha1_finalize — finalization is exactly the same for SHA-256 as it is for SHA-1, so there's no reason to define a new function here.

Preventing Replay Attacks with the HMAC Keyed-Hash Algorithm

Related to message digests (and particularly relevant to SSL) are HMACs, specified in RFC 2104. To understand the motivation for HMAC, consider the secure hash functions (MD5 and SHA) examined in the previous three sections. Secure hashes are reliable, one-way functions. You give them the input, they give you the output, and nobody — not even you — can work backward from the output to uncover the input. Right?

Well, not exactly — or at least, not always. Imagine that a company maintains a database of purchase orders, and to verify that the customer is in possession of the credit card number used to place an order, a secure hash of the credit card number is stored for each order. The customer is happy, because her credit card number is not being stored in a database for some hacker to steal; and the company is happy, because it can ask a customer for her credit card number and then retrieve all orders that were made using that card for customer service purposes. The company just asks the customer for the credit card number again, hashes it, and searches the database on the hash column.

Unfortunately, there's a problem with this approach. Although there are a lot of potential hash values — even for a small hash function such as MD5 — there aren't that many credit card numbers. About 10,000 trillion. In fact, not every 16-digit number is a valid credit card number, and the LUHN consistency check that verifies the validity of a credit card number is a public algorithm. In cryptography terms, this isn't actually a very big number. A motivated attacker might try to compute the MD5 hash — or whatever hash was used — of all 10,000 trillion possible credit card numbers and store the results, keyed back to the original credit card number. This might take months to complete on a powerful cluster of computers, but after it's computed this database could be used against any database that stores an MD5 hash of credit card numbers. Fortunately, this direct attack is infeasible for a different reason. This would require 320,000 trillion bytes of memory — about 320 petabytes. The cost of this storage array far outweighs the value of even the largest database of credit card numbers.

So far, so good. An attacker would have to spend months mounting a targeted attack against the database or would have to have an astronomical amount of storage at his disposal. Unfortunately, Martin Hellman, in his paper "A Cryptanalytic Time — Memory Trade-Off", came up with a way to trade storage space for speed. His concept has been refined into what are now called rainbow tables. The idea is to start with an input, hash it, and then arbitrarily map that hash back to the input space. This arbitrary mapping doesn't undo the hash — that's impossible — it just has to be repeatable. You then take the resulting input, hash it, map it back, and so on. Do this n times, but only store the first and the last values. This way, although you have to go through every possible input value, you can drastically reduce the amount of storage you need.

When you have a hash code you want to map back to its original input, look for it in your table. If you don't find it, apply your back-mapping function, hash that, and look in the table again. Eventually, you find a match, and when you do, you have uncovered the original input. This approach has been successfully used to crack passwords whose hashes were stored rather than their actual contents; rainbow tables of common password values are available for download online; you don't even have to compute them yourself.

The easiest way to guard against this is to include a secret in the hash; without the secret, the attacker doesn't know what to hash in the first place. This is, in fact, the idea behind the HMAC. Here, both sides share a secret, which is combined with the hash in a secure way. Only a legitimate holder of the secret can figure out H(m,s) where H is the secure hash function, m is the message, and s is the secret.

A weak, naïve, shared-secret MAC operation might be:

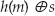
where h refers to a secure digest. The problem with this approach is its vulnerability to known plaintext attacks. The attack works like this: The attacker convinces somebody with the MAC secret to hash and XOR the text "abc" or some other value that is known to the attacker. This has the MD5 hash 900150983cd24fb0d6963f7d28e17f72. Remember that the attacker can compute this as well — an MD5 hash never changes. The holder of the secret then XORs this value with the secret and makes the result available.

Unfortunately, the attacker can then XOR the hash with the result and recover the secret. Remember that a ⊕ b ⊕ b = a, but a ⊕ b ⊕ a = b as well. So hash ⊕ secret ⊕ hash = secret. Since mac = (hash ⊕ secret), mac ⊕ hash = secret, and the secret has been revealed.

Implementing a Secure HMAC Algorithm

A more secure algorithm is specified in RFC 2104 and is the standard for combining shared secrets with secure hash algorithms. Overall, it's not radically different in concept than XORing the shared secret with the result of a secure hash; it just adds a couple of extra functions.

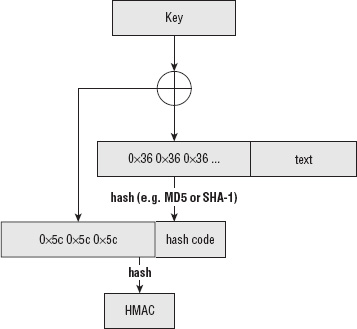
An HMAC-hash prepends one block of data to the data to be hashed. The prepended block consists of 64 bytes of 0x36, XORed with the shared secret. This means that the shared secret can't be longer than 64 bytes. If it is, it should be securely hashed itself, and the results of that hash used as the shared secret. This result (the prepended block, plus the input data itself) is then hashed, using a secure hash algorithm. Finally, this hash is appended to a new block of data that consists of one block of the byte 0x5C, XORed again with the shared secret (or its computed hash as described previously), and hashed again to produce the final hash value. Figure 4-1 illustrates this process.

This double-hash technique stops the attacker in the known-plaintext attack described earlier from computing the hash code and XORing it against the secret to recover it. All of this complexity is carefully designed to create a repeatable process. Remember, if "abc" hashes to "xyz" for me, it must hash that way for you no matter when you run it or what type of machine you're on — but in such a way that can't be reversed or forged. It seems complicated (and it is), but after it's implemented, it can be treated as a black box.

Using the digest algorithm above, you can put together an HMAC implementation that can work with any hash algorithm in Listing 4-19.

Listing 4-19: "hmac.c" HMAC function

/**
 * Note: key_length, text_length, hash_block_length are in bytes.
 * hash_code_length is in ints.
 */
void hmac( const unsigned char *key,

int key_length,
     const unsigned char *text,
     int text_length,
     void (*hash_block_operate)(const unsigned char *input, unsigned int hash[] ),
     void (*hash_block_finalize)(const unsigned char *block, int length ),
     int hash_block_length,
     int hash_code_length,
     unsigned int *hash_out )
{
 unsigned char *ipad, *opad, *padded_block;
 unsigned int *hash1;
 int i;

 // TODO if key_length > hash_block_length, should hash it using "hash_
 // function" first and then use that as the key.
 assert( key_length < hash_block_length );

 hash1 = ( unsigned int * ) malloc( hash_code_length * sizeof( unsigned int )
);
 ipad = ( unsigned char * ) malloc( hash_block_length );
 padded_block = ( unsigned char * ) malloc( text_length + hash_block_length );

 memset( ipad, 0x36, hash_block_length );

 memset( padded_block, '\0', hash_block_length );
 memcpy( padded_block, key, key_length );
 for ( i = 0; i < hash_block_length; i++ )
 {
   padded_block[ i ] ^= ipad[ i ];
 }

 memcpy( padded_block + hash_block_length, text, text_length );
 memcpy( hash1, hash_out, hash_code_length * sizeof( unsigned int ) );
 digest_hash( padded_block, hash_block_length + text_length, hash1,
  hash_code_length, hash_block_operate, hash_block_finalize );

 opad = ( unsigned char * ) malloc( hash_block_length );

 memset( opad, 0x5C, hash_block_length );

 free( padded_block );
 padded_block = ( unsigned char * ) malloc(
  ( hash_code_length * sizeof( int ) ) + hash_block_length );
 memset( padded_block, '\0', hash_block_length );
 memcpy( padded_block, key, key_length );

 for ( i = 0; i < hash_block_length; i++ )
 {
   padded_block[ i ] ^= opad[ i ];

}

 memcpy( padded_block + hash_block_length, hash1,
   hash_code_length * sizeof( int ) );
 digest_hash( padded_block,
   hash_block_length + ( hash_code_length * sizeof( int ) ), hash_out,
   hash_code_length, hash_block_operate, hash_block_finalize );

 free( hash1 );
 free( ipad );
 free( opad );
 free( padded_block );
}

Figure 4-1: HMAC Function

The method signature is a behemoth, repeated in Listing 4-20.

Listing 4-20: "hmac.h" HMAC function prototype

void hmac( const unsigned char *key,
    int key_length,
    const unsigned char *text,
    int text_length,
    int (*hash_block_operate)(const unsigned char *input, unsigned int hash[] ),
    int (*hash_block_finalize)(unsigned char *block, int length ),
    int hash_block_length,
    int hash_code_length,
    unsigned int *hash_out )

Here, key and key_length describe the shared secret; text and text_length describe the data to be HMAC-ed; hash_block_operate and hash_block_finalize describe the hash operation; hash_block_length describes the length of a block in bytes (which is always 64 for MD5 and SHA-1); hash_code_length is the length of the resultant hash in ints (4 for MD5, = for SHA-1); and hash_out is a pointer to the hash code to be generated.

Because you don't need to deal with shared secrets that are greater than 64 bytes for SSL, just ignore them:

// TODO if key_length > hash_block_length, should hash it using "hash_
 // function" first and then use that as the key.
 assert( key_length < hash_block_length );

Remember that HMAC requires that you compute an initial hash based on the text to be hashed, prepended with a block of 0x36s XORed with the shared secret, called the key here. This section of the HMAC function builds this block of data:

hash1 = ( unsigned int * ) malloc( hash_code_length * sizeof( unsigned int ) );

 ipad = ( unsigned char * ) malloc( hash_block_length );
 padded_block = ( unsigned char * ) malloc( text_length 1 hash_block_length );

 memset( ipad, 0x36, hash_block_length );

 memset( padded_block, '\0', hash_block_length );
 memcpy( padded_block, key, key_length );
 for ( i = 0; i < hash_block_length; i11 )
 {
   padded_block[ i ] ^= ipad[ i ];
 }

You allocate a new block of memory as long as the text to be hashed plus one extra block, fill it with 0x36s, and XOR that with the key. Finally, compute the hash of this new data block:

memcpy( padded_block 1 hash_block_length, text, text_length );
 memcpy( hash1, hash_out, hash_code_length * sizeof( unsigned int ) );
 digest_hash( padded_block, hash_block_length 1 text_length, hash1,
   hash_code_length, hash_block_operate, hash_block_finalize );

Notice that you're hashing into an internal block called hash1, and remember that HMAC requires you to hash that hash. There's a minor implementation problem here, though. The caller of digest_hash must preinitialize the hash code to its proper initialization value. You could ask the caller of this function to pass the correct initialization value in as a parameter, but you can "cheat" instead to save an input parameter. Because you know that the caller of hmac had to initialize hash_out, copy that value into hash1 to properly initialize it.

Completing the HMAC Operation

Now you have the first hash code computed in hash1, according to the secure hashing algorithm that was passed in. To complete the HMAC operation, you need to prepend that with another block of 0x5Cs, XORed with the shared secret, and hash it:

opad = ( unsigned char * ) malloc( hash_block_length );

 memset( opad, 0x5C, hash_block_length );

 free( padded_block );
 padded_block = ( unsigned char * ) malloc( hash_code_length 1
   ( hash_block_length * sizeof( int ) ) );
 memset( padded_block, '\0', hash_block_length );
 memcpy( padded_block, key, key_length );

 for ( i = 0; i < hash_block_length; i11 )
 {
   padded_block[ i ] ^= opad[ i ];
 }

Notice that this frees and reallocates padded_block. You may wonder why you'd want to reallocate here because you already allocated this temporary space to compute the first hash value. However, consider the case where text_length is less than hash_code_length, which sometimes it is. In this case, you'd have too little space for the prepended hash code. You could make this a bit more efficient by allocating max( hash_code_length, text_length ) at the top of the function, but this implementation is good enough.

Finally, compute the hash into hash_out, which is the return value of the function

memcpy( padded_block 1 hash_block_length, hash1,
   hash_code_length * sizeof( int ) );
 digest_hash( padded_block,
   hash_block_length 1 ( hash_code_length * sizeof( int ) ), hash_out,
   hash_code_length, hash_block_operate, hash_block_finalize );

Creating Updateable Hash Functions

Notice that, in order to compute an HMAC, you had to build an internal buffer consisting of a padded, XORed key followed by the text to be hashed. However, the hash functions presented here don't ever need to go back in the data stream. After block #N has been hashed, subsequent operations won't change the hash of block #N. They are just added to it, modulo 32. Therefore, you can save memory and time by allowing the hash operation to save its state and pick back up where it left off later — that is, feed it a block of data, let it update the hash code, and then feed it another, and so on.

Of course, the padding requirements of MD5 and SHA make this a little trickier than it sounds at first. You need to keep track of the running bit-length of the input so that it can be appended later on. This is, incidentally, how a 32-bit architecture can hash an input of more than 2³² bits. Plus, for additional flexibility, you'd want to allow the caller to pass in less than a single block at a time and accumulate the blocks yourself.

You could store this running state in a static global, but this would cause thread-safety problems (if you ever wanted to use this routine in a threaded context, anyway). Instead, you'd do better to pass a context object into the hashing function, with a routine named something like hash_update that would also take the data to be added to the running hash, and another routine named hash_finalize that would add the final padding blocks and return the result. This is, in fact, the only non-superficial difference between the MD5 code included in RFC 1321 and the MD5 implementation presented here. You need to be able to compute running hashes for SSL, so implement this extension for MD5 and SHA. Change your digest function to allow running updates and improve the HMAC implementation a bit.

Defining a Digest Structure

Because you can no longer call digest in one shot, but must instead keep track of a long-running operation, define a context structure that stores the state of an ongoing digest computation as shown in Listing 4-21.

Listing 4-21: "digest.h" digest context structure declaration

typedef struct
{
 unsigned int *hash;
 int hash_len;
 unsigned int input_len;

 void (*block_operate)(const unsigned char *input, unsigned int hash[] );
 void (*block_finalize)(const unsigned char *block, int length );

 // Temporary storage
 unsigned char block[ DIGEST_BLOCK_SIZE ];
 int block_len;
}
digest_ctx;

hash and hash_len are fairly straightforward; this is the hash code as it has been computed with the data that's been given so far. input_len is the number of bytes that have been passed in; remember input_len needs to be tracked in order to append the length in bits to the virtual buffer before computing the final hash code. Go ahead and stick the block_operate and block_finalize function pointers in here so that you don't have to further pollute your function call signatures. Finally, there's a block of temporary storage; if a call to update is made with less than a full block (or with a non-aligned bit left over), store it here, along with its length, and pass it on to block_operate when there's enough data to make a full block. This is shown in Listing 4-22.

Listing 4-22: "digest.c" update digest function

void update_digest( digest_ctx *context, const unsigned char *input, int input_len )
{
 context->input_len += input_len;

 // Process any left over from the last call to "update_digest"
 if ( context->block_len > 0 )
 {
   // How much we need to make a full block
   int borrow_amt = DIGEST_BLOCK_SIZE - context->block_len;

   if ( input_len < borrow_amt )
   {
     memcpy( context->block + context->block_len, input, input_len );
     context->block_len += input_len;
     input_len = 0;
   }
   else
   {
     memcpy( context->block + context->block_len, input, borrow_amt );
     context->block_operate( context->block, context->hash );
     context->block_len = 0;
     input += borrow_amt;
     input_len -= borrow_amt;
  }
}

 while ( input_len >= DIGEST_BLOCK_SIZE )
 {
   context->block_operate( input, context->hash );

   input += DIGEST_BLOCK_SIZE;
   input_len -= DIGEST_BLOCK_SIZE;
 }

 // Have some non-aligned data left over; save it for next call, or
 // "finalize" call.

if ( input_len > 0 )
 {
   memcpy( context->block, input, input_len );
   context->block_len = input_len;
 }
}

This is probably the most complex function presented so far, so it's worth going through carefully:

1. Update the input length. You have to append this to the very last block, whenever that may come.

   context->input_len 1= input_len;
   
    // Process any left over from the last call to "update_digest"
    if ( context->block_len > 0 )
    {
    ...
    }

2. Check to see if you have any data left over from a previous call. If you don't, go ahead and process the data, one block at a time, until you run out of blocks:

   while ( input_len >= DIGEST_BLOCK_SIZE )
    {
      context->block_operate( input, context->hash );
   
      input += DIGEST_BLOCK_SIZE;
      input_len -= DIGEST_BLOCK_SIZE;
    }

   This ought to look familiar; it's the main loop of the original digest function from Listing 4-13.

3. Process one entire block, update the hash, increment the input pointer and decrement the length counter. At the end, input_len is either 0 or some integer less than the block size, so just store the remaining data in the context pointer until the next time update_digest is called:

   if ( input_len > 0 )
   {
     memcpy( context->block, input, input_len );
     context->block_len = input_len;
   }

   At this point, you know that input_len is less than one block size, so there's no danger of overrunning the temporary buffer context->block.

4. Next time update_digest is called, check to see if there's any data left over from the previous call. If so, concatenate data from the input buffer onto the end of it, process the resulting block, and process whatever remaining blocks are left.

   if ( context->block_len > 0 )
   {
     // How much we need to make a full block
     int borrow_amt = DIGEST_BLOCK_SIZE - context->block_len;
   
     if ( input_len < borrow_amt )
     {

5. borrow_amt is the number of bytes needed to make a full block. If you still don't have enough, just add it to the end of the temporary block and allow the function to exit.

   memcpy( context->block 1 context->block_len, input, input_len );
      context->block_len 1= input_len;
      input_len = 0;
    }

Otherwise, go ahead and copy borrow_amt bytes into the temporary block, process that block, and continue:

else
 {
   memcpy( context->block 1 context->block_len, input, borrow_amt );
   context->block_operate( context->block, context->hash );
   context->block_len = 0;
   input 1= borrow_amt;
   input_len -= borrow_amt;
 }

Appending the Length to the Last Block

So, the caller calls update_digest repeatedly, as data becomes available, allowing it to compute a running hash code. However, to complete an MD5 or SHA-1 hash, you still have to append the length, in bits, to the end of the last block. The function finalize_digest handles what used to be the complex logic in digest_hash to figure out if the remaining data consists of one or two blocks — that is, if there's enough space for the end terminator and the length on the end of the remaining block as shown in Listing 4-23.

Listing 4-23: "digest.c" finalize digest

/**
 * Process whatever's left over in the context buffer, append
 * the length in bits, and update the hash one last time.
 */
void finalize_digest( digest_ctx *context )
{
 memset( context->block + context->block_len, 0, DIGEST_BLOCK_SIZE -

context->block_len );
 context->block[ context->block_len ] = 0x80;
 // special handling if the last block is < 64 but > 56
 if ( context->block_len >= INPUT_BLOCK_SIZE )
 {
   context->block_operate( context->block, context->hash );
   context->block_len = 0;
 memset( context->block + context->block_len, 0, DIGEST_BLOCK_SIZE -
   context->block_len );
 }
 // Only append the length for the very last block
 // Technically, this allows for 64 bits of length, but since we can only
 // process 32 bits worth, we leave the upper four bytes empty
 context->block_finalize( context->block, context->input_len * 8 );

 context->block_operate( context->block, context->hash );
}

This logic was described when it was originally presented in the context of MD5.

Listing 4-24 shows how you initialize the MD5 digest context.

Listing 4-24: "md5.c" MD5 digest initialization

void new_md5_digest( digest_ctx *context )
{
 context->hash_len = 4;
 context->input_len = 0;
 context->block_len = 0;
 context->hash = ( unsigned int * )
  malloc( context->hash_len * sizeof( unsigned int ) );
 memcpy( context->hash, md5_initial_hash,
  context->hash_len * sizeof( unsigned int ) );
 memset( context->block, '\0', DIGEST_BLOCK_SIZE );
 context->block_operate = md5_block_operate;
 context->block_finalize = md5_finalize;
}

Listing 4-25 shows how you initialize the SHA-1 context.

Listing 4-25: "sha.c" SHA-1 digest initialization

void new_sha1_digest( digest_ctx *context )
{
 context->hash_len = 5;
 context->input_len = 0;
 context->block_len = 0;
 context->hash = ( unsigned int * )
 malloc( context->hash_len * sizeof( unsigned int ) );
 memcpy( context->hash, sha1_initial_hash,
 context->hash_len * sizeof( unsigned int ) );

memset( context->block, '\0', DIGEST_BLOCK_SIZE );
 context->block_operate = sha1_block_operate;
 context->block_finalize = sha1_finalize;
}

And finally, Listing 4-26 shows how you initialize the SHA-256 context.

Listing 4-26: "sha.c" SHA-256 digest initialization

void new_sha256_digest( digest_ctx *context )
{
 context->hash_len = 8;
 context->input_len = 0;
 context->block_len = 0;
 context->hash = ( unsigned int * ) malloc( context->hash_len *
   sizeof( unsigned int ) );
 memcpy( context->hash, sha256_initial_hash, context->hash_len *
   sizeof( unsigned int ) );
 memset( context->block, '\0', DIGEST_BLOCK_SIZE );
 context->block_operate = sha256_block_operate;
 context->block_finalize = sha1_finalize;
}

Of course if you want to support more hash contexts, just add more of them here.

After the contexts have been initialized, they're just passed to update_digest as new data becomes available, and passed to finalize_digest after all the data to be hashed has been accumulated.

Computing the MD5 Hash of an Entire File

An example might help to clarify how these updateable digest functions work. Consider a real-world example — computing the MD5 hash of an entire file:

// hash a file; buffer input
 digest_ctx context;
 const char *filename = "somefile.tmp";
 char buf[ 400 ]; // purposely non-aligned to exercise updating logic
 int bytes_read;
 int f = open( filename, O_RDONLY );

 if ( !f )
 {
   fprintf( stderr, "Unable to open '%s' for reading: ", filename );
   perror( "" );
   exit( 0 );
 }

 new_md5_digest( &context );

while ( ( bytes_read = read( f, buf, 400 ) ) > 0 )
 {
   update_digest( &context, buf, bytes_read );
 }

 finalize_digest( &context );

 if ( bytes_read == −1 )
 {
   fprintf( stderr, "Error reading file '%s': ", filename );
   perror( "" );
 }

 close( f );

 {
   unsigned char *hash = ( unsigned char * ) context.hash;

   for ( i = 0; i < ( context.hash_len * 4 ); i11 )
   {
     printf( "%.02x", hash[ i ] );
   }
   printf( "\n" );
 }

 free( context.hash );

Pay special attention to how this works:

1. A new MD5 digest structure is initialized by calling new_md5_digest from Listing 4-24.
2. The file is opened and read, 400 bytes at a time.
3. These 400-byte blocks are passed into update_digest from Listing 4-22, which is responsible for computing the hash "so far," on top of the hash that's already been computed.
4. Before completing, finalize_digest from Listing 4-23 is called to append the total length of the file as required by the digest structure and the final hash is computed.
5. At this point, the context parameter can no longer be reused; if you wanted to compute another hash, you'd have to initialize another context.

The benefit of this approach is that rather than reading the whole file into memory and calling md5_hash from Listing 4-7 (which would produce the exact same result), the whole file doesn't need to be stored in memory all at once.

The hash is converted to a char array at the end so that it prints out in canonical order — remember that MD5 is little-endian; however, it's customary to display a hash value in big-endian order anyway.

This new updateable hash operation simplifies HMAC a bit because you don't need to do so much copying to get the buffers set up correctly as shown in Listing 4-27.

Listing 4-27: "hmac.c" modified HMAC function to use updateable digest functions

void hmac( unsigned char *key,
    int key_length,
    unsigned char *text,
    int text_length,
    digest_ctx *digest )
{
 unsigned char ipad[ DIGEST_BLOCK_SIZE ];
 unsigned char opad[ DIGEST_BLOCK_SIZE ];
 digest_ctx hash1;
 int i;

 // TODO if key_length > hash_block_length, should hash it using
 // "hash_function" first and then use that as the key.
 assert( key_length < DIGEST_BLOCK_SIZE );

 // "cheating"; copy the supplied digest context in here, since we don't
 // know which digest algorithm is being used
 memcpy( &hash1, digest, sizeof( digest_ctx ) );
 hash1.hash = ( unsigned int * ) malloc(
 hash1.hash_len * sizeof( unsigned int ) );
 memcpy( hash1.hash, digest->hash, hash1.hash_len * sizeof( unsigned int ) );

 memset( ipad, 0x36, DIGEST_BLOCK_SIZE );

 for ( i = 0; i < key_length; i++ )
 {
   ipad[ i ] ^= key[ i ];
 }

 update_digest( &hash1, ipad, DIGEST_BLOCK_SIZE );
 update_digest( &hash1, text, text_length );
 finalize_digest( &hash1 );

 memset( opad, 0x5C, DIGEST_BLOCK_SIZE );

 for ( i = 0; i < key_length; i++ )

{
   opad[ i ] ^= key[ i ];
 }

 update_digest( digest, opad, DIGEST_BLOCK_SIZE );
 update_digest( digest, ( unsigned char * ) hash1.hash,
 hash1.hash_len * sizeof( int ) );
 finalize_digest( digest );

 free( hash1.hash );
}

Although update_digest and finalize_digest themselves are practically impenetrable if you don't already know what they're doing, HMAC is actually much easier to read now that you've shunted memory management off to update_digest. Now you simply XOR the key with a block of 0x36s, update the digest, update it again with the text, finalize, XOR the key with another block of 0x5Cs, update another digest, update it again with the result of the first digest, and finalize that. The only real "magic" in the function is at the beginning.

memcpy( &hash1, digest, sizeof( digest_ctx ) );
 hash1.hash = ( unsigned int * ) malloc(
  hash1.hash_len * sizeof( unsigned int ) );
 memcpy( hash1.hash, digest->hash, hash1.hash_len * sizeof( unsigned int ) );

Remember that the hmac function can be called with an MD5, SHA-1, or SHA-256 context. However, the function has no way of knowing which it was called with. There are multitudes of ways to work around that: You could pass in a flag or add an initializer function to the digest_ctx structure, but the simplest way is to just memcpy the whole initialized structure at the start of the function. You know it was initialized prior to invocation; the only thing to be careful of is that hash was dynamically allocated, so you need to reallocate and recopy it. If you were doing this in C++, this would be the sort of thing you'd use a copy constructor for. OK, really, I promise to stop talking C++ now.

You can develop a main routine in Listing 4-28 to test this out.

Listing 4-28: "hmac.c" main routine

#ifdef TEST_HMAC
int main( int argc, char *argv[ ] )
{
 int i;
 digest_ctx digest;
 int key_len;
 unsigned char *key;
 int text_len;
 unsigned char *text;

if ( argc < 4 )
 {
   fprintf( stderr, "usage: %s [-sha1|md5] [0x]<key> [0x]<text>\n", argv[ 0 ] );
   exit( 0 );
 }

 if ( !( strcmp( argv[ 1 ], "-sha1" ) ) )
 {
   new_sha1_digest( &digest );
 }
 else if ( !( strcmp( argv[ 1 ], "-md5" ) ) )
 {
   new_md5_digest( &digest );
 }
 else
 {
   fprintf( stderr, "usage: %s [-sha1|md5] <key> <text>\n", argv[ 0 ] );
   exit( 1 );
 }

 key_len = hex_decode( argv[ 2 ], &key );
 text_len = hex_decode( argv[ 3 ], &text );

 hmac( key, key_len, text, text_len, &digest );

 for ( i = 0; i < digest.hash_len * sizeof( int ); i++ )
 {
   printf( "%.02x", ( ( unsigned char *) digest.hash )[ i ] );
 }
 printf( "\n" );

 free( digest.hash );
 free( key );
 free( text );

 return 0;
}
#endif

To compute an HMAC, call it like this:

jdavies@localhost$ hmac -md5 Jefe "what do ya want for nothing?"
750c783e6ab0b503eaa86e310a5db738

Where Does All of This Fit into SSL?

You may still be wondering what all this has to do with SSL. After all, you have secure key exchange and symmetric cryptography. Where does the HMAC function fit in?

SSL requires that every record first be HMAC'ed before being encrypted. This may seem like overkill — after all, HMAC guarantees the integrity of a record. But because you're using symmetric cryptography, the odds are infinitesimally small that an attacker could modify a record in such a way that it decrypts meaningfully, at least without access to the session key. Consider a secure application that transmits the message, "Withdraw troops from Bunker Hill and move them to Normandy beach." If you run this through the AES algorithm with the key "passwordsecurity" and the initialization vector "initializationvc," you get:

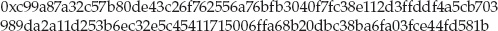
So far, so good. An attacker can't modify the message and move the troops — say, to Fort Knox — without the key. If he tries to change even one bit of the message, it decrypts to gibberish and is presumably rejected.

He can, however, cut half of it off. The attacker could modify the encrypted message to be

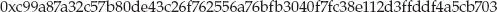
This message is received and decrypted correctly to "Withdraw troops from Bunker Hill." The recipient has no way to detect the modification. For this reason, some hash function must be used to verify the integrity of the message after it's been decrypted. SSL mandates that every record be protected this way with an HMAC function. You examine this in more detail when the details of the SSL protocol are discussed.

Also, SSL uses the HMAC function quite a bit as a pseudo-random number generator. Because the output is not predictably related to the input, the HMAC function is actually used to generate the keying material from a shared secret. In fact, the HMAC function is used to generate the final HMAC secret!

Understanding Digital Signature Algorithm (DSA) Signatures

Now it's time to return to the primary topic of this chapter — digital signatures. Recall from the beginning of this chapter that, in order to properly support digital signatures, you must first compute a secure hash of the document/message that you want to sign, and then perform a public-key operation on that secure hash using a private key. By now, you should have a very good understanding of secure hash algorithms, but not the actual mechanics of what to do with those secure hashes because this hasn't yet been covered.

RSA support for digital signatures is straightforward — compute a secure hash over the bytes to be signed and "encrypt" it using a private key. The recipient then verifies the same signature by computing the secure hash of the same set of bytes, "decrypting" using the associated public key, and comparing the two. The only difference between an RSA digital signature and an RSA encryption (other than the fact that encryption is done with a public key and signing is done with a private key) is that the padding type from Listing 3-21 is 0x01, instead of 0x02, and the padding bytes are all 1s instead of random bytes.

However, RSA isn't the only game in town, at least not when it comes to digital signatures. A competing standard is the U.S. government's Digital Signature Algorithm, specified in FIPS 186-3.

Implementing Sender-Side DSA Signature Generation

If you were pleasantly surprised by the simplicity and elegance of the RSA algorithm, where encryption, decryption, signatures, and verification were all essentially the same operation with different parameters, DSA is going to be a bit of a shock to your system. The signature and verification operations are both completely different, and both are fairly complex. They also take quite a few extra parameters.

A DSA signature accepts five input parameters, including the message to be signed, and returns two output parameters. The input parameters are named g, p, q, and x (and, of course, the message itself). g, p, and q are part of the public key, and x is the private key. Like RSA, the signature is performed on a secure hash of the message to be signed. However, the hash algorithm is somewhat part of the signature, so you can't necessarily just pick a random signature algorithm and try to apply it. DSA is certified for SHA-1 and SHA-256; if you try to use it with some other hash algorithm, "behavior is undefined."

So, to generate the two-element DSA signature, whose elements are named r and s by the standard (apparently nobody ever told the FIPS people the general rule on using meaningful variable names), you perform the following computations:

where (k⁻¹ % q) means the inverse mod q, as defined in Chapter 3, of k.

What about this c? c is just a random number — securely generated, of course — whose length in bits is the same as q. After performing these operations, you've generated r and s, which make up the signature.

To slightly minimize the method signatures, define a new structure named dsa_params in Listing 4-29 to hold the general parameters g, p, and q.

Listing 4-29: "dsa.h" dsa_params structure

typedef struct
{
 huge g;
 huge p;
 huge q;
}
dsa_params;

Define the structure in Listing 4-30 to hold the actual signature.

Listing 4-30: "dsa.h" dsa_signature structure

typedef struct
{
 huge r;
 huge s;
}
dsa_signature;

So now, in code, the signature algorithm can be implemented as shown in Listing 4-31.

Listing 4-31: "dsa.c" DSA signature generation algorithm

void dsa_sign( dsa_params *params,
      huge *private_key,
      unsigned int *hash,
      int hash_len,
      dsa_signature *signature )
{
 huge k;
 huge z;
 huge q;

 set_huge( &q, 1 );

 generate_message_secret( params, &k );
 // r = ( g ^ k % p ) % q
 mod_pow( &params->g, &k, &params->p, &signature->r );
 copy_huge( &q, &params->q );
 divide( &signature->r, &q, NULL );

 // z = hash(message), only approved with SHA
 load_huge( &z, ( unsigned char * ) hash,
  ( (hash_len * 4 ) < params->q.size ) ?
  (hash_len * 4 ) : params->q.size );

// s = ( inv(k) * ( z + xr ) ) % q
 inv( &k, &params->q );
 set_huge( &signature->s, 0 );
 copy_huge( &signature->s, private_key );
 multiply( &signature->s, &signature->r );
 add( &signature->s, &z );
 multiply( &signature->s, &k );
 copy_huge( &q, &params->q );
 divide( &signature->s, &q, NULL );

 free_huge( &z );
}

Notice that this keeps essentially the same variable names that the specification suggests, although it does call x private_key to make it a bit clearer what it does. You should be able to follow the last parts of the code. I've added comments to indicate what each section is doing with respect to the overall algorithm. Note that this calls the inv routine defined in Listing 3-36 to compute (k^–1 % q) as part of the computation of s. Also, the caller passes in the hash, not the message itself; this makes the routine a bit more flexible, although DSA is only officially approved for use with SHA. The signature function doesn't know or care what the original message was.

The computation of k is delegated to its own routine in Listing 4-32.

Listing 4-32: "dsa.c" message secret generation

static void generate_message_secret( dsa_params *params, huge *k )
{
 int i;
 huge q;
 huge one;

 set_huge( &q, 0 ); // initialize this so that copy works
 set_huge( &one, 1 );

 copy_huge( &q, &params->q );
 subtract( &q, &one );

 // XXX the extra + 8 aren't really necessary since we're not generating
 // a random "c"
 k->sign = 0;
 k->size = params->q.size + 8;
 k->rep = malloc( k->size );
 // TODO this should be filled with random bytes
 for ( i = 0; i < k->size; i++ )
 {
   k->rep[ i ] = i + 1;
 }

// k will become k % ( q - 1 );
 divide( k, &q, NULL );
 add( k, &one );
}

The whole dsa_params structure is passed here, although technically only q is required.

So, given a message, a set of DSA parameters, and a private key, you can compute a DSA signature for the message. Remember that a DSA signature consists of two separate elements. Because r and s are both computed mod q, they are of the same length as q, but they have to be separated somehow in the output. This is in contrast to an RSA signature which is just a single, very long, number. You'll see in Chapter 5 that this comes up as a bit of an issue in SSL/TLS.

Implementing Receiver-Side DSA Signature Verification

Now you may be saying, "OK, that DSA signature algorithm was a little complex, but it wasn't that bad." Get ready to see the signature verification algorithm.

Remember that the purpose of this whole thing is for the holder of the private key to be able to transmit, in some authenticated way, the public key and the signature to anybody else and allow that person to verify that only the holder of the private key could have produced that signature over the given message. With RSA, verification was a trivial extension of signature generation. You "encrypt" a hash using the private key, and the recipient "decrypts" using the public key and compares the hashes. If the two match, the signature is verified.

Because DSA isn't encrypting or decrypting anything, DSA signature verification is a bit more complex. The recipient has the DSA parameters g, p, and q, the public key y and the signature elements r and s — along with, of course, the message itself. From this, it needs to check to see if r and s were generated from g, p, q, x, and the message. The DSA way to accomplish this is to perform the following operations:

If everything went correctly, v is equal to r. Otherwise, something went wrong or the signature is faked.

The signature part, then, is in r; s is just transmitted to allow the recipient to invert enough of the original computation to recover r. The security is mostly in the secrecy of the parameter k — which, you'll recall, was generated randomly in the signature stage. Since s depends on k and the private key x — and x and y are of course mathematically related — v depends on s and y. The whole complicated mess described in this section just repeats the computation

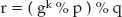
without having access to k.

In code, this can be implemented as in Listing 4-33.

Listing 4-33: "dsa.c" DSA signature verification algorithm

int dsa_verify( dsa_params *params,
                                    huge *public_key,
                                    unsigned int *hash,
                                    int hash_len,
                                    dsa_signature *signature )
{
 int match;
 huge w, z, u1, u2, q, p;

 set_huge( &q, 1 );
 set_huge( &p, 1 );
 set_huge( &w, 0 );

 // w = inv(s) % q
 copy_huge( &w, &signature->s );
 inv( &w, &params->q );

 // z = hash(message), truncated to sizeof(q)
 load_huge( &z, ( unsigned char * ) hash,
  ( (hash_len * 4 ) < params->q.size ) ?
  (hash_len * 4 ) : params->q.size );

 // u1 = (zw) % q
 multiply( &z, &w );
 copy_huge( &q, &params->q );
 divide( &z, &params->q, NULL );  // u1 = z

 // u2 = (rw) % q
 multiply( &w, &signature->r );
 copy_huge( &q, &params->q );
 divide( &w, &q, NULL ); // u2 = w

 // v = ( ( ( g^u1) % p * (y^u2) %p ) % p ) % q
 mod_pow( &params->g, &z, &params->p, &u1 );
 mod_pow( public_key, &w, &params->p, &u2 );
 multiply( &u1, &u2 );
 copy_huge( &p, &params->p );
 divide( &u1, &p, NULL );

copy_huge( &q, &params->q );
 divide( &u1, &q, NULL ); // u1 is "v" now

 // Check to see if v & s match
 match = !compare( &u1, &signature->r );

 free_huge( &w );
 free_huge( &z );
 free_huge( &u1 );
 free_huge( &u2 );

 return match;
}

As with the signing algorithm, I've added comments so that you can match what the code is doing with the algorithm. Notice that this doesn't use u1 and u2 exactly as they're shown in the algorithm, instead putting u1 and u2 into z and w because you don't need them again, and then using u1 and u2 to hold the mod_pow values later on.

Also notice how:

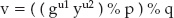
is put together. You don't want to compute g^u1, then compute y^u2 and then multiply them by each other to finally figure out "mod p" of the whole mess. You want to be able to use your mod_pow algorithm to keep the memory constraints manageable. So instead, factor the v computation out into

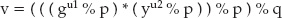
by the distributivity of the modulus operator. Now you can use mod_pow to compute (g^u1) % p and ( y^u2 % p), multiply these together, which results in at most 2p bits, and then apply the modulus operation twice.

You can put together a main routine to test this but, like RSA's e, d, and n, the DSA parameters g, p, q, x, and y must be specifically related and you haven't yet seen how. So just hardcode a sample set in the routine in Listing 4-34 to show how it can be called.

Listing 4-34: "dsa.c" test main routine

#ifdef TEST_DSA
int main( int argc, char *argv[] )
{
 unsigned char priv[] = {
0x53, 0x61, 0xae, 0x4f, 0x6f, 0x25, 0x98, 0xde, 0xc4, 0xbf, 0x0b, 0xbe, 0x09,
 0x5f, 0xdf,  0x90, 0x2f, 0x4c, 0x8e, 0x09 };
 unsigned char pub[] = {
0x1b, 0x91, 0x4c, 0xa9, 0x73, 0xdc, 0x06, 0x0d, 0x21, 0xc6, 0xff, 0xab, 0xf6,

0xad, 0xf4, 0x11, 0x97, 0xaf, 0x23, 0x48, 0x50, 0xa8, 0xf3, 0xdb, 0x2e, 0xe6,
 0x27, 0x8c, 0x40, 0x4c,  0xb3, 0xc8, 0xfe, 0x79, 0x7e, 0x89, 0x48, 0x90, 0x27,
 0x92, 0x6f, 0x5b, 0xc5, 0xe6, 0x8f,  0x91, 0x4c, 0xe9, 0x4f, 0xed, 0x0d, 0x3c,
 0x17, 0x09, 0xeb, 0x97, 0xac, 0x29, 0x77, 0xd5,  0x19, 0xe7, 0x4d, 0x17 };
 unsigned char P[] = {
0x00, 0x9c, 0x4c, 0xaa, 0x76, 0x31, 0x2e, 0x71, 0x4d, 0x31, 0xd6, 0xe4, 0xd7,
 0xe9, 0xa7,  0x29, 0x7b, 0x7f, 0x05, 0xee, 0xfd, 0xca, 0x35, 0x14, 0x1e, 0x9f,
 0xe5, 0xc0, 0x2a, 0xe0,  0x12, 0xd9, 0xc4, 0xc0, 0xde, 0xcc, 0x66, 0x96, 0x2f,
 0xf1, 0x8f, 0x1a, 0xe1, 0xe8, 0xbf,  0xc2, 0x29, 0x0d, 0x27, 0x07, 0x48, 0xb9,
 0x71, 0x04, 0xec, 0xc7, 0xf4, 0x16, 0x2e, 0x50,  0x8d, 0x67, 0x14, 0x84, 0x7b };
 unsigned char Q[] = {
0x00, 0xac, 0x6f, 0xc1, 0x37, 0xef, 0x16, 0x74, 0x52, 0x6a, 0xeb, 0xc5, 0xf8,
 0xf2, 0x1f,  0x53, 0xf4, 0x0f, 0xe0, 0x51, 0x5f };
 unsigned char G[] = {
0x7d, 0xcd, 0x66, 0x81, 0x61, 0x52, 0x21, 0x10, 0xf7, 0xa0, 0x83, 0x4c, 0x5f,
 0xc8, 0x84,  0xca, 0xe8, 0x8a, 0x9b, 0x9f, 0x19, 0x14, 0x8c, 0x7d, 0xd0, 0xee,
 0x33, 0xce, 0xb4, 0x57,  0x2d, 0x5e, 0x78, 0x3f, 0x06, 0xd7, 0xb3, 0xd6, 0x40,
 0x70, 0x2e, 0xb6, 0x12, 0x3f, 0x4a,  0x61, 0x38, 0xae, 0x72, 0x12, 0xfb, 0x77,
 0xde, 0x53, 0xb3, 0xa1, 0x99, 0xd8, 0xa8, 0x19,  0x96, 0xf7, 0x7f, 0x99 };
 dsa_params params;
 dsa_signature signature;
 huge x, y;
 unsigned char *msg = "abc123";
 digest_ctx ctx;

 // TODO load these from a DSA private key file instead
 load_huge( &params.g, G, sizeof( G ) );
 load_huge( &params.p, P, sizeof( P ) );
 load_huge( &params.q, Q, sizeof( Q ) );
 load_huge( &x, priv, sizeof( priv ) );
 load_huge( &y, pub, sizeof( pub ) );

 new_sha1_digest( &ctx );
 update_digest( &ctx, msg, strlen( msg ) );
 finalize_digest( &ctx );

 dsa_sign( &params, &x, ctx.hash, ctx.hash_len, &signature );

 printf( "DSA signature of abc123 is:" );
 printf( "r:" );
 show_hex( signature.r.rep, signature.r.size );
 printf( "s:" );
 show_hex( signature.s.rep, signature.s.size );

 if ( dsa_verify( &params, &y, ctx.hash, ctx.hash_len, &signature ) )
 {
   printf( "Verified\n" );
 }
 else

{
   printf( "Verificiation failed\n" );
 }

 free_huge( &x );
 free_huge( &y );

 return 0;
}
#endif

The output of this function isn't too interesting.

jdavies@localhost$ ./dsa
DSA signature of abc123 is:
r: 14297f2522458d809b6c5752d3975a00bb0d89e0
s: 2f6e24ed330faf27700470cc6074552e58cbea3a
Verifying:
Verified

But it illustrates how DSA signatures are generated. You can see a noticeable pause when this example runs; public-key cryptography strikes again.

How to Make DSA Efficient

As you can imagine, it takes a bit longer to compute or verify a DSA signature than it does to compute or verify an RSA signature. The parameters p and y need to be at least 512 bits to be secure (2,048 bits is common). q and x can be a bit shorter; typically these are 160 bits, to match the output from an SHA-1 hash, and can still be secure as long as p and y are long. Still, this requires a lot of computation and a lot of memory compared to RSA.

However, if you look at the signature algorithm, you notice that the only part that depends on the message is s — r can actually be precomputed before the message is known, as long as q is known because the secret parameter k depends on it. Because p, g, and q are part of the public key, a very speed-conscious implementation could create a table of r and k values and speed up the signature process quite a bit.

Also, notice that RSA verification involves a modular exponentiation of an enormous parameter d, which is 1,024 bits for reasonable security. This takes a long time to process. In contrast, DSA signature verification only requires modular exponentiation of u1 and u2, which are both the same length as q, which is 160 bits. On the other hand, you have to compute a modular inverse for every signature verification.

Finally, notice that although mod_pow is aware of, and optimized for, the fact that it's operating in a Galois field (that is, the final result is computed modulo a target p), the DSA implementation here does several multiplication and addition operations only to throw away all but the "mod p" bits of the results. If you reworked your add and multiply operations to be aware of their field, you could cut down quite a bit on the amount of memory you'd need to set aside to compute interim results. You could even speed up mod_pow this way. This optimization won't be explored here; see Michael Brown's paper "Software Implementations of the NIST Elliptic Curves over Prime Fields" (www.eng.auburn.edu/users/hamilton/security/pubs/Software_Implementation_of_the_NIST_Elliptic.pdf) for a good discussion on optimal arithmetic operations in a Galois field. The paper itself is about elliptic-curve cryptography, but a lot of it is applicable to large-number modular arithmetic in general.

DSA is not particularly common, or popular, in spite of being a U.S. government standard (in fact, I wasn't able to find any U.S. government web sites using SSL with DSA, including the NIST web site, which published the DSA standard in the first place!). Still, it's worth examining both because support for it is a mandatory part of TLS as well as because supporting it demonstrates how flexible you need to be on signature algorithms.

Getting More Security per Bit: Elliptic Curve DSA

DSA has been defined using ECC primitives, just like DH was. For the most part, ECDSA works like DSA, but it uses elliptic-curve keypairs instead of public/private keypairs. Instead of r being ( g^k % p ) % q, r is just G — the generator point that is part of an elliptic-curve's definition — multiplied by k. s is computed identically; remember that in an elliptic-curve keypair, the private key is just an integer. Signature verification is also almost identical up until the computation of v (which is compared to r and, if they're identical, indicates that the signature is verified). Even this computation is similar; you just replace the mod_pow operations with ECC point-multiplication operations.

However, for ECDSA, you can't "cheat" and just use integer operations like in the ECDH implementation of the last chapter; remember that there's a hash computation that's used in the signature generation process. The smallest hash examined so far is MD5, which outputs 128 bits — quite a few more than you can fit into a 32-bit int. In fact, ECDSA is only defined for an SHA-256 hash, unlike "regular" DSA, which used a plain-old 160-bit SHA-1 hash. Because you're going to be dealing with a 256-bit integer, at least, go ahead and rewrite the elliptic-curve math functions from Chapter 3 to work with huge integers.

Rewriting the Elliptic-Curve Math Functions to Support Large Numbers

The implementations are, obviously, not drastically different than with 32-bit integers; a few things are shuffled around to reduce the number of temporary huge objects, though, so you might want to compare this code carefully to the ECC code in Chapter 3.

If you recall, ECC involves two operations: point addition — which works on two distinct points in a Cartesian plane, whose X-values must be different — and point multiplication — which works on one point and a scalar value. To implement, follow these steps:

1. Redefine the point, elliptic_curve, and ecc_key structures in Listing 4-35 to work with huges instead of points.

   Listing 4-35: "ecc.h" elliptic curve structure declarations

   typedef struct
   {
    huge x;
    huge y;
   }
   point;
   
   typedef struct
   {
    huge p;
    huge a;
    huge b;
    point G;
    huge n; // n is prime and is the "order" of G
    huge h; // h = #E(F_p)/n (# is the number of points on the curve)
   }
   elliptic_curve;
   
   typedef struct
   {
    huge d;  // random integer < n; this is the private key
    point Q; // Q = d * G; this is the public key
   }
   ecc_key;

2. You need an add_points operation in Listing 4-36.

   Listing 4-36: "ecc.c" point addition implementation

   void add_points( point *p1, point *p2, huge *p )
   {
    point p3;
    huge denominator;
    huge numerator;
    huge invdenom;
    huge lambda;
   
    set_huge( &denominator, 0 );
    copy_huge( &denominator, &p2->x );    // denominator = x2
    subtract( &denominator, &p1->x );     // denominator = x2 - x1
    set_huge( &numerator, 0 );
    copy_huge( &numerator, &p2->y );      // numerator = y2
    subtract( &numerator, &p1->y );       // numerator = y2 - y1
    set_huge( &invdenom, 0 );
    copy_huge( &invdenom, &denominator );
    inv( &invdenom, p );
    set_huge( &lambda, 0 );
    copy_huge( &lambda, &numerator );
    multiply( &lambda, &invdenom );       // lambda = numerator / denominator
    set_huge( &p3.x, 0 );
    copy_huge( &p3.x, &lambda );    // x3 = lambda
    multiply( &p3.x, &lambda );     // x3 = lambda * lambda
    subtract( &p3.x, &p1->x );   // x3 = ( lambda * lambda ) - x1
    subtract( &p3.x, &p2->x );   // x3 = ( lambda * lambda ) - x1 - x2
   
    divide( &p3.x, p, NULL );       // x3 = ( ( lamdba * lambda ) - x1 - x2 ) % p
   
    // positive remainder always
    if ( p3.x.sign )
    {
      p3.x.sign = 0;
      subtract( &p3.x, p );
      p3.x.sign = 0;
    }
   
    set_huge( &p3.y, 0 );
    copy_huge( &p3.y, &p1->x ); // y3 = x1
    subtract( &p3.y, &p3.x );      // y3 = x1 - x3
    multiply( &p3.y, &lambda );    // y3 = ( x1 - x3 ) * lambda
    subtract( &p3.y, &p1->y );  // y3 = ( ( x1 - x3 ) * lambda ) - y
   
    divide( &p3.y, p, NULL );
    // positive remainder always
    if ( p3.y.sign )
    {
      p3.y.sign = 0;
      subtract( &p3.y, p );
      p3.y.sign = 0;
    }

   // p1->x = p3.x
    // p1->y = p3.y
    copy_huge( &p1->x, &p3.x );
    copy_huge( &p1->y, &p3.y );
   
    free_huge( &p3.x );
    free_huge( &p3.y );
    free_huge( &denominator );
    free_huge( &numerator );
    free_huge( &invdenom );
    free_huge( &lambda );
   }

   I've left comments indicating the int operations that the huge operation blocks correspond to so you can cross-reference this implementation back to the easier-to-understand integer-based operation in Listing 3-39.

3. Recall that multiplication is defined in terms of "double-and-add" — in this case, not as a performance optimization, but because adding a point to itself is actually not defined, so you need a double_point operation in Listing 4-37.

   Listing 4-37: "ecc.c" point-doubling algorithm

   static void double_point( point *p1, huge *a, huge *p )
   {
    huge lambda;
    huge l1;
    huge x1;
    huge y1;
   
    set_huge( &lambda, 0 );
    set_huge( &x1, 0 );
    set_huge( &y1, 0 );
    set_huge( &lambda, 2 );     // lambda = 2;
    multiply( &lambda, &p1->y );  // lambda = 2 * y1
    inv( &lambda, p );       // lambda = ( 2 * y1 ) ^ −1 (% p)
   
    set_huge( &l1, 3 );       // l1 = 3
    multiply( &l1, &p1->x );    // l1 = 3 * x
    multiply( &l1, &p1->x );    // l1 = 3 * x ^ 2
    add( &l1, a );         // l1 = ( 3 * x ^ 2 ) + a
    multiply( &lambda, &l1 );    // lambda = [ ( 3 * x ^ 2 ) + a ] / [ 2 * y1 ] ) % p
    copy_huge( &y1, &p1->y );
    // Note - make two copies of x2; this one is for y1 below
    copy_huge( &p1->y, &p1->x );
    set_huge( &x1, 2 );
    multiply( &x1, &p1->x );    // x1 = 2 * x1
   
    copy_huge( &p1->x, &lambda );  // x1 = lambda

   multiply( &p1->x, &lambda );  // x1 = ( lambda ^ 2 );
    subtract( &p1->x, &x1 );    // x1 = ( lambda ^ 2 ) - ( 2 * x1 )
    divide( &p1->x, p, NULL );   // [ x1 = ( lambda ^ 2 ) - ( 2 * x1 ) ] % p
   
    if ( p1->x.sign )
    {
      subtract( &p1->x, p );
      p1->x.sign = 0;
      subtract( &p1->x, p );
    }
    subtract( &p1->y, &p1->x );  // y3 = x3 – x1
    multiply( &p1->y, &lambda ); // y3 = lambda * ( x3 - x1 );
    subtract( &p1->y, &y1 );   // y3 = ( lambda * ( x3 - x1 ) ) - y1
    divide( &p1->y, p, NULL );  // y3 = [ ( lambda * ( x3 - x1 ) ) - y1 ] % p
    if ( p1->y.sign )
    {
      p1->y.sign = 0;
      subtract( &p1->y, p );
      p1->y.sign = 0;
    }
   
    free_huge( &lambda );
    free_huge( &x1 );
    free_huge( &y1 );
    free_huge( &l1 );
   }

4. Finally, you can implement multiply_point in Listing 4-38, the really important function, in terms of double_point and add_points.

   Listing 4-38: "ecc.c" point-multiplication algorithm

   void multiply_point( point *p1, huge *k, huge *a, huge *p )
   {
    int i;
    unsigned char mask;
    point dp;
    int paf = 1;
   
    set_huge( &dp.x, 0 );
    set_huge( &dp.y, 0 );
    copy_huge( &dp.x, &p1->x );
    copy_huge( &dp.y, &p1->y );
    for ( i = k->size; i; i-- )
    {
      for ( mask = 0x01; mask; mask <<= 1 )
      {
        if ( k->rep[ i - 1 ] & mask )
        {
         if ( paf )
         {

   paf = 0;
           copy_huge( &p1->x, &dp.x );
           copy_huge( &p1->y, &dp.y );
         }
         else
         {
           add_points( p1, &dp, p );
         }
       }
       // double dp
       double_point( &dp, a, p );
      }
    }
   
    free_huge( &dp.x );
    free_huge( &dp.y );
   }

You might want to compare this implementation to the multiply function presented in Listing 3-41. There is, of course, no divide equivalent. If there were, ECC wouldn't be cryptographically secure.

Implementing ECDSA

Now you have enough ammunition to put together an implementation of ECDSA. Recall that DSA signature generation involved the computation of two numbers r and s from the parameters g, p, and q. ECDSA signatures are similar. In essence, the modular multiplications are replaced by point multiplications. The generator is a point on an elliptic curve; r is that point multiplied by a random integer k; and s is computed exactly the same way as in DSA. The only elliptic-curve function involved is in the computation of r. In code, this is shown in Listing 4-39.

Listing 4-39: "ecdsa.c" elliptic-curve DSA signature generation

void ecdsa_sign( elliptic_curve *params,
                huge *private_key,
                unsigned int *hash,
                int hash_len,
                dsa_signature *signature )
{
 unsigned char K[] = {
   0x9E, 0x56, 0xF5, 0x09, 0x19, 0x67, 0x84, 0xD9, 0x63, 0xD1, 0xC0,
   0xA4, 0x01, 0x51, 0x0E, 0xE7, 0xAD, 0xA3, 0xDC, 0xC5, 0xDE, 0xE0,
   0x4B, 0x15, 0x4B, 0xF6, 0x1A, 0xF1, 0xD5, 0xA6, 0xDE, 0xCE
 };
 huge k;
 point X;
 huge z;

// This should be a random number between 0 and n-1
 load_huge( &k, ( unsigned char * ) K, sizeof( K ) );

 set_huge( &X.x, 0 );
 set_huge( &X.y, 0 );
 copy_huge( &X.x, &params->G.x );
 copy_huge( &X.y, &params->G.y );

 multiply_point( &X, &k, &params->a, &params->p );

 set_huge( &signature->r, 0 );
 copy_huge( &signature->r, &X.x );
 divide( &signature->r, &params->n, NULL ); // r = x1 % n

 // z is the L_n leftmost bits of hash - cannot be longer than n
 load_huge( &z, ( unsigned char * ) hash,
    ( ( hash_len * 4 ) < params->n.size ) ? ( hash_len * 4 ) : params->n.size );

 // s = k^-1 ( z + r d_a ) % n
 inv( &k, &params->n );
 set_huge( &signature->s, 0 );
 copy_huge( &signature->s, private_key );
 multiply( &signature->s, &signature->r );
 add( &signature->s, &z );
 multiply( &signature->s, &k );
 divide( &signature->s, &params->n, NULL );

 free_huge( &k );
 free_huge( &z );
 free_huge( &X.x );
 free_huge( &X.y );
}

You can see a lot of parallels between the DSA signature verification routine and the ECDSA signature verification routine in Listing 4-40.

Listing 4-40: "ecdsa.c" elliptic-curve DSA signature verification

int ecdsa_verify( elliptic_curve *params,
        point *public_key,
        unsigned int *hash,
        int hash_len,
        dsa_signature *signature )
{
 huge z;
 huge w;
 point G;
 point Q;
 int match;

 // w = s^-1 % n

set_huge( &w, 0 );
 copy_huge( &w, &signature->s );
 inv( &w, &params->n );

 // z is the L_n leftmost bits of hash - cannot be longer than n
 load_huge( &z, ( unsigned char * ) hash,
  ( ( hash_len * 4 ) < params->n.size ) ? ( hash_len * 4 ) : params->n.size );

 // u1 = zw % n
 multiply( &z, &w );
 divide( &z, &params->n, NULL );  // u1 = z

 // u2 = (rw) % q
 multiply( &w, &signature->r );
 divide( &w, &params->n, NULL ); // u2 = w

 // (x1,y1) = u1 * G + u2 * Q
 set_huge( &G.x, 0 );
 set_huge( &G.y, 0 );
 set_huge( &Q.x, 0 );
 set_huge( &Q.y, 0 );
 copy_huge( &G.x, &params->G.x );
 copy_huge( &G.y, &params->G.y );
 copy_huge( &Q.x, &public_key->x );
 copy_huge( &Q.y, &public_key->y );

 multiply_point( &G, &z, &params->a, &params->p );
 multiply_point( &Q, &w, &params->a, &params->p );
 add_points( &G, &Q, &params->p );

 // r = x1 % n
 divide( &G.x, &params->n, NULL );

 match = !compare( &G.x, &signature->r );

 free_huge( &z );
 free_huge( &w );
 free_huge( &G.x );
 free_huge( &G.y );
 free_huge( &Q.x );
 free_huge( &Q.y );

 return match;
}

Here, as in signature generation, modular exponentiation has been replaced with elliptic-curve addition and multiplication operations.

Generating ECC Keypairs

One point glossed over thus far is that of the elliptic-curve parameters themselves. In fact, generating elliptic-curve parameters is so complex, so time consuming, and so hard to get right that the NIST publishes a list of approved named curves for use in elliptic curve operations. Of course, the actual keypairs — the secret integer and the public point — are generated per-user from the parameters. Generating a keypair is actually pretty simple: Pick a random large integer d and multiply it by the point G. The result of the multiplication is the public key, and d is the private key.

To illustrate how to use this, you can borrow an elliptic curve from RFC 4754 that includes some ECDSA examples. The test routine is shown in Listing 4-41.

Listing 4-41: "ecdsa.c" test routine

#ifdef TEST_ECDSA
int main( int argc, char *argv[ ] )
{
 // ECC parameters
 unsigned char P[] = {
0xFF, 0xFF, 0xFF, 0xFF, 0x00, 0x00, 0x00, 0x01, 0x00, 0x00, 0x00, 0x00, 0x00,
0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0xFF, 0xFF, 0xFF, 0xFF, 0xFF, 0xFF,
0xFF, 0xFF, 0xFF, 0xFF, 0xFF, 0xFF
 };
 unsigned char b[] = {
 0x5A, 0xC6, 0x35, 0xD8, 0xAA, 0x3A, 0x93, 0xE7, 0xB3, 0xEB, 0xBD, 0x55, 0x76,
 0x98, 0x86,  0xBC, 0x65, 0x1D, 0x06, 0xB0, 0xCC, 0x53, 0xB0, 0xF6, 0x3B, 0xCE,
 0x3C, 0x3E, 0x27, 0xD2, 0x60, 0x4B
 };
 unsigned char q[] = {
 0xFF, 0xFF, 0xFF, 0xFF, 0x00, 0x00, 0x00, 0x00, 0xFF, 0xFF, 0xFF, 0xFF, 0xFF,
 0xFF, 0xFF, 0xFF, 0xBC, 0xE6, 0xFA, 0xAD, 0xA7, 0x17, 0x9E, 0x84, 0xF3, 0xB9,
 0xCA, 0xC2, 0xFC, 0x63, 0x25, 0x51
 };
 unsigned char gx[] = {
   0x6B, 0x17, 0xD1, 0xF2, 0xE1, 0x2C, 0x42, 0x47, 0xF8, 0xBC, 0xE6, 0xE5,
 0x63,
   0xA4, 0x40, 0xF2, 0x77, 0x03, 0x7D, 0x81, 0x2D, 0xEB, 0x33, 0xA0, 0xF4,
 0xA1,
   0x39, 0x45, 0xD8, 0x98, 0xC2, 0x96
 };
 unsigned char gy[] = {
 0x4F, 0xE3, 0x42, 0xE2, 0xFE, 0x1A, 0x7F, 0x9B, 0x8E, 0xE7, 0xEB, 0x4A, 0x7C,
 0x0F, 0x9E, 0x16, 0x2B, 0xCE, 0x33, 0x57, 0x6B, 0x31, 0x5E, 0xCE, 0xCB, 0xB6,
 0x40, 0x68, 0x37, 0xBF, 0x51, 0xF5
 };

 // key
 unsigned char w[] = { 0xDC, 0x51, 0xD3, 0x86, 0x6A, 0x15, 0xBA, 0xCD, 0xE3,
 0x3D, 0x96, 0xF9, 0x92, 0xFC, 0xA9, 0x9D, 0xA7, 0xE6, 0xEF, 0x09, 0x34, 0xE7,

0x09, 0x75, 0x59, 0xC2, 0x7F, 0x16, 0x14, 0xC8, 0x8A, 0x7F };

 elliptic_curve curve;
 ecc_key A;
 dsa_signature signature;

 digest_ctx ctx;

 load_huge( &curve.p, ( unsigned char * ) P, sizeof( P ) );
 set_huge( &curve.a, 3 );
 curve.a.sign = 1;
 load_huge( &curve.b, b, sizeof( b ) );
 load_huge( &curve.G.x, gx, sizeof( gx ) );
 load_huge( &curve.G.y, gy, sizeof( gy ) );
 load_huge( &curve.n, q, sizeof( q ) );

 // Generate new public key from private key "w" and point "G"
 load_huge( &A.d, w, sizeof( w ) );
 set_huge( &A.Q.x, 0 );
 set_huge( &A.Q.y, 0 );
 copy_huge( &A.Q.x, &curve.G.x );
 copy_huge( &A.Q.y, &curve.G.y );
 multiply_point( &A.Q, &A.d, &curve.a, &curve.p );

 new_sha256_digest( &ctx );
 update_digest( &ctx, "abc", 3 );
 finalize_digest( &ctx );

 ecdsa_sign( &curve, &A.d, ctx.hash, ctx.hash_len, &signature );

 printf( "R:" );
 show_hex( signature.r.rep, signature.r.size );
 printf( "S:" );
 show_hex( signature.s.rep, signature.r.size );

 if ( !ecdsa_verify( &curve, &A.Q, ctx.hash, ctx.hash_len, &signature ) )
 {
   printf( "Signatures don't match.\n" );
 }
 else
 {
   printf( "Signature verified.\n" );
 }

 return 0;
}
#endif

Like the DSA test routine output, this one isn't particularly interesting, but it demonstrates the concept:

jdavies@localhost$ ./ecdsa

R:
cb28e0999b9c7715fd0a80d8e47a77079716cbbf917dd72e97566ea1c066957c
S:
86fa3bb4e26cad5bf90b7f81899256ce7594bb1ea0c89212748bff3b3d5b0315
Verifying
Signature verified.

If you ran this on your own computer, you may have noticed that it was slow. Murderously slow, in fact. Each point-multiplication operation requires between log₂k and 2 * log₂k modular inversions, each of which involves many operations in its own right. Nor can you speed the thing up by precomputing some inversions and reusing them because λ is going to be different for each call. The whole process, including the generation of the public key, took me three minutes on a relatively modern computer running Windows Vista, and this was a 256-bit key — although, for ECC, that's actually pretty long whereas for RSA or DSA it would be unusably short.

So, what's the point of ECC, then? The idea was that it was supposed to be faster. Actually, there's been quite a bit of research in speeding up the somewhat naïve implementation presented here. These techniques generally involve translating the point to be multiplied from the two-dimensional coordinate system presented here into a three-dimensional coordinate system, performing equivalent operations, and then transforming them back to the two-dimensional coordinate system, all the while taking into account the prime-field you're working in.

The implementation is even more complex than the simple multiplication routine presented above, and involves orders of magnitude more operations (but you can trade lots of operations to get rid of just one modular inversion and still be ahead). The Jacobian projection is one such popular transformation; I don't cover it here, but it can speed up elliptic-curve operations by an order of magnitude to bring it to parity with modular exponentiation operations. Because ECC offers equivalent security with far fewer public-key bits, this makes ECC an attractive choice for public-key cryptography operations, which will probably become more and more important in the future.