Michael Paluszek and Stephanie ThomasMATLAB Machine Learning Recipeshttps://doi.org/10.1007/978-1-4842-3916-2_6

6. Fuzzy Logic

Michael Paluszek¹ and Stephanie Thomas¹

(1)

Plainsboro, NJ, USA

Fuzzy logic [26] is an alternative approach to control system design. Fuzzy logic works within the framework of set theory and is better at dealing with ambiguities. For example, three sets may be defined for a sensor: hard failure, soft failure, and no failure. The three sets may overlap and at any given time the sensor may have a degree of membership in each set. The degree of membership in each set can be used to determine what action to take. An algorithmic approach would have to assign a number to the state of the sensor. This could be problematic and not necessarily represent the actual state of the system. In effect, you would be applying a degree of fuzziness.

../images/420697_2_En_6_Chapter/420697_2_En_6_Figa_HTML.gif

When you go to a doctor with pain the doctor will often try and get you to convert a fuzzy concept, pain, into a number from 0 to 10. As pain is personal and your impression is imprecise, you are giving a fuzzy concept or belief a hard number. As you may have experienced, this is not terribly productive or useful.

Surveys do the same thing. For example, you will be asked to rate the service in a restaurant from 0 to 5. You then rate a bunch of other things on the same scale. This allows the review to come up with a number for your overall impression of the restaurant. Does the resulting 4.8 actually mean anything? Netflix abandoned the numerical ratings of movies you have seen for thumbs up and down. It seems that they felt that a binary decision, really two sets, was a better indicator than a number.

NASA and the U.S. Department of Defense like to use technology readiness levels that go from 1 to 9 to determine where your work is in terms of readiness. Nine is a technology already operating in a target system. One is just an idea. All the other levels are fuzzy for anything moderately complicated. Even giving a technology a 9 is not terribly informative. The M-16 rifle was deployed to Vietnam. It often jammed. In terms of TRL it was 9, but a 9 doesn’t say how well it is working. Again, the readiness of the rifle, when you read soldiers’ and marines’ impressions, was best represented by fuzzy beliefs.

This chapter will show you how to implement a fuzzy logic control system for windshield wipers. Unlike the other chapters, we will be working with linguistic concepts, not hard numbers. Of course, when you set your wiper motor speed you need to pick a number (defuzzify your output), but all the intermediate steps employ fuzzy logic.

6.1 Building Fuzzy Logic Systems

6.1.1 Problem

We want to have a tool to build a fuzzy logic controller.

6.1.2 Solution

Build a MATLAB function that takes parameter pairs that define everything needed for the fuzzy controller.

6.1.3 How It Works

To create a fuzzy system you must create inputs, outputs, and rules. You can also choose methods for some parts of the fuzzy inference. The fuzzy inference engine has three steps:

1.
Fuzzify
2.
Fire
3.
Defuzzify

The fuzzy system data are stored in a MATLAB data structure. This structure has the following fields:

Input {:}
Output {:}
Rules {:}
Implication
Aggregation
Defuzzify

The first three fields are cell arrays of structs. There is a separate structure for rules and fuzzy sets, described below. The last three fields are strings containing the names of the desired functions.

The fuzzy set structure has the following fields:

name
range(2) (two-element array with minimum and maximum values)
comp {:} (cell array of label strings)
type {:} (cell array of membership function names)
params {:} (cell array of parameter vectors)

The fuzzy rule struct has the following fields:

input(:) (vector of input component numbers)
output(:) (vector of outputs)
operator {:} (cell array of operator strings)

This is a lot of data to organize. We do it with the function BuildFuzzySystem. The following code snippet shows how it assigns data to the data structure using parameter pairs.

d = load ( ’SmartWipers’);

j = 1;

for k = 1:2:length(varargin)

switch ( lower (varargin{k}))

case ’id’

j = varargin{k+1};

case ’input␣comp’

d.input(j).comp = varargin{k+1};

case ’input␣type’

d.input(j).type = varargin{k+1};

case ’input␣name’

d.input(j).name = varargin{k+1};

case ’input␣params’

This code continues with other cases. If you don’t enter anything, BuildFuzzySystem loads the Smart Wipers demo, as shown above. and returns it unchanged. For example, if you just enter one input type you get:

SmartWipers = BuildFuzzySystem(...

’id’,1,...

’input␣comp’,{ ’Dry’ ’Drizzle’ ’Wet’} ,...

’input␣type’, { ’Trapezoid’ ’Triangle’ ’Trapezoid’} ,...

’input␣params’,{[0 0 10 50] [40 50] [50 90 101 101]},...

’input␣range’,[0 100])

SmartWipers =

struct with fields:

SmartWipers: [1x1 struct]

input: [1x1 struct]

Fuzzy sets in this context consist of a set of linguistic categories or components defining a variable. For instance, if the variable is “age,” the components might be “young,” “middle-aged,” and “old.” Each fuzzy set has a range over which it is valid, for instance, a good range for “age” may be 0 to 100. Each component has a membership function that describes the degree to which a value in the set’s range belongs to each component. For instance, a person who is 50 would rarely be described as “young,” but might be described as “middle aged” or “old,” depending on the person asked.

To build a fuzzy set, you must divide it into components. The following membership functions are provided:

1.
Triangular
2.
Trapezoidal
3.
Gaussian
4.
General bell
5.
Sigmoidal

Membership functions are limited in value to between 0 and 1. The membership functions are shown in Figure 6.1.

The triangular membership function requires two parameters: the center of the triangle and the half-width of the desired triangle base. Triangular membership functions are limited to symmetrical triangles.

The trapezoid membership function requires four parameters: the left-most point, the start of the plateau, the end of the plateau, and the right-most points.

A Gaussian membership function is a continuous function with two parameters: the center of the bell and the width (standard deviation) of the bell. Gaussian membership functions are symmetrical.

A general bell function is also continuous and symmetrical, but it has three parameters to allow for a flattened top, making it similar to a smoothed trapezoid. It requires three parameters: the center of the bell, the width of the bell at the points y = 0.5, and the slope of the function at the points y = 0.5.

Just as a bell function is similar to a smoothed trapezoid, a sigmoidal membership function is similar to a smoothed step function. It takes two parameters: the point at which y = 0.5 and the slope of the function. As the slope approaches infinity the sigmoidal function approaches the step function.

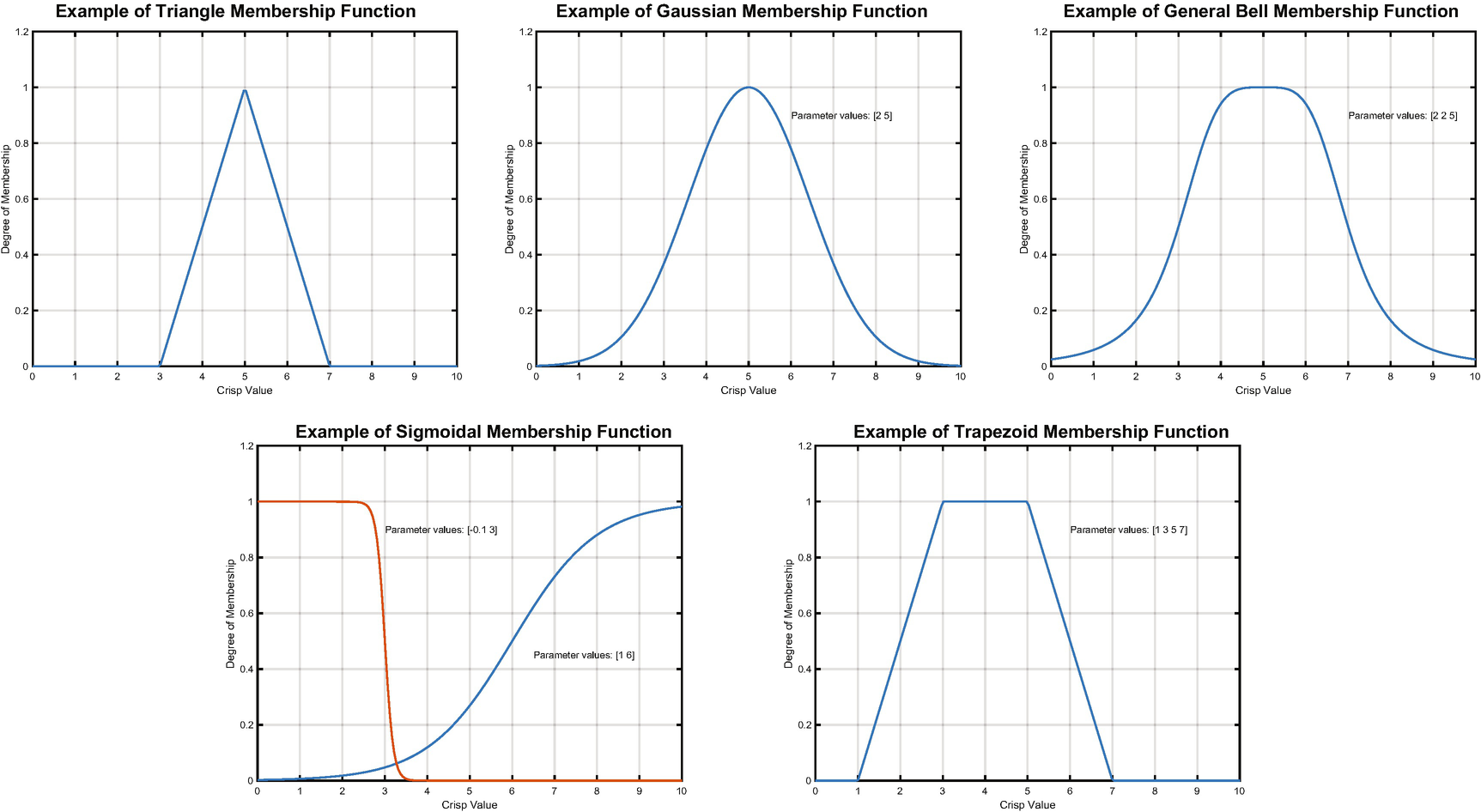
../images/420697_2_En_6_Chapter/420697_2_En_6_Fig1_HTML.png — Figure 6.1
Membership functions.

Fuzzy rules are if-then statements. For example, an air conditioner rule might say IF the room temperature IS high, THEN the blower level IS high. In this case, “room temperature” is the input fuzzy set, “high” is its component for this rule, “blower level” is the output fuzzy set, and “high” is its chosen component.

6.2 Implement Fuzzy Logic

6.2.1 Problem

We want to implement fuzzy logic.

6.2.2 Solution

Build a fuzzy inference engine.

6.2.3 How It Works

Let’s repeat the three steps in fuzzy inference, adding two steps within defuzzify:

1.
Fuzzify
2.
Fire
3.
Defuzzify
1. a.
  Implication
2. b.
  Aggregation

The control flow is in the main function, called FuzzyInference. It just calls Fuzzify, Fire, and Defuzzify in order. It calls warndlg if the inputs are not sensible.

function y = FuzzyInference( x, system )

if length(x) == length( system.input )

fuzzyX = Fuzzify( x, system.input );

strength = Fire( fuzzyX, system.rules );

y = Defuzzify( strength, system );

else

warndlg({ ’The␣length␣of␣x␣must␣be␣equal␣to␣the’,...

’number␣of␣input␣sets␣in␣the␣system.’})

end

You will notice the use of eval to evaluate function names stored as strings as the input. You could also store pointers and do the same thing. For example, for the function:

function y = MyFun(x)

y = x;

eval works on a string. Essentially, it applies the MATLAB parser to your own text. You can make the string as complex as you want, albeit at the expense of readability. You can also do things such as make self-modifying code.

>> eval ([ ’MyFun(’, sprintf ( ’%f’,2), ’)’])

ans =

It is cleaner and takes less processing time to use a pointer to the function.

>> feval (@MyFun,2)

ans =

feval works on a pointer to the function and is generally faster.

TIP

Use feval instead of eval whenever possible.

The fuzzify sub-function code is shown below. It puts the data into the various input membership sets. An input may be in more than one set.

function fuzzyX = Fuzzify( x, sets )

m = length (sets);

fuzzyX = cell (1,m);

for i = 1:m

n = length (sets(i).comp);

range = sets(i).range(:);

if range(1) <= x(i) <= range(2)

for j = 1:n

fuzzyX{i}(j) = eval ([sets(i). type {j} ’MF(x(i),[’ num2str (sets(i).params{j}) ’])’]);

end

else

fuzzyX{i}(1:n) = zeros (1,n);

end

The fuzzy rules fire in the following code. The code applies “Fuzzy AND” or “Fuzzy OR.” “Fuzzy AND” is the minimum of a set of membership values. “Fuzzy OR” is the maximum of a set of membership values. Suppose we have a vector [1 0 1 0]. The maximum value is 1 and the minimum is 0.

>> 1 && 0 && 1 && 0

ans =

logical

>> 1 || 0 || 1 || 0

ans =

logical

This corresponds to the fuzzy logic AND and OR.

The next code snippet shows the Fire sub-function in FuzzyInference.

function strength = Fire( FuzzyX, rules )

m = length ( rules );

n = length ( FuzzyX );

strength = zeros (1,m);

for i = 1:m

method = rules(i).operator;

for j = 1:n

comp = rules(i). input (j);

if comp ~= 0

dom(j) = FuzzyX{j}(comp);

else

dom(j) = inf;

end

strength(i) = eval ([method ’(dom(find(dom<=1)))’]);

end

Finally, we defuzzify the results. This function first uses the implication functions to determine membership. It aggregates the output using the aggregate function which, in this case, is max.

function result = Defuzzify( strength, system )

rules = system.rules;

output = system.output;

m = length ( output );

n = length ( rules );

imp = system.implicate;

agg = system.aggregate;

defuzz = system.defuzzify;

result = zeros (1,m);

for i = 1:m

range = output(i).range(:);

x = linspace ( range(1),range(2),200 );

for j = 1:n

comp = rules(j).output(i);

if( comp ~= 0 )

mf = [output(i). type {comp} ’MF’];

params = output(i).params{comp};

mem(j,:) = eval ([ imp ’IMP(’ mf ’(x,params),strength(j))’]);

else

mem(j,:) = zeros ( size (x));

end

aggregate = eval ([ agg ’(mem)’ ]);

result(i) = eval ([ defuzz ’DF(aggregate,␣x)’]);

end

6.3 Demonstrate Fuzzy Logic

6.3.1 Problem

We want a control system to select window wiper speed and interval based on rainfall.

6.3.2 Solution

Build a fuzzy logic control system using the tools we’ve developed.

6.3.3 How It Works

To call a fuzzy system, use the function y = FuzzyInference( x, system ).

The script SmartWipersDemo implements the rainfall demo. We only show the code that calls the inference engine. The fuzzy system is loaded using SmartWipers = BuildFuzzySystem( ), as discussed above.

% Generate regularly space arrays in the 2 inputs

x = linspace (SmartWipers.input(1).range(1),SmartWipers.input(1).range(2),n);

y = linspace (SmartWipers.input(2).range(1),SmartWipers.input(2).range(2),n);

PlotSet(1:n,[x;y], ’x␣label’, ’Input’, ’y␣label’,{ ’Wetness’, ’Intensity’},...

’figure␣title’, ’Inputs’, ’Plot␣Title’,{ ’Wetness’, ’Intensity’})

h = waitbar (0, ’Smart␣Wipers␣Demo:␣plotting␣the␣rule␣base’);

z1 = zeros (n,n);

z2 = zeros (n,n);

for k = 1:n

for j = 1:n

temp = FuzzyInference([x(k),y(j)], SmartWipers);

z1(k,j) = temp(1);

z2(k,j) = temp(2);

end

waitbar(k/n)

end

close(h);

NewFigure( ’Wiper␣Speed␣from␣Fuzzy␣Logic’)

Smart wipers is a control system for an automatic windshield wiper [7]. First, the demo will plot the input and output fuzzy variables. Fuzzy inference is performed on each set of crisp inputs plotted. Figure 6.2 shows the inputs to the fuzzy logic system. Figure 6.3 shows the outputs.

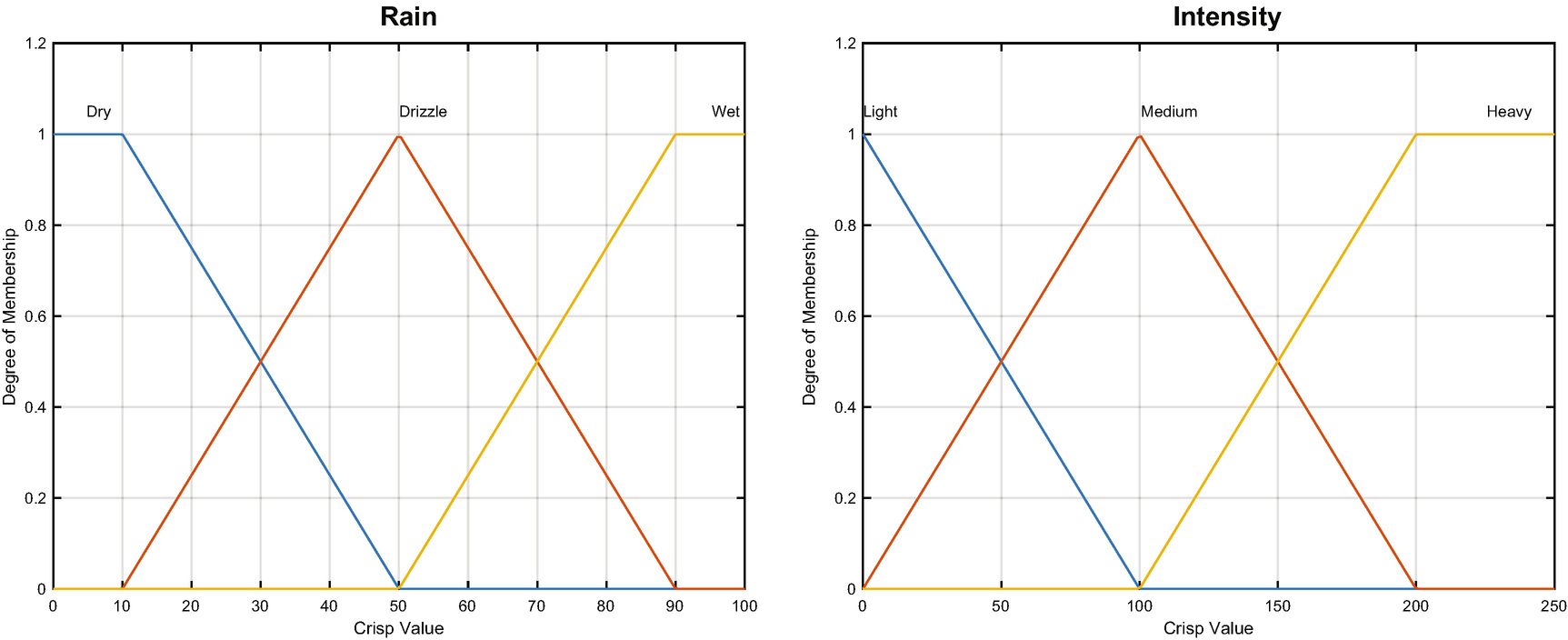
../images/420697_2_En_6_Chapter/420697_2_En_6_Fig2_HTML.png — Figure 6.2
Rain wetness and intensity are the inputs for the smart wiper control system.

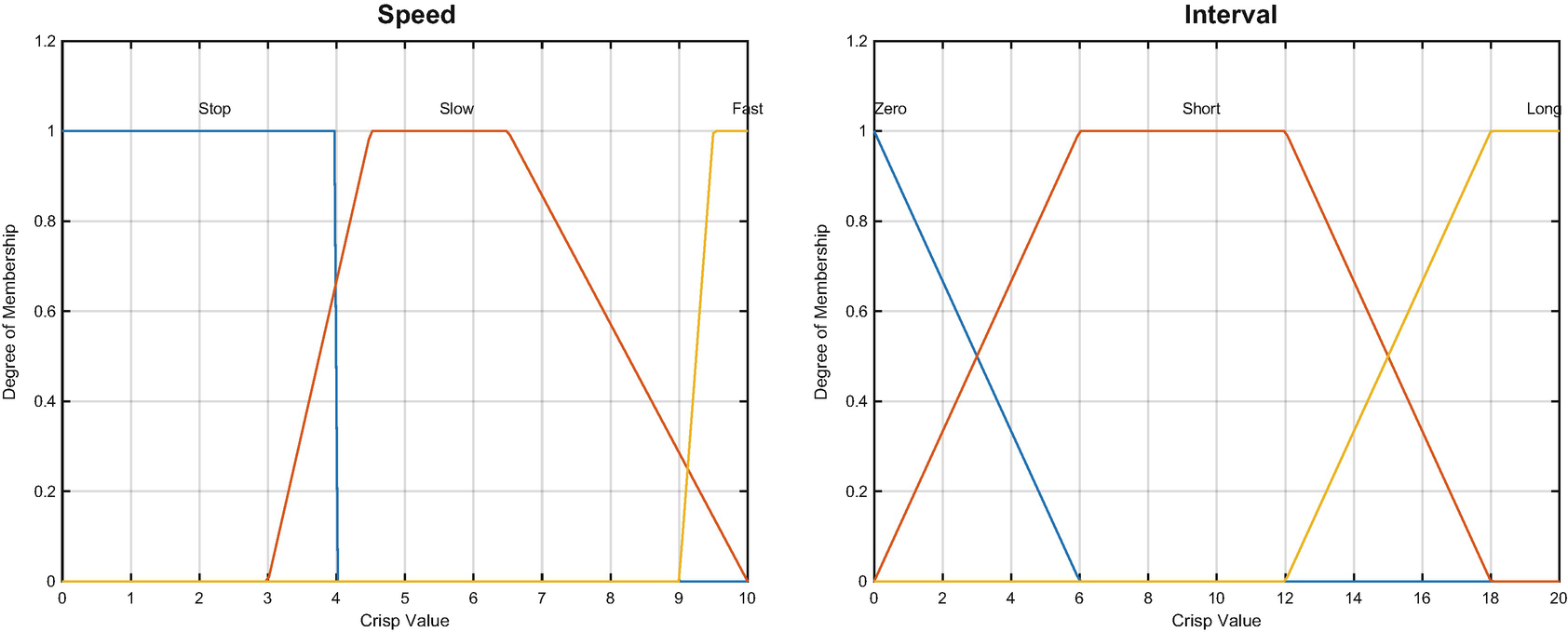
../images/420697_2_En_6_Chapter/420697_2_En_6_Fig3_HTML.png — Figure 6.3
Wiper speed and interval are the outputs for the smart wiper control system.

The inputs that are tested in the fuzzy logic system are given in Figure 6.4.

Figure 6.5 gives surface plots to show how the outputs relate to the inputs. The surface plots are generated by the code below. We add a colorbar to make the plot more readable. The color is related to z-value. We use view in the second plot to make it easier to read in the figure. You can use rotate3d on to allow you to rotate the figure with the mouse.

../images/420697_2_En_6_Chapter/420697_2_En_6_Fig4_HTML.png — Figure 6.4
Rain wetness and intensity input numbers.

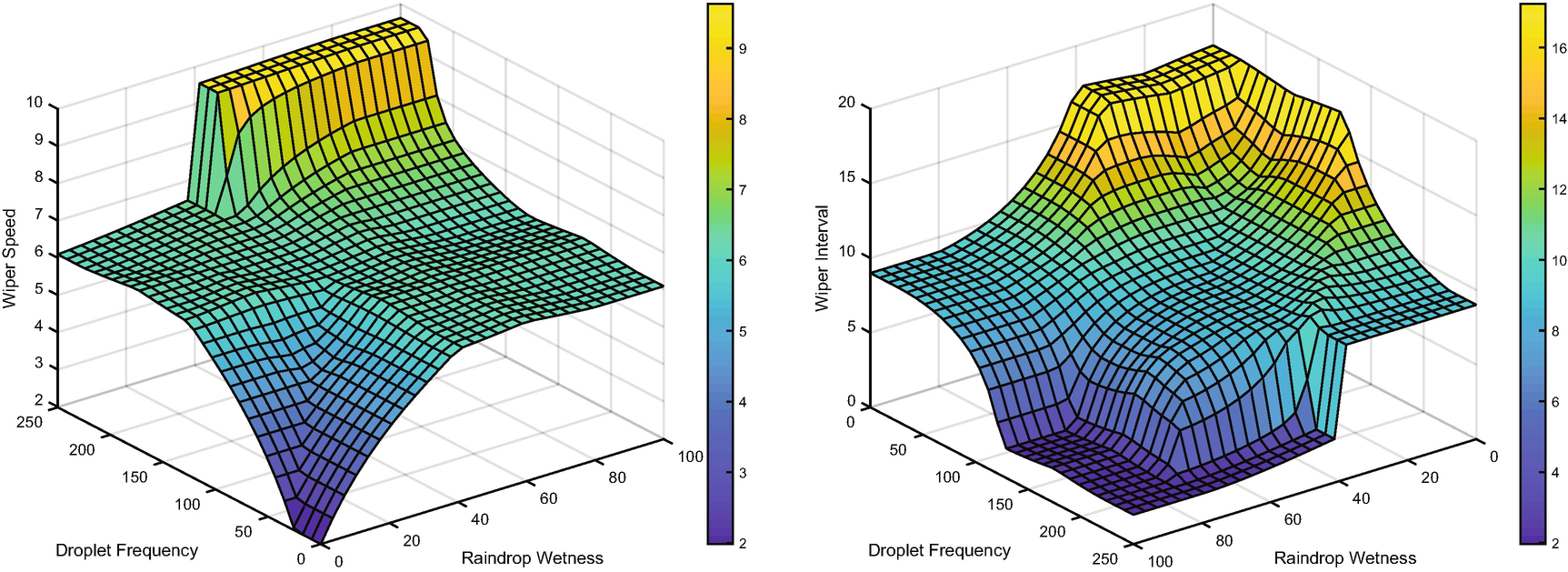
../images/420697_2_En_6_Chapter/420697_2_En_6_Fig5_HTML.png — Figure 6.5
Wiper speed and interval versus droplet frequency and wetness.

NewFigure( ’Wiper␣Speed␣from␣Fuzzy␣Logic’)

surf(x,y,z1)

xlabel( ’Raindrop␣Wetness’)

ylabel( ’Droplet␣Frequency’)

zlabel( ’Wiper␣Speed’)

colorbar

NewFigure( ’Wiper␣Interval␣from␣Fuzzy␣Logic’)

surf(x,y,z2)

xlabel( ’Raindrop␣Wetness’)

ylabel( ’Droplet␣Frequency’)

zlabel( ’Wiper␣Interval’)

view([142.5 30])

TIP

Use rotate3d on to rotate a figure with the mouse.

6.4 Summary

This chapter demonstrated fuzzy logic. A windshield wipers demonstration gives an example of how it is used. Table 6.1 lists the functions and scripts included in the companion code.

Table 6.1

Chapter Code Listing

File	Description
BuildFuzzySystem	Builds a fuzzy logic system (data structure) using parameter pairs.
SmartWipersDemo	Demonstrates a fuzzy logic control system for windshield wipers.
FuzzyPlot	Plots a fuzzy set.
TriangleMF	Triangle membership function.
TrapezoidMF	Trapezoid membership function.
SigmoidalMF	Display a neural net with multiple layers.
ScaleIMP	Scale implication function.
ClipIMP	Clip implication function.
GeneralBellMF	General bell membership function.
GaussianMF	Gaussian membership function.
FuzzyOR	Fuzzy Or (maximum of membership values).
FuzzAND	Fuzzy And (minimum of membership values).
FuzzyInference	Performs fuzzy inference given a fuzzy system and crisp data x.
CentroidDF	Centroid defuzzification.

Previous Chapter

5. Adaptive Control

Next Chapter

7. Data Classification with Decision Trees

Table of Contents for MATLAB Machine Learning Recipes: A Problem-Solution Approach

6. Fuzzy Logic

6.1 Building Fuzzy Logic Systems

6.1.1 Problem

6.1.2 Solution

6.1.3 How It Works

6.2 Implement Fuzzy Logic

6.2.1 Problem

6.2.2 Solution

6.2.3 How It Works

TIP

6.3 Demonstrate Fuzzy Logic

6.3.1 Problem

6.3.2 Solution

6.3.3 How It Works

TIP

6.4 Summary

Table of Contents for
MATLAB Machine Learning Recipes: A Problem-Solution Approach