Michael Paluszek and Stephanie ThomasMATLAB Machine Learning Recipeshttps://doi.org/10.1007/978-1-4842-3916-2_5

5. Adaptive Control

Michael Paluszek¹ and Stephanie Thomas¹

(1)

Plainsboro, NJ, USA

Control systems need to react to the environment in a predictable and repeatable fashion. Control systems take measurements and use them to control the process. For example, a ship measures its heading and changes its rudder angle to attain a desired heading.

../images/420697_2_En_5_Chapter/420697_2_En_5_Figa_HTML.png

Typically control systems are designed and implemented with all of the parameters hard coded into the software. This works very well in most circumstances, particularly when the system is well known during the design process. When the system is not well defined, or is expected to change significantly during operation, it may be necessary to implement learning control. For example, the batteries in an electric car degrade over time. This leads to less range. An autonomous driving system would need to learn that that range was decreasing. This would be done by comparing the distance traveled with the battery state of charge. More drastic, and sudden, changes can alter a system. For example, in an aircraft the air data system may fail owing to a sensor malfunction. If GPS were still operating, the plane would want to switch to a GPS-only system. In a multi-input-multi-output control system a branch may fail, because of a failed actuator or sensor. The system may have to modify to operating branches in that case.

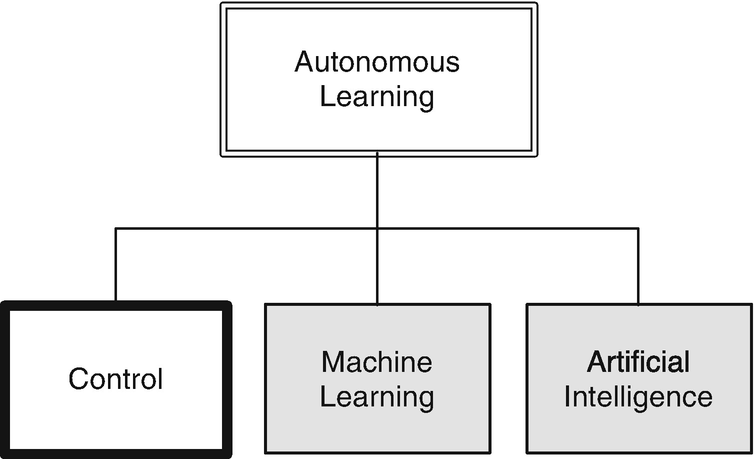
Learning and adaptive control are often used interchangeably. In this chapter, you will learn a variety of techniques for adaptive control for different systems. Each technique is applied to a different system, but all are generally applicable to any control system.

Figure 5.1 provides a taxonomy of adaptive and learning control. The paths depend on the nature of the dynamical system. The right-most branch is tuning. This is something a designer would do during testing, but it could also be done automatically, as will be described in the self-tuning Recipe 5.1. The next path is for systems that will vary with time. Our first example of a system with time-varying parameters applies Model Reference Adaptive Control (MRAC) for a spinning wheel. This is discussed in Section 5.3.

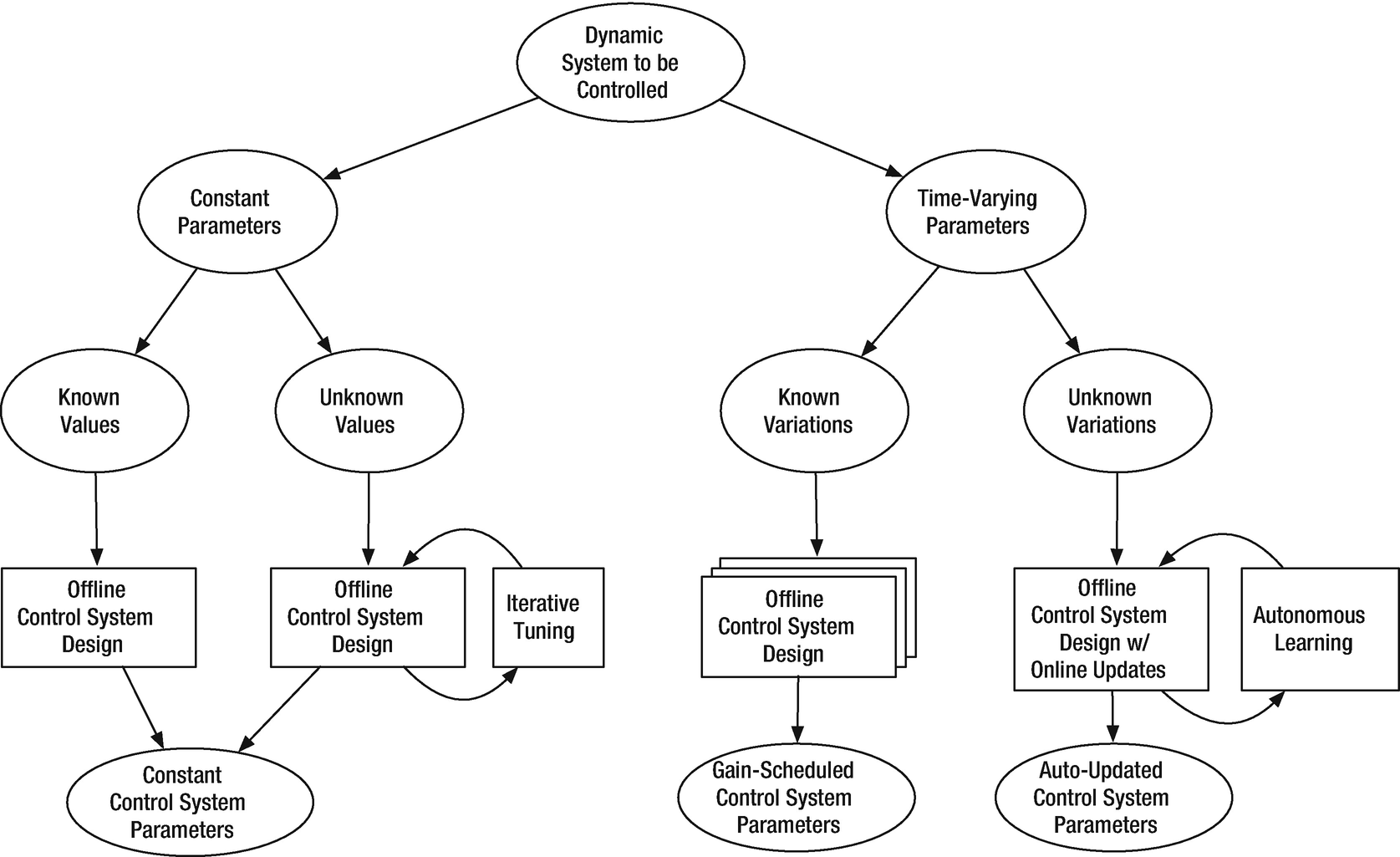
../images/420697_2_En_5_Chapter/420697_2_En_5_Fig1_HTML.png — Figure 5.1
Taxonomy of adaptive or learning control.

The next example is for ship control. Your goal is to control the heading angle. The dynamics of the ship are a function of the forward speed. Although it isn’t really learning from experience, it is adapting based on information about its environment.

The last example is a spacecraft with variable inertia. This shows very simple parameter estimation.

5.1 Self Tuning: Modeling an Oscillator

We want to tune a damper so that we critically damp a spring system for which the spring constant changes. Our system will work by perturbing the undamped spring with a step and measuring the frequency using a fast Fourier transform (FFT). We then compute the damping using the frequency and add a damper to the simulation. We then measure the undamped natural frequency again to see that it is the correct value. Finally, we set the damping ratio to 1 and observe the response. The system in shown in Figure 5.2.

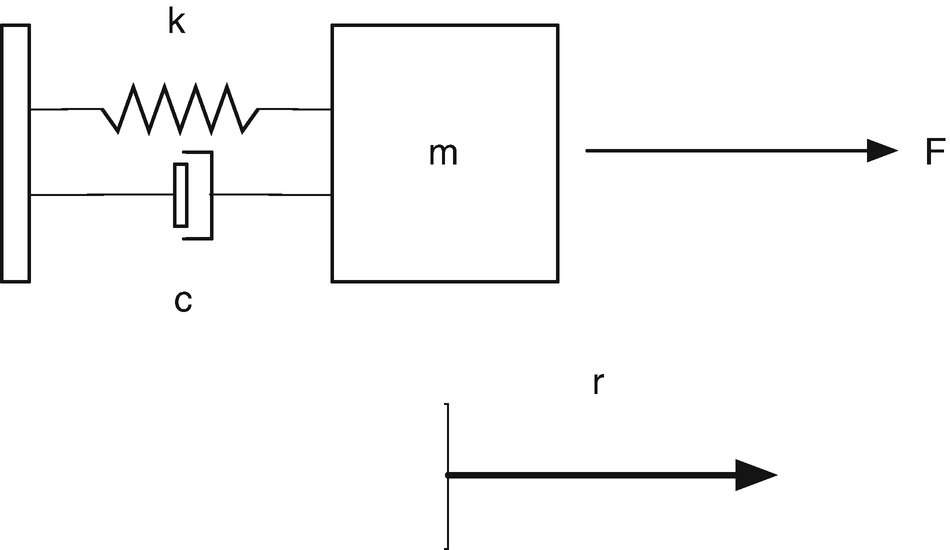
../images/420697_2_En_5_Chapter/420697_2_En_5_Fig2_HTML.png — Figure 5.2
Spring-mass-damper system. The mass is on the right. The spring is on the top to the left of the mass. The damper is below. F is the external force, m is the mass, k is the stiffness, and c is the damping.

In Chapter 4, we introduced parameter identification in the context of Kalman Filters, which is another way of finding the frequency. The approach here is to collect a large sample of data and process it in batches to find the natural frequency. The equations for the system are:

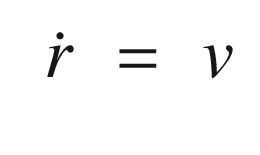
$\displaystyle \begin{aligned} \begin{array}{rcl} \dot{r} &\displaystyle =&\displaystyle v \end{array} \end{aligned}$

(5.1)

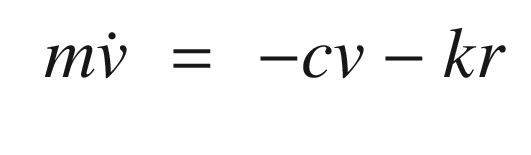
$\displaystyle \begin{aligned} \begin{array}{rcl} m\dot{v} &\displaystyle =&\displaystyle -cv -kr \end{array} \end{aligned}$

(5.2)

c is the damping and k is the stiffness. The damping term causes the velocity to go to zero. The stiffness term bounds the range of motion (unless the damping is negative). The dot above the symbols means the first derivative with respect to time, that is:

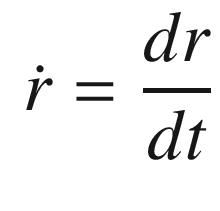
$\displaystyle \begin{aligned} \dot{r} = \frac{dr}{dt} \end{aligned}$

(5.3)

The equations state that the change in position with respect to time is the velocity and the mass times the change in velocity with respect to time is equal to a force proportional to its velocity and position. The second equation is Newton’s Law:

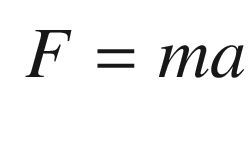
$\displaystyle \begin{aligned} F = ma \end{aligned}$

(5.4)

where F is force, m is mass, and a is acceleration.

TIP

Weight is mass times the acceleration of gravity.

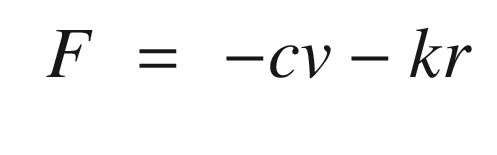
$\displaystyle \begin{aligned} \begin{array}{rcl} F &\displaystyle =&\displaystyle -cv - kr \end{array} \end{aligned}$

(5.5)

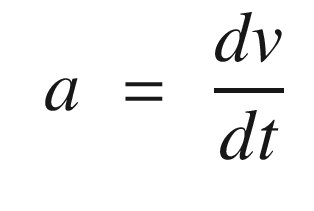
$\displaystyle \begin{aligned} \begin{array}{rcl} a &\displaystyle =&\displaystyle \frac{dv}{dt} \end{array} \end{aligned}$

(5.6)

5.2 Self Tuning: Tuning an Oscillator

5.2.1 Problem

We want to identify the frequency of an oscillator and tune a control system to that frequency.

5.2.2 Solution

The solution is to have the control system measure the frequency of the spring. We will use an FFT to identify the frequency of the oscillation.

5.2.3 How It Works

The following script shows how an FFT identifies the oscillation frequency for a damped oscillator.

The function is shown in the following code. We use the RHSOscillator dynamical model for the system. We start with a small initial position to get it to oscillate. We also have a small damping ratio so that it will damp out. The resolution of the spectrum is dependent on the number of samples:

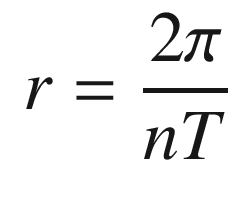
$\displaystyle \begin{aligned} r = \frac{2\pi}{nT} \end{aligned}$

(5.7)

where n is the number of samples and T is the sampling period. The maximum frequency is:

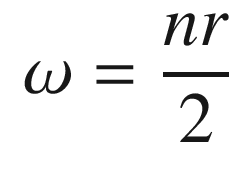
$\displaystyle \begin{aligned} \omega = \frac{nr}{2} \end{aligned}$

(5.8)

The following shows the simulation loop and FFTEnergy call.

%% Initialize

nSim = 2^16; % Number of time steps

dT = 0.1; % Time step (sec)

dRHS = RHSOscillator; % Get the default data structure

dRHS.omega = 0.1; % Oscillator frequency

dRHS.zeta = 0.1; % Damping ratio

x = [1;0]; % Initial state [position;velocity]

y1Sigma = 0.000; % 1 sigma position measurement noise

%% Simulation

xPlot = zeros (3,nSim);

for k = 1:nSim

% Measurements

y = x(1) + y1Sigma* randn ;

% Plot storage

xPlot(:,k) = [x;y];

% Propagate (numerically integrate) the state equations

x = RungeKutta( @RHSOscillator, 0, x, dT, dRHS );

end

FFTEnergy is shown below.

function [e, w, wP] = FFTEnergy( y, tSamp, aPeak )

if( nargin < 3 )

aPeak = 0.95;

end

n = size ( y, 2 );

% If the input vector is odd drop one sample

if( 2*floor(n/2) ~= n )

n = n - 1;

y = y(1:n,:);

end

x = fft (y);

e = real (x.* conj (x))/n;

hN = n/2;

e = e(1,1:hN);

r = 2* pi /(n*tSamp);

w = r*(0:(hN-1));

if( nargin > 1 )

k = find ( e > aPeak* max (e) );

wP = w(k);

end

The FFT takes the sampled time sequence and computes the frequency spectrum. We compute the FFT using MATLAB’s fft function. We take the result and multiply it by its conjugate to get the energy. The first half of the result has the frequency information. aPeak is to indicate peaks for the output. It is just looking for values greater than a certain threshold.

Figure 5.3 shows the damped oscillation. Figure 5.4 shows the spectrum. We find the peak by searching for the maximum value. The noise in the signal is seen at the higher frequencies. A noise-free simulation is shown in Figure 5.5.

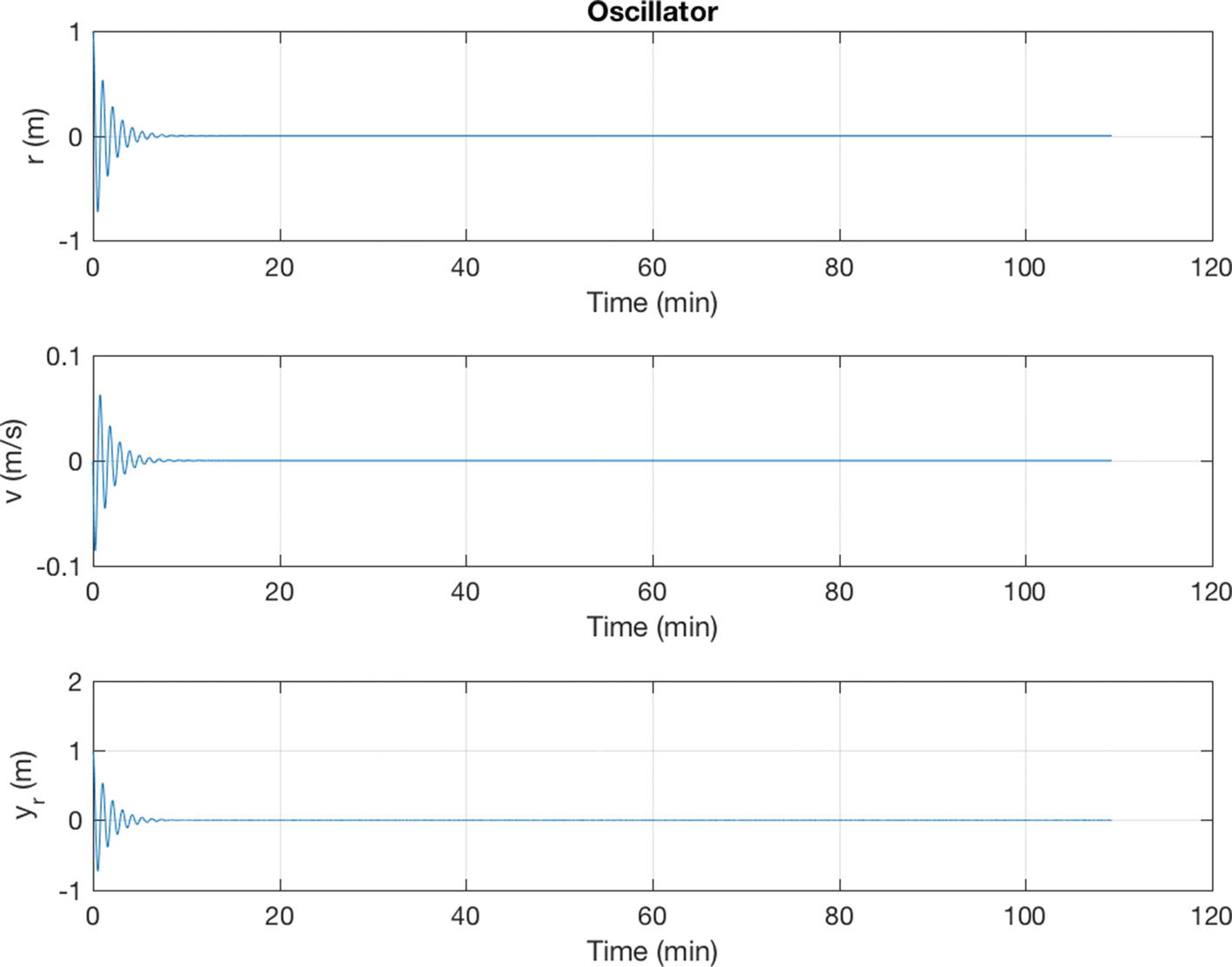
../images/420697_2_En_5_Chapter/420697_2_En_5_Fig3_HTML.jpg — Figure 5.3
Simulation of the damped oscillator. The damping ratio, ζ is 0.5 and undamped natural frequency ω is 0.1 rad/s.

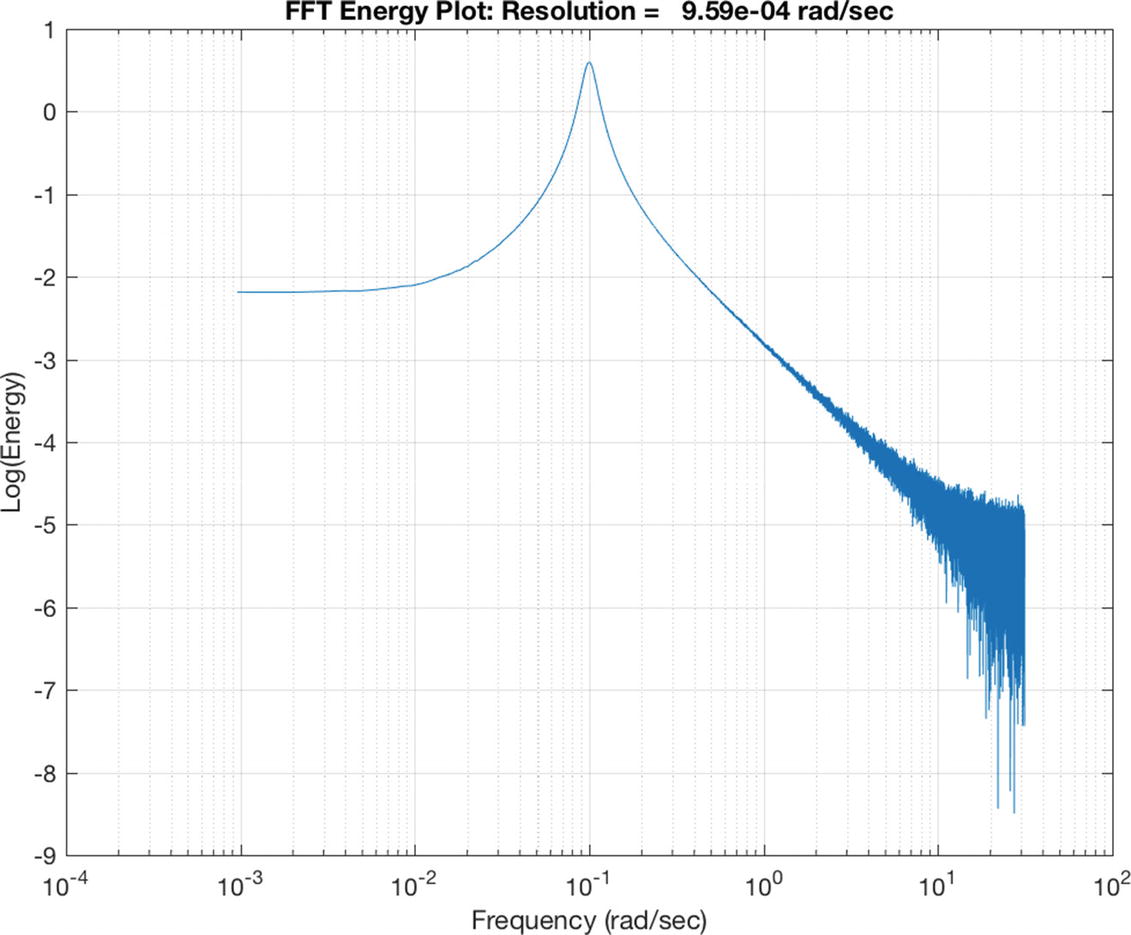
../images/420697_2_En_5_Chapter/420697_2_En_5_Fig4_HTML.jpg — Figure 5.4
The frequency spectrum. The peak is at the oscillation frequency of 0.1 rad/s.

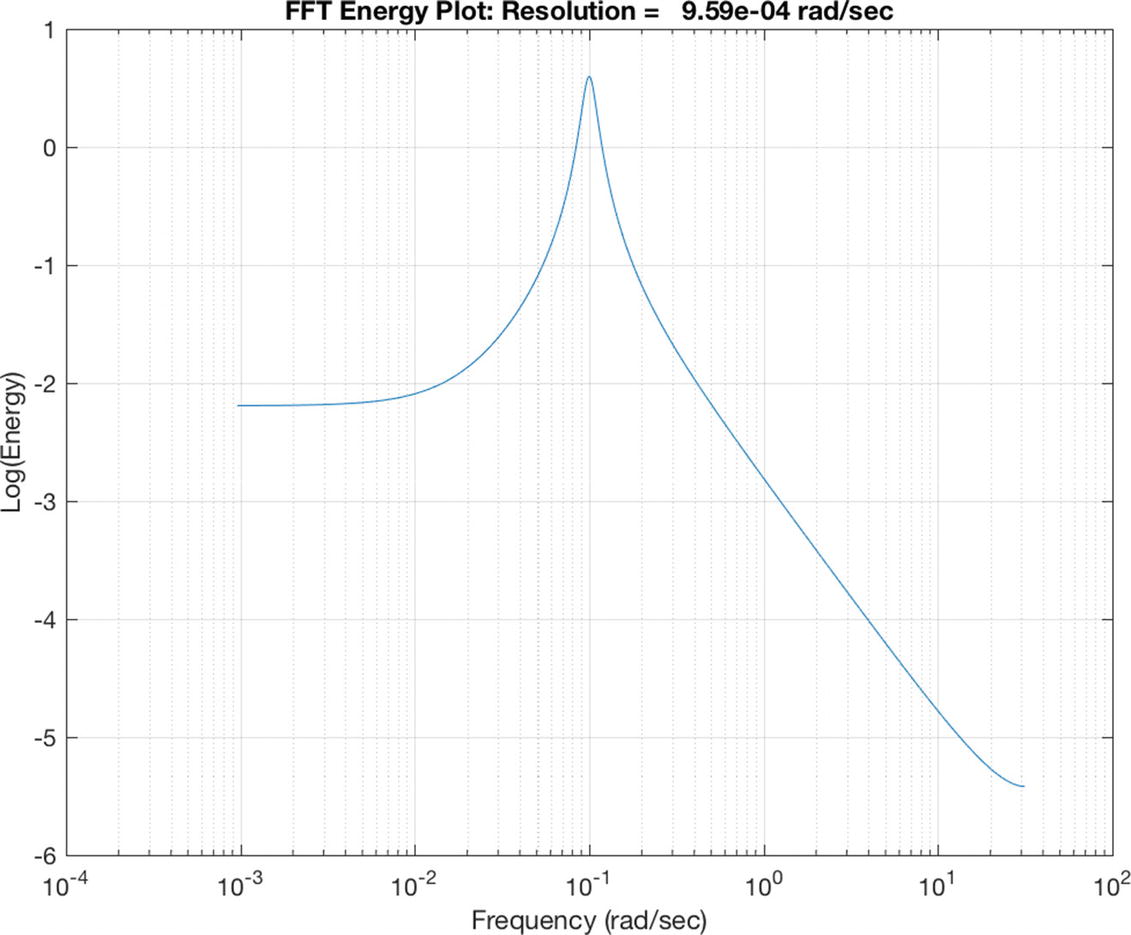
../images/420697_2_En_5_Chapter/420697_2_En_5_Fig5_HTML.jpg — Figure 5.5
The frequency spectrum without noise. The peak of the spectrum is at 0.1 rad/s in agreement with the simulation.

The tuning approach is to:

1.
Excite the oscillator with a pulse
2.
Run it for 2ⁿ steps
3.
Do an FFT
4.
If there is only one peak, compute the damping gain

The script TuningSim calls FFTEnergy.m with aPeak set to 0.7. The value for aPeak is found by looking at a plot and picking a suitable number. The disturbances are Gaussian distributed accelerations and there is noise in the measurement.

The results in the command window are:

TuningSim

Estimated oscillator frequency 0.0997 rad/s

Tuned

As you can see from the FFT plots in Figure 5.6, the spectra are “noisy” owing to the sensor noise and Gaussian disturbance. The criterion for determining that it is underdamped is a distinctive peak. If the noise is large enough we have to set lower thresholds to trigger the tuning. The top left FFT plot shows the 0.1 rad/s peak. After tuning, we damp the oscillator sufficiently so that the peak is diminished. The time plot in Figure 5.6 (the bottom plot) shows that initially the system is lightly damped. After tuning it oscillates very little. There is a slight transient every time the tuning is adjusted at 1.9, 3.6, and 5.5 s. The FFT plots (the top right and middle two) show the data used in the tuning.

An important point is that we must stimulate the system to identify the peak. All system identification, parameter estimation, and tuning algorithms have this requirement. An alternative to a pulse (which has a broad frequency spectrum) would be to use a sinusoidal sweep. That would excite any resonances and make it easier to identify the peak. However, care must be taken when exciting a physical system at different frequencies to ensure that it does not have an unsafe or unstable response at natural frequencies.

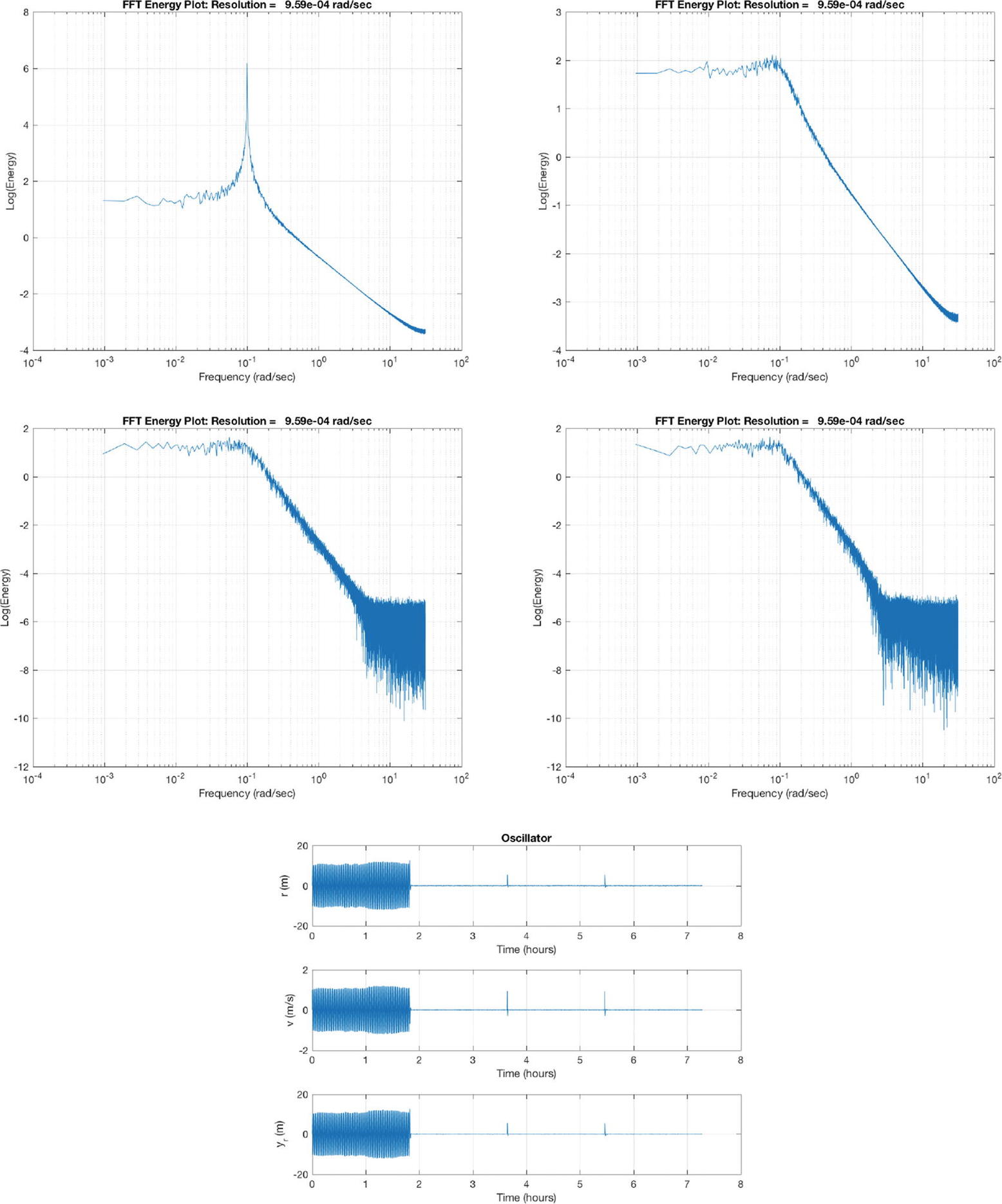
../images/420697_2_En_5_Chapter/420697_2_En_5_Fig6_HTML.jpg — Figure 5.6
Tuning simulation results. The first four plots are the frequency spectrums taken at the end of each sampling interval; the last shows the results over time.

5.3 Implement Model Reference Adaptive Control

Our next example is to control a rotor with an unknown load so that it behaves in a desired manner. The dynamical model of the rotary joint is [2]:

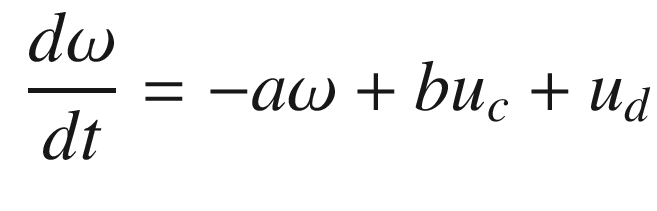
$\displaystyle \begin{aligned} \frac{d\omega}{dt} = -a\omega + bu_c + u_d \end{aligned}$

(5.9)

where the damping a and/or input constants b are unknown. ω is the angular rate. u_c is the input voltage and u_d is a disturbance angular acceleration. This is a first-order system, which is modeled by one first-order differential equation. We would like the system to behave like the reference model:

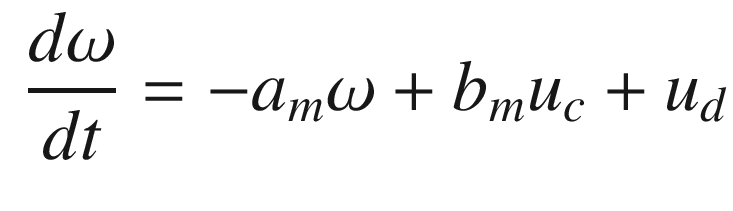
$\displaystyle \begin{aligned} \frac{d\omega}{dt} = -a_m\omega + b_mu_c + u_d \end{aligned}$

(5.10)

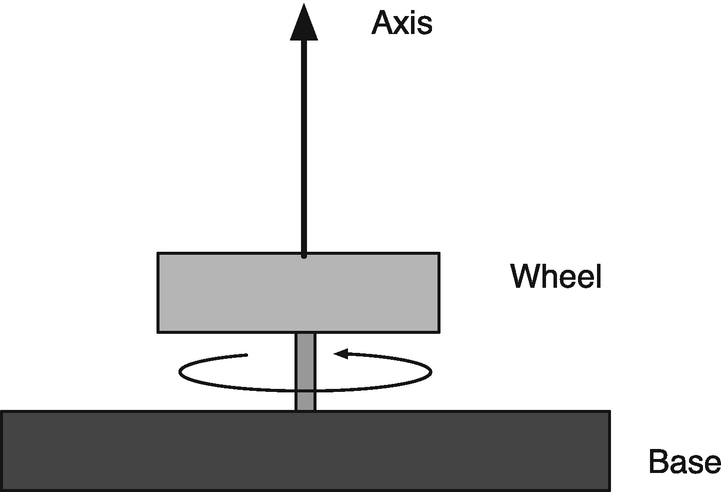
../images/420697_2_En_5_Chapter/420697_2_En_5_Fig7_HTML.png — Figure 5.7
Speed control of a rotor for the Model Reference Adaptive Control demo.

5.3.1 Problem

We want to control a system to behave like a particular model. Our example is a simple rotor.

5.3.2 Solution

The solution is to implement an MRAC function.

5.3.3 How It Works

The idea is to have a dynamical model that defines the behavior of your system. You want your system to have the same dynamics. This desired model is the reference, hence the name Model Reference Adaptive Control. We will use the MIT rule [3] to design the adaptation system. The MIT rule was first developed at the MIT Instrumentation Laboratory (now Draper Laboratory), which developed the NASA Apollo and Space Shuttle guidance and control systems.

Consider a closed-loop system with one adjustable parameter, θ. θ is a parameter, not an angle. The desired output is y_m. The error is:

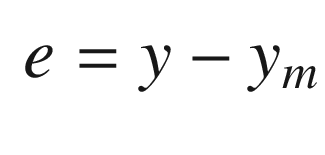
$\displaystyle \begin{aligned} e = y - y_m \end{aligned}$

(5.11)

Define a loss function (or cost) as:

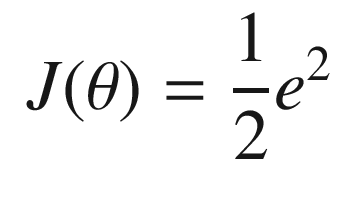
$\displaystyle \begin{aligned} J(\theta) = \frac{1}{2}e^2 \end{aligned}$

(5.12)

The square removes the sign. If the error is zero, the cost is zero. We would like to minimize J(θ). To make J small, we change the parameters in the direction of the negative gradient of J or:

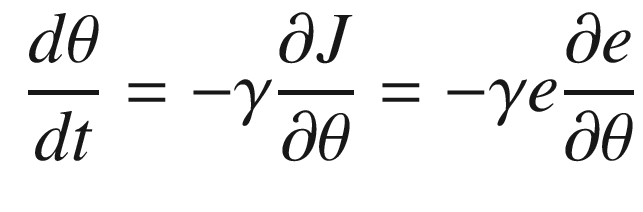
$\displaystyle \begin{aligned} \frac{d\theta}{dt} = -\gamma \frac{\partial J}{\partial \theta} = -\gamma e \frac{\partial e}{\partial \theta} \end{aligned}$

(5.13)

This is the MIT rule. If the system is changing slowly, then we can assume that θ is constant as the system adapts. γ is the adaptation gain. Our dynamical model is:

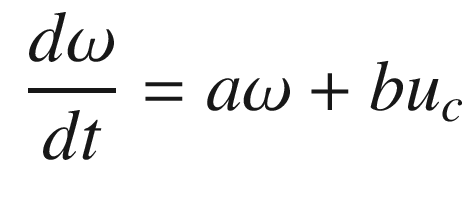
$\displaystyle \begin{aligned} \frac{d\omega}{dt} = a\omega + bu_c \end{aligned}$

(5.14)

We would like it to be the model:

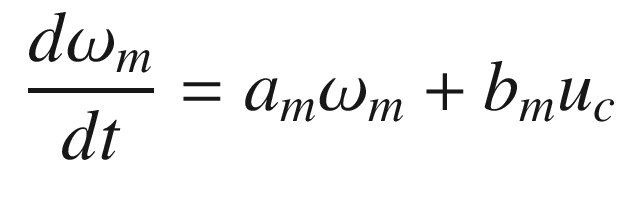
$\displaystyle \begin{aligned} \frac{d\omega_m}{dt} = a_m\omega_m + b_mu_c \end{aligned}$

(5.15)

a and b are the actual unknown parameters. a_m and b_m are the model parameters. We would like a and b to be a_m and b_m. Let the controller for our rotor be:

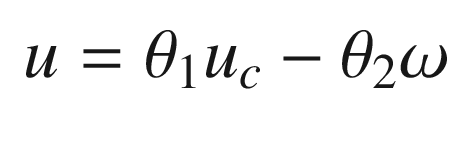
$\displaystyle \begin{aligned} u = \theta_1u_c - \theta_2 \omega \end{aligned}$

(5.16)

The second term provides the damping. The controller has two adaptation parameters. If they are chosen to be:

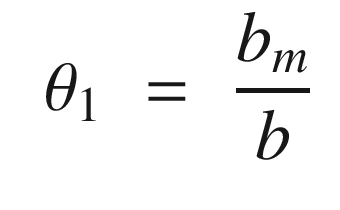
$\displaystyle \begin{aligned} \begin{array}{rcl} \theta_1 &\displaystyle =&\displaystyle \frac{b_m}{b} \end{array} \end{aligned}$

(5.17)

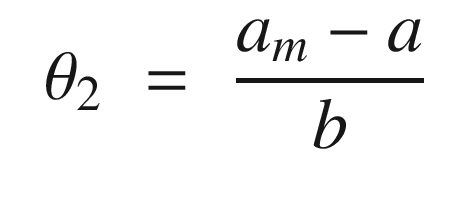
$\displaystyle \begin{aligned} \begin{array}{rcl} \theta_2 &\displaystyle =&\displaystyle \frac{a_m-a}{b} \end{array} \end{aligned}$

(5.18)

the input–output relations of the system and model are the same. This is called perfect model following. This is not required. To apply the MIT rule write the error as:

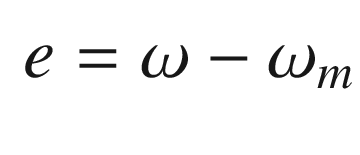
$\displaystyle \begin{aligned} e = \omega - \omega_m \end{aligned}$

(5.19)

With the parameters θ ₁ and θ ₂ the system is:

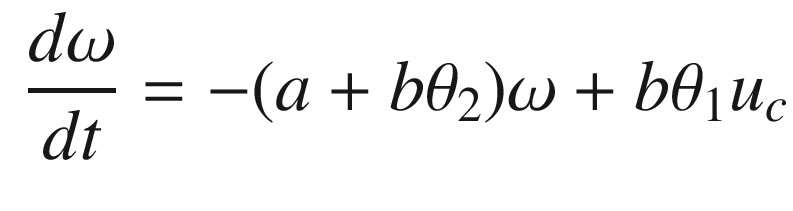
$\displaystyle \begin{aligned} \frac{d\omega}{dt} = -(a+b\theta_2)\omega + b\theta_1u _c \end{aligned}$

(5.20)

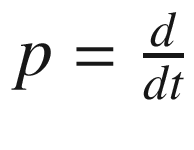where γ is the adaptation gain. To continue with the implementation, we introduce the operator $p = \frac {d}{dt}$ . We then write: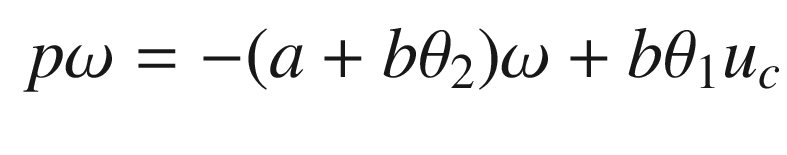

$\displaystyle \begin{aligned} p\omega = -(a+b\theta_2)\omega + b\theta_1u_c \end{aligned}$

(5.21)

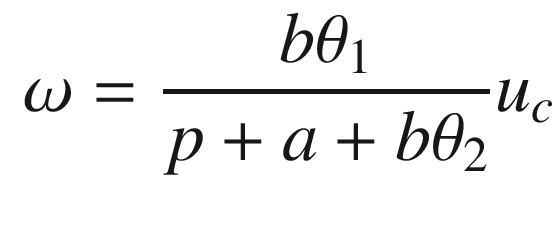
$\displaystyle \begin{aligned} \omega = \frac{b\theta_1}{p + a + b\theta_2}u_c \end{aligned}$

(5.22)

We need to get the partial derivatives of the error with respect to θ ₁ and θ ₂. These are:

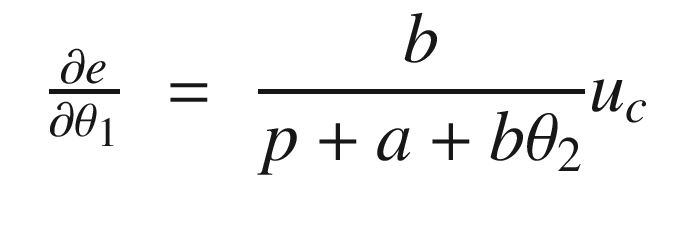
$\displaystyle \begin{aligned} \begin{array}{rcl} \frac{\partial e}{\partial \theta_1} &\displaystyle =&\displaystyle \frac{b}{p + a + b\theta_2}u_c \end{array} \end{aligned}$

(5.23)

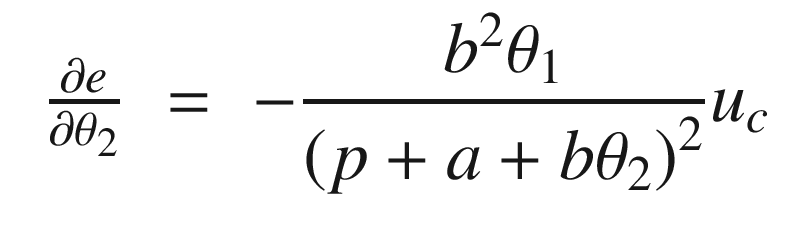
$\displaystyle \begin{aligned} \begin{array}{rcl} \frac{\partial e}{\partial \theta_2} &\displaystyle =&\displaystyle -\frac{b^2\theta_1}{\left(p + a + b\theta_2\right)^2}u_c \end{array} \end{aligned}$

(5.24)

from the chain rule for differentiation. Noting that:

$\displaystyle \begin{aligned} u_c = \frac{p + a + b\theta_2}{b\theta_1}\omega \end{aligned}$

(5.25)

the second equation becomes:

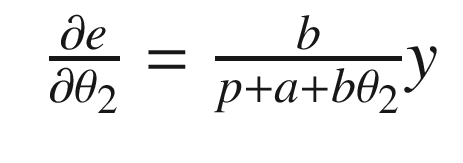
$\displaystyle \begin{aligned} \begin{array}{rcl} \frac{\partial e}{\partial \theta_2} =\frac{b}{p + a + b\theta_2}y \end{array} \end{aligned}$

(5.26)

Since we don’t know a, let’s assume that we are pretty close to it. Then let:

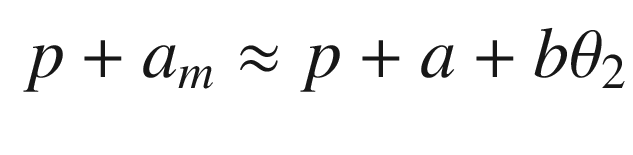
$\displaystyle \begin{aligned} p + a_m \approx p + a + b\theta_2 \end{aligned}$

(5.27)

Our adaptation laws are now:

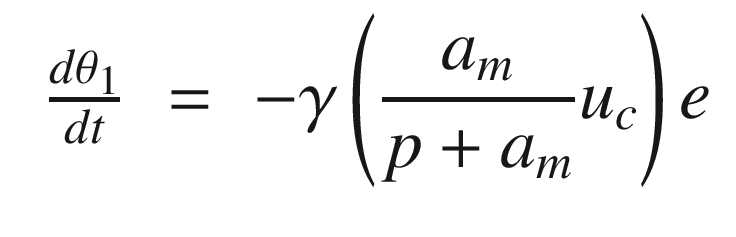
$\displaystyle \begin{aligned} \begin{array}{rcl} \frac{d\theta_1}{dt} &\displaystyle =&\displaystyle -\gamma\left(\frac{a_m}{p + a_m}u_c\right)e \end{array} \end{aligned}$

(5.28)

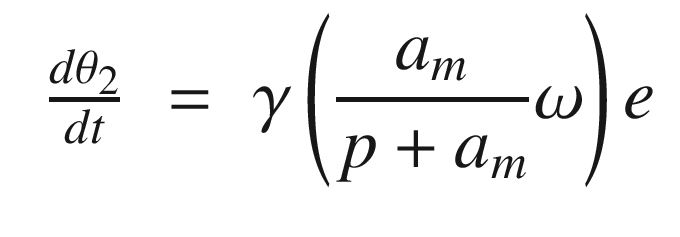
$\displaystyle \begin{aligned} \begin{array}{rcl} \frac{d\theta_2}{dt} &\displaystyle =&\displaystyle \gamma\left(\frac{a_m}{p + a_m}\omega\right)e \end{array} \end{aligned}$

(5.29)

Let:

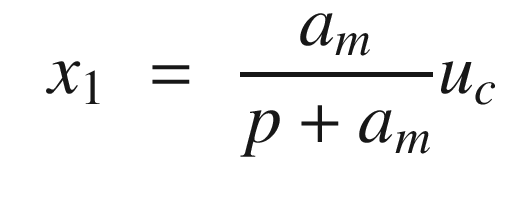
$\displaystyle \begin{aligned} \begin{array}{rcl} x_1 &\displaystyle =&\displaystyle \frac{a_m}{p + a_m}u_c \end{array} \end{aligned}$

(5.30)

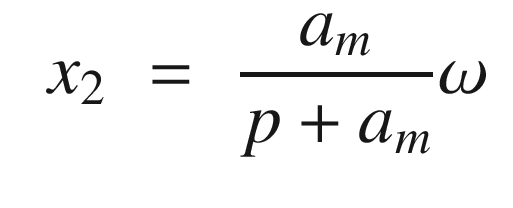
$\displaystyle \begin{aligned} \begin{array}{rcl} x_2 &\displaystyle =&\displaystyle \frac{a_m}{p + a_m}\omega \end{array} \end{aligned}$

(5.31)

which are differential equations that must be integrated. The complete set is:

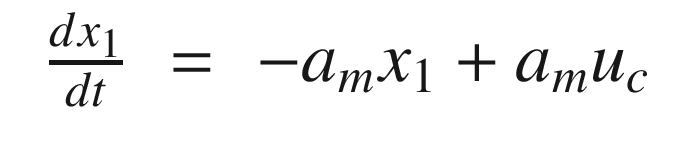
$\displaystyle \begin{aligned} \begin{array}{rcl} \frac{dx_1}{dt} &\displaystyle =&\displaystyle - a_m x_1+a_m u_c \end{array} \end{aligned}$

(5.32)

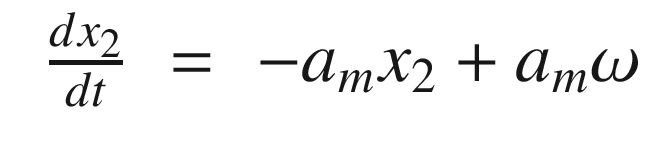
$\displaystyle \begin{aligned} \begin{array}{rcl} \frac{dx_2}{dt} &\displaystyle =&\displaystyle - a_m x_ 2+ a_m \omega \end{array} \end{aligned}$

(5.33)

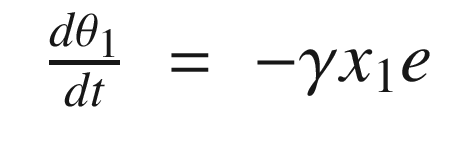
$\displaystyle \begin{aligned} \begin{array}{rcl} \frac{d\theta_1}{dt} &\displaystyle =&\displaystyle -\gamma x_1 e \end{array} \end{aligned}$

(5.34)

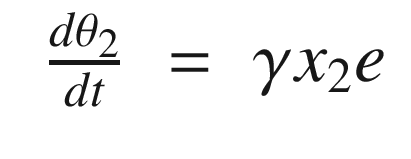
$\displaystyle \begin{aligned} \begin{array}{rcl} \frac{d\theta_2}{dt} &\displaystyle =&\displaystyle \gamma x_2 e \end{array} \end{aligned}$

(5.35)

$\displaystyle \begin{aligned} \begin{array}{rcl} . \end{array} \end{aligned}$

(5.36)

Our only measurement would be ω, which would be measured with a tachometer. As noted before, the controller is

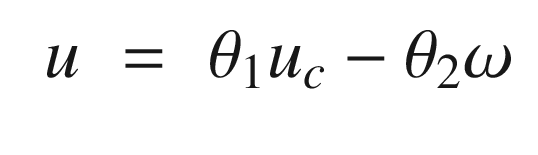
$\displaystyle \begin{aligned} \begin{array}{rcl} u &\displaystyle =&\displaystyle \theta_1 u_c - \theta_2 \omega \end{array} \end{aligned}$

(5.37)

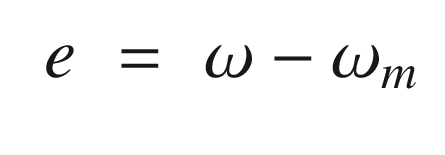
$\displaystyle \begin{aligned} \begin{array}{rcl} e &\displaystyle =&\displaystyle \omega - \omega_m \end{array} \end{aligned}$

(5.38)

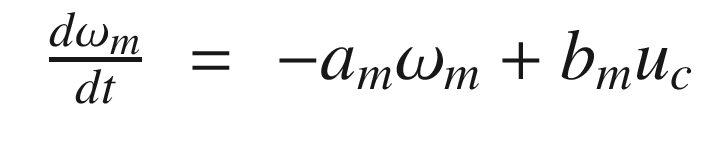
$\displaystyle \begin{aligned} \begin{array}{rcl} \frac{d\omega_m}{dt} &\displaystyle =&\displaystyle - a_m \omega_m + b_m u_c \end{array} \end{aligned}$

(5.39)

The MRAC is implemented in the function MRAC shown in its entirety below. The controller has five differential equations, which are propagated. The states are [x ₁, x ₂, θ ₁, θ ₂, ω_m]. RungeKutta is used for the propagation, but a less computationally intensive lower order integrator, such as Euler, could be used instead. The function returns the default data structure if no inputs and one output is specified. The default data structure has reasonable values. That makes it easier for a user to implement the function. It only propagates one step.

function d = MRAC( omega, d )

if( nargin < 1 )

d = DataStructure;

return

end

d.x = RungeKutta( @RHS, 0, d.x, d.dT, d, omega );

d.u = d.x(3)*d.uC - d.x(4)*omega;

%% MRAC>DataStructure

function d = DataStructure

% Default data structure

d = struct( ’aM’,2.0, ’bM’,2.0, ’x’,[0;0;0;0;0], ’uC’,0, ’u’,0, ’gamma’,1, ’dT’,0.1);

%% MRAC>RHS

function xDot = RHS( ~, x, d, omega )

% RHS for MRAC

e = omega - x(5);

xDot = [-d.aM*x(1) + d.aM*d.uC;...

-d.aM*x(2) + d.aM*omega;...

-d.gamma*x(1)*e;...

d.gamma*x(2)*e;...

-d.aM*x(5) + d.bM*d.uC];

Now that we have the MRAC controller done, we’ll write some supporting functions and then test it all out in RotorSim.

5.4 Generating a Square Wave Input

5.4.1 Problem

We need to generate a square wave to stimulate the rotor in the previous recipe.

5.4.2 Solution

For the purposes of simulation and testing our controller we will generate a square wave with a function.

5.4.3 How It Works

SquareWave generates a square wave. The first few lines are our standard code for running a demo or returning the data structure.

function [v,d] = SquareWave( t, d )

if( nargin < 1 )

if( nargout == 0 )

Demo;

else

v = DataStructure;

end

return

end

if( d.state == 0 )

if( t - d.tSwitch >= d.tLow )

v = 1;

d.tSwitch = t;

d.state = 1;

else

v = 0;

end

else

if( t - d.tSwitch >= d.tHigh )

v = 0;

d.tSwitch = t;

d.state = 0;

else

v = 1;

end

This function uses d.state to determine if it is in the high or low part of a square wave. The width of the low part of the wave is set in d.tLow. The width in the high part of the square wave is set in d.tHigh. It stores the time of the last switch in d.tSwitch.

A square wave is shown in Figure 5.8. There are many ways to specify a square wave. This function produces a square wave with a minimum of zero and maximum of 1. You specify the time at zero and the time at 1 to create the square wave.

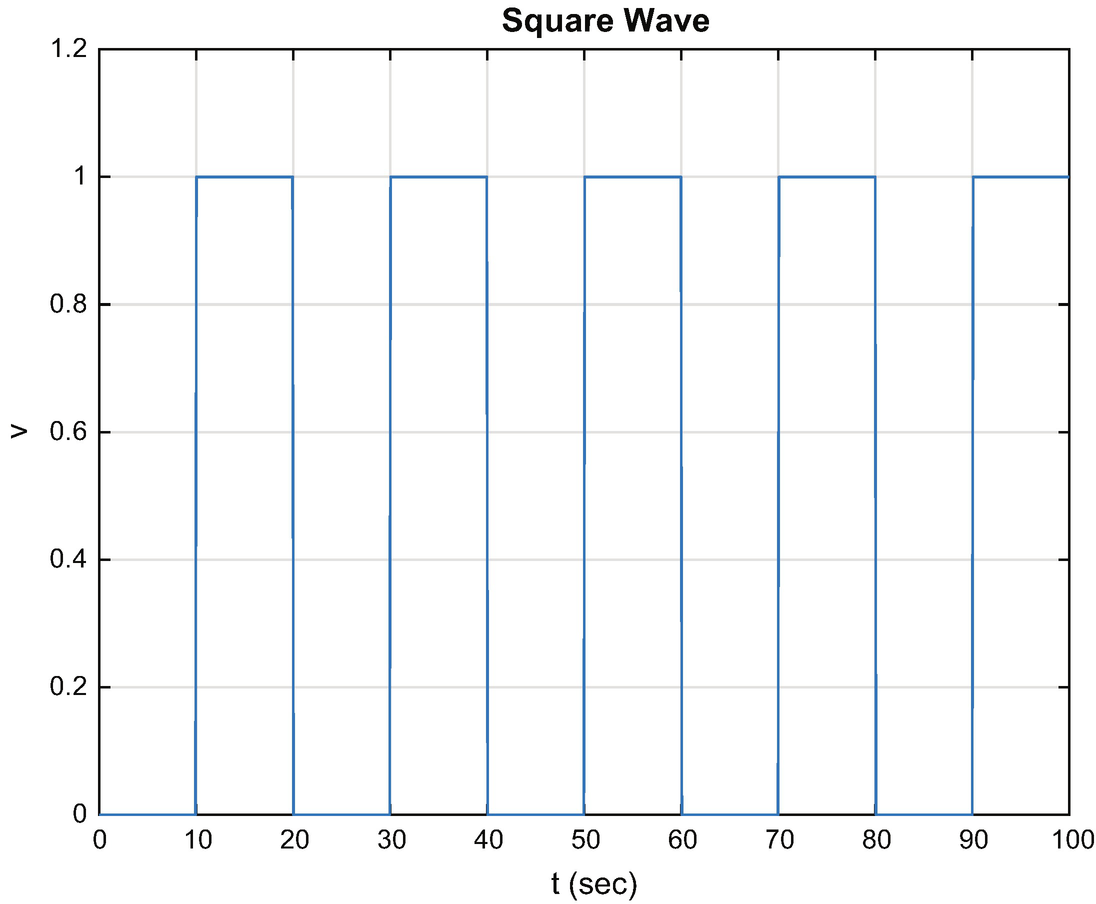
../images/420697_2_En_5_Chapter/420697_2_En_5_Fig8_HTML.png — Figure 5.8
Square wave.

We adjusted the y-axis limit and line width using the code:

PlotSet(t,v, ’x␣label’, ’t␣(sec)’, ’y␣label’, ’v’, ’plot␣title’, ’Square␣Wave’,...

’figure␣title’, ’Square␣Wave’);

set(gca, ’ylim’,[0 1.2])

h = get ( gca , ’children’);

set(h, ’linewidth’,1);

TIP

h = get( gca,’children’) gives you access to the line data structure in a plot for the most recent axes.

5.5 Demonstrate MRAC for a Rotor

5.5.1 Problem

We want to create a recipe to control our rotor using MRAC.

5.5.2 Solution

The solution is to use implement our MRAC function in a MATLAB script from Recipe 5.3.

5.5.3 How It Works

Model Reference Adaptive Control is implemented in the script RotorSim. It calls MRAC to control the rotor. As in our other scripts, we use PlotSet for our 2D plots. Notice that we use two new options. One ’plot set’ allows you to put more than one line on a subplot. The other ’legend’ adds legends to each plot. The cell array argument to ’legend’ has a cell array for each plot. In this case, we have two plots each with two lines, so the cell array is:

{{ ’true’, ’estimated’} ,{ ’Control’ , ’Command’}}

Each plot legend is a cell entry within the overall cell array.

The rotor simulation script with MRAC is shown in the following listing. The square wave functions generates the command to the system that ω should track. RHSRotor, SquareWave, and MRAC all return default data structures. MRAC and SquareWave are called once per pass through the loop. The simulation right-hand side, that is the dynamics of the rotor, in RHSRotor, is then propagated using RungeKutta. Note that we pass a pointer to RHSRotor to RungeKutta.

%% Initialize

nSim = 4000; % Number of time steps

dT = 0.1; % Time step (sec)

dRHS = RHSRotor; % Get the default data structure

dC = MRAC;

dS = SquareWave;

x = 0.1; % Initial state vector

%% Simulation

xPlot = zeros (4,nSim);

theta = zeros (2,nSim);

t = 0;

for k = 1:nSim

% Plot storage

xPlot(:,k) = [x;dC.x(5);dC.u;dC.uC];

theta(:,k) = dC.x(3:4);

[uC, dS] = SquareWave( t, dS );

dC.uC = 2*(uC - 0.5);

dC = MRAC( x, dC );

dRHS.u = dC.u;

% Propagate (numerically integrate) the state equations

x = RungeKutta( @RHSRotor, t, x, dT, dRHS );

t = t + dT;

end

TIP

Pass pointers @fun instead of strings ’fun’ to functions whenever possible.

RHSRotor is shown below.

dRHS.u = dC.u;

% Propagate (numerically integrate) the state equations

x = RungeKutta( @RHSRotor, t, x, dT, dRHS );

t = t + dT;

end

%% Plot the results

The dynamics is just one line of code. The remaining returns the default data structure.

The results are shown in Figure 5.9. We set the adaptation gain, γ to 1. a_m and b_m are set equal to 2. a is set equal to 1 and b to $\frac {1}{2}$ .

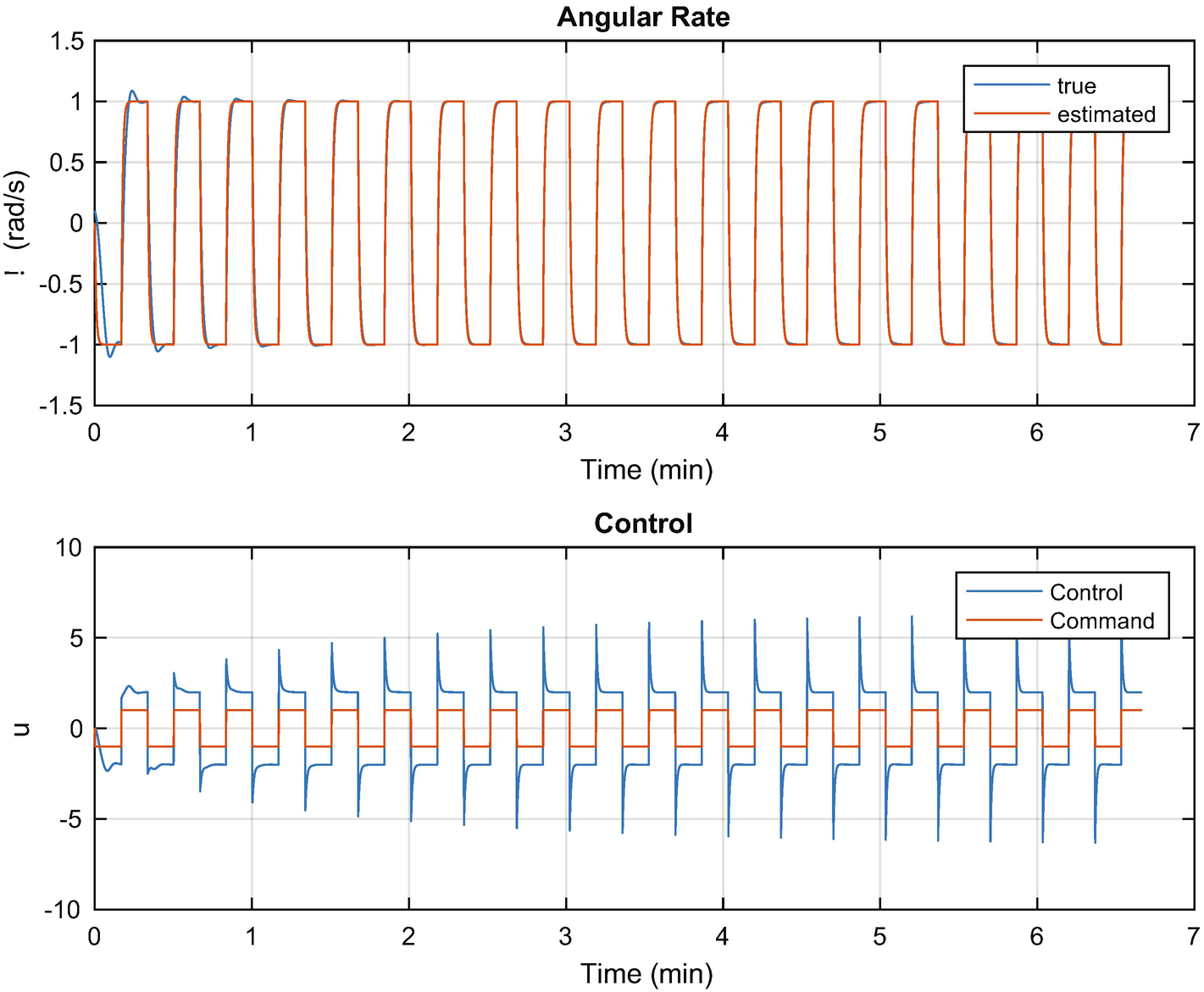
../images/420697_2_En_5_Chapter/420697_2_En_5_Fig9_HTML.png — Figure 5.9
MRAC control of a rotor.

The first plot shows the estimated and true angular rates of the rotor on top and the control demand and actual control sent to the wheel on the bottom. The desired control is a square wave (generated by SquareWave). Notice the transient in the applied control at the transitions of the square wave. The control amplitude is greater than the commanded control. Notice also that the angular rate approaches the desired commanded square wave shape.

Figure 5.10 shows the convergence of the adaptive gains, θ ₁ and θ ₂. They have converged by the end of the simulation.

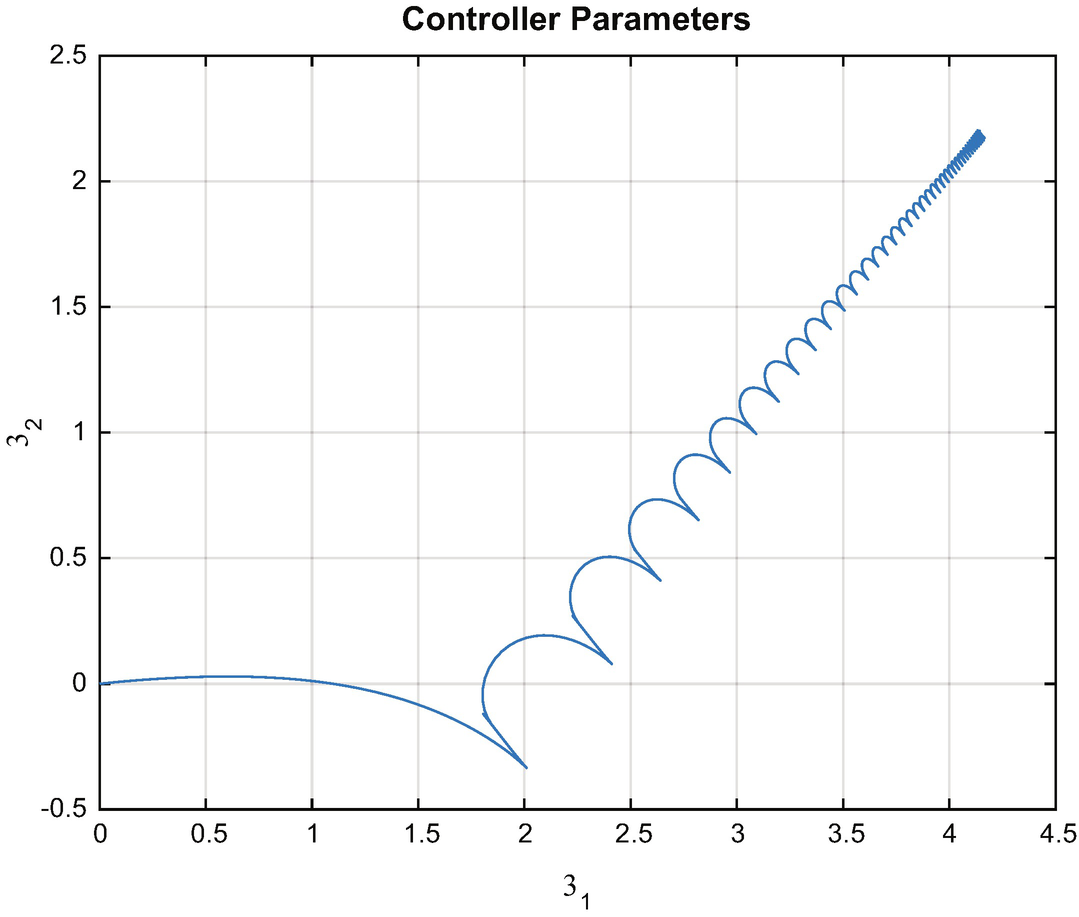
../images/420697_2_En_5_Chapter/420697_2_En_5_Fig10_HTML.png — Figure 5.10
Gain convergence in the MRAC controller.

Model Reference Adaptive Control learns the gains of the system by observing the response to the control excitation. It requires excitation to converge. This is the nature of all learning systems. If there is insufficient stimulation, it isn’t possible to observe the behavior of the system, so there is not enough information for learning. It is easy to find an excitation for a first-order system. For higher order systems, or nonlinear systems, this can be more difficult.

5.6 Ship Steering: Implement Gain Scheduling for Steering Control of a Ship

5.6.1 Problem

We want to steer a ship at all speeds. The problem is that the dynamics are speed dynamics, making this a nonlinear problem

5.6.2 Solution

The solution is to use gain scheduling to set the gains based on speeds. The gain scheduling is learned by automatically computing gains from the dynamical equations of the ship. This is similar to the self-tuning example except that we are seeking a set of gains for all speeds, not just one. In addition, we assume that we know the model of the system.

../images/420697_2_En_5_Chapter/420697_2_En_5_Fig11_HTML.png — Figure 5.11
Ship heading control for gain scheduling control.

5.6.3 How It Works

The dynamical equations for the heading of a ship are in state space form [2]

$\displaystyle \begin{aligned} \left[ \begin{array}{l} \dot{v}\\ \dot{r}\\ \dot{\psi} \end{array} \right] = \left[ \begin{array}{rrr} \left(\frac{u}{l}\right)a_{11}&ua_{12}&0\\ \left(\frac{u}{l^2}\right)a_{21}&\left(\frac{u}{l}\right)a_{22}&0\\ 0&1&0 \end{array} \right] \left[ \begin{array}{l} v\\ r\\ \psi \end{array} \right] + \left[ \begin{array}{r} \left(\frac{u^2}{l}\right)b_1\\ \left(\frac{u^2}{l^2}\right)b_2\\ 0 \end{array} \right]\delta + \left[ \begin{array}{r} \alpha_v\\ \alpha_r\\ 0 \end{array} \right] \end{aligned}$

(5.40)

v is the transverse speed, u is the ship’s speed, l is the ship length, r is the turning rate, and ψ is the heading angle. α_v and α_r are disturbances. The ship is assumed to be moving at speed u. This is achieved by the propeller, which is not modeled. The control is rudder angle δ. Notice that if u = 0, the ship cannot be steered. All of the coefficients in the state matrix are functions of u, except for the heading angle. Our goal is to control heading given the disturbance acceleration in the first equation and disturbance angular rate in the second.

The disturbances only affect the dynamic states, r and v. The last state, ψ is a kinematic state and does not have a disturbance.

The ship model is shown in the following code, RHSShip. The second and third outputs are for use in the controller. Notice that the differential equations are linear in the state and the control. Both matrices are a function of the forward velocity. We are not trying to control the forward velocity, it is an input to the system. The default parameters for the minesweeper are given in in Table 5.1. These are the same numbers that are in the default data structure.

Table 5.1

Ship Parameters [3]

Parameter	Minesweeper	Cargo	Tanker
l	55	161	350
a ₁₁	-0.86	-0.77	-0.45
a ₁₂	-0.48	-0.34	-0.44
a ₂₁	-5.20	-3.39	-4.10
a ₂₂	-2.40	-1.63	-0.81
b ₁	0.18	0.17	0.10
b ₂	1.40	-1.63	-0.81

function [xDot, a, b] = RHSShip( ~, x, d )

if( nargin < 1 )

xDot = struct( ’l’,100, ’u’,10, ’a’,[-0.86 -0.48;-5.2 -2.4], ’b’,[0.18;-1.4], ’alpha’,[0;0;0], ’delta’,0);

return

end

uOL = d.u/d.l;

uOLSq = d.u/d.l^2;

uSqOl = d.u^2/d.l;

a = [ uOL*d.a(1,1) d.u*d.a(1,2) 0;...

uOLSq*d.a(2,1) uOL*d.a(2,2) 0;...

0 1 0];

b = [uSqOl*d.b(1);...

uOL^2*d.b(2);...

0];

xDot = a*x + b*d.delta + d.alpha;

In the ship simulation, ShipSim, we linearly increase the forward speed while commanding a series of heading psi changes. The controller takes the state space model at each time step and computes new gains, which are used to steer the ship. The controller is a linear quadratic regulator. We can use full state feedback because the states are easily modeled. Such controllers will work perfectly in this case, but are a bit harder to implement when you need to estimate some of the states or have unmodeled dynamics.

for k = 1:nSim

% Plot storage

xPlot(:,k) = x;

dRHS.u = u(k);

% Control

% Get the state space matrices

[~,a,b] = RHSShip( 0, x, dRHS );

gain(k,:) = QCR( a, b, qC, rC );

dRHS.delta = -gain(k,:)*[x(1);x(2);x(3) - psi(k)]; % Rudder angle

delta(k) = dRHS.delta;

% Propagate (numerically integrate) the state equations

x = RungeKutta( @RHSShip, 0, x, dT, dRHS );

end

The quadratic regulator generator code is shown in the following lists. It generates the gain from the matrix Riccati equation. A Riccati equation is an ordinary differential equation that is quadratic in the unknown function. In steady state, this reduces to the algebraic Riccati equation, which is solved in this function.

function k = QCR( a, b, q, r )

[sinf,rr] = Riccati( [a,-(b/r)*b’;-q’,-a’] );

if( rr == 1 )

disp( ’Repeated␣roots.␣Adjust␣q,␣r␣or␣n’);

end

k = r\(b’*sinf);

function [sinf, rr] = Riccati( g )

%% Ricatti

% Solves the matrix Riccati equation in the form

% g = [a r ]

% [q -a’]

rg = size (g);

[w, e] = eig (g);

es = sort ( diag (e));

% Look for repeated roots

j = 1: length (es)-1;

if ( any(abs(es(j)-es(j+1))<eps*abs(es(j)+es(j+1))) )

rr = 1;

else

rr = 0;

end

% Sort the columns of w

ws = w(:, real ( diag (e)) < 0);

sinf = real (ws(rg/2+1:rg,:)/ws(1:rg/2,:));

a is the state transition matrix, b is the input matrix, q is the state cost matrix, and r is the control cost matrix. The bigger the elements of q, the more cost we place on deviations of the states from zero. That leads to tight control at the expense of more control. The bigger the elements of b, the more cost we place on control. Bigger b means less control. Quadratic regulators guarantee stability if all states are measured. They are a very handy controller to get something working. The results are given in Figure 5.12. Note how the gains evolve. The gain on the angular rate r is nearly constant. Notice that the ψ range is very small! Normally, you would zoom out the plot. The other two gains increase with speed. This is an example of gain scheduling. The difference is that we autonomously compute the gains from perfect measurements of the ship’s forward speed.

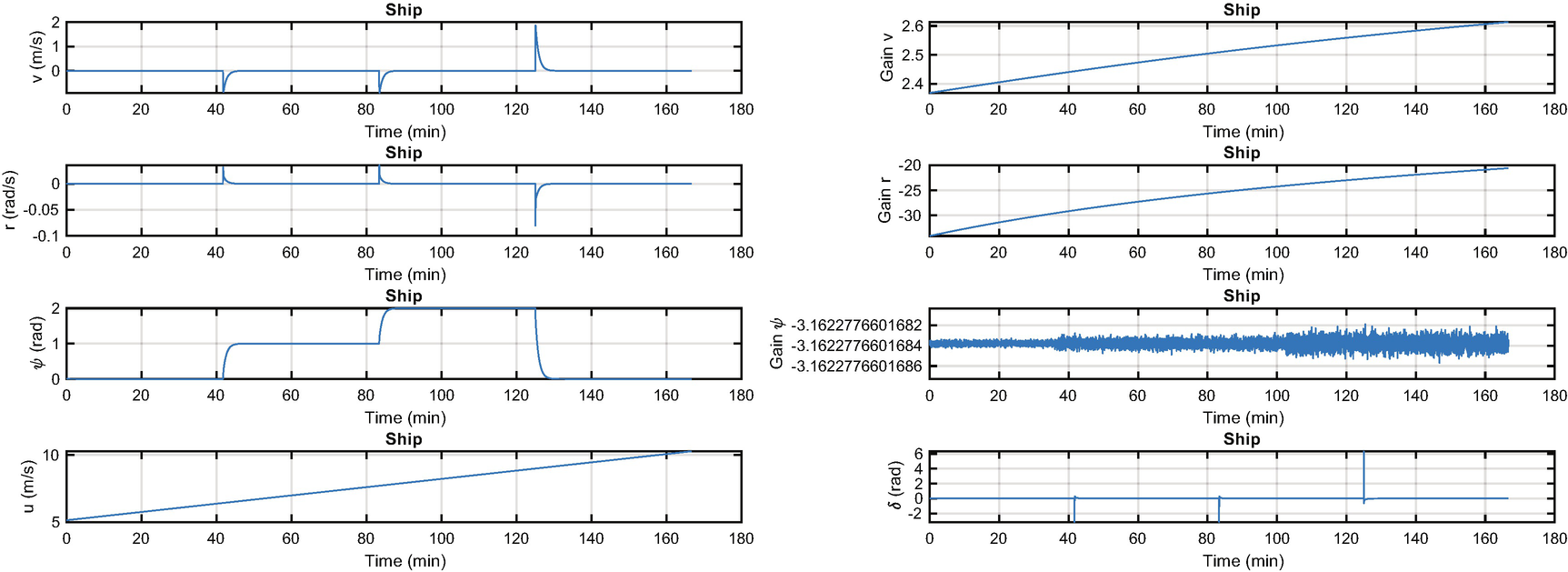
../images/420697_2_En_5_Chapter/420697_2_En_5_Fig12_HTML.png — Figure 5.12
Ship steering simulation. The states are shown on the left with the forward velocity. The gains and rudder angle are shown on the right. Notice the “pulses” in the rudder to make the maneuvers.

ShipSimDisturbance is a modified version of ShipSim, which is of shorter duration, with only one course change, and with disturbances in both angular rate and lateral velocity. The results are given in Figure 5.13.

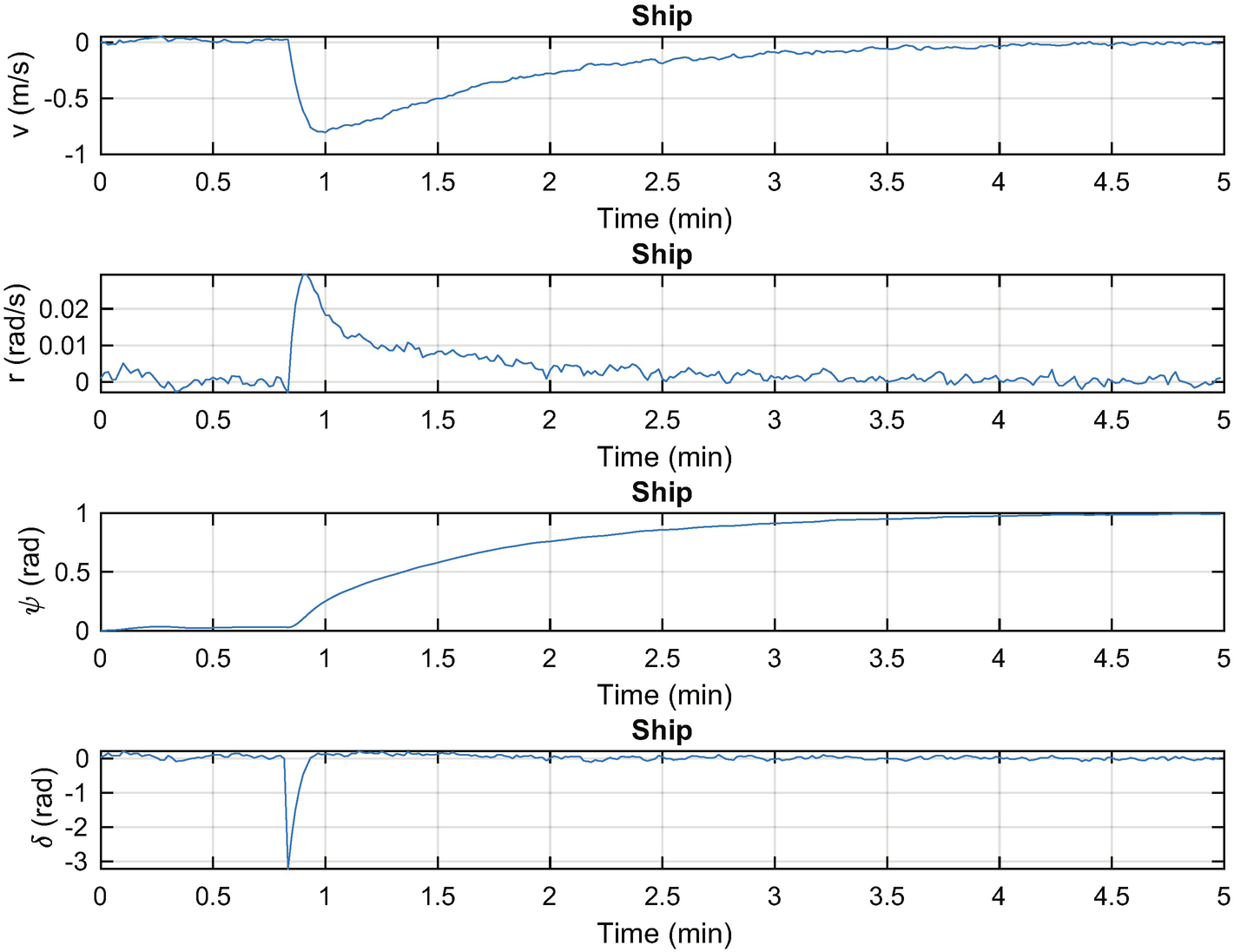
../images/420697_2_En_5_Chapter/420697_2_En_5_Fig13_HTML.png — Figure 5.13
Ship steering simulation. The states are shown on the left with the rudder angle. The disturbances are Gaussian white noise.

5.7 Spacecraft Pointing

5.7.1 Problem

We want to control the orientation of a spacecraft with thrusters for control.

5.7.2 Solution

The solution is to use a parameter estimator to estimate the inertia and feed it into the control system.

5.7.3 How It Works

The spacecraft model is shown in Figure 5.14.

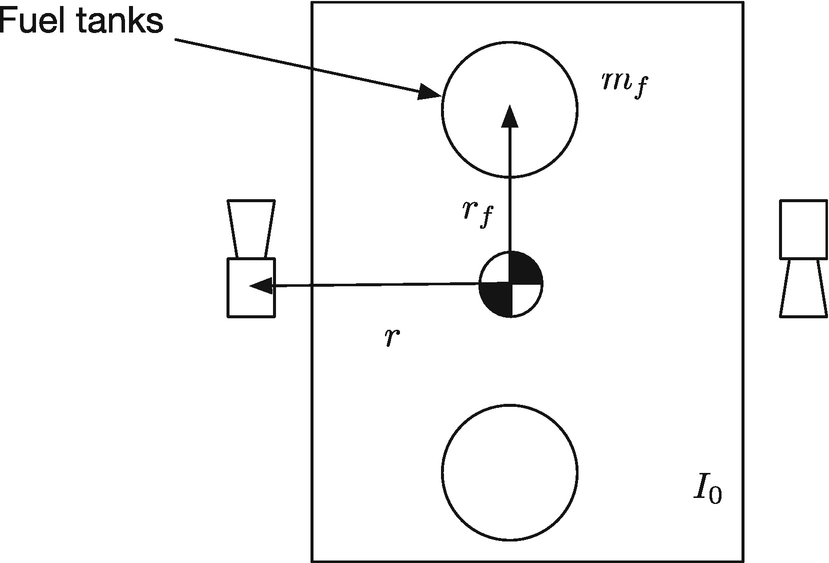
../images/420697_2_En_5_Chapter/420697_2_En_5_Fig14_HTML.png — Figure 5.14
Spacecraft model.

The dynamical equations are

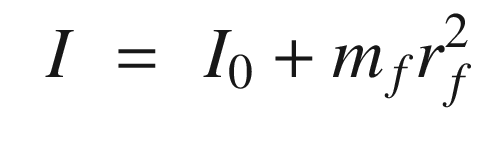
$\displaystyle \begin{aligned} \begin{array}{rcl} I &\displaystyle =&\displaystyle I_0 + m_f r_f^2 \end{array} \end{aligned}$

(5.41)

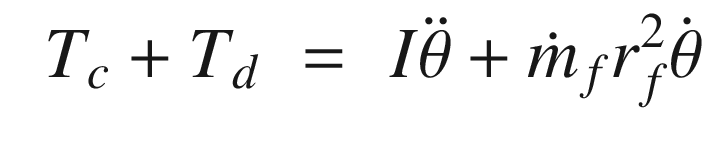
$\displaystyle \begin{aligned} \begin{array}{rcl} T_c + T_d&\displaystyle =&\displaystyle I\ddot{\theta} + \dot{m}_f r_f^2 \dot{\theta} \end{array} \end{aligned}$

(5.42)

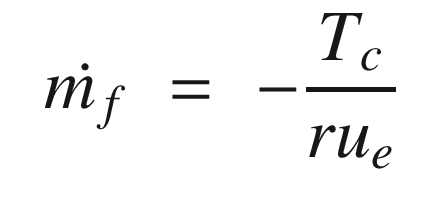
$\displaystyle \begin{aligned} \begin{array}{rcl} \dot{m_f} &\displaystyle =&\displaystyle -\frac{T_c}{r u_e} \end{array} \end{aligned}$

(5.43)

where I is the total inertia, I ₀ is the constant inertia for everything except the fuel mass, T_c is the thruster control torque, T_d is the disturbance torque, m_f is the total fuel mass, r_f is the distance to the fuel tank center, r is the vector to the thrusters, u_e is the thruster exhaust velocity, and θ is the angle of the spacecraft axis. Fuel consumption is balanced between the two tanks so that the center-of-mass remains at (0,0). The second term in the second equation is the inertia derivative term, which adds damping to the system.

Our controller is a proportional derivative controller of the form:

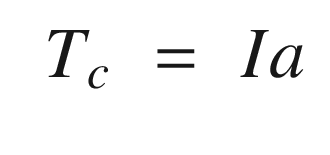
$\displaystyle \begin{aligned} \begin{array}{rcl} T_c &\displaystyle =&\displaystyle Ia \end{array} \end{aligned}$

(5.44)

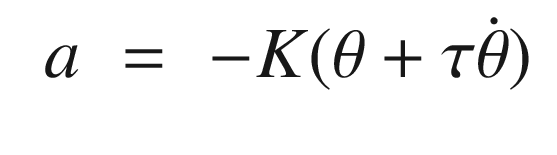
$\displaystyle \begin{aligned} \begin{array}{rcl} a &\displaystyle =&\displaystyle -K(\theta + \tau\dot{\theta}) \end{array} \end{aligned}$

(5.45)

K is the forward gain and τ the rate constant. We design the controller for a unit inertia and then estimate the inertia so that our dynamical response is always the same. We will estimate the inertia using a very simple algorithm:

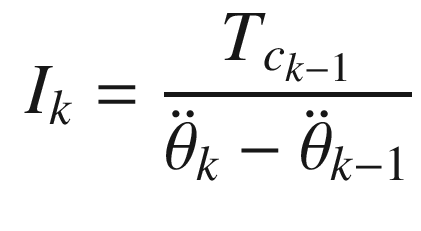
$\displaystyle \begin{aligned} I_k = \frac{T_{c_{k-1}}}{\ddot{\theta}_k - \ddot{\theta}_{k-1}} \end{aligned}$

(5.46)

We will do this only when the control torque is not zero and the change in rate is not zero. This is a first difference approximation and should be good if we don’t have a lot of noise. The following shows a code snippet showing the simulation loop with the control system.

%% Initialize

nSim = 50; % Number of time steps

dT = 1; % Time step (sec)

dRHS = RHSSpacecraft; % Get the default data structure

x = [2.4;0.;1]; % [angle;rate;mass fuel]

%% Controller

kForward = 0.1;

tau = 10;

%% Simulation

xPlot = zeros (6,nSim);

omegaOld = x(2);

inrEst = dRHS.i0 + dRHS.rF^2*x(3);

dRHS.tC = 0;

tCThresh = 0.01;

kI = 0.99; % Inertia filter gain

for k = 1:nSim

% Collect plotting information

xPlot(:,k) = [x;inrEst;dRHS.tD;dRHS.tC];

% Control

% Get the state space matrices

dRHS.tC = -inrEst*kForward*(x(1) + tau*x(2));

omega = x(2);

omegaDot = (omega-omegaOld)/dT;

if( abs(dRHS.tC) > tCThresh )

inrEst = kI*inrEst + (1-kI)*omegaDot/(dRHS.tC);

end

omegaOld = omega;

% Propagate (numerically integrate) the state equations

x = RungeKutta( @RHSSpacecraft, 0, x, dT, dRHS );

end

We only estimate inertia when the control torque is above a threshold. This prevents us from responding to noise. We also incorporate the inertia estimator in a simple low pass filter. The results are shown in Figure 5.15. The threshold has it only estimating inertia at the very beginning of the simulation when it is reducing the attitude error.

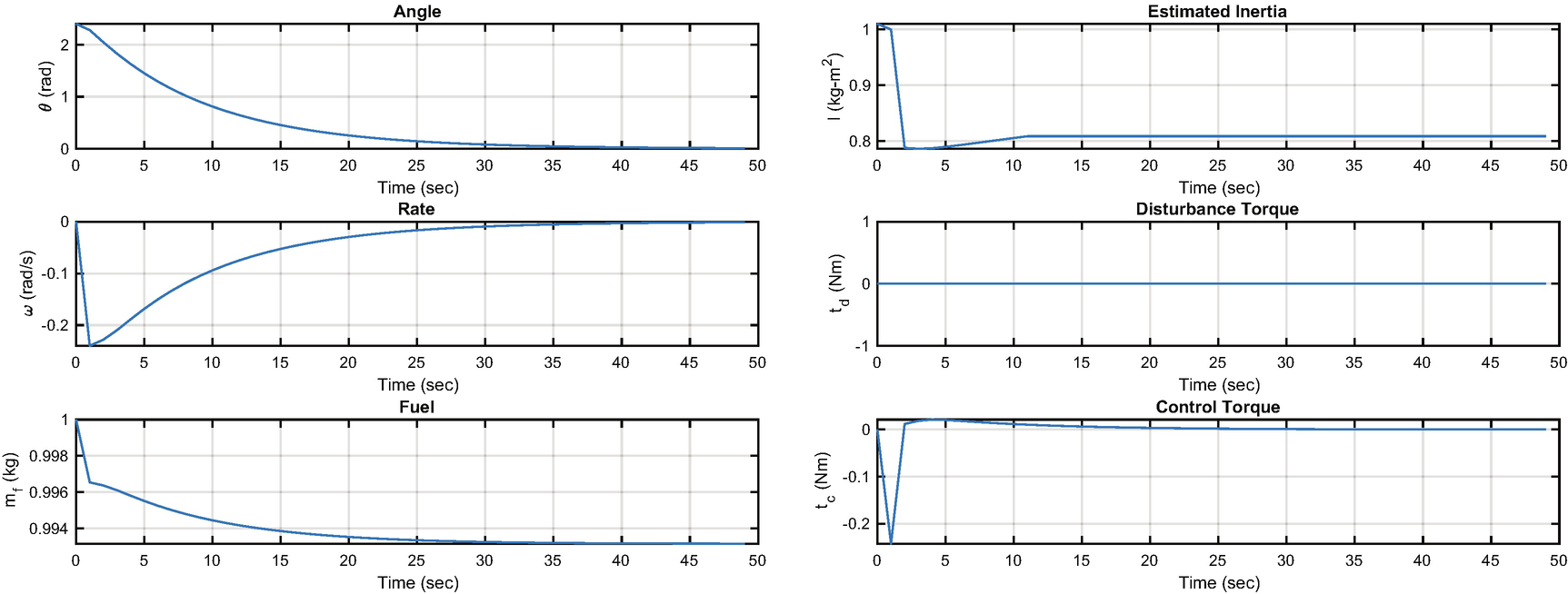
../images/420697_2_En_5_Chapter/420697_2_En_5_Fig15_HTML.png — Figure 5.15
States and control outputs from the spacecraft simulation.

This algorithm appears crude, but it is fundamentally all we can do in this situation given just angular rate measurements. More sophisticated filters or estimators could improve the performance.

5.8 Summary

This chapter has demonstrated adaptive or learning control. You learned about model tuning, model reference adaptive control, adaptive control and gain scheduling. Table 5.2 lists the functions and scripts included in the companion code.

Table 5.2

Chapter Code Listing

File	Description
Combinations	Enumerates n integers for 1:n taken k at a time.
FFTEnergy	Generates fast Fourier transform energy.
FFTSim	Demonstration of the fast Fourier transform.
MRAC	Implement model reference adaptive control.
QCR	Generates a full state feedback controller.
RHSOscillatorControl	Right-hand side of a damped oscillator with a velocity gain.
RHSRotor	Right-hand side for a rotor.
RHSShip	Right-hand side for a ship steering model.
RHSSpacecraft	Right-hand side for a spacecraft model.
RotorSim	Simulation of model reference adaptive control.
ShipSim	Simulation of ship steering.
ShipSimDisturbance	Simulation of ship steering with disturbances.
SpacecraftSim	Time varying inertia demonstration.
SquareWave	Generate a square wave.
TuningSim	Controller tuning demonstration.
WrapPhase	Keep angles between − π and π.

Table of Contents for MATLAB Machine Learning Recipes: A Problem-Solution Approach

5. Adaptive Control

5.1 Self Tuning: Modeling an Oscillator

TIP

5.2 Self Tuning: Tuning an Oscillator

5.2.1 Problem

5.2.2 Solution

5.2.3 How It Works

5.3 Implement Model Reference Adaptive Control

5.3.1 Problem

5.3.2 Solution

5.3.3 How It Works

5.4 Generating a Square Wave Input

5.4.1 Problem

5.4.2 Solution

5.4.3 How It Works

TIP

5.5 Demonstrate MRAC for a Rotor

5.5.1 Problem

5.5.2 Solution

5.5.3 How It Works

TIP

5.6 Ship Steering: Implement Gain Scheduling for Steering Control of a Ship

5.6.1 Problem

5.6.2 Solution

5.6.3 How It Works

5.7 Spacecraft Pointing

5.7.1 Problem

5.7.2 Solution

5.7.3 How It Works

5.8 Summary

Table of Contents for
MATLAB Machine Learning Recipes: A Problem-Solution Approach