V Kishore AyyadevaraPro Machine Learning Algorithms https://doi.org/10.1007/978-1-4842-3564-5_8

8. Word2vec

V Kishore Ayyadevara¹

(1)

Hyderabad, Andhra Pradesh, India

Word2vec is a neural network–based approach that comes in very handy in traditional text mining analysis.

One of the problems with a traditional text mining approach is an issue with the dimensionality of data. Given the high number of distinct words within a typical text, the number of columns that are built can become very high (where each column corresponds to a word, and each value in the column specifies whether the word exists in the text corresponding to the row or not—more about this later in the chapter).

Word2vec helps represent data in a better way: words that are similar to each other have similar vectors, whereas words that are not similar to each other have different vectors. In this chapter, we will explore the different ways in which word vectors are calculated.

To get an idea of how Word2vec can be useful, let’s explore a problem. Let’s say we have two input sentences:

../images/463052_1_En_8_Chapter/463052_1_En_8_Figa_HTML.png

Intuitively, we know that enjoy and like are similar words. However, in traditional text mining, when we one-hot-encode the words, our output looks like this:

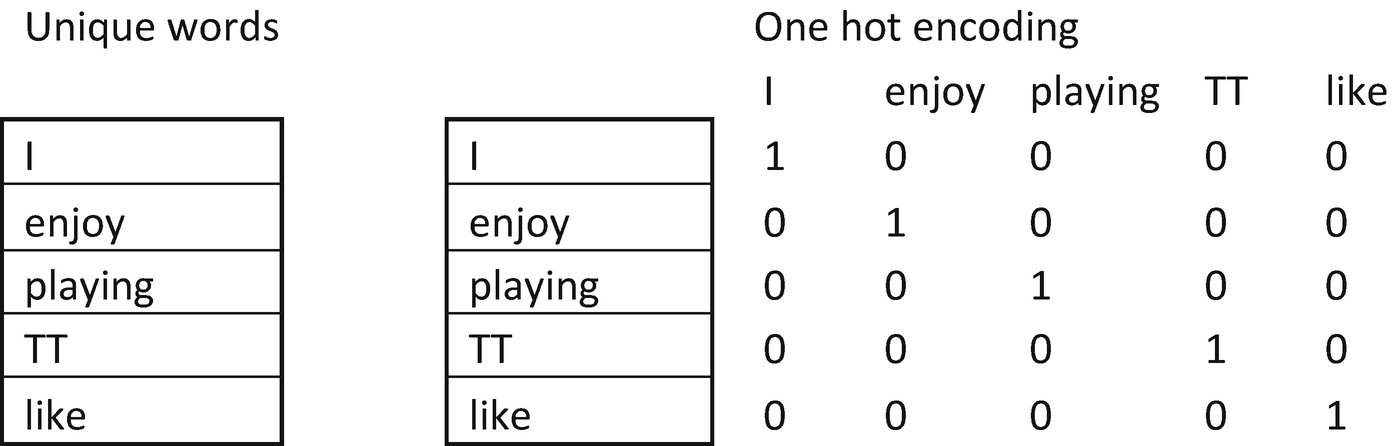
../images/463052_1_En_8_Chapter/463052_1_En_8_Figb_HTML.png

Notice that one-hot encoding results in each word being assigned a column. The major issue with one-hot-encoding is that the eucledian distance between the words {I, enjoy} is the same as the distance between the words {enjoy, like}. But we know that the distance between {I, enjoy} should be greater than the distance between {enjoy, like} because enjoy and like are more synonymous to each other.

Hand-Building a Word Vector

Before building a word vector, we’ll formulate the hypothesis as follows:

“Words that are related will have similar words surrounding them.”

For example, the words king and prince will have similar words surrounding them more often than not. Essentially, the context (the surrounding words) of the words would be similar.

With this hypothesis, let’s look at each word as output and all the context words (surrounding words) as input. Thus, our dataset translates as follows (available as “word2vec.xlsx” in github):

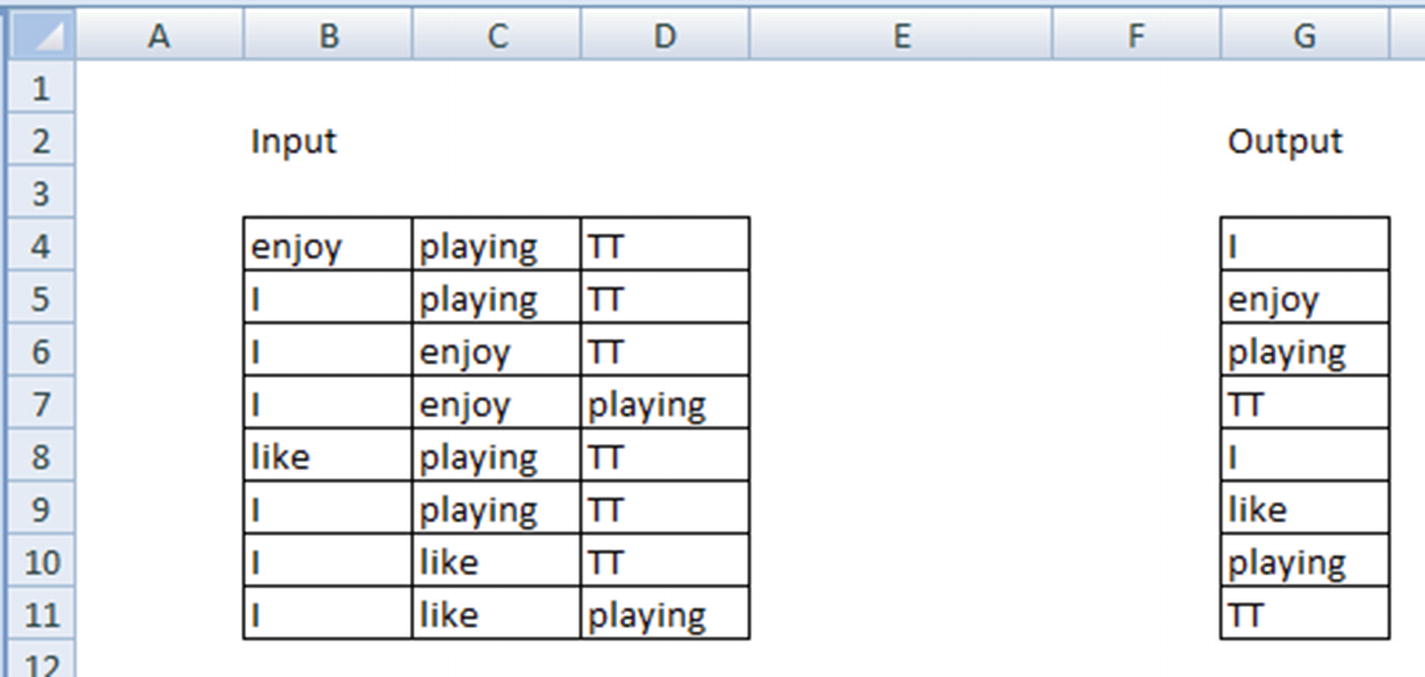
../images/463052_1_En_8_Chapter/463052_1_En_8_Figc_HTML.jpg

By using the context words as input, we are trying to predict the given word as output.

A vectorized form of the preceding input and output words looks like this (note that, the column names {I, enjoy, playing, TT, like} are given in row 3 only for reference):

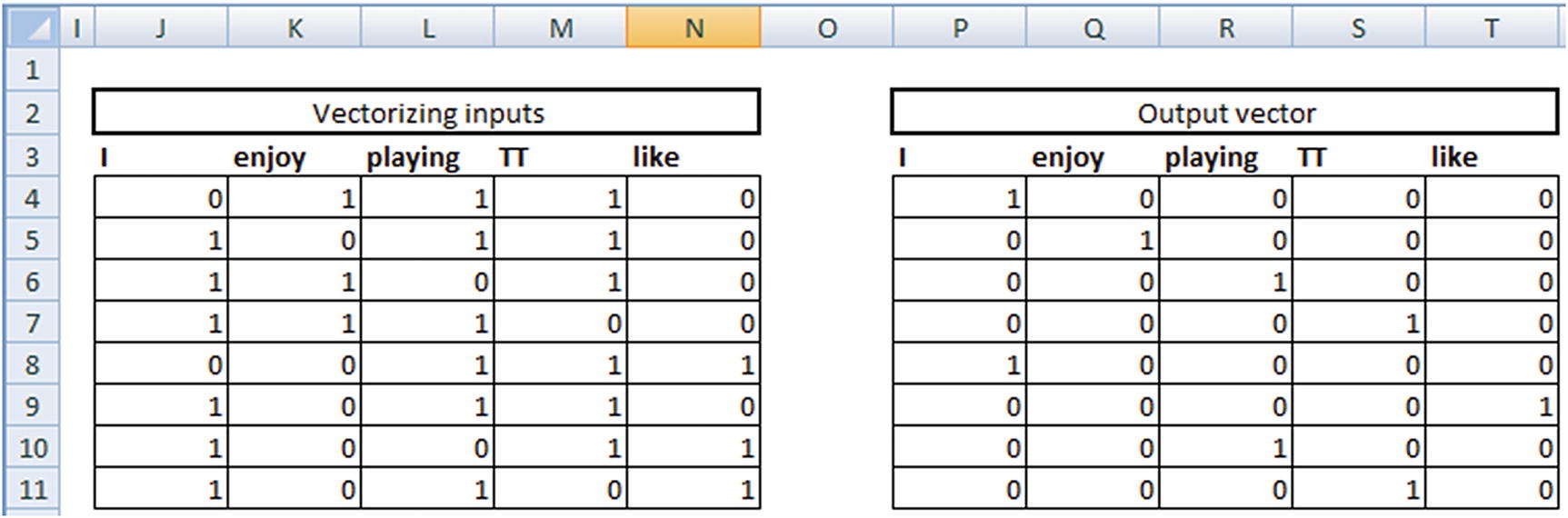
../images/463052_1_En_8_Chapter/463052_1_En_8_Figd_HTML.jpg

Note that, given the input words—{enjoy, playing, TT}—the vector form is {0,1,1,1,0} because the input doesn’t contain both I and like, so the first and last indices are 0 (note the one-hot encoding done in the first page).

For now, let’s say we would like to convert the 5-dimensional input vector into a 3-dimensional vector. In such a scenario, our hidden layer has three neurons associated with it. Our neural network would look like Figure 8-1.

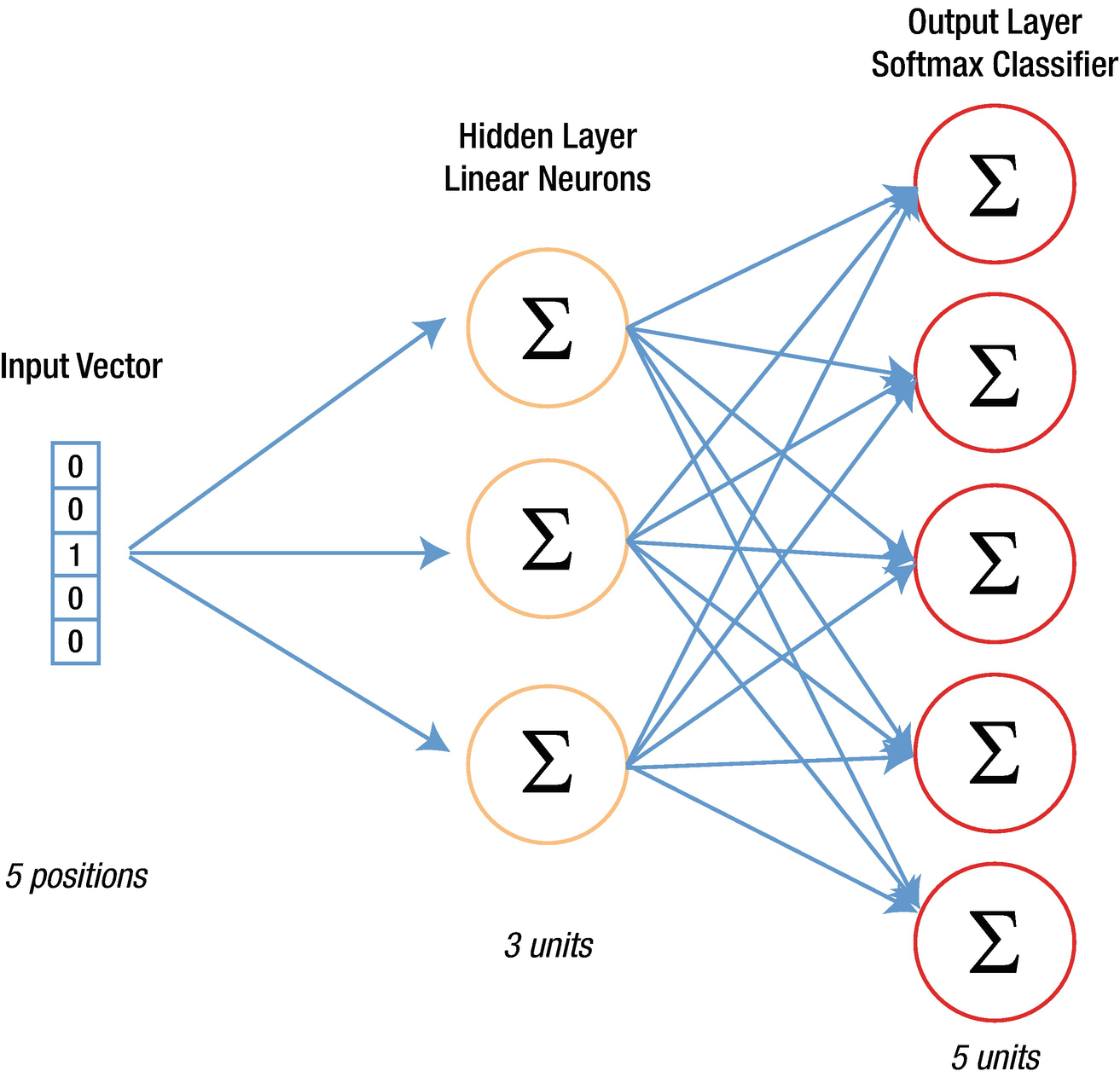
../images/463052_1_En_8_Chapter/463052_1_En_8_Fig1_HTML.png — Figure 8-1
Our neural network

The dimensions of each layer are as follows:

Layer	Size	Commentary
Input layer	8 × 5	Because there are 8 inputs and 5 indices (unique words)
Weights at hidden layer	5 × 3	Because there are 5 inputs each to the 3 neurons
Output of hidden layer	8 × 3	Matrix multiplication of input and hidden layer
Weights from hidden to output	3 × 5	3 output columns from hidden layer mapped to the 5 original output columns
Output layer	8 × 5	Matrix multiplication between output of hidden layer and the weights from hidden to output layer

The following shows how each of these works out:

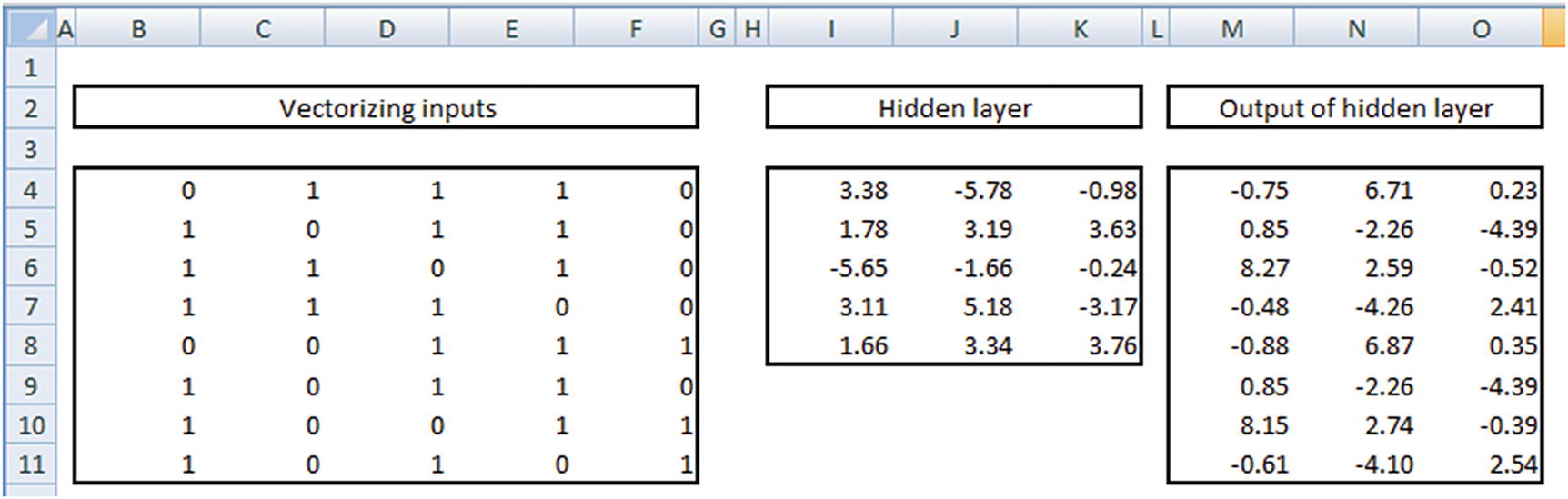
../images/463052_1_En_8_Chapter/463052_1_En_8_Fige_HTML.jpg

Note that the input vector is multiplied by a randomly initialized hidden layer weight matrix to obtain the output of hidden layer. Given that the input is 8 × 5 in size and the hidden layer is 5 × 3 in size, the output of matrix multiplication is 8 × 3. And, unlike in a traditional neural network, in the Word2vec approach we don’t apply any activations on the hidden layer:

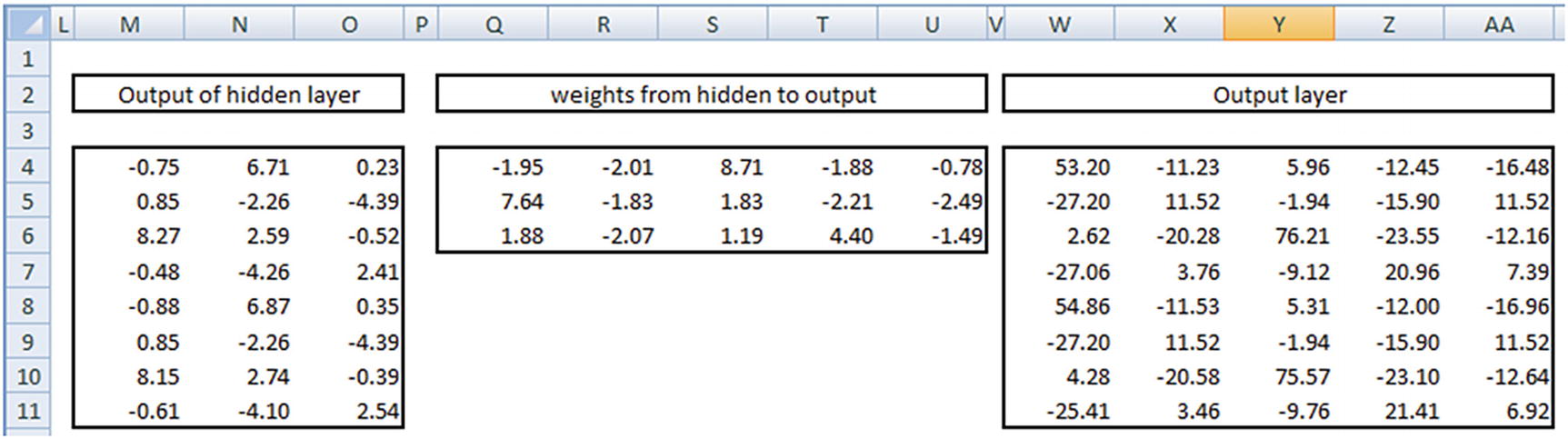
../images/463052_1_En_8_Chapter/463052_1_En_8_Figf_HTML.jpg

Once we have the output of the hidden layer, we multiply them with a matrix of weights from hidden to output layer. Given that the output of hidden layer is 8 × 3 in size and the hidden layer to output is 3 × 5 in size, our output layer is 8 × 5. But note that the output layer has a range of numbers, both positive and negative, as well as numbers that are >1 or <–1.

Hence, just as we did in neural networks, we pass the numbers through a softmax to convert them to a number between 0 and 1:

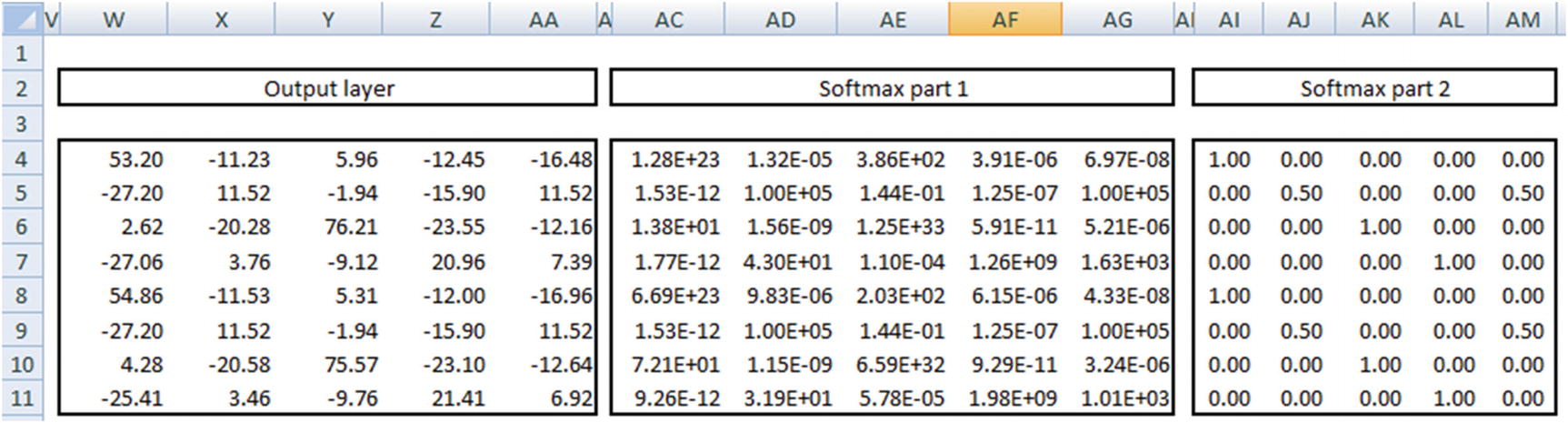
../images/463052_1_En_8_Chapter/463052_1_En_8_Figg_HTML.jpg

For convenience, I have broken down softmax into two steps:

1.
Apply exponential to the number.
2.
Divide the output of step 1 by the row sum of the output of step 1.

In the preceding output, we see that the output of the first column is very close to 1 in the first row, and the output of the second column is 0.5 in the second row and so on.

Once we obtain the predictions, we compare them with the actuals to calculate the cross entropy loss across the whole batch, as follows:

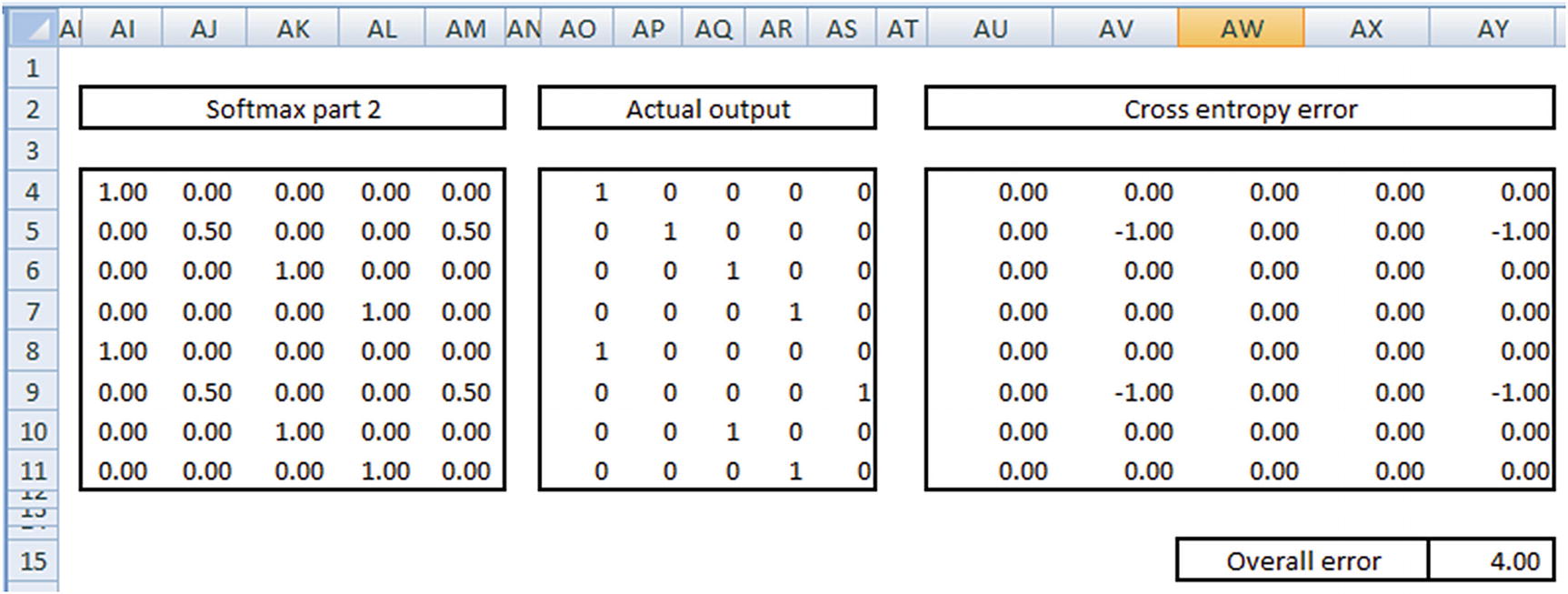
../images/463052_1_En_8_Chapter/463052_1_En_8_Figh_HTML.jpg

Cross entropy loss = –∑ Actual value × Log (probability, 2)

Now that we’ve calculated the overall cross entropy error, our task is to reduce the overall cross entropy error by varying the weights that are randomly initialized, using an optimizer of choice. Once we arrive at the optimal weight values, we are left with the hidden layer that looks like this:

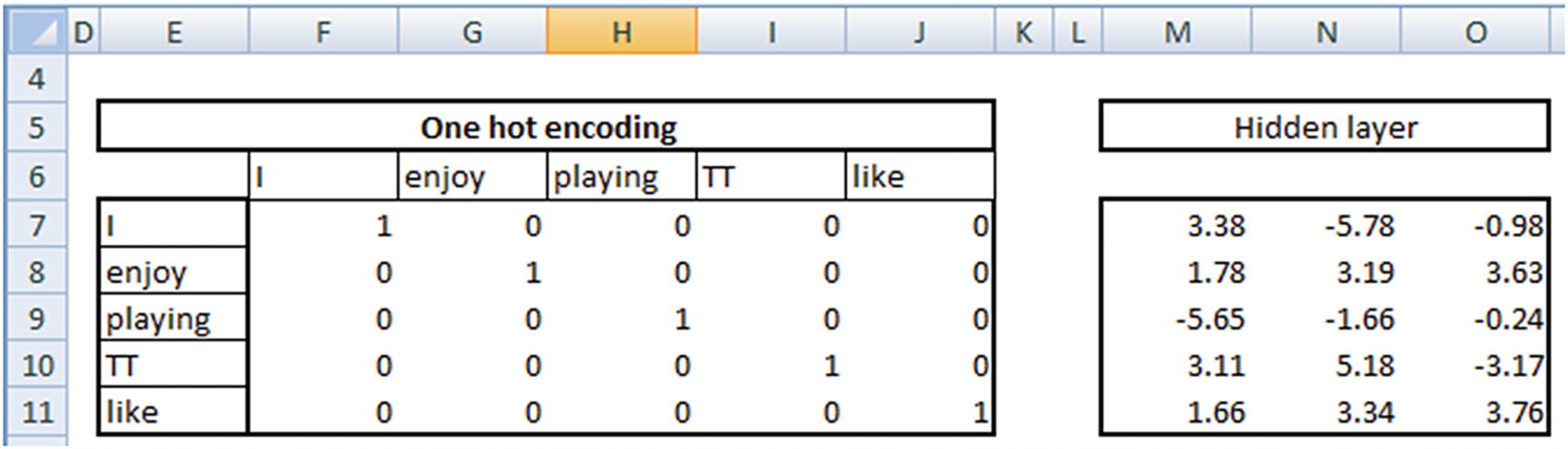
../images/463052_1_En_8_Chapter/463052_1_En_8_Figi_HTML.jpg

Now that we have the input words and the hidden layer weights calculated, the words can now be represented in a lower dimension by multiplying the input word with the hidden layer representation.

The matrix multiplication of the input layer (1 × 5 for each word) and hidden layer (5 × 3 weights) is a vector of size (1 × 3):

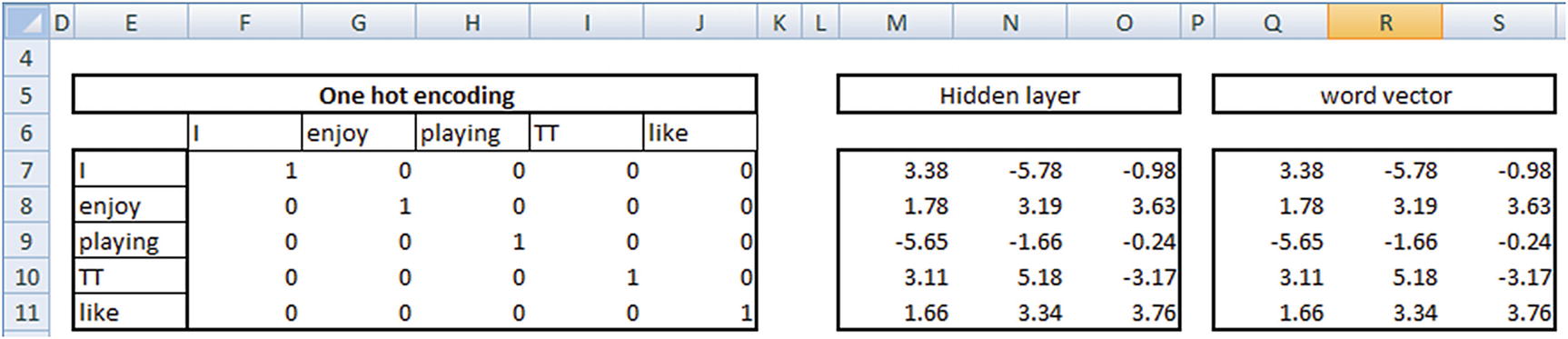
../images/463052_1_En_8_Chapter/463052_1_En_8_Figj_HTML.jpg

If we now consider the words {enjoy, like} we should notice that the vectors of the two words are very similar to each other (that is, the distance between the two words is small).

This way, we have converted the original input one-hot-encoded vector, where the distance between {enjoy, like} was high to the transformed word vector, where the distance between {enjoy, like} is small.

Methods of Building a Word Vector

The method we have adopted in building a word vector in the previous section is called the continuous bag of words (CBOW) model.

Take a sentence “The quick brown fox jumped over the dog.” The CBOW model handles that sentence like this:

1.
Fix a window size. That is, select n words to the left and right of a given word. For example, let’s say the window size is 2 words each to the left and right of the given word.
2.
Given the window size, the input and output vectors would look like this:

Input words	Output word
{The, quick, fox, jumped}	{brown}
{quick, brown, jumped, over}	{fox}
{brown, fox, over, the}	{jumped}
{fox, jumped, the, dog}	{over}

Another approach to build a word vector is called the skip-gram model. In the skip-gram model, the preceding step is reversed, as follows:

Input words	Output word
{brown}	{The, quick, fox, jumped}
{fox}	{quick, brown, jumped, over}
{jumped}	{brown, fox, over, the}
{over}	{fox, jumped, the, dog}

The approach to arrive at the hidden layer vectors remains the same, irrespective of whether it is a skip-gram model or a CBOW model.

Issues to Watch For in a Word2vec Model

For the way of calculation discussed so far, this section looks at some of the common issues we might be facing.

Frequent Words

Typical frequent words like the appear quite often in vocabulary. In such cases, the output has the words like the occurring a lot more often. If not treated, this might result in a majority of the output being the most frequent words, like the, more than other words. We need to have a way to penalize for the number of times a frequently occurring word can be seen in the training dataset.

In a typical Word2vec analysis, the way we penalize for frequently occurring words is as follows. The probability of selecting a word is calculated like this:

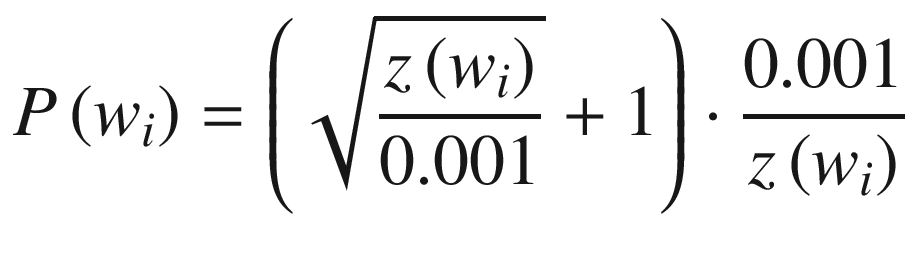
$P\left({w}_i\right)=\left(\sqrt{\frac{z\left({w}_i\right)}{0.001}}+1\right)\cdot \frac{0.001}{z\left({w}_i\right)}$

z(w) is the number of times a word has occurred over the total occurrences of any word. A plot of that formula reveals the curve in Figure 8-2.

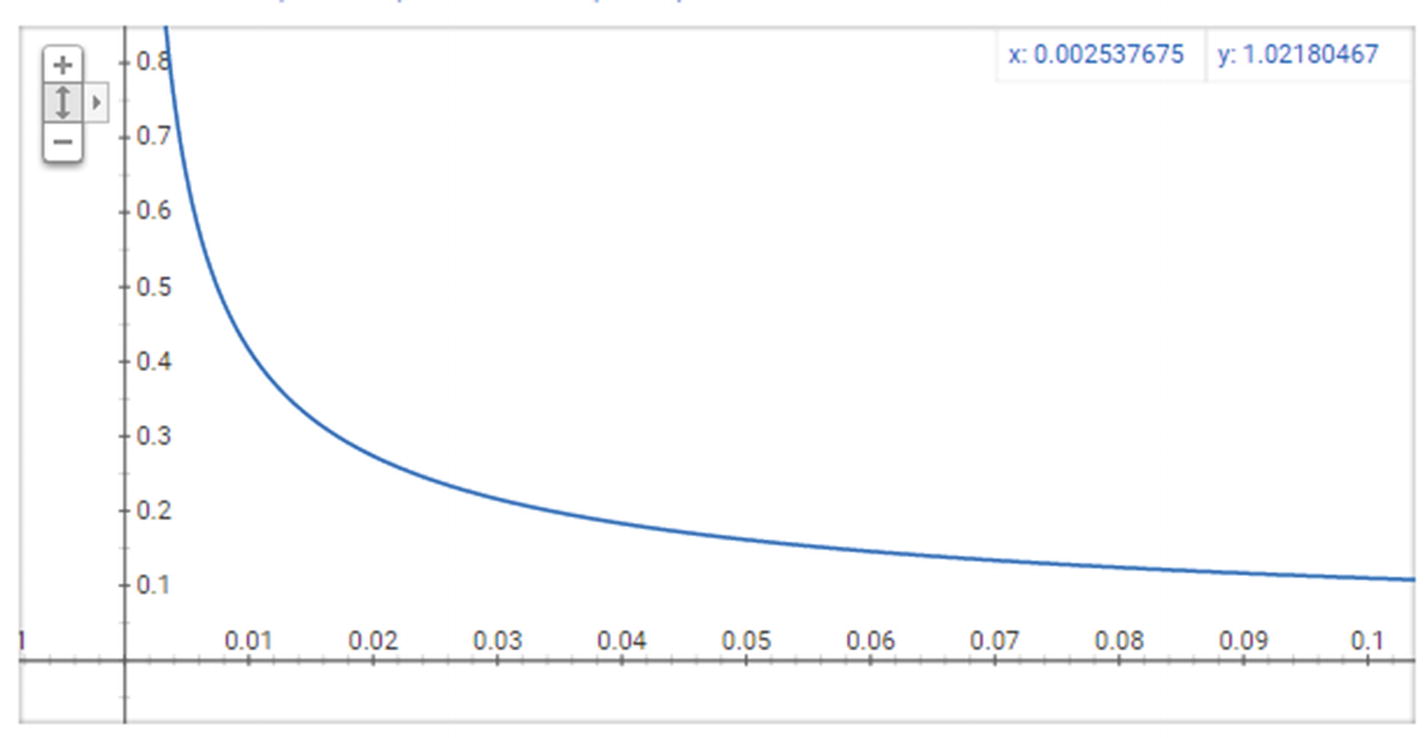
../images/463052_1_En_8_Chapter/463052_1_En_8_Fig2_HTML.jpg — Figure 8-2
The resultant curve

Note that as z(w) (x-axis) increases, the probability of selection (y-axis) decreases drastically.

Negative Sampling

Let’s assume there are a total of 10,000 unique words in our dataset—that is, each vector is of 10,000 dimensions. Let’s also assume that we are creating a 300-dimensional vector from the original 10,000-dimensional vector. This means, from the hidden layer to the output layer, there are a total of 300 × 10,000 = 3,000,000 weights.

One of the major issues with such a high number of weights is that it might result in overfitting on top of the data. It also might result in a longer training time.

Negative sampling is one way to overcome this problem. Let’s say that instead of checking for all 10,000 dimensions, we pick the index at which the output is 1 (the correct label) and five random indices where the label is 0. This way, we are reducing the number of weights to be updated in a single iteration from 3 million to 300 × 6 = 1800 weights.

I said that the selection of negative indices is random, but in actual implementation of Word2vec, the selection is based on the frequency of a word when compared to the other words. The words that are more frequent have a higher chance of getting selected when compared to words that are less frequent.

The probability of selecting five negative words is as follows:

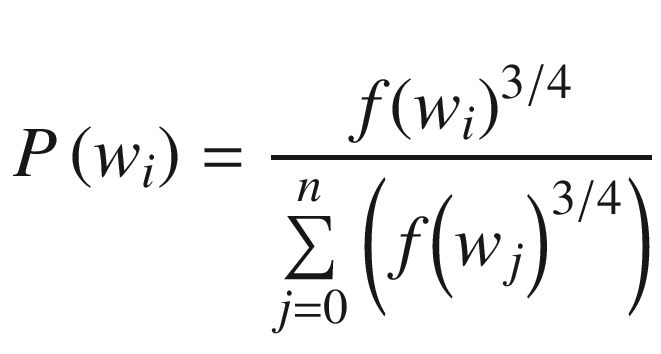
$P\left({w}_i\right)=\frac{f{\left({w}_i\right)}^{3/4}}{\sum \limits_{j=0}^n\left(f{\left({w}_j\right)}^{3/4}\right)}$

f(w) is the frequency of a given word.

Once the probabilities of each word are calculated, the word selection happens as follows: Higher-frequency words are repeated more often, and lower-frequent words are repeated less often and are stored in a table. Given that high-frequency words are repeated more often, the chance of them getting picked up is higher when a random selection of five words is made from the table.

Implementing Word2vec in Python

Word2vec can be implemented in Python using the gensim package (the Python implementation is available in github as “word2vec.ipynb”).

The first step is to initialize the package:

import nltk

import gensim

import pandas as pd

Once we import the package, we are expected to provide the parameters discussed in previous sections:

import logging

logging.basicConfig(format=’%(asctime)s : %(levelname)s : %(message)s’,\

level=logging.INFO)

# Set values for various parameters

num_features = 100 # Word vector dimensionality

min_word_count = 50 # Minimum word count

num_workers = 4 # Number of threads to run in parallel

context = 9 # Context window size

downsampling = 1e-4 # Downsample setting for frequent words

logging essentially helps us in tracking the extent to which the word vector calculation is complete.
num_features is the number of neurons in the hidden layer.
min_word_count is the cut-off of the frequency of words that get accepted for the calculation.
context is the window size
downsampling helps in assigning a lower probability of picking the more frequent words.

The input vocabulary for the model should be like the following:

../images/463052_1_En_8_Chapter/463052_1_En_8_Figk_HTML.jpg

Note that all the input sentences are tokenized.

A Word2vec model is trained as follows:

from gensim.models import word2vec

print(“Training model...”)

w2v_model = word2vec.Word2Vec(t2, workers=num_workers,

size=num_features, min_count = min_word_count,

window = context, sample = downsampling)

Once a model is trained, the vector of weights for any word in the vocabulary that meets the specified criterion can be obtained as follows:

model['word'] # replace the "word" with the word of your interest

Similarly, the most similar word to a given word can be obtained like this:

model.most_similar('word')

Summary

In this chapter, you learned the following:

Word2vec is an approach that can help convert text words into numeric vectors.
This acts as a powerful first step for multiple approaches downstream—for example, one can use the word vectors in building a model.
Word2vec comes up with the vectors using one the CBOW or skip-gram model, which have a neural network architecture that helps in coming up with vectors.
The hidden layer in neural network is the key to generating the word vectors.

Previous Chapter

7. Artificial Neural Network

Next Chapter

9. Convolutional Neural Network

Table of Contents for Pro Machine Learning Algorithms : A Hands-On Approach to Implementing Algorithms in Python and R