Table of Contents for
Pro Machine Learning Algorithms : A Hands-On Approach to Implementing Algorithms in Python and R

Version ebook / Retour

Cover image for bash Cookbook, 2nd Edition Pro Machine Learning Algorithms : A Hands-On Approach to Implementing Algorithms in Python and R by V Kishore Ayyadevara Published by Apress, 2018
  1. Navigation
  2. Cover
  3. Front Matter
  4. 1. Basics of Machine Learning
  5. 2. Linear Regression
  6. 3. Logistic Regression
  7. 4. Decision Tree
  8. 5. Random Forest
  9. 6. Gradient Boosting Machine
  10. 7. Artificial Neural Network
  11. 8. Word2vec
  12. 9. Convolutional Neural Network
  13. 10. Recurrent Neural Network
  14. 11. Clustering
  15. 12. Principal Component Analysis
  16. 13. Recommender Systems
  17. 14. Implementing Algorithms in the Cloud
  18. Back Matter
© V Kishore Ayyadevara 2018
V Kishore AyyadevaraPro Machine Learning Algorithms https://doi.org/10.1007/978-1-4842-3564-5_5

5. Random Forest

V Kishore Ayyadevara1 
(1)
Hyderabad, Andhra Pradesh, India
 

In Chapter 4, we looked at the process of building a decision tree. Decision trees can overfit on top of the data in some cases—for example, when there are outliers in dependent variable. Having correlated independent variables may also result in the incorrect variable being selected for splitting the root node.

Random forest overcomes those challenges by building multiple decision trees, where each decision tree works on a sample of the data. Let’s break down the term: random refers to the random sampling of data from original dataset, and forest refers to the building of multiple decision trees, one each for each random sample of data. (Get it? It is a combination of multiple trees, and so is called a forest.)

In this chapter you will learn the following:

  • Working details of random forest

  • Advantages of random forest over decision tree

  • The impact of various hyper-parameters on a decision tree

  • How to implement random forest in Python and R

A Random Forest Scenario

To illustrate why random forest is an improvement over decision tree, let’s go through a scenario in which we try to classify whether you will like a movie or not:
  1. 1.
    You ask for recommendations from a person A.
    1. a.
      A asks some questions to find out what your preferences are.
      1. i.

        We’ll assume only 20 exhaustive questions are available.

         
      2. ii.

        We’ll add the constraint that any person can ask from a random selection of 10 questions out of the 20 questions.

         
      3. iii.

        Given the 10 questions, the person ideally orders those questions in such a way that they are in a position to extract the maximum information from you.

         
       
    2. b.

      Based on your responses, A comes up with a set of recommendations for movies.

       
     
  2. 2.
    You ask for recommendations from another person, B.
    1. a.
      As before, B asks questions to find out your preferences.
      1. i.

        B is also in a position to ask only 10 questions out of the exhaustive list of 20 questions.

         
      2. ii.

        Based on the set of 10 randomly selected questions, B again orders them to maximize the information obtained from your preferences.

         
      3. iii.

        Note that the set of questions is likely to be different between A and B, though with some overlap.

         
       
    2. b.

      Based on your responses, B comes up with recommendations.

       
     
  3. 3.
    In order to achieve some randomness, you may have told A that The Godfather is the best movie you have ever watched. But you merely told B you enjoyed watching The Godfather “a lot.”
    1. a.

      This way, although the original information did not change, the way in which the two different people learned it was different.

       
     
  4. 4.
    You perform the same experiment with n friends of yours.
    1. a.

      Through the preceding, you have essentially built an ensemble of decision trees (where ensemble means combination of trees or forest).

       
     
  5. 5.

    The final recommendation will be the average recommendation of all n friends.

     

Bagging

Bagging is short for bootstrap aggregating . The term bootstrap refers to selecting a few rows randomly (a sample from the original dataset), and aggregating means taking the average of predictions from all the decision trees that are built on the sample of the dataset.

This way, the predictions are less likely to be biased due to a few outlier cases (because there could be some trees built using sample data—where the sample data did not have any outliers). Random forest adopts the bagging approach in building predictions.

Working Details of a Random Forest

The algorithm for building a random forest is as follows:
  1. 1.

    Subset the original data so that the decision tree is built on only a sample of the original dataset.

     
  2. 2.

    Subset the independent variables (features) too while building the decision tree.

     
  3. 3.

    Build a decision tree based on the subset data where the subset of rows as well as columns is used as the dataset.

     
  4. 4.

    Predict on the test or validation dataset.

     
  5. 5.

    Repeat steps 1 through 3 n number of times, where n is the number of trees built.

     
  6. 6.

    The final prediction on the test dataset is the average of predictions of all n trees.

     

The following code in R builds the preceding algorithm (available as “rf_code.R” in github):

t=read.csv("train_sample.csv")

The described dataset has 140 columns and 10,000 rows. The first 8,000 rows are used to train the model, and the rest are used for testing:

train=t[1:8000,]
test=t[8001:9999,]

Given that we are using decision trees to build our random forest, let’s use the rpart package:

library(rpart)
Initialize a new column named prediction in the test dataset:
test$prediction=0
for(i in 1:1000){ # we are running 1000 times - i.e., 1000 decision trees
  y=0.5
  x=sample(1:nrow(t),round(nrow(t)*y))  # Sample 50% of total rows, as y is 0.5
t2=t[x, c(1,sample(139,5)+1)]     # Sample 5 columns randomly, leaving the first column which is the dependent variable
dt=rpart(response~.,data=t2)   # Build a decision tree on the above subset of data (sample rows and columns)
 pred1=(predict(dt,test))  # Predict based on the tree just built
 test$prediction=(test$prediction+pred1)  # Add predictions of all the iterations of previously built decision trees
}
test$prediction = (test$prediction)/1000  # Final prediction of the value is the average of predictions of all the iterations

Implementing a Random Forest in R

Random forest can be implemented in R using the randomForest package. In the following code snippet, we try predicting whether a person would survive or not in the Titanic dataset (the code is available as “rf_code2.R” in github).

For simplicity, we will not deal with missing values and only consider those rows that do not have missing values:
../images/463052_1_En_5_Chapter/463052_1_En_5_Figa_HTML.jpg
In that code, we build a random forest that has 10 trees to provide predictions. The output of that code snippet is shown here:
../images/463052_1_En_5_Chapter/463052_1_En_5_Figb_HTML.jpg
Note that the error message above specifies two things:

  • The number of distinct values in some categorical independent variables is high.

  • Additionally, it assumes that we would have to specify regression instead of classification.

Let’s look at why random forest might have given an error when the categorical variable had a high number of distinct values. Note that random forest is an implementation of multiple decision trees. In a decision tree, when there are more distinct values, the frequency count of a majority of the distinct values is very low. When frequency is low, the purity of the distinct value is likely to be high (or impurity is low). But this isn’t reliable, because the number of data points is likely to be low (in a scenario where the number of distinct values of a variable is high). Hence, random forest does not run when the number of distinct values in categorical variable is high.

Consider the warning message in the output: “The response has five or fewer unique values. Are you sure you want to do regression?” Note that, the column named Survived is numeric in class. So, the algorithm by default assumed that it is a regression that needs to be performed.

To avoid this, you need to convert the dependent variable into a categorical or factor variable:
../images/463052_1_En_5_Chapter/463052_1_En_5_Figc_HTML.jpg

Now we can expect the random forest predictions to be made.

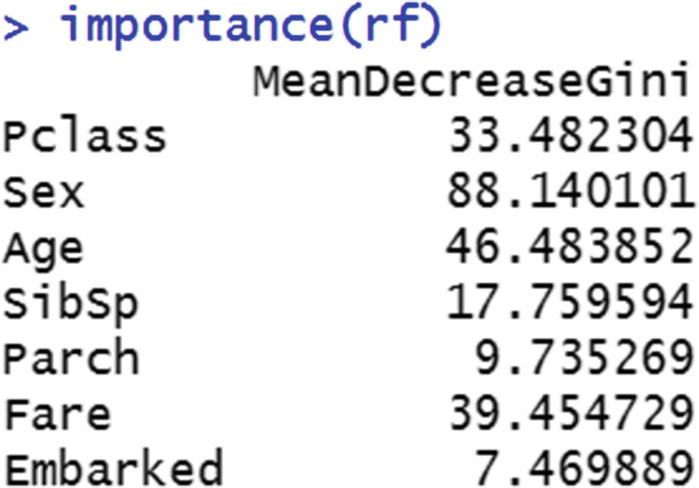
If we contrast the output with decision tree, one of the major drawbacks is that the decision tree output can be visualized as a tree, but random forest output cannot be visualized as a tree, because it is a combination of multiple decision trees. One way to understand the variable importance is by looking at how much of the decrease in overall impurity is because of splitting by the different variables.

Variable importance can be calculated in R by using the function importance :
../images/463052_1_En_5_Chapter/463052_1_En_5_Figd_HTML.jpg
Consider how MeanDecreaseGini for the variable Sex might be calculated:
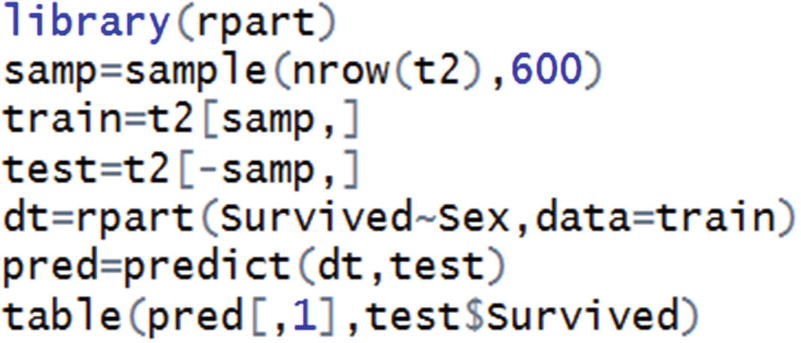
../images/463052_1_En_5_Chapter/463052_1_En_5_Fige_HTML.jpg

In the preceding code snippet, a sample of the original dataset is selected. That sample is considered as a training dataset, and the rest are considered as a test dataset.

A decision tree is built based on the train dataset. Predictions are made on the out-of-bag data—that is, the test dataset:
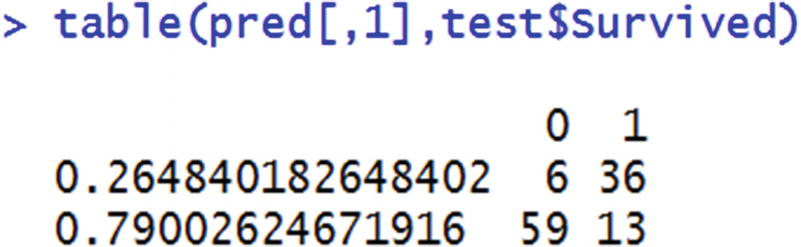
../images/463052_1_En_5_Chapter/463052_1_En_5_Figf_HTML.jpg
Let us calculate the entropy of the preceding output:
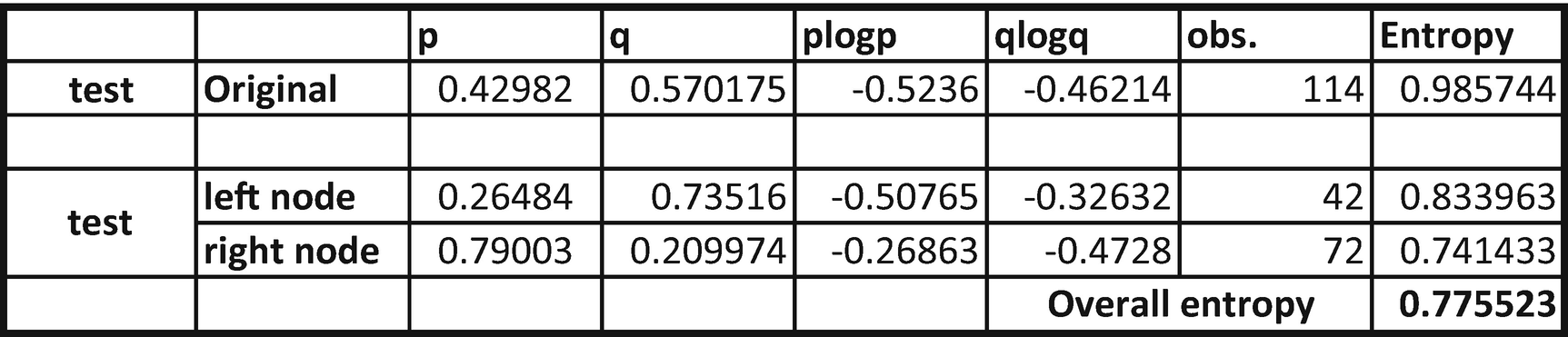
../images/463052_1_En_5_Chapter/463052_1_En_5_Figg_HTML.png

From the table, we can see that overall entropy reduces from 0.9857 to 0.7755.

Similarly, let’s consider the other extreme, the variable that is least important: Embarked:
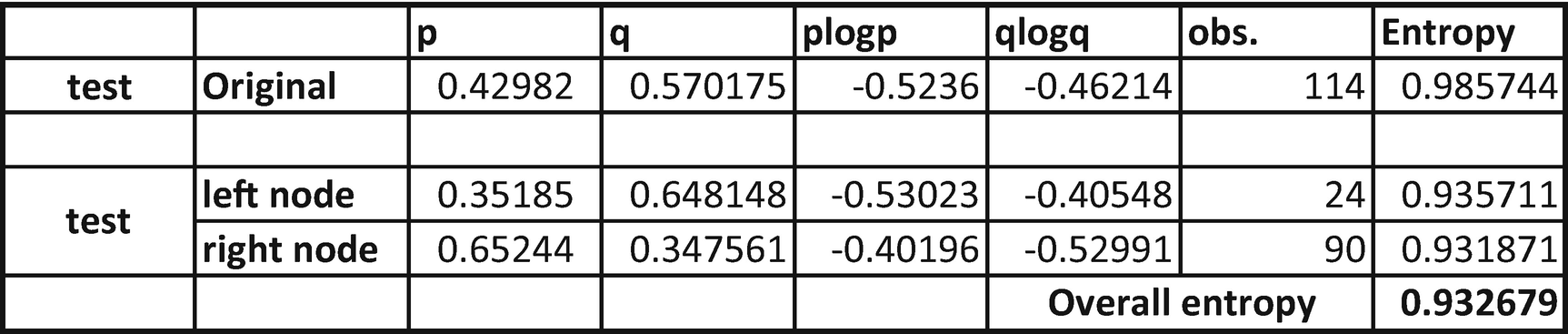
../images/463052_1_En_5_Chapter/463052_1_En_5_Figh_HTML.png

From the preceding table, we see that entropy reduced from 0.9857 to only 0.9326. So, there was a much lower reduction in entropy when compared to the variable Sex. That means Sex as a variable is more important than Embarked.

The variable importance plot can also be obtained by the function shown in Figure 5-1.
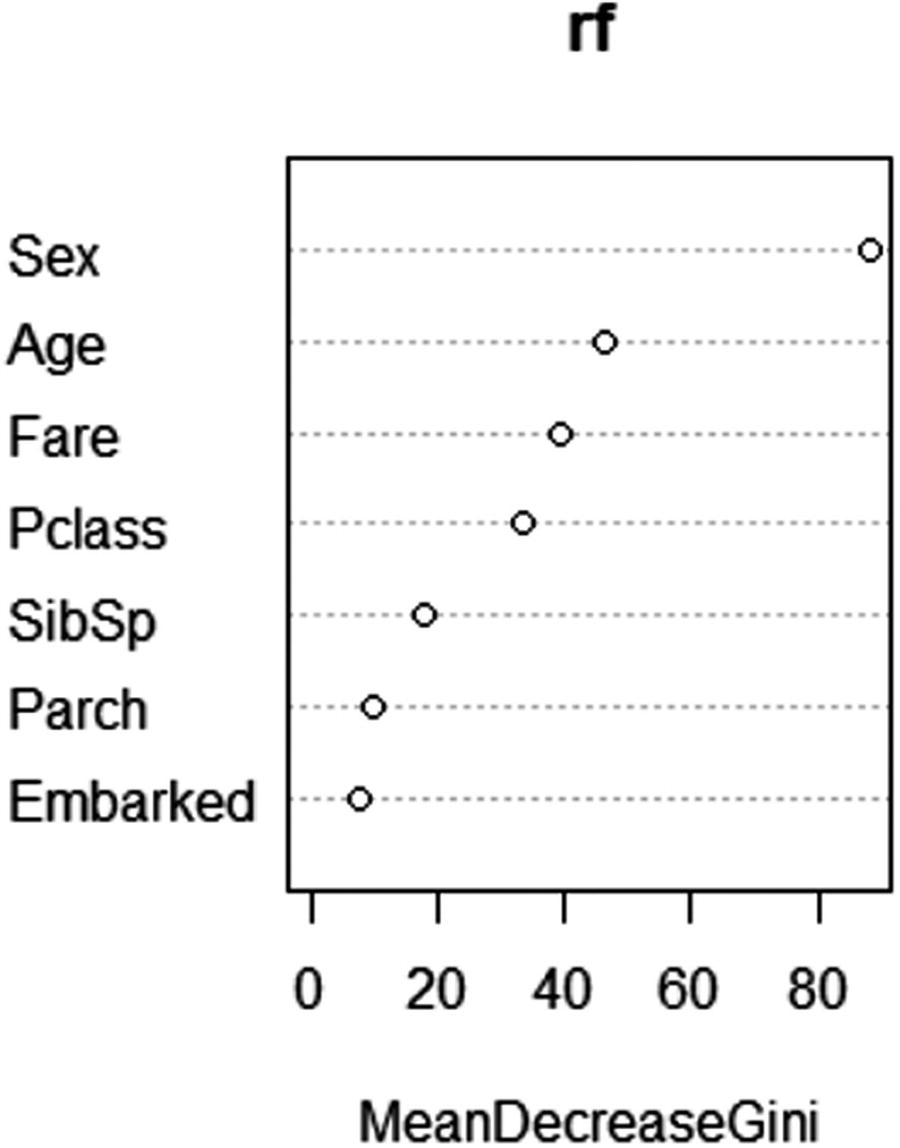
../images/463052_1_En_5_Chapter/463052_1_En_5_Fig1_HTML.jpg
Figure 5-1

Variable importance plot

Parameters to Tune in a Random Forest

In the scenario just discussed, we noticed that random forest is based on decision tree, but on multiple trees running to produce an average prediction. Hence, the parameters that we tune in random forest would be very much the same as the parameters that are used to tune a decision tree.

The major parameters therefore are the following:

  • Number of trees

  • Depth of tree

To see the impact of number of trees on the test dataset AUC, we’ll go through some code . AUC is calculated using the following code snippet:
../images/463052_1_En_5_Chapter/463052_1_En_5_Figi_HTML.jpg
In the following code snippet, we increment the number of trees by a step of 10 and see how the AUC value varies over the number of trees:
../images/463052_1_En_5_Chapter/463052_1_En_5_Figj_HTML.jpg

In the first two lines, we have initialized empty vectors that we will keep populating over the for loop of different numbers of trees. After initialization, we are running a loop where the number of trees is incremented by 10 in each step. After running the random forest, we are calculating the AUC value of the predictions on the test dataset and keep appending the values of AUC.

The final plot of AUC over different numbers of trees is plotted in Figure 5-2.
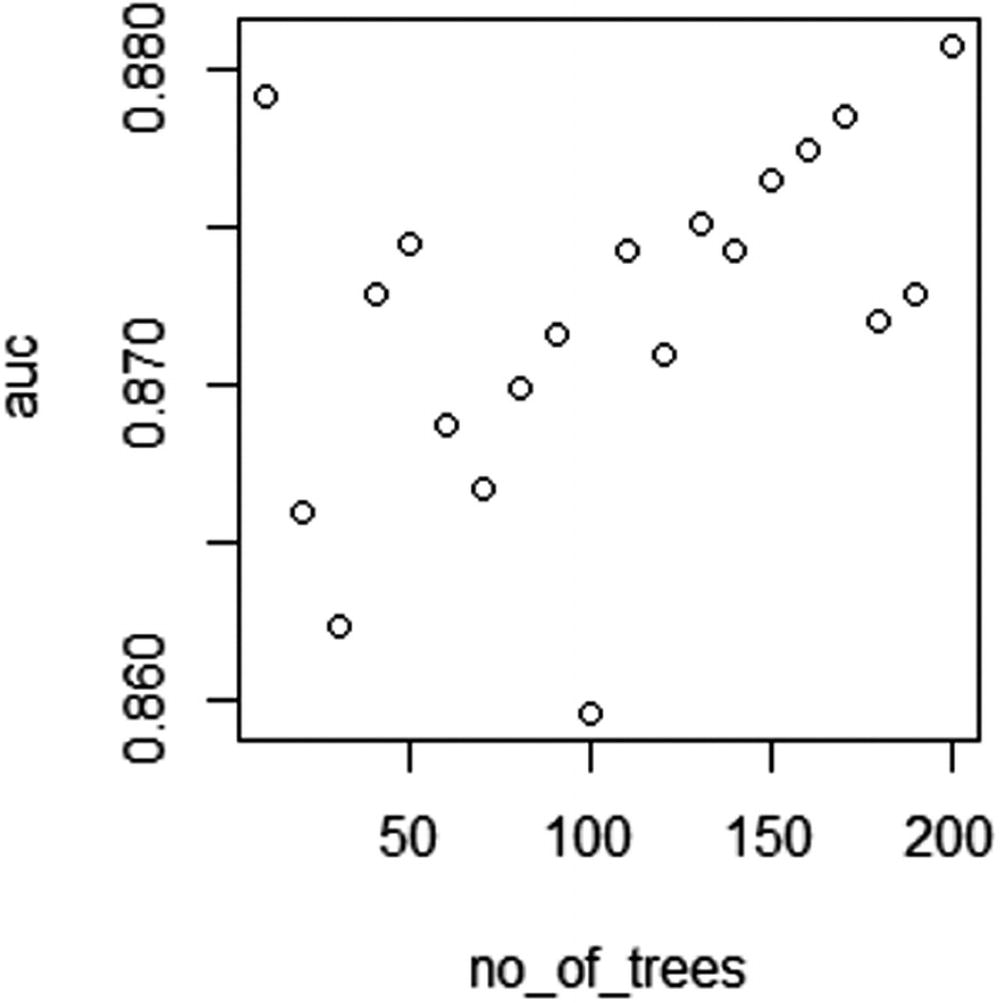
../images/463052_1_En_5_Chapter/463052_1_En_5_Fig2_HTML.jpg
Figure 5-2

AUC over different number of trees

From Figure 5-2, we can see that as the number of trees increases, the AUC value of test dataset increases in general. But after a few more iterations, the AUC might not increase further.

Variation of AUC by Depth of Tree

In the previous section, we noted that the maximum value of AUC occurs when the number of trees is close to 200.

In this section, we’ll consider the impact of depth of tree on the accuracy measure (AUC). In Chapter 4, we saw that the size of a node directly impacts the maximum depth of a tree. For example, if minimum possible node size is high, then depth is automatically low, and vice versa. So let’s tune the node size as a parameter and see how AUC varies by node size:
../images/463052_1_En_5_Chapter/463052_1_En_5_Figk_HTML.jpg

Note that the preceding code is very similar to the code we wrote for the variation in number of trees. The only addition is the parameter nodesize.

The output of the preceding code snippet is shown in Figure 5-3.
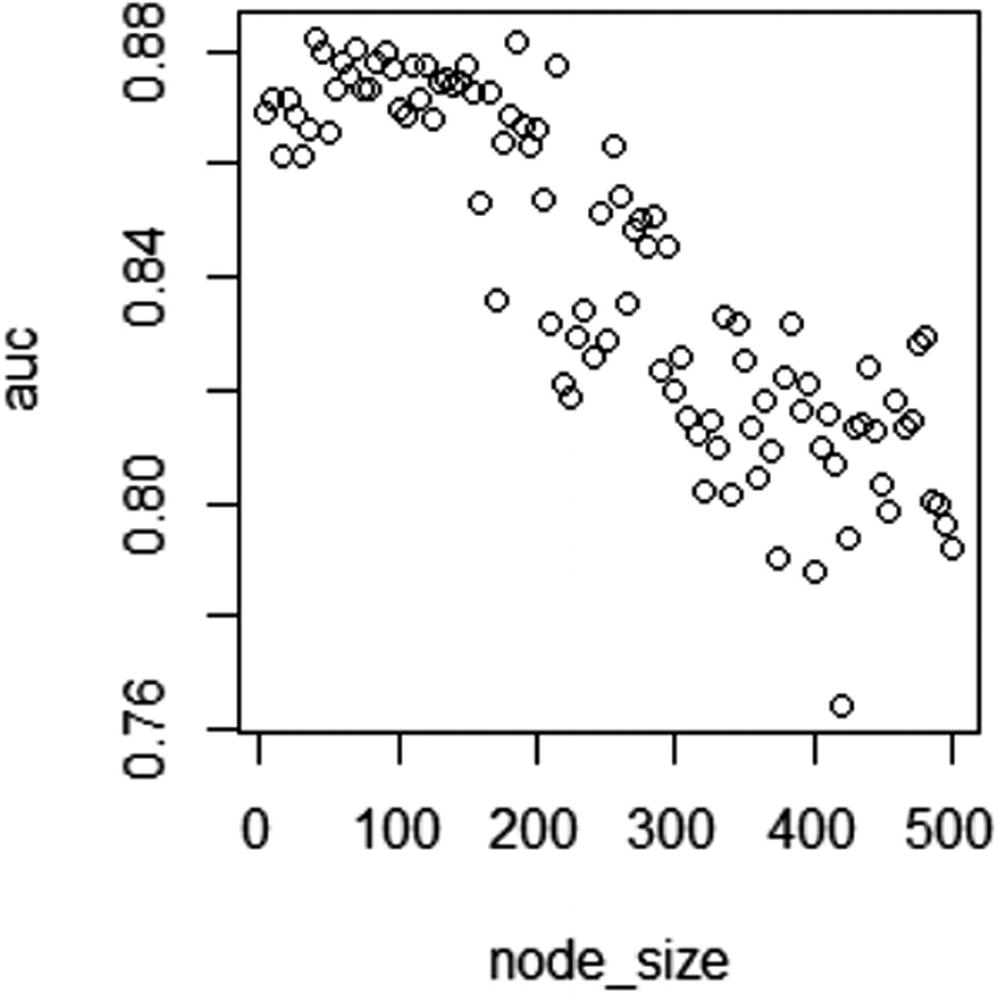
../images/463052_1_En_5_Chapter/463052_1_En_5_Fig3_HTML.jpg
Figure 5-3

AUC over different node sizes

In Figure 5-3, note that as node size increases a lot, AUC of test dataset decreases.

Implementing a Random Forest in Python

Random forest is implemented in Python with the scikit-learn library. The implementation details of random forest are shown here (available in github as “random forest.ipynb”):
from sklearn.ensemble import RandomForestClassifier
rfc = RandomForestClassifier(n_estimators=100,max_depth=5,min_samples_leaf=100,random_state=10)
rfc.fit(X_train, y_train)
Predictions are made as follows:
rfc_pred=rfc.predict_proba(X_test)
Once the predictions are made, AUC can be calculated as follows:
from sklearn.metrics import roc_auc_score
roc_auc_score(y_test, rfc_pred[:,1])

Summary

In this chapter, we saw how random forest improves upon decision tree by taking an average prediction approach. We also saw the major parameters that need to be tuned within a random forest: depth of tree and the number of trees. Essentially, random forest is a bagging (bootstrap aggregating) algorithm—it combines the output of multiple decision trees to give the prediction.