Segmenting a program into manageable chunks of code is fundamental to programming in every language. A function is a basic building block in C++ programs. So far, every example has had one function, main(), and has typically used functions from the Standard Library. This chapter is all about defining your own functions with names that you choose.
What a function is and why you should segment your programs into functions
How to declare and define functions
How data is passed to a function and how a function can return a value
What the difference is between “pass-by-value” and “pass-by-reference” and how to choose between both mechanisms
What the best way is to pass strings to a function
How to specify default values for function parameters
What the preferred way is to return a function’s output in modern C++
How to handle optional input parameters and optional return values
How using const as a qualifier for a parameter type affects the operation of a function
The effect of defining a variable as static within a function
What an inline function is
How to create multiple functions that have the same name but different parameters—a mechanism you’ll come to know as function overloading
What recursion is and how to apply it to implement elegant algorithms
Segmenting Your Programs
All the programs you have written so far have consisted of just one function, main() . A real-world C++ application consists of many functions, each of which provides a distinct well-defined capability. Execution starts in main(), which must be defined in the global namespace. main() calls other functions, each of which may call other functions, and so on. The functions other than main() can be defined in a namespace that you create.
When one function calls another that calls another that calls another, you have a situation where several functions are in action concurrently. Each that has called another that has not yet returned will be waiting for the function that was called to end. Obviously something must keep track of from where in memory each function call was made and where execution should continue when a function returns. This information is recorded and maintained automatically in the stack. We introduced the stack when we explained free store memory, and the stack is often referred to as the call stack in this context. The call stack records all the outstanding function calls and details of the data that was passed to each function. The debugging facilities that come with most C++ development systems usually provide ways for you to view the call stack while your program executes.
Functions in Classes
A class defines a new type, and each class definition will usually contain functions that represent the operations that can be carried out with objects of the class type. You have already used functions that belong to a class extensively. In the previous chapter, you used functions that belong to the string class, such as the length() function, which returns the number of characters in the string object, and the find() function for searching a string. The standard input and output streams cin and cout are objects, and using the stream insertion and extraction operators calls functions for those objects. Functions that belong to classes are fundamental in object-oriented programming, which you’ll learn about from Chapter 11 onward.
Characteristics of a Function
A function should perform a single, well-defined action and should be relatively short. Most functions do not involve many lines of code, certainly not hundreds of lines. This applies to all functions, including those that are defined within a class. Several of the working examples you saw earlier could easily be divided into functions. If you look again at Ex7_05.cpp, for instance, you can see that what the program does falls naturally into three distinct actions. First the text is read from the input stream, then the words are extracted from the text, and finally the words that were extracted are output. Thus, the program could be defined as three functions that perform these actions, plus the main() function that calls them.
Defining Functions
The return type, which is the type of value, if any, that the function returns when it finishes execution. A function can return data of any type, including fundamental types, class types, pointer types, or reference types. It can also return nothing, in which case you specify the return type as void.
The name of the function. Functions are named according to the same rules as variables.
The number and types of data items that can be passed to the function when it is called. This is called the parameter list, and it appears as a comma-separated list between parentheses following the function name.
A general representation of a function looks like this:
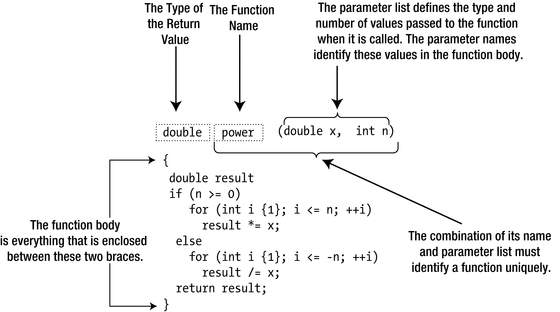
An example of a function definition
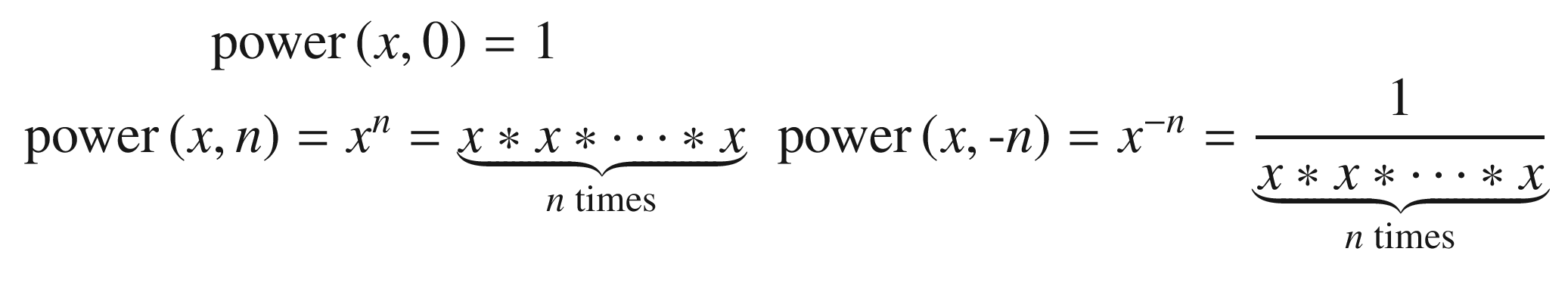
If nothing is to be passed to a function when it is called, then nothing appears between the parentheses. If there is more than one item in the parameter list, they are separated by commas. The power() function in Figure 8-1 has two parameters, x and n. The parameter names are used in the body of the function to access the corresponding values that were passed to the function. Our power function could be called from elsewhere in the program as follows:
When this call to power() is evaluated, the code in the function body gets executed with the parameters x and n initialized to 3.0 and 2, respectively, with 3.0 being the value of the number variable. The term argument is used for the values that are passed to a function when called. So in our example, number and 2 are arguments, and x and n are the corresponding parameters. The sequence of arguments in a function call must correspond to the sequence of the parameters in the parameter list of the function definition. More specifically, their types should match. If they do not match exactly, the compiler will apply implicit conversions whenever possible. Here’s an example:
Even though the type of the first argument passed here is float, this code snippet will still compile; the compiler implicitly converts the argument to the type of its corresponding parameter. If no implicit conversion is possible, compilation will, of course, fail.
The conversion from float to double is lossless since a double generally has twice as many bits available to represent the number—and hence the name double. So, this conversion is always safe. The compiler will happily perform the opposite conversion for you as well, though. That is, it will implicitly convert a double argument when assigned to a float parameter. This is a so-called narrowing conversion; because a double can represent numbers with much greater precision than a float, information may be lost during this conversion. Most compilers will issue a warning when it performs such narrowing conversions.
The combination of the function name and the parameter list is called the signature of a function. The compiler uses the signature to decide which function is to be called in any particular instance. Thus, functions that have the same name must have parameter lists that differ in some way to allow them to be distinguished. As we will discuss in detail later, such functions are called overloaded functions.
Tip
While it made for compact code that fitted nicely in Figure 8-1, from a coding style point of view the parameter names x and n used by our definition of power() do not particularly excel in clarity. One could perhaps argue that x and n are still acceptable in this specific case because power() is a well-known mathematical function and x and n are commonplace in mathematical formulae. That notwithstanding, in general we highly recommend you use more descriptive parameter names. Instead of x and n, for instance, you should probably use base and exponent, respectively. In fact, you should always choose descriptive names for just about everything: function names, variable names, class names, and so on. Doing so consistently will go a long way toward keeping your code easy to read and understand.
Our power() function returned a value of type double. Not every function, though, has to return a value—it might just write something to a file or a database or modify some global state. The void keyword is used to specify that a function does not return a value as follows:
Note
A function with a return type specified as void doesn’t return a value, so it can’t be used in most expressions. Attempting to use such a function in this way will cause a compiler error message.
The Function Body
Calling a function executes the statements in the function body with the parameters having the values you pass as arguments. Returning to our definition of power() in Figure 8-1, the first line of the function body defines the double variable, result, initialized with 1.0. result is an automatic variable so only exists within the body of the function. This means that result ceases to exist after the function finishes executing.
The calculation is performed in one of two for loops, depending on the value of n. If n is greater than or equal to zero, the first for loop executes. If n is zero, the body of the loop doesn’t execute at all because the loop condition is immediately false. In this case, result is left at 1.0. Otherwise, the loop variable i assumes successive values from 1 to n, and result is multiplied by x on each iteration. If n is negative, the second for loop executes, which divides result by x on each loop iteration.
The variables that you define within the body of a function and all the parameters are local to the function. You can use the same names in other functions for quite different purposes. The scope of each variable you define within a function is from the point at which it is defined until the end of the block that contains it. The only exceptions to this rule are variables that you define as static, and we’ll discuss these later in the chapter.
Let’s give the power() function a whirl in a complete program.
This program produces the following output:
All the action occurs in the for loop in main(). The power() function is called seven times. The first argument is 8.0 on each occasion, but the second argument has successive values of i, from –3 to +3. Thus, seven values are outputs that correspond to 8-3, 8-2, 8-1, 80, 81, 82, and 83.
Tip
While it is instructive to write your own power() function, there is of course already one provided by the Standard Library. The cmath header offers a variety of std::pow(base, exponent) functions similar to our version, except that they are designed to work optimally with all numeric parameter types—that is, not just with double and int but also, for instance, with float and long, with long double and unsigned short, or even with noninteger exponents. You should always prefer the predefined mathematical functions of the cmath header; they will almost certainly be far more efficient and accurate than anything you could write yourself.
Return Values
A function with a return type other than void must return a value of the type specified in the function header. The only exception to this rule is the main() function, where, as you know, reaching the closing brace is equivalent to returning 0. Normally, though, the return value is calculated within the body of the function and is returned by a return statement, which ends the function, and execution continues from the calling point. There can be several return statements in the body of a function with each potentially returning a different value. The fact that a function can return only a single value might appear to be a limitation, but this isn’t the case. The single value that is returned can be anything you like: an array, a container such as std::vector<>, or even a container with elements that are containers.
How the return Statement Works
The return statement in the previous program returns the value of result to the point where the function was called. The result variable is local to the function and ceases to exist when the function finishes executing, so how is it returned? The answer is that a copy of the double being returned is made automatically, and this copy is made available to the calling function. The general form of the return statement is as follows:
expression must evaluate to a value of the type that is specified for the return value in the function header or must be convertible to that type. The expression can be anything, as long as it produces a value of an appropriate type. It can include function calls and can even include a call of the function in which it appears, as you’ll see later in this chapter.
If the return type is specified as void, no expression can appear in a return statement. It must be written simply as follows:
If the last statement in a function body executes so that the closing brace is reached, this is equivalent to executing a return statement with no expression. In a function with a return type other than void, this is an error, and the function will not compile—except for main(), of course.
Function Declarations
Ex8_01.cpp works perfectly well as written, but let’s try rearranging the code so that the definition of main() precedes the definition of the power() function in the source file. The code in the program file will look like this:
As you’ll see later, a program can consist of several source files. The definition of a function that is called in one source file may be contained in a separate source file.
Suppose you have a function A() that calls a function B(), which in turn calls A(). If you put the definition of A() first, it won’t compile because it calls B(); the same problem arises if you define B() first because it calls A().
Naturally, there is a solution to these difficulties. You can declare a function before you use or define it by means of a function prototype.
Note
Functions that are defined in terms of each other, such as the A() and B() functions we described just now, are called mutually recursive functions. We’ll talk more about recursion near the end of this chapter.
Function Prototypes
A function prototype is a statement that describes a function sufficiently for the compiler to be able to compile calls to it. It defines the function name, its return type, and its parameter list. A function prototype is sometimes referred to as a function declaration. A function can be compiled only if the call is preceded by a function declaration in the source file. The definition of a function also doubles as a declaration, which is why you didn’t need a function prototype for power() in Ex8_01.cpp.
You could write the function prototype for the power() function as follows:
If you place function prototypes at the beginning of a source file, the compiler is able to compile the code regardless of where the function definitions are. Ex8_02.cpp will compile if you insert the prototype for the power() function before the definition of main().
The function prototype shown earlier is identical to the function header with a semicolon appended. A function prototype is always terminated by a semicolon, but in general, it doesn’t have to be identical to the function header. You can use different names for the parameters from those used in the function definition (but not different types, of course). Here’s an example:
This works just as well. The compiler only needs to know the type each parameter is, so you can omit the parameter names from the prototype, like this:
There is no particular merit in writing function prototypes like this. It is much less informative than the version with parameter names. If both function parameters were of the same type, then a prototype like this would not give any clue as to which parameter was which. We recommend that you always include descriptive parameter names in function prototypes.
It could be a good idea to always write prototypes for each function that is defined in a source file—with the exception of main(), of course, which never requires a prototype. Specifying prototypes near the start of the file removes the possibility of compiler errors arising from functions not being sequenced appropriately. It also allows other programmers to get an overview of the functionality of your code.
Most of the examples in the book use functions from the Standard Library, so where are the prototypes for them? The standard headers contain them. A primary use of header files is to collect the function prototypes for a related group of functions.
Passing Arguments to a Function
It is important to understand precisely how arguments are passed to a function. This affects how you write functions and ultimately how they operate. There are also a number of pitfalls to be avoided. In general, the function arguments should correspond in type and sequence to the list of parameters in the function definition. You have no latitude so far as the sequence is concerned, but you do have some flexibility in the argument types. If you specify a function argument of a type that doesn’t correspond to the parameter type, then the compiler inserts an implicit conversion of the argument to the type of the parameter where possible. The rules for automatic conversions of this kind are the same as those for automatic conversions in an assignment statement. If an automatic conversion is not possible, you’ll get an error message from the compiler. If such implicit conversions result in potential loss of precision, compilers generally issue a warning. Examples of such narrowing conversions are conversions from long to int, double to float, or int to float (see also Chapter 2).
There are two mechanisms by which arguments are passed to functions, pass-by-value and pass-by-reference. We’ll explain the pass-by-value mechanism first.
Pass-by-Value

The pass-by-value mechanism for arguments to a function
Each time you call the power() function, the compiler arranges for copies of the arguments to be stored in a temporary location in the call stack. During execution, all references to the function parameters in the code are mapped to these temporary copies of the arguments. When execution of the function ends, the copies of the arguments are discarded.
We can demonstrate the effects of this with a simple example. The following calls a function that attempts to modify one of its arguments, and of course, it fails miserably:
This example produces the following output:
The output shows that adding 10 to it in the changeIt() function has no effect on the variable it in main(). The it variable in changeIt() is local to the function, and it refers to a copy of whatever argument value is passed when the function is called. Of course, when the value of it that is local to changeIt() is returned, a copy of its current value is made, and it’s this copy that’s returned to the calling program.
Pass-by-value is the default mechanism by which arguments are passed to a function. It provides a lot of security to the calling function by preventing the function from modifying variables that are owned by the calling function. However, sometimes you do want to modify values in the calling function. Is there a way to do it when you need to? Sure there is; one way is to use a pointer.
Passing a Pointer to a Function
When a function parameter is a pointer type, the pass-by-value mechanism operates just as before. However, a pointer contains the address of another variable; a copy of the pointer contains the same address and therefore points to the same variable.
If you modify the definition of the first changeIt() function to accept an argument of type double*, you can pass the address of it as the argument. Of course, you must also change the code in the body of changeIt() to dereference the pointer parameter. The code is now like this:
This version of the program produces the following output:
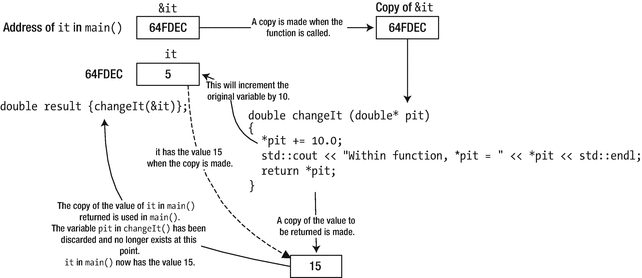
Passing a pointer to a function
This version of changeIt() serves only to illustrate how a pointer parameter can allow a variable in the calling function to be modified—it is not a model of how a function should be written. Because you are modifying the value of it directly, returning its value is somewhat superfluous.
Passing an Array to a Function
An array name is essentially an address, so you can pass the address of an array to a function just by using its name. The address of the array is copied and passed to the function. This provides several advantages:
First, passing the address of an array is an efficient way of passing an array to a function. Passing all the array elements by value would be time-consuming because every element would be copied. In fact, you can’t pass all the elements in an array by value as a single argument because each parameter represents a single item of data.
Second, and more significantly, because the function does not deal with the original array variable but with a copy, the code in the body of the function can treat a parameter that represents an array as a pointer in the fullest sense, including modifying the address that it contains. This means you can use the power of pointer notation in the body of a function for parameters that are arrays. Before we get to that, let’s try the most straightforward case first—handling an array parameter using array notation.
This example includes a function to compute the average of the elements in an array:
This produces the following brief output:
The average() function works with an array containing any number of double elements. As you can see from the prototype, it accepts two arguments: the array address and a count of the number of elements. The type of the first parameter is specified as an array of any number of values of type double. You can pass any one-dimensional array of elements of type double as an argument to this function, so the second parameter that specifies the number of elements is essential. The function will rely on the correct value for the count parameter being supplied by the caller. There’s no way to verify that it is correct, so the function will quite happily access memory locations outside the array if the value of count is greater than the array length. With this definition, it is up to the caller to ensure that this doesn’t happen.
And in case you were wondering, no, you cannot circumvent the need for the count parameter by using either the sizeof operator or std::size() inside the average() function. Remember, an array parameter such as array simply stores the address of the array, not the array itself. So, the expression sizeof(array) would return the size of the memory location that contains the address of the array and not the size of the entire array. A call of std::size() with an array parameter name will simply not compile because std::size() has no way of determining the array’s size either. Without the definition of the array, the compiler has no way to determine its size. It cannot do so from only the array’s address.
Within the body of average(), the computation is expressed in the way you would expect. There’s no difference between this and the way you would write the same computation directly in main(). The average() function is called in main() in the output statement. The first argument is the array name, values, and the second argument is an expression that evaluates to the number of array elements.
The elements of the array that is passed to average() are accessed using normal array notation. We’ve said that you can also treat an array passed to a function as a pointer and use pointer notation to access the elements. Here’s how average() would look in that case:
For all intents and purposes, both notations are completely equivalent. In fact, as you saw in Chapter 5, you can freely mix both notations. You can, for instance, use array notation with a pointer parameter:
There really is no difference at all in the way any of these function definitions are evaluated. In fact, the following two function prototypes are considered identical by the compiler:
We will revisit this later in the section on function overloading.
Caution
There exists a common and potentially dangerous misconception about passing fixed-size arrays to functions. Consider the following variant of the average() function:
Clearly, the author of this function wrote it to average exactly ten values; no more, no less. We invite you to replace average() in Ex8_05.cpp with the previous average10() function and update the function call in main() accordingly. The resulting program should compile and run just fine. So, what’s the problem? The problem is that the signature of this function—which unfortunately is perfectly legal C++ syntax—creates the false expectation that the compiler would enforce that only arrays of size exactly 10 can be passed as arguments to this function. To verify, let’s see what happens if we change the body of the main() function of our example program to pass only three values (you can find the resulting program in Ex8_05A.cpp):
Even though we now called average10() with an array that is considerably shorter than the required ten values, the resulting program should still compile. If you run it, the average10() function will blindly read well beyond the bounds of the values array. Obviously, no good can come of this. Either the program will crash or it will produce garbage output. The root of the problem is that, unfortunately, the C++ language dictates that a compiler is supposed to treat a function signature of the form
yet again as synonymous with either one of the following:
Because of this, you should never use a dimension specification when passing an array by value; it only creates false expectations. An array that is passed by value is always passed as a pointer, and its dimensions are not checked by the compiler. We will see later that you can safely pass given-size arrays to a function using pass-by-reference instead of pass-by-value.
const Pointer Parameters
The average() function only needs to access values of the array elements; it doesn’t need to change them. It would be a good idea to make sure that the code in the function does not inadvertently modify elements of the array. Specifying the parameter type as const will do that:
Now the compiler will verify that the elements of the array are not modified in the body of the function. So if you now, for instance, accidentally type (*array)++ instead of *array++, compilation will fail. Of course, you must modify the function prototype to reflect the new type for the first parameter; remember that pointer-to-const types are quite different from pointer-to-non-const types.
Specifying a pointer parameter as const has two consequences: the compiler checks the code in the body of the function to ensure that you don’t try to change the value pointed to, and it allows the function to be called with an argument that points to a constant.
Note
In our latest definition of average(), we didn’t declare the function’s count parameter const as well. If a parameter of a fundamental type such as int or size_t is passed by value, it does not need to be declared const, at least not for the same reason. The pass-by-value mechanism makes a copy of the argument when the function is called, so you are already protected from modifying the original value from within the function.
Nonetheless, it does remain good practice to mark variables as const if they will or should not change during a function’s execution. This general guideline applies to any variable—including those declared in the parameter list. For that reason, and for that reason only, you might still consider declaring count as const. This would, for instance, prevent you from accidentally writing ++count somewhere in the function’s body, which could have disastrous results indeed. But know that you would then be marking a local copy as a constant and that it is by no means required to add const to prevent changes to the original value.
Passing a Multidimensional Array to a Function
Passing a multidimensional array to a function is quite straightforward. Suppose you have a two-dimensional array defined as follows:
The prototype of a hypothetical yield() function would look like this:
In theory, you could specify the first array dimension in the type specification for the first parameter as well, but it is best not to. The compiler would again simply ignore this, analogous to what happened for the average10() function we discussed earlier. The size of the second array dimension does have the desired effect, though—C++ is fickle that way. Any two-dimensional array with 4 as a second dimension can be passed to this function, but arrays with 3 or 5 as a second dimension cannot.
Let’s try passing a two-dimensional array to a function in a concrete example:
This produces the following output:
The first parameter to the yield() function is defined as a const array of an arbitrary number of rows of four elements of type double. When you call the function, the first argument is the beans array , and the second argument is the total length of the array in bytes divided by the length of the first row. This evaluates to the number of rows in the array.
Pointer notation doesn’t apply particularly well with a multidimensional array. In pointer notation, the statement in the nested for loop would be as follows:
Surely, you’ll agree that the computation is clearer in array notation!
Note
The definition of yield in Ex8_06 contains a “magic number” 4 in the inner for loop. In Chapter 5 we warned you that such numbers are mostly a bad idea. After all, if at some point the row length in the function signature is changed, it would be easy to also forget to update the number 4 in the for loop. A first solution would to replace the hard-coded number 4 with std::size(array[i]); another is to replace the inner loop with a range-based for loop:
Note that you cannot replace the outer loop with a range-based loop as well, and you cannot use std::size() there. Remember, there is no way for the compiler to know the first dimension of the double[][4] array; only the second dimension or higher of an array can be fixed when passing it by value.
Pass-by-Reference
As you may recall, a reference is an alias for another variable. You can specify a function parameter as a reference as well, in which case the function uses the pass-by-reference mechanism with the argument. When the function is called, an argument corresponding to a reference parameter is not copied. Instead, the reference parameter is initialized with the argument. Thus, it becomes an alias for the argument in the calling function. Wherever the parameter name is used in the body of the function, it is as if it accesses the argument value in the calling function directly.
You specify a reference type by adding & after the type name. To specify a parameter type as “reference to string,” for example, you write the type as string& . Calling a function that has a reference parameter is no different from calling a function where the argument is passed by value. Using references, however, improves performance with objects such as type string. The pass-by-value mechanism copies the object, which would be time-consuming with a long string and memory-consuming as well for that matter. With a reference parameter, there is no copying.
References vs. Pointers
In many regards, references are similar to pointers. To see the similarity, let’s use a variation of Ex8_04 with two functions: one that accepts a pointer as an argument and one that accepts a reference instead:
The result is that the original it value in main() is updated twice, once per function call:
The most obvious difference is that to pass a pointer, you need to take the address of a value first using the address-of operator. Inside the function you then, of course, have to dereference that pointer again to access the value. For a function that accepts its arguments by reference, you have to do neither. But note that this difference is purely syntactical; in the end, both have the same effect. In fact, compilers will mostly compile references in the same way as pointers.
So, which mechanism should you use, as they appear to be functionally equivalent? That’s a fair question. Let’s therefore consider some of the facets that play a role in this decision.
The single most distinctive feature of a pointer is that it can be nullptr , whereas a reference must always refer to something. So if you want to allow the possibility of a null argument, you cannot use a reference. Of course, precisely because a pointer parameter can be null, you’re almost forced to always test for nullptr before using it. References have the advantage that you do not need to worry about nullptrs.
As Ex8_07 shows, the syntax for calling a function with a reference parameter is indeed no different from calling a function where the argument is passed by value. On the one hand, because you do not need the address-of and dereferencing operators, reference parameters allow for a more elegant syntax. On the other hand, however, precisely the fact that there is no syntactical difference means that references can sometimes cause surprises. And code that surprises is bad code because surprises lead to bugs. Consider, for instance, the following function call:
Without a prototype or the definition of do_it(), you have no way of knowing whether the argument to this function is passed either by reference or by value. So, you also have no way of knowing whether the previous statement will modify the it value—provided it itself is not const, of course. This property of pass-by-reference can sometimes make code harder to follow, which may lead to surprises if values passed as arguments are changed when you did not expect them to be. Therefore:
Tip
Always declare variables as const whenever their values are not supposed to change anymore after initialization. This will make your code more predictable and hence easier to read and less prone to subtle bugs. Moreover, and perhaps even more importantly, in your function signatures, always declare pointer or reference parameters with const as well if the function does not modify the corresponding arguments. First, this makes it easier for programmers to use your functions because they can easily understand what will or will not be modified by a function just by looking at its signature. Second, reference-to-const parameters allow your functions to be called with const values. As we will show in the next section, const values—which as you now know should be used as much as possible—cannot be assigned to a reference-to-non-const parameter.
If you want to allow nullptr arguments, you cannot use references. Conversely, pass-by-reference can be seen as a contract that a value is not allowed to be null. Note already that instead of representing optional values as a nullable pointer, you may also want to consider the use of std::optional<>. We’ll discuss this option later in this chapter.
Using reference parameters allows for a more elegant syntax but may mask that a function is changing a value. Never change an argument value if it is not clear from the context—from the function name, for instance—that this will happen.
Because of the potential risks, some coding guidelines advise to never use reference-to-non-const parameters and advocate to instead always use pointer-to-non-const parameters. Personally, we would not go that far. There is nothing inherently wrong with a reference-to-non-const, as long as it is predictable for the caller which arguments may become modified. Choosing descriptive function and parameter names is always a good start to make a function’s behavior more predictable.
Passing arguments by reference-to-const is generally preferred over passing a pointer-to-const value. Because this is such a common case, we’ll present you with a bigger example in the next subsection.
Input vs. Output Parameters
In the previous section, you saw that a reference parameter enables the function to modify the argument within the calling function. However, calling a function that has a reference parameter is syntactically indistinguishable from calling a function where the argument is passed by value. This makes it particularly important to use a reference-to-const parameter in a function that does not change the argument. Because the function won’t change a reference-to-const parameter, the compiler will allow both const and non-const arguments. But only non-const arguments can be supplied for a reference-to-non-const parameter.
Let’s investigate the effect of using reference parameters in a new version of Ex7_06.cpp that extracts words from text:
The output is the same as Ex7_06.cpp. Here’s a sample:
There are now two functions in addition to main(): find_words() and list_words(). Note how the code in both functions is the same as the code that was in main() in Ex7_05.cpp. Dividing the program into three functions makes it easier to understand and does not increase the number of lines of code significantly.
The find_words() function finds all the words in the string identified by the second argument and stores them in the vector specified by the first argument. The third parameter is a string object containing the word separator characters.
The first parameter of find_words() is a reference, which avoids copying the vector<string> object. More important, though, it is a reference to a non-const vector<>, which allows us to add values to the vector from inside the function. Such a parameter is therefore sometimes called an output parameter because it is used to collect a function’s output. Parameters whose values are purely used as input are then called input parameters.
Tip
In principle, a parameter can act as both an input and an output parameter. Such a parameter is called an input-output parameter. A function with such a parameter, in one way or another, first reads from this parameter, uses this input to produce some output, and then stores the result into the same parameter. It is generally better to avoid input-output parameters, though, even if that means adding an extra parameter to your function. Code tends to be much easier to follow if each parameter serves a single purpose—a parameter should be either input or output, not both.
The find_words() function does not modify the values passed to the second and third parameters. Both are, in other words, input parameters and should therefore never be passed by reference-to-non-const. Reference-to-non-const parameters should be reserved for those cases where you need to modify the original value—in other words, for output parameters. For input parameters, only two main contenders remain: pass-by-reference-to-const or pass-by-value. And because string objects would otherwise be copied, the only logical conclusion is to declare both input parameters as const string&.
In fact, if you’d declare the third parameter to find_words() as a reference to a non-const string, the code wouldn’t even compile. Give it a try if you will. The reason is that the third argument in the function call in main(), separators, is a const string object. You cannot pass a const object as the argument for a reference-to-non-const parameter. That is, you can pass a non-const argument to a reference-to-const parameter but never the other way around. In short, a T value can be passed to both T& and const T& references, whereas a const T value can be passed only to a const T& reference. And this is only logical. If you have a value that you’re allowed to modify, there’s no harm in passing it to a function that will not modify it—not modifying something that you’re allowed to modify is fine. The converse is not true: if you have a const value, you’d better not be allowed to pass it to a function that might modify it!
The parameter for list_words(), finally, is reference-to-const because it too is an input parameter. The function only accesses the argument; it doesn’t change it.
Tip
Input parameters should usually be references-to-const. Only smaller values, most notably those of fundamental types, are to be passed by value. Use reference-to-non-const only for output parameters, and even then you should often consider returning a value instead. We’ll study how to return values from functions soon.
Passing Arrays by Reference
At first sight, it may seem that for arrays there would be little benefit from passing them by reference. After all, if you pass an array by value, the array elements themselves already do not get copied. Instead, a copy is made of the pointer to the first element of the array. Passing an array also already allows you to modify the values of the original array—unless you add const, of course. So surely this already covers both advantages typically attributed to passing by reference: no copying and the possibility to modify the original value?
While this is most certainly true, you did already discover the main limitation with passing an array by value earlier, namely, that there is no way to specify the array’s first dimension in a function signature, at least not in such a way that the compiler enforces that only arrays of exactly that size are passed to the function. A lesser-known fact, though, is that you can accomplish this by passing arrays by reference.
To illustrate, we invite you to again replace the average() function in Ex8_05.cpp with an average10() function, but this time with the following variant:
As you can see, the syntax for passing an array by reference is somewhat more complex. The const could in principle be omitted from the parameter type, but it is preferred here because you do not modify the values of the array in the function’s body. The extra parentheses surrounding &array are required, though. Without them, the compiler would no longer interpret the parameter type as a reference to an array of doubles but as an array of references to double. Because arrays of references are not allowed in C++, this would then result in a compiler error:
With our new and improved version of average10() in place, the compiler does live up to expectations. Attempting to pass any array of a different length should now result, as desired, in a compiler error:
Note, moreover, that if you pass a fixed-size array by reference, it can be used as input to operations such as sizeof(), std::size(), and range-based for loops. This was not possible with arrays that are passed by value. You can use this to eliminate the two occurrences of 10 from the body of average10():
Tip
You have already seen a more modern alternative to working with arrays of fixed length in Chapter 5: std::array<>. Using values of this type, you can just as safely pass fixed-size arrays by reference and without having to remember the tricky syntax for passing plain fixed-size arrays by reference:
We made three variants of this program available to you: Ex8_09A, which uses pass-by-reference; Ex8_09B, which eliminates the magic numbers; and Ex8_09C, to show the use of std::array<>.
References and Implicit Conversions
A program often uses many different types, and as you know, the compiler is usually quite happy to assist you by implicitly converting between them. Whether or not you should always be happy about such conversions is another matter, though. That aside, most of the time it is convenient that code such as the following snippet will compile just fine, even though it assigns an int value to a differently typed double variable:
For function arguments that employ pass-by-value, it is only natural that such conversions occur as well. For instance, given the same two variables i and d, a function with signature f(double) can hence be called not only with f(d) or f(1.23) but also with differently typed arguments such as f(i), f(123), or f(1.23f).
Implicit conversions thus remain quite straightforward for pass-by-value. Let’s take a look now how they fare with reference arguments:
We first define two trivial functions: one that doubles doubles and one that streams them to std::cout. The first part of main() then shows that these, of course, work for a double variable—obviously, you should thus see the number 246 appear in the output. The interesting parts of this example are its final two statements, of which the first is commented out because it would not compile.
Let’s consider the print_it(i) statement first and explain why it is in fact already a minor miracle that this even works at all. The function print_it() operates on a reference to a const double, a reference that as you know is supposed to act as an alias for a double that is defined elsewhere. On a typical system, print_it() will ultimately read the 8 bytes found in the memory location behind this reference and print out the 64 bits it finds there in some human-readable format to std::cout. But the value that we passed to the function as an argument is no double; it is an int! This int is generally only 4 bytes big, and its 32 bits are laid out completely differently than those of a double. So, how can this function be reading from an alias for a double if there is no such double defined anywhere in the program? The answer is that the compiler, before it calls print_it(), implicitly creates a temporary double value somewhere in memory, assigns it the converted int value, and then passes a reference to this temporary memory location to print_it().
Such implicit conversions are only supported for reference-to-const parameters, not for reference-to-non-const parameters. Suppose for argument’s sake that the double_it(i) statement on the second-to-last line will compile without error. Surely, the compiler will then similarly convert the int value 456 to a double value 456.0, store this temporary double somewhere in memory, and apply the function body of double_it() to it. Then you’d have a temporary double somewhere, now with value 912.0, and an int value i that is still equal to 456. Now, while in theory the compiler could convert the resulting temporary value back to an int, the designers of the C++ programming language decided that that would be a bridge too far. The reason is that generally such inverse conversions would inevitably mean loss of information. In our case, this would involve a conversion from double to int, which would result in the loss of at least the fractional part of the number. The creation of temporaries is therefore never allowed for reference-to-non-const parameters. This is also why the statement double_it(i) is invalid in standard C++ and should fail to compile.
String Views: The New Reference-to-const-string
As we explained earlier, the main motivation for passing input arguments by reference-to-const instead of by value is to avoid unnecessary copies. Copying bigger strings too often, for instance, can become quite expensive, in terms of both time and memory. This is why for functions that do not modify the std::strings they operate on, your natural instinct by now should be to declare the corresponding input parameters as const string&. We did this, for example, in Ex8_08 for find_words().
Unfortunately, const string& parameters are not perfect. While they do avoid copies of std::string objects, they have some shortcomings. To illustrate why, suppose that we alter the main() function of Ex8_08 a bit as follows:
The difference is that we no longer first store the separators in a separate separators constant of type const std::string. Instead, the corresponding string literal is passed directly as the third argument to the call of find_words(). You can easily verify that this still compiles and works correctly.
The first question then is, why does this compile and work? After all, the third parameter of find_words() expects a reference to a std::string object, but the argument that we’ve passed is a string literal. And a string literal is, as you may recall, of type const char[]—array of characters—and therefore definitely not a std::string object. Naturally, you already know the answer from the previous section: the compiler must be applying some form of implicit conversion. That is, the function’s reference will not actually refer to the literal but instead to some temporary std::string object the compiler has implicitly created somewhere in memory. We will explain in later chapters exactly how such conversions work for nonfundamental types, but for now believe us when we say that in this case the temporary string object will be initialized with a full copy of all characters in the string literal.
Being the careful reader that you are, you have now realized why passing strings by reference-to-const is still somewhat flawed. Our motivation for using references was to avoid copies, but, alas, string literals still become copied when passed to reference-to-const-std::string parameters. They become copied into temporary std::string objects that emanate from implicit conversions.
This brings us to the second and real question of this section: how to create functions that never copy input string arguments, not even string literals or other character arrays? And we do not want to use const char* for this because you’d have to pass the string’s length along separately as well, and then you’d miss out on the many nice helper functions offered by std::string.
The answer is provided by std::string_view , a type defined in the string_view header, added to the Standard Library with C++17. Values of this type will act analogously to values of type const std::string—mind the const!—only with one major difference: the strings they encapsulate can never be modified through their public interface. That is, string_views are in a way inherently const. To paraphrase The Boss , you can look (view) but not touch a string_view’s characters. Interestingly, this limitation implies that these objects, unlike std::strings, do not need their own copy of the character array they operate on. Instead, it suffices they simply point to any character sequence stored inside either an actual std::string object, a string literal, or any other character array for that matter. Because it does not involve copying an entire character array, initializing and copying a string_view is very cheap.
So, std::strings copy characters when created, implicitly or explicitly, and string_views don’t. All this might get you wondering how object creation works exactly and how your Standard Library implementation makes this behave differently for string_views and strings. And not to worry: we explain it in depth in upcoming chapters. For now, though, remember the following best-practice guideline:
Tip
Always use the type std::string_view instead of const std::string& for input string parameters. While there is nothing wrong with using const std::string_view&, you might as well pass std::string_view by value because copying these objects is cheap.
Using String View Function Parameters
For our new version of Ex8_08 (see earlier), the find_words() function is thus probably better declared as follows:
In many cases, nothing more would have to change about the program. The std::string_view type can mostly be used as a drop-in replacement for either const std::string& or const std::string. But not in our example, which is fortunate because it allows us to explain when it might go wrong and why. To make the find_words() function definition compile with its new and improved signature, you have to slightly alter it, like so (also available in Ex8_08A.cpp):
The modification we had to make is in the second-to-last statement, which originally did not include the explicit std::string{ … } initialization:
The compiler, however, will refuse any and all implicit conversions of std::string_view objects to values of type std::string (give it a try!). The rationale behind this deliberate restriction is that you normally use string_ view to avoid more expensive string copy operations, and converting a string_view back to a std::string always involves copying the underlying character array. To protect you from accidentally doing so, the compiler is not allowed to ever implicitly make this conversion. You always have to explicitly add the conversion in this direction yourself.
Note
There exist two other cases where a string_view is not exactly equivalent to const string. First, string_view does not provide a c_str() function to convert it to a const char* array. Luckily, it does share with std::string its data() function, though, which for most intents and purposes is equivalent. Second, string_views cannot be concatenated using the addition operator (+). To use a string_view value view in a concatenation expression, you have to convert it to a std::string first, for instance using string{view}.
String literals are generally not that big, so you may wonder whether it is really such a big deal if they are copied. Perhaps not. But a std::string_view can be created from any C-style character array, which can be as big as you want. So, while for find_words() you likely did not gain much from making seperators a string_view, for the other argument, str, it could indeed make a big difference, as illustrated by this snippet:
In this case, the char array is assumed to be terminated by a null character element, a convention common in C and C++ programming. If this is not the case, you’ll have to use something more of this form:
The bottom line in either case is that if you use std::string_view, the huge text array is not copied when passing it to find_words(), whereas it would be if you’d use const std::string&.
Default Argument Values
There are many situations in which it would be useful to have default argument values for one or more function parameters. This would allow you to specify an argument value only when you want something different from the default . A simple example is a function that outputs a standard error message. Most of the time, a default message will suffice, but occasionally an alternative is needed. You can do this by specifying a default parameter value in the function prototype. You could define a function to output a message like this:
You specify the default argument value like this:
If both are separate, you need to specify default values in the function prototype and not in the function definition. The reason is that when resolving the function calls, the compiler needs to know whether a given number of arguments is acceptable.
To output the default message, you call such functions without the corresponding argument:
To output a particular message, you specify the argument:
In the previous example, the parameter happens to be passed by value. You specify default values for nonreference and reference parameters in the same manner:
From what you learned in previous sections, it also should come as no surprise that default values for which the implicit conversion requires the creation of a temporary object—as is in the previous example—are illegal for reference-to-non-const parameters. Hence, the following should not compile:
Specifying default parameter values can make functions simpler to use. Naturally, you aren’t limited to just one parameter with a default value.
Multiple Default Parameter Values
All function parameters that have default values must be placed together at the end of the parameter list. When an argument is omitted in a function call, all subsequent arguments in the list must also be omitted. Thus, parameters with default values should be sequenced from the least likely to be omitted to the most likely at the end. These rules are necessary for the compiler to be able to process function calls.
Let’s contrive an example of a function with several default parameter values. Suppose that you wrote a function to display one or more data values, several to a line, as follows:
The data parameter is an array of values to be displayed, and count indicates how many there are. The third parameter of type string_view specifies a title that is to head the output. The fourth parameter determines the field width for each item, and the last parameter is the number of data items per line. This function has a lot of parameters. It’s clearly a job for default parameter values! Here’s an example:
The definition of show_data() in Ex8_11.cpp can be taken from earlier in this section. Here’s the output:
The prototype for show_data() specifies default values for all parameters except the first. You have five ways to call this function: you can specify all five arguments, or you can omit the last one, the last two, the last three, or the last four. You can supply just the first to output a single data item, as long as you are happy with the default values for the remaining parameters.
Remember that you can omit arguments only at the end of the list; you are not allowed to omit the second and the fifth. Here’s an example:
Arguments to main()
You can define main() so that it accepts arguments that are entered on the command line when the program executes. The parameters you can specify for main() are standardized; either you can define main() with no parameters or you can define main() in the following form:
The first parameter, argc, is a count of the number of string arguments that were found on the command line. It is type int for historical reasons, not size_t as you might expect from a parameter that cannot be negative. The second parameter, argv, is an array of pointers to the command-line arguments, including the program name. The array type implies that all command-line arguments are received as C-style strings. The program name used to invoke the program is normally recorded in the first element of argv, argv[0].1 The last element in argv (argv[argc]) is always nullptr, so the number of elements in argv will be argc+1. We’ll give you a couple of examples to make this clear. Suppose that to run the program, you enter just the program name on the command line:
In this case, argc will be 1, and argv[] contains two elements. The first is the address of the string "Myprog", and the second will be nullptr.
Suppose you enter this:
Now argc will be 4, and argv will have five elements. The first four elements will be pointers to the strings "Myprog", "2", "3.5", and "Rip Van Winkle". The fifth element, argv[4], will be nullptr.
What you do with the command-line arguments is entirely up to you. The following program shows how you access the command-line arguments:
This lists the command-line arguments, including the program name. Command-line arguments can be anything at all—file names to a file copy program, for example, or the name of a person to search for in a contact file. They can be anything that is useful to have entered when program execution is initiated.
Returning Values from a Function
As you know, you can return a value of any type from a function. This is quite straightforward when you’re returning a value of one of the basic types, but there are some pitfalls when you are returning a pointer or a reference.
Returning a Pointer
When you return a pointer from a function, it must contain either nullptr or an address that is still valid in the calling function. In other words, the variable pointed to must still be in scope after the return to the calling function. This implies the following absolute rule:
Caution
Never return the address of an automatic, stack-allocated local variable from a function.
Suppose you define a function that returns the address of the larger of two argument values. This could be used on the left of an assignment so that you could change the variable that contains the larger value, perhaps in a statement such as this:
You can easily be led astray when implementing this. Here’s an implementation that doesn’t work:
It’s relatively easy to see what’s wrong with this: a and b are local to the function. The argument values are copied to the local variables a and b. When you return &a or &b, the variables at these addresses no longer exist back in the calling function. You usually get a warning from your compiler when you compile this code.
You can specify the parameters as pointers:
If you do, do not forget to also dereference the pointers. The previous condition (a > b) would still compile, but then you’d not be comparing the values themselves. You’d instead be comparing the addresses of the memory locations holding these values. You could call the function with this statement:
A function to return the address of the larger of two values is not particularly useful, but let’s consider something more practical. Suppose we need a program to normalize a set of values of type double so that they all lie between 0.0 and 1.0 inclusive. To normalize the values, we can first subtract the minimum sample value from them to make them all non-negative. Two functions will help with that, one to find the minimum and another to adjust the values by any given amount. Here’s a definition for the first function:
You shouldn’t have any trouble seeing what’s going on here. The index of the minimum value is stored in index_min, which is initialized arbitrarily to refer to the first array element. The loop compares the value of the element at index_min with each of the others, and when one is less, its index is recorded in index_min. The function returns the address of the minimum value in the array. It probably would be more sensible to return the index, but we’re demonstrating pointer return values among other things. The first parameter is const because the function doesn’t change the array. With this parameter const you must specify the return type as const. The compiler will not allow you to return a non-const pointer to an element of a const array.
A function to adjust the values of array elements by a given amount looks like this:
This function adds the value of the third argument to each array element. The return type could be void so it returns nothing, but returning the address of data allows the function to be used as an argument to another function that accepts an array. Of course, the function can still be called without storing or otherwise using the return value.
You could combine using this with the previous function to adjust the values in an array, samples, so that all the elements are non-negative:
The third argument to shift_range() calls smallest(), which returns a pointer to the minimum element. The expression negates the value, so shift_range() will subtract the minimum from each element to achieve what we want. The elements in data are now from zero to some positive upper limit. To map these into the range from 0 to 1, we need to divide each element by the maximum element. We first need a function to find the maximum:
This works in essentially the same way as smallest(). We could use a function that scales the array elements by dividing by a given value:
Dividing by zero would be a disaster, so when the third argument is zero, the function just returns the original array. We can use this function in combination with largest() to scale the elements that are now from 0 to some maximum to the range 0 to 1:
Of course, what the user would probably prefer is a function that will normalize an array of values, thus avoiding the need to get into the gory details:
Remarkably this function requires only one statement. Let’s see if it all works in practice:
If you compile and run this example complete with the definitions of largest(), smallest(), shift_range(), scale_range(), and normalize_range() shown earlier, you should get the following output:
The output demonstrates that the results are what was required. The last two statements in main() could be condensed into one by passing the address returned by normalize_range() as the first argument to show_data():
This is more concise but clearly not necessarily clearer.
Returning a Reference
Returning a pointer from a function is useful, but it can be problematic. Pointers can be null, and dereferencing nullptr generally results in the failure of your program. The solution, as you will surely have guessed from the title of this section, is to return a reference. A reference is an alias for another variable, so we can state the following golden rule for references:
Caution
Never return a reference to an automatic local variable in a function.
By returning a reference, you allow a function call to the function to be used on the left of an assignment. In fact, returning a reference from a function is the only way you can enable a function to be used (without dereferencing) on the left of an assignment operation.
Suppose you code a larger() function like this:
The return type is “reference to string,” and the parameters are references to non-const values. Because you want to return a reference-to-non-const referring to one or other of the arguments, you must not specify the parameters as const.
You could use the function to change the larger of the two arguments, like this:
Because the parameters are not const, you can’t use string literals as arguments; the compiler won’t allow it. A reference parameter permits the value to be changed, and changing a constant is not something the compiler will knowingly go along with. If you make the parameters const, you can’t use a reference-to-non-const as the return type.
You’re not going to examine an extended example of using reference return types at this moment, but you can be sure that you’ll meet them again before long. As you’ll discover, reference return types become essential when you are creating your own data types using classes.
Returning vs. Output Parameters
You now know two ways a function can pass the outcome it produces back to its caller: it can either return a value or put values into output parameters. In Ex8_08, you encountered the following example of the latter:
Another way of declaring this function, however, is as follows:
When your function outputs an object, you of course do not want this object to be copied, especially if this object is as expensive to copy as, for instance, a vector of strings. Prior to C++11, the recommended approach then was mostly to use output parameters. This was the only way you could make absolutely sure that all strings in the vector<> did not get copied when returning the vector<> from the function. This advice has changed drastically with C++11, however:
Tip
In modern C++, you should generally prefer returning values over output parameters. This makes function signatures and calls much easier to read. Arguments are for input, and all output is returned. The mechanism that makes this possible is called move semantics and is discussed in detail in Chapter 17. In a nutshell, move semantics ensures that returning objects that manage dynamically allocated memory—such as vectors and strings—no longer involves copying that memory and is therefore very cheap. Notable exceptions are arrays or objects that contain an array, such as std::array<>. For these it is still better to use output parameters.
Return Type Deduction
Just like you can let the compiler deduce the type of a variable from its initialization, you can have the compiler deduce the return type of a function from its definition. You can write the following, for instance:
From this definition, the compiler will deduce that the return type of getAnswer() is int. Naturally, for a type name as short as int, there is little point in using auto. In fact, it even results in one extra letter to type. But later you’ll encounter type names that are much more verbose (iterators are a classical example). For these, type deduction can save you time. Or you may want your function to return the same type as some other function, and for whatever reason you do not feel the need to look up what type that is or to type it out. In general, the same considerations apply here as for using auto for declaring variables. If it is clear enough from the context what the type will be or if the exact type name matters less for the clarity of your code, return type deduction can be practical.
Note
Another context where return type deduction can be practical is to specify the return type of a function template. You’ll learn about this in the next chapter.
The compiler can even deduce the return type of a function with multiple return statements, provided their expressions evaluate to a value of exactly the same type. That is, no implicit conversions will be performed because the compiler has no way to decide which of the different types to deduce. For instance, consider the following function to obtain a string’s first letter in the form of another string:
Replace auto in the function with std::string_view. This will allow the compiler to perform the necessary type conversions for you.
Replace the first return statement with return std::string_view{" "}. The compiler will then deduce std::string_view as the return type.
Replace the second return statement with return text.substr(0, 1).data(). Because the data() function—as your Standard Library documentation will confirm—returns a const char* pointer, the return type of getFirstLetter() then deduces to const char* as well.
Return Type Deduction and References
You need to take extra care with return type deduction if you want the return type to be a reference. Suppose you write the larger() function shown earlier using an auto-deduced return type instead:
Explicitly specify the std::string& return type as before.
Specify auto& instead of auto. Then the return type will always be a reference.
While discussing all details and intricacies of C++ type deduction is well outside our scope, the good news is that one simple rule covers most cases:
Caution
auto never deduces to a reference type, always to a value type. This implies that even when you assign a reference to auto, the value still gets copied. This copy will moreover not be const, unless you explicitly use const auto. To have the compiler deduce a reference type, you can use auto& or const auto&.
Naturally, this rule is not specific to return type deduction. The same holds if you use auto for local variables as well:
In the previous code snippet, auto_test has type std::string and therefore contains a copy of test. Unlike ref_to_test, this new copy isn’t const anymore either.
Working with Optional Values
When writing your own functions, you will often encounter input arguments that are optional or functions that can return a value only if nothing went wrong. Consider the following function prototype:
From this declaration, you can imagine that this function searches a given string for a given character, back to front, starting from a given starting index. Once found, it will then return the index of the last occurrence of that character. But what happens if the character doesn’t occur in the string? And what do you do if you want the algorithm to consider the entire string? Of course, passing string.length()-1 as a start index will work, but that’s somewhat tedious. Would it perhaps work as well if you pass, say, -1 to the third argument? Without interface documentation or a peek at the implementation code, there is no way of knowing how this function will behave exactly.
The traditional solution is to pick some specific value or values to use when the caller wants the function to use its default settings or to return when no actual value could be computed. A typical choice for indices is -1. A possible specification for find_last_in_string() would thus be that it returns -1 if char_to_find does not occur in the given string and that the entire string is searched if -1 or any negative value is passed as a start_index. In fact, std::string and std::string_view define their own find() functions, and they use the special size_t constants std::string::npos and std::string_view::npos for these purposes.
The problem is that, in general, it can be hard to remember how every function encodes “not provided” or “not computed.” Conventions tend to differ between different libraries or even within the same library. Some may return 0 upon failure, and others may return a negative value. Some may accept nullptr for a const char* parameter, and others won’t. And so on.
To aid the users of a function, optional parameters are typically given a valid default value. Here’s an example:
However, this technique, of course, does not extend to return values. Another problem with the traditional approaches is that, in general, there may not even be an obvious way of encoding an optional value. One reason for this may be the type of the optional value. Think about it, how would you encode an optional bool, for instance? Another reason would be the specific situation. Suppose, for instance, that you need to define a function that reads a configuration override from a given configuration file. Then you’d probably prefer to give that function the following form:
But what should happen if the configuration file does not contain a value with the given name? Because this is intended to be a generic function, you cannot a priori assume that an int value such as 0, -1, or any other value isn’t a valid configuration override as well. Traditional workarounds include the following:
While these work, the C++17 Standard Library now offers std::optional<>, a utility we believe can help make your function declarations much cleaner and easier to read.
std::optional
As of C++17, the Standard Library provides std::optional<>, which constitutes an interesting alternative to all the implicit encodings of optional values we discussed earlier. Using this auxiliary type, any optional int can be explicitly declared with optional<int> as follows:
The fact that these parameters or return values are optional is now stated explicitly, making these prototypes self-documenting. Your code therefore becomes much easier to use and read than code that uses traditional approaches. Let’s take a look at the basic use of std::optional<> in some real code:
The output produced by this program is as follows:
To showcase std::optional<>, we define find_last(), a variation of the find_last_in_string() function we used as an example earlier. Notice that because find_last() uses unsigned size_t indexes instead of int indexes, using -1 as a default value would already be less obvious here. A second, more interesting difference, though, is the default value for the function’s third argument. This value, std::nullopt, is the special constant defined by the Standard Library to initialize optional<T> values that do not (yet) have a T value assigned. We will see shortly why using this as a default parameter value can be interesting.
After the function’s prototype, you see the program’s main() function. In main(), we call find_last() three times to search for the letters 'a', 'b', and 'i' in some sample string. And there is really nothing surprising about the calls themselves. If you want a nondefault start index, you simply pass a number to find_last(), like we did for our third call. The compiler then implicitly converts this number to a std::optional<> object, exactly like you’d expect. If you’re OK with the default starting index, though, you could always pass std::nullopt explicitly. We opted to have the default parameter value take care of that for us, though.
How you can check whether an optional<> value returned by find_last() was assigned an actual value
How you subsequently extract this value from the optional<> to use it
For the former, main() shows three alternatives, in this order: either you have the compiler convert the optional<> to a Boolean for you or you call the has_value() function or you compare the optional<> to nullopt. For the latter, main() presents two options: you can either use the * operator or call the value() function. Assigning the optional<size_t> return value directly to a size_t, however, would not be possible. The compiler cannot convert values of type optional<size_t> to values of type size_t.
From the body of find_last(), aside from some interesting challenges with empty strings and unsigned index types, we’d mostly like you to pay attention to two more aspects related to optional<>. First, notice that returning a value is straightforward. Either you return std::nullopt or you return an actual value. Both will then be converted to a suitable optional<> by the compiler. Second, we’ve used value_or() there. If the optional<> start_index contains a value, this function will return the same as value(); if it does not contain a value, value_or() simply evaluates to the value you pass it as an argument. The value_or() function is therefore a welcome alternative to equivalent if-else statements or conditional operator expressions that would first call has_value() and then value().
Note
Ex8_14 covers most there is to know about std::optional<>. As always, if you need to know more, please consult your favorite Standard Library reference. One thing to note already, though, is that next to the * operator, std::optional<> also supports the -> operator. That is, in the following example the last two statements are equivalent:
Note that while this syntax makes optional <> objects look and feel like pointers, they most certainly aren’t pointers. Each optional<> object contains a copy of any value assigned to it, and this copy is not kept in the free store. That is, while copying a pointer doesn’t copy the value it points to, copying an optional<> always involves copying the entire value that is stored inside it.
Static Variables
In the functions you have seen so far, nothing is retained within the body of the function from one execution to the next. Suppose you want to count how many times a function has been called. How can you do that? One way is to define a variable at file scope and increment it from within the function. A potential problem with this is that any function in the file can modify the variable, so you can’t be sure that it’s being incremented only when it should be.
A better solution is to define a variable in the function body as static. A static variable that you define within a function is created the first time its definition is executed. It then continues to exist until the program terminates. This means you can carry over a value from one call of a function to the next. To specify a variable as static, you prefix the type name in the definition with the static keyword. Let’s consider this simple example:
The first time the statement starting with static executes, count is created and initialized to 0. Subsequent executions of the statement have no further effect. This function then increments the static variable count and returns the incremented value. The first time the function is called, it therefore returns 1. The second time, it returns 2. Each time the function is called, it returns an integer that is one larger than the previous value. count is created and initialized only once, the first time the function is called. Subsequent calls simply increment count and return the resulting value. count survives for as long as the program is executing.
You can specify any type of variable as static, and you can use a static variable for anything that you want to remember from one function call to the next. You might want to hold on to the number of the previous file record that was read, for example, or the highest value of previous arguments.
If you don’t initialize a static variable, it will be zero-initialized by default. In the previous example, you could therefore omit the {0} initialization and still get the same result. Take care, though, because such zero-initialization does not occur for regular local variables. If you do not initialize these, they will contain junk values.
Inline Functions
With functions that are short, the overhead of the code the compiler generates to deal with passing arguments and returning a result is significant compared to the code involved in doing the actual calculation. The execution times of the two types of code may be similarly related. In extreme cases, the code for calling the function may occupy more memory than the code in the body of the function. In such circumstances, you can suggest to the compiler that it replaces a function call with the code from the body of the function, suitably adjusted to deal with local names. This could make the program shorter, faster, or possibly both.
You do this using the inline keyword in the function definition. Here’s an example:
This definition indicates that the compiler can replace calls with inline code. However, it is only a suggestion, and it’s down to the compiler as to whether your suggestion is taken up. When a function is specified as inline , the definition must be available in every source file that calls the function. For this reason, the definition of an inline function usually appears in a header file rather than in a source file, and the header is included in each source file that uses the function. Most if not all modern compilers will make short functions inline, even when you don’t use the inline keyword in the definition. If a function you specify as inline is used in more than one source file, you should place the definition in a header file that you include in each source file that uses the function. If you don’t, you’ll get “unresolved external” messages when the code is linked.
Function Overloading
You’ll often find that you need two or more functions that do essentially the same thing, but with parameters of different types. The largest() and smallest() functions in Ex8_13.cpp are likely candidates. You would want these operations to work with arrays of different types such as int[], double[], float[], or even string[]. Ideally, all such functions would have the same name, smallest() or largest(). Function overloading makes that possible.
The functions have different numbers of parameters.
At least one pair of corresponding parameters is of different types.
Note
The return type of a function is not part of the function’s signature. To decide which function overload to use, the compiler looks only at the number and types of the function parameters and arguments. If you declare two functions with the same name and parameter list but with a different return type, your program will fail to compile.
Here’s an example that uses overloaded versions of the largest() function :
This produces the following output:
The compiler selects the version of largest() to be called in main() based on the argument list. Each version of the function has a unique signature because the parameter lists are different. It’s important to note that the parameters that accept vector<T> arguments are references. If they are not specified as references, the vector object will be passed by value and thus copied. This could be expensive for a vector with a lot of elements. Parameters of array types are different. Only the address of an array is passed in this case, so they do not need to be reference types.
Note
Did it bother you that several of the largest() functions in Ex8_15.cpp had the exact same implementation, only for a different type? If so, good. A good programmer should always be wary of repeating the same code multiple times—and not just because programmers are a lazy bunch. Later, we’ll call this code duplication and explain to you some other downsides of doing this beyond having to type a lot. To avoid this particular type of duplication—where multiple functions perform the same task but for different parameter types—you need function templates. You will learn about function templates in the next chapter.
Overloading and Pointer Parameters
Pointers to different types are different, so the following prototypes declare different overloaded functions:
Note that a parameter of type int* is treated in the same way as a parameter type of int[]. Hence, the following prototype declares the same function as Prototype 1 earlier:
With either parameter type, the argument is an address and therefore not differentiated. In fact, you might recall from earlier that even the following prototype declares the same function:
Because such array dimension specifications are completely ignored by the compiler, we argued earlier that they are thus dangerously misleading and advised you to never use this form. If a dimension specification is what you want, the recommended approach instead is either to use std::array<> or to pass arrays by reference.
Overloading and Reference Parameters
You need to be careful when you are overloading functions with reference parameters. You can’t overload a function with a parameter type data_type with a function that has a parameter type data_type&. The compiler cannot determine which function you want from the argument. These prototypes illustrate the problem:
Suppose you write the following statements:
The second statement could call either function. The compiler cannot determine which version of do_it() should be called. Thus, you can’t distinguish overloaded functions based on a parameter for one version being of a given type and the other being a reference to that type.
You should also be wary when you have overloaded a function where one version has a parameter of type type1 and another has a parameter reference to type2—even if type1 and type2 are different. Which function is called depends on the sort of arguments you use, but you may get some surprising results. Let’s explore this a little with an example:
This produces the following output:
The third line of output may not be what you were anticipating. You might expect the second output statement in main() to call the version of larger() with long& parameters. This statement has called the version with double parameters—but why? After all, you did cast both arguments to long.
That is exactly where the problem lies. The arguments are not a_int and b_int but temporary locations that contain the same values after conversion to type long. As we explained earlier, the compiler will not use a temporary address to initialize a reference-to-non-const.
So, what can you do about this? You have a couple of choices. If a_int and b_int were type long, the compiler will call the version of larger() with parameters of type long&. If the variables can’t be type long, you could specify the parameters as references-to-const like this:
Clearly, you must change the function prototype too. The function works with either const or non-const arguments. The compiler knows that the function won’t modify the arguments, so it will call this version for arguments that are temporary values instead of the version with double parameters. Note that you return type long now. If you insist on returning a reference, the return type must be const because the compiler cannot convert from a reference-to-const to a reference-to-non-const.
Overloading and const Parameters
A const parameter is only distinguished from a non-const parameter for references and pointers. For a fundamental type such as int, for example, const int is identical to int. Hence, the following prototypes are not distinguishable:
The compiler ignores the const attribute of the parameters in the second declaration. This is because the arguments are passed by value, meaning that a copy of each argument is passed into the function, and thus the original is protected from modification by the function. There is no point to specifying parameters as const in a function prototype when the arguments are passed by value.
Naturally, while it is pointless in a function prototype, in a function definition it can certainly make sense to declare parameter variables const. You can do this to prevent the function-local copies from the arguments from being modified, and you can even do this if some earlier function prototype did not contain the const specifiers. The following is therefore perfectly valid—and even quite sensible:
Overloading with const Pointer Parameters
Overloaded functions are different if one has a parameter of type type* and the other has a parameter of const type*. The parameters are pointers to different things—so they are different types. For example, these prototypes have different function signatures:
Applying the const modifier to a pointer prevents the value at the address from being modified. Without the const modifier, the value can be modified through the pointer; the pass-by-value mechanism does not inhibit this in any way. In this example, the first function shown earlier is called with these statements:
The latter version of larger() with const parameters is called by the following code:
The compiler won’t pass a pointer-to-const value to a function in which the parameter is a pointer-to-non-const. Allowing a pointer-to-const value to be passed through a pointer-to-non-const pointer would violate the const-ness of the variable. The compiler hence selects the version of larger() with const pointer parameters to compute num6.
Two overloaded functions are the same, however, if one of them has a parameter of type “pointer to type” and the other has a parameter “const pointer to type.” Here’s an example:
The reason is clear when you consider that the const specifiers after the asterisk (*) of a pointer type make the pointer variables themselves constants. That is, they cannot be reassigned another value. Since a function prototype does not define any code that could be doing such reassignments, it is again pointless to add these const specifiers after the asterisk in a prototype; doing so should again only be considered in a function definition.
Overloading and Reference-to-const Parameters
Reference parameters are more straightforward when it comes to const. Adding const after the ampersand (&), for one, is not allowed. References are already constant by nature, in the sense that they will always keep referring to the same value. And type T& and type const T& are always differentiated, so type const int& is always different from type int&. This means you can overload functions in the manner implied by these prototypes:
Each function will have the same function body, which returns the larger of the two arguments, but the functions behave differently. The first prototype declares a function that doesn’t accept constants as arguments, but you can use the function on the left of an assignment to modify one or the other of the reference parameters. The second prototype declares a function that accepts constants and nonconstants as arguments, but the return type is not a reference, so you can’t use the function on the left of an assignment.
Overloading and Default Argument Values
You know that you can specify default parameter values for a function. However, default parameter values for overloaded functions can sometimes affect the compiler’s ability to distinguish one call from another. For example, suppose you have two versions of a show_error() function that outputs an error message. Here’s a version that has a C-style string parameter:
This version accepts a string_view argument:
You should not specify a default argument for both functions because it would create an ambiguity. The statement to output the default message in either case would be as follows:
The compiler has no way of knowing which function is required. Of course, this is a silly example: you have no reason to specify defaults for both functions. A default for just one does everything that you need. However, circumstances can arise where it is not so silly, and overall, you must ensure that all function calls uniquely identify the function that should be called.
Recursion
A function can call itself, and a function that contains a call to itself is referred to as a recursive function. Recursion may seem to be a recipe for a loop that executes indefinitely, and if you are not careful, it certainly can be. A prerequisite for avoiding a loop of unlimited duration is that the function must contain some means of stopping the process.
A recursive function call can be indirect. For example, a function fun1() calls another function fun2(), which in turn calls fun1(). In this case, fun1() and fun2() are also called mutually recursive functions. We will not see any real examples of mutually recursive functions, though, and restrict ourselves to the easier and far more common case where a single function fun() recursively calls itself.
An example of a tree structure
Data that is organized as a tree can be traversed effectively using recursion. Each branch of a tree can be regarded as a subtree, so a function for accessing the items in a tree can simply call itself when a branch node is encountered. When a data item is encountered, the function does what is required with the item and returns to the calling point. Thus, finding the leaf nodes of the tree—the data items—provides the means by which the function stops the recursive calls of itself.
Basic Examples
There are many things in physics and mathematics that you can think of as involving recursion. A simple example is the factorial of a positive integer n (written as n!), which is the number of different ways in which n things can be arranged. For a given positive integer, n, the factorial of n is the product 1 × 2 × 3 × . . . × n. The following recursive function calculates this:
If this function is called with an argument value of 4, the return statement that calls the function with a value of 3 in the expression executes. This will execute the return to call the function with an argument of 2, which will call factorial() with an argument of 1. The if expression will be true in this case, so 1 will be returned, which will be multiplied by 2 in the next level up, and so on, until the first call returns the value 4 × 3 × 2 × 1. This is often the example given to show recursion, but it is an inefficient process. It would certainly be much faster to use a loop.
Caution
Consider for a second what would happen if our factorial() function is called with zero. The first recursive call would be factorial(-1), the next factorial(-2), and so on. That is, n just becomes more and more negative. This will go on for a very long time, most likely up to the point that the program fails. The lesson here is that you must always ensure that recursion eventually reaches the stopping conditions or you risk running into what is called infinite recursion, which generally results in a program crash. A correct definition of factorial(), for instance, would therefore be the following:
Here’s another recursive function in a working example—it’s a recursive version of the power() function you encountered at the beginning of this chapter:
The output is as follows:
The first line in power() returns 1.0 if n is 0. For positive n, the next line returns the result of the expression x * power(x, n-1). This causes a further call of power() with the index value reduced by 1. If, in this recursive function execution, n is still positive, then power() is called again with n reduced by 1. Each recursive call is recorded in the call stack, along with the arguments and return location. This repeats until n eventually is 0, whereupon 1 is returned and the successive outstanding calls unwind, multiplying by x after each return. For a given value of n greater than 0, the function calls itself n times. For negative powers of x, the reciprocal of x n is calculated using the same process.
With this example, the recursive call process is inefficient compared to a loop. Every function call involves a lot of housekeeping. Implementing the power() function using loops like we did earlier in this chapter makes it execute a lot faster. Essentially, you need to make sure that the depth of recursion necessary to solve a problem is not itself a problem. For instance, if a function calls itself a million times, a large amount of stack memory will be needed to store copies of argument values and the return address for each call. Even up to the point where your runtime runs out of stack memory, the amount of memory allocated for the call stack is generally fixed and limited; surpassing this limit generally causes a fatal crash. In such cases, it is therefore generally better to use a different approach, such as a loop. However, in spite of the overhead, using recursion can often simplify the coding considerably. Sometimes this gain in simplicity can be well worth the loss in efficiency that you get with recursion.
Recursive Algorithms
Recursion is often favored in sorting and merging operations. Sorting data can be a recursive process in which the same algorithm is applied to smaller and smaller subsets of the original data. We can develop an example that uses recursion with a well-known sorting algorithm called quicksort. The example will sort a sequence of words. We have chosen this because it demonstrates a lot of different coding techniques and it’s sufficiently complicated to tax a few brain cells more than the examples you’ve seen up to now. The example involves more than 100 lines of code, so we’ll show and discuss each of the functions in the book separately and leave you to assemble them into a complete working program. The complete program is available in the code download as Ex8_18.cpp.
The Quicksort Algorithm
How the quicksort algorithm works
The same process is repeated for smaller and smaller sets of words until each word is in a separate set. When that is the case, the process ends, and the words are in ascending sequence. Of course, you’ll rearrange addresses in the code, not move words around. The address of each word can be stored as a smart pointer to a string object, and the pointers can be stored in a vector container.
The type of a vector of smart pointers to string objects is going to look a bit messy, so it won’t help the readability of the code. The following type alias will help to make the code easier to read:
The main() Function
The definition of main() will be simple because all the work will be done by other functions. There will be several #include directives and prototypes for the other functions in the application preceding the definition of main():
We think by now you know why all these Standard Library headers are needed. memory is for smart pointer template definitions, and vector contains the templates for vector containers. The type alias will make the code less cluttered.
swap() is a helper function that interchanges the elements at indexes first and second in the words vector.
The overload of sort() with three function parameters will use the quicksort algorithm to sort a contiguous sequence of elements in words from index start to index end inclusive. Indexes specifying a range are needed because the quicksort algorithm involves sorting subsets of a sequence, as you saw earlier.
The overload of sort() with one single parameter simply calls the one with three parameters (see later); it is there only for your convenience—to allow you to call sort() with a single vector<> argument.
extract_words() extracts words from text and stores smart pointers to the words in the words vector.
show_words() outputs the words in words.
max_word_length() determines the length of the longest word in words and is just to help make the output pretty.
The last two functions have reference-to-const parameters for the words vector because they don’t need to change it. The others have regular reference parameters because they do. Here’s the code for main():
The vector of smart pointers is defined using the type alias, Words. The vector will be passed by reference to each function to avoid copying the vector and to allow it to be updated when necessary. Forgetting the & in the type parameter can lead to a mystifying error. If the parameter to a function that changes words is not a reference, then words is passed by value, and the changes will be applied to the copy of words that is created when the function is called. The copy is discarded when the function returns, and the original vector will be unchanged.
The process in main() is straightforward. After reading some text into the string object text, the text is passed to the extract_words() function that stores pointers to the words in words. After a check to verify that words is not empty, sort() is called to sort the contents of words, and show_words() is called to output the words.
The extract_words() Function
You have seen a function similar to this. Here’s the code:
The last two parameters are string_views because the function won’t change the arguments corresponding to them. The separators object could conceivably be defined as a static variable within the function, but passing it as an argument makes the function more flexible. The process is essentially the same as you have seen previously. Each substring that represents a word is passed to the make_shared() function that is defined in the memory header. The substring is used by make_shared() to create a string object in the free store along with a smart pointer to it. The smart pointer that make_shared() returns is passed to the push_back() function for the words vector to append it as a new element in the sequence.
The swap() Function
There’ll be a need to swap pairs of addresses in the vector in several places, so it’s a good idea to define a helper function to do this:
This just swaps the addresses in words at indexes first and second.
The sort() Functions
You can use swap() in the implementation of the quicksort method because it involves rearranging the elements in the vector. The code for the sorting algorithm looks like this:
The parameters are the vector of addresses and the index positions of the first and last addresses in the subset to be sorted. The first time the function is called, start will be 0, and end will be the index of the last element. In subsequent recursive calls, a subsequence of the vector elements is to be sorted, so start and/or end will be interior index positions in many cases.
- 1.
The check for start not being less than end stops the recursive function calls. If there’s one element in a set, the function returns. In each execution of sort(), the current sequence is partitioned into two smaller sequences in the last two statements that call sort() recursively, so eventually you must end up with a sequence that has only one element.
- 2.
After the initial check, an address in the middle of the sequence is chosen arbitrarily as the pivot element for the sort. This is swapped with the address at index start, just to get it out of the way. You could also put it at the end of the sequence.
- 3.
The for loop compares the chosen word with the words pointed to by elements following start. If a word is less than the chosen word, its address is swapped into a position following start: the first into start+1, the second into start+2, and so on. The effect of this process is to position all the words less than the chosen word before all the words that are greater than or equal to it. When the loop ends, current contains the index of the address of the last word found to be less than the chosen word. The address of the chosen word at start is swapped with the address at current, so the addresses of words less than the chosen word are now to the left of current, and the addresses of words that are greater or equal are to the right.
- 4.
The last step sorts the subsets on either side of current by calling sort() for each subset. The indexes of words less than the chosen word run from start to current-1, and the indexes of those greater run from current+1 to end.
With recursion, the code for the sort is relatively easy to follow. And that’s not all; if you’d try to implement quicksort without recursion, meaning using just loops, you’d notice that this is not only much harder but also that you need to keep track of a stack of sorts of your own. Consequently, it is quite challenging to be faster with a loop than with recursion for quicksort. So, recursion not only makes for very natural, elegant algorithms, but their performance can be close enough to optimal for many uses as well.
A slight downside of this recursive sort() function is that it requires three arguments; it’s slightly unfortunate that sorting a vector requires you to decipher what to pass as second and third arguments. We therefore provide a more convenient single-parameter sort() function you can call instead:
This is actually a fairly common pattern. To get the recursion going, you provide a nonrecursive helper function. Often the recursive function is then not even exposed to the user (you’ll learn later to encapsulate or locally define functions).
Mind also the check for empty inputs. Any idea what would happen for empty inputs should you omit it? Precisely. Subtracting one from an unsigned size_t value equal to zero would result in a huge number (see, for instance, Chapter 5 for a complete explanation), which in this case would result in the recursive sort() function accessing the vector<> with indices that are massively out of bounds. And the latter, in turn, would of course almost certainly result in a crash!
The max_word_length() Function
This is a helper function that is used by the show_words() function:
This steps through the words that the vector elements point to and finds and returns the length of the longest word. You could put the code in the body of this function directly in the show_words() function. However, code is easier to follow if you break it into small, well-defined chunks. The operation that this function performs is self-contained and makes a sensible unit for a separate function.
The show_words() Function
This function outputs the words pointed to by the vector elements. It’s quite long because it lists all words beginning with the same letter on the same line, with up to ten words per line. Here’s the code:
The field_width variable is initialized to two more than the number of characters in the longest word. The variable is used for the field width for each word, so they will be aligned neatly in columns. There’s also words_per_line, which is the maximum number of words on a line. The first word is output before the for loop. This is because the loop compares the initial character in the current word with that of the previous word to decide whether it should be on a new line. Outputting the first word separately ensures we have a previous word at the start. The std::left manipulator that is defined in the iostream header causes data to be left aligned in the output field. There’s a complementary std::right manipulator. The rest of the words are output within the for loop. This outputs a newline character when eight words have been written on a line or when a word with an initial letter that is different from the preceding word is encountered.
If you assemble the functions into a complete program, you’ll have a good-sized example of a program split into several functions. Here’s an example of the output:
Of course, words beginning with an uppercase letter precede all words beginning with lowercase letters.
Summary
Functions are self-contained compact units of code with a well-defined purpose. A well-written program consists of a large number of small functions, not a small number of large functions.
A function definition consists of the function header that specifies the function name, the parameters, and the return type, followed by the function body containing the executable code for the function.
A function prototype enables the compiler to process calls to a function even though the function definition has not been processed.
The pass-by-value mechanism for arguments to a function passes copies of the original argument values, so the original argument values are not accessible from within the function.
Passing a pointer to a function allows the function to change the value that is pointed to, even though the pointer itself is passed by value.
Declaring a pointer parameter as const prevents modification of the original value.
You can pass the address of an array to a function as a pointer. If you do, you should generally pass the array’s length along as well.
Specifying a function parameter as a reference avoids the copying that is implicit in the pass-by-value mechanism. A reference parameter that is not modified within a function should be specified as const.
Input parameters should be reference-to-const, except for smaller values such as those of fundamental types. Returning values is preferred over output parameters, except for very large values such as std::array<>.
Specifying default values for function parameters allows arguments to be optionally omitted.
Default values can be combined with std::optional<> to make signatures more self-documenting. std::optional<> can be used for optional return values as well.
Returning a reference from a function allows the function to be used on the left of an assignment operator. Specifying the return type as a reference-to-const prevents this.
The signature of a function is defined by the function name together with the number and types of its parameters.
Overloaded functions are functions with the same name but with different signatures and therefore different parameter lists. Overloaded functions cannot be differentiated by the return type.
A recursive function is a function that calls itself. Implementing an algorithm recursively can result in elegant and concise code. Sometimes, but certainly not always, this is at the expense of execution time when compared to other methods of implementing the same algorithm.
Exercises
Exercise 8-1. Write a function, validate_input(), that accepts two integer arguments that represent the upper and lower limits for an integer that is to be entered. It should accept a third argument that is a string describing the input, with the string being used in the prompt for input to be entered. The function should prompt for input of the value within the range specified by the first two arguments and include the string identifying the type of value to be entered. The function should check the input and continue to prompt for input until the value entered by the user is valid. Use the validate_input() function in a program that obtains a user’s date of birth and outputs it in the form of this example:
November 21, 2012The program should be implemented so that separate functions, month(), year(), and day(), manage the input of the corresponding numerical values. Don’t forget leap years—February 29, 2017, is not allowed!
Exercise 8-2. Write a function that reads a string or array of characters as input and reverses it. Justify your choice of parameter type? Provide a main() function to test your function that prompts for a string of characters, reverses them, and outputs the reversed string.
Exercise 8-3. Write a program that accepts from two to four command-line arguments. If it is called with less than two or more than four arguments, output a message telling the user what they should do and then exit. If the number of arguments is correct, output them, each on a separate line.
Exercise 8-4. Create a function, plus(), that adds two values and returns their sum. Provide overloaded versions to work with int, double, and strings, and test that they work with the following calls:
const int n {plus(3, 4)};const double d {plus(3.2, 4.2)};const string s {plus("he", "llo")};const string s1 {"aaa"};const string s2 {"bbb"};const string s3 {plus(s1, s2)};Can you explain why the following doesn’t work?
const auto d {plus(3, 4.2)};Exercise 8-5. Define a function that checks whether a given number is prime. Your primal check does not have to be efficient; any algorithm you can think of will do. In case you have forgotten, a prime number is a natural number strictly greater than 1 and with no positive divisors other than 1 and itself. Write another function that generates a vector<> with all natural numbers less or equal to a first number and starting from another. By default it should start from 1. Create a third function that given a vector<> of numbers outputs another vector<> containing all the prime numbers it found in its input. Use these three functions to create a program that prints out all prime numbers less or equal to a number chosen by the user (print, for instance, 15 primes per line). Note: In principle, you do not need any vectors to print these prime numbers; obviously, these extra functions have been added for the sake of the exercise.
Exercise 8-6. Implement a program that queries the user for a number of grades. A grade is an integer number between 0 and 100 (both inclusive). The user can stop at any time by entering a negative number. Once all grades have been collected, your program is to output the following statistics: the five highest grades, the five lowest grades, the average grade, the median grade, and the standard deviation and variance of the grades. Of course, you’re to write a separate function to compute each of these statistics. Also, you must write the code to print five values only once. To practice, use arrays to store any five extremes and not, for instance, vectors.
Hint: As a preprocessing step, you should first sort the grades the user enters; you’ll see that this will make writing the functions to compute the statistics much easier. You can adapt the quicksort algorithm from Ex8_18 to work with grade numbers.
Caution: Make sure to do something sensible if the user enters less than five or even zero grades. Anything is fine, as long as it does not crash. Perhaps you can practice std::optional<> to deal with inputs such as an empty series of grades?
- Note: The median is the value that appears in the middle position of a sorted list. If there is an even number of grades, there obviously is no single middle value—the median is then defined as the mean of the two middle values. The formulas to compute mean (μ) and standard deviation (σ) of a series of n grades x i are as follows:
The variance is then defined as σ 2. The cmath header of the Standard Library defines std::sqrt() to compute square roots.
Exercise 8-7. The so-called Fibonacci function is popular among lecturers in computer science and mathematics for introducing recursion. This function has to compute the nth number from the famous Fibonacci sequence, named after Italian mathematician Leonardo of Pisa, known also as Fibonacci. This sequence of positive integer numbers is characterized by the fact that every number after the first two is the sum of the two preceding ones. For n ≥ 1, the sequence is defined as follows:
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181…
For convenience, computer scientists mostly define an additional zeroth Fibonacci number as zero. Write a function to compute the nth Fibonacci number recursively. Test it with a simple program that prompts the user for how many numbers should be computed and then prints them out one by one, each on a different line.
Extra: While the naive recursive version of the Fibonacci function is very elegant—the code matches nearly verbatim with common mathematical definitions—it is notorious for being very slow. If you ask the computer to compute, say, 100 Fibonacci numbers, you’ll notice that it becomes noticeably slower and slower as n becomes larger. Do you think you can rewrite the function to use a loop instead of recursion? How many numbers can you correctly compute now?
Hint: In each iteration of the loop, you’ll naturally want to compute a next number. To do this, all you need are the previous two numbers. So, there should be no need to keep track of the full sequence in, for instance, a vector<>.
Exercise 8-8. If written using a more mathematical notation, the power() functions we wrote in Ex8_01 and especially Ex8_17 both essentially compute a power(x,n) for n > 0, as follows:
power(x,n) = x * power(x,n-1)= x * (x * power(x,n-2))= ...= x * (x * (x * ... (x * x)...)))Clearly, this method requires exactly n-1 multiplications. It may surprise you, but there is another, much more effective way. Suppose n is even; then you know the following:
power(x,n) = power(x,n/2) * power(x,n/2)As both operands of this multiplication are identical, you need to compute this value only once. That is, you have just reduced the computation of power(x,n) to that of power(x,n/2), which obviously at most requires half as many multiplications. Moreover, because you can now apply this formula recursively, you’ll need even far fewer multiplications than that—only something in the order of log2(n) to be exact. To give you an idea, this means that for n in the order of 1000, you only need in the order of 10 multiplications! Can you apply this idea to create a more efficient recursive version of power()? You can start from the program in Ex8_17.cpp.
Note: This principle is something you’ll often see in recursive algorithms. In each recursive call, you reduce a problem to a problem of half the size. If you think back, you’ll realize that we applied the same principle in the quicksort algorithm as well, for instance. Because this solution strategy is that common, it also has a name; it’s called divide and conquer, after the famous phrase of Julius Caesar.
Exercise 8-9. Modify the solution of Exercise 8-8 such that it counts the number of times the call power(1.5,1000) performs a multiplication. Do so by replacing each multiplication with a helper function mult() that takes two arguments, prints a message of how many multiplications have been performed thus far, and then simply returns the product of both arguments. Use at least one static variable.
