In this chapter, we’ll explain the fundamental data types that are built into C++. You’ll need these in every program. All of the object-oriented capabilities are founded on these fundamental data types because all the data types that you create are ultimately defined in terms of the basic numerical data your computer works with. By the end of the chapter, you’ll be able to write a simple C++ program of the traditional form: input – process – output.
What a fundamental data type is in C++
How you declare and initialize variables
How you can fix the value of a variable
What integer literals are and how you define them
How calculations work
How to define variables that contain floating-point values
How to create variables that store characters
What the auto keyword does
Variables, Data, and Data Types
A variable is a named piece of memory that you define. Each variable stores data only of a particular type. Every variable has a type that defines the kind of data it can store. Each fundamental type is identified by a unique type name that consists of one or more keywords. Keywords are reserved words in C++ that you cannot use for anything else.
The compiler makes extensive checks to ensure that you use the right data type in any given context. It will also ensure that when you combine different types in an operation such as adding two values, for example, either they are of the same type or they can be made to be compatible by converting one value to the type of the other. The compiler detects and reports attempts to combine data of different types that are incompatible.
Numerical values fall into two broad categories: integers, which are whole numbers, and floating-point values, which can be nonintegral. There are several fundamental C++ types in each category, each of which can store a specific range of values. We’ll start with integer types.
Defining Integer Variables
Here’s a statement that defines an integer variable:
This defines a variable of type int with the name apple_count. The variable will contain some arbitrary junk value. You can and should specify an initial value when you define the variable, like this:
The initial value for apple_count appears between the braces following the name so it has the value 15. The braces enclosing the initial value are called a braced initializer . You’ll meet situations later in the book where a braced initializer will have several values between the braces. You don’t have to initialize variables when you define them, but it’s a good idea to do so. Ensuring variables start out with known values makes it easier to work out what is wrong when the code doesn’t work as you expect.
The size of variables of type int is typically 4 bytes, so they can store integers from -2,147,483,648 to +2,147,483,647. This covers most situations, which is why int is the integer type that is used most frequently.
Here are definitions for three variables of type int :
The initial value for total_fruit is the sum of the values of two variables defined previously. This demonstrates that the initial value for a variable can be an expression. The statements that define the two variables in the expression for the initial value for total_fruit must appear earlier in the source file; otherwise, the definition for total_fruit won’t compile.
The initial value between the braces should be of the same type as the variable you are defining. If it isn’t, the compiler will try to convert it to the required type. If the conversion is to a type with a more limited range of values, the conversion has the potential to lose information. An example would be if you specified the initial value for an integer variable that is not an integer—1.5, for example. A conversion to a type with a more limited range of values is called a narrowing conversion. If you use curly braces to initialize your variables, the compiler will always issue either a warning or an error whenever it detects a narrowing conversion .
There are two other ways for initializing a variable. Functional notation looks like this:
A second alternative is the so-called assignment notation:
Both these possibilities are equally valid as the braced initializer form and mostly completely equivalent. Both are therefore used extensively in existing code as well. In this book, however, we’ll adopt the braced initializer syntax. This is the most recent syntax that was introduced in C++11 specifically to standardize initialization. Its main advantage is that it enables you to initialize just about everything in the same way—which is why it is also commonly referred to as uniform initialization . Another advantage is that the braced initializer form is slightly safer when it comes to narrowing conversions:
All three definitions clearly contain a narrowing conversion. We’ll have more to say about floating-point to integer conversions later, but for now believe us when we say that after these variable definitions banana_count will contain the integer value 7, coconut_count will initialize to 5, and papaya_count will initialize to 0—provided compilation does not fail with an error because of the third statement, of course. It’s unlikely that this is what the author had in mind. Definitions with narrowing conversions such as these are therefore almost always mistakes.
Nevertheless, as far as the C++ standard is concerned, our first two definitions are perfectly legal C++. They are allowed to compile without even the slightest warning. While some compilers do issue a warning about such flagrant narrowing conversions, definitely not all of them do. If you use the braced initializer form, however, a conforming compiler is required to at least issue a diagnostic message. Some compilers will even issue an error and refuse to compile such definitions altogether. We believe inadvertent narrowing conversions do not deserve to go unnoticed, which is why we favor the braced initializer form.
Note
To represent fractional numbers, you typically use floating-point variables rather than integers. We’ll describe these later in this chapter.
Prior to C++17, there was one relatively common case where uniform initialization could not be used. We’ll return to this exception near the end of this chapter when we discuss the auto keyword. But since this quirk will soon be nothing more than a bad memory, we believe there’s little objective reason left not to embrace the new syntax. Uniformity and predictability, on the other hand, are desirable traits—especially for you, someone who’s taking the first steps in C++. In this book, we’ll therefore consistently use braced initializers.
You can define and initialize more than one variable of a given type in a single statement. Here’s an example:
While this is legal, it’s often considered best to define each variable in a separate statement. This makes the code more readable, and you can explain the purpose of each variable in a comment.
You can write the value of any variable of a fundamental type to the standard output stream. Here’s a program that does that with a couple of integers:
If you compile and execute this, you’ll see that it outputs the values of the three variables following some text explaining what they are. The integer values are automatically converted to a character representation for output by the insertion operator, <<. This works for values of any of the fundamental types.
Tip
The three variables in Ex2_01.cpp, of course, do not really need any comments explaining what they represent. Their variable names already make that crystal clear—as they should! In contrast, a lesser programmer might have produced the following, for instance:
Without extra context or explanation, no one would ever be able to guess this code is about counting fruit. You should therefore always choose your variable names as self-descriptive as possible. Properly named variables and functions mostly need no additional explanation in the form of a comment at all, by which we of course do not mean you should never add comments to declarations. You cannot always capture everything in a single name. A few words or, if need be, a little paragraph of comments can then do wonders in helping someone understand the code. A little extra effort at the time of writing can considerably speed up future development!
Signed Integer Types
Signed Integer Types
Type Name | Typical Size (Bytes) | Range of Values |
|---|---|---|
signed char | 1 | -128 to +127 |
short short int signed short signed short int | 2 | -256 to +255 |
int signed signed int | 4 | -2,147,483,648 to +2,147,483,647 |
long long int signed long signed long int | 4 or 8 | Same as either int or long long |
long long long long int signed long long singed long long int | 8 | -9,223,372,036,854,775,808 to +9,223,372,036,854,775,807 |
Type signed char is always 1 byte (which in turn nearly always is 8 bits); the number of bytes occupied by the others depends on the compiler. Each type will always have at least as much memory as the one that precedes it in the list, though.
Where two type names appear in the left column, the abbreviated name that comes first is more commonly used. That is, you will usually see long used rather than long int or signed long int.
The signed modifier is mostly optional; if omitted, your type will be signed by default. The only exception to this rule is char. While the unmodified type char does exist, it is compiler-dependant whether it is signed or unsigned. We’ll discuss this further in the next subsection. For all integer types other than char, however, you are free to choose whether you add the signed modifier. Personally, we normally do so only when we really want to stress that a particular variable is signed.
Unsigned Integer Types
Of course, there are circumstances where you don’t need to store negative numbers. The number of students in a class or the number of parts in an assembly is always a positive integer. You can specify integer types that only store non-negative values by prefixing any of the names of the signed integer types with the unsigned keyword—types unsigned char or unsigned short or unsigned long long, for example. Each unsigned type is a different type from the signed type but occupies the same amount of memory.
Type char is a different integer type from both signed char and unsigned char. The char type is intended only for variables that store character codes and can be a signed or unsigned type depending on your compiler. If the constant CHAR_MIN in the climits header is 0, then char is an unsigned type with your compiler. We’ll have more to say about variables that store characters later in this chapter.
Tip
Only use variables of the unmodified char type to store characters. For char variables that store other data such as plain integer numbers, you should always add the appropriate sign modifier.
With the possible exception of unsigned char, increasing the range of representable numbers is rarely the main motivator for adding the unsigned modifier—it rarely matters, for instance, whether you can represent numbers up to +2,147,483,647 or up to +4,294,967,295 (the maximum values for signed and unsigned int, respectively). No. Instead, you mostly add the unsigned modifier to make your code more self-documenting, that is, to make it more predictable what values a given variable will or should contain.
Note
You can also use the keywords signed and unsigned on their own. As Table 2-1 shows, the type signed is considered shorthand for signed int. So naturally, unsigned is short for unsigned int.
Zero Initialization
The following statement defines an integer variable with an initial value equal to zero:
You could omit the 0 in the braced initializer here, and the effect would be the same. The statement that defines counter could thus be written like this:
The empty curly braces somewhat resemble the number zero, which makes this syntax easy to remember. Zero initialization works for any fundamental type. For all fundamental numeric types, for instance, an empty braced initializer is always assumed to contain the number zero.
Defining Variables with Fixed Values
Sometimes you’ll want to define variables with values that are fixed and must not be changed. You use the const keyword in the definition of a variable that must not be changed. Such variables are often referred to as constants . Here’s an example:
The const keyword tells the compiler that the value of toe_count must not be changed. Any statement that attempts to modify this value will be flagged as an error during compilation; cutting off someone’s toe is a definite no-no! You can use the const keyword to fix the value of variables of any type.
Tip
If nothing else, knowing which variables can and cannot change their values along the way makes your code easier to follow. So, we recommend you add the const specifier whenever applicable.
Integer Literals
Constant values of any kind, such as 42, 2.71828, 'Z', or "Mark Twain", are referred to as literals. These examples are, in sequence, an integer literal, a floating-point literal, a character literal, and a string literal. Every literal will be of some type. We’ll first explain integer literals and introduce the other kinds of literals in context later.
Decimal Integer Literals
You can write integer literals in a very straightforward way. Here are some examples of decimal integers:
Unsigned integer literals have u or U appended. Literals of types long and type long long have L or LL appended, respectively, and if they are unsigned, they also have u or U appended. If there is no suffix, an integer constant is of type int. The U and L or LL can be in either sequence. You can use lowercase for the L and LL suffixes, but we recommend that you don’t because lowercase L is easily confused with the digit 1.
You could omit the + in the second example, as it’s implied by default, but if you think putting it in makes things clearer, that’s not a problem. The literal +123 is the same as 123 and is of type int because there is no suffix.
The fourth example, 22333, is the number that you, depending on local conventions, might write as either 22,333; 22 333; or 22.333 (though other formatting conventions exist as well). You must not use commas or spaces in a C++ integer literal, though, and adding a dot would turn it into a floating-point literal (as discussed later). Ever since C++14, however, you can use the single quote character, ', to make numeric literals more readable. Here’s an example:
Here are some statements using some of these literals:
Note that there are no restrictions on how to group the digits. Most Western conventions tend to group digits per three, but this is not universal. Natives of the subcontinent of India, for instance, would typically write the literal for 15 million as follows (using groups of two digits except for the rightmost group of three digits):
So far we have been very diligent in adding our literal suffixes—u or U for unsigned literals, L for literals of type long, and so on. In practice, however, you’ll rarely add these in variable initializers of this form. The reason is that no compiler will ever complain if you simply type this:
While all these literals are technically of type (signed) int, your compiler will happily convert them to the correct type for you. As long as the target type can represent the given values without loss of information, there’s no need to issue a warning.
Note
While mostly optional, there are situations where you do need to add the correct literal suffixes, such as when you initialize a variable with type auto (as explained near the end of this chapter) or when calling overloaded functions with literal arguments (as covered in Chapter 8).
An initializing value should always be within the permitted range for the type of variable, as well as from the correct type. The following two statements violate these restrictions. They require, in other words, what you know to be narrowing conversions:
As we explained earlier, depending on which compiler you use, these braced initializations will result in at least a compiler warning, if not a compilation error.
Hexadecimal Literals
Hexadecimal literals: | 0x1AF | 0x123U | 0xAL | 0xcad | 0xFF |
Decimal literals: | 431 | 291U | 10L | 3245 | 255 |
A major use for hexadecimal literals is to define particular patterns of bits. Each hexadecimal digit corresponds to 4 bits, so it’s easy to express a pattern of bits as a hexadecimal literal. The red, blue, and green components (RGB values) of a pixel color, for instance, are often expressed as three bytes packed into a 32-bit word. The color white can be specified as 0xFFFFFF because the intensity of each of the three components in white have the same maximum value of 255, which is 0xFF. The color red would be 0xff0000. Here are some examples:
Octal Literals
Octal literals: | 0657 | 0443U | 012L | 06255 | 0377 |
Decimal literals: | 431 | 291U | 10L | 3245 | 255 |
Caution
Don’t write decimal integer values with a leading zero. The compiler will interpret such values as octal (base 8), so a value written as 065 will be the equivalent of 53 in decimal notation.
Binary Literals
Binary literals: | 0B110101111 | 0b100100011U | 0b1010L | 0B110010101101 | 0b11111111 |
Decimal literals: | 431 | 291U | 10L | 3245 | 255 |
We have illustrated in the code fragments how you can write various combinations for the prefixes and suffixes such as 0x or 0X and UL, LU, or Lu, but of course it’s best to stick to a consistent way of writing integer literals.
As far as your compiler is concerned, it doesn’t matter which number base you choose when you write an integer value. Ultimately it will be stored as a binary number. The different ways for writing an integer are there just for your convenience. You choose one or other of the possible representations to suit the context.
Note
You can use a single quote as a separator in any integer literal to make it easier to read. This includes hexadecimal or binary literals. Here’s an example: 0xFF00'00FF'0001UL or 0b1100'1010'1101.
Calculations with Integers
To begin with, let’s get some bits of terminology out of the way. An operation such as addition or multiplication is defined by an operator—the operators for addition and multiplication are + and *, respectively. The values that an operator acts upon are called operands , so in an expression such as 2*3, the operands are 2 and 3. Operators such as multiplication that require two operands are called binary operators . Operators that require one operand are called unary operators . An example of a unary operator is the minus sign in the expression -width. The minus sign negates the value of width, so the result of the expression is a value with the opposite sign to that of its operand. This contrasts with the binary multiplication operator in expressions such as width * height, which acts on two operands, width and height.
Basic Arithmetic Operations
Operator | Operation |
|---|---|
+ | Addition |
- | Subtraction |
* | Multiplication |
/ | Division |
% | Modulus (the remainder after division) |
The operators in Table 2-2 are all binary operators and work largely in the way you would expect. There are two operators that may need a little word of explanation, though: the somewhat lesser-known modulus operator, of course, but also the division operator. Integer division is slightly idiosyncratic in C++. When applied to two integer operands, the result of a division operation is always again an integer. Suppose, for instance, that you write the following:
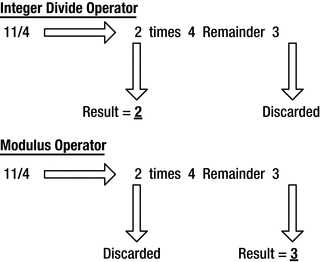
Contrasting the division and modulus operators
Integer division returns the number of times that the denominator divides into the numerator. Any remainder is discarded. The modulus operator, %, complements the division operator in that it produces the remainder after integer division. It is defined such that, for all integers x and y, (x / y) * y + (x % y) equals x. Using this formula, you can easily deduce what the modulus operand will do for negative operands.
The result of both the division and modulus operator is undefined when the right operand is zero—what’ll happen depends, in other words, on your compiler and computer architecture.
Compound Arithmetic Expressions
If multiple operators appear in the same expression, multiplication, division, and modulus operations always execute before addition and subtraction. Here’s an example of such a case:
You can control the order in which more complicated expressions are executed using parentheses. You could write the statement that calculates a value for perimeter as follows:
The subexpression within the parentheses is evaluated first. The result then is multiplied by two, which produces the same end result as before. If you omit the parentheses here, however, the result would no longer be 18. The result, instead, would become 14:
The reason is that multiplication is always evaluated before addition. So, the previous statement is actually equivalent to the following one:
Parentheses can be nested, in which case subexpressions between parentheses are executed in sequence from the innermost pair of parentheses to the outermost. This example of an expression with nested parentheses will show how it works:
The expression 5*d is evaluated first, and c is added to the result. That result is multiplied by 4, and b is added. That result is multiplied by 3, and a is added. Finally, that result is multiplied by 2 to produce the result of the complete expression.
We will have more to say about the order in which such compound expressions are evaluated in the next chapter. The main thing to remember is that whatever the default evaluation order is, you can always override it by adding parentheses. And even if the default order happens to be what you want, it never hurts to add some extra parentheses just for the sake of clarity:
Assignment Operations
In C++, the value of a variable is fixed only if you use the const qualifier . In all other cases, the value of a variable can always be overwritten with a new value:
This last line is an assignment statement, and the = is the assignment operator. The arithmetic expression on the right of the assignment operator is evaluated, and the result is stored in the variable on the left. Initializing the perimeter variable upon declaration may not be strictly necessary—as long as the variable is not read prior to the assignment, that is—but it’s considered good practice to always initialize your variables nevertheless. And zero is often as good a value as any.
You can assign a value to more than one variable in a single statement. Here’s an example:
The second statement calculates the value of the expression c*c - d*d and stores the result in b, so b will be set to 9. Next the value of b is stored in a, so a will also be set to 9. You can have as many repeated assignments like this as you want.
It’s important to appreciate that an assignment operator is quite different from an = sign in an algebraic equation. The latter implies equality, whereas the former is specifying an action—specifically, the act of overwriting a given memory location. A variable can be overwritten as many times as you want, each time with different, mathematically nonequal values. Consider the assignment statement in the following:
The variable y is initialized with 5, so the expression y + 1 produces 6. This result is stored back in y, so the effect is to increment y by 1. This last line makes no sense in common math: as any mathematician will tell you, y can never equal y + 1 (except of course when y equals infinity…). But in programming languages such as C++ repeatedly incrementing a variable with one is actually extremely common. In Chapter 5, you’ll find that equivalent expressions are, for instance, ubiquitous in loops.
Let’s see some of the arithmetic operators in action in an example. This program converts distances that you enter from the keyboard and in the process illustrates using the arithmetic operators :
The following is an example of typical output from this program:
The first statement in main() defines three integer variables and initializes them with zero. They are type unsigned int because in this example the distance values cannot be negative. This is an instance where defining three variables in a single statement is reasonable because they are closely related.
The next statement outputs a prompt to std:: cout for the input. We used a single statement spread over three lines, but it could be written as three separate statements as well:
When you have a sequence of << operators as in the original statement, they execute from left to right so the output from the previous three statements will be the same as the original.
The next statement reads values from cin and stores them in the variables yards, feet, and inches . The type of value that the >> operator expects to read is determined by the type of variable in which the value is to be stored. So, in this case, unsigned integers are expected to be entered. The >> operator ignores spaces, and the first space following a value terminates the operation. This implies that you cannot read and store spaces using the >> operator for a stream, even when you store them in variables that store characters. The input statement in the example could again also be written as three separate statements:
The effect of these statements is the same as the original.
You define two variables, inches_per_foot and feet_per_yard, that you need to convert from yards, feet, and inches to just inches, and vice versa. The values for these are fixed, so you specify the variables as const. You could use explicit values for conversion factors in the code, but using const variables is much better because it is then clearer what you are doing. The const variables are also positive values, so you define them as type unsigned int. You could add U modifiers to the integer literals if you prefer, but there’s no need. The conversion to inches is done is a single assignment statement:
The expression between parentheses executes first. This converts the yards value to feet and adds the feet value to produce the total number of feet. Multiplying this result by inches_per_foot obtains the total number of inches for the values of yards and feet. Adding inches to that produces the final total number of inches, which you output using this statement:
The first string is transferred to the standard output stream, cout, followed by the value of total_inches. The string that is transferred to cout next has \n as the last character, which will cause the next output to start on the next line.
Converting a value from inches to yards, feet, and inches requires four statements:
You reuse the variables that stored the input for the previous conversion to store the results of this conversion. Dividing the value of total_inches by inches_per_foot produces the number of whole feet, which you store in feet. The % operator produces the remainder after division, so the next statement calculates the number of residual inches, which is stored in inches. The same process is used to calculate the number of yards and the final number of feet.
Notice the use of whitespace to nicely outline these assignment statements. You could’ve written the same statements without spaces as well, but that simply does not read very fluently:
We generally add a single space before and after each binary operator, as it promotes code readability. Adding extra spaces to outline related assignments in a semitabular form doesn’t harm either.
There’s no return statement after the final output statement because it isn’t necessary. When the execution sequence runs beyond the end of main(), it is equivalent to executing return 0.
The op= Assignment Operators
In Ex2_02.cpp, there was a statement that you could write more economically:
This statement could be written using an op= assignment operator. The op = assignment operators, or also compound assignment operators , are so called because they’re composed of an operator and an assignment operator =. You could use one to write the previous statement as follows:
This is the same operation as the previous statement.
In general, an op= assignment is of the following form:
lhs represents a variable of some kind that is the destination for the result of the operator. rhs is any expression. This is equivalent to the following statement:
The parentheses are important because you can write statements such as the following:
This is equivalent to the following:
Without the implied parentheses, the value stored in x would be the result of x * y + 1, which is quite different.
op= Assignment Operators
Operation | Operator | Operation | Operator |
|---|---|---|---|
Addition | += | Bitwise AND | &= |
Subtraction | -= | Bitwise OR | |= |
Multiplication | *= | Bitwise exclusive OR | ^= |
Division | /= | Shift left | <<= |
Modulus | %= | Shift right | >>= |
Note that there can be no spaces between op and the =. If you include a space, it will be flagged as an error. You can use += when you want to increment a variable by some amount. For example, the following two statements have the same effect:
The shift operators that appear in the table, << and >>, look the same as the insertion and extraction operators that you have been using with streams. The compiler can figure out what << or >> means in a statement from the context. You'll understand how it is possible that the same operator can mean different things in different situations later in the book.
Sidebar: Using Declarations and Directives
There were a lot of occurrences of std::cin and std::cout in Ex2_02.cpp. You can eliminate the need to qualify a name with the namespace name in a source file with a using declaration . Here’s an example:
This tells the compiler that when you write cout, it should be interpreted as std::cout. With this declaration before the main() function definition, you can write cout instead of std::cout, which saves typing and makes the code look a little less cluttered.
You could include two using declarations at the beginning of Ex2_02.cpp and avoid the need to qualify cin and cout:
Of course, you still have to qualify endl with std, although you could add a using declaration for that too. You can apply using declarations to names from any namespace, not just std.
A using directive imports all the names from a namespace. Here’s how you could use any name from the std namespace without the need to qualify it:
With this at the beginning of a source file, you don’t have to qualify any name that is defined in the std namespace. At first sight this seems an attractive idea. The problem is it defeats a major reason for having namespaces. It is unlikely that you know all the names that are defined in std, and with this using directive you have increased the probability of accidentally using a name from std.
We’ll use a using directive for the std namespace occasionally in examples in the book where the number of using declarations that would otherwise be required is excessive. We recommend that you make use of using directives only when there’s a good reason to do so.
The sizeof Operator
You use the sizeof operator to obtain the number of bytes occupied by a type, by a variable, or by the result of an expression. Here are some examples of its use:
These statements show how you can output the size of a variable, the size of a type, and the size of the result of an expression. To use sizeof to obtain the memory occupied by a type, the type name must be between parentheses. You also need parentheses around an expression with sizeof. You don’t need parentheses around a variable name, but there’s no harm in putting them in. Thus, if you always use parentheses with sizeof, you can’t go wrong.
You can apply sizeof to any fundamental type, class type, or pointer type (you’ll learn about pointers in Chapter 5). The result that sizeof produces is of type size_t, which is an unsigned integer type that is defined in the Standard Library header cstddef. Type size_t is implementation defined, but if you use size_t, your code will work with any compiler.
Now you should be able to create your own program to list the sizes of the fundamental integer types with your compiler.
Incrementing and Decrementing Integers
You’ve seen how you can increment a variable with the += operator and we’re sure you’ve deduced that you can decrement a variable with -=. There are two other operators that can perform the same tasks. They’re called the increment operator and the decrement operator, ++ and --, respectively.
These operators are more than just other options. You’ll see a lot more of them, and you’ll find them to be quite an asset once you get further into C++. In particular, you’ll use them all the time when working with arrays and loops in Chapter 5. The increment and decrement operators are unary operators that you can apply to an integer variable. The following three statements that modify count have exactly the same effect:
Each statement increments count by 1. Using the increment operator is clearly the most concise. The action of this operator is different from other operators that you’ve seen in that it directly modifies the value of its operand. The effect in an expression is to increment the value of the variable and then to use the incremented value in the expression. For example, suppose count has the value 5 and you execute this statement:
The increment and decrement operators execute before any other binary arithmetic operators in an expression. Thus, count will be incremented to 6, and then this value will be used in the evaluation of the expression on the right of the assignment. total will therefore be assigned the value 12.
You use the decrement operator in the same way:
Assuming count is 6 before this statement, the -- operator will decrement it to 5, and then this value will be used to calculate the value to be stored in total, which will be 11.
You’ve seen how you place a ++ or -- operator before the variable to which it applies. This is called the prefix form of these operators. You can also place them after a variable, which is called the postfix form. The effect is a little different.
Postfix Increment and Decrement Operations
The postfix form of ++ increments the variable to which it applies after its value is used in context. For example, you can rewrite the earlier example as follows:
With an initial value of 5 for count, total is assigned the value 11. In this case, count will be incremented to 6 only after being used in the surrounding expression. The preceding statement is thus equivalent to the following two statements:
In an expression such as a++ + b, or even a+++b, it’s less than obvious what you mean, or indeed what the compiler will do. These two expressions are actually the same, but in the second case you might have meant a + ++b, which is different—it evaluates to one more than the other two expressions. It would be clearer to write the preceding statement as follows:
Alternatively, you can use parentheses:
The rules that we’ve discussed in relation to the increment operator also apply to the decrement operator. For example, suppose count has the initial value 5 and you write this statement:
This results in total having the value 10 assigned. However, consider this statement:
In this instance, total is set to 11.
You should take care applying these operators to a given variable more than once in an expression. Suppose count has the value 5 and you write this:
The result of this statement is undefined because the statement modifies the value of count more than once using increment operators. Even though this expression is undefined according to the C++ standard, this doesn’t mean that compilers won’t compile them. It just means that there is no guarantee at all of consistency in the results.
The effects of statements such as the following used to be undefined as well:
Here you’re incrementing the value of the variable that appears on the left of the assignment operator in the expression on the right, so you’re again modifying the value of k twice. Starting with C++17, however, the latter expression has become well-defined. Informally, the C++17 edition of the standard added the rule that all side effects of the right side of an assignment (and this includes compound assignments, increments, and decrements) are fully committed before evaluating the left side and the actual assignment. Nevertheless, the precise rules of when precisely an expression is defined or undefined remain subtle, even in C++17, so our advice remains unchanged:
Tip
Modify a variable only once as a result of evaluating a single expression and access the prior value of the variable only to determine its new value—that is, do not attempt to read a variable again after it has been modified in the same expression.
The increment and decrement operators are usually applied to integers, particularly in the context of loops, as you’ll see in Chapter 5. You’ll see later in this chapter that you can apply them to floating-point variables too. In later chapters, you’ll explore how they can also be applied to certain other data types, in some cases with rather specialized (but very useful) effects.
Defining Floating-Point Variables
Floating-Point Data Types
Data Type | Description |
|---|---|
float | Single precision floating-point values |
double | Double precision floating-point values |
long double | Double-extended precision floating-point values |
Note
You cannot use the unsigned or signed modifiers with floating-point types; floating-point types are always signed.
As explained in Chapter 1, the term precision refers to the number of significant digits in the mantissa. The types are in order of increasing precision, with float providing the lowest number of digits in the mantissa and long double the highest. The precision only determines the number of digits in the mantissa. The range of numbers that can be represented by a particular type is determined by the range of possible exponents.
The precision and range of values aren’t prescribed by the C++ standard, so what you get with each type depends on your compiler. And this, in turn, will depend on what kind of processor is used by your computer and the floating-point representation it uses. The standard does guarantee that type long double will provide a precision that’s no less than that of type double, and type double will provide a precision that is no less than that of type float.
Floating-Point Type Ranges
Type | Precision (Decimal Digits) | Range (+ or –) |
|---|---|---|
float | 7 | ±1.18 × 10-38 to ±3.4 × 1038 |
double | 15 (nearly 16) | ±2.22 × 10-308 to ±1.8 × 10308 |
long double | 18-19 | ±3.65 × 10-4932 to ±1.18 × 104932 |
The numbers of digits of precision in Table 2-5 are approximate. Zero can be represented exactly with each type, but values between zero and the lower limit in the positive or negative range can’t be represented, so the lower limits are the smallest possible nonzero values.
Here are some statements that define floating-point variables:
As you see, you define floating-point variables just like integer variables. Type double is more than adequate in the majority of circumstances. You typically use float only when speed or data size is truly of the essence. If you do use float, though, you always need to remain vigilant that the loss of precision is acceptable for your application.
Floating-Point Literals
You can see from the code fragment in the previous section that float literals have f (or F) appended and long double literals have L (or l) appended. Floating-point literals without a suffix are of type double. A floating-point literal includes either a decimal point or an exponent, or both; a numeric literal with neither is an integer.
An exponent is optional in a floating-point literal and represents a power of 10 that multiplies the value. An exponent must be prefixed with e or E and follows the value. Here are some floating-point literals that include an exponent:
The value between parentheses following each literal with an exponent is the equivalent literal without the exponent. Exponents are particularly useful when you need to express very small or very large values.
As always, your compiler will happily initialize floating-point variables with literals that lack a proper F or L suffix, or even with integer literals. If the literal value falls outside the representable range of the variable’s type, though, your compiler should at least issue a warning regarding a narrowing conversion.
Floating-Point Calculations
You write floating-point calculations in the same way as integer calculations . Here’s an example:
The modulus operator, %, can’t be used with floating-point operands , but all the other binary arithmetic operators that you have seen, +, -, *, and /, can be. You can also apply the prefix and postfix increment and decrement operators, ++ and --, to a floating-point variable with essentially the same effect as for an integer; the variable will be incremented or decremented by 1.0.
Pitfalls
Many decimal values don’t convert exactly to binary floating-point values. The small errors that occur can easily be amplified in your calculations to produce large errors.
Taking the difference between two nearly identical values will lose precision. If you take the difference between two values of type float that differ in the sixth significant digit, you’ll produce a result that will have only one or two digits of accuracy. The other digits in the mantissa will be garbage. In Chapter 1, we already named this phenomenon catastrophic cancellation.
Working with values that differ by several orders of magnitude can lead to errors. An elementary example of this is adding two values stored as type float with 7 digits of precision where one value is 108 times larger than the other. You can add the smaller value to the larger as many times as you like, and the larger value will be unchanged.
Invalid Floating-Point Results
So far as the C++ standard is concerned, the result of division by zero is undefined. Nevertheless, floating-point operations in most computers are implemented according to the IEEE 754 standard (also known as IEC 559). So in practice, compilers generally behave quite similarly when dividing floating-point numbers by zero. Details may differ across specific compilers, so consult your product documentation.
The IEEE floating-point standard defines special values having a binary mantissa of all zeroes and an exponent of all ones to represent +infinity or -infinity, depending on the sign. When you divide a positive nonzero value by zero, the result will be +infinity, and dividing a negative value by zero will result in -infinity.
Floating-Point Operations with NaN and ±infinity Operands
Operation | Result | Operation | Result |
|---|---|---|---|
±value / 0 | ±infinity | 0 / 0 | NaN |
±infinity ± value | ±infinity | ±infinity / ±infinity | NaN |
±infinity * value | ±infinity | infinity - infinity | NaN |
±infinity / value | ±infinity | infinity * 0 | NaN |
value in the table is any nonzero value. You can discover how your compiler presents these values by plugging the following code into main():
You’ll see from the output when you run this how ±infinity and NaN look . One possible outcome is this:
Tip
The easiest way to obtain a floating-point value that represents either infinity or NaN is using the facilities of the limits header of the Standard Library, which we discuss later in this chapter. That way you do not really have to remember the rules of how to obtain them through divisions by zero. To check whether a given number is either infinity or NaN, you should use the std::isinf() and std::isnan() functions provided by the cmath header—what to do with the results of these functions will only become clear in Chapter 4, though.
Mathematical Functions
The cmath Standard Library header file defines a large selection of trigonometric and numerical functions that you can use in your programs. In this section, we’ll only discuss some of the functions that you are likely to use on a regular basis, but there are many, many more. The functions defined by cmath today truly range from the very basic to some of the most advanced mathematical functions (in the latter category, the C++17 standard, for instance, has recently added beauties such as cylindrical Neumann functions, associated Laguerre polynomials, and the Riemann zeta function). You can consult your favorite Standard Library reference for the complete list.
Numerical Functions in the cmath Header
Function | Description |
|---|---|
abs(arg) | Computes the absolute value of arg. Unlike most cmath functions, abs() returns an integer type if arg is integer. |
ceil(arg) | Computes a floating-point value that is the smallest integer greater than or equal to arg, so std::ceil(2.5) produces 3.0 and std::ceil(-2.5) produces -2.0. |
floor(arg) | Computes a floating-point value that is the largest integer less than or equal to arg, so std::floor(2.5) results in 2.0 and std::floor(-2.5) results in -3.0. |
exp(arg) | Computes the value of e arg . |
log(arg) | Computes the natural logarithm (to base e) of arg. |
log10(arg) | Computes the logarithm to base 10 of arg. |
pow(arg1, arg2) | Computes the value of arg1 raised to the power arg2, or arg1 arg2 . arg1 and arg2 can be integer or floating-point types. The result of std::pow(2, 3) is 8.0, std::pow(1.5f, 3) equals 3.375f, and std::pow(4, 0.5) is equal to 2. |
sqrt(arg) | Computes the square root of arg. |
round(arg) | Rounds arg to the nearest integer. The result is a floating-point number though, even for integer inputs. The cmath header also defines lround() and llround() that evaluate to the nearest integer of type long and long long, respectively. Halfway cases are rounded away from zero. In other words, std::lround(0.5) gives 1L, whereas std::round(-1.5f) gives -2.0f. |
Besides these, the cmath header provides all basic trigonometric functions (std::cos(), sin(), and tan()), as well as their inverse functions (std::acos(), asin(), and atan()). Angles are always expressed in radians.
Let’s look at some examples of how these are used. Here’s how you can calculate the cosine of an angle in radians :
If the angle is in degrees, you can calculate the tangent by using a value for π to convert to radians:
If you know the height of a church steeple is 100 feet and you’re standing 50 feet from its base, you can calculate the angle in radians of the top of the steeple like this:
You can use this value in angle and the value of distance to calculate the distance from your toe to the top of the steeple:
Of course, fans of Pythagoras of Samos could obtain the result much more easily, like this:
Tip
The problem with an expression of form std::atan(a / b) is that by evaluating the division a / b, you lose information about the sign of a and b. In our example this does not matter much, as both distance and height are positive, but in general you may be better off calling std::atan2(a, b). The atan2() function is defined by the cmath header as well. Because it knows the signs of both a and b, it is capable of properly reflecting this in the resulting angle. You can consult a Standard Library reference for the detailed specification.
Let’s try a floating-point example. Suppose that you want to construct a circular pond in which you will keep fish. Having looked into the matter, you know that you must allow 2 square feet of pond surface area for every 6 inches of fish length. You need to figure out the diameter of the pond that will keep the fish happy. Here’s how you can do it:
With input values of 20 fish with an average length of 9 inches, this example produces the following output:
You first define three const variables in main() that you’ll use in the calculation. Notice the use of a constant expression to specify the initial value for fish_factor. You can use any expression for an initial value that produces a result of the appropriate type. You specify fish_factor, inches_per_foot, and pi as const because their values are fixed and should not be altered.
Next, you define the fish_count and fish_length variables in which you’ll store the user input. Both have an initial value of zero. The input for the fish length is in inches, so you convert it to feet before you use it in the calculation for the pond. You use the /= operator to convert the original value to feet.
You define a variable for the area for the pond and initialize it with an expression that produces the required value:
The product of fish_count and fish_length gives the total length of all the fish in feet, and multiplying this by fish_factor gives the required area for the pond in square feet. Once computed and initialized, the value of pond_area will and should not be changed anymore, so you might as well declare the variable const to make that clear.
The area of a circle is given by the formula πr2, where r is the radius. You can therefore calculate the radius of the circular pond by dividing the area by π and calculating the square root of the result. The diameter is twice the radius, so the whole calculation is carried out by this statement:
You obtain the square root using the sqrt() function from the cmath header.
Of course, you could calculate the pond diameter in a single statement like this:
This eliminates the need for the pond_area variable so the program will be smaller and shorter. It’s debatable whether this is better than the original, though, because it’s far less obvious what is going on.
The last statement in main() outputs the result. Unless you’re an exceptionally meticulous pond enthusiast, however, the pond diameter has more decimal places than you need. Let’s look into how you can fix that.
Formatting Stream Output
You can change how data is formatted when it is written to an output stream using stream manipulators, which are declared in the iomanip and ios Standard Library headers. You apply a stream manipulator to an output stream with the insert operator, <<. We’ll just introduce the most useful manipulators. You should consult a Standard Library reference if you want to get to know the others.
std::fixed | Output floating-point data in fixed-point notation. |
std::scientific | Output all subsequent floating-point data in scientific notation, which always includes an exponent and one digit before the decimal point. |
std::defaultfloat | Revert to the default floating-point data presentation. |
std::dec | All subsequent integer output is decimal. |
std::hex | All subsequent integer output is hexadecimal. |
std::oct | All subsequent integer output is octal. |
std::showbase | Outputs the base prefix for hexadecimal and octal integer values. Inserting std::noshowbase in a stream will switch this off. |
std::left | Output is left-justified in the field. |
std::right | Output is right-justified in the field. This is the default. |
std::setprecision(n) | Sets the floating-point precision or the number of decimal places to n digits. If the default floating-point output presentation is in effect, n specifies the number of digits in the output value. If fixed or scientific format has been set, n is the number of digits following the decimal point. The default precision is 6. |
std::setw(n) | Sets the output field width to n characters, but only for the next output data item. Subsequent output reverts to the default where the field width is set to the number of output character needed to accommodate the data. |
std::setfill(ch) | When the field width has more characters than the output value, excess characters in the field will be the default fill character, which is a space. This sets the fill character to be ch for all subsequent output. |
When you insert a manipulator in an output stream, it normally remains in effect until you change it. The only exception is std::setw(), which only influences the width of the next field that is output.
Let’s see how some of these work in practice. Replace the output statement at the end of Ex2_03.cpp with the following, and enter, for instance, 20 and 9 as input again:
You’ll get the floating-point value presented with 2 digits of precision, which will correspond to 1 decimal place in this case. Because the default handling of floating-point output is in effect, the integer between the parentheses in setprecision() specifies the output precision for floating-point values, which is the total number of digits before and after the decimal point. You can make the parameter specify the number of digits after the decimal point—the number of decimal places in other words—by setting the mode as fixed. For example, try this in Ex2_03.cpp:
Setting the mode as fixed or as scientific causes the setprecision() parameter to be interpreted as the number of decimal places in the output value. Setting scientific mode causes floating-point output to be in scientific notation, which is with an exponent:
In scientific notation there is always one digit before the decimal point. The value set by setprecision() is still the number of digits following the decimal point. There’s always a two-digit exponent value, even when the exponent is zero.
The following statements illustrate some of the formatting possible with integer values :
The output from these statements is as follows:
It’s a good idea to insert showbase in the stream when you output integers as hexadecimal or octal so the output won’t be misinterpreted as decimal values. We recommend you try various combinations of these manipulators and stream constants to get a feel for how they all work.
Mixed Expressions and Type Conversion
You can write expressions involving operands of different types. For example, you could have defined the variable to store the number of fish in Ex2_03 like this:
The number of fish is certainly an integer, so this makes sense. The number of inches in a foot is also integral, so you would want to define the variable like this:
The calculation would still work OK in spite of the variables now being of differing types. Here’s an example:
Technically, all binary arithmetic operands require both operands to be of the same type. Where this is not the case, however, the compiler will arrange to convert one of the operand values to the same type as the other. These are called implicit conversions . The way this works is that the variable of a type with the more limited range is converted to the type of the other. The fish_length variable in the first statement is of type double. Type double has a greater range than type unsigned int, so the compiler will insert a conversion for the value of inches_per_foot to type double to allow the division to be carried out. In the second statement, the value of fish_count will be converted to type double to make it the same type as fish_length before the multiply operation executes.
1. long double | 2. double | 3. float |
4. unsigned long long | 5. long long | 6. unsigned long |
7. long | 8. unsigned int | 9. int |
The operand to be converted will be the one with the lower rank. Thus, in an operation with operands of type long long and type unsigned int, the latter will be converted to type long long. An operand of type char, signed char, unsigned char, short, or unsigned short is always converted to at least type int.
Implicit conversions can produce unexpected results. Consider these statements :
You might expect the output to be -10, but it isn’t. The output will most likely be 4294967286! This is because the value of y is converted to unsigned int to match the type of x, so the result of the subtraction is an unsigned integer value. And -10 cannot be represented by an unsigned type. For unsigned integer types, going below zero always wraps around to the largest possible integer value. That is, for a 32-bit unsigned int type, -1 becomes 2 32 -1 or 4294967295, -2 becomes 2 32 -2 or 4294967293, and so on. This of course means that -10 indeed becomes 2 32 -10, or 4294967286.
Note
The phenomenon where the result of a subtraction of unsigned integers wraps around to very large positive numbers is sometimes called underflow. In general, underflow is something to watch out for (we’ll encounter examples of this in later chapters). Naturally, the converse phenomenon exists as well and is called overflow. Adding the unsigned char values 253 and 5, for instance, will not give 258—the largest value a variable of type unsigned char can hold is 255! Instead, the result will be 2, or 258 modulo 256. The outcome of overflow and underflow with signed integer types is undefined—that is, it depends on the compiler and computer architecture you are using.
The compiler will also insert an implicit conversion when the expression on the right of an assignment produces a value that is of a different type from the variable on the left. Here’s an example:
The last statement requires a conversion of the value of the expression on the right of the assignment to allow it to be stored as type int. The compiler will insert a conversion to do this, but since this is a narrowing conversion, it may issue a warning message about possible loss of data.
You need to take care when writing integer operations with operands of different types. Don’t rely on implicit type conversion to produce the result you want unless you are certain it will do so. If you are not sure, what you need is an explicit type conversion, also called an explicit cast.
Explicit Type Conversion
To explicitly convert the value of an expression to a given type, you write the following:
The static_cast keyword reflects the fact that the cast is checked statically, that is, when the code is compiled. Later, when you get to deal with classes, you’ll meet dynamic casts, where the conversion is checked dynamically, that is, when the program is executing. The effect of the cast is to convert the value that results from evaluating expression to the type that you specify between the angle brackets. The expression can be anything from a single variable to a complex expression involving lots of nested parentheses. You could eliminate the warning that arises from the assignment in the previous section by writing it as follows:
By adding an explicit cast, you signal the compiler that a narrowing conversion is intentional. If the conversion is not narrowing, you’d rarely add an explicit cast. Here’s another example of the use of static_cast<>():
The initializing value for whole_number is the sum of the integral parts of value1 and value2, so they’re each explicitly cast to type int. whole_number will therefore have the initial value 25. Note that as with integer division, casting from a floating-point type to an integral type uses truncation. That is, it simply discards the entire fractional part of the floating-point number.
Tip
As seen earlier in this chapter, the std::round(), lround(), and llround() functions from the cmath header allow you to round floating-point numbers to the nearest integer. In many cases, this is better than (implicit or explicit) casting, where truncation is used instead.
The casts do not affect the values stored in value1 and value2, which will remain as 10.9 and 15.9, respectively. The values 10 and 15 produced by the casts are just stored temporarily for use in the calculation and then discarded. Although both casts cause a loss of information, the compiler always assumes you know what you’re doing when you explicitly specify a cast.
Of course, the value of whole_number would be different if you wrote this:
The result of adding value1 and value2 will be 26.8, which results in 26 when converted to type int. As always with braced initializers, without the explicit type conversion in this statement, the compiler will either refuse to insert or at least warn about inserting implicit narrowing conversions .
Generally, the need for explicit casts should be rare, particularly with basic types of data. If you have to include a lot of explicit conversions in your code, it’s often a sign that you could choose more suitable types for your variables. Still, there are circumstances when casting is necessary, so let’s look at a simple example. This example converts a length in yards as a decimal value to yards, feet, and inches :
This is typical output from this program:
The first two statements in main() define conversion constants feet_per_yard and inches_per_foot as integers. You declare these as const to prevent them from being modified accidentally. The variables that will store the results of converting the input to yards, feet, and inches are of type unsigned int and initialized with zero.
The statement that computes the whole number of yards from the input value is as follows:
The cast discards the fractional part of the value in length and stores the integral result in yards. You could omit the explicit cast here and leave it to the compiler to take care of, but it’s always better to write an explicit cast in such cases. If you don’t, it’s not obvious that you realized the need for the conversion and the potential loss of data. Many compilers will then issue a warning as well.
You obtain the number of whole feet with this statement:
Subtracting yards from length produces the fraction of a yard in the length as a double value. The compiler will arrange for the value in yards to be converted to type double for the subtraction. The value of feet_per_yard will then be converted to double to allow the multiplication to take place, and finally the explicit cast converts the result from type double to type unsigned int.
The final part of the calculation obtains the residual number of whole inches:
The explicit cast applies to the total number of inches in length, which results from the product of length, feet_per_yard, and inches_per_foot. Because length is type double, both const values will be converted implicitly to type double to allow the product to be calculated. The remainder after dividing the integral number of inches in length by the number of inches in a foot is the number of residual inches.
Old-Style Casts
Prior to the introduction of static_cast<> into C++ around 1998—so a very, very long time ago—an explicit cast of the result of an expression was written like this:
The result of expression is cast to the type between the parentheses. For example, the statement to calculate inches in the previous example could be written like this:
This type of cast is a remnant of the C language and is therefore also referred to as a C-style cast. There are several kinds of casts in C++ that are now differentiated, but the old-style casting syntax covers them all. Because of this, code using the old-style casts is more prone to errors. It isn’t always clear what you intended, and you may not get the result you expected. Therefore:
Tip
You’ll still see old-style casting used because it’s still part of the language, but we strongly recommend that you use only the new casts in your code. One should never use C-style casts in C++ code anymore. Period. That is why this is also the last time that we mention this syntax in this book….
Finding the Limits
You have seen typical examples of the upper and lower limits for various types. The limits Standard Library header makes this information available for all the fundamental data types so you can access this for your compiler. Let’s look at an example. To display the maximum value you can store in a variable of type double, you could write this:
The expression std::numeric_limits<double>::max() produces the value you want. By putting different type names between the angled brackets, you can obtain the maximum values for other data types. You can also replace max() with min() to get the minimum value that can be stored, but the meaning of minimum is different for integer and floating-point types. For an integer type, min() results in the true minimum, which will be a negative number for a signed integer type. For a floating-point type, min() returns the minimum positive value that can be stored.
Caution
std::numeric_limits<double>::min() typically equals 2.225e-308, an extremely tiny positive number. So, for floating-point types, min() does not give you the complement of max(). To get the lowest negative value a type can represent, you should use lowest() instead. For instance, std::numeric_limits<double>::lowest() equals -1.798e+308, a hugely negative number. For integer types, min() and lowest() always evaluate to the same number.
The following program will display the maximums and minimums for some of the numerical data types:
You can easily extend this to include unsigned integer types and types that store characters. On our test system, the results of running the program are as follows:
Finding Other Properties of Fundamental Types
You can retrieve many other items of information about various types. The number of binary digits, or bits, for example, is returned by this expression:
type_name is the type in which you’re interested. For floating-point types, you’ll get the number of bits in the mantissa. For signed integer types, you’ll get the number of bits in the value, that is, excluding the sign bit. You can also find out what the range of the exponent component of floating-point values is, whether a type is signed or not, and so on. You can consult a Standard Library reference for the complete list.
Before we move on, there are two more numeric_limits<> functions we still want to introduce. We promised you earlier that we would. To obtain the special floating-point values for infinity and not-a-number (NaN), you should use expressions of the following form:
None of these expressions would compile for integer types, nor would they compile in the unlikely event that the floating-point types that your compiler uses do not support these special values. Besides quiet_NaN(), there’s a function called signaling_NaN()—and not loud_NaN() or noisy_NaN(). The difference between the two is outside the scope of this brief introduction, though: if you’re interested, you can always consult your Standard Library documentation.
Working with Character Variables
Variables of type char are used primarily to store a code for a single character and occupy 1 byte. The C++ standard doesn’t specify the character encoding to be used for the basic character set, so in principle this is down to the particular compiler, but it’s usually ASCII.
You define variables of type char in the same way as variables of the other types that you’ve seen. Here’s an example:
You can initialize a variable of type char with a character literal between single quotes or by an integer. An integer initializer must be within the range of type char—remember, it depends on the compiler whether it is a signed or unsigned type. Of course, you can specify a character as one of the escape sequences you saw in Chapter 1.
There are also escape sequences that specify a character by its code expressed as either an octal or a hexadecimal value. The escape sequence for an octal character code is one to three octal digits preceded by a backslash. The escape sequence for a hexadecimal character code is one or more hexadecimal digits preceded by \x. You write either form between single quotes when you want to define a character literal. For example, the letter 'A' could be written as hexadecimal '\x41' in ASCII. Obviously, you could write codes that won’t fit within a single byte, in which case the result is implementation defined.
Variables of type char are numeric; after all, they store integer codes that represent characters. They can therefore participate in arithmetic expressions , just like variables of type int or long. Here’s an example:
When you write a char variable to cout, it is output as a character, not as an integer. If you want to see it as a numerical value, you can cast it to another integer type. Here’s an example:
This produces the following output:
When you use >> to read from a stream into a variable of type char, the first nonwhitespace character will be stored. This means you can’t read whitespace characters in this way; they’re simply ignored. Further, you can’t read a numerical value into a variable of type char; if you try, the character code for the first digit will be stored.
Working with Unicode Characters
ASCII is generally adequate for national language character sets that use Latin characters. However, if you want to work with characters for multiple languages simultaneously or if you want to handle character sets for many non-English languages, 256 character codes doesn’t go nearly far enough, and Unicode is the answer. You can refer to Chapter 1 for a brief introduction on Unicode and character encodings.
Type wchar_t is a fundamental type that can store all members of the largest extended character set that’s supported by an implementation. The type name derives from wide characters because the character is “wider” than the usual single-byte character. By contrast, type char is referred to as “narrow” because of the limited range of character codes that are available.
You define wide-character literals in a similar way to literals of type char, but you prefix them with L. Here’s an example:
This defines wch as type wchar_t and initializes it to the wide-character representation for Z.
Your keyboard may not have keys for representing other national language characters, but you can still create them using hexadecimal notation. Here’s an example:
The value between the single quotes is an escape sequence that specifies the hexadecimal representation of the character code. The backslash indicates the start of the escape sequence, and x or X after the backslash signifies that the code is hexadecimal.
Type wchar_t does not handle international character sets very well. It’s much better to use type char16_t, which stores characters encoded as UTF-16, or char32_t, which stores UTF-32 encoded characters. Here’s an example of defining a variable of type char16_t:
The lowercase u prefix to the literals indicates that they are UTF-16. You prefix UTF-32 literals with uppercase U. Here’s an example:
Of course, if your editor and compiler have the capability to accept and display the characters, you can define cyr like this:
The Standard Library provides standard input and output streams wcin and wcout for reading and writing characters of type wchar_t, but there is no provision with the library for handling char16_t and char32_t character data.
Caution
You should not mix output operations on wcout with output operations on cout . The first output operation on either stream sets an orientation for the standard output stream that is either narrow or wide, depending on whether the operation is to cout or wcout. The orientation will carry forward to subsequent output operations for either cout or wcout.
The auto Keyword
You use the auto keyword to indicate that the compiler should deduce the type. Here are some examples:
The compiler will deduce the types for m, n, and pi from the initial values you supply. You can use functional or assignment notation with auto for the initial value as well:
Having said that, this is not really how the auto keyword is intended to be used. Typically, when defining variables of fundamental types, you might as well specify the type explicitly so you know for sure what it is. You’ll meet the auto keyword again later in the book where it is more appropriately and much more usefully applied.
Caution
You need to be careful when using braced initializers with the auto keyword. For example, suppose you write this (notice the equal sign!):
Then the type deduced for m will not be int, but instead will be std::initializer_list<int>. To give you some context, this is the same type you would get if you’d use a list of elements between the braces:
You will see later that such lists are typically used to specify the initial values of containers such as std::vector<>. To make matters worse, the type deduction rules have changed in C++17. If you are using an older compiler, the type the compiler deduces in place of auto may not at all be what you’d expect in many more cases. Here’s an overview:
To summarize, if your compiler properly supports C++17, you can use braced initialization to initialize any variable with a single value, provided you do not combine it with an assignment. This also is the guideline we’ll follow in this book. If your compiler is not fully up-to-date yet, however, you should simply never use braced initializers with auto. Instead, either explicitly state the type or use assignment or functional notation.
Summary
Constants of any kind are called literals. All literals have a type.
You can define integer literals as decimal, hexadecimal, octal, or binary values.
A floating-point literal must contain a decimal point or an exponent or both. If there is neither, you have specified an integer.
The fundamental types that store integers are short, int, long, and long long. These store signed integers, but you can also use the type modifier unsigned preceding any of these type names to produce a type that occupies the same number of bytes but stores unsigned integers.
The floating-point data types are float, double, and long double.
Uninitilized variables generally contain garbage values. Variables may be given initial values when they’re defined, and it’s good programming practice to do so. A braced initializer is the preferred way of specifying initial values.
A variable of type char can store a single character and occupies one byte. Type char may be signed or unsigned, depending on your compiler. You can also use variables of the types signed char and unsigned char to store integers. Types char, signed char, and unsigned char are different types.
Type wchar_t stores a wide character and occupies either two or four bytes, depending on your compiler. Types char16_t and char32_t may be better for handling Unicode characters in a cross-platform manner.
You can fix the value of a variable by using the const modifier. The compiler will check for any attempts within the program source file to modify a variable defined as const.
The four main mathematic operations correspond to the binary +, -, *, and / operators. For integers, the modulus operator % gives you the remainder after integer division.
The ++ and -- operators are special shorthand for adding or subtracting one from a numeric variable. Both exist in postfix and prefix forms.
You can mix different types of variables and constants in an expression. The compiler will arrange for one operand in a binary operation to be automatically converted to the type of the other operand when they differ.
The compiler will automatically convert the type of the result of an expression on the right of an assignment to the type of the variable on the left where these are different. This can cause loss of information when the left-side type isn’t able to contain the same information as the right-side type—double converted to int, for example, or long converted to short.
You can explicitly convert a value of one type to another using the static_cast<>() operator.
Exercises
Exercise 2-1. Write a program that will compute the area of a circle. The program should prompt for the radius of the circle to be entered from the keyboard, calculate the area using the formula area = pi * radius * radius, and then display the result.
Exercise 2-2. Using your solution for Exercise 2-1, improve the code so that the user can control the precision of the output by entering the number of digits required. To really show off how accurate floating-point numbers can be, you can perhaps switch to double-precision floating-point arithmetic as well. You’ll need a more precise approximation of π. 3.141592653589793238 will do fine.
Exercise 2-3. Create a program that converts inches to feet and inches. In case you’re unfamiliar with imperial units: 1 foot equals 12 inches. An input of 77 inches, for instance, should thus produce an output of 6 feet and 5 inches. Prompt the user to enter an integer value corresponding to the number of inches and then make the conversion and output the result.
Exercise 2-4. For your birthday you’ve been given a long tape measure and an instrument that measures angles (the angle between the horizontal and a line to the top of a tree, for instance). If you know the distance, d, you are from a tree, and the height, h, of your eye when peering into your angle-measuring device, you can calculate the height of the tree with the formula h + d*tan(angle). Create a program to read h in inches, d in feet and inches, and angle in degrees from the keyboard, and output the height of the tree in feet.
Note There is no need to chop down any trees to verify the accuracy of your program. Just check the solutions on the Apress website!
Exercise 2-5. Your body mass index (BMI) is your weight, w, in kilograms divided by the square of your height, h, in meters (w/(h*h)). Write a program to calculate the BMI from a weight entered in pounds and a height entered in feet and inches. A kilogram is 2.2 pounds, and a foot is 0.3048 meters.
Exercise 2-6. Here’s an extra exercise for puzzle fans. Write a program that will prompt the user to enter two different positive integers. Identify in the output the value of the larger integer and the value of the smaller integer. Using the decision-making facilities of Chapter 5, this would be like stealing a piece of cake from a baby while walking in the park. What makes this a brain teaser, though, is that this can be done solely with the operators you’ve learned about in this chapter!
