Decision-making is fundamental to any kind of computer programming. It’s one of the things that differentiates a computer from a calculator. It means altering the sequence of execution depending on the result of a comparison. In this chapter, you’ll explore how to make choices and decisions. This will allow you to validate program input and write programs that can adapt their actions depending on the input data. Your programs will be able to handle problems where logic is fundamental to the solution.
How to compare data values
How to alter the sequence of program execution based on the result of a comparison
What logical operators and expressions are and how you apply them
How to deal with multiple-choice situations
Comparing Data Values
To make decisions, you need a mechanism for comparing things, and there are several kinds of comparisons. For instance, a decision such as “If the traffic signal is red, stop the car” involves a comparison for equality. You compare the color of the signal with a reference color, red, and if they are equal, you stop the car. On the other hand, a decision such as “If the speed of the car exceeds the limit, slow down” involves a different relationship. Here you check whether the speed of the car is greater than the current speed limit. Both of these comparisons are similar in that they result in one of two values: they are either true or false. This is precisely how comparisons work in C++.
Relational Operators
Operator | Meaning |
|---|---|
< | Less than |
<= | Less than or equal to |
> | Greater than |
>= | Greater than or equal to |
== | Equal to |
!= | Not equal to |
Caution
The equal-to operator, ==, has two successive equal signs . It’s a common mistake to use one equal sign instead of two to compare for equality. This will not necessarily result in a warning message from the compiler because the expression may be valid but just not what you intended, so you need to take particular care to avoid this error.
Each of these operators compares two values and results in a value of type bool. There are only two possible bool values, true and false. true and false are keywords and are literals of type bool. They are sometimes called Boolean literals (after George Boole, the father of Boolean algebra).
You create variables of type bool just like other fundamental types. Here’s an example:
This defines the variable isValid as type bool with an initial value of true. If you initialize a bool variable using empty braces, {}, its initial value is false:
While explicitly using {false} here could arguably improve the readability of your code, it is good to remember that where numeric variables are initialized to zero, for instance, when using {}, Boolean variables will be initialized to false .
Applying the Comparison Operators
You can see how comparisons work by looking at a few examples. Suppose you have integer variables i and j, with values 10 and –5, respectively. Consider the following expressions :
All of these expressions evaluate to true. Note that in the last expression, the addition, j + 15, executes first because + has a higher precedence than <=.
You could store the result of any of these expressions in a variable of type bool. Here’s an example:
If i is greater than j, true is stored in isValid; otherwise, false is stored. You can compare values stored in variables of character types, too. Assume that you define the following variables:
You can write comparisons using these variables:
Here you are comparing code values (recall from Chapter 1 that characters are mapped to integral codes using standard encoding schemes such as ASCII and Unicode). The first expression checks whether the value of first, which is 'A', is less than the value of last, which is 'Z'. This is always true. The result of the second expression is false because the code value for 'E' is greater than the value of first. The last expression is true, because 'A' is definitely not equal to 'Z'.
You can output bool values just as easily as any other type. Here’s an example that shows how they look by default:
Here’s an example of output from this program:
The prompting for input and reading of characters from the keyboard is standard stuff that you have seen before. Note that the parentheses around the comparison expressions in the output statement are necessary here. If you omit them, the compiler outputs an error message (to understand why you should review the operator precedence rules from the beginning of the previous chapter). The expressions compare the first and second characters that the user entered. From the output you can see that the value true is displayed as 1, and the value false is displayed as 0. These are the default representations for true and false. You can make bool values output as true and false using the std::boolalpha manipulator. Just add this statement somewhere before the last four lines of the main() function:
If you compile and run the example again, you get bool values displayed as true or false. To return output of bool values to the default setting, insert the std::noboolalpha manipulator into the stream.
Comparing Floating-Point Values
Of course, you can also compare floating-point values . Let’s consider some slightly more complicated numerical comparisons. First, define variables with the following statements:
Now consider the following logical expressions:
The comparison operators are all of lower precedence than the arithmetic operators, so none of the parentheses are strictly necessary, but they do help make the expressions clearer. The first comparison evaluates to true because y has a very small negative value (–0.000000000025), which is greater than –1. The second comparison results in false because the expression 10 - i has the value 20, which is the same as j. The third expression is true because 3 + y is slightly less than 3.
You can use relational operators to compare values of any of the fundamental types. When you learn about classes, you’ll see how you can arrange for the comparison operators to work with types that you define, too. All you need now is a way to use the result of a comparison to modify the behavior of a program. Let’s look into that immediately.
The if Statement
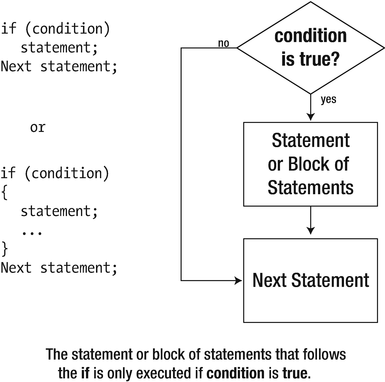
Logic of the simple if statement
Here is an example of an if statement that tests the value of a char variable, letter :
If letter has the value 'A', the condition is true, and these statements produce the following output:
If the value of letter is not equal to 'A', only the second line appears in the output. You put the condition to be tested between parentheses immediately following the keyword, if. We adopt the convention to add a space between the if and the parentheses (to differentiate visually from function calls), but this is not required. As usual, the compiler will ignore all whitespace, so the following are equally valid ways to write the test:
The statement following the if is indented to indicate that it executes only as a result of the condition being true. The indentation is not necessary for the program to compile, but it does help you recognize the relationship between the if condition and the statement that depends on it. Sometimes, you will see simple if statements written on a single line, like this:
Caution
Never put a semicolon (;) directly after the condition of the if statement. Unfortunately, doing so compiles without errors (at best, the compiler will issue a warning), but it does not mean at all what was intended:
The semicolon on the first line results in a so-called empty statement or null statement . Superfluous semicolons, and therefore empty statements, are allowed to appear pretty much anywhere within a series of statements. The following, for instance, is legal C++:
Usually, such empty statements have no effect at all. But when added immediately after the condition of an if, it binds the statement that is executed if the condition evaluates to true. In other words, writing a semicolon after the if (letter == 'A') test has the same effect as writing this:
So this states, if letter equals 'A', then do nothing. But what is worse is that the second line is always executed, unconditionally, even if letter is different from 'A'—precisely what the if statement intended to prevent. Therefore, take care to never put a semicolon directly after a conditional test because it essentially nullifies the test!
You could extend the code fragment to change the value of letter if it contains the value 'A'.
All the statements in the block will be executed when the if condition is true. Without the braces, only the first statement would be the subject of the if, and the statement assigning the value 'a' to letter would always be executed. Of course, each of the statements in the block is terminated by a semicolon. No semicolon is necessary, though, after the closing brace of the block. You can have as many statements as you like within the block; you can even have nested blocks. If and when letter has the value 'A', both statements within the block will be executed, so its value will be changed to 'a' after the same message as before is displayed. Neither of these statements executes if the condition is false. The statement following the block always executes.
If you cast true to an integer type, the result will be 1; casting false to an integer results in 0. Conversely, you can also convert numerical values to type bool. Zero converts to false, and any nonzero value converts to true. When you have a numerical value where a bool value is expected, the compiler will insert an implicit conversion to convert the numerical value to type bool. This is useful in decision-making code.
Let’s try an if statement for real. This program will range check the value of an integer entered from the keyboard :
The output depends on the value that you enter. For a value between 50 and 100, the output will be something like the following:
Outside the range 50 to 100, a message indicating that the value is invalid will precede the output showing the value. If it is less than 50, for instance, the output will be as follows:
After prompting for and reading a value, the first if statement checks whether the value entered is different from zero:
Recall that any number is converted to true, except 0 (zero)—which is converted to false. So, value always converts to true, except if the number you entered is zero. You will often find such a test written like this, but if you prefer, you can easily make the test for zero more explicit as follows:
The second if statement then checks if your input is less than 50:
The output statement is executed only when the if condition is true, which is when value is less than 50. The next if statement checks the upper limit in essentially the same way and outputs a message when it is exceeded. Finally, the last output statement is always executed, and this outputs the value. Of course, checking for the upper limit being exceeded when the value is below the lower limit is superfluous. You could arrange for the program to end immediately if the value entered is below the lower limit, like this:
You could do the same with the if statement that checks the upper limit. You can have as many return statements in a function as you need.
Of course, if you conditionally end the program like that, the code after both if statements is no longer executed anymore. That is, if the user enters an invalid number and one of these return statements is executed, then the last line of the program will no longer be reached. To refresh your memory, this line was as follows:
Later this chapter, we will see other means to avoid the upper limit test if value was already found to be below the lower limit—means that do not involve ending the program.
Nested if Statements
The statement that executes when the condition in an if statement is true can itself be an if statement. This arrangement is called a nested if . The condition of the inner if is tested only if the condition for the outer if is true. An if that is nested inside another can also contain a nested if. You can nest ifs to whatever depth you require. We'll demonstrate the nested if with an example that tests whether a character entered is alphabetic:
Here’s some typical output:
After creating the char variable letter with initial value zero, the program prompts you to enter a letter. The if statement that follows checks whether the character entered is 'A' or larger. If letter is greater than or equal to 'A', the nested if that checks for the input being 'Z' or less executes. If it is 'Z' or less, you conclude that it is an uppercase letter and display a message. You are done at this point, so you execute a return statement to end the program.
The next if, using essentially the same mechanism as the first, checks whether the character entered is lowercase , displays a message, and returns. You probably noticed that the test for a lowercase character contains only one pair of braces, whereas the uppercase test has two. The code block between the braces belongs to the inner if here. In fact, both sets of statements work as they should—remember that if (condition) {...} is effectively a single statement and does not need to be enclosed within more braces. However, the extra braces do make the code clearer, so it’s a good idea to use them.
The output statement following the last if block executes only when the character entered is not a letter, and it displays a message to that effect . You can see that the relationship between the nested ifs and the output statement is much easier to follow because of the indentation. Indentation is generally used to provide visual cues to the logic of a program.
This program illustrates how a nested if works, but it is not a good way to test for characters. Using the Standard Library, you can write the program so that it works independently of the character coding. We’ll explore how that works in the next subsection.
Character Classification and Conversion
The letters A to Z are represented by a set of codes where the code for 'A' is the minimum and the code for 'Z' is the maximum.
The codes for the uppercase letters are contiguous, so no nonalphabetic characters lie between the codes for 'A' and 'Z'.
All uppercase letters in the alphabet fall within the range A to Z.
While the first two assumptions will hold for any character encoding used in practice today, the third is definitely not true for many languages. The Greek alphabet, for instance, knows uppercase letters such as Δ, Θ, and Π; the Russian one contains Ж, Ф, and Щ; and even Latin-based languages such as French often use capital letters such as É and Ç whose encodings won’t lie at all between 'A' and 'Z'. It is therefore not a good idea to build these kinds of assumptions into your code because it limits the portability of your program. Never assume that your program will be used only by fellow Anglophones!
To avoid making such assumptions in your code, the C and C++ Standard Libraries offer the concept of locales. A locale is a set of parameters that defines the user’s language and regional preferences, including the national or cultural character set and the formatting rules for currency and dates. A complete coverage of this topic is far beyond the scope of this book, though. We only cover the character classification functions provided by the cctype header, listed in Table 4-2.
Functions for Classifying Characters Provided by the cctype Header
Function | Operation |
|---|---|
isupper(c) | Tests whether c is an uppercase letter, by default 'A' to 'Z'. |
islower(c) | Tests whether c is a lowercase letter, by default 'a' to 'z'. |
isalpha(c) | Tests whether c is an uppercase or lowercase letter (or any alphabetic character that is neither uppercase nor lowercase, should the locale’s alphabet contain such characters). |
isdigit(c) | Tests whether c is a digit, '0' to '9'. |
isxdigit(c) | Tests whether c is a hexadecimal digit, either '0' to '9', 'a' to 'f', or 'A' to 'F'. |
isalnum(c) | Tests whether c is an alphanumeric character; same as isalpha(c) || isdigit(c). |
isspace(c) | Tests whether c is whitespace, by default a space (' '), newline ('\n'), carriage return ('\r'), form feed ('\f'), or horizontal ('\t') or vertical tab ('\v'). |
isblank(c) | Tests whether c is a space character used to separate words within a line of text. By default either a space (' ') or a horizontal tab ('\t'). |
ispunct(c) | Tests whether c is a punctuation character. By default, this will be either a space or one of the following: _ { } [ ] # ( ) < > % : ; . ? * + - / ^ & | ∼ ! = , \ " ' |
isprint(c) | Tests whether c is a printable character, which includes uppercase or lowercase letters, digits, punctuation characters, and spaces. |
iscntrl(c) | Tests whether c is a control character, which is the opposite of a printable character. |
isgraph(c) | Tests whether c has a graphical representation, which is true for any printable character other than a space . |
Each of these functions returns a value of type int. The value will be nonzero (true) if the character is of the type being tested for, and 0 (false) if it isn’t. You may be wondering why these functions don’t return a bool value, which would make much more sense. The reason they don’t return a bool value is that they originate from the C Standard Library and predate type bool in C++.
You could use cctype’s character classification functions to implement Ex4_03 without any hard-coded assumptions about either the character set or its encoding. The character codes in different environments are always taken care of by the Standard Library functions. An additional advantage is that these functions also make the code simpler and easier to read:
As cctype is part of the C++ Standard Library, it defines all its functions inside the std namespace. You therefore normally should prefix their names with std::. You’ll find the adjusted program under the name Ex4_03A.cpp.
Functions for Converting Characters Provided by the cctype Header
Function | Operation |
|---|---|
tolower(c) | If c is uppercase, the lowercase equivalent is returned; otherwise, c is returned. |
toupper(c) | If c is lowercase, the uppercase equivalent is returned; otherwise, c is returned. |
Note
All standard character classification and conversion functions except for isdigit() and isxdigit() operate according to the rules of the current locale. All examples given in Table 4-2 are for the default, so-called "C" locale, which is a set of preferences similar to those used by English-speaking Americans. The C++ Standard Library offers an extensive library for working with other locales and character sets. You can use these to develop applications that work correctly irrespective of the user’s language and regional conventions. This topic is a bit too advanced for this book, though. Consult a Standard Library reference for more details.
The if-else Statement
The if statement that you have been using executes a statement or block of statements if the condition specified is true. Program execution then continues with the next statement in sequence. Of course, you may want to execute one block of statements when the condition is true and another set when the condition is false. An extension of the if statement called an if-else statement allows this.
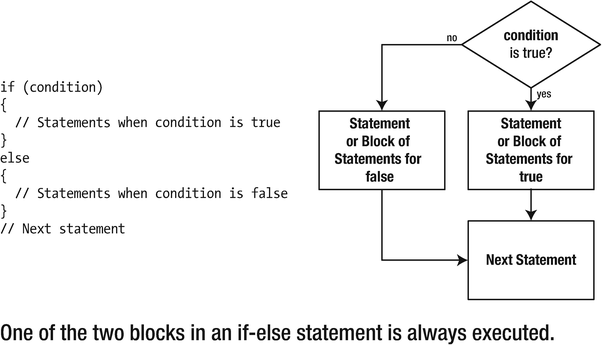
The if-else statement logic
The flowchart in Figure 4-2 shows the sequence in which statements execute, depending on whether the if condition is true or false. You can always use a block of statements wherever you can put a single statement. This allows any number of statements to be executed for each option in an if-else statement.
You could write an if-else statement that would report whether the character stored in the char variable letter was alphanumeric :
This uses the isalnum() function from the cctype header you saw earlier. If letter contains a letter or a digit, isalnum() returns a positive integer. This will be implicitly converted to a bool value, which will be true, so the first message is displayed. If letter contains other than a letter or a digit, isalnum() returns 0, which converts to false so the output statement after else executes. The braces are again not mandatory here because they contain single statements, but it’s clearer if you put them in. The indentation in the blocks is a visible indicator of the relationship between various statements. You can clearly see which statement is executed for a true result and which is executed for false. You should always indent the statements in your programs to show their logical structure.
Here’s an example of using if-else with a numerical value :
Here’s an example of output from this program:
After reading the input into number, the program tests this value in the if condition. This is an expression that produces the remainder that results from dividing number by 2. The remainder will be 1 if number is odd, or 0 if it even, and these values convert to true and false, respectively. Thus, if the remainder is 1, the if condition is true, and the statement in the block immediately following the if executes. If the remainder is 0, the if condition is false, so the statement in the block following the else keyword executes.
You could specify the if condition as number % 2 == 0, in which case the sequence of blocks would need to be reversed because this expression evaluates to true when number is even.
Nested if-else Statements
You have already seen that you can nest if statements within if statements. You have no doubt anticipated that you can also nest if-else statements within ifs, ifs within if-else statements, and if-else statements within other if-else statements. This provides you with plenty of versatility (and considerable room for confusion), so let’s look at a few examples. Taking the first case, an example of an if-else nested within an if might look like the following:
This would be better written with braces, but it’s easier to make the point we want to make without. coffee and donuts are variables of type char that can have the value 'y' or 'n'. The test for donuts executes only if the result of the test for coffee is true, so the messages reflect the correct situation in each case. The else belongs to the if that tests for donuts. However, it is easy to get this confused.
If you write much the same thing but with incorrect indentation, you can be trapped into the wrong conclusion about what happens here:
The indentation now misleadingly suggests that this is an if nested within an if-else, which is not the case. The first message is correct, but the output as a consequence of the else executing is quite wrong. This statement executes only if the test for coffee is true, because the else belongs to the test for donuts, not the test for coffee. This mistake is easy to see here, but with larger and more complicated if structures, you need to keep in mind the following rule about which if owns which else:
Caution
An else always belongs to the nearest preceding if that’s not already spoken for by another else. The potential for confusion here is known as the dangling else problem .
Braces will always make the situation clearer:
Now it’s absolutely clear. The else definitely belongs to the if that is checking for donuts.
Understanding Nested ifs
Now that you know the rules, understanding an if nested within an if-else should be easy:
Notice the formatting of the code here. When an else block is another if, writing else if on one line is an accepted convention. The braces enclosing the test for donuts are essential. Without them the else would belong to the if that’s looking out for donuts. In this kind of situation, it is easy to forget to include the braces and thus create an error that may be hard to find. A program with this kind of error compiles without a problem, as the code is correct. It may even produce the right results some of the time. If you removed the braces in this example, you’d get the right results only as long as coffee and donuts were both 'y' so that the check for tea wouldn’t execute.
Nesting if-else statements in other if-else statements can get very messy, even with just one level of nesting. Let’s beat the coffee and donuts analysis to death by using it again:
The logic here doesn’t look quite so obvious, even with the correct indentation. Braces aren’t necessary, as the rule you saw earlier will verify, but it would look much clearer if you included them:
There are much better ways of dealing with this kind of logic. If you put enough nested ifs together, you can almost guarantee a mistake somewhere. The next section will help to simplify things.
Logical Operators
As you have seen, using ifs where you have two or more related conditions can be cumbersome. You have tried your iffy talents on looking for coffee and donuts, but in practice, you may want to check much more complex conditions. For instance, you could be searching a personnel file for someone who is older than 21, younger than 35, is female, has a bachelor’s or master’s degree, is unmarried, and speaks Hindi or Urdu. Defining a test for this could involve the mother of all ifs.
Logical Operators
Operator | Description |
|---|---|
&& | Logical AND |
|| | Logical OR |
! | Logical negation (NOT) |
The first two, && and ||, are binary operators that combine two operands of type bool and produce a result of type bool. The third operator, !, is unary, so it applies to a single operand of type bool and produces a bool result. In the following pages we’ll explain first how each of these is used; then we’ll demonstrate them in an example. Finally, we’ll compare these logical operators with the bitwise operators you learned about earlier.
Logical AND
You use the AND operator , &&, where you have two conditions that must both be true for a true result. For example, you want to be rich and healthy. Earlier, to determine whether a character was an uppercase letter, the value had to be both greater than or equal to 'A' and less than or equal to 'Z'. The && operator only produces a true result if both operands are true. If either or both operands are false, then the result is false. Here’s how you could test a char variable, letter, for an uppercase letter using the && operator:
The output statement executes only if both of the conditions combined by && are true . No parentheses are necessary in the expression because the precedence of the comparison operators is higher than that of &&. As usual, you’re free to put parentheses in if you want. You could write the statement as follows:
Now there’s no doubt that the comparisons will be evaluated first. Still, most experienced programmers probably wouldn’t put these extra parentheses here.
Logical OR
The OR operator , ||, applies when you want a true result when either or both of the operands are true. The result is false only when both operands are false.
For example, you might be considered creditworthy enough for a bank loan if your income was at least $100,000 a year or if you had $1,000,000 in cash. This could be tested like this:
The response emerges when either or both of the conditions are true. (A better response might be “Why do you want to borrow?” It’s strange how banks will only lend you money when you don’t need it.)
Notice also that we’ve used digit separators to increase the readability of the integer literals: it is far more obvious that 1'000'000.00 equals one million than that 1000000.00 does. Would you even spot the difference between 100000.00 and 1000000.00 without the separators? (Should the bank ever make mistakes filling in either one of these numbers, you’d surely want it to be in your favor!)
Logical Negation
The third logical operator , !, applies to single bool operand and inverts its value. So, if the value of a bool variable, test, is true, then !test is false; if test is false, then !test results in the value true.
Like all logical operators, you can apply logical negation to any expressions that evaluate to true or false. Operands can be anything from a single bool variable to a complex combination of comparisons and bool variables. For example, suppose x has the value 10. Then the expression !(x > 5) evaluates to false because x > 5 is true. Of course, in that particular case, you may be better off simply writing x <= 5. The latter expression is equivalent, but because it does not contain the negation, it is probably easier to read.
Caution
Let foo, bar, and xyzzy be variables (or any expressions if you will) of type bool. Then beginning C++ programmers, such as yourself, often write statements like this:
While technically correct, it is generally accepted that you should favor the following equivalent yet shorter if statements instead:
Combining Logical Operators
You can combine conditional expressions and logical operators to any degree to which you feel comfortable. This example implements a questionnaire to decide whether a person is a good loan risk:
Here’s some sample output :
The interesting bit is the if statement that determines whether a loan will be granted. The if condition is as follows:
This condition requires that the applicant’s age be at least 21 and that either their income is larger than $25,000 or their account balance is greater than $100,000. The parentheses around the expression (income > 25'000 || balance > 100'000) are necessary to ensure that the result of ORing the income and balance conditions together is ANDed with the result of the age test. Without the parentheses, the age test would be ANDed with the income test, and the result would be ORed with the balance test. This is because && has a higher precedence than ||, as you can see from the table in Chapter 3. Without the parentheses, the condition would have allowed an 8-year-old with a balance over $100,000 to get a loan. That’s not what was intended. Banks never lend to minors or mynahs.
If the if condition is true, the block of statements that determine the loan amount executes. The loan variable is defined within this block and therefore ceases to exist at the end of the block. The if statement within the block determines whether twice the declared income is less than half the account balance. If it is, the loan is twice the income; otherwise, it is half the account balance. This ensures the loan corresponds to the least amount according to the rules.
Tip
When combining logical operators, it is recommended to always add parentheses to clarify the code. Suppose for argument’s sake that the bank’s condition for allowing a loan was as follows:
That is, for younger clients, the decision depends entirely on their yearly salary—yes, even toddlers get a loan, as long as they can submit proof of sufficient income, of course—whereas more mature clients must already have sufficient savings. Then you could also write this condition as follows:
While both expressions are perfectly equivalent, you’ll surely agree that the one with parentheses is much easier to read than the one without. When combining && and ||, it is therefore recommended to always clarify the meaning of the logical expression by adding parentheses, even when it strictly speaking is not necessary.
Logical Operators on Integer Operands
In a way, logical operators can be—and actually fairly often are—applied to integer operands instead of Boolean operands. For instance, earlier you saw that the following can be used to test whether an int variable value differs from zero:
Equally frequently, you will encounter a test of the following form:
Here, logical negation is applied to an integer operand—not to a Boolean operand as usual. Similarly, suppose you have defined two int variables, value1 and value2; then you could write the following:
Because these expressions are so short, they are popular among C++ programmers. Typical use cases of such patterns occur if these integer values represent, for instance, the number of elements in a collection of objects. It is therefore important that you understand how they work: every numeric operand to a logical operator in expressions such as these is first converted to a bool using the familiar rule: zero converts to false, and every other number converts to true. Even if all operands are integers, the logical expression still evaluates to a bool, though.
Logical Operators vs. Bitwise Operators
It’s important not to confuse the logical operators &&, ||, and ! that apply to operands that are convertible to bool with the bitwise operators &, |, and ∼ that operate on the bits within integral operands.
From the previous subsection, you’ll remember that logical operators always evaluate to a value of type bool, even if their operands are integers. The converse is true for bitwise operators: they always evaluate to an integer number, even if both operands are of type bool. Nevertheless, because the integer result of a bitwise operator always converts back to a bool, it may often seem that logical and bitwise operators can be used interchangeably. The central test in Ex4_05 to test whether a loan is admissible, for instance, could in principle be written like this:
This will compile and have the same end result as before when && and || were still used. In short, what happens is that the bool values that result from the comparisons are converted to ints, which are then bitwise combined into a single int using the bitwise operators, after which this single int is again converted to a bool for the if statement. Confused? Don’t worry, it’s not really all that important. Such conversions back and forth between bool and integers are rarely a cause for concern.
What is important, though, is the second, more fundamental difference between the two sets of operators; namely, unlike bitwise operators , the binary logical operators are so-called short-circuit operators.
Short-Circuit Evaluation
Consider the following code snippet:
Quickly, is x = 2 the correct solution? Of course not, 2 is not less than 0! It does not even matter whether 2*2 + 632*2 equals 1268 or not (it does, actually…). Because the first operand of the AND operator is false already, the end result will be false as well. After all, false && true remains false; the only case where the AND operator evaluates to true is true && true.
Similarly, in the following snippet, it should be instantly clear that x = 2 is a correct solution:
Why? Because the first operand is true, you immediately know that the full OR expression will evaluate to true as well. There’s no need to even compute the second operand.
Naturally, a C++ compiler knows this as well. Therefore, if the first operand to a binary logical expression already determines the outcome, the compiler will make sure no time is wasted evaluating the second operand. This property of the logical operators && and || is called short-circuit evaluation . The bitwise operators & and |, on the other hand, do not short-circuit. For these operators, both operands are always evaluated.
If you need to test for multiple conditions that are glued together with logical operators, then you should put the cheapest ones to compute first. Our two examples in this section already illustrate this to a point, but of course this technique only really pays off if one of the operands is truly expensive to calculate.
Short-circuiting is more commonly utilized to prevent the evaluation of right-hand operands that would otherwise fail to evaluate—as in cause a fatal crash. This is done by putting other conditions first that short-circuit whenever the other operands would fail. As we will see later in this book, a popular application of this technique is to check that a pointer is not null before dereferencing it.
We will see several more examples of logical expressions that rely on short-circuit evaluation in later chapters. For now, just remember that the second operand of && is evaluated only after the first operand evaluates to true, and the second operand of || only after the first evaluates to false. For & and |, both operands are always evaluated.
And, oh yes, in case you were wondering, the correct solution for the equation earlier is x = -634.
Logical XOR
There is no counterpart of the bitwise XOR—short for eXclusive OR—operator, ^, among the logical operators. This is in part, no doubt, because short-circuiting this operator makes no sense (both operands must always be evaluated to know the correct outcome of this operator; perhaps take a second to think about this). Luckily, the XOR operator, like any of the bitwise operators, can simply be applied to Boolean operands as well. The following test, for instance, passes for most youngsters and millionaires. Adults with a normal bank balance will not pass the cut, though, and neither will teenage millionaires :
In other words, this test is equivalent to either one of the following combinations of logical operators:
Convincing yourself that these three if statements are indeed equivalent makes for a nice little exercise in Boolean algebra.
The Conditional Operator
The conditional operator is sometimes called the ternary operator because it involves three operands—the only operator to do so. It parallels the if-else statement, in that instead of selecting one of two statement blocks to execute depending on a condition, it selects the value of one of two expressions. Thus, the conditional operator enables you to choose between two values. Let’s consider an example.
Suppose you have two variables, a and b, and you want to assign the value of the greater of the two to a third variable, c. The following statement will do this:
The conditional operator has a logical expression as its first operand, in this case a > b. If this expression is true, the second operand—in this case a—is selected as the value resulting from the operation. If the first operand is false, the third operand—in this case b—is selected as the value. Thus, the result of the conditional expression is a if a is greater than b, and b otherwise. This value is stored in c. The assignment statement is equivalent to the if statement :
Of course, you can use the conditional operator to select the lower of two values. In the previous program, you used an if-else to decide the value of the loan; you could use this statement instead:
This produces the same result. The condition is 2*income < balance/2. If this evaluates to true, then the expression 2*income evaluates and produces the result of the operation. If the condition is false, the expression balance/2 produces the result of the operation.
You don’t need parentheses because the precedence of the conditional operator is lower than that of the other operators in this statement. Of course, if you think parentheses would make things clearer, you can include them:
The general form of the conditional operator, which is often represented by ?:, is as follows:
As usual, all whitespace before or after both the ? or the : is optional and ignored by the compiler. If condition evaluates to true, the result is the value of expression1; if it evaluates to false, the result is the value of expression2. If condition is an expression that results in a numerical value, then it is implicitly converted to type bool.
Note that only one of expression1 or expression2 will be evaluated. Similar to the short-circuiting evaluation of binary logical operands, this has significant implications for expressions such as the following:
Suppose both divisor and dividend are variables of type int. For integers, division by zero results in undefined behavior in C++. This means that, in the worst case, dividing an integer by zero may cause a fatal crash. If divisor equals zero in the previous expression, however, then (dividend / divisor) is not evaluated. If the condition to a conditional operator evaluates to false, the second operand is not evaluated at all. Instead, only the third operand is evaluated. In this case, this implies that the entire expression trivially evaluates to 0. That is a much better outcome indeed than a potential crash!
You can use the conditional operator to control output depending on the result of an expression or the value of a variable. You can vary a message by selecting one text string or another depending on a condition .
The output from this program might be as follows:
The only bit of interest is the output statement that is executed after the numbers of mice have been entered. The expression using the conditional operator evaluates to " mouse" if the value of mice is 1, or " mice" otherwise. This allows you to use the same output statement for any number of mice and select singular or plural as appropriate.
There are many other situations in which you can apply this sort of mechanism, such as when selecting between "is" and "are" or between "he" and "she" or indeed in any situation in which you have a binary choice. You can even combine two conditional operators to choose between three options. Here’s an example:
This statement outputs one of three messages, depending on the relative values of a and b. The second choice for the first conditional operator is the result of another conditional operator.
The switch Statement
You’re often faced with a multiple-choice situation in which you need to execute a particular set of statements from a number of choices (that is, more than two), depending on the value of an integer variable or expression. The switch statement enables you to select from multiple choices. The choices are identified by a set of fixed integer or enumeration values, and the selection of a particular choice is determined by the value of a given integer or enumeration constant.
The choices in a switch statement are called cases. A lottery where you win a prize depending on your number coming up is an example of where it might apply. You buy a numbered ticket, and if you’re lucky, you win a prize. For instance, if your ticket number is 147, you win first prize; if it’s 387, you can claim a second prize; and ticket 29 gets you a third prize; any other ticket number wins nothing. The switch statement to handle this situation would have four cases: one for each of the winning numbers, plus a “default” case for all the losing numbers. Here’s a switch statement that selects a message for a given ticket number :
The switch statement is harder to describe than to use. The selection of a particular case is determined by the value of the integer expression between the parentheses that follow the keyword switch. In this example, it is simply the integer variable ticket_number.
Note
You can only switch on values of integral (int, long, unsigned short, etc.), character (char, etc.), and enumeration types (see Chapter 2). Technically, switching on Boolean values is allowed as well, but instead of a switch on Booleans, you should just use if/else statements. Unlike some other programming languages, however, C++ does not allow you to create switch() statements with conditions and labels that contain expressions of any other type. A switch that branches on different string values, for instance, is not allowed (we’ll discuss strings in Chapter 7).
The possible choices in a switch statement appear in a block, and each choice is identified by a case value . A case value appears in a case label, which is of the following form:
It’s called a case label because it labels the statements or block of statements that it precedes. The statements that follow a particular case label execute if the value of the selection expression is the same as that of the case value. Each case value must be unique, but case values don’t need to be in any particular order, as the example demonstrates.
Each case value must be a constant expression , which is an expression that the compiler can evaluate at compile time. Case values are mostly either literals or const variables that are initialized with literals. Naturally, any case label must either be of the same type as the condition expression inside the preceding switch() or be convertible to that type.
The default label in the example identifies the default case, which is a catchall that is selected if none of the other cases is selected. If present, the default label does not have to be the last label. It often is, but it can in principle appear anywhere among the regular case labels. You also don’t have to specify a default case. If you don’t and none of the case values is selected, the switch does nothing.
The break statement that appears after each set of case statements is essential for the logic here. Executing a break statement breaks out of the switch and causes execution to continue with the statement following the closing brace. If you omit the break statement for a case, the statements for the following case will execute. Notice that we don’t need a break after the final case (usually the default case) because execution leaves the switch at this point anyway. It’s good programming style to include it, though, because it safeguards against accidentally falling through to another case that you might add to a switch later. switch, case, default, and break are all keywords.
This example demonstrates the switch statement :
After defining your options in the output statement and reading a selection number into the variable choice , the switch statement executes with the selection expression specified simply as choice in parentheses, immediately following the keyword switch. The possible choices in the switch are between braces and are each identified by a case label. If the value of choice corresponds with any of the case values, then the statements following that case label execute.
If the value of choice doesn’t correspond with any of the case values, the statements following the default label execute. If you hadn’t included a default case here and the value of choice was different from all the case values, then the switch would have done nothing, and the program would continue with the next statement after the switch—effectively executing return 0; because the end of main() has been reached.
You have only one statement plus a break statement for each case in this example, but in general you can have as many statements as you need following a case label, and you generally don’t need to enclose them between braces. The cases where you do need to add braces are discussed in one of the next sections.
As we said earlier, each of the case values must be a compile-time constant and must be unique. The reason that no two case values can be the same is that if they are, the compiler has no way of knowing which statements should be executed when that particular value comes up. However, different case values don’t need to have unique actions. Several case values can share the same action, as the following example shows:
Here is an example of some output :
The if condition first checks that you really do have a letter and not some other character using the std::isalpha() classification function from the Standard Library. The integer returned will be nonzero if the argument is alphabetic, and this will be implicitly converted to true, which causes the switch to be executed. The switch condition converts the value to lowercase using the Standard Library character conversion routine, tolower() ,and uses the result to select a case. Converting to lowercase avoids the need to have case labels for uppercase and lowercase letters. All of the cases that identify a vowel cause the same statements to be executed. You can see that you can just write each of the cases in a series, followed by the statements any of these cases is to select. If the input is not a vowel, it must be a consonant and the default case deals with this.
If isalpha() returns 0, which converts to false, the switch doesn’t execute because the else clause is selected; this outputs a message indicating that the character entered was not a letter.
In Ex4_08.cpp, we put all case labels with vowel values on a single line. This is not required. You are allowed to add line breaks (or any form of whitespace for that matter) in between the case labels as well. Here’s an example:
A break statement is not the only way to move control out of a switch statement. If the code following a case label contains a return statement, control instantly exits not only the switch statement but the surrounding function as well. So, in principle, you could rewrite the switch statement in Ex4_08 as follows:
With this particular variant, we also again illustrate that a default case is optional. If you enter a vowel, the output will reflect this, and the return statement in the switch statement will terminate the program. Note that after a return statement you should never put a break statement anymore. If you enter a consonant, the switch statement does nothing. None of these cases apply, and there is no default case. Execution therefore continues after the statement and outputs that you have in fact entered a consonant—remember, if you would’ve entered a vowel, the program would’ve terminated already because of the return statement.
The code for this variant is available as Ex4_08A. We created it to show a few points, though, not because it necessarily reflects good programming style. The use of a default case is surely recommended over continuing after a switch statement after none of the cases executed a return.
Fallthrough
The break statement at the end of each group of case statements transfers execution to the statement after the switch. You could demonstrate the essential nature of the break statements by removing them from the switch statements of earlier example Ex4_07 or Ex4_08 and seeing what happens. You’ll find that the code beneath the case label directly following the case without a break statement then gets executed as well. This phenomenon is called fallthrough because in a way we “fall through” into the next case.
More often than not, a missing break statement signals an oversight and therefore a bug. To illustrate this, let’s return to an earlier example—the one with the lottery numbers:
You’ll notice that this time , we have “accidentally” omitted the break statement after the first case. If you executed this switch statement now with ticket_number equal to 147, the output would be as follows:
Because ticket_number equals 147, the switch statement jumps to the corresponding case, and you win first prize. But because there is no break statement, execution simply goes on with the code underneath the next case label, and you win second prize as well—huzza! Clearly, this omission of break must be an accidental oversight. In fact, because more often than not fallthrough signals a bug, many compilers issue a warning if a nonempty switch case is not followed by either a break or a return statement. Empty switch cases, such as those used in Ex4_08 (to check for vowels), are common enough not to warrant a compiler warning.
Fallthrough does not always mean a mistake was made, though. It can at times be quite useful to purposely write a switch statement that employs fallthrough. Suppose that in our lottery multiple numbers win second and third prize (two and three numbers, respectively) and that one of the numbers winning third prize gets a special bonus prize. Then we could write this logic as follows:
The idea is that if your ticket_number equals 929, the outcome should be the following:
If your number is either 29 or 78, however, you’d only win third prize. The slight annoyance with these atypical cases (pun intended) is that compilers may issue a fallthrough warning, even though you know for a fact that this time it is not a mistake. And of course, as a self-respecting programmer, you want to compile all your programs free of warnings. You could always rewrite the code and duplicate the statement to output that you won third prize. But in general, duplication is something you’d like to avoid as well. So, what to do?
Luckily, C++17 adds a new language feature to signal to both the compiler and the person reading your code that you are intentionally using fallthrough: you can add a [[fallthrough]] statement in the same place where you would otherwise add a break statement:
For empty cases, such as the one for number 29, a [[fallthrough]] statement is allowed but not required. Compilers already do not issue warnings for this.
Statement Blocks and Variable Scope
A switch statement has its own block between braces that encloses the case statements. An if statement also often has braces enclosing the statements to be executed if the condition is true, and the else part may have such braces too. These statement blocks are no different from any other blocks when it comes to variable scope. Any variable declared within a block ceases to exist at the end of the block, so you cannot reference it outside the block.
For example, consider the following rather arbitrary calculation :
The output statement at the end causes a compiler error message because the savit variable is undefined at this point. Any variable defined within a block can be used only within that block, so if you want to access data that originates inside a block from outside it, you must define the variable storing that information in an outer block.
Variable definitions within a switch statement block must be reachable in the course of execution, and it must not be possible to bypass them by jumping to a case after the declaration and within the same scope; otherwise, the code will not compile. Most likely you don’t understand at all yet what we mean. It’ll be much easier to explain, though, by means of an example. The following code illustrates how illegal declarations can arise in a switch :
Only two of the variable definitions in this switch statement are legal: the ones for m and n. For a definition to be legal, it must first be possible for it to be reached and thus executed in the normal course of execution. Clearly, this is not the case for variables i and k. Second, it must not be possible during execution to enter the scope of a variable while bypassing its definition, which is the case for the variable j. If execution jumps to either the case with label 3 or the default case, it enters the scope in which the variable j was defined, while bypassing its actual definition. That’s illegal. Variable m, however, is only “in scope” from its declaration to the end of the enclosing block, so this declaration cannot be bypassed. And the declaration of variable n cannot by bypassed because there are no cases after the default case. Note that it’s not because it concerns the default case that the declaration of n is legal; if there were additional cases following the default one, the declaration of n would’ve been just as illegal.
Initialization Statements
Consider the following code snippet:
We convert some input character to a lowercase character lower and use the outcome first to check whether the input was a letter and then, if so, to produce some output. For illustration’s sake, ignore the fact that we could—should even—be using the portable std::isalpha() function here instead. You’ve learned all about that in this chapter already. The key point that we want to make with this example is that the lower variable is used only by the if statement and not anymore by any of the code that follows the snippet. In general, it is considered good coding style to limit the scope of variables to the region in which they are used, even if this means adding an extra scope as follows:
The result is that, for the rest of the code, it is as if the lower variable never existed. Patterns such as this where an extra scope (and indentation) is introduced to bind local variables to if statements are relatively common. They are common enough for C++17 to introduce a new, specialized syntax for it. The general syntax is as follows:
The additional initialization statement is executed prior to evaluating the condition expression, the usual Boolean expression of the if statement. You will use such initialization statements mainly to declare variables local to the if statement. With this, our earlier example becomes the following:
Variables declared in the initialization statement can be used both in the if statement’s condition expression and in the statement or block that immediately follows the if. For if-else statements, they can be used in the statement or block that follows the else as well. But for any code after the if or if-else statement, it is as if these variables never existed.
For completeness, C++17 adds a similar syntax for switch statements:
Caution
At the time of writing, these extended if and switch statements are still new and not well known among C++ developers yet. And using unfamiliar syntax may hinder code readability. So if you’re working in a team, it may be prudent to check with your colleagues whether you want to use it already in your code base. On the other hand, though, how is new syntax ever going to gain any traction if not for well-educated trendsetters such as yourself?
Summary
You can compare two values using the comparison operators. This will result in a value of type bool, which can be either true or false.
You can convert a bool value to an integer type—true will convert to 1, and false will convert to 0.
Numerical values can be converted to type bool—a zero value converts to false, and any nonzero value converts to true. When a numerical value appears where a bool value is expected—such as in an if condition—the compiler will insert an implicit conversion of the numerical value to type bool.
The if statement executes a statement or a block of statements depending on the value of a condition expression. If the condition is true, the statement or block executes. If the condition is false, it doesn’t.
The if-else statement executes a statement or block of statements when the condition is true and executes another statement or block when the condition is false.
if and if-else statements can be nested.
The logical operators &&, ||, and ! are used to string together more complex logical expressions. The arguments to these operators must either be Booleans or values that are convertible to Booleans (such as integral values).
The conditional operator selects between two values depending on the value of an expression.
The switch statement provides a way to select one from a fixed set of options, depending on the value of an expression of integral or enumeration type.
Exercises
Exercise 4-1. Write a program that prompts for two integers to be entered and then uses an if-else statement to output a message that states whether the integers are the same.
Exercise 4-2. Write another program that prompts for two integers to be entered. This time, any negative number or zero is to be rejected. Next, check whether one of the (strictly positive) numbers is an exact multiple of the other. For example, 63 is a multiple of 1, 3, 7, 9, 21, or 63. Note that the user should be allowed to enter the numbers in any order. That is, it does not matter whether the user enters the largest number first or the smaller one; both should work correctly!
Exercise 4-3. Create a program that prompts for input of a number (nonintegral numbers are allowed) between 1 and 100. Use a nested if, first to verify that the number is within this range and then, if it is, to determine whether it is greater than, less than, or equal to 50. The program should output information about what was found.
Exercise 4-4. It’s time to make good on a promise. Somewhere in this chapter we said we’d look for someone “who is older than 21, younger than 35, is female, has a bachelor’s or master’s degree, is unmarried, and speaks Hindi or Urdu.” Write a program that prompts the user for these qualifications and then outputs whether they qualify for these very specific requirements. To this end, you should define an integer variable age, a character variable gender (to hold 'm' for male and 'f' for female), a variable degree of an enumeration type AcademicDegree (possible values: none, associate, bachelor, professional, master, doctor), and three Boolean variables: married, speaksHindi, and speaksUrdu. Emulate a trivial online job interview, and query your applicant for input on all these variables. People who enter invalid values do not qualify, of course, and should be ruled out as early as possible (that is, immediately after entering any invalid value; ruling them out precognitively prior to entering invalid values, sadly, is not possible yet in Standard C++).
Exercise 4-5. Add some code at the end of the main() function of Ex4_06.cpp to print an additional message. If you have exactly one mouse, output a message of the form “It is a brown/white mouse.” Otherwise, if you have multiple mice, compose a grammatically correct message of the form “Of these mice, N is a/are brown mouse/mice.” If you have no mice, no new message needs to be printed. Use an appropriate mixture of conditional operators and if/else statements.
Exercise 4-6. Write a program that determines, using only the conditional operator, if an integer that is entered has a value that is 20 or less, is greater than 20 but not greater than 30, is greater than 30 but not exceeding 100, or is greater than 100.
Exercise 4-7. Implement a program that prompts for input of a letter. Use a library function to determine whether the letter is a vowel and whether it is lowercase or not, and output the result. Finally, output the lowercase letter together with its character code as a binary value.
Hint: Even though starting with C++14, C++ supports binary integral literals (of form 0b11001010; see Chapter 2), C++ standard output functions and streams do not support outputting integral values in binary format. They mostly do support hexadecimal and octal formatting—for std::cout, for instance, you can use the std::hex and std::oct output manipulators defined in <ios>. But to output a character in binary format, you’ll thus have to write some code yourself. It shouldn’t be too hard, though: a char normally has only eight bits, remember? You can just stream these bits one by one. Perhaps these binary integer literals can be helpful as well—why else would we have mentioned them at the start of this hint?
Exercise 4-8. Create a program that prompts the user to enter an amount of money between $0 and $10 (decimal places allowed). Any other value is to be rejected politely. Determine how many quarters (25c), dimes (10c), nickels (5c), and pennies (1c) are needed to make up that amount. For our non-American readers, one dollar ($) equals 100 cents (c). Output this information to the screen and ensure that the output makes grammatical sense (for example, if you need only one dime, then the output should be “1 dime” and not “1 dimes”).
