In C++, you have economy-class functions, business-class functions, and first-class functions, all with varying degrees of comfort, space, privacy, and onboard service…no, of course that’s not what the term first-class means.1 We’re just kidding. Let’s start over:
In computer science, a programming language is said to offer first-class functions if it allows you to treat functions like any other variable. In such a language, for instance, you can assign a function as a value to a variable, just like you would an integer or a string. You can pass a function as an argument to other functions or return one as the result of another function. At first sight you may find it difficult to imagine the applicability of such language constructs, but they are immensely useful and powerful.
This chapter introduces what C++ has to offer in this area, ranging from basic first-class functions in the form of function pointers to anonymous functions and closures that are defined by means of lambda expressions (not to worry, all these fancy terms will become clear to you before this chapter is over). The introduction of lambda expressions in C++11 in particular has thoroughly reshaped C++. It lifted the expressivity of the language to a whole new level. This was, in no small part, due to the heavy use of first-class function parameters throughout the Standard Library. The function templates of its generic algorithms library (which is a topic of the next chapter), in particular, are a prime use case for lambda expressions.
What a function pointer is and what you use it for
The limitations of function pointers and how to overcome them using standard object-oriented techniques and operator overloading
What a lambda expression is
How you define a lambda expression
What a lambda closure is and why it is more powerful than an anonymous function
What a capture clause is and how you use it
How you pass any first-class function as an argument to another function
How std::function<> allows you to represent any first-class function as a variable
Pointers to Functions
You are familiar already with pointers to data, variables that store the address of those regions in memory containing values of other variables, arrays, or dynamically allocated memory. A computer program is more than just data alone, however. Another essential part of the memory allotted to a computer program holds its executable code, consisting of blocks of compiled C++ statements. Naturally, all compiled code belonging to a given function will typically be grouped together as well.
A pointer to a function or function pointer is a variable that can store the address of a function and therefore point to different functions at different times during execution. You use a pointer to a function to call the function at the address it contains. An address is not sufficient to call a function, though. To work properly, a pointer to a function must also store the type of each parameter as well as the return type. Clearly, the information required to define a pointer to a function will restrict the range of functions to which the pointer can point. It can only store the address of a function with a given number of parameters of specific types and with a given return type. This is analogous to a pointer that stores the address of a data item. A pointer to type int can only point to a location that contains a value of type int.
Defining Pointers to Functions
Here’s a definition of a pointer that can store the address of functions that have parameters of type long* and int and return a value of type long:
This may look a little weird at first because of all the parentheses. The name of the pointer variable is pfun. It doesn’t point to anything because it is not initialized. Ideally, it would be initialized to nullptr or with the address of a specific function. The parentheses around the pointer name and the asterisk are essential. Without them, this statement would declare a function rather than define a pointer variable because the * will bind to the type long:
The general form of a pointer to a function definition is as follows:
The pointer can only point to functions with the same return_type and list_of_parameter_types as those specified in its definition.
Of course, you should always initialize a pointer when you declare it. You can initialize a pointer to a function to nullptr or with the name of a function. Suppose you have a function with the following prototype:
Then you can define and initialize a pointer to this function with this statement:
The pointer is initialized with the address of some function find_maximum() , which is a function that most likely searches for the largest element of type long in a given array. The second parameter would then be the size of that array. The prototype of this function could thus look like this:
Using auto will make defining a pointer to this function much simpler:
You could also use auto* to highlight the fact that pfun is a pointer:
This defines pfun as a pointer to any function with the same parameter list and return type as find_maximum() and initializes it with the address of find_maximum() . You can store the address of any function with the same parameter list and return type in an assignment. If find_minimum() has the same parameter list and return type as find_maximum(), you can make pfun point to it like this:
Note
Even though the name of a function already evaluates to a value of a function pointer type, you can also explicitly take its address using the address-of operator, &. The following statements, in other words, have the same effect as the earlier ones:
Some recommend to always add the address-of operator because in doing so you make it jump out more that you’re creating a pointer to a function.
To call find_minimum() using pfun, you just use the pointer name as though it were a function name. Here’s an example:
This outputs the minimum value in the data array . As with pointers to variables, you should ensure that a pointer to a function effectively contains the address of a function before you use it to invoke a function. Without initialization, catastrophic failure of your program is almost guaranteed.
To get a feel for these newfangled pointers to functions and how they perform in action, let’s try one out in a working program :
This example produces the following output:
This is hardly a useful program, but it does show how a pointer to a function is defined, assigned a value, and used to call a function. After the usual preamble, you define and initialize pDo_it as a pointer to a function, which can point to either of the functions sum() or product().
pDo_it is initialized to nullptr, so before using it the address of the function product() is stored in pDo_it. product() is then called indirectly through the pointer pDo_it in the output statement. The name of the pointer is used just as if it were a function name and is followed by the function arguments between parentheses, exactly as they would appear if the original function name were being used. It would save a lot of complication if the pointer were defined and initialized like this:
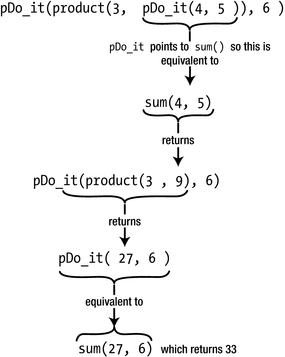
Execution of an expression using a function pointer
Callback Functions for Higher-Order Functions
Pointer to function is a perfectly reasonable type, which means a function can have a parameter of this type as well. The function can then use its pointer to function parameter to call the function to which the argument points when the function is called. You can specify just a function name as the argument for a parameter that is a “pointer to function” type. A function passed to another function as an argument is referred to as a callback function ; the function that accepts another function as an argument is a higher-order function. Consider the following example:
This function template generalizes the find_maximum() and find_minimum() functions we alluded to earlier. The function pointer you pass to the compare parameter determines which “optimum” the function returns. The type of compare forces you to pass a pointer to a function that takes two T values as input and returns a Boolean. This function is expected to compare the two T values it receives and evaluate whether the first one is somehow “better” than the second one. The higher-order find_optimum() then calls the given comparison function through its compare parameter and uses this to determine which out of all the T values in its vector argument is best, or optimal.
The key point is that you, as the caller of find_optimum(), determine what it means for one T value to be better or more optimal than the other. If it’s the minimum element you want, you pass a comparison function equivalent to the less-than operator, <; if it’s the maximum element you want, the compare callback should behave like the greater-than operator, >. Let’s see this in action:
This program prints out these results:
The first two calls to find_optimum() demonstrate that, indeed, this function can be used to find both the minimum and maximum numbers in a given vector. In passing, we illustrate that a function pointer may point to the instantiation of a function template such as greater<>() as well. All you have to do is explicitly instantiate the template by specifying all its template arguments between < and >.
The second half of the example is perhaps even more interesting. The default comparison operators of std::string, as you know, compare strings alphabetically. As in a phone book, Shemp would therefore always appear last. But there are times where you’d prefer to compare strings in a different manner. Adding callback parameters to your sorting or find_optimum() functions facilitates this. We illustrate this capability in Ex18_02 by looking for the longest string instead, by passing a pointer to longer().
This example showcases the tremendous value of higher-order functions and callbacks in your never-ending battle against code duplication. If it weren’t for first-class functions, you would have had to write at least three distinct find_optimum() functions already only to make Ex18_02 work: find_minimum(), find_maximum(), and find_longest(). All three would then have contained the same loop to extract the corresponding optimum from a given vector. While for beginners it may be a great exercise to write such loops at least a couple of times, this soon gets old and certainly has no place in professional software development. Luckily, the Standard Library offers a vast collection of generic algorithms similar to find_optimum() that you can reuse instead, and all will accept similar callback functions that allow you to tune them to your needs. We’ll discuss this in more detail in the next chapter.
Note
First-class callback functions have plenty more uses beyond serving as the argument to higher-order functions. Callbacks are actively used in day-to-day object-oriented programming as well. Objects often store one or multiple callback functions inside their member variables. Invoking such callbacks can serve any number of purposes. They could constitute a user-configurable step in the logic implemented by one of the object’s member functions, or they may be used to signal other objects that some event has occurred. Callback members in all their various forms and manifestations facilitate various standard object-oriented idioms and patterns, most notably perhaps variations on the classical Observer pattern. Discussing object-oriented design falls outside of the scope of this book; there are other excellent books that specialize in this. You can find a basic example of a callback member variable in the exercises at the end of the chapter.
Type Aliases for Function Pointers
As we’re sure you will agree, the syntax required to define a function pointer variable is rather horrendous. The less you have to type this syntax, the better. The auto keyword can help, but there are times where you do want to specify the type of a function pointer explicitly when a function pointer is used as a function parameter, for instance, or as an object’s member variable. Because “pointer to function” is just a type like any other, however, you can define a type alias for such types using the using keyword (see Chapter 3).
Consider the definition of the callback parameter in the optimum() function template of Ex18_02:
Unfortunately, this type contains a template type parameter, T, which complicates matters a bit. Let’s simplify that for a moment and instead start with a concrete instantiation of this type template:
You obtain the type of this variable by copying the entire variable definition and dropping the variable name, string_comp:
Quite a mouthful this type is, so it’s well worth creating an alias for. With the modern syntax based on the using keyword, defining an alias for this type is as straightforward as this:
The right side of this assignment-like declaration simply matches the type name; the left side, of course, is a name of your choosing. With this type alias in place, declaring a parameter such as string_comp immediately becomes a lot less tedious and a lot more readable:
One nice thing about the using syntax for type aliases is that it extends gracefully to templated types. To define an alias for the type of the compare callback parameter of Ex18_02, all you need to do is generalize the StringComparison definition in the most natural way; you simply prepend it with the template keyword, as always, followed by a template parameter list between angular brackets:
This defines an alias template, which is a template that generates type aliases. In Optimum.h, you could use this template to simplify the signature of find_optimum():
Of course, you can also use it to define a variable with a concrete type:
Note
For historical reference, this is how you would define StringComparison using the old typedef syntax (see also Chapter 3):
With the alias name needlessly appearing in the middle, this syntax is again far more complex than the one that uses the using keyword. Defining an alias template, moreover, is not even possible with typedef. Our conclusion from Chapter 3 thus stands, stronger than ever. To define a type alias, you should always use using; typedef has no place in modern C++.
Function Objects
Much like pointers to data values, pointers to functions are low-level language constructs that C++ has inherited from the C programming language. And just like raw pointers, function pointers have their limitations, which can be overcome using an object-oriented approach. In Chapter 6 you learned that smart pointers are the object-oriented answer to the inherently unsafe raw pointers. In this section, we introduce a similar technique where objects are used as a more powerful alternative to plain C-style function pointers. These objects are called function objects or functors (the two terms are synonymous). Like a function pointer, a function object acts precisely like a function; but unlike a raw function pointer, it is a full-fledged class type object—complete with its own member variables and possibly even various other member functions. We’ll show you that function objects are hence far more powerful and expressive than plain C-style function pointers.
Basic Function Objects
A function object or functor is simply an object that can be called as if it were a function. The key in constructing one is to overload the function call operator, as was briefly introduced in Chapter 12 already. To see how this is done, we will define a class of function objects that encapsulate this simple function:
Quickly recapping what you saw in Chapter 12, here is how you define a class with an overloaded function call operator:
This basic functor class has only one member: a function call operator. The main thing to remember here is that the function call operator is denoted with operator() and that its actual parameter list is specified only after an initial set of empty parentheses. Beyond that, this is just like any other operator function. You can define it in the corresponding source file in the usual manner:
With this class definition, you can create your very first function object and then call it as if it were an actual function like so:
Of course, what is being “called” is not the object itself but rather its function call operator function. If you’re into self-harm and code-obscuring, you could thus also write less(5,6) as less.operator()(5,6).
Granted, creating a functor just to call it right after is not very useful at all. Things become a bit more interesting already if you use a functor as a callback function. To demonstrate this, you’ll first have to generalize the find_optimum() template of Ex18_02 since currently it only accepts a function pointer for its callback argument. Of course, creating an extra overload specifically for the Less type would defeat the purpose of having a higher-order function with a callback in the first place. And there’s also no such thing as one single type that encompasses all function object class types. The most common way to generalize a function such as find_optimum() is therefore to declare a second template type parameter and to use that then as the type of the compare parameter:
Function pointers of type bool (*)(const T&, const T&) (or similar types, such as for instance bool (*)(T, T)). Therefore, if you were to plug this new definition of find_optimum<>() into Ex18_02, this example would still work precisely like before.
Function objects of a type like Less that have a corresponding function call operator.
Both options are demonstrated in our next example:
Standard Function Objects
You can customize many templates of the Standard Library by providing them with a first-class function, similar to what you did with find_optimum<>() in examples Ex18_02 and Ex18_03. For regular functions you can mostly use a plain function pointer, but for built-in operators that is not an option. You cannot create a pointer to a built-in operator. Of course, it’s easy to quickly define either a function (as in Ex18_02) or a functor class (Less in Ex18_03) that emulates the operator’s behavior, but doing so for every operator all the time would become tedious very fast.
Of course, this did not escape the designers of the Standard Library either. The functional header of the Standard Library therefore defines a series of function object class templates, one for every built-in operator you may want to pass to other templates. The class template std::less<>, for instance, is fundamentally analogous to the Less template of Ex18_03. After adding an #include for the functional header, you could thus replace the definition of the less variable in Ex18_03 with this one:
Tip
As of C++14, the recommended way to use the function object types of the functional header is actually by omitting the type argument, for instance, as follows:
The templates defined by <functional> employ more advanced template programming techniques to ensure that functors defined without an explicit type argument generally behave precisely like those defined the traditional way, except in specific situations that involve implicit conversions, where a function object of type std::less<> may lead to more efficient code than a function object of type std::less<int> (or, to use a more common example, more efficient than, say, one of type std::less<std::string>). Explaining this in more detail would lead us too far astray, though. Trust us, if you simply always omit the type argument, you’re guaranteed that the compiler can generate optimal code under all circumstances. Plus, it saves you some typing; it’s a clear win-win!
The Function Object Class Templates Offered by the <functional> Header
Comparisons | less<>, greater<>, less_equal<>, greater_equal<>, equal_to<>, not_equal_to<> |
Arithmetic operations | plus<>, minus<>, multiplies<>, divides<>, modulus<>, negate<> |
Logical operations | logical_and<>, logical_or<>, logical_not<> |
Bitwise operations | bit_and<>, bit_or<>, bit_xor<>, bit_not<> |
We could also use std::greater<> to replace our greater<> function template of Ex18_03. Now isn’t that great?
This time we created the std::less<> and greater<> function objects as temporary objects directly inside the function call expression itself, rather than storing them first in a named variable. You can find this variant of the program in Ex18_03A.
Parameterized Function Objects
Perhaps you’ve already noticed that, in fact, none of the function objects that you have seen thus far has been more powerful than a plain function pointer. Why go through all the trouble of defining a class with a function call operator if defining a plain function is so much easier? Surely, there must be more to function objects than this?
Indeed there is. Function objects only truly become interesting once you start adding more members—either variables or functions. Building on the same find_optimum() example as always, suppose you want to search not for the smallest or largest number but instead for the number that is nearest to some user-provided value. There is no clean way for you to accomplish this using functions and pointers to functions. Think about it, how would the callback’s function body ever get access to the value that the user has entered? There is no clean way for you to pass this value along to the function if all you have is a pointer. If you use a function-like object, however, you can pass along any information you want by storing it in the object’s member variables. The easiest is if we just show you how you might do this:
Every function object of type Nearer has a member variable n in which it stores the value to compare with. This value is passed in through its constructor, so it could easily be a number that was entered by the user earlier. Of course, the object’s function call operator has access to this number as well, which is the part that would not have been possible when using a function pointer as a callback. This program illustrates how to use this functor class:
A possible session then might go like this:
Lambda Expressions
Ex18_04 clearly demonstrates a couple of things. First, it shows the potential of passing a function object as a callback. Given that it can have any number of members, function objects are certainly much more powerful than plain function pointers. But that’s not all that we can learn from Ex18_04. Indeed, if there’s one more thing that Ex18_04 clearly exposes, it’s that defining a class for a function object requires you to write quite some code. Even a simple callback class such as Nearer—which has only one member variable—quickly takes about ten lines of code already.
This is where lambda expressions come in. They offer you a convenient, compact syntax to quickly define callback functions or functors. And not only is the syntax compact, lambda expressions also allow you to define the callback’s logic right there where you want to use it. This is often much better than having to define this logic somewhere in the function call operator of some class definition. Lambda expressions thus generally lead to particularly expressive yet still very readable code.
A lambda expression has a lot in common with a function definition. In its most basic form, a lambda expression basically provides a way to define a function with no name, an anonymous function. But lambda expressions are far more powerful than that. In general, a lambda expression effectively defines a full-blown function object that can carry any number of member variables. The beauty is that there’s no need for an explicit definition of the type of this object anymore; this type is generated automatically for you by the compiler.
Practically speaking, you’ll find that a lambda expression is different from a regular function in that it can access variables that exist in the enclosing scope where it is defined. Thinking back to Ex18_04, for instance, a lambda expression there would be able to access number_to_search_for, the number that was entered by the user. Before we examine how lambda expressions get access to local variables, though, let’s first take one step back again and begin by explaining how you can define a basic unnamed or anonymous function using a lambda expression.
Defining a Lambda Expression
Consider the following basic lambda expression:
As you can see, the definition of a lambda expression indeed looks very much like the definition of a function. The main differences are that a lambda expression does not specify a return type or function name and that it always starts with square brackets. The opening square brackets are called the lambda introducer . They mark the beginning of the lambda expression. There’s more to the lambda introducer than there is here—the brackets are not always empty—but we’ll explain this in more depth a little later. The lambda introducer is followed by the lambda parameter list between round parentheses. This list is exactly like a regular function parameter list (ever since C++14, default parameter values are even allowed). In this case, there’s two int parameters, x and y.
Tip
For lambda functions without parameters, you may omit the empty parameter list, (). That is, a lambda expression of form []() {...} may be further shortened to [] {...}. An empty lambda initializer, [], must not be omitted, though. The lambda initializer is always required to signal the start of a lambda expression.
The body of the lambda expression between braces follows the parameter list, again just like a normal function. The body for this lambda contains just one statement, a return statement that also calculates the value that is returned. In general, the body of a lambda can contain any number of statements. The return type defaults to that of the value returned. If nothing is returned, the return type is void.
It’s educational to have at least a basic notion of how lambda expressions are compiled. This will aid you later in understanding how more advanced lambda expressions behave. Whenever the compiler encounters a lambda expression, it internally generates a new class type. In the case of our example, the generated class will be similar to the LessThan class you defined in Ex18_03. Slightly simplified, such a class might look something like this:
A first notable difference is that the implicit class definition will have some unique, compiler-generated name. We picked __Lambda8C1 here, but your compiler could use whatever name it wants. There’s no telling what this name will be (at least not at compile time), nor is there any guarantee it will still be the same the next time you compile the same program. This somewhat limits the way in which these function objects can be used, but not by much—as we’ll show you in one of the next subsections.
Another point worth noting first is that, at least by default, a lambda expression results in a function call operator() with a return type equal to auto. You first encountered the use of auto as a return type in Chapter 8. Back then, we explained to you that the compiler then attempts to deduce the actual return type from the return statements in the function’s body. There were some limitations, though: auto return type deduction requires that all return statements of the function return a value of the same type. The compiler will never apply any implicit conversions—any conversions need to be added by you explicitly. This same limitation therefore applies to the body of a lambda expression as well.
You do have the option to specify the return type of a lambda function explicitly. You could do this to have the compiler generate implicit conversions for the return statements or simply to make the code more self-documenting. While clearly not necessary here, you could supply a return type for the previous lambda like this:
The return type is specified following the -> operator that comes after the parameter list and is type bool here.
Naming a Lambda Closure
As you know, a lambda expression evaluates to a function object. This function object is formally called a lambda closure, although many also refer to it informally as either a lambda function or a lambda. You don’t know a priori what the type of the lambda closure will be; only the compiler does. The only way to store the lambda object in a variable is thus to have the compiler deduce the type for you:
The auto keyword tells the compiler to figure out the type that the variable less should have from what appears on the right of the assignment—in this case a lambda expression. Supposing the compiler generates a type with the name __Lambda8C1 for this lambda expression (as shown earlier), this statement is then effectively compiled as follows:
Passing a Lambda Expression to a Function Template
You can use less just like the equivalent functor of Ex18_03:
This works because the callback parameter of the find_optimum() template of Ex18_03 is declared with a template type parameter, which the compiler can substitute with whatever name it picked for the lambda closure’s generated type:
Rather than first storing a lambda closure in a named variable, it is at least as common to directly use a lambda expression as a callback argument as follows:
Tip
The previous statements would also compile with the find_optimum() function template of Ex18_02, whose callback argument still had to be a function pointer (concretely, the type of the corresponding parameter in that version of find_optimum() was still bool (*)(int,int)). The reason is that the compiler makes sure that a lambda closure that does not capture any variables always has a (nonexplicit) type conversion operator to the equivalent function pointer type. As soon as the lambda closure requires member variables, it can no longer be cast to a function pointer. The next subsection explains how and when lambda closures capture variables into member variables.
Ex18_05 is yet another variant of Ex18_02 and Ex18_03, only this time one that uses lambda expressions to define all its callback functions:
The result will be the same as before. Clearly, if you only need to sort strings on their length once, a lambda expression is more convenient than defining a separate longer() function and definitely far more interesting than defining a Longer functor class.
Tip
If <functional> defines a suitable functor type, using that type is normally far more compact and readable than a lambda expression. std::less<> and std::greater<>, for instance, could readily replace the first three lambda expressions in Ex18_05.cpp (see also Ex18_03A).
The Capture Clause
As we’ve said before, the lambda introducer, [], is not necessarily empty. It can contain a capture clause that specifies how variables in the enclosing scope can be accessed from within the body of the lambda. The body of a lambda expression with nothing between the square brackets can work only with the arguments and with variables that are defined locally within the lambda. A lambda with no capture clause is called a stateless lambda expression because it cannot access anything in its enclosing scope.
If used in isolation, a capture default clause applies to all variables in the scope enclosing the definition of the lambda. There are two capture defaults: = and &. We’ll discuss both of them in turn next. The capture clause can contain only one of the capture defaults, never both.
Capturing by Value
If you put = between the square brackets, the body of the lambda can access all automatic variables in the enclosing scope by value. That is, while the values of all variables are made available within the lambda expression, the values stored in the original variables cannot be changed. Here’s an example based on Ex18_04:
The = capture clause allows all the variables that are in scope where the definition of the lambda appears to be accessed by value from within the body of the lambda expression. In Ex18_06 this means that the lambda’s body has, at least in principle, access to main()’s two local variables, numbers and number_to_search_for. The effect of capturing local variables by value is rather different from passing arguments by value, though. To properly understand how capturing works, it’s again instructive to study the class that the compiler might generate for the lambda expression of Ex18_06:
The lambda expression itself is then compiled as follows:
It should come as no surprise that this class is completely equivalent to the Nearer class we defined earlier in Ex18_04. Concretely, the closure object has one member per local variable of the surrounding scope that is used inside the lambda’s function body. We say that these variables are captured by the lambda. At least conceptually the member variables of the generated class have the same name as the variables that were captured. That way, the lambda expression’s body appears to have access to variables of the surrounding scope, while in reality it is accessing the corresponding member variables that are stored inside the lambda closure.
Note
Variables that are not used by the lambda expression’s body, such as the numbers vector in Ex18_06, are never captured by a default capture clause such as =.
The = clause denotes that all variables are to be captured by value, which is why the number_to_search_for member variable has a value type, in this case, type int. The number_to_search_for member variable contains, in other words, a copy of the original local variable with the same name. While this implies that the value of the original number_to_search_for variable is in a sense available during the function’s execution, you cannot possibly update its value. Even if updates to this member were allowed, you’d only be updating a copy. To avoid any confusion, the compiler therefore even arranges it so that by default you cannot update number_to_search_for at all from within the lambda’s body—not even the copy that is stored in the closure’s member variable. It does so by declaring the function call operator, operator(), as const. You’ll recall from Chapter 11 that you cannot modify any of the member variables of an object from within one of its const member functions.
Tip
In the unlikely event that you do want to alter a variable that was captured by value , you can add the keyword mutable to the definition of a lambda expression, right after the parameter list. Doing so causes the compiler to omit the const keyword from the function call operator of the generated class. Remember that you’d still only be updating a copy of the original variable. If you want to update the local variable itself, you should capture it by reference. Capturing variables by reference is explained next.
Capturing by Reference
If you put & between the square brackets, all variables in the enclosing scope are accessible by reference, so their values can be changed by the code in the body of the lambda. To count the number of comparisons performed by find_optimum(), for instance, you could use this lambda expression:
All variables within the outer scope are available by reference, so the lambda can both use and alter their values. If you plug this code snippet in Ex18_06, for instance, the value of count after the call to find_optimum<>() will be 5.
For completeness, this is a class similar to the one that your compiler would generate for this lambda expression:
Note that this time the captured variable count is stored in the closure’s member variable by reference. The ++count increment in this operator() will therefore compile, even though that member function is declared with const. Any modification to a reference leaves the function object itself unaltered. It is the variable that the count reference refers to that is modified instead. The mutable keyword is therefore not needed in this case.
Tip
Although the & capture clause is legal, capturing all variables in the outer scope by reference is not considered good practice because of the potential for accidentally modifying one of them. Similarly, using a = capture default risks introducing costly copies. It’s therefore safer to explicitly specify how each individual variable that you need should be captured. We'll explain how you do this next.
Capturing Specific Variables
You can identify specific variables in the enclosing scope that you want to access by listing them in the capture clause. For each variable, you can choose whether it should be captured either by value or by reference. You capture a specific variable by reference by prefixing its name with &. You could rewrite the previous statement as follows:
Here, count is the only variable in the enclosing scope that can be accessed from within the body of the lambda. The &count specification makes it available by reference. Without the &, the count variable in the outer scope would be available by value and not updatable. The lambda expression in Ex18_06, in other words, could also be written as follows:
Caution
You mustn’t prefix the names of the variables that you want to capture by value with =. The capture clause [=number_to_search_for], for example, is invalid; the only correct syntax is [number_to_search_for].
When you put several variables in the capture clause, you separate them with commas. You can freely mix variables that are captured by value with others that are captured by reference. You can also include a capture default in the capture clause along with specific variable names that are to be captured. The capture clause [=, &counter], for instance, would allow access to counter by reference and any other variables in the enclosing scope by value. Analogously, you could write a capture clause such as [&, number_to_search_for], which would capture number_to_search_for by value and all other variables by reference. If present, the capture default (= or &) must always be the first item in the capture list.
Caution
If you use the = capture default, you are no longer allowed to capture any specific variables by value; similarly, if you use &, you can no longer capture specific variables by reference. Capture clauses such as [&, &counter] or [=, &counter, number_to_search_for] should therefore trigger a compiler error.
Capturing the this Pointer
In this final subsection on capturing variables, we’ll discuss how to use a lambda expression from within the member function of a class. Sadistically beating the find_optimum<>() example to death one last time, suppose you defined this class:
A fully functional implementation of the Finder example is available under Ex18_07. The definitions of the getter and setter members are of no particular interest, but to define findNearest() you’d of course like to reuse the find_optimum<>() template you defined earlier. A reasonable first attempt at defining this function might therefore look as follows:
Unfortunately, though, your compiler won’t be too happy with this yet. The problem is that this time number_to_search_for is the name of a member variable rather than that of a local variable. And member variables cannot be captured, neither by value nor by reference; only local variables and function arguments can. To give a lambda expression access to the current object’s members, you should instead add the keyword this to the capture clause, like so:
By capturing the this pointer, you effectively give the lambda expression access to all members that the surrounding member function has access to. That is, even though the lambda closure will be an object of a class other than Finder, its function call operator will still have access to all protected and private members of Finder, including the member variable number_to_search_for, which is normally private to Finder. When we say all members, we do mean all members. Next to member variables, a lambda expression thus has access to all member functions as well—either public, protected, or private. Another way to write our example lambda is therefore as follows:
Note
Precisely like in the member function itself, there is no need to add this-> when accessing a member. The compiler takes care of that for you.
Together with the this pointer , you can still capture other variables as well. You can combine it with a & capture default to capture local variables by reference or any sequence of captures of named variables. The = capture default already implies that the this pointer is captured (by value). So, this would also be valid:
Caution
You are not allowed to combine a = default capture with a capture of this (at least not yet in C++17; C++20 is rumored to relax this restriction). A capture clause of the form [=, this] will thus be flagged as an error by the compiler. [&, this] is allowed, though, as & does not imply the capture of this.
The std::function<> Template
The type of a function pointer is very different from that of a function object or lambda closure. The former is a pointer, and the latter is a class. At first sight, it might thus seem that the only way to write code that works for any conceivable callback—that is, either a function pointer, function object, or lambda closure—is to use either auto or a template type parameter. This is what we did for our find_optimum<>() template in earlier examples. The same technique is heavily used throughout the Standard Library, as you will see in the next chapter.
Using templates does have its cost. It typically implies defining all your code inside the header file, for one, which is not always very practical. Also, you risk template code bloat, where the compiler has to generate specialized code for all different types of callbacks, even when it’s not required for performance reasons. It also has its limitations: what if you needed say a vector<> of callback functions—a vector<> that is potentially filled with a mixture of function pointers, function objects, and lambda closures?
To cater for these types of scenarios, the functional header defines the std::function<> template. With objects of type std::function<> you can store, copy, move, and invoke any kind of function-like entity—be it a function pointer, function object, or lambda closure. The following example demonstrates precisely that:
The output looks as follows:
In the first part of the program, we define a std::function<> variable compare and assign it three different kinds of first-class functions in sequence: first a function pointer, then a function object, and finally a lambda closure. In between, all three first-class functions are always called. More precisely, they are indirectly invoked through the compare variable’s function call operator. A std::function<> itself is, in other words, a function object—one that can encapsulate any other kind of first-class function.
There is only one restriction for the function-like entities that can be assigned to a given std::function<>. They must all have matching return and parameter types. These type requirements are specified between the angular brackets of the std::function<> type template. In Ex18_08, for instance, compare has type std::function<bool(int,int)>. This indicates that compare will only accept first-class functions that can be called with two int arguments and that return a value that is convertible to bool.
Tip
A variable of type std::function<bool(int,int)> not only can store first-class functions whose signature is precisely (int, int); it can store any function that is callable with two int arguments. There is a subtle difference. The latter implies that functions with signatures such as (const int&, const int&), (long, long), or even (double, double) are acceptable as well. Similarly, the return type must not be exactly equal to bool. It suffices that its values can be converted into a Boolean. So, functions that return either int or even double* or std::unique_ptr<std::string> would work as well. You can try this by playing with the signature and return type of the less() function in Ex18_08.cpp.
The general form of a std::function<> type template instantiation is as follows:
The ReturnType is not optional, so to represent functions that do not return a value, you should specify void for the ReturnType. Similarly, for functions without parameters you must still include an empty parameter type list, (). Reference types and const qualifiers are allowed for any of the ParamTypes, as well as for the ReturnType. All in all, it’s a most natural way of specifying function type requirement, wouldn’t you agree?
A default-constructed std::function<> object does not contain any callable first-class function yet. Invoking its function call operator would then result in a std::bad_function_call exception. In the last five lines of the program, we show you how you can verify whether a function<> is callable. As the example shows, there are two ways: a function<> implicitly converts to a Boolean (through a nonexplicit cast operator), or it can be compared to a nullptr (even though in general a function<> need not contain a pointer).
The std:: function<> template forms a powerful alternative to the use of auto or template type parameters. The prime advantage to these other approaches is that std::function<> allows you to name the type of your first-class function variables. Being able to name this type facilitates the use of lambda-enabled callback functions in a much wider range of use cases than just higher-order function templates: std::function<> may, for example, be used for function parameters and member variables (without resorting to templates) or to store first-class functions into containers. The possibilities are limitless. You’ll find a basic example of such a use in the exercises later.
Summary
This chapter introduced first-class functions in all their forms and flavors—from plain C-style function pointers over object-oriented functors to full-blown closures. We showed that lambda expressions offer a particularly versatile and expressive syntax not just to define anonymous functions but to create lambda closures capable of capturing any number of variables from their surroundings. Like function objects, lambda expressions are much more powerful than function pointers; but unlike function objects, they do not require you to specify a complete class—the compiler takes care of this tedious task for you. Lambda expressions really come into their own when combined, for instance, with the algorithms library of the C++ Standard Library, where many of the higher-order template functions have a parameter for which you can supply a lambda expression as the argument. We’ll return to this in the next chapter.
A pointer to a function stores the address of a function. A pointer to a function can store the address of any function with the specified return type and number and types of parameters.
You can use a pointer to a function to call the function at the address it contains. You can also pass a pointer to a function as a function argument.
Function objects or functors are objects that behave precisely like a function by overloading the function call operator.
Any number of member variables or functions can be added to a function object, making them far more versatile than plain function pointers. For one, functors can be parameterized with any number of additional local variables.
Function objects are powerful but do require quite some coding to set up. This is where lambda expressions come in; they alleviate the need to define the class for each function object you need.
A lambda expression defines either an anonymous function or a function object. Lambda expressions are typically used to pass a function as an argument to another function.
A lambda expression always begins with a lambda introducer that consists of a pair of square brackets that can be empty.
The lambda introducer can contain a capture clause that specifies which variables in the enclosing scope can be accessed from the body of the lambda expression. Variables can be captured by value or by reference.
There are two default capture clauses: = specifies that all variables in the enclosing scope are to be captured by value, and & specifies that all variables in the enclosing scope are captured by reference.
A capture clause can specify specific variables to be captured by value or by reference.
Variables captured by value will have a local copy created. The copy is not modifiable by default. Adding the mutable keyword following the parameter list allows local copies of variables captured by value to be modified.
You can specify the return type for a lambda expression using the trailing return type syntax. If you don’t specify a return type, the compiler deduces the return type from the first return statement in the body of the lambda.
You can use the std::function<> template type that is defined in the functional header to specify the type of a function parameter that will accept any first-class function as an argument, including a lambda expression. In fact, it allows you to specify a named type for a variable—be it a function parameter, member variable, or automatic variable—that can hold a lambda closure. This is a feat that would otherwise be very hard as the name of this type is known only to the compiler.
Exercises
Exercise 18-1. Define and test a lambda expression that returns the number of elements in a vector<string> container that begin with a given letter.
Exercise 18-2. Throughout this book you’ve already defined various sort functions but always to sort elements in ascending order and always according to the evaluation of the < operator. Clearly, a truly generic sorting function would benefit from a comparison callback, completely analogous to the find_optimum<>() templates that you worked with throughout this chapter. Take the solution to Exercise 9-6 and generalize its sort<>() template accordingly. Use this to sort a sequence of integers in descending order (that is, from large to small); to sort a sequence of characters alphabetically, ignoring the case ('a' must rank before 'B', even though 'B' < 'a'); and a sequence of floating-point values in ascending order but ignoring the sign (5.5 should thus precede -55.2 but not -3.14).
Exercise 18-3. In this exercise, you will compare the performance of two sorting algorithms. Given a sequence of n elements, quicksort should in theory use about n log2 n comparisons on average, and bubble sort n 2. Let’s see whether you can replicate these theoretical results in practice! Start by recycling the quicksort template from the previous exercise (perhaps rename it to quicksort()?). Then you should extract the bubble sort algorithm from Ex5_09, and generalize it to work for any element type and comparison callback as well. Next you define an integer comparison functor that counts the number of times it is called (it can sort in any which order you prefer). Use it to count the number of comparisons that both algorithms need to sort, for instance, sequences of 500, 1,000, 2,000, and 4,000 random integer values between 1 and 100. Do these numbers agree, at least more or less, with the theoretical expectations?
Exercise 18-4. Create a generic function that collects all elements of a vector<T> that satisfy a given unary callback function. This callback function accepts a T value and returns a Boolean value that indicates whether the element should be part of the function’s output. The resulting elements are to be collected and returned in another vector. Use this higher-order function to gather all numbers greater than a user-provided value from a sequence of integers, all capital letters from a sequence of characters, and all palindromes from a sequence of strings. A palindrome is a string that reads the same backward and forward (such as, for example, "racecar", "noon", or "kayak").
Exercise 18-5. As noted earlier, callback functions have many more interesting uses beyond serving as the argument to higher-order functions. They are used frequently in more advanced object-oriented designs as well. While creating a full-blown, complex system of intercommunicating objects would lead us too far astray, one basic example of how this could work should get you started. Begin by recovering the Truckload class of Example 17-1. Create a DeliveryTruck class that encapsulates a single Truckload object. Add DeliveryTruck::deliverBox() that not only applies removeBox() on its Truckload but also notifies any interested party that the given Box is delivered. It does so, of course, by calling a callback function. In fact, make it so that a DeliveryTruck can have any number of callback functions, all of which are to be called whenever a Box is delivered (the newly delivered Box is then to be passed to these callbacks as an argument). You could store these callbacks in a std::vector<> member, for instance. New callbacks are added through a DeliveryTruck::registerOnDelivered() member. We’ll leave it to you to choose the appropriate types, but we do expect that all known flavors of first-class functions are supported (that is, function pointers, function objects, and lambda closures). In real life, such callbacks could be used by the trucking company to accumulate statistics on delivery times, to send an e-mail to the customer that his Box has arrived, and so on. In your case, a smaller test program suffices. It should register at least these callback functions: a global logDelivery() function that streams the delivered Box to std::cout and a lambda expression that counts the number of times any Box is delivered.
Note: What you are to implement in this exercise is a variation on the often-used Observer pattern. In the terminology of this classical object-oriented design pattern, the DeliveryTruck is called the observable, and the entities that are being notified through the callbacks are called the observers. The nice thing about this pattern is that the observable does not need to know the concrete type of its observers, meaning that both can be developed and compiled completely independently from each other.
