In this book we sometimes will use certain code in the examples before having explained it in detail. This chapter is intended to help you when this occurs by giving presenting an overview of the major elements of C++ and how they hang together. We’ll also explain a few concepts relating to the representation of numbers and characters in your computer.
What is meant by modern C++
What the terms C++11, C++14, and C++17 mean
What the C++ Standard Library is
What are the elements of a C++ program
How to document your program code
How your C++ code becomes an executable program
How object-oriented programming differs from procedural programming
What binary, hexadecimal, and octal number systems are
What floating-point numbers are
How a computer represents numbers using nothing but bits and bytes
What Unicode is
Modern C++
The C++ programming language was originally developed in the early 1980s by Danish computer scientist Bjarne Stroustrup. That makes C++ one of the older programming languages still in active use—very old, in fact, in the fast-paced world of computer programming. Despite its age, though, C++ is still standing strong, steadily maintaining its top-five position in most popularity rankings for programming languages. There’s no doubt whatsoever that C++ still is one of the most widely used and most powerful programming language in the world today.
Just about any kind of program can be written in C++, from device drivers to operating systems and from payroll and administrative programs to games. Major operating systems, browsers, office suites, email clients, multimedia players, database systems—name one and chances are it’s written at least partly in C++. Above all else, C++ is perhaps best suited for applications where performance matters, such as applications that have to process large amounts of data, modern games with high-end graphics, or apps that target embedded or mobile devices. Programs written in C++ are still easily many times faster than those written in other popular languages. Also, C++ is far more effective than most other languages for developing applications across an enormous range of computing devices and environments, including for personal computers, workstations, mainframe computers, tablets, and mobile phones.
The C++ programming language may be old, but it’s still very much alive and kicking. Or, better yet: it’s again very much alive and kicking. After its initial development and standardization in the 1980s, C++ evolved slowly—until 2011, that is, when the International Organization for Standardization (ISO) released a new version of the standard that formally defines the C++ programming language. This edition of the standard, commonly referred to as C++11, revived C++ and catapulted the somewhat dated language right back into the 21st century. It modernized the language and the way we use it so profoundly that you could almost call C++11 a completely new language.
Programming using the features of C++11 and beyond is referred to as modern C++. In this book, we’ll show you that modern C++ is about more than simply embracing the language’s new features—lambda expressions, auto type deduction, and range-based for loops, to name a few. More than anything else, modern C++ is about modern ways of programming, the consensus of what constitutes good programming style. It’s about applying an implicit set of guidelines and best practices, all designed to make C++ programming easier, less error-prone, and more productive. A modern, safe C++ programming style replaces traditional low-level language constructs with the use of containers (Chapters 5 and 19), smart pointers (Chapter 6), or other RAII techniques (Chapter 15), and it emphasizes exceptions to report errors (Chapter 15), passing objects by value through move semantics (Chapter 17), writing algorithms instead of loops (Chapter 19), and so on. Of course, all this probably means little to nothing to you yet. But not to worry: in this book, we’ll gradually introduce everything you need to know to program in C++ today!
The C++11 standard appears to have revived the C++ community, which has been actively working hard on extending and further improving the language ever since. Every three years, a new version of the standard is published. In 2014, the C++14 standard was finalized, and in 2017 the C++17 edition. This book relates to C++ as defined by C++17. All code should work on any compiler that complies with the C++17 edition of the standard. The good news is that most major compilers have been keeping up with the latest developments, so if your compiler does not support a particular feature yet, it soon will.
Standard Libraries
If you had to create everything from scratch every time you wrote a program, it would be tedious indeed. The same functionality is required in many programs—reading data from the keyboard, calculating a square root, and sorting data records into a particular sequence are examples. C++ comes with a large amount of prewritten code that provides facilities such as these so you don’t have to write the code yourself. All this standard code is defined in the Standard Library.
The Standard Library is a huge collection of routines and definitions that provide functionality that is required by many programs. Examples are numerical calculations, string processing, sorting and searching, organizing and managing data, and input and output. We’ll introduce major Standard Library functionalities in virtually every chapter and will later zoom in a bit more specifically on some key data structures and algorithms in Chapter 19. Nevertheless, the Standard Library is so vast that we will only scratch the surface of what is available in this book. It really needs several books to fully elaborate all the capabilities it provides. Beginning STL (Apress, 2015) is a companion book that is a tutorial on using the Standard Template Library, which is the subset of the C++ Standard Library for managing and processing data in various ways. For a compact yet complete overview of everything the modern Standard Library has to offer, we also recommend the book C++ Standard Library Quick Reference (Apress, 2016).
Given the scope of the language and the extent of the library, it’s not unusual for a beginner to find C++ somewhat daunting. It is too extensive to learn in its entirety from a single book. However, you don’t need to learn all of C++ to be able to write substantial programs. You can approach the language step-by-step, in which case it really isn’t difficult. An analogy might be learning to drive a car. You can certainly become a competent and safe driver without necessarily having the expertise, knowledge, and experience to drive in the Indianapolis 500. With this book you can learn everything you need to program effectively in C++. By the time you reach the end, you’ll be confidently writing your own applications. You’ll also be well equipped to explore the full extent of C++ and its Standard Library.
C++ Program Concepts
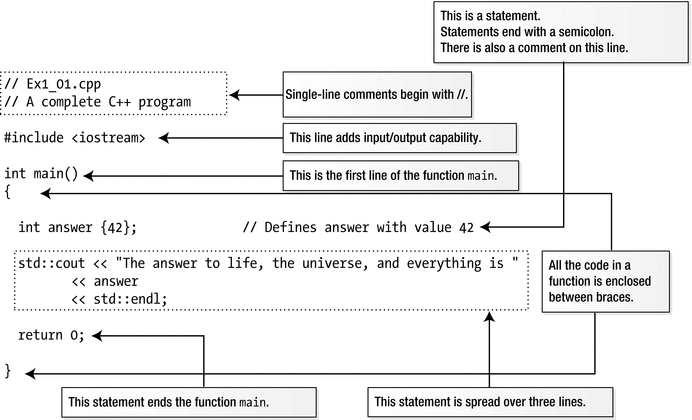
A complete C++ program
Source Files and Header Files
The file depicted in Figure 1-1, Ex1_01.cpp, is in the code download for the book. The file extension, .cpp, indicates that this is a C++ source file. Source files contain functions and thus all the executable code in a program. The names of source files usually have the extension .cpp, although other extensions such as .cc, .cxx, or .c++ are sometimes used to identify a C++ source file.
C++ code is actually stored in two kinds of files. Next to source files, there’re also so-called header files. Header files contain, among other things, function prototypes and definitions for classes and templates that are used by the executable code in a .cpp file. The names of header files usually have the extension .h, although other extensions such as .hpp are also used. You’ll create your first very own header files in Chapter 10; until then all your programs will be small enough to be defined in a single source file.
Comments and Whitespace
The first two lines in Figure 1-1 are comments. You add comments that document your program code to make it easier to understand how it works. The compiler ignores everything that follows two successive forward slashes on a line, so this kind of comment can follow code on a line. In our example, the first line is a comment that indicates the name of the file containing this code. We'll identify the file for each working example in the same way.
Note
The comment with the file name in each header or source file is only there for your convenience. In normal coding there is no need to add such comments; it only introduces an unnecessary maintenance overhead when renaming files.
There’s another form of comment that you can use when you need to spread a comment over several lines. Here’s an example:
Everything between /* and */ will be ignored by the compiler. You can embellish this sort of comment to make it stand out. For instance:
Whitespace is any sequence of spaces, tabs, newlines, or form feed characters. Whitespace is generally ignored by the compiler, except when it is necessary for syntactic reasons to distinguish one element from another.
Preprocessing Directives and Standard Library Headers
The third line in Figure 1-1 is a preprocessing directive. Preprocessing directives cause the source code to be modified in some way before it is compiled to executable form. This preprocessing directive adds the contents of the Standard Library header file with the name iostream to this source file, Ex1_01.cpp. The header file contents are inserted in place of the #include directive.
Header files , which are sometimes referred to just as headers, contain definitions to be used in a source file. iostream contains definitions that are needed to perform input from the keyboard and text output to the screen using Standard Library routines. In particular, it defines std::cout and std::endl among many other things. If the preprocessing directive to include the iostream header was omitted from Ex1_01.cpp, the source file wouldn’t compile because the compiler would not know what std::cout or std::endl is. The contents of header files are included into a source file before it is compiled. You’ll be including the contents of one or more Standard Library header files into nearly every program, and you’ll also be creating and using your own header files that contain definitions that you construct later in the book.
Caution
There are no spaces between the angle brackets and the standard header file name. With some compilers, spaces are significant between the angle brackets, < and >; if you insert spaces here, the program may not compile.
Functions
A program that is broken down into discrete functions is easier to develop and test.
You can reuse a function in several different places in a program, which makes the program smaller than if you coded the operation in each place that it is needed.
You can often reuse a function in many different programs, thus saving time and effort.
Large programs are typically developed by a team of programmers. Each team member is responsible for programming a set of functions that are a well-defined subset of the whole program. Without a functional structure, this would be impractical.
The program in Figure 1-1 consists of just the function main(). The first line of the function is as follows:
This is called the function header , which identifies the function. Here, int is a type name that defines the type of value that the main() function returns when it finishes execution—an integer. An integer is a number without a fractional component; that is, 23 and -2048 are integers, while 3.1415 and ¼ are not. In general, the parentheses following a name in a function definition enclose the specification for information to be passed to the function when you call it. There’s nothing between the parentheses in this instance, but there could be. You’ll learn how you specify the type of information to be passed to a function when it is executed in Chapter 8. We’ll always put parentheses after a function name in the text—like we did with main()—to distinguish it from other things that are code.
The executable code for a function is always enclosed between curly braces. The opening brace follows the function header.
Statements
A statement is a basic unit in a C++ program. A statement always ends with a semicolon, and it’s the semicolon that marks the end of a statement, not the end of the line. A statement defines something, such as a computation, or an action that is to be performed. Everything a program does is specified by statements. Statements are executed in sequence until there is a statement that causes the sequence to be altered. You’ll learn about statements that can change the execution sequence in Chapter 4. There are three statements in main() in Figure 1-1. The first defines a variable, which is a named bit of memory for storing data of some kind. In this case, the variable has the name answer and can store integer values:
The type, int, appears first, preceding the name. This specifies the kind of data that can be stored—integers. Note the space between int and answer. One or more whitespace characters is essential here to separate the type name from the variable name; without the space, the compiler would see the name intanswer, which it would not understand. An initial value for answer appears between the braces following the variable name, so it starts out storing 42. There’s a space between answer and {42}, but it’s not essential. Any of the following definitions are valid as well:
The compiler mostly ignores superfluous whitespace. However, you should use whitespace in a consistent fashion to make your code more readable.
There’s a somewhat redundant comment at the end of the first statement explaining what we just described, but it does demonstrate that you can add a comment to a statement. The whitespace preceding the // is also not mandatory, but it is desirable.
You can enclose several statements between a pair of curly braces, { }, in which case they’re referred to as a statement block . The body of a function is an example of a block, as you saw in Figure 1-1 where the statements in the main() function appear between curly braces. A statement block is also referred to as a compound statement because in most circumstances it can be considered as a single statement , as you’ll see when we look at decision-making capabilities in Chapter 4, and loops in Chapter 5. Wherever you can put a single statement, you can equally well put a block of statements between braces. As a consequence, blocks can be placed inside other blocks—this concept is called nesting . Blocks can be nested, one within another, to any depth.
Data Input and Output
Input and output are performed using streams in C++. To output something, you write it to an output stream, and to input data, you read it from an input stream. A stream is an abstract representation of a source of data or a data sink. When your program executes, each stream is tied to a specific device that is the source of data in the case of an input stream and the destination for data in the case of an output stream. The advantage of having an abstract representation of a source or sink for data is that the programming is then the same regardless of the device the stream represents. You can read a disk file in essentially the same way as you read from the keyboard. The standard output and input streams in C++ are called cout and cin, respectively, and by default they correspond to your computer’s screen and keyboard. You’ll be reading input from cin in Chapter 2.
The next statement in main() in Figure 1-1 outputs text to the screen:
The statement is spread over three lines, just to show that it’s possible. The names cout and endl are defined in the iostream header file. We’ll explain about the std:: prefix a little later in this chapter. << is the insertion operator that transfers data to a stream. In Chapter 2 you’ll meet the extraction operator, >>, that reads data from a stream. Whatever appears to the right of each << is transferred to cout. Inserting endl to std::cout causes a new line to be written to the stream and the output buffer to be flushed. Flushing the output buffer ensures that the output appears immediately. The statement will produce the following output:
You can add comments to each line of a statement. Here’s an example:
You don’t have to align the double slashes , but it’s common to do so because it looks tidier and makes the code easier to read. Of course, you should not start writing comments just to write them. A comment normally contains useful information that is not immediately obvious from the code.
return Statements
The last statement in main() is a return statement. A return statement ends a function and returns control to where the function was called. In this case, it ends the function and returns control to the operating system. A return statement may or may not return a value. This particular return statement returns 0 to the operating system. Returning 0 to the operating system indicates that the program ended normally. You can return nonzero values such as 1, 2, etc., to indicate different abnormal end conditions. The return statement in Ex1_01.cpp is optional, so you could omit it. This is because if execution runs past the last statement in main(), it is equivalent to executing return 0.
Note
main() is the only function for which omitting return is equivalent to returning zero. Any other function with return type int always has to end with an explicit return statement—the compiler shall never presume to know which value an arbitrary function should return by default.
Namespaces
A large project will involve several programmers working concurrently. This potentially creates a problem with names. The same name might be used by different programmers for different things, which could at least cause some confusion and may cause things to go wrong. The Standard Library defines a lot of names, more than you can possibly remember. Accidental use of Standard Library names could also cause problems. Namespaces are designed to overcome this difficulty.
A namespace is a sort of family name that prefixes all the names declared within the namespace. The names in the Standard Library are all defined within a namespace that has the name std. cout and endl are names from the Standard Library, so the full names are std::cout and std::endl. Those two colons together, ::, have a fancy title: the scope resolution operator. We’ll have more to say about it later. Here, it serves to separate the namespace name, std, from the names in the Standard Library such as cout and endl. Almost all names from the Standard Library are prefixed with std.
The code for a namespace looks like this:
Everything between the braces is within the my_space namespace. You’ll find out more about defining your own namespaces in Chapter 10.
Caution
The main() function must not be defined within a namespace. Things that are not defined in a namespace exist in the global namespace, which has no name.
Names and Keywords
A name can be any sequence of upper or lowercase letters A to Z or a to z, the digits 0 to 9, and the underscore character, _.
A name must begin with either a letter or an underscore.
Names are case sensitive.
The C++ standard allows names to be of any length, but typically a particular compiler will impose some sort of limit. However, this is normally sufficiently large that it doesn’t represent a serious constraint. Most of the time you won’t need to use names of more than 12 to 15 characters.
Here are some valid C++ names:
Uppercase and lowercase are differentiated, so democrat is not the same name as Democrat. You can see a couple examples of conventions for writing names that consist of two or more words; you can capitalize the second and subsequent words or just separate them with underscores.
Names that begin with two consecutive underscores
Names that begin with an underscore followed by an uppercase letter
Within the global namespace: all names that begin with an underscore
While compilers often won’t really complain if you use these, the problem is that such names might clash either with those that are generated by the compiler or with names that are used internally by your Standard Library implementation. Notice that the common denominator with these reserved names is that they all start with an underscore. Thus, our advice is this:
Tip
Do not use names that start with an underscore.
Classes and Objects
A class is a block of code that defines a data type. A class has a name that is the name for the type. An item of data of a class type is referred to as an object. You use the class type name when you create variables that can store objects of your data type. Being able to define your own data types enables you to specify a solution to a problem in terms of the problem. If you were writing a program processing information about students, for example, you could define a Student type. Your Student type could incorporate all the characteristic of a student—such as age, gender, or school record—that was required by the program.
You will learn all about creating your own classes and programming with objects in Chapters 11 through 14. Nevertheless, you’ll be using objects of specific Standard Library types long before that. Examples include vectors in Chapter 5 and strings in Chapter 7. Even the std::cout and std::cin streams are technically objects. But not to worry: you’ll find that working with objects is easy enough, much easier than creating your own classes, for instance. Objects are mostly intuitive in use because they’re mostly designed to behave like real-life entities (although some do model more abstract concepts, such as input or output streams, or low-level C++ constructs, such as data arrays and character sequences).
Templates
You sometimes need several similar classes or functions in a program where the code differs only in the kind of data that is processed. A template is a recipe that you create to be used by the compiler to generate code automatically for a class or function customized for a particular type or types. The compiler uses a class template to generate one or more of a family of classes. It uses a function template to generate functions. Each template has a name that you use when you want the compiler to create an instance of it. The Standard Library uses templates extensively.
Defining function templates is the subject of Chapter 9, and defining class templates is covered in Chapter 16. But, again, you’ll be using some concrete Standard Library templates throughout earlier chapters, such as instantiations of the container class templates in Chapter 5 or certain elementary utility function templates such as std::min() and max().
Code Appearance and Programming Style
The way in which you arrange your code can have a significant effect on how easy it is to understand. There are two basic aspects to this. First, you can use tabs and/or spaces to indent program statements in a manner that provides visual cues to their logic, and you can arrange matching braces that define program blocks in a consistent way so that the relationships between the blocks are apparent. Second, you can spread a single statement over two or more lines when that will improve the readability of your program.
Style 1 | Style 2 | Style 3 |
|---|---|---|
namespace mine { bool has_factor(int x, int y) { int factor{ hcf(x, y) }; if (factor > 1) { return true; } else { return false; } } } | namespace mine { bool has_factor(int x, int y) { int factor{ hcf(x,y) }; if (factor>1) { return true; } else { return false; } } } | namespace mine { bool has_factor(int x, int y) { int factor{ hcf(x, y) }; if (factor > 1) return true; else return false; } } |
We will use Style 1 for examples in the book. Over time, you will surely develop your own, based either on personal preferences or on company policies. It is recommended to, at some point, pick one style that suits you and then use this consistently throughout your code. Not only does a consistent code presentation style look good, but it also makes your code easier to read.
A particular convention for arranging matching braces and indenting statements is only one of several aspects of one’s programming style . Other important aspects include conventions for naming variables, types, and functions, and the use of (structured) comments. The question of what constitutes a good programming style can be highly subjective at times, though some guidelines and conventions are objectively superior. The general idea, though, is that code that conforms to a consistent style is easier to read and understand, which helps to avoid introducing errors. Throughout the book we’ll regularly give you advice as you fashion your own programming style.
Tip
One of the best tips we can give you regarding good programming style is no doubt to choose clear, descriptive names for all your variables, functions, and types.
Creating an Executable
Creating an executable module from your C++ source code is basically a three-step process. In the first step, the preprocessor processes all preprocessing directives. One of its key tasks is to, at least in principle, copy the entire contents of all #included headers into your .cpp files. Other preprocessing directives are discussed in Chapter 10. In the second step, your compiler processes each .cpp file to produce an object file that contains the machine code equivalent of the source file. In the third step, the linker combines the object files for a program into a file containing the complete executable program.
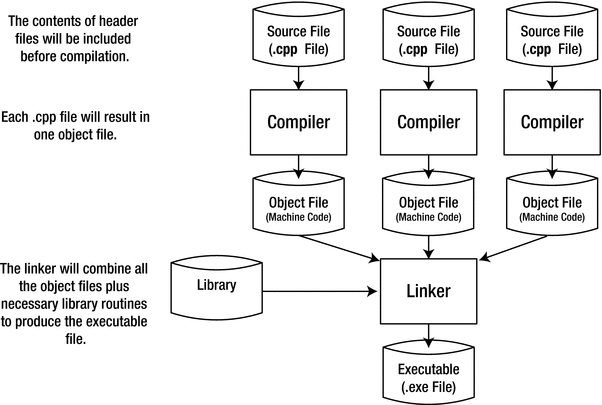
The compile and link process
In the first half of the book, your programs will consist of a single source file. In Chapter 10 we will show you how to compose a larger program , consisting of multiple header and source files.
Note
The concrete steps you have to follow to get from your source code to a functioning executable differ from compiler to compiler. While most of our examples are small enough to compile and link through a series of command-line instructions, it is probably easier to use a so-called integrated development environment (IDE) instead. Modern IDEs offer a very user-friendly graphical user interface to edit, compile, link, run, and debug your programs. References to the most popular compilers and IDEs as well as pointers on how to get started are available from the Apress website ( www.apress.com/book/download.html ) together with the source code of all examples and the solutions to all exercises.
In practice, compilation is an iterative process because you’re almost certain to have made typographical and other errors in the code. Once you’ve eliminated these from each source file, you can progress to the link step, where you may find that yet more errors surface. Even when the link step produces an executable module, your program may still contain logical errors; that is, it doesn’t produce the results you expect. To fix these, you must go back and modify the source code and try to compile it once more. You continue this process until your program works as you think it should. As soon as you declare to the world at large that your program works, someone will discover a number of obvious errors that you should have found. It hasn’t been proven beyond doubt so far as we know, but it’s widely believed that any program larger than a given size will always contain errors. It’s best not to dwell on this thought when flying….
Procedural and Object-Oriented Programming
You create a clear, high-level definition of the overall process that your program will implement.
You segment the overall process into workable units of computation that are, as much as possible, self-contained. These will usually correspond to functions.
You code the functions in terms of processing basic types of data: numerical data, single characters, and character strings.
From the problem specification, you determine what types of objects the problem is concerned with. For example, if your program deals with baseball players, you’re likely to identify BaseballPlayer as one of the types of data your program will work with. If your program is an accounting package, you may well want to define objects of type Account and type Transaction. You also identify the set of operations that the program will need to carry out on each type of object. This will result in a set of application-specific data types that you will use in writing your program.
You produce a detailed design for each of the new data types that your problem requires, including the operations that can be carried out with each object type.
You express the logic of the program in terms of the new data types you’ve defined and the kinds of operations they allow.
The program code for an object-oriented solution to a problem will be completely unlike that for a procedural solution and almost certainly easier to understand. It will also be a lot easier to maintain. The amount of design time required for an object-oriented solution tends to be greater than for a procedural solution. However, the coding and testing phase of an object-oriented program tends to be shorter and less troublesome, so the overall development time is likely to be roughly the same in either case.
To get an inkling of what an objected-oriented approach implies, suppose you’re implementing a program that deals with boxes of various kinds. A feasible requirement of such a program would be to package several smaller boxes inside another, larger box. In a procedural program, you would need to store the length, width, and height of each box in a separate group of variables. The dimensions of a new box that could contain several other boxes would need to be calculated explicitly in terms of the dimensions of each of the contained boxes, according to whatever rules you had defined for packaging a set of boxes.
An object-oriented solution might involve first defining a Box data type. This would enable you to create variables that can reference objects of type Box and, of course, create Box objects. You could then define an operation that would add two Box objects together and produce a new Box object that could contain them. Using this operation, you could write statements like this:
In this context, the + operation means much more than simple addition. The + operator applied to numerical values will work exactly as before, but for Box objects it has a special meaning. Each of the variables in this statement is of type Box. The statement would create a new Box object big enough to contain box1, box2, and box3.
Being able to write statements like this is clearly much easier than having to deal with all the box dimensions separately, and the more complex the operations on boxes you take on, the greater the advantage is going to be. This is a trivial illustration, though, and there’s a great deal more to the power of objects than you can see here. The purpose of this discussion is just to give you an idea of how readily problems solved using an object-oriented approach can be understood. Object-oriented programming is essentially about solving problems in terms of the entities to which the problems relates rather than in terms of the entities that computers are happy with: numbers and characters.
Representing Numbers
Numbers are represented in a variety of ways in a C++ program, and you need to have an understanding of the possibilities. If you are comfortable with binary, hexadecimal, and floating-point number representations, you can safely skip this bit.
Binary Numbers
324 is 3 × 102 + 2 × 101 + 4 × 100, which is 3 × 100 + 2 × 10 + 4 × 1.
911 is 9 × 102 + 1 × 101 + 1 × 100, which is 9 × 100 + 1 × 10 + 1 × 1.
1 × 23 + 1 × 22 + 0 × 21 + 1 × 20, which is 1 × 8 + 1 × 4 + 0 × 2 + 1 × 1
Decimal Equivalents of 8-Bit Binary Values
Binary | Decimal | Binary | Decimal |
|---|---|---|---|
0000 0000 | 0 | 1000 0000 | 128 |
0000 0001 | 1 | 1000 0001 | 129 |
0000 0010 | 2 | 1000 0010 | 130 |
. . . | . . . | . . . | . . . |
0001 0000 | 16 | 1001 0000 | 144 |
0001 0001 | 17 | 1001 0001 | 145 |
. . . | . . . | . . . | . . . |
0111 1100 | 124 | 1111 1100 | 252 |
0111 1101 | 125 | 1111 1101 | 253 |
0111 1110 | 126 | 1111 1110 | 254 |
0111 1111 | 127 | 1111 1111 | 255 |
Using the first seven bits , you can represent positive numbers from 0 to 127, which is a total of 128 different numbers. Using all eight bits, you get 256, or 28, numbers. In general, if you have n bits available, you can represent 2n integers, with positive values from 0 to 2n – 1.
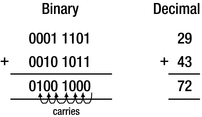
Adding binary values
The addition operation adds corresponding bits in the operands, starting with the rightmost. Figure 1-3 shows that there is a “carry” of 1 to the next bit position for each of the first six bit positions. This is because each digit can be only 0 or 1. When you add 1 + 1, the result cannot be stored in the current bit position and is equivalent to adding 1 in the next bit position to the left.
Hexadecimal Numbers
1111 0101 1011 1001 1110 0001
Binary notation here starts to be more than a little cumbersome for practical use, particularly when you consider that this in decimal is only 16,103,905—a miserable eight decimal digits. You can sit more angels on the head of a pin than that! Clearly you need a more economical way of writing this, but decimal isn’t always appropriate. You might want to specify that the 10th and 24th bits from the right in a number are 1, for example. Figuring out the decimal integer for this is hard work, and there’s a good chance you’ll get it wrong anyway. An easier solution is to use hexadecimal notation, in which the numbers are represented using base 16.
Hexadecimal Digits and Their Values in Decimal and Binary
Hexadecimal | Decimal | Binary |
|---|---|---|
0 | 0 | 0000 |
1 | 1 | 0001 |
2 | 2 | 0010 |
3 | 3 | 0011 |
4 | 4 | 0100 |
5 | 5 | 0101 |
6 | 6 | 0110 |
7 | 7 | 0111 |
8 | 8 | 1000 |
9 | 9 | 1001 |
A or a | 10 | 1010 |
B or b | 11 | 1011 |
C or c | 12 | 1100 |
D or d | 13 | 1101 |
E or e | 14 | 1110 |
F or f | 15 | 1111 |
1111 0101 1011 1001 1110 0001
F 5 B 9 E 1
15 × 165 + 5 × 164 + 11 × 163 + 9 × 162 + 14 × 161 + 1 × 160
Thankfully, this adds up to the same number you got when converting the equivalent binary number to a decimal value: 16,103,905. In C++, hexadecimal values are written with 0x or 0X as a prefix, so in code the value would be written as 0xF5B9E1. Obviously, this means that 99 is not at all the same as 0x99.
The other handy coincidence with hexadecimal numbers is that modern computers store integers in words that are an even number of bytes, typically 2, 4, 8, or 16 so-called bytes. A byte is 8 bits, which is exactly two hexadecimal digits, so any binary integer word in memory always corresponds to an exact number of hexadecimal digits.
Negative Binary Numbers
There’s another aspect to binary arithmetic that you need to understand: negative numbers. So far, we’ve assumed that everything is positive—the optimist’s view—and so the glass is still half-full. But you can’t avoid the negative side of life—the pessimist’s perspective—that the glass is already half-empty. But how is a negative number represented in a modern computer? You’ll see shortly that the answer to this seemingly easy question is actually far from obvious….
Integers that can be both positive and negative are referred to as signed integers . Naturally, you only have binary digits at your disposal to represent numbers. At the end of the day, any language your computer speaks shall consist solely of bits and bytes. As you know, your computer’s memory is generally composed of 8-bit bytes, so all binary numbers are going to be stored in some multiple (usually a power of 2) of 8 bits. Thus, you can also only have signed integers with 8 bits, 16 bits, 32 bits, or whatever.
A straightforward representation of signed integers therefore consists of a fixed number of binary digits, where one of these bits is designated as a so-called sign bit. In practice, the sign bit is always chosen to be the leftmost bit. Say we fix the size of all our signed integers to 8 bits; then the number 6 could be represented as 00000110, and -6 could be represented as 10000110. Changing +6 to –6 just involves flipping the sign bit from 0 to 1. This is called a signed magnitude representation: each number consists of a sign bit that is 0 for positive values and 1 for negative values, plus a given number of other bits that specify the magnitude or absolute value of the number (the value without the sign in other words).
While signed magnitude representations are easy to work with for humans, they have one unfortunate downside: they are not at all easy to work with for computers! More specifically, they carry a lot of overhead in terms of the complexity of the circuits that are needed to perform arithmetic. When two signed integers are added, for instance, you don’t want the computer to be messing about, checking whether either or both of the numbers are negative. What you really want is to use the same simple and very fast “add” circuitry regardless of the signs of the operands.
12 in binary is | 00001100 |
–8 in binary (you suppose) is | 10001000 |
If you now “add” these together, you get | 10010100 |
This seems to give –20, which of course isn’t what you wanted at all. It’s definitely not +4, which you know is 00000100. “Ah,” we hear you say, “you can’t treat a sign just like another digit.” But that is just what you do want to do to speed up binary computations!
- 1.
You start with +8 in binary: 00001000.
- 2.
You then “flip” each binary digit, changing 0s to 1s, and vice versa: 11110111.
This is called the 1’s complement form.
- 3.
If you now add 1 to this, you get the 2’s complement form of -8: 11111000.
Note that this works both ways. To convert the 2’s complement representation of a negative number back into the corresponding positive binary number, you again flip all bits and add one. For our example, flipping 11111000 gives 00000111, adding one to this gives 00001000, or +8 in decimal. Magic!
+12 in binary is | 00001100 |
The 2’s complement representation of –8 is | 11111000 |
If you add these together, you get | 00000100 |
The answer is 4—it works! The “carry” propagates through all the leftmost 1s, setting them back to 0. One fell off the end, but you shouldn’t worry about that—it’s probably compensating for the one you borrowed from the end in the subtraction you did to get –8. In fact, what’s happening is that you’re implicitly assuming that the sign bit, 1 or 0, repeats forever to the left. Try a few examples of your own; you’ll find it always works, like magic. The great thing about the 2’s complement representation of negative numbers is that it makes arithmetic—and not just addition, by the way—very easy for your computer. And that accounts for one of the reasons computers are so good at crunching numbers.
Octal Values
Octal integers are numbers expressed with base 8. Digits in an octal value can only be from 0 to 7. Octal is used rarely these days. It was useful in the days when computer memory was measured in terms of 36-bit words because you could specify a 36-bit binary value by 12 octal digits. Those days are long gone, so why are we introducing it? The answer is the potential confusion it can cause. You can still write octal constants in C++. Octal values are written with a leading zero, so while 76 is a decimal value, 076 is an octal value that corresponds to 62 in decimal. So, here’s a golden rule:
Caution
Never write decimal integers in your source code with a leading zero. You'll get a value different from what you intended!
Bi-Endian and Little-Endian Systems
Integers are stored in memory as binary values in a contiguous sequence of bytes, commonly groups of 2, 4, 8, or 16 bytes. The question of the sequence in which the bytes appear can be important—it’s one of those things that doesn’t matter until it matters, and then it really matters.
00000000 00000100 00000010 00000001
Byte address: | 00 | 01 | 02 | 03 |
Data bits: | 00000001 | 00000010 | 00000100 | 00000000 |
As you can see, the most significant eight bits of the value—the one that’s all 0s—are stored in the byte with the highest address (last, in other words), and the least significant eight bits are stored in the byte with the lowest address, which is the leftmost byte. This arrangement is described as little-endian. Why on earth, you wonder, would a computer reverse the order of these bytes? The motivation, as always, is rooted in the fact that it allows for more efficient calculations and simpler hardware. The details don’t matter much; the main thing is that you’re aware that most modern computers these days use this counterintuitive encoding.
Byte address: | 00 | 01 | 02 | 03 |
Data bits: | 00000000 | 00000100 | 00000010 | 00000001 |
Now the bytes are in reverse sequence with the most significant eight bits stored in the leftmost byte, which is the one with the lowest address. This arrangement is described as bi-endian. Some processors such as PowerPC and all recent ARM processors are bi-endian, which means that the byte order for data is switchable between bi-endian and little-endian.
Note
Regardless of whether the byte order is bi-endian or little-endian, the bits within each byte are arranged with the most significant bit on the left and the least significant bit on the right.
This is all very interesting, you may say, but when does it matter? Most of the time, it doesn’t. More often than not, you can happily write a program without knowing whether the computer on which the code will execute is bi-endian or little-endian. It does matter, however, when you’re processing binary data that comes from another machine. You need to know the endianness. Binary data is written to a file or transmitted over a network as a sequence of bytes. It’s up to you how you interpret it. If the source of the data is a machine with a different endianness from the machine on which your code is running, you must reverse the order of the bytes in each binary value. If you don’t, you have garbage.
For those who collect curious background information, the terms bi-endian and little-endian are drawn from the book Gulliver’s Travels by Jonathan Swift. In the story, the emperor of Lilliput commanded all his subjects to always crack their eggs at the smaller end. This was a consequence of the emperor’s son having cut his finger following the traditional approach of cracking his egg at the big end. Ordinary, law-abiding Lilliputian subjects who cracked their eggs at the smaller end were described as Little Endians. The Big Endians were a rebellious group of traditionalists in the Lilliputian kingdom who insisted on continuing to crack their eggs at the big end. Many were put to death as a result.
Floating-Point Numbers
All integers are numbers, but of course not all numbers are integers: 3.1415 is no integer, and neither is -0.00001. Many applications will have to deal with fractional numbers at one point or another. So clearly you need a way to represent such numbers on your computer as well, complemented with the ability to efficiently perform computations with them. The mechanism nearly all computers support for handling fractional numbers, as you may have guessed from the section title, is called floating-point numbers.
Floating-point numbers do not just represent fractional numbers, though. As an added bonus, they are able to deal with very large numbers as well. They allow you to represent, for instance, the number of protons in the universe, which needs around 79 decimal digits (though of course not accurate within one particle, but that’s OK—who has the time to count them all anyway?). Granted, the latter is perhaps somewhat extreme, but clearly there are situations in which you’ll need more than the ten decimal digits you get from a 32-bit binary integer, or even more than the 19 you can get from a 64-bit integer. Equally, there are lots of very small numbers, for example, the amount of time in minutes it takes the typical car salesperson to accept your generous offer on a 2001 Honda (and it’s covered only 480,000 miles…). Floating-point numbers are a mechanism that can represent both these classes of numbers quite effectively.
We’ll first explain the basic principles using decimal floating-point numbers. Of course, your computer will again use a binary representation instead, but things are just so much easier to understand for us humans when we use decimal numbers. A so-called normalized number consists of two parts: a mantissa or fraction and an exponent. Both can be either positive or negative. The magnitude of the number is the mantissa multiplied by 10 to the power of the exponent. In analogy with the binary floating-point number representations of your computer, we’ll moreover fix the number of decimal digits of both the mantissa and the exponent.
It’s easier to demonstrate this than to describe it, so let’s look at some examples. The number 365 could be written in a floating-point form, as follows:
The mantissa here has seven decimal digits, the exponent two. The E stands for “exponent” and precedes the power of 10 that the 3.650000 (the mantissa) part is multiplied by to get the required value. That is, to get back to the regular decimal notation, you simply have to compute the following product: 3.650000 × 102. This is clearly 365.
Now let’s look at a small number:
This is evaluated as -3.65 × 10-3, which is -0.00365. They’re called floating-point numbers for the fairly obvious reason that the decimal point “floats” and its position depends on the exponent value.
Now suppose you have a larger number such as 2,134,311,179. Using the same amount of digits, this number looks like this:
It’s not quite the same. You’ve lost three low-order digits, and you’ve approximated your original value as 2,134,311,000. This is the price to pay for being able to handle such a vast range of numbers: not all these numbers can be represented with full precision; floating-point numbers in general are only approximate representations of the exact number.
Aside from the fixed-precision limitation in terms of accuracy, there’s another aspect you may need to be conscious of. You need to take great care when adding or subtracting numbers of significantly different magnitudes. A simple example will demonstrate the problem. Consider adding 1.23E-4 to 3.65E+6. The exact result, of course, is 3,650,000 + 0.000123, or 3,650,000.000123. But when converted to floating-point with seven digits of precision, this becomes the following:
Adding the latter, smaller number to the former has had no effect whatsoever, so you might as well not have bothered. The problem lies directly with the fact that you carry only seven digits of precision. The digits of the larger number aren’t affected by any of the digits of the smaller number because they’re all further to the right.
Funnily enough, you must also take care when the numbers are nearly equal. If you compute the difference between such numbers, most numbers may cancel each other out, and you may end up with a result that has only one or two digits of precision. This is referred to as catastrophic cancellation, and it’s quite easy in such circumstances to end up computing with numbers that are totally garbage.
While floating-point numbers enable you to carry out calculations that would be impossible without them, you must always keep their limitations in mind if you want to be sure your results are valid. This means considering the range of values that you are likely to be working with and their relative values. The field that deals with analyzing and maximizing the precision—or numerical stability—of mathematical computations and algorithms is called numerical analysis. This is an advanced topic, though, and well outside the scope of this book. Suffice to say that the precision of floating-point numbers is limited and that the order and nature of arithmetic operations you perform with them can have a significant impact on the accuracy of your results.
Your computer, of course, again does not work with decimal numbers; rather, it works with binary floating-point representations. Bits and bytes, remember? Concretely, nearly all computers today use the encoding and computation rules specified by the IEEE 754 standard. Left to right, each floating-point number then consists of a single sign bit, followed by a fixed number of bits for the exponent, and finally another series of bits that encode the mantissa. The most common floating-point numbers representations are the so-called single precision (1 sign bit, 8 bits for the exponent, and 23 for the mantissa, adding up to 32 bits in total) and double precision (1 + 11 + 52 = 64 bits) floating-point numbers.
Floating-point numbers can represent huge ranges of numbers. A single-precision floating-point number, for instance, can already represent numbers ranging from 10-38 to 10+38. Of course, there’s a price to pay for this flexibility: the number of digits of precision is limited. You know this already from before, and it’s also only logical; of course not all 38 digits of all numbers in the order of 10+38 can be represented exactly using 32 bits. After all, the largest signed integer a 32-bit binary integer can represent exactly is only 231 - 1, which is about 2 × 10+9. The number of decimal digits of precision in a floating-point number depends on how much memory is allocated for its mantissa. A single-precision floating-point value, for instance, provides approximately seven decimal digits accuracy. We say “approximately” because a binary fraction with 23 bits doesn’t exactly correspond to a decimal fraction with seven decimal digits. A double-precision floating-point value corresponds to around 16 decimal digits accuracy.
Representing Characters
Data inside your computer has no intrinsic meaning. Machine code instructions are just numbers: of course numbers are just numbers, but so are, for instance, characters. Each character is assigned a unique integer value called its code or code point. The value 42 can be the atomic number of molybdenum; the answer to life, the universe, and everything; or an asterisk character. It all depends on how you choose to interpret it. You can write a single character in C++ between single quotes, such as 'a' or '?' or '*', and the compiler will generate the code value for these.
ASCII Codes
Way back in the 1960s, the American Standard Code for Information Interchange (ASCII) was defined for representing characters. This is a 7-bit code, so there are 128 different code values. ASCII values 0 to 31 represent various nonprinting control characters such as carriage return (code 15) and line feed (code 12). Code values 65 to 90 inclusive are the uppercase letters A to Z, and 97 to 122 correspond to lowercase a to z. If you look at the binary values corresponding to the code values for letters, you’ll see that the codes for lowercase and uppercase letters differ only in the sixth bit; lowercase letters have the sixth bit as 0, and uppercase letters have the sixth bit as 1. Other codes represent digits 0 to 9, punctuation, and other characters.
The original 7-bit ASCII is fine if you are American or British, but if you are French or German, you need things like accents and umlauts in text, which are not included in the 128 characters that 7-bit ASCII encodes. To overcome the limitations imposed by a 7-bit code, extended versions of ASCII were defined with 8-bit codes. Values from 0 to 127 represent the same characters as 7-bit ASCII, and values from 128 to 255 are variable. One variant of 8-bit ASCII that you have probably met is called Latin-1, which provides characters for most European languages, but there are others for languages such as Russian.
If you speak Korean, Japanese, Chinese, or Arabic, an 8-bit coding is totally inadequate. To give you an idea, modern encodings of Chinese, Japanese, and Korean scripts (which share a common background) cover nearly 88,000 characters—a tiny bit more than the 256 characters you’re able to get out of 8 bits! To overcome the limitations of extended ASCII, the Universal Character Set (UCS) emerged in the 1990s. UCS is defined by the standard ISO 10646 and has codes with up to 32 bits. This provides the potential for hundreds of millions of unique code values.
UCS and Unicode
UCS defines a mapping between characters and integer code values, called code points. It is important to realize that a code point is not the same as an encoding. A code point is an integer; an encoding specifies a way of representing a given code point as a series of bytes or words. Code values of less than 256 are popular and can be represented in one byte. It would be inefficient to use four bytes to store code values that require just one byte just because there are other codes that require several bytes. Encodings are ways of representing code points that allow them to be stored more efficiently.
Unicode is a standard that defines a set of characters and their code points identical to those in UCS. Unicode also defines several different encodings for these code points and includes additional mechanisms for dealing with such things as right-to-left languages such as Arabic. The range of code points is more than enough to accommodate the character sets for all the languages in the world, as well as many different sets of graphical characters such as mathematical symbols, or even emoticons and emojis. Regardless, the codes are arranged such that strings in the majority of languages can be represented as a sequence of single 16-bit codes.
UTF-8 represents a character as a variable-length sequence of between 1 and 4 bytes. The ASCII character set appears in UTF-8 as single byte codes that have the same codes values as ASCII. Most web pages use UTF-8 to encode text.
UTF-16 represents characters as one or two 16-bit values. UTF-16 includes UTF-8. Because a single 16-bit value accommodates all of code plane 0, UTF-16 covers most situations in programming for a multilingual context.
UTF-32, you guessed it, simply represents all characters as 32-bit values.
You have four integer types that store Unicode characters. These are types char, wchar_t, char16_t, and char32_t. You’ll learn more about these in Chapter 2.
C++ Source Characters
The letters a to z and A to Z
The digits 0 to 9
The whitespace characters space, horizontal tab, vertical tab, form feed, and newline
The characters _ { } [ ] # ( ) < > % : ; . ? * + - / ^ & | ∼ ! = , \ ” ’
This is easy and straightforward. You have 96 characters that you can use, and it’s likely that these will accommodate your needs most of the time. Most of the time the basic source character set will be adequate, but occasionally you’ll need characters that aren’t in it. You can, at least in theory, include Unicode characters in a name. You specify a Unicode character in the form of a hexadecimal representation of its code point, either as \udddd or as \Udddddddd, where d is a hexadecimal digit. Note the lowercase u in the first case and the uppercase U in the second; either is acceptable. Compiler support for Unicode characters in names is limited, though. Both character and string data can include Unicode characters.
Escape Sequences
Escape Sequences That Represent Control Characters
Escape Sequence | Control Character |
|---|---|
\n | Newline |
\t | Horizontal tab |
\v | Vertical tab |
\b | Backspace |
\r | Carriage return |
\f | Form feed |
\a | Alert/bell |
Escape Sequences That Represent “Problem” Characters
Escape Sequence | “Problem” Character |
|---|---|
\\ | Backslash |
\' | Single quote |
\" | Double quote |
Because the backslash signals the start of an escape sequence, the only way to enter a backslash as a character constant is by using two successive backslashes (\\).
This program that uses escape sequences outputs a message to the screen. To see it, you’ll need to enter, compile, link, and execute the code:
When you manage to compile, link, and run this program, you should see the following output displayed:
The output is determined by what’s between the outermost double quotes in the following statement:
In principle, everything between the outer double quotes in the preceding statement gets sent to cout. A string of characters between a pair of double quotes is called a string literal . The double quote characters are delimiters that identify the beginning and end of the string literal; they aren’t part of the string. Each escape sequence in the string literal will be converted to the character it represents by the compiler, so the character will be sent to cout, not the escape sequence itself. A backslash in a string literal always indicates the start of an escape sequence, so the first character that’s sent to cout is a double quote character.
Least followed by a space is output next. This is followed by a single quote character, then said, followed by another single quote. Next is a space, followed by the backslash specified by \\. Then a newline character corresponding to \n is written to the stream so the cursor moves to the beginning of the next line. You then send two tab characters to cout with \t\t, so the cursor will be moved two tab positions to the right. The word soonest is output next followed by a space and then mended between single quotes. Finally, a period is output followed by a double quote.
Note
If you’re no fan of escape sequences, Chapter 7 will introduce a possible alternative to them called raw string literals.
The truth is, in our enthusiasm for showcasing character escaping, we may have gone a bit overboard in Ex1_02.cpp. You actually do not have to escape the single quote character, ', inside string literals ; there’s already no possibility for confusion. So, the following statement would have worked just fine already:
It’s only when within a character literal of the form '\'' that a single quote really needs escaping. Conversely, double quotes, of course, won’t need a backslash then; your compiler will happily accept both '\"' and '"'. But we’re getting ahead of ourselves: character literals are more a topic of the next chapter.
Note
The \t\t escape sequences in Ex1_02 are, strictly speaking, not required either—you could in principle type tabs in a string literal as well (as in "\"Least 'said' \\\n soonest 'mended'.\""). Using \t\t is nevertheless recommended; the problem with tabs is that one generally cannot tell the difference between a tab, " ", and a number of spaces, " ", let alone properly count the number of tabs. Also, some text editors tend to convert tabs into spaces upon saving. It’s therefore not uncommon for style guides to require the use of the \t escape sequence in string literals.
Summary
A C++ program consists of one or more functions, one of which is called main(). Execution always starts with main().
The executable part of a function is made up of statements contained between braces.
A pair of curly braces is used to enclose a statement block.
A statement is terminated by a semicolon.
Keywords are reserved words that have specific meanings in C++. No entity in your program can have a name that coincides with a keyword.
A C++ program will be contained in one or more files. Source files contain the executable code, and header files contain definitions used by the executable code.
The source files that contain the code defining functions typically have the extension .cpp.
Header files that contain definitions that are used by a source file typically have the extension .h.
Preprocessor directives specify operations to be performed on the code in a file. All preprocessor directives execute before the code in a file is compiled.
The contents of a header file are added into a source file by an #include preprocessor directive.
The Standard Library provides an extensive range of capabilities that supports and extends the C++ language.
Access to Standard Library functions and definitions is enabled through including Standard Library header files in a source file.
Input and output are performed using streams and involve the use of the insertion and extraction operators, << and >> . std::cin is a standard input stream that corresponds to the keyboard. std::cout is a standard output stream for writing text to the screen. Both are defined in the iostream Standard Library header.
Object-oriented programming involves defining new data types that are specific to your problem. Once you’ve defined the data types that you need, a program can be written in terms of the new data types.
Unicode defines unique integer code values that represent characters for virtually all of the languages in the world as well as many specialized character sets. Code values are referred to as code points. Unicode also defines how these code points may be encoded as byte sequences.
Exercises
Exercise 1-1: Create, compile, link, and execute a program that will display the text "Hello World" on your screen.
Exercise 1-2: Create and execute a program that outputs your name on one line and your age on the next line.
Exercise 1-3: The following program produces several compiler errors. Find these errors and correct them so the program can compile cleanly and run.
