An array enables you to work with several data items of the same type using a single name, the array name. The need for this occurs often—when working with a series of temperatures or the ages of a group of people, for example. A loop is another fundamental programming facility. It provides a mechanism for repeating one or more statements as many times as your application requires. Loops are essential in the majority of programs. Using a computer to calculate the company payroll, for example, would not be practicable without a loop. There are several kinds of loop, each with their own particular area of application.
What an array is and how you create an array
How to use a for loop
How the while loop works
What the merits of the do-while loop are
What the break and continue statements do in a loop
What the continue statement does in a loop
How to use nested loops
How to create and use an array container
How to create and use a vector container
Arrays
The variables you have created up to now can store only a single data item of the specified type—an integer, a floating-point value, a character, or a bool value. An array stores several data items of the same type. You can create an array of integers or an array of characters (or in fact an array of any type of data), and there can be as many as the available memory will allow.
Using an Array
An array is a variable that represents a sequence of memory locations, each storing an item of data of the same data type. Suppose, for instance, you’ve written a program to calculate the average temperature. You now want to extend the program to calculate how many samples are above that average and how many are below. You’ll need to retain the original sample data to do this, but storing each data item in a separate variable would be tortuous to code and highly impractical. An array provides you with the means of doing this easily. You could store 366 temperature samples in an array defined as follows:
This defines an array with the name temperatures to store 366 values of type double. The data values are called elements. The number of elements specified between the brackets is the size of the array. The array elements are not initialized in this statement, so they contain junk values.
The size of an array must always be specified using a constant integer expression. Any integer expression that the compiler can evaluate at compile time may be used, though mostly this will be either an integer literal or a const integer variable that itself was initialized using a literal.
You refer to an array element using an integer called an index. The index of a particular array element is its offset from the first element. The first element has an offset of 0 and therefore an index of 0; an index value of 3 refers to the fourth array element—three elements from the first. To reference an element, you put its index between square brackets after the array name, so to set the fourth element of the temperatures array to 99.0, you would write the following:
While an array of 366 elements nicely illustrates the need of arrays—just imagine having to define 366 distinct variables—creating figures with that many elements would be somewhat cumbersome. Let’s therefore look at another array:
The compiler will allocate six contiguous storage locations for storing values of type unsigned int as a result of this definition. Each element in the height array contains a different number. Because the definition of height doesn’t specify any initial values for the array, the six elements will contain junk values (analogous to what happens if you define a single variable of type unsigned int without an initial value). You could define the array with proper initial values like this:

An array with six elements
Note
The type of the array will determine the amount of memory required for each element. The elements of an array are stored in one contiguous block of memory. So if the unsigned int type is 4 bytes on your computer, the height array will occupy 24 bytes.
The initializer must not have more values than there are elements in the array; otherwise, the statement won’t compile. There can be fewer values in the list, however, in which case the elements for which no initial value has been supplied will be initialized with zero (false for an array of bool elements). Here’s an example:
The first three elements will have the values that appear in the list. The last three will be zero. To initialize all the elements with zero, you can just use an empty initializer:
To define an array of values that cannot be modified, you simply add the keyword const to its type. The following defines an array of six unsigned int constants:
Any modification to either one of these six array elements (be it an assignment, increment, or any other modification) will now be prevented by the compiler.
Array elements participate in arithmetic expressions like other variables. You could sum the first three elements of height like this:
You use references to individual array elements such as ordinary integer variables in an expression. As you saw earlier, an array element can be on the left of an assignment to set a new value, so you can copy the value of one element to another in an assignment, like this:
However, you can’t copy all the element values from one array to the elements of another in an assignment. You can operate only on individual elements. To copy the values of one array to another, you must copy the values one at a time. What you need is a loop.
Understanding Loops
A loop is a mechanism that enables you to execute a statement or block of statements repeatedly until a particular condition is met. Two essential elements make up a loop: the statement or block of statements that is to be executed repeatedly forms the so-called body of the loop, and a loop condition of some kind that determines when to stop repeating the loop. A single execution of a loop’s body is called an iteration.
Execute a loop a given number of times
Execute a loop until a given value exceeds another value
Execute the loop until a particular character is entered from the keyboard
Execute a loop for each element in a collection of elements
The for loop primarily provides for executing the loop a prescribed number of times, but there is considerable flexibility beyond that.
The range-based for loop executes one iteration for each element in a collection of elements.
The while loop continues executing as long as a specified condition is true. The condition is checked at the beginning of an iteration, so if the condition starts out as false, no loop iterations are executed.
The do-while loop continues to execute as long as a given condition is true. This differs from the while loop in that the do-while loop checks the condition at the end of an iteration. This implies that at least one loop iteration always executes.
We’ll start by explaining how the for loop works.
The for Loop
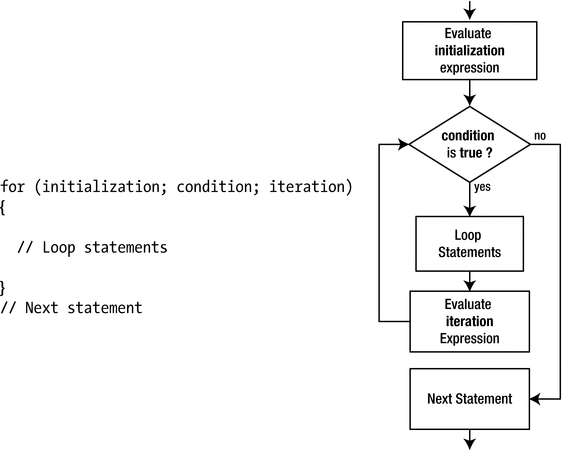
The logic of the for loop
You can omit any or all of the expressions controlling a for loop, but you must always include the semicolons. We’ll explain later in this chapter why and when you might omit one or other of the control expressions. The initialization expression is evaluated only once, at the beginning of the loop. The loop condition is checked next, and if it is true, the loop statement or statement block executes. If the condition is false, the loop ends, and execution continues with the statement after the loop. After each execution of the loop statement or block, the iteration expression is evaluated, and the condition is checked to decide whether the loop should continue.
In the most typical usage of the for loop, the first expression initializes a counter, the second expression checks whether the counter has reached a given limit, and the third expression increments the counter. For example, you could copy the elements from one array to another like this:
The first expression defines i as type size_t with an initial value of 0. You might remember the size_t type from the values returned by the sizeof operator. It is an unsigned integer type that is generally used, for instance, for sizes and counts of things. As i will be used to index the arrays, using size_t makes sense. The second expression, the loop condition, is true as long as i is less than 12, so the loop continues while i is less than 12. When i reaches 12, the expression will be false, so the loop ends. The third expression increments i at the end of each loop iteration, so the loop block that copies the ith element from rainfall to copy will execute with values of i from 0 to 11.
Note
size_t is not the name of a built-in fundamental type such as int, long, or double; it is a type alias defined by the Standard Library. More specifically, it is an alias for one of the unsigned integer types, sufficiently large to contain the size of any type the compiler supports (including any array). The alias is defined in the cstddef header, as well as in a number of other headers. In practice, however, you mostly do not need to include (with #include) any of these headers explicitly to use the size_t alias; the alias is often indirectly defined already by including other more high-level headers (such as the iostream header used by most of our examples).
Caution
Array index values are not checked to verify that they are valid. It’s up to you to make sure that you don’t reference elements outside the bounds of the array. If you store data using an index value that’s outside the valid range for an array, you’ll either inadvertently overwrite something in memory or cause a so-called segmentation fault or access violation (both terms are synonymous and denote an error that is raised by the operating system if and when it detects unauthorized memory access). Either way, your program will almost certainly come to a sticky end.
As always, the compiler ignores all whitespace within the for statement. Also, if the loop’s body consists of only a single statement, the curly braces are again optional. So, if you like, you could format the for loop from before like this:
In this book, we will follow the convention to put a single space after the for keyword (to differentiate loops from function calls), to put no spaces before the two semicolons (like with any other statement), and to generally use curly braces even for single-statement loop bodies (for better visual identification of loop bodies). You are free to follow any coding style you prefer, of course.
Not only is it legal to define variables such as i within a for loop initialization expression, it is common. This has some significant implications. A loop defines a scope. The loop statement or block, including any expressions that control the loop, falls within the scope of a loop. Any automatic variables declared within the scope of a loop do not exist outside it. Because i is defined in the first expression, it is local to the loop, so when the loop ends, i will no longer exist. When you need to be able to access the loop control variable after the loop ends, you just define it before the loop, like this:
Now you can access i after the loop—its value will then be 12 in this case. i is initialized to 0 in its definition, so the first loop control expression is superfluous. You can omit any or all of the loop control expressions, so the loop can be written as follows:
The loop works just as before. We’ll discuss omitting other control expressions a little later in this chapter.
Note
At the end of the previous chapter we told you that C++17 has introduced new syntax for initialization statements for if and switch statements. These initialization statements are modeled after, and are therefore completely analogous to, those of for loops. The only difference is that with a for loop you cannot omit the first semicolon when forsaking the initialization statement.
Avoiding Magic Numbers
One minor problem with the code fragments in the preceding section is that they involve the “magic number” 12 for the array sizes. Suppose they invented a 13th month—Undecimber—and you had to add a rainfall value for that month. Then it wouldn’t be unthinkable that after increasing the size of the rainfall array, you’d forget to update the 12 in the for loop. This is how bugs creep in!
A safer solution already is to define a const variable for the array size and use that instead of the explicit value:
This is much less error prone, and it is clear that size is the number of elements in both arrays.
Tip
If the same constant is scattered around your code, it is easy to make a mistake by forgetting to update some of them. Therefore, define magic numbers, or any constant variable for that matter, only once. If you then have to change the constant, you have to do so in only one place.
Let’s try a for loop in a complete example:
The output is as follows:
The definition of the height array uses a const variable to specify the number of elements. The size variable is also used as the limit for the control variable in the two for loops. The first for loop iterates over each height element in turn, adding its value to total. The loop ends when the loop variable i is equal to size, and the statement following the loop is executed, which defines the average variable with the initial value as total divided by size.
After outputting the average height, the second for loop iterates over the elements in the array, comparing each value with average. The count variable is incremented each time an element is less than average, so when the loop ends, count will contain the number of elements less than average.
Incidentally, you could replace the if statement in the loop with this statement:
This works because the bool value that results from the comparison will be implicitly converted to an integer. The value true converts to 1, and false converts to 0, so count will be incremented only when the comparison results in true. However, while this new code is clever and fun, just the fact that it needs to be explained should be enough to stick with the original if statement instead. Always prefer code that reads (almost) like plain English over clever code!1
Defining the Array Size with the Braced Initializer
You can omit the size of the array when you supply one or more initial values in its definition. The number of elements will be the number of initial values. Here’s an example:
This defines an array with three elements of type int that will have the initial values 2, 3, and 4. It is equivalent to writing this:
The advantage of omitting the size is that you can’t get the array size wrong; the compiler determines it for you.
Determining the Size of an Array
You saw earlier how you can avoid magic numbers for the number of elements in an array by defining a constant initialized with the array size. You also don’t want to be specifying a magic number for the array size when you let the compiler decide the number of elements from the braced initializer list. You need a fool-proof way of determining the size when necessary.
If your implementation supports it, the easiest and recommended way is to use the std::size() function provided by the array header of the Standard Library.2 Suppose you’ve defined this array:
Then you can use the expression std::size(values) to obtain the array’s size, 10.
Note
The std::size() function works not only for arrays; you can also use it as an alternative means to obtain the size of just about any collection of elements defined by the Standard Library, including the std::vector<> and std::array<> containers we will introduce later in this chapter.
At the time of writing, the handy std::size() helper function is still quite new; it was added to the Standard Library in C++17. Before, people often used a different technique based on the sizeof operator. You know from Chapter 2 that the sizeof operator returns the number of bytes that a variable occupies. This works with an entire array as well as with a single array element. Thus, the sizeof operator provides a way to determine the number of elements in an array; you just divide the size of the array by the size of a single element. Let’s try both:
This example produces the following output:
The number of elements in the values array is determined by the compiler from the number of initializing values in the definition. The first output statement uses the sizeof operator to calculate the number of array elements. The expression sizeof(values) evaluates to the number of bytes occupied by the entire array, and the expression sizeof(values[0]) evaluates to the number of bytes occupied by a single element—any element will do, but usually one takes the first element. The expression sizeof(values) / sizeof(values[0]) divides the number of bytes occupied by the whole array by the number of bytes for one element, so this evaluates to the number of elements in the array.
In the for loop, we use std::size() to control the number of iterations. Clearly, std::size() is much easier to use and understand than the old sizeof-based expression. So, if possible, you should always use std::size().
The for loop itself determines the sum of the array elements. None of the control expressions has to be of a particular form. You have seen that you can omit the first control expression. In the for loop in the example, you could accumulate the sum of the elements within the third loop control expression. The loop would then become the following:
The third loop control expression now does two things: it adds the value of the element at index i to sum, and then it increments the control variable, i. Note that earlier i was incremented using the prefix ++ operator, whereas now it is incremented using the postfix ++ operator. This is essential here to ensure the element selected by i is added to sum before i is incremented. If you use the prefix form, you get the wrong answer for the sum of the elements; you’ll also use an invalid index value that accesses memory beyond the end of the array.
The single semicolon at the end of the line is an empty statement that constitutes the loop’s body. In general, this is something to watch out for; you should never add a semicolon prior to a loop’s body. In this case, however, it works because all calculations occur within the loop’s control expressions already. An alternative, clearer way of writing a loop with an empty body is this:
Caution
Performing actions beyond incrementing the loop index variable in the for loop’s increment expression (the third and last components between the round parentheses) is unconventional, to say the least. In our example, it is far more common to simply update the sum variable in the loop’s body, as in Ex5_02. We only showed you these alternatives here to give you a feeling of what is possible in principle. In general, however, you should always prefer conventional and clear code over code that is compact and clever!
Controlling a for Loop with Floating-Point Values
The for loop examples so far have used an integer variable to control the loop, but you can use anything you like. The following code fragment uses floating-point values to control the loop:
This loop is controlled by the radius variable, which is of type double. It has an initial value of 2.5 and is incremented at the end of each loop iteration until it exceeds 20.0, whereupon the loop ends. The loop statement calculates the area of a circle for the current value of radius, using the standard formula πr 2, where r is the radius of the circle. The manipulator setw() in the loop statement gives each output value the same field width; this ensures that the output values line up vertically. Of course, to use the manipulators in a program, you need to include the iomanip header.
You need to be careful when using a floating-point variable to control a for loop. Fractional values may not be representable exactly as a binary floating-point number. This can lead to some unwanted side effects, as this complete example demonstrates:
On our test system, this produces the following output:
The loop includes an if statement to output three sets of values per line. You would expect to see the area of a circle with radius 3.0 as the last output. After all, the loop should continue as long as radius is less than or equal to 3.0. But the last value displayed has the radius at 2.8; what’s going wrong?
The loop ends earlier than expected because when 0.2 is added to 2.8, the result is greater than 3.0. This is an astounding piece of arithmetic at face value, but read on! The reason for this is a very small error in the representation of 0.2 as a binary floating-point number. 0.2 cannot be represented exactly in binary floating point. The error is in the last digit of precision, so if your compiler supports 15-digit precision for type double, the error is of the order of 10-15. Usually, this is of no consequence, but here you depend on adding 0.2 successively to get exactly 3.0—which doesn’t happen.
You can see what the difference is by changing the loop to output just one circle area per line and to display the difference between 3.0 and the next value of radius:
On our machine, the last line of output is now this:
As you can see, radius + 0.2 is greater than 3.0 by around 4.44 × 10-16. This causes the loop to terminate before the next iteration.
Note
Any number that is a fraction with an odd denominator cannot be represented exactly as a binary floating-point value.
While this example may seem a tad academic, rounding errors do cause analogous bugs in practice. One of the authors remembers a real-life bug with a for loop similar to that of Ex5_03. It was a bug that very nearly resulted in the destruction of some high-tech piece of hardware worth well over $10,000—just because the loop occasionally ran for one iteration too many. Conclusion:
Caution
Comparing floating-point numbers can be tricky. You should always be cautious when comparing the result of floating-point computations directly using operators such as ==, <=, or >=. Rounding errors almost always prevent the floating-point value from ever becoming exactly equal to the mathematical precise value.
For the for loop in Ex5_03, one option is to introduce an integral counter i specifically for controlling the loop. Another option is to replace the loop’s condition with one that anticipates rounding errors. In this particular case, it suffices to use something like radius < 3.0 + 0.001. Instead of 0.001, you can use any number sufficiently greater than the expected rounding errors yet sufficiently less than the loop’s .2 increment. A corrected version of the program can be found in Ex5_03A.cpp. Most math libraries and so-called unit test frameworks will offer utility functions to aid you with comparing floating-point numbers in a reliable manner.
More Complex for Loop Control Expressions
You can define and initialize more than one variable of a given type in the first for loop control expression. You just separate each variable from the next with a comma. Here’s a working example that makes use of that:
The program calculates the sum of the integers from 1 to n for each integer n from 1 to limit, where limit is an upper limit that you enter. It also calculates the factorial of each n. (The factorial of an integer n, written n!, is the product of all the integers from 1 to n; for example, 5! = 1 × 2 × 3 × 4 × 5 = 120.) Don’t enter large values for limit. Factorials grow rapidly and easily exceed the capacity of even a variable of type unsigned long long. Here’s some typical output:
First, you read the value for limit from the keyboard after displaying a prompt. The value entered for limit will not be large, so type unsigned int is more than adequate. Using setw() to specify the field width for the column headings for the output enables the values to be aligned vertically with the headings simply by specifying the same field widths. The for loop does all the work. The first control expression defines and initializes three variables of type unsigned long long. n is the loop counter, sum accumulates the sum of integers from 1 to the current n, and factorial will store n!. Type unsigned long long provides the maximum range of positive integers and so maximizes the range of factorials that can be calculated. Note that there will be no warning if a factorial value cannot be accommodated in the memory allocated; the result will just be incorrect.
Note
The optional initialization statement of if and switch statements is completely equivalent to that of for loops. So there too you can define multiple variables of the same type at once if you want.
The Comma Operator
Although the comma looks as if it’s just a humble separator, it is actually a binary operator. It combines two expressions into a single expression, where the value of the operation is the value of its right operand. This means that anywhere you can put an expression, you can also put a series of expressions separated by commas. For example, consider the following statements:
The first four statements define four variables with an initial value 1. The last statement outputs the result of three assignment expressions that are separated by the comma operator. The comma operator is left associative and has the lowest precedence of all the operators, so the expression evaluates like this:
The effect will be that value1 will be incremented by 2 to produce 3, value2 will be incremented by 3 to produce 4, and value3 will be incremented by 4 to produce 5. The value of the composite expression is the value of the rightmost expression in the series, so the value that is output is 5. You could use the comma operator to incorporate the calculations into the third loop control expression of the for loop in Ex5_04.cpp:
The third control expression combines three expressions using the comma operator. The first expression increments n as before, the second adds the incremented n to sum, and the third multiplies factorial by that same value. It is important here that we first increment n and only then perform the other two calculations. Notice also that we initialize sum to 1 here, where before we initialized it to 0. The reason is that the third control expression is executed only for the first time after the first execution of the loop’s body. Without this modification, the first iteration would start by printing out an incorrect sum of zero. If you replace the loop in Ex5_04.cpp by this new version and run the example again, you’ll see that it works as before (see also Ex5_04A).
The Range-Based for Loop
The range-based for loop iterates over all the values in a range of values. This raises the immediate question: what is a range? An array is a range of elements, and a string is a range of characters. The containers provided by the Standard Library are all ranges as well. We’ll introduce two Standard Library containers later in this chapter. This is the general form of the range-based for loop:
The range_declaration identifies a variable that will be assigned each of the values in the range in turn, with a new value being assigned on each iteration. The range_expression identifies the range that is the source of the data. This will be clearer with an example. Consider these statements:
The variable x will be assigned a value from the values array on each iteration. It will be assigned values 2, 3, 5, and so on, in succession. Thus, the loop will accumulate the sum of all the elements in the values array in total. The variable x is local to the loop and does not exist outside it.
A braced initializer list itself is a valid range, so you could write the previous code even more compactly as follows:
Of course, the compiler knows the type of the elements in the values array, so you could also let the compiler determine the type for x by writing the former loop like this:
Using the auto keyword causes the compiler to deduce the correct type for x. The auto keyword is used often with the range-based for loop. This is a nice way of iterating over all the elements in an array or other kind of range. You don’t need to be aware of the number of elements. The loop mechanism takes care of that.
Note that the values from the range are assigned to the range variable, x. This means you cannot modify the elements of values by modifying the value of x. For example, this doesn’t change the elements in the values array:
This just adds 2 to the local variable, x, not to the array element. The value stored in x is overwritten by the value of the next element from values on the next iteration. In the next chapter, you’ll learn how you can change the values in a range using this loop.
The while Loop
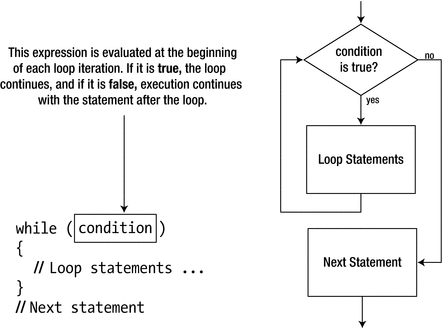
How the while loop executes
The flowchart in Figure 5-3 shows the logic of this loop. You can use any expression to control the loop, as long as it evaluates to a value of type bool or can be implicitly converted to type bool. If the loop condition expression evaluates to a numerical value, for example, the loop continues as long as the value is nonzero. A zero value ends the loop.
You could implement a version of Ex5_04.cpp using a while loop to see how it differs:
The output from this program is the same as Ex5_04.cpp if you entered it correctly. The variables n, sum, and factorial are defined before the loop. Here the types of the variables can be different, so n and sum are defined as unsigned int. The maximum value that can be stored in factorial limits the calculation, so this remains as type unsigned long long. Because of the way the calculation is implemented, the counter n is initialized to zero. The while loop condition increments n and then compares the new value with limit. The loop continues as long as the condition is true, so the loop executes with values of n from 1 up to limit. When n reaches limit+1, the loop ends. The statements within the loop body are the same as in Ex5_04.cpp.
Note
Any for loop can be written as an equivalent while loop, and vice versa. For instance, a for loop has the following generic form:
This can typically3 be written using a while loop as follows:
The while loop needs to be surrounded by an extra pair of curly braces to emulate the way the variables declared in the initialization code are scoped by the original for loop.
The do-while Loop
The do-while loop is similar to the while loop in that the loop continues for as long as the specified loop condition remains true. The only difference is that the loop condition is checked at the end of the do-while loop, rather than at the beginning, so the loop statement is always executed at least once.
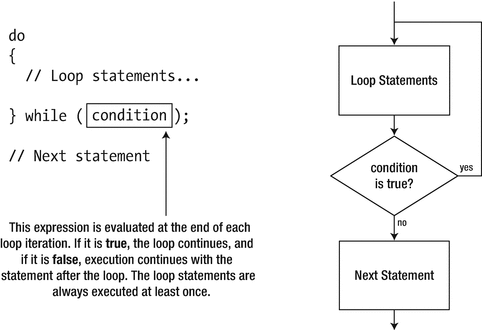
How a do-while loop executes
This kind of logic is ideal for situations where you have a block of code that you always want to execute once and may want to execute more than once. We can tell that you’re not convinced that this is something that you’d ever need to do, so let’s look at another example.
This program will calculate the average of an arbitrary number of input values—temperatures, for example—without storing them. You have no way of knowing in advance how many values will be entered, but it’s safe to assume that you’ll always have at least one, because if you didn’t, there’d be no point to running the program. That makes it an ideal candidate for a do-while loop. Here’s the code:
A sample session with this program produces the following output (for our non-American readers: the temperature readings we entered here are in degrees Fahrenheit, not Celsius, and are therefore not at all that extraordinary):
This program deals with any number of input values without prior knowledge of how many will be entered. After defining four variables that are required for the input and the calculation, the data values are read in a do-while loop. One input value is read on each loop iteration, and at least one value will always be read, which is not unreasonable. The response to the prompt that is stored in reply determines whether the loop ends. If the reply is y or Y, the loop continues; otherwise, the loop ends. Using the std::tolower() function that is declared in the cctype header ensures either uppercase or lowercase is accepted.
An alternative to using tolower() in the loop condition is to use a more complex expression for the condition. You could express the condition as reply == 'y' || reply == 'Y'. This ORs the two bool values that result from the comparisons so that either an uppercase or lowercase y entered will result in true.
Caution
While the semicolon after a do-while statement is required by the language, you should normally never add one after the while() of a regular while loop:
This creates a while loop with a body that equals an empty statement. In other words, it is equivalent to the following:
Two things may happen if you accidentally add such a semicolon: either body becomes executed exactly once or never at all. The former would happen, for instance, if you add a semicolon to the while loop of Ex5_05. In general, however, it is more likely that a while loop’s body is supposed to, after one or more iterations, make the evaluation of its condition flip from true to false. Adding an erroneous semicolon then causes the while loop to go on indefinitely.
Nested Loops
You can place a loop inside another loop. In fact, you can nest loops within loops to whatever depth you require to solve your problem. Furthermore, nested loops can be of any kind. You can nest a for loop inside a while loop inside a do-while loop inside a range-based for loop, if you have the need. They can be mixed in any way you want.
Nested loops are often applied in the context of arrays, but they have many other uses. We’ll illustrate how nesting works with an example that provides lots of opportunity for nesting loops. Multiplication tables are the bane of many children’s lives at school, but you can easily use a nested loop to generate one.
Here’s an example of the output:
This example includes three standard headers, iostream, iomanip, and cctype. Just as a refresher, the first is for stream input/output, the second is for stream manipulators, and the third provides the tolower() and toupper() character conversion functions along with the various character classification functions.
The input value for the size of the table is stored in table. A table will be output presenting the results of all products from 1 × 1 up to table × table. The value entered is validated by comparing it with table_min and table_max. A table less than table_min doesn’t make much sense, and table_max represents a size that is the maximum that is likely to look reasonable when it is output. If table is not within range, the program ends with a return code value of 1 to indicate it’s not a normal end. (Granted, terminating the program after a bad user input is a tad drastic. Perhaps you could try to make it so that the program asks the user to try again instead?)
The multiplication table is presented in the form of a rectangular table—what else? The values along the left column and the top row are the operand values in a multiplication operation. The value at the intersection of a row and column is the product of the row and column values. The table variable is used as the iteration limit in the first for loop that creates the top line of the table. Vertical bars are used to separate columns, and the use of the setw() manipulator makes all the columns the same width.
The next for loop creates a line of dash characters to separate the top row of multipliers from the body of the table. Each iteration adds six dashes to the row. By starting the count at zero instead of one, you output table + 1 sets—one for the left column of multipliers and one for each of the columns of table entries.
The final for loop contains a nested for loop that outputs the left column of multipliers and the products that are the table entries. The nested loop outputs a complete table row, right after the multiplier for the row in the leftmost column is printed. The nested loop executes once for each iteration of the outer loop, so table rows are generated.
The code that creates a complete table is within a do-while loop. This provides for as many tables to be produced as required. If y or Y is entered in response to the prompt after a table has been output, another iteration of the do-while loop executes to allow another table to be created. This example demonstrates three levels of nesting: a for loop inside another for loop that is inside the do-while loop.
Skipping Loop Iterations
Situations arise where you want to skip one loop iteration and press on with the next. The continue statement does this:
When this statement executes within a loop, execution transfers immediately to the end of the current iteration. As long as the loop control expression allows it, execution continues with the next iteration. This is best understood in an example. Let’s suppose you want to output a table of characters with their character codes in hexadecimal and decimal formats. Of course, you don’t want to output characters that don’t have a graphical representation—some of these, such as tabs and newline, would mess up the output. So, the program should output just the printable characters. Here’s the code:
This outputs all the printable characters with code values from 0 to the maximum unsigned char value so it displays a handy list of the codes for the printable ASCII characters. The do-while loop is the most interesting bit. The variable, ch, varies from zero up to the maximum value for its type, unsigned char. You saw the numeric_limits<>::max() function in Chapter 2, which returns the maximum value for the type you place between the angled brackets. Within the loop, you don’t want to output details of any character that does not have a printable representation, and the isprint() function that is declared in the locale header only returns true for printable characters. Thus, the expression in the if statement will be true when ch contains the code for a character that is not printable. In this case, the continue statement executes, which skips the rest of the code in the current loop iteration.
The hex and dec manipulators in the output statements set the output mode for integers to what you require. You have to cast the value of ch to int in the output statement to display as a numeric value; otherwise, it would be output as a character. The judicious use of the setw() manipulator for the headings and the output in the loop ensures that everything lines up nicely.
We’re sure you noticed when you run the example that the last character code in the output is 126. This is because the isprint() function is returning false for code values in excess of this. If you want to see character codes greater than 126 in the output, you could write the if statement in the loop as follows:
This will execute the continue statement only for codes that represent control characters, which are code values from 0x00 to 0x1F. You’ll now see some weird and wonderful characters in the last 128 characters; what these are depends on the language and regional settings of your platform.
Using unsigned char as the type for ch keeps the code simple. If you used char as the type for ch, you would need to provide for the possibility that it could be a signed or unsigned type. One complication of signed values is that you can no longer easily cover the range by counting up from 0. Overall, the loop’s logic is far easier here if you simply stick with unsigned chars.
Note that, nevertheless, the straightforward for loop isn’t suitable here, even with ch as type unsigned char. The condition in a for loop is checked before the loop block executes, so you might be tempted to write the loop as follows:
This loop never ends. After executing the loop block with ch at the maximum value, the next increment of ch gives it a value of 0, so the second loop control expression is never false. You could make it work by using type int for the control variable in a for loop and then casting the value to type unsigned char when you want to output it as a character.
Breaking Out of a Loop
Sometimes, you need to end a loop prematurely; something might arise within the loop statement that indicates there is no point in continuing. In this case, you can use the break statement. Its effect in a loop is much the same as it is in a switch statement; executing a break statement within a loop ends the loop immediately, and execution continues with the statement following the loop. The break statement is often used with an indefinite loop, so let’s look next at what one of those looks like.
Indefinite Loops
An indefinite loop can potentially run forever. Omitting the second control expression in a for loop results in a loop that potentially executes an unlimited number of iterations. There has to be some way to end the loop within the loop block itself; otherwise, the loop repeats indefinitely.
Indefinite loops have many practical uses, such as programs that monitor some kind of alarm indicator, for instance, or that collect data from sensors in an industrial plant. An indefinite loop can be useful when you don’t know in advance how many loop iterations will be required, such as when you are reading a variable quantity of input data. In these circumstances, you code the exit from the loop within the loop block, not within the loop control expression.
In the most common form of the indefinite for loop, all the control expressions are omitted, as shown here:
You still need the semicolons (;), even though no loop control expressions exist. The only way this loop can end is if some code within the loop terminates it.
You can have an indefinite while loop, too:
The loop condition is always true, so you have an indefinite loop. This is equivalent to the for loop with no control expressions. Of course, you can also have a version of the do-while loop that is indefinite, but it is not normally used because it has no advantages over the other two types of loop.
The obvious way to end an indefinite loop is to use the break statement. You could have used an indefinite loop in Ex5_07.cpp to allow several tries at entering a valid table size, instead of ending the program immediately. This loop would do it:
This indefinite for loop could replace the code at the beginning of the do-while loop in Ex5_07.cpp that handles input of the table size. This allows up to max_tries attempts to enter a valid table size. A valid entry executes the break statement, which terminates this loop and continues with the next statement in the do-while loop. You’ll find the resulting program in Ex5_07A.cpp.
Here’s an example that uses an indefinite while loop to sort the contents of an array in ascending sequence:
Typical output looks like this:
The code limits the number of values that can be entered to size, which is set to 1000. Only users with amazing keyboard skill and persistence will find out this entire array. This is thus rather wasteful with memory, but you’ll learn how you can avoid this in such circumstances later in this chapter.
Data entry is managed in the first while loop. This loop runs until either 0 is entered or the array, x, is full because size values have been entered. In the latter instance, the user will see a message, indicating the limit.
Each value is read into the variable input. This allows the value to be tested for zero before it is stored in the array. Each value is stored in the element of the array x at index count. In the if statement that follows, count is pre-incremented and thus incremented before it is compared to size. This ensures it represents the number of elements in the array by the time it is compared to size.
The elements are sorted in ascending sequence in the next indefinite while loop. Ordering the values of the array elements is carried out in the nested for loop that iterates over successive pairs of elements and checks whether they are in ascending sequence. If a pair of elements contains values that are not in ascending sequence, the values are swapped to order them correctly. The bool variable, swapped, records whether it was necessary to interchange any elements in any complete execution of the nested for loop. If it wasn’t, then the elements are in ascending sequence, and the break statement is executed to exit the while loop. If any pair had to be interchanged, swapped will be true, so another iteration of the while loop will execute, and this causes the for loop to run through pairs of elements again.
This sorting method is called the bubble sort because elements gradually “bubble up ” to their correct position in the array. It’s not the most efficient sorting method, but it has the merit that it is very easy to understand, and it’s a good demonstration of yet another use for an indefinite loop.
Tip
In general, indefinite loops, or even just break statements, should be used judiciously. They are sometimes considered bad coding style. You should, as much as possible, put the conditions that determine when a loop terminates between the round parentheses of the for or while statement. Doing so increases code readability because this is where every C++ programmer will be looking for such conditions. Any (additional) break statements inside the loop’s body are much easier to miss and can therefore make code harder to understand.
Controlling a for Loop with Unsigned Integers
You probably didn’t notice, but Ex5_09 actually contains a perfect example of a rather crucial caveat regarding controlling a for loop with unsigned integers, such as values of type size_t. Suppose we omit the following check from the program in Ex5_09.cpp:
What would happen then, you think, if the user decides not to enter any values? That is, if count equals zero? Something bad, I’m sure you already guessed. And of course you guessed correctly! What’d happen is that execution would enter the following for loop with count equal to 0:
Mathematically speaking, if count equals 0, count - 1 should become -1. But since count is an unsigned integer, it cannot actually represent a negative value such as -1. Instead, subtracting one from zero gives numeric_limits<size_t>::max() a very large unsigned value. On our test system this equals 18446744073709551615—a number well over 18 quintillion. This effectively turns the loop into the following:
While technically not an indefinite loop, it would take even the fastest computer a fair amount of time to count to 18 quintillion (and a bit). In our case, though, the program will crash long before the counter i comes even close to that number. The reason is that the loop counter i is used in expressions such as x[i], which means that the loop will quickly start accessing and overwriting parts of memory it has no business touching.
Caution
Take care when subtracting from unsigned integers. Any value that mathematically speaking should be negative then wraps around to become a huge positive number. These types of errors can have catastrophic results in loop control expressions.
A first solution is to test that count does not equal zero prior to entering the loop, like we did in Ex5_09. Other options include casting to a signed integer or rewriting the loop such that it no longer uses subtraction:
Similar caveats lurk when using a for loop to traverse an array in reverse order. Suppose we have an array my_array and we want to process it starting with the last element working our way back to the front of the array. Then an understandable first attempt could be a loop of the following form:
Let’s assume we know that my_array is not an array of size zero. Let’s ignore the truly awful things that would happen if that were the case. Even then we are in serious problems. Because the index variable i is of unsigned type, i is by definition always greater or equal to zero. That’s what unsigned means. In other words, the loop’s termination condition i >= 0, by definition, always evaluates to true, effectively turning this buggy reverse loop into an indefinite loop. We’ll leave it to you to come up with a solution in the exercises at the end of the chapter.
Arrays of Characters
An array of elements of type char can have a dual personality. It can simply be an array of characters, in which each element stores one character, or it can represent a string. In the latter case, the characters in the string are stored in successive array elements, followed by a special string termination character called the null character that you write as '\0'. The null character marks the end of the string.
A character array that is terminated by '\0' is referred to as a C-style string . This contrasts with the string type from the Standard Library that we’ll explain in detail in Chapter 7. Objects of type string are much more flexible and convenient for string manipulation than using arrays of type char. For the moment, we’ll introduce C-style strings in the context of arrays in general and return to them and to type string in detail in Chapter 7.
You can define and initialize an array of elements of type char like this:
This isn’t a string—it’s just an array of five characters. Each array element is initialized with the corresponding character from the initializer list. As with numeric arrays, if you provide fewer initializing values than there are array elements, the elements that don’t have explicit initial values will be initialized with the equivalent of zero, which is the null character, '\0' in this case. This means that if there are insufficient initial values, the array will effectively contain a string. Here’s an example:
The last element will be initialized with '\0'. The presence of the null character means that this can be treated as a C-style string. Of course, you can still regard it as an array of characters.
You could leave it to the compiler to set the size of the array to the number of initializing values:
This also defines an array of five characters initialized with the vowels in the braced initializer.
You can also declare an array of type char and initialize it with a string literal, as follows:

An array of elements of type char initialized with a string literal
You can leave the compiler to set the size of the array when you initialize it with a string literal:
This time, the array will have nine elements: eight to store the characters in the string, plus an extra element to store the string termination character. Of course, you could have used this approach when you declared the vowels array:
There’s a significant difference between this and the previous definition for vowels without an explicit array dimension. Here you’re initializing the array with a string literal. This has '\0' appended to it implicitly to mark the end of the string, so the vowels array will contain six elements. The array created with the earlier definition will have only five elements and can’t be used as a string.
You can output a string stored in an array just by using the array name. The string in the name array, for example, could be written to cout with this statement:
This will display the entire string of characters, up to the '\0'. There must be a '\0' at the end. If there isn’t, the standard output stream will continue to output characters from successive memory locations, which almost certainly contain garbage, until either a null character happens to turn up or an illegal memory access occurs.
Caution
You can’t output the contents of an array of a numeric type by just using the array name. This works only for char arrays. And even a char array passed to an output stream must be terminated with a null character, or the program will likely crash.
This example analyzes an array of elements of type char to work out how many vowels and consonants are used in it:
Here’s an example of the output:
The text array of type char elements has the size defined by a const variable, max_length. This determines the maximum length of string that can be stored, including the terminating null character, so the longest string can contain max_length-1 characters.
You can’t use the extraction operator to read the input because it won’t read a string containing spaces; any whitespace character terminates the input operation with the >> operator. The getline() function for cin that is defined in the iostream header reads a sequence of characters, including spaces. By default, the input ends when a newline character, '\n', is read, which will be when you press the Enter key. The getline() function expects two arguments between the parentheses. The first argument specifies where the input is to be stored, which in this case is the text array. The second argument specifies the maximum number of characters that you want to store. This includes the string termination character, '\0', which will be automatically appended to the end of the input.
Note
The period between the name of the cin object and that of its so-called member function getline() is called the direct member selection operator. This operator is used to access members of a class object. You will learn all about defining classes and member functions from Chapter 11 onward.
Although you haven’t done so here, you can optionally supply a third argument to the getline() function. This specifies an alternative to '\n' to indicate the end of the input. For example, if you want the end of the input string to be indicated by an asterisk, for example, you would use this statement to read the input:
This would allow multiple lines of text to be entered because the '\n' that results from pressing Enter would no longer terminate the input operation. Of course, the total number of characters that you can enter in the read operation is still limited by maxlength.
Just to show that you can, the program outputs the string that was entered using just the array name, text. The text string is then analyzed in a straightforward manner in the for loop. The second control expression within the loop will be false when the character at the current index, i, is the null character, so the loop ends when the null character is reached.
Next, to work out the number of vowels and consonants, you only need to inspect alphabetic characters, and the if statement selects them; isalpha() only returns true for alphabetic characters. Thus, the switch statement executes only for letters. Converting the switch expression to lowercase avoids having to write cases for uppercase as well as lowercase letters. Any vowel will select the first case, and the default case is selected by anything that isn’t a vowel, which must be a consonant, of course.
By the way, because the null character '\0' is the only character that converts to the Boolean false (analogous to 0 for integral values), you could write the for loop in Ex5_10 like this as well:
Multidimensional Arrays
All the arrays so far have required a single index value to select an element. Such an array is called a one-dimensional array because varying one index can reference all the elements. You can also define arrays that require two or more index values to access an element. These are referred to generically as multidimensional arrays. An array that requires two index values to reference an element is called a two-dimensional array . An array needing three index values is a three-dimensional array , and so on, for as many dimensions as you think you can handle.
Suppose, as an avid gardener, that you want to record the weights of the carrots you grow in your small vegetable garden. To store the weight of each carrot, which you planted in three rows of four, you could define a two-dimensional array:
This defines an array with three rows of four elements and initializes all elements to zero. To reference a particular element of the carrots array, you need two index values. The first index specifies the row, from 0 to 2, and the second index specifies a particular carrot in that row, from 0 to 3. To store the weight of the third carrot in the second row, you could write the following:

Elements in a two-dimensional array
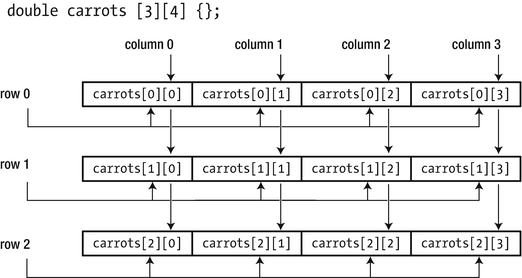
Rows and columns in a two-dimensional array
The array name by itself references the entire array. Note that with this array, you can’t display the contents of either a row or the whole array using this notation. Here’s an example:
This statement will output a single hexadecimal value, which happens to be the address in memory of the first element of the array. You’ll see why this is the case when we discuss pointers in the next chapter. Arrays of type char are a little different, as you saw earlier.
To display the entire array, one row to a line, you must write something like this:
This uses magic numbers, 3 and 4, which you can avoid by using std::size():
Note
You can use range-based for loops here as well. However, to write the outer loop as a range-based for, you’ll first need to learn about references. You’ll do so in the next chapter.
It may also be better not to use magic numbers for the array dimension sizes in the first place, so you could define the array as follows:
Defining an array of three dimensions just adds another set of square brackets. You might want to record three temperatures per day, seven days a week, for 52 weeks of the year. You could declare the following array to store such data as type int:
The array stores three values in each row. There are seven such rows for a whole week’s data and 52 sets of these for all the weeks in the year. This array will have a total of 1,092 elements of type long. They will all be initialized with zero. To display the middle temperature for day 3 of week 26, you could write this:
Remember that all the index values start at 0, so the weeks run from 0 to 51, the days run from 0 to 6, and the samples in a day run from 0 to 2.
Initializing Multidimensional Arrays
You have seen that an empty braced initializer initializes an array with any number of dimensions to zero. It gets a little more complicated when you want initial values other than zero. The way in which you specify initial values for a multidimensional array derives from the notion that a two-dimensional array is an array of one-dimensional arrays. The initializing values for a one-dimensional array are written between braces and separated by commas. Following on from that, you could declare and initialize the two-dimensional carrots array, with this statement:
Each row is a one-dimensional array, so the initializing values for each row are contained within their own set of braces. These three lists are themselves contained within a set of braces because the two-dimensional array is a one-dimensional array of one-dimensional arrays. You can extend this principle to any number of dimensions—each extra dimension requires another level of nested braces enclosing the initial values.
A question that may immediately spring to mind is, “What happens when you omit some of the initializing values?” The answer is more or less what you might have expected from past experience. Each of the innermost pairs of braces contains the values for the elements in the rows. The first list corresponds to carrots[0], the second to carrots[1], and the third to carrots[2]. The values between each pair of braces are assigned to the elements of the corresponding row. If there aren’t enough to initialize all the elements in the row, then the elements without values will be initialized to 0.
Let’s look at an example:
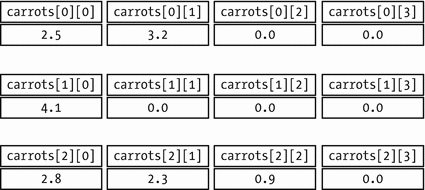
Omitting initial values for a two-dimensional array
If you don’t include sufficient sets of braces to initialize all of the rows in the array, the elements in the rows without braces enclosing initializing values will all be set to 0. If you include several initial values in the braced initializer but omit the nested braces enclosing values for the rows, values are assigned sequentially to the elements, as they’re stored in memory—with the rightmost index varying most rapidly. For example, suppose you define the array like this:
The first four values in the list will initialize elements in row 0. The last three values in the list will initialize the first three elements in row 1. The remaining elements will be initialized with zero.
Setting Dimensions by Default
You can let the compiler determine the size of the first (leftmost) dimension of an array with any number of dimensions from the set of initializing values. The compiler, however, can determine only one of the dimensions in a multidimensional array, and it has to be the first. You could define the two-dimensional carrots array with this statement:
The array will have three rows, as before, because there are three sets of braces within the outer pair. If there were only two sets, the array would have two rows. The number of inner pairs of braces determines the number of rows.
What you cannot do is have the compiler deduce any dimension other than the first one. Up to a point, this makes sense. If you were to supply 12 initial values for a two-dimensional array, for instance, there’s no way for the compiler to know whether the array should be three rows of four elements, six rows of two elements, or indeed any combination that amounts to 12 elements. Still, this does mean that, rather unfortunately, array definitions such as the following should result in a compiler error as well:
You always have to explicitly specify all array dimensions except the first one. Here’s an example of defining a three-dimensional array:
This array has three dimensions of sizes 2, 3, and 4. The outer braces enclose two further sets of braces, and each of these in turn contains three sets, each of which contains the four initial values for the corresponding row. As this simple example demonstrates, initializing arrays of three dimensions or more gets increasingly complicated, and you need to take great care when placing the braces enclosing the initial values. The braces are nested to as many levels as there are dimensions in the array.
Multidimensional Character Arrays
You can define arrays of two or more dimensions to hold any type of data. A two-dimensional array of type char is interesting because it can be an array of C-style strings . When you initialize a two-dimensional array of char elements with string literals, you don’t need the braces around the literal for a row—the double quotes delimiting the literal do the job of the braces in this case. Here’s an example:
This array will have six rows because there are six string literals as initial values. Each row stores a string containing the name of a movie star, and a terminating null character, '\0', will be appended to each string. Each row will accommodate up to 80 characters according to the row dimension you’ve specified. We can see this applied in the following example:
This is some typical output from this program:
Apart from its incredible inherent entertainment value, the main point of interest in the example is the definition of the array, stars. It’s a two-dimensional array of char elements, which can hold multiple strings, each of which can contain up to max_length characters, including the terminating null that’s automatically added by the compiler. The initializing strings for the array are enclosed between braces and separated by commas. Because the size of the first array dimension is omitted, the compiler creates the array with the number of rows necessary to accommodate all the initializing strings. As you saw earlier, you can omit the size of only the first dimension; you must specify the sizes of any other dimensions that are required.
The if statement arranges for the output to be displayed. Its condition checks that the integer that was entered is within range before attempting to display a name. When you need to reference a string for output, you only need to specify the first index value. A single index selects a particular 80-element subarray, and because this contains a string, the operation will output the contents of each element up to the terminating null character. The index is specified as choice-1 because the choice values start from 1, whereas the index values need to start from 0. This is quite a common idiom when you’re programming with arrays.
Allocating an Array at Runtime
The C++17 standard does not permit an array dimension to be specified at runtime. That is, the array dimension must be a constant expression that can be evaluated by the compiler. However, some current C++ compilers do allow setting variable array dimensions at runtime because the current C standard, C11, permits this, and a C++ compiler will typically compile C code too.
These so-called variable-length arrays can be a useful feature, so in case your compiler supports this, we’ll show how it works with an example. Keep in mind, though, that this is not strictly in conformance with the C++ language standard. Suppose you want to calculate the average height for a group of people, and you want to accommodate as many people as the user wants to enter heights for. As long as the user can input the number of heights to be processed, you can create an array that is an exact fit for the data that will be entered, like this:
The height array is created when the code executes and will have count elements. Because the array size is not known at compile time, you cannot specify any initial values for the array.
Here’s a working example using this:
Here’s some sample output:
The height array is allocated using the value entered for count. The height values are read into the array in the while loop. Within the loop, the if statement checks whether the value entered is zero. When it is nonzero, the entered variable that counts the number of values entered so far is incremented. When the value is zero, a message is output, and the next iteration executes without incrementing entered. Thus, the new attempt at entering a value will be read into the current element of height, which will overwrite the zero value that was read on the previous iteration. A straightforward for loop aggregates the total of all the heights, and this is used to output the average height. You could have used a range-based for loop here:
Alternatively, you could accumulate the total of the heights in the while loop and dispense with the for loop altogether. This would shorten the program significantly. The while loop would then look like this (this variant can also be found in Ex5_12A):
Using the postfix increment operator in the expression for the index to the height array when adding the most recent element value to total ensures the current value of entered is used to access the array element before it is incremented for the next loop iteration.
Note
If your compiler does not allow variable-length arrays, you can achieve the same result—and much more—using a vector, which we’ll discuss shortly.
Alternatives to Using an Array
The Standard Library defines a rich collection of data structures called containers that offer a variety of ways to organize and access your data. You’ll learn more about these different containers in Chapter 19. In this section, however, we briefly introduce you to the two most elemental containers: std::array<> and std::vector<>. These form a direct alternative to the plain arrays built in to the C++ language, but they are much easier to work with, are much safer to use, and provide significantly more flexibility than the more low-level, built-in arrays. Our discussion here won’t be exhaustive, though; it’s just enough for you to use them like the built-in arrays you’ve seen thus far. More information will follow in Chapter 19.
Like all containers , std::array<> and std::vector<> are defined as class templates—two C++ concepts you’re not yet familiar with. You’ll learn all about classes from Chapter 11 onward and all about templates in Chapters 9 and 16. Still, we prefer to introduce these containers here because they’re so important and because then we can use them in the examples and exercises of upcoming chapters. Also, given a clear initial explanation and some examples, we’re certain that you’ll be able to successfully use these containers already. After all, these containers are specifically designed to behave analogously to built-in arrays and can thus act as near drop-in replacements for them.
The compiler uses the std::array<T,N> and std::vector<T> templates to create a concrete type based on what you specify for the template parameters, T and N. For example, if you define a variable of type std::vector<int>, the compiler will generate a vector<> container class that is specifically tailored to hold and manipulate an array of int values. The power of templates lies in the fact that any type T can be used. We’ll mostly omit both the namespace std and the type parameters T and N when referring to them generically in text, as in array<> and vector<>.
Using array<T,N> Containers
The array<T,N> template is defined in the array header, so you must include this in a source file to use the container type. An array<T,N> container is a fixed sequence of N elements of type T, so it’s just like a regular array except that you specify the type and size a little differently. Here’s how you create an array<> of 100 elements of type double:
This creates an object that has 100 elements of type double. The specification for the parameter N must be a constant expression—just like in declarations of regular arrays. In fact, for most intents and purposes, a variable of type std::array<double, 100> behaves in exactly the same manner as a regular array variable declared like this:
If you create an array<> container without specifying initial values, it will contain garbage values as well—just like with a plain array. Most Standard Library types, including vector<> and all other containers, always initialize their elements, typically to the value zero. But array<> is special in the sense that it is specifically designed to mimic built-in arrays as closely as possible. Naturally, you can initialize an array<>’s elements in the definition as well, just like a normal array:
The four values in the initializer list are used to initialize the first four elements; subsequent elements will be zero. If you want all values to be initialized to zero, you can use empty braces:
You can easily set all the elements to any other given value as well using the fill() function for the array<> object. Here’s an example:
The fill() function belongs to the array<> object. The function is a so-called member of the class type, array<double, 100>. All array<> objects will therefore have a fill() member, as well as several other members. Executing this statement causes all elements to be set to the value you pass as the argument to the fill() function. Obviously, this must be of a type that can be stored in the container. You’ll understand the relationship between the fill() function and an array<> object better after Chapter 11.
The size() function for an array<> object returns the number of elements as type size_t. With the same values variable from before, the following statement therefore outputs 100:
In a way, the size() function provides the first real advantage over a standard array because it means that an array<> object always knows how many elements there are. You’ll only be able to fully appreciate this, though, after Chapter 8, where you learn all about passing arguments to functions. You’ll learn that passing a regular array to a function in such a way that it preserves knowledge over its size requires some advanced, hard-to-remember syntax. Even programmers with years of experience—yours truly included—mostly don’t know this syntax by heart. Many, we’re sure, won’t even know that it exists. Passing an array<> object to a function, on the other hand, will turn out to be straightforward, and the object always knows its size by means of the size() function.
Accessing Individual Elements
You can access and use elements using an index in the same way as for a standard array. Here’s an example:
The fifth element is set to the value of the expression that is the right operand of the assignment. As another example, this is how you could compute the sum of all elements in the values object:
Because an array<> object is a range, you can use the range-based for loop to sum the elements more simply:
Accessing the elements in an array<> object using an index between square brackets doesn’t check for invalid index values. The at() function for an array<> object does and therefore will detect attempts to use an index value outside the legitimate range. The argument to the at() function is an index, the same as when you use square brackets, so you could write the for loop that totals the elements like this:
The expression values.at(i) is equivalent to values[i] but with the added security that the value of i will be checked. For example, this code will fail:
The second loop condition now using the <= operator allows i to reference beyond the last element. This will result in the program terminating at runtime with a message relating to an exception of type std::out_of_range being thrown. Throwing an exception is a mechanism for signaling exceptional error conditions. You’ll learn more about exceptions in Chapter 15. If you code this using values[i], the program will silently access the element beyond the end of the array and add whatever it contains to total. The at() function provides a further advantage over standard arrays.
The array<> template also offers convenience functions to access the first and last elements. Given an array<> variable values, the expression values.front() is equivalent to values[0], and values.back() is equivalent to values[values.size() - 1].
Operations on array<>s As a Whole
You can compare entire array<> containers using any of the comparison operators as long as the containers are of the same size and they store elements of the same type. Here’s an example:
Containers are compared element by element. For a true result for ==, all pairs of corresponding elements must be equal. For inequality, at least one pair of corresponding elements must be different for a true result. For all the other comparisons, the first pair of elements that differ produces the result. This is essentially the way in which words in a dictionary are ordered, where the first pair of corresponding letters that differ in two words determines their order. All the comparisons in the code fragment are true, so all four messages will be output when this executes.
To convince you of how truly convenient this is, let’s try exactly the same thing with plain arrays:
This code still compiles. That looks promising. However, running this on our test system now produces the following disappointing result:
You can try it for yourself by running Ex5_13.cpp. The results differ depending on which compiler you use, but it’s unlikely that you’ll see all four messages appear again like before. But what exactly is going on here? Why does comparing regular arrays not work as expected? You’ll find out in the next chapter. (You see, it’s not just comics and television shows that know how to employ a cliffhanger.) For now just remember that applying comparison operators to plain array names is not at all that useful because it clearly does not result in their elements being compared.
Unlike standard arrays, you can also assign one array<> container to another, as long as they both store the same number of elements of the same type. Here’s an example:
Moreover, array<> objects can be stored inside other containers. Regular arrays cannot. The following, for instance, creates a vector<> container that can hold array<> objects as elements, each in turn containing three int values:
The vector<> container is discussed in the next section.
Conclusion and Example
We’ve given you plenty of reasons—at least seven by our count—to use an array<> container in your code in preference to a standard array. And what’s more, there’s absolutely no disadvantage to using array<> either. Using an array<> container carries no performance overhead at all compared to a standard array (that is, unless you use the at() function instead of the [] operator of array<>—bounds checking, of course, may come at a small runtime cost).
Note
Even if in your code you use std::array<> containers, it still remains perfectly possible to call legacy functions that expect plain arrays as input. You can always access the built-in array that is encapsulated within the array<> object using its data() member.
Here’s an example that demonstrates array<> containers in action:
We leave you to run the program to see the output because it takes quite a lot of space. There are two sets of four const variables defined that relate to the range of weights and heights for the BMI table. The weights and heights are stored in array<> containers with elements of type unsigned (short for unsigned int) because all the weights and heights are integral. The containers are initialized with the appropriate values in for loops. The second loop that initializes height_ins uses a different approach to setting the values just to demonstrate the at() function. This is appropriate in this loop because the loop is not controlled by the index limits for the container, so it’s possible that a mistake could be made that would use an index outside the legal range for the container. The program would be terminated if this occurred, which would not be the case using square brackets to reference an element.
The next two for loops output the table column headings and a line to separate the headings from the rest of the table. The table is created using nested range-based for loops. The outer loop iterates over the heights and outputs the height in the leftmost column in feet and inches. The inner loop iterates over the weights and outputs a row of BMI values for the current height.
Using std::vector<T> Containers
The vector<T> container is a sequence container that may seem much like the array<T,N> container, but that is in fact far more powerful. There’s no need to know the number of elements a vector<> will store in advance, at compile time. In fact, there is even no need to know the number of elements it will store in advance, at runtime. That is, the size of a vector<> can grow automatically to accommodate any number of elements. You can add some now and then some more later. A vector<> will grow as you add more and more elements; additional space is allocated automatically whenever required. There is no real maximum number of elements either—other than the one imposed by the amount of memory available to your process, of course—which is the reason you need only the type parameter T. There’s no need for the N with a vector<>. Using the vector<> container needs the vector header to be included in your source file.
Here’s an example of creating a vector<> container to store values of type double:
This typically has no space for elements allocated yet, so memory will need to be allocated dynamically when you add the first data item. You can add an element using the push_back() function for the container object. Here’s an example:
The push_back() function adds the value you pass as the argument—3.1415 in this case—as a new element at the end of the existing elements. Since there are no existing elements here, this will be the first, which probably will cause memory to be allocated for the first time.
You can initialize a vector<> with a predefined number of elements, like this:
Unlike a built-in array or an array<> object, a vector<> container always initializes its elements. In this case, our container starts out with 20 elements that are initialized with zero. If you don’t like zero as the default value for your elements, you can specify another value explicitly:
The second argument between the parentheses specifies the initial value for all elements, so all 20 elements will be 99L. Unlike most other array types you’ve seen so far, the first argument that specifies the number of elements—20 in our example—does not need to be a constant expression. It could be the result of an expression executed at runtime or read in from the keyboard. Of course, you can add new elements to the end of this or any other vector using the push_back() function.
A further option for creating a vector<> is to use a braced list to specify initial values:
The primes vector container will be created with eight elements with the given initial values.
Caution
You may have noticed before that we didn’t initialize the values and numbers vector<> objects using the usual braced initializer syntax but instead using round parentheses:
This is because using braced initializers here has a significantly different effect, as the comments next to the statements explain:
When you use curly braces to initialize a vector<>, the compiler always interprets it as a sequence of initial values. This is to accommodate for initializing vectors in the same manner as you did with regular arrays or array<> containers before:
This is one of only few occasions where the so-called uniform initialization syntax is not quite so uniform. To initialize a vector<> with a given number of identical values—without repeating that same value over and over, that is—you cannot use curly braces. If you do, it is interpreted by the compiler as a list of one or two initial values.
You can use an index between square brackets to set a value for an existing element or just to use its current value in an expression. Here’s an example:
Index values for a vector<> start from 0, just like a standard array. You can always reference existing elements using an index between square brackets, but you cannot create new elements this way. For that, you need to use, for instance, the push_back() function. The index values are not checked when you index a vector like this. So, you can accidentally access memory outside the extent of the vector and store values in such locations using an index between square brackets. The vector<> object again provides the at() function as well, just like an array<> container object, so you could consider using the at() function to refer to elements whenever there is the potential for the index to be outside the legal range.
Each vector<> knows its size and has a size() member to query it.
Passing a vector<> to a function is straightforward (see Chapter 8).
Each vector<> has the convenience functions front() and back() to facilitate accessing the first and last elements of the vector<>.
Two vector<> containers can be compared using <, >, <=, >=, ==, and != operators. Unlike with array<>, this even works for vectors that do not contain the same number of elements. The semantics then is the same as when you alphabetically compare words of different length. We all know that aardvark precedes zombie in the dictionary, even though the former has more letters. Also, love comes before lovesickness—both in life and in the dictionary. The comparison of vector<> containers is analogous. The only difference is that the elements are not always letters but can be any values the compiler knows how to compare using <, >, <=, >=, ==, and !=. In technical speak, this principle is called a lexicographical comparison.
Assigning a vector<> to another vector<> variable copies all elements of the former into the latter, overwriting any elements that may have been there before, even if the new vector<> is shorter. If need be, additional memory will be allocated to accommodate more elements as well.
A vector<> can be stored inside other containers, so you can, for instance, create a vector of vectors of integers.
A vector<> does not have a fill() member, though. Instead, it offers assign() functions that can be used to reinitialize the contents of a vector<>, much like you would when initializing it for the first time:
Deleting Elements
You can remove all the elements from a vector<> by calling the clear() function for the vector object. Here’s an example:
Caution
Both vector<> and array<> also provide an empty() function, which is sometimes wrongfully called in an attempt to clear a vector<>. But empty() does not empty a vector<>; clear() does. Instead, the empty() member checks whether a given container is empty. That is, it evaluates to the Boolean value true if and only if the container contains no elements and does not modify the container at all in the process.
You can remove the last element from a vector object by calling its pop_back() function . Here’s an example:
The second statement removes the last element, so the size of data will be 99.
This is by no means all there is to using vector<> containers. For instance, we showed you only how to add or remove elements from the end of a vector<>, while it’s perfectly possible to insert or remove elements at arbitrary positions. You’ll learn more about working with vector<> containers in Chapter 19.
Example and Conclusion
You are now in a position to create a new version of Ex5_09.cpp that uses only the memory required for the current input data:
The output will be the same as Ex5_09.cpp . Because the data is now stored in a container of type vector<double>, there is no longer a maximum of 1,000 elements imposed onto our more diligent users. Memory is allocated incrementally to accommodate whatever input data is entered. We also no longer need to track a count of the values the user enters; the vector<> already takes care of that for us.
Other than these simplifications, all other code inside the function remains the same as before. This shows that you can use a std::vector<> in the same manner as you would a regular array. But it gives you the added bonus that you do not need to specify its size using a compile-time constant. This bonus comes at a small cost, though, as we’re sure you’ll understand. Luckily, this small performance overhead is rarely a cause for concern, and you’ll soon find that std::vector<> will be the container you use most frequently. We’ll return to this in more detail later, but for now just follow this simple guideline:
Tip
If you know the exact number of elements at compile time, use std::array<>. Otherwise, use std::vector<>.
Summary
An array stores a fixed number of values of a given type.
You access elements in a one-dimensional array using an index value between square brackets. Index values start at 0, so in a one-dimensional array, an index is the offset from the first element.
An array can have more than one dimension. Each dimension requires a separate index value to reference an element. Accessing elements in an array with two or more dimensions requires an index between square brackets for each array dimension.
A loop is a mechanism for repeating a block of statements.
There are four kinds of loop that you can use: the while loop, the do-while loop, the for loop, and the range-based for loop.
The while loop repeats for as long as a specified condition is true.
The do-while loop always performs at least one iteration and continues for as long as a specified condition is true.
The for loop is typically used to repeat a given number of times and has three control expressions. The first is an initialization expression, executed once at the beginning of the loop. The second is a loop condition, executed before each iteration, which must evaluate to true for the loop to continue. The third is executed at the end of each iteration and is usually used to increment a loop counter.
The range-based for loop iterates over all elements within a range. An array is a range of elements, and a string is a range of characters. The array and vector containers define a range so you can use the range-based for loop to iterate over the elements they contain.
Any kind of loop may be nested within any other kind of loop to any depth.
Executing a continue statement within a loop skips the remainder of the current iteration and goes straight to the next iteration, as long as the loop control condition allows it.
Executing a break statement within a loop causes an immediate exit from the loop.
A loop defines a scope so that variables declared within a loop are not accessible outside the loop. In particular, variables declared in the initialization expression of a for loop are not accessible outside the loop.
The array<T,N> container stores a sequence of N elements of type T. An array<> container provides an excellent alternative to using the arrays that are built in to the C++ language.
The vector<T> container stores a sequence of elements of type T that increases dynamically in size as required when you add elements. You use a vector<> container instead of a standard array when the number of elements cannot be determined in advance.
Exercises
Exercise 5-1. Write a program that outputs the squares of the odd integers from 1 up to a limit that is entered by the user.
Exercise 5-2. Write a program that uses a while loop to accumulate the sum of an arbitrary number of integers entered by the user. After every iteration, ask the user whether he or she is done entering numbers. The program should output the total of all the values and the overall average as a floating-point value.
Exercise 5-3. Create a program that uses a do-while loop to count the number of nonwhitespace characters entered on a line. The count should end when the first # character is found.
Exercise 5-4. Use std::cin.getline(…) to obtain a C-style string of maximum 1,000 characters from the user. Count the number of characters the user entered using an appropriate loop. Next, write a second loop that prints out all characters, one by one, but in a reverse order.
- Exercise 5-5. Write a program equivalent to that of Exercise 5-4, except for the following:
If before you used a for loop to count the characters, you now use while, or vice versa.
This time you should first reverse the characters in the array, before printing them out left to right (for the sake of the exercise you could still use a loop to print out the characters one by one).
Exercise 5-6. Create a vector<> container with elements containing the integers from 1 to an arbitrary upper bound entered by the user. Output the elements from the vector that contain values that are not multiples of 7 or 13. Output them 10 on a line, aligned in columns.
- Exercise 5-7. Write a program that will read and store an arbitrary sequence of records relating to products. Each record includes three items of data—an integer product number, a quantity, and a unit price. For product number 1001, the quantity is 25, and the unit price is $9.95. Because you do not know yet how to create compound types, simply use three different array-like sequences to represent these records. The program should output each product on a separate line and include the total cost. The last line should output the total cost for all products. Columns should align, so the output should be something like this:
Product
Quantity
Unit Price
Cost
1001
25
$9.95
$248.75
1003
10
$15.50
$155.00
$403.75
Exercise 5-8. The famous Fibonacci series is a sequence of integers with the first two values as 1 and the subsequent values as the sum of the two preceding values. So, it begins 1, 1, 2, 3, 5, 8, 13, and so on. This is not just a mathematical curiosity. The sequence also regularly appears in biological settings, for instance. It relates to the way shells grow in a spiral, and the number of petals on many flowers is a number from this sequence. Create an array<> container with 93 elements. Store the first 93 numbers in the Fibonacci series in the array and then output them one per line. Any idea why we’d be asking you to generate 93 Fibonacci numbers and not, say, 100?
