In this chapter, we expand on the types that we discussed in the previous chapter and explain how variables of the basic types interact in more complicated situations. We also introduce some new features of C++ and discuss some of the ways that these are used.
How the execution order in an expression is determined
What the bitwise operators are and how you use them
How you can define a new type that limits variables to a fixed range of possible values
How you can define alternative names for existing data types
What the storage duration of a variable is and what determines it
What variable scope is and what its effects are
Operator Precedence and Associativity
You already know that there is a priority sequence for executing arithmetic operators in an expression. You’ll meet many more operators throughout the book, including a few in this chapter. In general, the sequence in which operators in an expression are executed is determined by the precedence of the operators. Operator precedence is just a fancy term for the priority of an operator.
Some operators, such as addition and subtraction, have the same precedence. That raises the question of how an expression such as a+b-c+d is evaluated. When several operators from a group with the same precedence appear in an expression, in the absence of parentheses, the execution order is determined by the associativity of the group. A group of operators can be left-associative, which means operators execute from left to right, or they can be right-associative, which means they execute from right to left.
The Precedence and Associativity of C++ Operators
Precedence | Operators | Associativity |
|---|---|---|
1 | :: | Left |
2 | () [] -> . postfix ++ and -- | Left |
3 | ! ∼ unary + and - prefix ++ and -- address-of & indirection * C-style cast (type) sizeof new new[] delete delete[] | Right |
4 | .* ->* | Left |
5 | * / % | Left |
6 | + - | Left |
7 | << >> | Lef t |
8 | < <= > >= | Left |
9 | == != | Left |
10 | & | Left |
11 | ^ | Left |
12 | | | Left |
13 | && | Left |
14 | || | Lef t |
15 | ?: (conditional operator) = *= /= %= += -= &= ^= |= <<= >>= throw | Righ t |
16 | , (comma) | Left |
You haven’t met most of these operators yet, but when you need to know the precedence and associativity of any operator, you’ll know where to find it. Each row in Table 3-1 is a group of operators of equal precedence, and the rows are in precedence sequence, from highest to lowest. Let’s see a simple example to make sure that it’s clear how all this works . Consider this expression:
The * and / operators are in the same group with precedence that is higher than the group containing + and -, so the expression x*y/z is evaluated first, with a result of r, say. The operators in the group containing * and / are left-associative, so the expression is evaluated as though it was (x*y)/z. The next step is the evaluation of r - b + c - d. The group containing the + and - operators is also left-associative, so this will be evaluated as ((r - b) + c) - d. Thus, the whole expression is evaluated as though it was written as follows:
Remember, nested parentheses are evaluated in sequence from the innermost to the outermost. You probably won’t be able to remember the precedence and associativity of every operator, at least not until you have spent a lot of time writing C++ code. Whenever you are uncertain, you can always add parentheses to make sure things execute in the sequence you want. And even when you are certain (because you happen to be a precedence guru), it never hurts to add some extra parentheses to clarify a complex expression.
Bitwise Operators
As their name suggests, bitwise operators enable you to operate on an integer variable at the bit level. You can apply the bitwise operators to any type of integer, both signed and unsigned, including type char. However, they’re usually applied to unsigned integer types. A typical application is to set individual bits in an integer variable. Individual bits are often used as flags , which is the term used to describe binary state indicators. You can use a single bit to store any value that has two states: on or off, male or female, true or false.
You can also use the bitwise operators to work with several items of information stored in a single variable. For instance, color values are usually recorded as three 8-bit values for the intensities of the red, green, and blue components in the color. These are typically packed into 3 bytes of a 4-byte word. The fourth byte is not wasted either; it usually contains a value for the transparency of the color. This transparency value is called the color’s alpha component . Such color encodings are commonly denoted by letter quadruples such as RGBA or ARGB. The order of these letters then corresponds to the order in which the red (R), green (G), blue (B), and alpha (A) components appear in the 32-bit integer, with each component encoded as a single byte. To work with individual color components, you need to be able to separate out the individual bytes from a word, and the bitwise operators are just the tool for this.
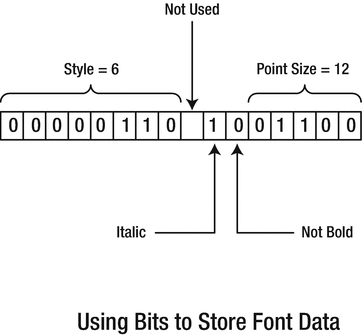
Packing font data into 2 bytes
Here one bit records whether the font is italic—1 signifies italic, and 0 signifies normal. Another bit specifies whether the font is bold. One byte selects one of up to 256 different styles. Five bits could record the point size up to 31 (or 32, if you disallow letters of size zero). Thus, in one 16-bit word you have four separate pieces of data. The bitwise operators provide you with the means of accessing and modifying the individual bits and groups of bits from an integer very easily so they provide you with the means of assembling and disassembling the 16-bit word.
The Bitwise Shift Operators
The bitwise shift operators shift the contents of an integer variable by a specified number of bits to the left or right. These are used in combination with the other bitwise operators to achieve the kind of operations we described in the previous section. The >> operator shifts bits to the right, and the << operator shifts bits to the left. Bits that fall off either end of the variable are lost.
All the bitwise operations work with integers of any type, but we’ll use type short, which is usually 2 bytes, to keep the illustrations simple. Suppose you define and initialize a variable, number, with this statement:
You can shift the contents of this variable with this statement:
Caution
The static_cast<> part of the previous statement is required because the expression number << 2 evaluates to a value of type int. This despite the fact that both number is of type short. The reason is that there are technically no mathematical or bitwise operators for integer types smaller than int. If their operands are either char or short, they are always implicitly converted to int first. Signedness is not preserved during this conversion either. Without static_cast<>, your compiler would issue at least a compiler warning to signal the narrowing conversion, or it might even refuse to compile the assignment altogether.
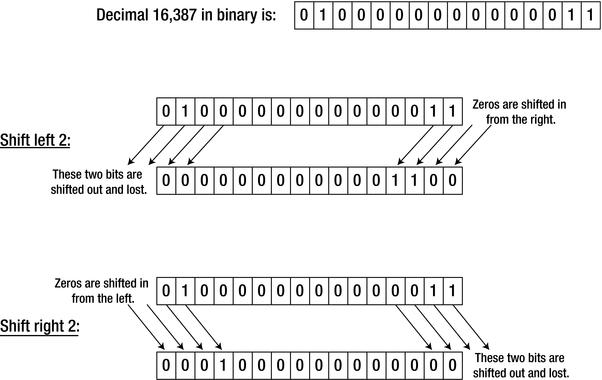
Shift operations
As you can see from Figure 3-2, shifting 16,387 two positions to the left produces the value 12. The rather drastic change in the value is the result of losing the high order bit. This statement shifts the value right two bit positions:
The result is 4,096, so shifting right two bits effectively divides the value by 4. As long as bits aren’t lost, shifting n bits to the left is equivalent to multiplying by 2, n times. In other words, it’s equivalent to multiplying by 2n. Similarly, shifting right n bits is equivalent to dividing by 2n. But beware: as you saw with the left shift of number, if significant bits are lost, the result is nothing like what you would expect. However, this is not different from the “real” multiply operation. If you multiplied the 2-byte number by 4, you would get the same result, so shifting left and multiplying are still equivalent. The incorrect result arises because the result of the multiplication is outside the range of a 2-byte integer.
When you want to modify the original value of a variable using a shift operation, you can do so by using a >>= or <<= operator . Here’s an example:
This is equivalent to the following:
There’s no confusion between these shift operators and the insertion and extraction operators for input and output. As far as the compiler is concerned, the meaning is clear from the context. If it isn’t, the compiler will generate a message in most cases, but you do need to be careful. For example, to output the result of shifting number left by two bits, you could write this:
The parentheses are essential here. Without them, the compiler would interpret the shift operator as a stream insertion operator, so you wouldn’t get the result that you intended:
Note that if number starts out as 16,387 like before in Figure 3-2, the former statement does not print out 12. Instead, it prints 65,548, which happens to be 16,387 times 4. The reason again is that number is implicitly promoted to a value of type int prior to shifting its bits to the left by two positions, and int is more than large enough to represent the exact result: 65,548. To obtain 12 instead, you could add static_cast<> to explicitly cast the result back to unsigned short:
Shifting Signed Integers
You can apply the bitwise shift operators to signed and unsigned integers. However, the effect of the right shift operator on signed integer types depends on your compiler and computer architecture. In some cases, a right shift on negative integers will introduce “0” bits at the left to fill vacated bit positions. In other cases, the sign bit is propagated, so “1” bits fill the vacated bit positions to the left. Which of the two happens depends on the binary encoding that your compiler uses for negative integers (the most common encoding schemes were discussed in Chapter 1).
The reason for propagating the sign bit, where this occurs, is to maintain consistency between a right shift and a divide operation. We can illustrate this with a variable of type signed char, just to show how it works. Suppose you define value like this:
104 in binary is 01101000, so assuming your computer employs a two’s complement notation for negative integers, -104 becomes 10011000 (remember, to obtain the two’s complement binary encoding, you have to first flip all bits of the positive binary value and then add one). You can shift value two bits to the right with this operation:
The binary result when the sign is propagated is shown in the comment. Two 0s are shifted out at the right end, and because the sign bit is 1, further 1s are inserted on the left. The decimal value of the result is –26 (flipping the bits of 11100110 and adding one gives 00011010 in binary, which is 26 in decimal notation). And -26 is the same as if you had divided by 4, as you would expect. With operations on unsigned integer types, of course, the sign bit isn’t propagated, and 0s are always inserted on the left.
As we said, what actually happens when you right-shift negative integers is implementation defined. Because for the most part you’ll be using these operators for operating at the bit level—where maintaining the integrity of the bit pattern is important—you should always use unsigned integers to ensure that you avoid the high-order bit being propagated.
Logical Operations on Bit Patterns
Bitwise Operators
Operator | Description |
|---|---|
∼ | The bitwise complement operator is a unary operator that inverts the bits in its operand, so 1 becomes 0, and 0 becomes 1. |
& | The bitwise AND operator ANDs corresponding bits in its operands. If the corresponding bits are both 1, then the resulting bit is 1; otherwise, it’s 0. |
^ | The bitwise exclusive OR operator or XOR operator exclusive-ORs corresponding bits in its operands. If the corresponding bits are different, then the result is 1. If the corresponding bits are the same, the result is 0. |
| | The bitwise OR operator ORs corresponding bits in its operands. If either bit is 1, then the result is 1. If both bits are 0, then the result is 0. |
The operators appear in Table 3-2 in order of precedence, so the bitwise complement operator has the highest precedence, and the bitwise OR operator has the lowest. The shift operators << and >> are of equal precedence, and they’re below the ∼ operator but above the & operator.
Using the Bitwise AND
You’ll typically use the bitwise AND operator to select particular bits or groups of bits in an integer value. Suppose you are using a 16-bit integer to store the point size, the style of a font, and whether it is bold and/or italic, as we illustrated in Figure 3-1. Suppose further that you want to define and initialize a variable to specify a 12-point, italic, style 6 font (in fact, the very same one illustrated in Figure 3-1). In binary, the style will be 00000110 (binary 6), the italic bit will be 1, the bold bit will be 0, and the size will be 01100 (binary 12). Remembering that there’s an unused bit as well, you need to initialize the value of the font variable to the binary number 0000 0110 0100 1100. Because groups of four bits correspond to a hexadecimal digit, the most compact way to do this is to specify the initial value in hexadecimal notation:
Of course, ever since C++14 you also have the option to simply use a binary literal instead:
Note the creative use of the digit grouping character here to signal the borders of the style, italic/bold, and point size components.
To work with the size afterward, you need to extract it from the font variable; the bitwise AND operator will enable you to do this. Because bitwise AND produces 1 bit only when both bits are 1, you can define a value that will “select” the bits defining the size when you AND it with font. You need to define a value that contains 1s in the bit positions that you’re interested in and 0s in all the others. This kind of value is called a mask , and you can define such a mask with one of these statements (both are equivalent):
The five low-order bits of font represent its size, so you set these bits to 1. The remaining bits are 0, so they will be discarded. (Binary 0000 0000 0001 1111 is hexadecimal 1F.)
You can now extract the point size from font with the following statement:
font | 0000 0110 0100 1100 |
size_mask | 0000 0000 0001 1111 |
font & size_mask | 0000 0000 0000 1100 |
We have shown the binary values in groups of four bits just to make it easy to identify the hexadecimal equivalent; it also makes it easier to see how many bits there are in total. The effect of the mask is to separate out the five rightmost bits, which represent the point size.
You can use the same mechanism to select the font style, but you’ll also need to use a shift operator to move the style value to the right. You can define a mask to select the left eight bits as follows:
You can obtain the style value with this statement:
font | 0000 0110 0100 1100 |
style_mask | 1111 1111 0000 0000 |
font & style_mask | 0000 0110 0000 0000 |
(font & style_mask) >> 8 | 0000 0000 0000 0110 |
You should be able to see that you could just as easily isolate the bits indicating italic and bold by defining a mask for each. Of course, you still need a way to test whether the resulting bit is 1 or 0, and you’ll see how to do that in the next chapter.
Another use for the bitwise AND operator is to turn bits off. You saw previously that a 0 bit in a mask will produce 0 in the result of the AND operator. To just turn the italic bit off in font, for example, you bitwise-AND font with a mask that has the italic bit as 0 and all other bits as 1. We’ll show you the code to do this after we’ve shown you how to use the bitwise OR operator, which is next.
Using the Bitwise OR
You can use the bitwise OR operator for setting one or more bits to 1. Continuing with your manipulations of the font variable, it’s conceivable that you would want to set the italic and bold bits on. You can define masks to select these bits with these statements:
Naturally, you could again use binary literals to specify these masks. In this case, however, using the left-shift operator is probably easiest:
Caution
Do remember, though, that, to turn on the nth bit, you have to shift the value 1 to the left by n-1! To see this, it’s always easiest to think about what happens if you shift with smaller values: shifting by zero gives you the first bit, shifting by one the second, and so on.
This statement then sets the bold bit to 1:
font | 0000 0110 0100 1100 |
bold | 0000 0000 0010 0000 |
font | bold | 0000 0110 0110 1100 |
Now font specifies that the font is bold as well as italic. Note that this operation will set the bit on regardless of its previous state. If it was on, it remains on.
You can also OR masks together to set multiple bits. The following statement sets both the bold and italics bits:
Caution
It’s easy to fall into the trap of allowing language to make you select the wrong operator. Because you say “Set italic and bold,” there’s a temptation to use the & operator, but this would be wrong. ANDing the two masks would result in a value with all bits 0, so you wouldn’t change anything.
Using the Bitwise Complement Operator
bold | 0000 0000 0010 0000 |
∼bold | 1111 1111 1101 1111 |
The effect of the complement operator is to flip each bit, 0 to 1 or 1 to 0. This will produce the result you’re looking for, regardless of whether bold occupies 2, 4, or 8 bytes.
Note
The bitwise complement operator is sometimes called the bitwise NOT operator because for every bit it operates on, what you get is not what you started with.
Thus, all you need to do to turn bold off is to bitwise-AND the complement of the bold mask with font. The following statement will do it:
You can set multiple bits to 0 by combining several inverted masks using the & operator and bitwise-ANDing the result with the variable you want to modify:
This sets both the italic and bold bits to 0 in font. No parentheses are necessary here because ∼ has a higher precedence than &. However, if you’re ever uncertain about operator precedence, put parentheses in to express what you want. It certainly does no harm, and it really does good when they’re necessary. Note that you can accomplish the same effect using the following statement:
Here the parentheses are required. We recommend you take a second to convince yourself that both statements are equivalent. If this doesn’t come natural yet, rest assured: you’ll get more practice working with similar logic when learning about so-called Boolean expressions in the next chapter.
Using the Bitwise Exclusive OR
Truth Table of Binary Bitwise Operators
x | y | x & y | x | y | x ^ y |
|---|---|---|---|---|
0 | 0 | 0 | 0 | 0 |
1 | 0 | 0 | 1 | 1 |
0 | 1 | 0 | 1 | 1 |
1 | 1 | 1 | 1 | 0 |
One interesting property of the XOR operator is that it may be used to toggle or flip the state of individual bits. With the font variable and the bold mask defined as before, the following toggles the bold bit—that is, if the bit was 0 before, it will now become 1, and vice versa:
font | 0000 0110 0100 1100 |
bold | 0000 0000 0010 0000 |
font ^ bold | 0000 0110 0010 1100 |
If the input is a font that is not bold, the result thus contains 0 ^ 1, or 1. Conversely, if the input already would be bold, the outcome would contain 1 ^ 1, or 0.
Drive one | ... 1010 0111 0110 0011 ... |
Drive two | ... 0110 1100 0010 1000 ... |
XOR drive (backup) | ... 1100 1011 0100 1011 ... |
Drive one | ... 1010 0111 0110 0011 ... |
XOR drive (backup) | ... 1100 1011 0100 1011 ... |
Recovered data (XOR) | ... 0110 1100 0010 1000 ... |
Notice that even with such a relatively simple trick, you already need only one extra drive to back up two others. The naïve approach would be to simply copy the contents of each drive onto another, meaning you’d need not three but four drives. The XOR technique is thus already a tremendous cost saver!
Using the Bitwise Operators: An Example
It’s time we looked at some of this stuff in action. This example exercises bitwise operators :
If you typed the code correctly, the output is as follows:
There’s an #include directive for the iomanip header because the code uses manipulators to control the formatting of the output. You define variables red and white as unsigned integers and initialize them with hexadecimal color values.
It will be convenient to display the data as hexadecimal values, and inserting std::hex in the output stream does this. The hex is modal, so all subsequent integer output will be in hexadecimal format. It will be easier to compare output values if they have the same number of digits and leading zeros. You can arrange for this by setting the fill character as 0 using the std::setfill() manipulator and ensuring the field width for each output value is the number of hexadecimal digits, which is 8. The setfill() manipulator is modal, so it remains in effect until you reset it. The std:: setw() manipulator is not modal; you have to insert it into the stream before each output value.
You combine red and white using the bitwise AND and OR operators with these statements:
The parentheses around the expressions are necessary here because the precedence of << is higher than & and |. Without the parentheses, the statements wouldn’t compile. If you check the output, you’ll see that it’s precisely as discussed. The result of ANDing two bits is 1 if both bits are 1; otherwise, the result is 0. When you bitwise-OR two bits, the result is 1 unless both bits are 0.
Next, you create a mask to use to flip between the values red and white by combining the two values with the XOR operator. The output for the value of mask shows that the exclusive OR of two bits is 1 when the bits are different and 0 when they’re the same. By combining mask with either color values using exclusive OR, you obtain the other. This means that by repeatedly applying exclusive OR with a well-chosen mask, you can toggle between two different colors. Applying the mask once gives one color, and applying it a second time reverts to the original color. This property is often exploited in computer graphics when drawing or rendering using a so-called XOR mode.
The last group of statements demonstrates using a mask to select a single bit from a group of flag bits. The mask to select a particular bit must have that bit as 1 and all other bits as 0. To select a bit from flags, you just bitwise-AND the appropriate mask with the value of flags . To switch a bit off, you bitwise-AND flags with a mask containing 0 for the bit to be switched off and 1 everywhere else. You can easily produce this by applying the complement operator to a mask with the appropriate bit set, and bit6mask is just such a mask. Of course, if the bit to be switched off was already 0, it would remain as 0.
Enumerated Data Types
You’ll sometimes need variables that have a limited set of possible values that can be usefully referred to by name—the days of the week, for example, or the months of the year. An enumeration provides this capability. When you define an enumeration, you’re creating a new type, so it’s also referred to as an enumerated data type. Let’s create an example using one of the ideas we just mentioned—a type for variables that can assume values corresponding to days of the week . You can define this as follows:
This defines an enumerated data type called Day, and variables of this type can only have values from the set that appears between the braces, Monday through Sunday. If you try to set a variable of type Day to a value that isn’t one of these values, the code won’t compile. The symbolic names between the braces are called enumerators .
Each enumerator will be automatically defined to have a fixed integer value of type int by default. The first name in the list, Monday, will have the value 0, Tuesday will be 1, and so on, through to Sunday with the value 6. You can define today as a variable of the enumeration type Day with the following statement:
You use type Day just like any of the fundamental types. This definition for today initializes the variable with the value Day::Tuesday. When you reference an enumerator, it must be qualified by the type name.
To output the value of today, you must cast it to a numeric type because the standard output stream will not recognize the type Day :
This statement will output "Today is 1".
By default, the value of each enumerator is one greater than the previous one, and by default the values begin at 0. You can make the implicit values assigned to enumerators start at a different integer value, though. This definition of type Day has enumerator values 1 through 7:
Monday is explicitly specified as 1, and subsequent enumerators will always be 1 greater than the preceding one. You can assign any integer values you like to the enumerators, and assigning these values is not limited to the first few enumerators either. The following definition, for instance, results in weekdays having values 3 through 7, Saturday having value 1, and Sunday having value 2:
The enumerators don’t even need to have unique values. You could define Monday and Mon as both having the value 1, for example, like this:
You can now use either Mon or Monday as the first day of the week. A variable, yesterday, that you’ve defined as type Day could then be set with this statement:
You can also define the value of an enumerator in terms of a previous enumerator. Throwing everything you’ve seen so far into a single example, you could define the type Day as follows:
Now variables of type Day can have values from Monday to Sunday and from Mon to Sun, and the matching pairs of enumerators correspond to the integer values 0, 2, 4, 6, 8, 10, and 12. Values for enumerators must be compile-time constants , that is, constant expressions that the compiler can evaluate. Such expressions include literals, enumerators that have been defined previously, and variables that you’ve specified as const. You can’t use non-const variables, even if you’ve initialized them using a literal.
The enumerators can be an integer type that you choose, rather than the default type int. You can also assign explicit values to all the enumerators. For example, you could define this enumeration:
The type specification for the enumerators goes after the enumeration type name and is separated from it by a colon. You can specify any integral data type for the enumerators. The possible values for variables of type Punctuation are defined as char literals and will correspond to the code values of the symbols. Thus, the values of the enumerators are 44, 33, and 63, respectively, in decimal, which also demonstrates (again) that the values don’t have to be in ascending sequence.
Here’s an example that demonstrates some of the things you can do with enumerations:
The output is as follows:
We’ll leave you to figure out why. Note the commented statements at the end of main(). They are all illegal operations. You should try them to see the compiler messages that result.
Note
The enumerations we have just described make obsolete the old syntax for enumerations. These are defined without using the class keyword. For example, the Day enumeration could be defined like this:
Your code will be less error prone if you stick to enum class enumeration types, though. For one, old-style enumerators convert to values of integral or even floating-point types without a cast, which can easily lead to mistakes. The more strongly typed enum classes are always the better choice over old-style enum types.
Aliases for Data Types
You’ve seen how enumerations provide one way to define your own data types. The using keyword enables you to specify a type alias, which is your own data type name that serves as an alternative to an existing type name. Using using, you can define the type alias BigOnes as being equivalent to the standard type unsigned long long with the following statement:
It’s important you realize this isn’t defining a new type. This just defines BigOnes as an alternative name for type unsigned long long. You could use it to define a variable mynum with this statement:
There’s no difference between this definition and using the standard type name. You can still use the standard type name as well as the alias, but it’s hard to come up with a reason for using both.
There’s an older syntax for defining an alias for a type name as well, which uses the typedef keyword. For example, you can define the type alias BigOnes like this:
Among several other advantages,1 however, the newer syntax is more intuitive, as it looks and feels like a regular assignment. With the old typedef syntax you always had to remember to invert the order of the existing type, unsigned long long, and the new name, BigOnes. Believe us, you would have struggled with this order each time you needed a type alias—we certainly have! Luckily, you’ll never have to experience this, as long as you follow this simple guideline:
Tip
Always use the using keyword to define a type alias. In fact, if it weren’t for legacy code, we’d be advising you to forget the keyword typedef even exists.
Because you are just creating a synonym for a type that already exists, this may appear to be a bit superfluous. This isn’t the case. A major use for this is to simplify code that involves complex type names. For example, a program might involve a type name such as std::map<std::shared_ptr<Contact>, std::string>. You’ll discover what the various components of this complex type mean later in this book, but for now it should already be clear that it can make for verbose and obscure code when such long types are repeated often. You can avoid cluttering the code by defining a type alias, like this:
Using PhoneBook in the code instead of the full type specification can make the code more readable. Another use for a type alias is to provide flexibility in the data types used by a program that may need to be run on a variety of computers. Defining a type alias and using it throughout the code allows the actual type to be modified by just changing the definition of the alias.
Still, type aliases, like most things in life, should be used with moderation. Type aliases can surely make your code more compact, yes. But compact code is never the goal. There are plenty of times where spelling out the concrete types makes the code easier to understand. Here’s an example:
StrPtr, while compact, does not help at all in clarifying your code. On the contrary, such a cryptic and unnecessary alias just obfuscates your code. Some guidelines therefore go as far as forbidding type aliases altogether. We certainly wouldn’t go that far; just use common sense when deciding whether an alias either helps or obfuscates, and you’ll be fine.
The Lifetime of a Variable
Variables defined within a block that are not defined to be static have automatic storage duration. They exist from the point at which they are defined until the end of the block, which is the closing curly brace, }. They are referred to as automatic variables or local variables . Automatic variables are said to have local scope or block scope. All the variables you have created so far have been automatic variables.
Variables defined using the static keyword have static storage duration. They are called static variables. Static variables exist from the point at which they are defined and continue in existence until the program ends. You’ll learn about static variables in Chapters 8 and 11.
Variables for which you allocate memory at runtime have dynamic storage duration . They exist from the point at which you create them until you release their memory to destroy them. You'll learn how to create variables dynamically in Chapter 5.
Variables declared with the thread_local keyword have thread storage duration. Thread local variables are an advanced topic, though, so we won’t be covering them in this book.
Another property that variables have is scope. The scope of a variable is the part of a program in which the variable name is valid. Within a variable’s scope, you can refer to it, set its value, or use it in an expression. Outside of its scope, you can’t refer to its name. Any attempt to do so will result in a compiler error message. Note that a variable may still exist outside of its scope, even though you can’t refer to it. You’ll see examples of this situation later, when you learn about variables with static and dynamic storage duration.
Note
Remember that the lifetime and scope of a variable are different things. Lifetime is the period of execution time over which a variable survives. Scope is the region of program code over which the variable name can be used. It’s important not to get these two ideas confused.
Global Variables
You have great flexibility in where you define variables. The most important consideration is what scope the variables need to have. You should generally place a definition as close as possible to where the variable is first used. This makes your code easier for another programmer to understand. In this section, we’ll introduce a first example where this is not the case: so-called global variables.
You can define variables outside all of the functions in a program. Variables defined outside of all blocks and classes are also called globals and have global scope (which is also called global namespace scope). This means they’re accessible in all the functions in the source file following the point at which they’re defined. If you define them at the beginning of a source file, they’ll be accessible throughout the file. In Chapter 10, we’ll show how to declare variables that can be used in multiple files.
Global variables have static storage duration by default, so they exist from the start of the program until execution of the program ends. Initialization of global variables takes place before the execution of main() begins, so they’re always ready to be used within any code that’s within the variable’s scope. If you don’t initialize a global variable, it will be zero-initialized by default. This is unlike automatic variables, which contain garbage values when uninitialized.
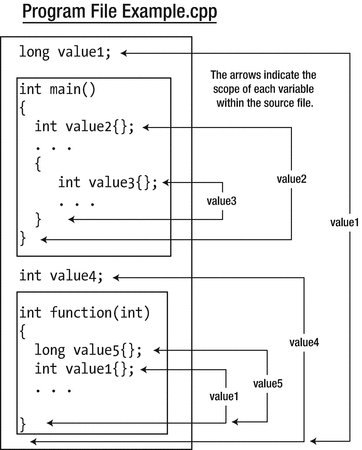
Variable scope
The variable value1 at the beginning of the file is defined at global scope, as is value4, which appears after the definition of main() . They will be initialized with zero by default. Remember, only global variables have default initial values, not automatic variables. The lifetime of global variables is from the beginning of program execution to when the program ends. Global variables have a scope that extends from the point at which they’re defined to the end of the file. Even though value4 exists when execution starts, it can’t be referred to in main() because main() isn’t within its scope. For main() to use value4, you would need to move the definition of value4 to the beginning of the file.
The local variable called value1 in function() will hide the global variable of the same name. If you use the name value1 in the function, you are accessing the local automatic variable of that name. To access the global value1, you must qualify it with the scope resolution operator, ::. Here’s how you could output the values of the local and global variables that have the name value1:
Because global variables continue to exist for as long as the program is running, you might be wondering, “Why not make all variables global and avoid messing around with local variables that disappear?” This sounds attractive at first, but there are serious disadvantages that completely outweigh any advantages . Real programs are composed of a huge number of statements, a significant number of functions, and a great many variables. Declaring all at global scope greatly magnifies the possibility of accidental, erroneous modification of a variable. It makes it hard to trace which part of the code is responsible for changes to global variables. It also makes the job of naming them sensibly quite intractable. Global variables, finally, occupy memory for the duration of program execution, so the program will require more memory than if you used local variables where the memory is reused.
By keeping variables local to a function or a block, you can be sure they have almost complete protection from external effects. They’ll only exist and occupy memory from the point at which they’re defined to the end of the enclosing block, and the whole development process becomes much easier to manage.
Tip
Common coding and design guidelines dictate that global variables are typically to be avoided, and with good reason. Global constants are a noble exception to this rule. That is, global variables that are declared with the const keyword. It is recommended to define all your constants only once, and global variables are perfectly suited for that.
Here’s an example that shows aspects of global and automatic variables :
The output from this example is as follows:
We’ve duplicated names in this example to illustrate what happens—it’s of course not a good approach to programming at all. Doing this kind of thing in a real program is confusing and totally unnecessary, and it results in code that is error prone.
There are three variables defined at global scope, count1, count2, and count3. These exist as long as the program continues to execute, but the names will be masked by local variables with the same name. The first two statements in main() define two integer variables, count1 and count3, with initial values of 10 and 50, respectively. Both variables exist from this point until the closing brace at the end of main(). The scope of these variables also extends to the closing brace at the end of main(). Because the local count1 hides the global count1, you must use the scope resolution operator to access the global count1 in the output statement in the first group of output lines. Global count2 is accessible just by using its name.
The second opening brace starts a new block. count1 and count2 are defined within this block with values 20 and 30, respectively. count1 here is different from count1 in the outer block, which still exists, but its name is masked by the second count1 and is not accessible here; global count1 is also masked but is accessible using the scope resolution operator. The global count2 is masked by the local variable with that name. Using the name count1 following the definition in the inner block refers to count1 defined in that block.
The first line of the second block of output is the value of the count1 defined in the inner scope—that is, inside the inner braces. If it was the outer count1, the value would be 10. The next line of output corresponds to the global count1. The following line of output contains the value of local count2 because you are using just its name. The last line in this block outputs global count2 by using the :: operator.
The statement assigning a new value to count1 applies to the variable in the inner scope because the outer count1 is hidden. The new value is the global count1 value plus 3. The next statement increments the global count1, and the following two output statements confirm this. The count3 that was defined in the outer scope is incremented in the inner block without any problem because it is not hidden by a variable with the same name. This shows that variables defined in an outer scope are still accessible in an inner scope as long as there is no variable with the same name defined in the inner scope.
After the brace ending the inner scope, count1 and count2 that are defined in the inner scope cease to exist. Their lifetime has ended. Local count1 and count3 still exist in the outer scope, and their values are displayed in the first two lines in the last group of output. This demonstrates that count3 was indeed incremented in the inner scope. The last lines of output correspond to the global count3 and count2 values.
Summary
You don’t need to memorize the operator precedence and associativity for all operators, but you need to be conscious of it when writing code. Always use parentheses if you are unsure about precedence.
The type-safe enumerations type are useful for representing fixed sets of values, especially those that have names, such as days of the week or suits in a pack of playing cards.
The bitwise operators are necessary when you are working with flags—single bits that signify a state. These arise surprisingly often—when dealing with file input and output, for example. The bitwise operators are also essential when you are working with values packed into a single variable. One extremely common example thereof is RGB-like encodings, where three to four components of a given color are packed into one 32-bit integer value.
The using keyword allows you to define aliases for other types. In legacy code, you might still encounter typedef being used for the same purpose.
By default, a variable defined within a block is automatic, which means that it exists only from the point at which it is defined to the end of the block in which its definition appears, as indicated by the closing brace of the block that encloses its definition.
Variables can be defined outside of all the blocks in a program, in which case they have global namespace scope and static storage duration by default. Variables with global scope are accessible from anywhere within the program file that contains them, following the point at which they’re defined, except where a local variable exists with the same name as the global variable. Even then, they can still be reached by using the scope resolution operator (::).
Exercises
Exercise 3-1. Create a program that prompts for input of an integer and store it as an int. Invert all the bits in the value and store the result. Output the original value, the value with the bits inverted, and the inverted value plus 1, each in hexadecimal representation and on one line. On the next line, output the same numbers in decimal representation. These two lines should be formatted such that they look like a table, where the values in the same column are right aligned in a suitable field width. All hexadecimal values should have leading zeros so eight hexadecimal digits always appear.
Note: Flipping all bits and adding one—ring any bells? Can you perhaps already deduce what the output will be before you run the program?
Exercise 3-2. Write a program to calculate how many square boxes can be contained in a single layer on a rectangular shelf, with no overhang. The dimensions of the shelf in feet and the dimension of a side of the box in inches are read from the keyboard. Use variables of type double for the length and depth of the shelf and type int for the length of the side of a box. Define and initialize an integer constant to convert from feet to inches (1 foot equals 12 inches). Calculate the number of boxes that the shelf can hold in a single layer of type long and output the result.
Exercise 3-3. Without running it, can you work out what the following code snippet will produce as output?
auto k {430u};auto j {(k >> 4) & ∼(∼0u << 3)};std::cout << j << std::endl;Exercise 3-4. Write a program to read four characters from the keyboard and pack them into a single integer variable. Display the value of this variable as hexadecimal. Unpack the four bytes of the variable and output them in reverse order, with the low-order byte first.
Exercise 3-5. Write a program that defines an enumeration of type Color where the enumerators are Red, Green, Yellow, Purple, Blue, Black, and White. Define the type for enumerators as an unsigned integer type and arrange for the integer value of each enumerator to be the RGB combination for the color it represents (you can easily find the hexadecimal RGB encoding of any color online). Create variables of type Color initialized with enumerators for yellow, purple, and green. Access the enumerator value and extract and output the RGB components as separate values.
Exercise 3-6. We’ll conclude with one more exercise for puzzle fans (and exclusively so). Write a program that prompts for two integer values to be entered and store them in integer variables, a and b, say. Swap the values of a and b without using a third variable. Output the values of a and b.
Hint: This is a particularly tough nut to crack. To solve this puzzle, you exclusively need one single compound assignment operator.
