16.1.1 Myth About Fast Languages

There is a common misunderstanding that the language defines the program execution speed. It is not true.

Better and more useful performance tests are usually highly specialized. They measure performance in very specific cases. It prevents us from making bold generalizations. So, when giving statements about the performance it is wise to give the most possibly detailed description of the scenario and test results. The description should be enough to build a similar system and launch similar tests, getting comparable results.

There are cases in which a program written in C can be outperformed by another program performing similar actions but written in, say, Java. It has no connection with the language itself.

For example, a typical malloc implementation has a particular property: it is hard to predict its execution time. In general, it is dependent on the current heap state: how many blocks exist, how fragmented the heap is, etc. In any case it is most likely greater than allocating memory on a stack. In a typical Java Virtual Machine implementation, however, allocating memory is fast. It happens because Java has a simpler heap structure. With some simplifications, it is just a memory region and a pointer inside it, which delimits an occupied area from the free one. Allocating memory means moving this pointer further into the free part, which is fast.

However, it has its cost: to get rid of the memory chunks we do not need anymore, garbage collection is performed, which might stop the program for an unknown period of time.

We imagine a situation in which garbage collection never happens, for example, a program allocates memory, performs computations, and exits, destroying all address space without invoking the garbage collector. In this case it is possible that a Java program performs faster just because of the careful allocation overhead imposed by malloc. However, if we use a custom memory allocator, fitting our specific needs for a particular task, we might do the same trick in C, changing the outcome drastically.

Additionally, as Java is usually interpreted and compiled in runtime, virtual machine has access to runtime optimizations that are based on how exactly the program is executed. For example, methods that are often executed one after another can be placed near each other in memory, so that they are placed in a cache together. In order to do that, certain information about program execution trace should be collected, which is only possible in runtime.

What really distinguishes C from other languages is a very transparent costs model. Whatever you are writing, it is easy to imagine which assembly instructions will be emitted. Contrary to that, languages destined primarily to work inside a runtime (Java, C#), or providing multiple additional abstractions, such as C++ with its virtual inheritance mechanism, are harder to predict. The only two real abstractions C provides are structures/unions and functions.

Being translated naively in machine instructions, a C program works very slowly. It is no match to a code generated by a good optimizing compiler. Usually, a programmer does not have more knowledge about low-level architecture details than the compiler, which is much needed to perform low-level optimizations, so he will not be able to compete with the compiler. Otherwise, sometimes, for a particular platform and compiler, one might change a program, usually reducing its readability and maintainability, but in a way that will speed up the code. Again, performance tests are mandatory for everyone.

16.1.2 General Advice

When programming we should not usually be concerned with optimizations right away. Premature optimization is evil for numerous reasons.

• Most programs are written in a way that only a fraction of their code is repeatedly executed. This code determines how fast the program will be executing, and it can slow down everything else. Speeding up other parts will in these circumstances have little to no effect.

  Finding such parts of the code is best performed using a profiler —a utility program that measures how often and how long different parts of code are executed.

• Optimizing code by hand virtually always makes it less readable and harder to maintain.

• Modern compilers are aware of common patterns in high-level language code. Such patterns get optimized well because the compiler writers put much work into it, since the work is worth it.

The most important part of optimizations is often choosing the right algorithm. Low-level optimizations on the assembly level are rarely so beneficial. For example, accessing elements of a linked list by index is slow, because we have to traverse it from the beginning, jumping from node to node. Arrays are more beneficial when the program logic demands accessing its elements by index. However, insertion in a linked list is easy compared to array, because to insert an element to the i-th position in an array we have to move all following elements first (or maybe even reallocate memory for it first and copy everything).

A simple, clean code is often also the most efficient.

Then, if the performance is unsatisfactory, we have to locate the code that gets executed the most using profiler and try to optimize it by hand. Check for duplicated computations and try to memorize and reuse computation results. Study the assembly listings and check if forcing inlining for some of the functions used is doing any good.

General concerns about hardware such as locality and cache usage should be taken into account at this time. We will speak about them in section 16.2.

The compiler optimizations should be considered then. We will study the basic ones later in this section. Turning specific optimizations on or off for a dedicated file or a code region can have a positive impact on performance. By default, they are usually all turned on when compiling with -O3 flag.

Only then come lower-level optimizations: manually throwing in SSE or AVX (Advanced Vector Extensions) instructions, inlining assembly code, writing data bypassing hardware cache, prefetching data into caches before using it, etc.

The compiler optimizations are boldly controlled by using compiler flags -O0, -O1, -O2, -O3, -Os (optimize space usage, to produce the smallest executable file possible). The index near -O, increases as the set of enabled optimizations grows.

Specific optimizations can be turned on and off. Each optimization type has two associated compiler options for that, for example, -fforward-propagate and -fno-forward-propagate.

16.1.3 Omit Stack Frame Pointer

Related GCC options : -fomit-frame-pointer

Sometimes we do not really need to store old rbp value and initialize it with the new base value. It happens when

• There are no local variables.

• Local variables fit into the red zone AND the function calls no other function.

However, there is a downside: it means that less information about the program state is kept at runtime. We will have trouble unwinding call stack and getting local variable values because we lack information about where the frame starts.

It is most troublesome in situations in which a program crashed and a dump of its state should be analyzed. Such dumps are often heavily optimized and lack debug information.

Performance-wise the effects of this optimizations are often negligible [26].

The code shown in Listing 16-1 demonstrates how to unwind the stack and display frame pointer addresses for all functions launched when unwind gets called. Compile it with -O0 to prevent optimizations.

Listing 16-1. stack_unwind.c

void unwind();
void f( int count ) {
    if ( count ) f( count-1 ); else unwind();
}
int main(void) {
    f( 10 ); return 0;
}

Listing 16-2 shows an example.

Listing 16-2. stack_unwind.asm

extern printf
global unwind

section .rodata
format : db "%x ", 10, 0

section .code
unwind:
push rbx

; while (rbx != 0) {
    ;     print rbx; rbx = [rbx];
    ; }
    mov rbx, rbp
    .loop:
    test rbx, rbx
    jz .end
    mov rdi, format
    mov rsi, rbx
    call printf
    mov rbx, [rbx]
    jmp .loop

    .end:
    pop rbx
    ret

How do we use it? Try it as a last resort to improve performance on code involving a huge amount of non-inlineable function calls.

16.1.4 Tail recursion

Related GCC options: -fomit-frame-pointer -foptimize-sibling-calls

Let us study a function shown in Listing 16-3.

Listing 16-3. factorial_tailrec.c

 __attribute__ (( noinline ))
     int factorial( int acc, int arg ) {
         if ( arg == 0 ) return acc;
         return factorial( acc * arg, arg-1 );
     }

int main(int argc, char** argv) { return factorial(1, argc); }

It calls itself recursively, but this call is particular. Once the call is completed, the function immediately returns.

We say that the function is tail recursive if the function either

• Returns a value that does not involve a recursive call, for example, return 4;.

• Launches itself recursively with other arguments and returns the result immediately, without performing further computations with it. For example, return factorial( acc * arg, arg-1 );.

A function is not tail recursive when the recursive call result is then used in computations.

Listing 16-4 shows an example of a non-tail-recursive factorial computation. The result of a recursive call is multiplied by arg before being returned, hence no tail recursion.

Listing 16-4. factorial_nontailrec.c

 __attribute__ (( noinline ))
     int factorial( int arg ) {

        if ( arg == 0 ) return acc;
        return arg * factorial( arg-1 );
    }

int main(int argc, char** argv) { return factorial(argc); }

In Chapter 2, we studied Question 20, which proposes a solution in the spirit of tail recursion. When the last thing a function does is call other function, which is immediately followed by the return, we can perform a jump to the said function start . In other words, the following pattern of instructions can be a subject to optimization:

  ; somewhere else:
      call f

  ...
  ...

  f:

     ...
     call g
     ret      ; 1
  g:

     ...
     ret      ; 2

The ret instruction in this listing are marked as the first and the second one.

Executing call g will place the return address into the stack. This is the address of the first ret instruction. When g completes its execution, it executes the second ret instruction, which pops the return address, leaving us at the first ret. Thus, two ret instructions will be executed in a row before the control passes to the function that called f. However, why not return to the caller of f immediately? To do that, we replace call g with jmp g. Now g we will never return to function f, nor will we push a useless return address into the stack. The second ret will pick up the return address from call f, which should have happened somewhere, and return us directly there.

  ; somewhere else:
      call f

  ...
  ...

  f:

     ...
     jmp g
  g:

     ...
     ret      ; 2

When g and f are the same function, it is exactly the case of tail recursion. When not optimized, factorial(5, 1) will launch itself five times, polluting the stack with five stack frames. The last call will end executing ret five times in a row in order to get rid of all return addresses.

Modern compilers are usually aware of tail recursive calls and know how to optimize tail recursion into a cycle. The assembly listing produced by GCC for the tail recursive factorial (Listing 16-3) is shown in Listing 16-5.

Listing 16-5. factorial_tailrec.asm

00000000004004c6 <factorial>:
4004c6:  89 f8                      mov     eax,edi
4004c8:  85 f6                      test    esi,esi
4004ca:  74 07                      je      4004d3 <factorial+0xd>
4004cc:  0f af c6                   imul    eax,esi
4004cf:  ff ce                      dec     esi
4004d1:  eb f5                      jmp     4004c8 <factorial+0x2>
4004d3:  c3                         ret

As we see, a tail recursive call consists of two stages.

• Populate registers with new argument values.

• Jump to the function start.

Cycles are faster than recursion because the latter needs additional space in the stack (which might lead to stack overflow as well). Why not always stick with cycles then?

Recursion often allows us to express some algorithms in a more coherent and elegant way. If we can write a function so that it becomes tail recursive as well, that recursion will not impact the performance.

Listing 16-6 shows an exemplary function accessing a linked list element by index.

Listing 16-6. tail_rec_example_list.c

#include <stdio.h>
#include <malloc.h>

struct llist {
    struct llist* next;
    int value;
};

struct llist* llist_at(
        struct llist* lst,
        size_t idx ) {
    if ( lst && idx ) return llist_at( lst->next, idx-1 );
    return lst;
}
struct llist* c( int value, struct llist* next) {
    struct llist* lst = malloc( sizeof(struct llist*) );
    lst->next = next;
    lst->value = value;
    return lst;
}

int main( void ) {
    struct llist* lst = c( 1, c( 2, c( 3, NULL )));
    printf("%d\n", llist_at( lst, 2 )->value );
    return 0;
}

Compiling with -Os will produce the non-recursive code, shown in Listing 16-7.

Listing 16-7. tail_rec_example_list. asm

0000000000400596 <llist_at>:

400596:       48 89 f8                       mov      rax,rdi
400599:       48 85 f6                       test     rsi,rsi
40059c:       74 0d                          je       4005ab <llist_at+0x15>
40059e:       48 85 c0                       test     rax,rax
4005a1:       74 08                          je       4005ab <llist_at+0x15>
4005a3:       48 ff ce                       dec      rsi
4005a6:       48 8b 00                       mov      rax,QWORD PTR [rax]
4005a9:       eb ee                          jmp      400599 <llist_at+0x3>
4005ab:       c3                             ret

How do we use it? Never be afraid to use tail recursion if it makes the code more readable for it brings no performance penalty.

16.1.5 Common Subexpressions Elimination

Related GCC options: -fgcse and others containing cse substring.

Computing two expressions with a common part does not result in computing this part twice. It means that it makes no sense performance-wise to compute this part ahead, store its result in a variable, and use it in two expressions.

In an example shown in Listing 16-8 a subexpression x ² + 2x is computed once, while the naive approach suggests otherwise.

Listing 16-8. common_subexpression.c

#include <stdio.h>

__attribute__ ((noinline))
    void test(int x) {
        printf("%d %d",
                x*x + 2*x + 1,
                x*x + 2*x - 1 );
    }

int main(int argc, char** argv) {
    test( argc );
    return 0;
}

As a proof, Listing 16-9 shows the compiled code, which does not compute x ² + 2x twice.

Listing 16-9. common_subexpression.asm

0000000000400516 <test>:
; rsi = x + 2
400516:       8d 77 02                     lea       esi,[rdi+0x2]
400519:       31 c0                        xor       eax,eax
40051b:       0f af f7                     imul      esi,edi
; rsi = x*(x+2)
40051e:       bf b4 05 40 00               mov       edi,0x4005b4
; rdx = rsi-1 = x*(x+2) - 1
400523:       8d 56 ff                     lea       edx,[rsi-0x1]
; rsi = rsi + 1 = x*(x+2) - 1
400526:       ff c6                        inc       esi
400528:       e9 b3 fe ff ff               jmp       4003e0 <printf@plt>                                                                            

How do we use it? Do not be afraid to write beautiful formulae with same common subexpressions: they will be computed efficiently. Favor code readability.

16.1.6 Constant Propagation

Related GCC options: -fipa-cp, -fgcse, -fipa-cp-clone, etc.

If compiler can prove that a variable has a specific value in a certain place of the program, it can omit reading its value and put it there directly.

Sometimes it even generates specialized function versions, partially applied to some arguments, if it knows an exact argument value (option -fipa-cp-clone). For example, Listing 16-10 shows the typical case when a specialized function version will be created for sum, which has only one argument instead of two, and the other argument’s value is fixed and equal to 42.

Listing 16-10. constant_propagation.c

__attribute__ ((noinline))
static int sum(int x, int y) { return x + y; }

int main( int argc, char** argv ) {
    return sum( 42, argc );
}

Listing 16-11 shows the translated assembly code.

Listing 16-11. constant_propagation.asm

00000000004004c0 <sum.constprop.0>:
4004c0:       8d 47 2a                     lea       eax,[rdi+0x2a]
4004c3:       c3                           ret

It gets better when the compiler computes complex expressions for you (including function calls). Listing 16-2 shows an example.

Listing 16-12. cp_fact.c

#include <stdio.h>

int fact( int n ) {
    if (n == 0) return 1;
    else return n * fact( n-1 );
}

int main(void) {
    printf("%d\n", fact( 4 ) );
    return 0;
}

Obviously, the factorial function will always compute the same result, because this value does not depend on user input. GCC is smart enough to precompute this value erasing the call and substituting the fact(4) value directly with 24, as shown in Listing 16-13. The instruction mov edx, 0x18 places 24₁₀ = 18₁₆ directly into rdx.

Listing 16-13. cp_fact.asm

0000000000400450 <main>:
400450:  48 83 ec 08                        sub      rsp,0x8
400454:  ba 18 00 00 00                     mov      edx,0x18
400459:  be 44 07 40 00                     mov      esi,0x400744
40045e:  bf 01 00 00 00                     mov      edi,0x1
400463:  31 c0                              xor      eax,eax
400465:  e8 c6 ff ff ff                     call     400430 <__printf_chk@plt>
40046a:  31 c0                              xor      eax,eax
40046c:  48 83 c4 08                        add      rsp,0x8
400470:  c3                                 ret

How do we use it? Named constants are not harmful, nor are constant variables. A compiler can and will precompute as much as it is able to, including functions without side effects launched on known arguments.

Multiple function copies for each distinct argument value can be bad for locality and will make the executable size grow. Take that into account if you face performance issues.

16.1.7 (Named) Return Value Optimization

Copy elision and return value optimization allow us to eliminate unnecessary copy operations.

Recall that naively speaking, local variables are created inside the function stack frame. So, if a function returns an instance of a structural type, it should first create it in its own stack frame and then copy it to the outside world (unless it fits into two general purpose registers rax and rdx).

Listing 16-14 shows an example.

Listing 16-14. nrvo.c

struct p  {
    long x;
    long y;
    long z;
};

__attribute__ ((noinline))
    struct p f(void) {
        struct p copy;
        copy.x = 1;
        copy.y = 2;
        copy.z = 3;
        return copy;
    }

int main(int argc, char** argv) {
    volatile struct p inst = f();
    return 0;
}

An instance of struct p called copy is created in the stack frame of f. Its fields are populated with values 1, 2, and 3, and then it is copied to the outside world, presumably by the pointer accepted by f as a hidden argument.

Listing 16-15 shows the resulting assembly code.

Listing 16-15. nrvo_off.asm

00000000004004b6 <f>:
; prologue
4004b6:  55                             push   rbp
4004b7:  48 89 e5                       mov    rbp,rsp
; A hidden argument is the address of a structure which will hold the  result.
; It is saved into stack.
4004ba:  48 89 7d d8                    mov    QWORD PTR [rbp-0x28],rdi
; Filling the fields of `copy` local variable
4004be:  48 c7 45 e0 01 00 00           mov    QWORD PTR [rbp-0x20],0x1
4004c5:  00
4004c6:  48 c7 45 e8 02 00 00           mov    QWORD PTR [rbp-0x18],0x2
4004cd:  00
4004ce:  48 c7 45 f0 03 00 00           mov    QWORD PTR [rbp-0x10],0x3
4004d5:  00
; rax = address of the destination struct
4004d6:  48 8b 45 d8                    mov    rax,QWORD PTR [rbp-0x28]
; [rax] = 1 (taken from `copy.x`)
4004da:  48 8b 55 e0                    mov    rdx,QWORD PTR [rbp-0x20]
4004de:  48 89 10                       mov    QWORD PTR [rax],rdx
; [rax + 8] = 2 (taken from `copy.y`)
4004da:  48 8b 55 e0                    mov    rdx,QWORD PTR [rbp-0x20]
4004e1:  48 8b 55 e8                    mov    rdx,QWORD PTR [rbp-0x18]
4004e5:  48 89 50 08                    mov    QWORD PTR [rax+0x8],rdx
; [rax + 10] = 3 (taken from `copy.z`)
4004e9:  48 8b 55 f0                    mov    rdx,QWORD PTR [rbp-0x10]
4004ed:  48 89 50 10                    mov    QWORD PTR [rax+0x10],rdx
; rax =  address where we have put the structure contents
; (it was the hidden argument)
4004f1:  48 8b 45 d8                    mov    rax,QWORD PTR [rbp-0x28]
4004f5:  5d                             pop    rbp
4004f6:  c3                             ret
                                                                                  
00000000004004f7 <main>:
4004f7:  55                             push   rbp
4004f8:  48 89 e5                       mov    rbp,rsp
4004fb:  48 83 ec 30                    sub    rsp,0x30
4004ff:  89 7d dc                       mov    DWORD PTR [rbp-0x24],edi
400502:  48 89 75 d0                    mov    QWORD PTR [rbp-0x30],rsi
400506:  48 8d 45 e0                    lea    rax,[rbp-0x20]
40050a:  48 89 c7                       mov    rdi,rax
40050d:  e8 a4 ff ff ff                 call   4004b6 <f>
400512:  b8 00 00 00 00                 mov    eax,0x0
400517:  c9                             leave
400518:  c3                             ret
400519:  0f 1f 80 00 00 00 00           nop    DWORD PTR [rax+0x0]

The compiler can produce a more efficient code as shown in Listing 16-16.

Listing 16-16. nrvo_on.asm

00000000004004b6 <f>:
4004b6:  48 89 f8                      mov     rax,rdi
4004b9:  48 c7 07 01 00 00 00          mov     QWORD PTR [rdi],0x1
4004c0:  48 c7 47 08 02 00 00          mov      QWORD PTR [rdi+0x8],0x2
4004c7:  00
4004c8:  48 c7 47 10 03 00 00          mov QWORD PTR [rdi+0x10],0x3
4004cf:  00
4004d0:  c3                            ret

00000000004004d1 <main>:
4004d1:  48 83 ec 20                   sub     rsp,0x20
4004d5:  48 89 e7                      mov     rdi,rsp
4004d8:  e8 d9 ff ff ff                call    4004b6 <f>
4004dd:  b8 00 00 00 00                mov     eax,0x0
4004e2:  48 83 c4 20                   add     rsp,0x20
4004e6:  c3                            ret
4004e7:  66 0f 1f 84 00 00 00          nop     WORD PTR [rax+rax*1+0x0]
4004ee:  00 00

We do not allocate a place in the stack frame for copy at all! Instead, we are operating directly on the structure passed to us through a hidden argument.

How do we use it? If you want to write a function that fills a certain structure, it is usually not beneficial to pass it a pointer to a preallocated memory area directly (or allocate it via malloc usage, which is also slower).

16.1.8 Influence of Branch Prediction

On the microcode level the actions performed by the CPU (central processing unit) are even more primitive than the machine instructions; they are also reordered to better use all CPU resources.

Branch prediction is a hardware mechanism that is aimed at improving program execution speed. When the CPU sees a conditional branch instruction (such as jg), it can

• Start executing both branches simultaneously; or

• Guess which branch will be executed and start executing it.

It happens when the computation result (e.g., the GF flag value in jg [rax]) on which this jump destination depends is not yet ready, so we start executing code speculatively to avoid wasting time.

The branch prediction unit can fail by issuing a misprediction. In this case, once the computation is completed, the CPU will do an additional work of reverting the changes made by instructions from the wrong branch. It is slow and has a real impact on program performance, but mispredictions are relatively rare.

The exact branch prediction logic depends on the CPU model. In general, two types of prediction exist [6]: static and dynamic.

• If the CPU has no information about a jump (when it is executed for the first time), a static algorithm is used. A possible simple algorithm is as follows:

  • If this is a forward jump , we assume that it happens.

  • If it is a backward jump, we assume that it does not happen.

  It makes sense because the jumps used to implement loops are more likely to happen than not.

• If a jump has already happened in the past, the CPU can use more complex algorithms. For example, we can use a ring buffer, which stores information about whether the jump occurred or not. In other words, it stores the history of jumps. When this approach is used, small loops of length dividing the buffer length are good for prediction.

The best source of relevant information with regard to the exact CPU model can be found in [16]. Unfortunately, most information about the CPU innards is not disclosed to public.

How do we use it? When using if-then-else or switch start with the most likely cases. You can also use special hints such as __builtin_expect GCC directives, which are implemented as special instruction prefixes for jump instructions (see [6]).

16.1.9 Influence of Execution Units

A CPU consists of many parts. Each instruction is executed in multiple stages, and at each stage different parts of the CPU are handling it. For example, the first stage is usually called instruction fetch and consists of loading instruction from memory¹ without thinking about its semantics at all.

A part of the CPU that performs the operations and calculations is called the execution unit . It is implementing different kinds of operations that the CPU wants to handle: instruction fetching, arithmetic, address translation, instruction decoding, etc. In fact, CPUs can use it in a more or less independent way. Different instructions are executed in a different number of stages, and each of these stages can be performed by a different execution unit. It allows for interesting circuitry usages such as the following:

• Fetching one instruction immediately after the other was fetched (but has not completed its execution).

• Performing multiple arithmetic actions simultaneously despite their being described sequentially in assembly code.

CPUs of the Pentium IV family were already capable of executing four arithmetic instructions simultaneously in the right circumstances.

How do we use the knowledge about execution unit’s existence? Let us look at the example shown in Listing 16-17.

Listing 16-17. cycle_nonpar_arith.asm

looper:
    mov      rax,[rsi]

    ; The next instruction depends on the previous one.
    ; It means that we can not swap them because
    ; the program behavior will change.
    xor     rax, 0x1

    ; One more dependency here
    add     [rdi],rax
    add     rsi,8
    add     rdi,8
    dec     rcx
    jnz     looper

Can we make it faster? We see the dependencies between instructions, which hinder the CPU microcode optimizer. What we are going to do is to unroll the loop so that two iterations of the old loop become one iteration of the new one. Listing 16-18 shows the result.

Listing 16-18. cycle_par_arith.asm

looper:
mov      rax,  [rsi]
mov      rdx,  [rsi + 8]
xor      rax,  0x1
xor      rdx,  0x1
add      [rdi], rax
add      [rdi+8], rdx
add      rsi, 16

add      rdi, 16
sub      rcx, 2
jnz      looper

Now the dependencies are gone, the instructions of two iterations are now mixed. They will be executed faster in this order because it enhances the simultaneous usage of different CPU execution units. Dependent instructions should be placed away from each other to allow other instructions to perform in between.

We cannot tell you which execution units are in your CPU, because this is highly model dependent. We have to read the optimization manuals for a specific CPU, such as [16]. Additional sources are often helpful; for example, the Haswell processors are well explained in [17].

16.1.10 Grouping Reads and Writes in Code

Hardware operates better with sequences of reads and writes which are not interleaved. For this reason, the code shown in Listing 16-19 is usually slower than its counterpart shown in Listing 16-20. The latter has sequences of sequential reads and writes grouped rather than interleaved.

Listing 16-19. rwgroup_bad.asm

mov rax,[rsi]
mov [rdi],rax
mov rax,[rsi+8]
mov [edi+4],eax
mov rax,[rsi+16]
mov [rdi+16],rax
mov rax,[esi+24]
mov [rdi+24],eax

Listing 16-20. rwgroup_good.asm

mov rax, [rsi]
mov rbx, [rsi+8]
mov rcx, [rsi+16]
mov rdx, [rsi+24]
mov [rdi], rax
mov [rdi+8], rbx
mov [rdi+16], rcx
mov [rdi+24], rdx

16.2.1 How Do We use Cache Effectively?

Caching is one of the most important mechanisms of performance boosting. We spoke about the general concepts of caching in Chapter 4. This section will further investigate how to use these concepts effectively.

We want to start by elaborating that contrary to the spirit of von Neumann architecture, the common CPUs have been using separate caches for instructions and data for at least 25 years. Instructions and code inhabit virtually always different memory regions, which explains why separate caches are more effective. We are interested in data cache.

By default, all memory operations involve cache, excluding the pages marked with cache-write-through and cache-disable bits (see Chapter 4).

Cache contains small chunks of memory of 64 bytes called cache-lines , aligned on a 64-byte boundary.

Cache memory is different from the main memory on a circuit level. Each cache-line is identified by a tag—an address of the respective memory chunk. Using special circuitry it is possible to retrieve the cache line by its address very fast (but only for small caches, like 4MB per processor, otherwise it is too expensive).

When trying to read a value from memory, the CPU will try to read it from the cache first. If it is missing, the relevant memory chunk will be loaded into cache. This situation is called cache-miss and often makes a huge impact on program performance.

There are usually several levels of cache; each of them is bigger and slower.

The LL-cache is the last level of cache closest to main memory.

For programs with good locality, caching works well. However, when the locality is broken for a piece of code, bypassing cache makes sense. For example, writing values into a large chunk of memory which will not be accessed any time soon is better performed without using cache.

The CPU tries to predict what memory addresses will be accessed in the near future and preloads the relevant memory parts into cache. It favors sequential memory accesses.

This gives us two important empirical rules needed to use caches efficiently.

• Try to ensure locality.

• Favor sequential memory access (and design data structures with this point in mind).

16.2.2 Prefetching

It is possible to issue a special hint to the CPU to indicate that a certain memory area will be accessed soon. In Intel 64 it is done using a prefetch instruction. It accepts an address in memory; the CPU will do its best to preload it into cache in the near future. This is used to prevent cache misses.

Using prefetch can be effective enough, but it should be coupled with testing. It should be executed before the data accesses themselves, but not too close. The cache preloading is being executed asynchronously, which means that it is a running at the same time when the following instructions are being executed. If prefetch is too close to data accesses, the CPU will not have enough time to preload data in cache and cache-miss will occur anyway.

Moreover, it is very important to understand that “close” and “far” from the data access mean the instruction position in the execution trace. We should not necessarily place prefetch close with regard to the program structure (in the same function), but we have to choose a place that precedes data access. It can be located in an entirely different module, for example, in the logging module, which just happens to usually be executed before the data access. This is of course very bad for code readability, introduces non-obvious dependencies between modules, and is a “last resort” kind of technique.

To use prefetch in C, we can use one of GCC built-ins:

Void __builtin_prefetch (const void *addr, ...)

It will be replaced with an architecture-specific prefetching instruction.

Besides address, it also accepts two parameters, which should be integer constants.

1. Will we read from that address (0, default) or write (1)?

2. How strong is locality? Three for maximal locality to zero for minimal. Zero indicates that the value can be cleared from cache after usage, 3 means that all levels of caches should continue to hold it.

Prefetching is performed by the CPU itself if it can predict where the next memory access is likely to be. While it works well for continuous memory accesses, such as traversing arrays, it starts being ineffective as soon as the memory access pattern starts seeming random for the predictor.

16.2.3 Example: Binary Search with Prefetching

Let us study an example shown in Listing 16-21.

Listing 16-21. prefetch_binsearch.c

#include <time.h>
#include <stdio.h>
#include <stdlib.h>

#define SIZE 1024*512*16

int binarySearch(int *array, size_t number_of_elements, int key) {
    size_t low = 0, high = number_of_elements-1, mid;
    while(low <= high) {
        mid = (low + high)/2;
#ifdef DO_PREFETCH
        // low path
        __builtin_prefetch (&array[(mid + 1 + high)/2], 0, 1);
        // high path
        __builtin_prefetch (&array[(low + mid - 1)/2], 0, 1);
#endif

        if(array[mid] < key)
            low = mid + 1;
        else if(array[mid] == key)
            return mid;
        else if(array[mid] > key)
            high = mid-1;
    }
    return -1;
}

int main() {
    size_t i = 0;
    int NUM_LOOKUPS = SIZE;
    int *array;
    int *lookups;

    srand(time(NULL));
    array =  malloc(SIZE*sizeof(int));

    lookups = malloc(NUM_LOOKUPS * sizeof(int));

    for (i=0;i<SIZE;i++) array[i] = i;
    for (i=0;i<NUM_LOOKUPS;i++) lookups[i] = rand() % SIZE;

    for (i=0;i<NUM_LOOKUPS;i++)
        binarySearch(array, SIZE, lookups[i]);
    free(array);
    free(lookups);
}

The memory access pattern of the binary search is hard to predict. It is highly nonsequential, jumping from the start to the end, then to the middle, then to the fourth, etc. Let us see the difference in execution times.

Listing 16-22 shows the results of execution with prefetch off.

Listing 16-22. binsearch_prefetch_off

> gcc -O3 prefetch.c -o prefetch_off && /usr/bin/time -v ./prefetch_off

   Command being timed: "./prefetch_off"
   User time (seconds): 7.56
   System time (seconds): 0.02
   Percent of CPU  this job got: 100%
   Elapsed (wall clock) time (h:mm:ss or m:ss): 0:07.58
   Average shared text size (kbytes): 0
   Average unshared data size (kbytes): 0
   Average stack size (kbytes): 0
   Average total size (kbytes): 0
   Maximum resident set size (kbytes): 66432
   Average resident set size (kbytes): 0
   Major (requiring I/O) page faults: 0
   Minor (reclaiming a frame) page faults: 16444
   Voluntary context switches: 1
   Involuntary context switches: 51
   Swaps: 0
   File system inputs: 0
   File system outputs: 0
   Socket messages sent: 0
   Socket messages received: 0
   Signals delivered: 0
   Page size (bytes): 4096
   Exit status: 0

Listing 16-23 shows the results of execution with prefetch on.

Listing 16-23. binsearch_prefetch_on

> gcc -O3 prefetch.c -o prefetch_off && /usr/bin/time -v ./prefetch_off

   Command being timed: "./prefetch_on"
   User time  (seconds):  6.56
   System time (seconds): 0.01
   Percent of CPU  this job got: 100%
   Elapsed (wall clock) time (h:mm:ss or m:ss): 0:06.57
   Average shared text size (kbytes): 0
   Average unshared data size (kbytes): 0
   Average stack size (kbytes): 0
   Average total size (kbytes): 0
   Maximum resident set size (kbytes): 66512
   Average resident set size (kbytes): 0
   Major (requiring I/O) page faults: 0
   Minor (reclaiming a frame) page faults: 16443
   Voluntary context switches: 1
   Involuntary context switches: 42
   Swaps: 0
   File system inputs: 0
   File system outputs: 0
   Socket messages sent: 0
   Socket messages received: 0
   Signals  delivered: 0
   Page size (bytes): 4096
   Exit status: 0

Using valgrind utility with cachegrind module we can check the amount of cache misses. Listing 16-24 shows the results for no prefetch, while Listing 16-25 shows the results with prefetching.

I corresponds to instruction cache, D to the data cache, LL – Last Level Cache ). There are almost 100% data cache misses, which is very bad.

Listing 16-24. binsearch_prefetch_off_cachegrind

==25479== Cachegrind, a cache and branch-prediction profiler
==25479== Copyright (C) 2002-2015, and GNU GPL'd, by Nicholas Nethercote et al.
==25479== Using Valgrind-3.11.0 and LibVEX; rerun with -h for copyright info
==25479== Command: ./prefetch_off
==25479==
--25479-- warning: L3 cache found, using its data for the LL simulation.
==25479==
==25479== I   refs:      2,529,064,580
==25479== I1  misses:              778
==25479== LLi misses:              774
==25479== I1  miss rate:          0.00%
==25479== Lli miss rate:          0.00%
==25479==
==25479== D   refs:         404,809,999   (335,588,367 rd   + 69,221,632 wr)
==25479== D1  misses:       160,885,105   (159,835,971 rd   +  1,049,134 wr)
==25479== LLd misses:       133,467,980   (132,418,879 rd   +  1,049,101 wr)
==25479== D1  miss rate:           39.7%  (       47.6%     +        1.5%  )
==25479== LLd miss rate:           33.0%  (       39.5%     +        1.5%  )
==25479==
==25479== LL refs:          160,885,883   (159,836,749 rd   +  1,049,134 wr)
==25479== LL misses:        133,468,754   (132,419,653 rd   +  1,049,101 wr)
==25479== LL miss rate:             4.5%  (        4.6%     +        1.5%  )

Listing 16-25. binsearch_prefetch_on_cachegrind

==26238== Cachegrind, a cache and branch-prediction profiler
==26238== Copyright (C) 2002-2015, and GNU GPL'd, by Nicholas Nethercote et al.
==26238== Using Valgrind-3.11.0 and LibVEX; rerun with -h for copyright info
==26238== Command: ./prefetch_on
==26238==
--26238-- warning: L3 cache found, using its data for the LL simulation.
==26238==
==26238== I   refs:     3,686,688,760
==26238== I1  misses:             777
==26238== LLi misses:             773
==26238== I1  miss rate:         0.00%
==26238== LLi miss rate:         0.00%
==26238==
==26238== D   refs:       404,810,009   (335,588,374  rd   + 69,221,635 wr)
==26238== D1  misses:     160,887,823   (159,838,690  rd   +  1,049,133 wr)
==26238== LLd misses:     133,488,742   (132,439,642  rd   +  1,049,100 wr)
==26238== D1  miss  rate:        39.7%  (       47.6%      +        1.5%  )
==26238== LLd miss rate:         33.0%  (       39.5%      +        1.5%  )
==26238==
==26238== LL refs:        160,888,600   (159,839,467  rd   +  1,049,133 wr)
==26238== LL misses:      133,489,515   (132,440,415  rd   +  1,049,100 wr)
==26238== LL miss rate:           3.3%  (        3.3%      +        1.5%  )

As we see, the amount of cache misses has drastically decreased.

16.2.4 Bypassing Cache

There exists a way to write into memory bypassing cache, which works even in user mode, so in order to use it we should not have access to the page table entries, holding CWT bit. In Intel 64 an instruction movntps allows us to do it. The operating system itself usually sets the bit CWT (cache-write-through) in page tables when memory-mapped IO is happening (when virtual memory acts as an interface for external devices). In this case, any memory read or write would lead to cache invalidation, which only hinders performance without giving any benefits.

GCC has intrinsic functions that are translated into machine-specific instructions that perform memory operations without involving cache. Listing 16-26 shows them.

Listing 16-26. cache_bypass_intrinsics.c

#include <emmintrin.h>
void _mm_stream_si32(int *p, int a);
void _mm_stream_si128(int *p, __m128i a);
void _mm_stream_pd(double *p, __m128d a);

#include <xmmintrin.h>
void _mm_stream_pi(__m64 *p, __m64 a);
void _mm_stream_ps(float *p, __m128 a);

#include <ammintrin.h>
void _mm_stream_sd(double *p, __m128d a);
void _mm_stream_ss(float *p, __m128 a);

Bypassing cache is useful if we are sure that we will not touch the related memory area for quite a long time. For further information refer to [12].

16.2.5 Example: Matrix Initialization

To illustrate a good memory access pattern , we are going to use a huge matrix with values 42. The matrix is stored row after row.

One program, shown in Listing 16-27, initializes each row; the other, shown in Listing 16-28, initializes each column. Which one will be faster?

Listing 16-27. matrix_init_linear.c

#include <stdio.h>
#include <malloc.h>
#define DIM (16*1024)

int main( int argc, char** argv ) {
    size_t i, j;
    int* mat = (int*)malloc( DIM * DIM * sizeof( int ) );
    for( i = 0; i < DIM; ++i )
        for( j = 0; j < DIM; ++j )
            mat[i*DIM+j] = 42;
    puts("TEST DONE");
    return 0;
}

Listing 16-28. matrix_init_ra.c

#include <stdio.h>
#include <malloc.h>
#define DIM (16*1024)

int main( int argc, char** argv ) {
    size_t i, j;
    int* mat = (int*)malloc( DIM * DIM * sizeof( int ) );
    for( i = 0; i < DIM; ++i )
        for( j = 0; j < DIM; ++j )
            mat[j*DIM+i] = 42;
    puts("TEST DONE");
    return 0;
}

We will use the time utility (not shell built-in) again to test the execution time.

> /usr/bin/time -v ./matrix_init_ra
   Command being timed: "./matrix_init_ra"
   User time (seconds): 2.40
   System time (seconds): 1.01
   Percent of CPU this job got: 86%
   Elapsed (wall clock) time (h:mm:ss or m:ss): 0:03.94
   Average shared text size (kbytes): 0
   Average unshared data size (kbytes): 0
   Average stack size (kbytes): 0
   Average total size (kbytes): 0
   Maximum resident set size (kbytes): 889808
   Average resident set size (kbytes): 0
   Major (requiring I/O) page faults: 2655
   Minor (reclaiming a frame) page faults: 275963
   Voluntary context switches: 2694
   Involuntary context switches: 548
   Swaps: 0
   File system inputs: 132368
   File system outputs: 0
   Socket messages sent: 0
   Socket messages received: 0
   Signals delivered: 0
   Page size (bytes): 4096
   Exit status: 0
                                                                                          
> /usr/bin/time -v ./matrix_init_linear

   Command being timed: "./matrix_init_linear"
   User time (seconds): 0.12
   System time (seconds): 0.83
   Percent of CPU this job got: 92%
   Elapsed (wall clock) time (h:mm:ss or m:ss): 0:01.04
   Average shared text size (kbytes): 0
   Average unshared data size (kbytes): 0
   Average stack size (kbytes): 0
   Average total size (kbytes): 0
   Maximum resident set size (kbytes): 900280
   Average resident set size (kbytes): 0
   Major (requiring I/O) page faults: 4
    Minor (reclaiming a frame) page faults: 262222
   Voluntary context switches: 29
   Involuntary context switches: 449
   Swaps: 0
   File system inputs: 176
   File system outputs: 0
   Socket messages sent: 0
   Socket messages received: 0
   Signals  delivered: 0
   Page size (bytes): 4096
   Exit status: 0

The execution is so much slower because of cache misses, which can be checked using valgrind utility with cachegrind module as shown in in Listing 16-29.

Listing 16-29. cachegrind_matrix_bad

> valgrind --tool=cachegrind ./matrix_init_ra

==17022== Command: ./matrix_init_ra
==17022==
--17022-- warning: L3 cache found, using its data for the LL simulation.
==17022==
==17022== I   refs:     268,623,230
==17022== I1  misses:           809
==17022== LLi misses:           804
==17022== I1  miss rate:       0.00%
==17022== Lli miss rate:       0.00%
==17022==
==17022== D   refs:      67,163,682   (40,974 rd  + 67,122,708 wr)
==17022== D1  misses:    67,111,793   ( 2,384 rd  + 67,109,409 wr)
==17022== LLd misses:    67,111,408   ( 2,034 rd  + 67,109,374 wr)
==17022== D1  miss rate:       99.9%  (   5.8%    +      100.0%  )
==17022== LLd miss rate:      99.9%   (   5.0%    +      100.0%  )
==17022==
==17022== LL refs:       67,112,602   ( 3,193 rd  + 67,109,409 wr)
==17022== LL misses:     67,112,212   ( 2,838 rd  + 67,109,374 wr)
==17022== LL miss rate:        20.0%  (   0.0%    +      100.0%  )

As we see, accessing memory sequentially decreases cache misses radically:

==17023== Command: ./matrix_init_linear
==17023==
--17023-- warning: L3 cache found, using its data for the LL simulation.
==17023==
==17023== I   refs:      336,117,093
==17023== I1  misses:            813
==17023== LLi misses:            808
==17023== I1  miss rate:        0.00%
==17023== LLi miss rate:        0.00%
==17023==
==17023== D   refs:       67,163,675   (40,970 rd  + 67,122,705 wr)
==17023== D1  misses:     16,780,146   ( 2,384 rd  + 16,777,762 wr)
==17023== LLd misses:     16,779,760   ( 2,033 rd  + 16,777,727 wr)
==17023== D1  miss rate:        25.0%  (   5.8%    +       25.0%  )
==17023== LLd  miss rate:       25.0%  (   5.0%    +       25.0%  )
==17023==
==17023== LL refs:        16,780,959   ( 3,197 rd   + 16,777,762 wr)
==17023== LL misses:      16,780,568   ( 2,841 rd   + 16,777,727 wr)
==17023== LL miss rate:          4.2%  (   0.0%     +      25.0%   )

16.4.1 Assignment: Sepia Filter

In this assignment, we will create a program to perform a sepia filter on an image. A sepia filter makes an image with vivid colors look like an old, aged photograph. Most graphical editors include a sepia filter.

The filter itself is not hard to code. It recalculates the red, green, and blue components of each pixel based on the old values of red, green, and blue. Mathematically, if we think about a pixel as a three-dimensional vector, the transformation is nothing but a multiplication of a vector by matrix.

Let the new pixel value be (B G R) ^T (where T superscript stands for transposition). B, G, and R stand for blue, green, and red levels. In vector form the transformation can be described as follows:

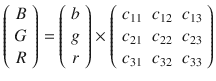
In scalar form, we can rewrite it as

• B = bc ₁₁ + gc ₁₂ + rc ₁₃

• G = bc ₂₁ + gc ₂₂ + rc ₂₃

• R = bc ₃₁ + gc ₃₂ + rc ₃₃

In the assignment given in section 13.10 we coded a program to rotate the image. If you thought out its architecture well, it will be easy to reuse most of its code.

We will have to use saturation arithmetic. It means, that all operations such as addition and multiplication are limited to a fixed range between a minimum and maximum value. Our typical machine arithmetic is modular: if the result is greater than the maximal value, we will come from the different side of the range. For example, for unsigned char: 200 + 100 = 300 mod 256 = 44. Saturation arithmetic implies that for the same range between 0 and 255 included 200 + 100 = 255 since it is the maximal value in range.

C does not implement such arithmetic, so we will have to check for overflows manually. SSE contains instructions that convert floating point values to single byte integers with saturation.

Performing the transformation in C is easy. It demands direct encoding of the matrix to vector multiplication and taking saturation into account. Listing 16-32 shows the code.

Listing 16-32. image_sepia_c_example.c

#include <inttypes.h>
struct pixel { uint8_t b, g, r; };

struct image {
    uint32_t width, height;
    struct pixel* array;
};

static unsigned char sat( uint64_t x) {
    if (x < 256) return x; return 255;
}
static void sepia_one( struct pixel* const pixel ) {
    static const float c[3][3] =  {
    { .393f, .769f, .189f },
    { .349f, .686f, .168f },
    { .272f, .543f, .131f } };
struct pixel const old = *pixel;

pixel->r = sat(
        old.r * c[0][0] + old.g * c[0][1] + old.b * c[0][2]
        );
pixel->g = sat(
        old.r * c[1][0] + old.g * c[1][1] + old.b  * c[1][2]
        );
pixel->b = sat(
        old.r * c[2][0] + old.g * c[2][1] + old.b * c[2][2]
        );
}

void sepia_c_inplace( struct image* img ) {
    uint32_t x,y;
    for( y = 0; y < img->height; y++ )
        for( x = 0; x < img->width; x++ )
            sepia_one( pixel_of( *img, x, y ) );
}

Note that using uint8_t or unsigned char is very important.

In this assignment you have to

• Implement in a separate file a routine to apply a filter to a big part of image (except for the last pixels maybe). It will operate on chunks of multiple pixels at a time using SSE instructions.

The last few pixels that did not fill the last chunk can be processed one by one using the C code provided in Listing 16-32.

• Make sure that both C and assembly versions produce similar results.

• Compile two programs; the first should use a naive C approach and the second one should use SSE instructions.

• Compare the time of execution of C and SSE using a huge image as an input (preferably hundreds of megabytes).

• Repeat the comparison multiple times and calculate the average values for SSE and C.

To make a noticeable difference, we have to have as many operations in parallel as we can. Each pixel consists of 3 bytes; after converting its components into floats it will occupy 12 bytes. Each xmm register is 16 bytes wide. If we want to be effective we will have use the last 4 bytes as well. To achieve that we use a frame of 48 bytes, which corresponds to three xmm registers, to 12-pixel components, and to 4 pixels.

Let the subscript denote the index of a pixel. The image then looks as follows:

• b ₁ g ₁ r ₁ b ₂ g ₂ r ₂ b ₃ g ₃ r ₃ b ₄ g ₄ r ₄ …

We would like to compute the first four components. Three of them correspond to the first pixel, the fourth one corresponds to the second one.

To perform necessary transformations it is useful to first put the following values into the registers:

• xmm ₀ = b ₁ b ₁ b ₁ b ₂

• xmm ₁ = g ₁ g ₁ g ₁ g ₂

• xmm ₂ = r ₁ r ₁ r ₁ r ₂

We will store the matrix coefficients in either xmm registers or memory, but it is important to store the columns, not the rows.

To demonstrate the algorithm , we will use the following start values:

• xmm ₃ = c ₁₁ |c ₂₁ |c ₃₁ |c ₁₁

• xmm ₄ = c ₁₂ |c ₂₂ |c ₃₂ |c ₁₂

• xmm ₅ = c ₁₃ |c ₂₃ |c ₃₃ |c ₁₃

We use mulps to multiply these packed values with xmm0…xmm2.

• xmm ₃ = b ₁ c ₁₁ |b ₁ c ₂₁ |b ₁ c ₃₁ |b ₂ c ₁₁

• xmm ₄ = g ₁ c ₁₂ |g ₁ c ₂₂ |g ₁ c ₃₂ |g ₂ c ₁₂

• xmm ₅ = r ₁ c ₁₃ |r ₁ c ₂₃ |r ₁ c ₃₃ |r ₂ c ₁₃

The next step is to add them using addps instructions.

The similar actions should be performed with two other two 16-byte-wide parts of the frame, containing

• g ₂ r ₂ b ₃ g ₃ and r ₃ b ₄ g ₄ r ₄

This technique using transposed coefficients matrix allows us to cope without horizontal addition instructions such as haddps. It is described in detail in [19].

To measure time, use getrusage(RUSAGE_SELF, &r) (read man getrusage pages first). It fills a struct r of type struct rusage whose field r.ru_utime contains a field of type struct timeval. It contains, in turn, a pair of values for seconds spent and millise conds spent. By comparing these values before transformation and after it we can deduce the time spent on transformation.

Listing 16-33 shows an example of single time measurement.

Listing 16-33. execution_time.c

#include <sys/time.h>
#include <sys/resource.h>
#include <stdio.h>
#include <unistd.h>
#include <stdint.h>
                                                                                          
int main(void) {
    struct rusage r;
    struct timeval start;
    struct timeval end;

    getrusage(RUSAGE_SELF, &r );
    start = r.ru_utime;

    for( uint64_t i = 0; i < 100000000; i++ );

    getrusage(RUSAGE_SELF, &r );
    end = r.ru_utime;

    long res = ((end.tv_sec - start.tv_sec) * 1000000L) +
        end.tv_usec - start.tv_usec;

    printf( "Time elapsed in microseconds: %ld\n", res );
    return 0;
}

Use a table to perform a fast conversion from unsigned char into float.

float const byte_to_float[] = {
    0.0f, 1.0f, 2.0f, ..., 255.0f };