12.2.1 Example: Natural Numbers

The language of natural numbers can be represented using a grammar.

We will take this set of characters as the alphabet: Σ = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}. However, we want a more decent representation than just all possible strings built of the characters from Σ, because the numbers with leading zeros (000124) do not look nice.

We define several nonterminal symbols: first, <notzero> for any digit except zero, <digit> for any digit, and <raw> for any sequence of <digit>s.

As we know, several rules are possible for one nonterminal. So, to define <notzero>, we can write as many rules as there are different options:

<notzero> ::= '1'
<notzero> ::= '2'
<notzero> ::= '3'
<notzero> ::= '4'
<notzero> ::= '5'
<notzero> ::= '6'
<notzero> ::= '7'
<notzero> ::= '8'
<notzero> ::= '9'

However, as it is very cumbersome and not so easy to read, we will use the different notation to describe exactly the same rules:

<notzero> ::= '1' | '2' | '3' | '4' | '5' | '6' | '7' | '8' | '9'

This notation is a part of canonical BNF .

After adding a zero, we get a rule for nonterminal <digit>, that encodes any digit.

<digit> ::= '0' | <notzero>

Then we define the nonterminal <raw> to encode all digit sequences. A sequence of digits is defined in a recursive way as either one digit or a digit followed by another sequence of digits.

<raw> ::= <digit> | <digit> <raw>

The <number> will serve us as a starting symbol. Either we deal with a one-digit number, which has no constraints on itself, or we have multiple digits, and then the first one should not be zero (otherwise it is a leading zero we do not want to see); the rest can be arbitrary.

Listing 12-1 shows the final result.

Listing 12-1. grammar_naturals

<notzero> ::= '1' | '2' | '3' | '4' | '5' | '6' | '7' | '8' | '9'
<digit> ::= '0' | <notzero>
<raw> ::= <digit> | <digit> <raw>
<number> ::=    <digit> | <notzero> <raw>                                                                            

12.2.2 Example: Simple Arithmetics

Let’s add a couple of simple binary operations . For a start, we will limit ourselves to addition and multiplication. We will base it on an example shown in Listing 12-1.

Let’s add a nonterminal <expr> that will serve as a new starting symbol. An expression is either a number or a number followed by a binary operation symbol and another expression (so, an expression is also defined recursively).

Listing 12-2 shows an example.

Listing 12-2. grammar_nat_pm

<notzero> ::= '1' | '2' | '3' | '4' | '5' | '6' | '7' | '8' | '9'
<digit> ::= '0' | <notzero>
<raw> ::= <digit> | <digit> <raw>
<number> ::=    <digit> | <notzero> <raw>

<expr> ::= <number> | <number> '+' <expr> | <number> '-' <expr>

The grammar allows us to build a tree-like structure on top of the text, where each leaf is a terminal, and each other node is a nonterminal. For example, let’s apply the current set of rules to a string 1+42 and see how it is deconstructed. Figure 12-1 shows the result.

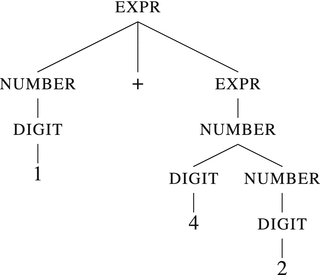
Figure 12-1. Parse tree for the expression 1+42

The first expansion is performed according to the rule <expr> ::= number '+' <expr>. The latter expression is just a number , which in turn is a sequence of digit and a number.

12.2.3 Recursive Descent

Writing parsers by hand is not hard. To illustrate it, we are going to show a parser that applies our new knowledge about grammars to literally translate the grammar description into the parsing code.

Let’s take a grammar for natural numbers that we have already described in section 12.2.1 and add just one more rule to it. The new starting symbol will be str, which corresponds to “a number ended by a null-terminator.” Listing 12-3 shows the revised grammar definition.

Listing 12-3. grammar_naturals_nullterm

<notzero> ::= '1' | '2' | '3' | '4' | '5' | '6' | '7' | '8' | '9'
<digit> ::= '0' | <notzero>
<raw> ::= <digit> | <digit> <raw>
<number> ::= <digit> | <notzero> <raw>

<str> ::= <number> '\0'

People usually operate with a notion of stream when performing parsing with grammar rules. A stream is a sequence of whatever is considered symbols. Its interface consists of two functions:

• bool expect(symbol) accepts a single terminal and returns true if the stream contains exactly this kind of terminal in the current position.

• bool accept(symbol) does the same and then advances the stream position by one in case of success.

Up to now, we operated with abstractions such as symbols and streams. We can map all the abstract notions to the concrete instances. In our case, the symbol will correspond to a single char.¹

Listing 12-4 shows an example text processor built based on grammar rules definitions. This is a syntactic checker, which verifies whether the string is holding a natural number without leading zeroes and nothing else (like spaces around the number).

Listing 12-4. rec_desc_nat.c

#include <stdio.h>
#include  <stdbool.h>

char const* stream = NULL ;

bool accept(char c) {
    if (*stream == c) {
        stream++;
        return  true;
    }
    else return false;
}
bool notzero( void ) {
    return accept( '1' ) || accept( '2' ) || accept( '3' )
    || accept( '4' )     || accept( '5' ) || accept( '6' )
    || accept( '7' )     || accept( '8' ) || accept( '9' );

}
bool digit( void ) {
    return accept('0') || notzero();
}
bool raw( void ) {
    if ( digit() ) { raw(); return true; }
    return false;
}
bool number( void ) {
    if ( notzero() ) {
         raw();
         return true;
    }  else return accept('0');
}
bool str( void ) {
    return number() && accept( 0 );
}
void check( const char* string ) {
    stream = string;
    printf("%s -> %d\n", string, str() );
}
int main(void) {
    check("12345");
    check("hello12");
    check("0002");
    check("10dbd");
    check("0");
    return 0;
}

This example shows how each nonterminal is mapped to a function with the same name that tries to apply the relevant grammar rules. The parsing occurs in a top-down manner: we start with the most general starting symbol and try to break it into parts and parse them.

When the rules start alike we factorize them by applying the common part first and then trying to consume the rest, as in number function. The two branches start with overlapping nonterminals: <digit> and <notzero>. Each of them contains the range 1...9, the only difference being <digit>’s range including zero. So, if we found a terminal in range 1...9 we try to consume as many digits after that as we can and we succeed anyway. If not, we check for the first digit being 0 and stop if it is so, consuming no more terminals.

The <notzero> function succeeds if at least one of the symbols in range 1-9 is found. Due to the lazy application of ||, not all accept calls will be performed. The first of them that succeeds will end the expression evaluation, so only one advancement in stream will occur.

The <digit> function succeeds if a zero is found or if <notzero> succeeded, which is a literal translation of a rule:

<digit> ::= '0' | <notzero>

The other functions are performing in the same manner. Should we not limit ourselves with a null-terminator, the parsing would answer us a question: “does this sequence of symbols start with a valid language sentence?”

In Listing 12-4 we have used a global variable on purpose in order to facilitate understanding. We still strongly advise against their usage in real programs.

The parsers for real programming languages are usually quite complex. In order to write them programmers use a special toolset that can generate parsers from the declarative description close to BNF. In case you need to write a parser for a complex language we recommend you taking a look at ANTLR or yacc parser generators.

Another popular technique of handwriting parsers is called parser combinators. It encourages creating parsers for the most basic generic text elements (a single character, a number, a name of a variable, etc.). Then these small parsers are combined (OR, AND, sequence…) and transformed (one or many occurences, zero or more occurences…) to produce more complex parsers. This technique, however, is easy to apply when the language supports a functional style of programming, because it often relies on higher-order functions.

12.2.4 Example: Arithmetics with Priorities

The interesting part of expressions is that different operations have different priorities. For example, the addition operation has a lower priority than the multiplication operation, so all multiplications are done prior to addition.

Let’s see the naive grammar for natural numbers with addition and multiplication in Listing 12-5.

Listing 12-5. grammar_nat_pm_mult

<notzero> ::= '1' | '2' | '3' | '4' | '5' | '6' | '7' | '8' | '9'
<digit> ::= '0' | <notzero>
<raw> ::= <digit> | <digit> <raw>
<number> ::= <digit> | <notzero> <raw>

<expr> ::= <number> | <number> '+' <expr>
       | <number> '-' <expr> | <number> '*' <expr>

Without taking the multiplication priority into account, the parse tree for the expression 1*2+3 will look as shown in Figure 12-2.

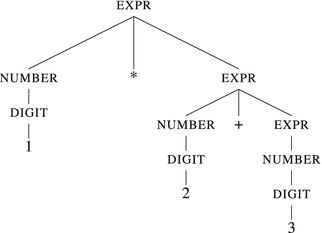
Figure 12-2. Parse trees without priorities for the expression 1*2+ 3

However, as we notice, the multiplication and addition are equals here: they are expanded in order of appearance. Because of this, the expression 1*2+3 is parsed as 1*(2+3), breaking the common evaluation order, tied to the tree structure.

From a parser’s point of view, the priority means that in the parse tree the “add” nodes should be closer to the root than the “multiply” nodes, since addition is performed on the bigger parts of the expression. The evaluation of the arithmetical expressions is performed, informally, starting from leaves and ending in the root.

How do we prioritize some operations over others? It is acquired by splitting one syntactical category <expr> into several classes. Each class is a refinement of the previous class of sorts. Listing 12-6 shows an example.

Listing 12-6. grammar_priorities

<expr> ::= <expr0> "<" <expr> | <expr0> "<=" <expr>
| <expr0> "==" <expr> | <expr0> ">" <expr> | <expr0> ">=" <expr> | <expr0>

<expr0> = <expr1> "+" <expr> | <expr1> "-" <expr> | <expr1>
<expr1> ::= <atom> "*" <expr1> | <atom> "/" <expr1> | <atom>
<atom> ::= "(" <expr> ")" | <NUMBER>

We can understand this example in the following way:

• <expr> is really any expression.

• <expr0> is an expression without <, >, == and other terminals, which are present in the first rule.

• <expr1> is also free of addition and subtraction .

12.2.5 Example: Simple Imperative Language

To illustrate that this knowledge can be applied to programming languages, we are giving an example of one’s syntax. This syntax description provides definitions for the statements, comprising typical imperative constructs: if, while, print and assignments. The keywords can be treated as atomic terminals. Listing 12-7 shows the grammar.

Listing 12-7. imp

<statements> ::= <statement> | <statement> ";" <statements>
<statement> ::= "{" <statements> "}" | <assignment> | <if> | <while> | <print>
<print> ::= "print" "(" <expr> ")"
<assignment>  ::=  IDENT  "="  <expr>
<if> ::= "<if>" "(" <expr> ")" <statement> "<else>" <statement>
<while> ::= "<while>" "(" <expr> ")" <statement>

<expr> ::= <expr0> "<" <expr> | <expr0> "<=" <expr>
| <expr0> "==" <expr> | <expr0> ">" <expr> | <expr0> ">=" <expr> | <expr0>
<expr0> = <expr1> "+" <expr> | <expr1> "-" <expr> | <expr1>
<expr1> ::= <atom> "*" <expr1> | <atom> "/" <expr1> | <atom>
<atom> ::= "(" <expr> ")" | NUMBER

12.2.6 Chomsky Hierarchy

The formal grammars as we have studied them are actually but a subclass of formal grammars as Chomsky viewed them. This class is called context-free grammars for reasons that will soon be apparent.

The hierarchy consists of four levels ranging from 3 to 0, lower levels being more expressive and powerful.

1. The regular grammars are surprisingly described by our old friends regular expressions . The finite automatons are the weakest type of parsers because they cannot handle the fractal structures such as arithmetical expressions.

   Even in the simplest case, <expr> ::= number '+' <expr>, the part of the expression on the right-hand side of '+' is similar to the whole expression. This rule can be applied recursively an arbitrary amount of time.

2. The context-free grammars , which we have studied already, have rules that are of the form

   nonterminal ::=
         <sequence  of  terminal  and  nonterminal  symbols>

   Any regular expression can be also described in terms of context-free grammars.

3. The context-sensitive grammars have rules of form:

   a A  b ::= a y b

   a and b denote an arbitrary (possibly empty) sequence of terminals and/or nonterminals, y denotes a non-empty sequence of terminals and/or nonterminals, and A is the nonterminal being expanded.

   The difference between levels 2 and 1 is that the nonterminal on the left side is substituted for y only when it occurs between a and b (which are left untouched). Remember, both a and b can be rather complex.

4. The unrestricted grammars have rules of form:

   sequence of terminal and nonterminal symbols ::=
       sequence of terminal and nonterminal symbols

As there are absolutely no restrictions on the left- and right-hand sides of the rules, these grammars are most powerful. It can be shown that these types of grammars can be used to encode any computer program, so these grammars are Turing-complete.

The real programming languages are almost never truly context-free. For example, a usage of a variable declared earlier is apparently a context-sensitive construction, because it is only valid when following a corresponding variable declaration. However, for simplicity, they are often approximated with context-free grammars and then additional passes on the parsing tree transform are done to check whether such context-sensitive conditions are satisfied.

12.2.7 Abstract Syntax Tree

There exists a notion of abstract syntax. It describes the trees that are constructed from the source code. The concrete syntax describes the exact mapping between keywords and the tree node types they are mapped to. For example, imagine that we have rewritten the C compiler so that the while keyword is replaced by _while_. Then imagine that we have rewritten all programs so that this new keyword is used instead of while. The concrete syntax did change indeed, but the abstract syntax is the same, because the language constructions stayed the same. On the contrary, if we add a finally clause to if, it incorporates a statement to be executed no matter the condition value, and we will change the abstract syntax as well.

The abstract syntax tree is usually also much more minimalistic in comparison to the parse trees. The parse tree would hold information that was only relevant for parsing (see Figure 12-3).

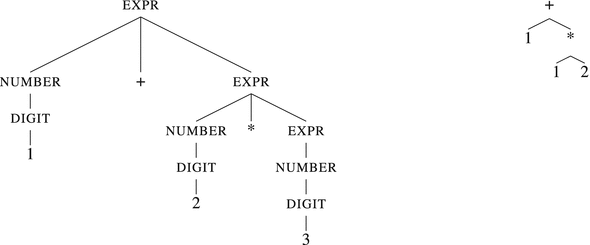
Figure 12-3. Parse tree and abstract syntax tree of the expression 1  +  2*3

As we see, the tree on the right is much more concise and to the point. This tree can be directly evaluated by an interpreter or some executable code to calculate what might be generated.

12.2.8 Lexical Analysis

In reality, applying grammar rules directly to the individual characters is overkill. It can be convenient to add a prepass called lexical analysis. The raw text is first transformed into a sequence of lexemes (also called tokens). Each token is described with a regular expression and extracted from the character stream. For example, a number can be described with a regular expression [0-9]+, and an identifier can be [a-zA-Z_][0-9a-zA-Z_]*. After performing such processing, the text will no longer be a flat sequence of characters but rather a linked list of tokens. Each token will be marked with its type and for the parser, the token types will be mapped to terminals.

It is easy to ignore all formatting details (such as line breaks and other whitespace symbols) during this step.

12.2.9 Summary on Parsing

The compiler parses the source code in several steps. Two important steps are lexical and syntactic analysis.

During the lexical analysis, the program text is broken into lexemes, such as integer literals or keywords. The text formatting is no more relevant after this step. Each lexeme type is best described using a regular expression.

During the syntactic analysis, a tree structure is built on top of the stream of tokens. This structure is called an abstract syntax tree. Each node corresponds to a language construct.

12.3.1 Undefined Behavior

The completeness of the semantics description is not enforced. It means that some language constructions are only defined for a subset of all possible situations. For example, a pointer dereference *x is only guaranteed to behave in a consistent way when x points to a “valid” memory location. When x is NULL or points to deallocated memory, the undefined behavior occurs. However, such expression is absolutely correct syntactically.

The standard intentionally introduces cases of undefined behavior. Why?

First of all, it is easier to write compilers that produce code with less guarantees. Second, all defined behavior has to be implemented. If we want that dereferencing null pointer triggers an error, the compiler has two do two things each time any pointer is dereferenced:

• Try to deduce that in this exact place the pointer can never have NULL as its value.

• If the compiler can not deduce, that this pointer is never NULL, it emits assembly code to check it. If the pointer is NULL, this code will execute a handler to it. Otherwise, it will proceed with dereferencing the pointer.

Listing 12-8 shows an example.

Listing 12-8. ptr_analysis1.c

int x = 0;
int* p = &x;
...
/* there are no writes to `p` in these lines */
...
*p =  10; /* this pointer can not be NULL  */

However, this is much trickier than it might appear. In the example in Listing 12-8, we could have assumed, that as no writes to variable p are performed, it is always holding the address of x. However, this is not always true, as illustrated by the example shown in Listing 12-9.

Listing 12-9. ptr_analysis2.c

int x = 0;
int* p = &x;
...
/* there are no writes to `p` in these lines */
int**  z  =  &p;
*z = NULL; /* Still not a direct write to `p` */
...
*p =  10; /* this pointer can not be NULL -- not true anymore */

So, solving this problem actually requires a very complex analysis in presence of pointer arithmetic. Once the variable’s address is taken, or worse still, its address is passed to a function, you have to analyze the entire function calling sequence, take function pointers into account, pointers to the pointers, etc.

The analysis will not always yield correct results (in the most general case this problem is even theoretically undecidable), and the performance can suffer because of it. So, in accordance with the C laissez-faire spirit, the correctness of pointer dereferencing is left to the responsibility of the programmer himself.

In managed languages such as Java or C#, the defined behavior of pointer dereferencing is much easier to achieve. First, they are usually run inside a framework, which provides code for exception raising and handling. Second, the nullability analysis is much simpler in the absence of address arithmetic. Finally, they are usually compiled just-in-time, which means that the compiler has access to runtime information and can use it to perform some optimizations unavailable to an ahead-of-time compiler. For example, after the program has launched and given the user input, a compiler deduced that the pointer x is never NULL if a certain condition P holds. Then it can generate two versions of the function f containing this dereference: one with a check and the other without check. Then every time f is called, only one of two versions is called. If the compiler can prove that P holds in a calling situation, the non-checked version is called; otherwise the checked one is called.

The undefined behavior can be dangerous (and usually is). It leads to subtle bugs, because it does not guarantee an error in compile or in runtime. The program can encounter a situation with undefined behavior and continue execution silently; however, its behavior will randomly change after a certain amount of instructions are executed.

A typical situation is the heap corruption. The heap is in fact structured; each block is delimited with utility information, used by the standard library. Writing out of block bounds (but close to them) is likely to corrupt this information, which will result in a crash during one of future calls to malloc of free, making this bug a time-bomb.

Here are some cases of undefined behavior , explicitly specified by the C99 standard. We are not providing the full list, because there are at least 190 cases.

• Signed integer overflow.

• Dereferencing an invalid pointer.

• Comparing the pointers to elements of two different memory blocks.

• Calling function with arguments that do not match its initial signature (possible by taking a pointer to it and casting to other function type).

• Reading from an uninitialized local variable.

• Division by 0.

• Accessing an array element out of its bounds.

• Attempting to change a string literal .

• The return value of a function, which does not have an executed return statement.

12.3.2 Unspecified Behavior

It is important to distinguish between undefined behavior and unspecified behavior. Unspecified behavior defines a set of behaviors that might happen but does not specify which one exactly will be selected. The selection will depend on the compiler.

For example,

• The function argument’s evaluation order is not specified. It means that while evaluating f(g(), h()) we have no guarantees that g() will be evaluated first and h() second. However, it is guaranteed that both g() and h() will be evaluated before f().

• The order of subexpression evaluation in general, f(x) + g(x), does not enforce f to be executed before g. Unspecified behavior describes the cases of nondeterminism in the abstract C machine.

12.3.3 Implementation-Defined Behavior

The standard also defines the implementation-defined behavior , such as the size of int (which, as we told you, is architecture-dependent). We can think about such choices as the abstract machine parameters: before we start it, we have to choose these parameters.

Another example of such behavior is the modulo operation x % y. The result in case of negative y is implementation-defined.

What is the difference between implementation-defined and unspecified behavior? The answer is that the implementation (compiler) has to explicitly document the choices it makes, while in cases of unspecified behavior anything from a set of possible behaviors can occur.

12.3.4 Sequence Points

Sequence points are the places in the program where the state of the abstract machine is coherent to the state of the target machine. We can think about them this way: when we debug a program, we can execute it in a step-by-step fashion, where each step is roughly equivalent to a C statement. We usually stop on semicolon, function calls, || operator, etc. However, we can switch to the assembly view, where each statement will be encoded by possibly many instructions, and execute these instructions in the same manner. It allows us to execute only a part of statement, pausing in a halfway. In this moment , the state of the abstract C machine is not well defined. Once we finish executing instructions that implement one single statement, the machines’ states “synchronize,” allowing us to explore not only the state of assembly level but also the state of the C program itself. This is the sequence point.

The second, equivalent definition of sequence point is the place in the program where the side effects of previous expressions are already applied, but the side effects of the following ones are not yet applied.

The sequence points are

• Semicolon.

• Comma (which in C can act the same way as a semicolon, but also groups statements. Its usage is discouraged.).

• Logic AND/OR (not bitwise versions!).

• When the function arguments are evaluated but the function has not started its execution yet.

• Question mark in the ternary operator.

Multiple real-world cases of undefined behavior are tied to the notion of sequence points. Listing 12-10 shows an example.

Listing 12-10. seq_points.c

int i = 0;
i = i ++ * 10;

What is i equal to? Unfortunately, the best answer we can give is the following: there is an undefined behavior in this code. Apparently, we do not know whether the i will be incremented before assigning i*10 to i or after that. There are two writes in the same memory location before the sequence point and it is undefined in which order will they occur.

The cause of this is as we have seen in section 12.3.2, the subexpression evaluation order is not fixed. As subexpressions might have effects on the memory state (think function calls or pre-or postincrement operators), and there is no enforced order in which these effects occur, even the result of one subexpression may depend on the effects of the other.

12.4.1 Alignment

From the point of view of the abstract machine, we are working with bytes of memory. Each byte has its address. The hardware protocols, used on the chip, are, however, quite different. It is quite common that the processor can only read packs of, say, 16 bytes, which start from an address divisible by 16. In other words, it can either read the first 16 byte-chunk from memory or the second one, but not a chunk that starts from an arbitrary address.

We say that the data is aligned on N-byte boundary if it starts from an address divisible by N. Apparently, if the data is aligned on kn-byte boundary, it is automatically aligned on n-byte boundary. For example, if the variable is aligned on 16-byte boundary, it is simultaneously aligned on an 8-byte boundary.

Aligned data (8-byte boundary):
0x00 00 00 00 00 00 00 00 :    11 22 33 44 55 66 77 88

Unaligned data (8-byte boundary):
0x00 00 00 00 00 00 00 00 :    .. .. .. 11 22 33 44 55
0x00 00 00 00 00 00 00 07 :    66 77 88 .. .. .. .. ..

What happens when the programmer requests a read of a multibyte value which spans over two such blocks (e.g., 8-byte value, whose first three bytes lie in one chunk, and the rest is in another one)? Different architectures give different answers to this question.

Some hardware architectures forbid unaligned memory access. It means that an attempt to read any value which is not aligned to, for example, an 8-byte boundary results in an interrupt. An example of such architecture is SPARC. The operating systems can emulate unaligned accesses by intercepting the generated interrupt and placing the complex accessing logic into the handler. Such operations, as you might imagine, are extremely costly because the interrupt handling is relatively slow.

Intel 64 adapts a less strict behavior. The unaligned accesses are allowed but bear an overhead. For example, if we want to read 8 bytes starting from the address 6 and we can only read chunks that are 8 bytes long, the CPU (central processing unit) will perform two reads instead of one and then compose the requested value from the parts of two quad words.

So, aligned accesses are cheaper, because they require less reads. The memory consumption is often a lesser concern for a programmer than the performance; thus compilers automatically adjust variables alignment in memory even if it creates gaps of unused bytes. This is commonly referred to as data structure padding.

The alignment is a parameter of the code generation and program execution, so it is usually viewed as a part of language pragmatics .

12.4.2 Data Structure Padding

For structures, the alignment exists in two different senses:

• The alignment of the structure instance itself. It affects the address the structure starts at.

• The alignment of the structure fields. Compiler can intentionally introduce gaps between structure fields in order to make accesses to them faster. Data structure padding relates to this.

For example, we have created a structure, shown in Listing 12-11.

Listing 12-11. align_str_ex1

struct mystr {
    uint16_t a;
    uint64_t b;
};

Assuming an alignment on an 8-byte boundary, the size of such structure, returned by sizeof, will be 16 bytes. The a field starts at an address divisible by 8, and then six bytes are wasted to align b on an 8-byte boundary.

There are several instances in which we should be aware of it:

• You might want to change the trade-off between memory consumption and performance to lesser memory consumption. Imagine you are creating a million copies of structures and every structure wastes 30% of its size because of alignment gaps. Forcing the compiler to decrease these gaps will then lead to a memory usage gain of 30% which is nothing to sneeze at. It also brings benefits of better locality which can be far more beneficial than the alignment of individual fields.

• Reading file headers or accepting network data into structures should take possible gaps between structure fields into account. For example, the file header contains a field of 2 bytes and then a field of 8 bytes. There are no gaps between them. Now we are trying to read this header into a structure, as shown in Listing 12-12.

Listing 12-12. align_str_read.c

struct str {
     uint16_t a; /* a gap of 4 bytes */
     uint64_t b;
};
struct str mystr;
fread( &mystr, sizeof( str ), 1, f );

The problem is that the structure’s layout has gaps inside it, while the file stores fields in a contiguous way. Assuming the values in file are a=0x1111 and b=0x 22 22 22 22 22 22 22, Figure 12-4 shows the memory state after reading.

Figure 12-4. Memory layout structure and the data read from file

There are ways to control alignment; up until C11 they are compiler-specific. We will study them first.

The #pragma keyword allows us to issue one of the pragmatic commands to the compiler. It is supported in MSVC, Microsoft’s C compiler, and is also understood by GCC for compatibility reasons.

Listing 12-13 shows how to use it to locally change the alignment choosing strategy by using the pack pragma.

Listing 12-13. pragma_pack.c

#pragma pack(push, 2)
struct mystr {
    short a;
    long b;
};
#pragma pack(pop)

The second argument of pack is a presumed size of the chunk that the machine is able to read from memory on the hardware level.

The first argument of pack is either push or pop. During the translation process, the compiler keeps track of the current padding value by checking the top of the special internal stack. We can temporarily override the current padding value by pushing a new value into this new stack and restore the old value when we are done. Changing padding value globally is possible by using the following form of this pragma:

#pragma pack(2)

However, it is very dangerous because it leads to unpredictable subtle changes in other parts of program, which are very difficult to trace.

Let’s see how the alignment value affects the individual field’s alignment by analyzing an example shown in Listing 12-14.

Listing 12-14. pack_2.c

#pragma pack(push, 2)
struct mystr {
    uint16_t a;
    int64_t b;
};
#pragma pack(pop)

The padding value tells us how many bytes a hypothetical target computer can fetch from memory in one read. The compiler tries to minimize the amount of reads for each field. There is no reason to skip bytes between a and b here, because it brings no benefits with regard to the padding value. Assuming that a=0x11 11 and b=0x22 22 22 22 22 22 22 22, the memory layout will look like the following:

11 11 22 22 22 22 22 22 22 22

Listing 12-15 shows another example with the padding value equal to 4.

Listing 12-15. pack_4.c

#pragma pack(push, 4)
struct mystr {
    uint16_t a;
    int64_t b;
};
#pragma pack(pop)

What if we adapt the same memory layout without gaps? As we can only read 4 bytes at a time, it is not optimal. We have delimited the bounds of memory chunks that are readable atomically.

Pack: 2
11 11 | 22 22 | 22 22 | 22 22 | 22 22 | ?? ??
Pack: 4, same memory layout
11 11   22 22 | 22 22   22 22 | 22 22   ?? ??
Pack: 4, memory layout really used
11 11   ?? ?? | 22 22   22 22 | 22 22   22 22

As we see, when the padding is set to 4, adapting a gapless memory layout forces the CPU to perform three reads to access b. So, basically, the idea is to minimize the amount of reads while placing struct members as close as possible.

The GCC specific way of doing roughly the same thing is the packed specification of the __attribute__ directive. In general, __attribute__is describing the additional specification of a code entity such as a type or a function. This packed keyword means that the structure fields are stored consecutively in memory without gaps at all. Listing 12-16 shows an example.

Listing 12-16. str_attribute_packed.c

Struct__attribute__(( packed )) mystr {
    uint8_t first;
    float delta;
    float position;
};

Remember that packed structures are not part of the language and are not supported on some architectures (such as SPARC) even on the hardware level, which means not only a performance hit but also program crashes or reading invalid values.