Intermediate C Programming

Programming Problems Using Recursion 243

printf (" f(% d) = %d , count = %d \n" , val , fv , count );22

return EXIT _SUCCES S ;23

}24

The program prints two values at line 22: fv and count. Their values can be computed

independently. Fig. 15.2 shows one way of computing both using an approach similar to

that shown in Section 14.2.

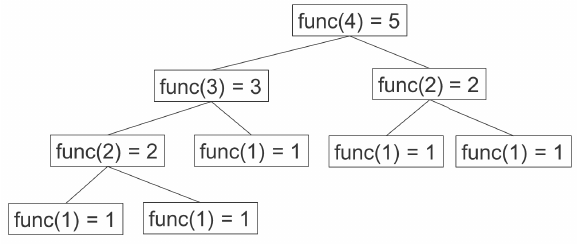
FIGURE 15.2: Determine the values of fv and count using a graphical illustration of the

calling relations.

The value of fv is 5. The value of count increments every time func is called. The ﬁgure

shows that both func and count are called 9 times.

This is a “top-down” approach to computing func. To compute func(4), the program

calls func(3). To compute func(3), func(2) is called. Computing func(4) calls func(2)

three times and each time that happens it needs to call func(1) + func(1). This is inef-

ﬁcient. It would be more eﬃcient if the program remembers the values of func(2) so that

it does not need to be recomputed. The following implementation shows a diﬀerent way of

computing func. It is a “bottom-up” approach: func(2) and func(3) are computed before

computing func(4). This is more eﬃcient because the program remembers the value of

func(2), and therefore does not need to recompute it.

// bottomu p . c1

#in clude < stdio .h >2

#in clude < stdlib .h >3

int func ( i n t n )4

int * arr ;6

// need n + 1 for arr [ n]7

arr = malloc ( s i z e o f ( i nt ) * (n + 1) );8

arr [0] = 1;9

arr [1] = 1;10

int ind ;11

for ( ind = 2; ind <= n ; ind ++)12

{13

arr [ ind ] = arr [ ind - 1] + arr [ ind / 2];14

}15

int val = arr [ n ];16

free ( arr );17

return val ;18

}19

244 Intermediate C Programming

int main ( i n t argc , char * * argv )20

{21

int val = 4;22

int fv = func ( val );23

printf (" f(% d) = % d\n " , val , fv ) ;24

return EXIT _SUCCES S ;25

}26

Some people mistakenly believe that recursion is slow. This is not true. The problem

is not recursion. The problem is redundant computation: func(2) is recomputed multiple

times. Recursion is fast when it is used correctly. Binary search and quick sort are two

examples. Some problems, such as integer partition, permutations, and combinations can

be solved naturally with recursion. Recursion is particularly helpful when the solution has

some symmetry with smaller solutions. This is indeed the case with all our recursive ex-

amples. Solving these types of problems using for or while loops is more diﬃcult. In each

case working out the required number of iterations is non-obvious, and the implementation

details would be quite complicated. What makes recursion simple is that it is possible to

assume that the simpler cases are already solved. It is only necessary to ﬁgure out how to

express a solution in terms of smaller solutions, and then, so long as the base cases are

correct, the whole thing will work. This book puts great emphasis on recursion not because

recursion is always a good strategy, but because recursion is an excellent approach for solv-

ing certain classes of problems. Attempting to solve these problems with other techniques

can be diﬃcult. If you understand recursion, then you can use it when recursion is a good

approach.

15.6 A Recursive Function with a Mistake

Consider the following incorrect implementation of binary search. One line in

binarysearch is incorrect, as marked by a comment. What is the output of this program?

// sear chbug . c1

#in clude < stdio .h >2

#in clude < stdlib .h >3

int binary Search ( i n t * arr , in t key , i n t len ) ;4

#d ef in e ARRAYSIZ E 105

int main ( i n t argc , char * * argv )6

int arr [ ARRAYS I ZE ] = {1 , 12 , 23 , 44 , 65 ,8

76 , 77 , 98 , 109 , 110};9

int ind ;10

for ( ind = 0; ind < ARRAYSIZE ; ind ++)11

{12

printf (" %d\ n" , b inarySe a rch ( arr , arr [ ind ],13

ARRAYSIZE )) ;14

}15

return EXIT _SUCCES S ;16

}17

int bina rySear chHel p ( in t * arr , i n t key , in t low , i n t high )19

Programming Problems Using Recursion 245

{20

i f ( low >= high ) /* ERROR : should be >, not >= */21

{22

return -1;23

}24

int mid = ( low + high ) / 2;25

i f ( arr [ mid ] == key )26

{27

return mid ;28

}29

i f ( arr [ mid ] > key )30

{31

return bin arySe archHe lp ( arr , key , low , mid - 1) ;32

}33

return bin arySe archHe lp ( arr , key , mid + 1 , high );34

}35

int binary Search ( i n t * arr , in t key , i n t len )37

{38

return bin arySe archHe lp ( arr , key , 0 , len - 1) ;39

}40

The program searches the array’s elements one by one. If binarySearchHelp were cor-

rect, the program would print:

When searching for 1, the arguments low and high change as shown in the following:

low high mid arr[mid] key

0 9 4 65 1

0 3 1 12 1

0 0 0 1 1

The problem occurs when low and high are both zero and binarySearchHelp re-

turns −1 without checking whether arr[mid] is the same as key. Does this mistake cause

binarySearchHelp to always return −1? Consider searching for 12:

low high mid arr[mid] key

0 9 4 65 12

0 3 1 12 12

The function correctly returns 1. What will the function return when searching for 23?

246 Intermediate C Programming

low high mid arr[mid] key

0 9 4 65 23

0 3 1 12 23

2 3 2 23 23

The function correctly returns 2. The program’s output is:

-1

As you can see, this program sometimes produces correct results and sometimes produces

incorrect results. This program has a 60% chance of producing correct results. This reinforces

the need to have a strategy for testing. It is usually important to automate testing so that

you can test many cases easily. A common mistake among beginning programmers is that

they test several cases and then believe their programs are correct.

Previous Chapter

15. Programming Problems Using Recursion (4/5)

Next Chapter

III. Structure

Table of Contents for Intermediate C Programming

Table of Contents for
Intermediate C Programming