Table of Contents for
Intermediate C Programming

Version ebook / Retour

Cover image for bash Cookbook, 2nd Edition Intermediate C Programming by Yung-Hsiang Lu Published by CRC Press, 2015
  1. Front Cover
  2. Contents (1/2)
  3. Contents (2/2)
  4. List of Figures (1/2)
  5. List of Figures (2/2)
  6. List of Tables
  7. Foreword
  8. Preface
  9. Author, Reviewers, and Artist
  10. Rules in Software Development
  11. Source Code
  12. I. Computer Storage: Memory and File
  13. 1. Program Execution (1/2)
  14. 1. Program Execution (2/2)
  15. 2. Stack Memory (1/5)
  16. 2. Stack Memory (2/5)
  17. 2. Stack Memory (3/5)
  18. 2. Stack Memory (4/5)
  19. 2. Stack Memory (5/5)
  20. 3. Prevent, Detect, and Remove Bugs (1/2)
  21. 3. Prevent, Detect, and Remove Bugs (2/2)
  22. 4. Pointers (1/6)
  23. 4. Pointers (2/6)
  24. 4. Pointers (3/6)
  25. 4. Pointers (4/6)
  26. 4. Pointers (5/6)
  27. 4. Pointers (6/6)
  28. 5. Writing and Testing Programs (1/4)
  29. 5. Writing and Testing Programs (2/4)
  30. 5. Writing and Testing Programs (3/4)
  31. 5. Writing and Testing Programs (4/4)
  32. 6. Strings (1/3)
  33. 6. Strings (2/3)
  34. 6. Strings (3/3)
  35. 7. Programming Problems and Debugging (1/4)
  36. 7. Programming Problems and Debugging (2/4)
  37. 7. Programming Problems and Debugging (3/4)
  38. 7. Programming Problems and Debugging (4/4)
  39. 8. Heap Memory (1/3)
  40. 8. Heap Memory (2/3)
  41. 8. Heap Memory (3/3)
  42. 9. Programming Problems Using Heap Memory (1/4)
  43. 9. Programming Problems Using Heap Memory (2/4)
  44. 9. Programming Problems Using Heap Memory (3/4)
  45. 9. Programming Problems Using Heap Memory (4/4)
  46. 10. Reading and Writing Files (1/3)
  47. 10. Reading and Writing Files (2/3)
  48. 10. Reading and Writing Files (3/3)
  49. 11. Programming Problems Using File (1/2)
  50. 11. Programming Problems Using File (2/2)
  51. II. Recursion
  52. 12. Recursion (1/4)
  53. 12. Recursion (2/4)
  54. 12. Recursion (3/4)
  55. 12. Recursion (4/4)
  56. 13. Recursive C Functions (1/4)
  57. 13. Recursive C Functions (2/4)
  58. 13. Recursive C Functions (3/4)
  59. 13. Recursive C Functions (4/4)
  60. 14. Integer Partition (1/5)
  61. 14. Integer Partition (2/5)
  62. 14. Integer Partition (3/5)
  63. 14. Integer Partition (4/5)
  64. 14. Integer Partition (5/5)
  65. 15. Programming Problems Using Recursion (1/5)
  66. 15. Programming Problems Using Recursion (2/5)
  67. 15. Programming Problems Using Recursion (3/5)
  68. 15. Programming Problems Using Recursion (4/5)
  69. 15. Programming Problems Using Recursion (5/5)
  70. III. Structure
  71. 16. Programmer-Defined Data Types (1/6)
  72. 16. Programmer-Defined Data Types (2/6)
  73. 16. Programmer-Defined Data Types (3/6)
  74. 16. Programmer-Defined Data Types (4/6)
  75. 16. Programmer-Defined Data Types (5/6)
  76. 16. Programmer-Defined Data Types (6/6)
  77. 17. Programming Problems Using Structure (1/4)
  78. 17. Programming Problems Using Structure (2/4)
  79. 17. Programming Problems Using Structure (3/4)
  80. 17. Programming Problems Using Structure (4/4)
  81. 18. Linked Lists (1/3)
  82. 18. Linked Lists (2/3)
  83. 18. Linked Lists (3/3)
  84. 19. Programming Problems Using Linked List (1/2)
  85. 19. Programming Problems Using Linked List (2/2)
  86. 20. Binary Search Trees (1/4)
  87. 20. Binary Search Trees (2/4)
  88. 20. Binary Search Trees (3/4)
  89. 20. Binary Search Trees (4/4)
  90. 21. Parallel Programming Using Threads (1/5)
  91. 21. Parallel Programming Using Threads (2/5)
  92. 21. Parallel Programming Using Threads (3/5)
  93. 21. Parallel Programming Using Threads (4/5)
  94. 21. Parallel Programming Using Threads (5/5)
  95. IV. Applications
  96. 22. Finding the Exit of a Maze (1/5)
  97. 22. Finding the Exit of a Maze (2/5)
  98. 22. Finding the Exit of a Maze (3/5)
  99. 22. Finding the Exit of a Maze (4/5)
  100. 22. Finding the Exit of a Maze (5/5)
  101. 23. Image Processing (1/3)
  102. 23. Image Processing (2/3)
  103. 23. Image Processing (3/3)
  104. 24. Huffman Compression (1/10)
  105. 24. Huffman Compression (2/10)
  106. 24. Huffman Compression (3/10)
  107. 24. Huffman Compression (4/10)
  108. 24. Huffman Compression (5/10)
  109. 24. Huffman Compression (6/10)
  110. 24. Huffman Compression (7/10)
  111. 24. Huffman Compression (8/10)
  112. 24. Huffman Compression (9/10)
  113. 24. Huffman Compression (10/10)
  114. A. Linux
  115. B. Version Control
  116. C. Integrated Development Environments (IDE) (1/3)
  117. C. Integrated Development Environments (IDE) (2/3)
  118. C. Integrated Development Environments (IDE) (3/3)
Recursion 175
number, we need to consider the number of possibilities for the remaining partition.
The relationship can be expressed in this table:
Total First Number Remaining Value to Partition
n 1 n − 1
n 2 n − 2
n 3 n − 3
.
.
.
n n − 2 2
n n − 1 1
n n 0
These are all the possible cases and they are exclusive. If the first number is 1, then
the remaining value to be partitioned is n − 1. How many ways can n − 1 be partitioned?
By definition, it is f (n − 1). Continuing with this logic, if the first number is 2, then the
remaining value is n − 2, and by definition there are f(n − 2) ways to partition it. Using
recursion, we can assume that we have the answers to smaller versions of the problems.
This works because the smaller versions are expressed in terms of yet smaller versions, and
eventually we get to the trivial cases, i.e., f (1) = 1, and f(2) = 2.
The value of f (n) is therefore the sum of all the different cases when the first number is
1, 2, 3, . . . , n − 1, or n. Now, we can express f (n) as
f(n) =
1 if n is 1
f(n − 1) + f(n − 2) + . . . f(1) + 1 = 1 +
n−1
P
i=1
f(i) if n > 1
(12.8)
There is also a convenient closed form solution to f (n):
f(n) = f (n − 1) +f (n − 2) + f (n − 3) + ... + 1
− f(n − 1) = +f(n − 2) + f(n − 3) + ... + 1
f(n) − f (n − 1) = f (n − 1)
f(n) = 2f (n − 1)
f(n) = 4f (n − 2)
f(n) = 8f (n − 3)
f(n) = 16f (n − 4)
.
.
.
f(n) = 2
n−1
f(1)
f(n) = 2
n−1
(12.9)
Therefore there are 2
n−1
ways to partition the integer n.
12.4.1 Count the Number of “1”s
The partition problem has many variations. In this variation we count how many “1”s
are used for partitioning n. Suppose g(n) is the answer. First observe that g(1) = 1 and
g(2) = 2. The more complicated cases can be related to the simpler cases with the following
logic. Observe that there are 2
n−2
partitions of n that begin with the digit “1”. There may
be “1”s in the partitions of the remaining value, n − 1. Thus, when the first number is
“1”, we use 2
n−2
+ g(n − 1) “1”s. Notice again how we just assume we have the answer for
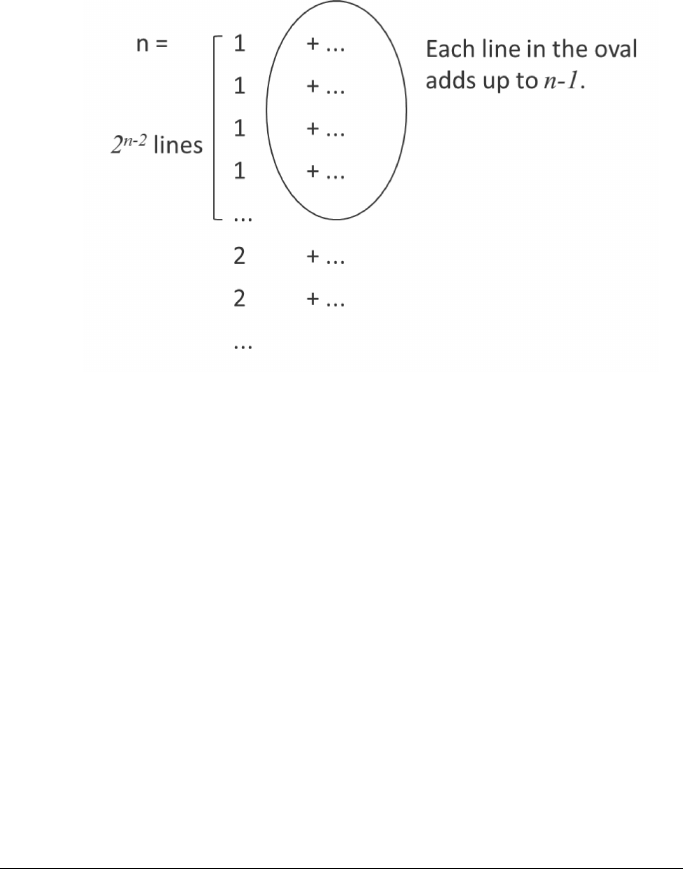
176 Intermediate C Programming
FIGURE 12.9: Count the occurrences of “1” when partitioning n.
smaller versions of the same function. We do not need to worry about the specific value of
g(n − 1), we just use it, confident that g(n − 1) will be expanded to g(n − 2), etc., until we
reach the trivial cases g(1) and g(2).
Continuing with this logic, when the first number is “2”, “1” is not used for the first
number but “1” may be used for partitioning the remaining value of n − 2. By definition,
“1” is used g(n − 2) times when partitioning n − 2.
Putting this all together, we calculate g(n) to be:
g(n) =
1 when n is 1
2
n−2
+ g(n − 1) + g(n − 2) + . . . g(1) = 2
n−2
+
n−1
P
i=1
g(i) when n > 1
(12.10)
To obtain the closed form, first find the relationship between g(n) and g(n − 1):
g(n) = 2
n−2
+ g(n − 1) +g(n − 2) + g(n − 3) + ... + g(1)
− g(n − 1) = 2
n−3
+g(n − 2) + g(n − 3) + ... + g(1)
g(n) − g(n − 1) = 2
n−3
+ g(n − 1)
g(n) = 2
n−3
+ 2g(n − 1)
(12.11)
This relationship can be expanded for g(n − 2), g(n − 3), ..., g(1).
g(n) = 2
n−3
+ 2g(n − 1)
g(n − 1) = 2
n−4
+ 2g(n − 2)
g(n − 2) = 2
n−5
+ 2g(n − 3)
.
.
.
g(n − k) = 2
n−k−3
+ 2g(n − k − 1)
.
.
.
g(3) = 2
0
+ 2g(2) when k = n − 3
(12.12)
In (12.12), the coefficient for g(n−1) on the right side is two. In order to cancel g(n −1),
the coefficient on the left size has to increase accordingly as shown below:
Recursion 177
g(n) = 2
n−3
+ 2g(n − 1)
2g(n − 1) = 2
n−3
+ 4g(n − 2)
4g(n − 2) = 2
n−3
+ 8g(n − 3)
.
.
.
2
k
g(n − k) = 2
n−3
+ 2
k+1
g(n − k − 1)
.
.
.
+ 2
n−3
g(3) = 2
n−3
+ 2
n−2
g(2)
g(n) +
n−1
P
i=3
2
n−i
g(i) = (n − 2)2
n−3
+ 2
n−2
g(2) +
n−1
P
i=3
2
n−i
g(i)
g(n) = (n − 2)2
n−3
+ 2
n−2
g(2)
g(n) = (n − 2)2
n−3
+ 2
n−1
g(n) = (n + 2)2
n−3
(12.13)
This table shows that the value of g(n) for 1 ≤ n ≤ 10. If a formula does not match
these cases, the formula is definitely wrong. However, matching these cases does not mean
that the formula is correct. It is necessary to have a systematic way to find the formula. It
is generally a bad idea to find a formula to match these finite values.
n 1 2 3 4 5 6 7 8 9
g(n) 1 2 5 12 28 64 144 320 704
12.4.2 Odd Numbers Only
In this variation of the partition problem we want to find how many ways n can be
partitioned without using any even number. It may be helpful to review how Equation (12.8)
is derived. What does f(n − 1) mean in this equation? It means the number of partitions
using “1” as the first number. Similarly, what does f (n −2) mean in this equation? It means
the number of partitions using “2” as the first number. To restrict the partitions to odd
numbers only, all partitions using even numbers must be discarded. Thus, f (n−2), f(n−4),
f(n − 6), etc., must be excluded. Suppose h(n) is the number of partitions for n using odd
numbers only.
h(n) = h(n − 1) + h(n − 3) + h(n − 5)... when n > 1 (12.14)
The last few terms will be different depending on whether n itself is odd or even. If n is
odd, n − 1 is even so h(1) is excluded. Also n − 1, n − 3, ..., are all even numbers. The
complete equation is shown below:
h(n) =
(
1 when n is 1
h(n − 1) + h(n − 3) + h(n − 5)... + h(2) + 1 when n > 1 and n is odd
(12.15)
If n is even, n − 1 is odd so h(1) is included. Also n − 1, n − 3, ..., are all odd numbers.
Therefore the complete equation is shown below:
178 Intermediate C Programming
h(n) =
1 when n is 1
h(n − 1) + h(n − 3) + h(n − 5)... + h(2) + 1 when n > 1 and n is odd
h(n − 1) + h(n − 3) + h(n − 5)... + h(1) when n is even
(12.16)
12.4.3 Increasing Values
How many ways can the positive integer n be partitioned using increasing values or the
number n itself? Suppose n is partitioned into the sum of k numbers:
n = a
1
+ a
2
+ a
3
+ ... + a
k
(12.17)
The following conditions must be true:
• a
i
(1 ≤ i ≤ k) are positive integers
• a
i
< a
i+1
(1 ≤ i < k)
Consider the first few cases of n:
• When n is 1, 1 is a valid partition.
• When n is 2, 2 is a valid partition but 1 + 1 is invalid.
• When n is 3, 1 + 2 and 3 are two valid partitions; 1 + 1 + 1, and 2 + 1 are invalid
partitions.
• When n is 4, 1 + 3 is a valid partition; 2 + 2 and 3 + 1 are invalid partitions.
• When n is 5, 1 + 4, 2 + 3 are valid partitions; 2 + 2 + 1, 3 + 2, 4 +1 are invalid
partitions.
To solve this problem, two arguments are needed for the equation. We define p(n, m)
to be the number of ways to partition n where m is the smallest number used. When
partitioning n, note the following:
• If 1 is used as the first number, then 2 is the smallest number that can be used when
partitioning n − 1. There are p(n − 1, 2) ways to partition n − 1 using 2 as the smallest
number.
• If 2 is used as the first number, then 3 is the smallest number that can be used to
partition n − 2. There are p(n − 2, 3) ways to partition n − 2 using 3 as the smallest
number.
• If 3 is used as the first number, then 4 is the smallest number that can be used to
partition n − 3. There are p(n − 3, 4) ways to partition n − 3 using 4 as the smallest
number.
Based on this reasoning,
p(n, 1) = p(n − 1, 2) + p(n − 2, 3) + ... + p(n − k, k + 1) + ... + p(1, n) + 1
= 1 +
n−1
P
i=1
p(n − i, i + 1)
(12.18)
By inspection we can tell that p(n, n) = 1. This means that there is one and only one
way to partition n using n as the smallest number. Also, p(n, m) = 0 if n < m because it
is impossible to partition an integer using a larger integer. This problem is different from
the previous ones because the recursive equations require two arguments. The fundamental
recursive reasoning is the same.
Recursion 179
12.4.4 Alternating Odd and Even Numbers
In this variation of the problem we want to find partitions that alternate between odd
and even numbers. If an odd number is used, then the next must be an even number. If an
even number is used, then the next must be an odd number. If only one number is used
(i.e., the number to be partitioned), then this restriction does not apply and it is always a
valid partition. This restriction allows only the following partitions for 1 to 7:
1 = 1 2 = 2 3 = 1 + 2 4 = 1 + 2 + 1
= 2 + 1 = 4
= 3
5 = 1 + 4 6 = 1 + 2 + 1 + 2 7 = 1 + 2 + 1 + 2 + 1
= 2 + 1 + 2 = 1 + 2 + 3 = 1 + 6
= 2 + 3 = 1 + 4 + 1 = 2 + 1 + 4
= 3 + 2 = 2 + 1 + 2 + 1 = 2 + 3 + 2
= 4 + 1 = 3 + 2 + 1 = 2 + 5
= 5 = 6 = 3 + 4
= 4 + 1 + 2
= 4 + 3
= 5 + 2
= 6 + 1
= 7
The following table shows the solutions for n between 1 and 10.
n 1 2 3 4 5 6 7 8 9 10
number of partitions 1 1 3 2 6 6 11 16 22 37
This problem using alternating odd and even numbers can be solved by defining two
functions as follows:
• s(n) is the number of ways to partition n using an odd number as the first number.
• t(n) is the number of ways to partition n using an even number as the first number.
By observation we can create the following table:
n 1 2 3 4 5
s(n) 1 0 2 1 3
t(n) 0 1 1 1 3
sum 1 1 3 2 6
To calculate s(n), the first number can be 1, 3, 5, ... and the second number must be an
even number. For example, when 1 is used for the first number, then the remaining n − 1
must start with an even number. By definition, there are t(n − 1) ways to partition n − 1
starting with an even number. When 3 is used for the first number, then there are t(n − 3)
ways to partition n − 3 starting with an even number. Based on this reasoning, s(n) is
defined as:
s(n) = t(n − 1) + t(n − 3) + t(n − 5)... (12.19)
By definition, s(n) must not start with an even number and t(n − 2), t(n − 4), ... must not
be included.
It is necessary to distinguish whether n is odd or even while writing down the last few
terms in this equation. If n is an even number then: