Intermediate C Programming

206 Intermediate C Programming

partition

val 106 1

left 105 4

ind 104 0

arr 103 10000

RL 102 line 44

main

arr 101 10000

n 100 4

(a) Stack Memory

Symbol Address Value

arr[3] 10012 1

arr[2] 10008 1

arr[1] 10004 1

arr[0] 10000 1

(b) Heap Memory

Now the value of left is 0 and the terminating condition at line 18 is true. This means

that we have reached a base case, and line 20 calls printPartition and prints the 4

elements in the array. Four elements are printed because ind is 4. Remember, ind gives

the next position to write an element into arr, and it also gives the length of the partition

so far. If you think about it carefully, you will see that these two things are equivalent.

Therefore, we can pass ind as the length of the array to printPartition. The program

now prints:

1 + 1 + 1 + 1

The function then returns because of line 21. The return statement at line 21 is not strictly

necessary, because the function will not call itself again. This is because the for loop starts

at 1 and val must be smaller than or equal to left. Because left is zero the function will

not enter the for loop, and will return normally anyway.

It is good practice to put the line 21 return statement. When people read recursive

functions they expect the functions to be divided neatly into the base case and the recursive

case. The return statement makes the base case clear. Clearly no recursion is going to

happen. No further analysis is required. Making code as clear as possible is one of the most

important parts of good programs. After meeting the terminating condition, the top frame

of the call stack is popped, and the program continues at line 27.

Frame Symbol Address Value

partition

val 121 1

left 120 1

ind 119 3

arr 118 10000

RL 117 line 27

partition

val 116 1

left 115 2

ind 114 2

arr 113 10000

RL 112 line 27

Integer Partition 207

partition

val 111 1

left 110 3

ind 109 1

arr 108 10000

RL 107 line 27

partition

val 106 1

left 105 4

ind 104 0

arr 103 10000

RL 102 line 44

main

arr 101 10000

n 100 4

(a) Stack Memory

Symbol Address Value

arr[3] 10012 1

arr[2] 10008 1

arr[1] 10004 1

arr[0] 10000 1

(b) Heap Memory

For the next iteration, val increments to two. This violates the condition val <= left

and the for loop exists. Since the function has nothing else to do after the for loop, the

top frame is popped. The program now continues at line 27.

Frame Symbol Address Value

partition

val 116 1

left 115 2

ind 114 2

arr 113 10000

RL 112 line 27

partition

val 111 1

left 110 3

ind 109 1

arr 108 10000

RL 107 line 27

partition

val 106 1

left 105 4

ind 104 0

arr 103 10000

RL 102 line 44

main

arr 101 10000

n 100 4

(a) Stack Memory

208 Intermediate C Programming

Symbol Address Value

arr[3] 10012 1

arr[2] 10008 1

arr[1] 10004 1

arr[0] 10000 1

(b) Heap Memory

Now the for loop enters the next iteration: val becomes 2 and the condition val <=

left is satisﬁed. Line 25 assigns 2 to arr[2] and line 26 calls the function itself again.

Frame Symbol Address Value

partition

val 121 garbage

left 120 0

ind 119 3

arr 118 10000

RL 117 line 27

partition

val 116 2

left 115 2

ind 114 2

arr 113 10000

RL 112 line 27

partition

val 111 1

left 110 3

ind 109 1

arr 108 10000

RL 107 line 27

partition

val 106 1

left 105 4

ind 104 0

arr 103 10000

RL 102 line 44

main

arr 101 10000

n 100 4

(a) Stack Memory

Symbol Address Value

arr[3] 10012 1

arr[2] 10008 1 → 2

arr[1] 10004 1

arr[0] 10000 1

(b) Heap Memory

Because left is zero, the terminating condition at line 18 is true. The program prints

the ﬁrst 3 elements (because ind is 3) in arr. So the program prints:

1 + 1 + 2

Line 21 returns and the top frame is popped.

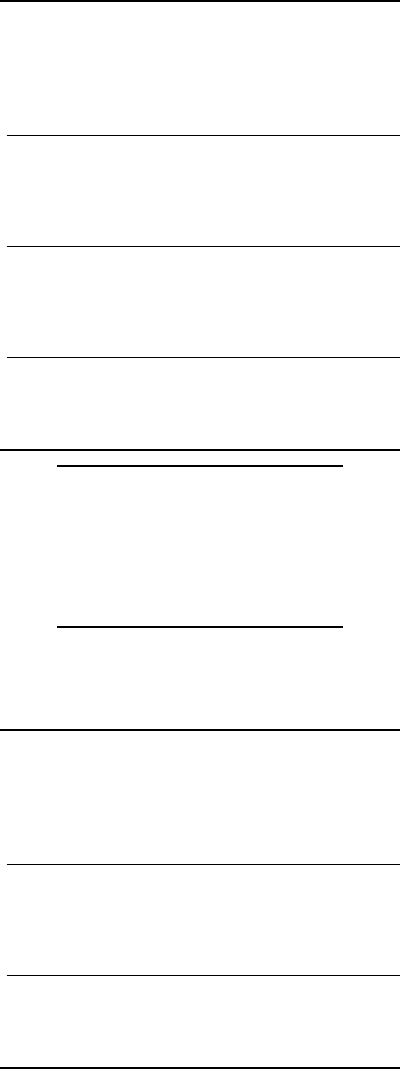
Integer Partition 209

Frame Symbol Address Value

partition

val 116 2

left 115 2

ind 114 2

arr 113 10000

RL 112 line 27

partition

val 111 1

left 110 3

ind 109 1

arr 108 10000

RL 107 line 27

partition

val 106 1

left 105 4

ind 104 0

arr 103 10000

RL 102 line 44

main

arr 101 10000

n 100 4

(a) Stack Memory

Symbol Address Value

arr[3] 10012 1

arr[2] 10008 2

arr[1] 10004 1

arr[0] 10000 1

(b) Heap Memory

The next iteration increments val to 3 but the condition val <= left is not satisﬁed.

The function exits the for loop. Since the function has nothing else to do after the for

loop, the function returns and the top frame is popped.

Frame Symbol Address Value

partition

val 111 1

left 110 3

ind 109 1

arr 108 10000

RL 107 line 27

partition

val 106 1

left 105 4

ind 104 0

arr 103 10000

RL 102 line 44

main

arr 101 10000

n 100 4

(a) Stack Memory

210 Intermediate C Programming

Symbol Address Value

arr[3] 10012 1

arr[2] 10008 2

arr[1] 10004 1

arr[0] 10000 1

(b) Heap Memory

For the next iteration, val becomes 2 and assigns 2 to arr[1].

Frame Symbol Address Value

partition

val 111 2

left 110 3

ind 109 1

arr 108 10000

RL 107 line 27

partition

val 106 1

left 105 4

ind 104 0

arr 103 10000

RL 102 line 44

main

arr 101 10000

n 100 4

(a) Stack Memory

Symbol Address Value

arr[3] 10012 1

arr[2] 10008 2

arr[1] 10004 1 → 2

arr[0] 10000 1

(b) Heap Memory

This process may seem tedious. Fortunately, computers are good at tedious work. Please

practice a few times and ensure that you fully understand the changes in the call stack and

heap memory. Then, leave the details to computers.

14.2 Trace Recursive Function Calls

Another way to understand this program is to draw its call tree. A call tree is a graphical

representation of the relationship between function calls. This tree is drawn “inverted” with

the root at the top, and the leaves at the bottom. Consider the following example:

void f1 ()1

f2 () ;3

Fig. 14.1 illustrates the calling relation of the two functions.

Here is another example and Fig. 14.2 shows the calling relations:

Previous Chapter

14. Integer Partition (1/5)

Next Chapter

14. Integer Partition (3/5)

Table of Contents for Intermediate C Programming

Table of Contents for
Intermediate C Programming