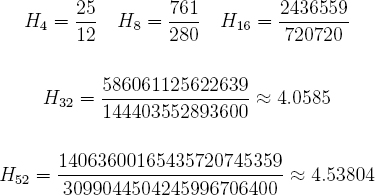
Chapter 3

Tools for Security and Insecurity

Cryptosystems and cryptographic protocols rely on various tools to be implemented properly. Perhaps the most basic tool is a random bit generator.¹ Random bit generators are used to randomly generate symmetric keys, private keys, padding, and so on in cryptography. They form the cornerstone of algorithms designed to protect computer systems and the cornerstone of algorithms that are designed to subvert computer systems. A poor random number generator could lead to a weak or otherwise guess-able private key. A poor random number generator could lead to a guess-able symmetric key and thereby diminish the effectiveness of a cryptovirus attack.

The survey books on cryptography that appeared in the 1990s gave the impression that crypto is a panacea for the Internet and its needs. However, experience has shown that this is far from the case [260]. For example, symmetric ciphers were analyzed in detail and proposed as solutions to common problems, yet little direction was given on how to arrive at truly random symmetric keys. This led to implementations containing very strong components as well as weak ones and security almost always defaults to the weakest link.

The first part of this chapter describes various physical phenomena that have been proposed in the literature as sources of randomness. It is common practice to misuse such sources by utilizing cryptographic hash functions as entropy extractors. The nature of this questionable practice is discussed in some detail.

John von Neumann's classic algorithm for unbiasing a biased coin is one of the earliest known entropy extraction algorithms². In this chapter it is shown how to apply this algorithm to an entropy source that behaves like a biased coin. A simple extension to Neumann's algorithm is then given along with references to other approaches. Common sense dictates that the more entropy sources that can be used, the better, so an approach is given to combine multiple sources of entropy securely. This approach has the property that the resulting bit stream is perfectly random provided that at least one of the entropy sources behaves like a biased coin and that is provably quasi-random otherwise.

It is often the case that sources of physical randomness provide random bits at a rate that is too slow for most applications. As a result efficient algorithms are needed that can convert a small number of truly random bits into a larger number of pseudorandom bits. Such algorithms are called pseudorandom number generators and the general topic is addressed in this chapter.

It is an unfortunate fact that even when random numbers are generated properly they are often misused. For example, OpenSSL suffered from a classic wrap-around bug in which the numbers from 1 to n were chosen in such a way that the smallest of these numbers were more likely to be chosen than the rest [233, 329]. This occurred in the selection of witnesses for the Rabin-Miller probabilistic primality test. Uniform sampling is a general subject that is important in designing secure malware as well. For example, a worm may need to choose a server uniformly at random from a set of three servers in order to decide which server to infect. Furthermore, the worm may only have a random bit generator at its disposal to make the selection. A common programming mistake is to generate two bits to get a number x between 0 and 3 inclusive, and then let the final answer be x mod 3. This is wrong since 0 will occur with a higher probability than 1. Uniform sampling techniques solve this problem and for this reason the topic of uniform sampling is covered.

Even when used correctly, random bits are often utilized in a wasteful fashion. This problem can be avoided by the judicious selection of efficient algorithms for the problem at hand. As a case in point, the problem of shuffling a deck of cards is covered. It is shown how successively choosing a card from the deck randomly uses up more random bits on average than applying an unranking algorithm from algorithmic combinatorics. This particular example is clearly applicable to on-line casinos, but is also applicable to designing secure polymorphic viruses. A polymorphic virus often needs to randomly permute instructions and may need to select a random subset of machine registers to use in a decryption algorithm that deciphers the bulk of the virus.

The chapter concludes with a discussion of how general advances in cryptography lend strength to malicious software attacks. It is shown how semantic security against plaintext attacks and adaptive chosen-ciphertext security affect the cryptovirus extortion attack from the perspective of the attacker. Also, the subject of mix networks is addressed. Mix networks constitute a fundamental building block in secure on-line voting protocols, electronic money protocols, and so on, and they are also crucial in carrying out malicious software attacks in a way that protects the perpetrator, be it a person or finite automaton.

3.1 Sources of Entropy

Computer programs utilize entropy sources to generate random numbers. Often user input is used as an entropy source. For example, the RSA toolkit SecurPC, which ran on Microsoft Windows 95, derived random seeds based on keyboard and mouse timings. This data is collected during a period of several minutes in which the user “bangs on the keyboard” [248]. Aside from being a hassle from the user's perspective, the security of this approach is questionable to say the least. Reliance on user-supplied entropy should be avoided or minimized whenever possible since it is vulnerable to attacks and can provide a false sense of security. This holds true for normal security applications as well as for malicious software.

Desirable sources of entropy are those that are firmly rooted in physical phenomena that are not affected by the actions of users. The emission from radioactive material has been proposed as entropy source [124]. Although this may be a very solid source of randomness, it requires specialized hardware that does not come with typical personal computer systems.

An attractive candidate for entropy is AT&T's truerand (described in Chapter 2) since it is based on physical phenomena and is likely to work on any PC equipped with a CPU crystal and a real-time clock crystal. Truerand increments a counter in a busy-waiting fashion until a timer interrupt causes the loop to terminate. This effectively pits the real-time clock signal against the microprocessor signal and in theory captures their discrepancies in the resulting counter value.

Another attractive entropy source is the air turbulence that exists within hard drives. The seek time for a drive is the time it takes the read/write head to move over the track that it is going to read or write to. Once in position, the disk must rotate so that the desired sector falls under the read/write head. This is called the rotational latency or rotational delay [221]. Seek times and rotational delay are governed by physical phenomena and are affected by such things as chaotic air turbulence that is generated within the confines of high-speed hard disk drives [81]. A typical way to extract entropy from this source is to measure the time it takes to perform a disk read, for instance. Davis surmised that the movement of a hard disk arm perturbs the flow of air inside the drive, thus creating chaotic turbulence. To implement programs that extract this type of entropy, one has to be conscious of the fact that most operating systems cache disk accesses. It is prudent to measure hard disk entropy by making low level read/write calls.

Using hard disks as entropy sources was carefully studied at Lucent Technologies [139]. Jakobsson et al devised an approach to extracting randomness from hard disks based on multiple drive phenomena. They derived experimental results using a Sun Ultra-1 with a Cheetah disk and were able to generate between 5 and 577 random bits per minute depending on the type of phenomena that was used. They subjected the resulting bits to a battery of tests, and they passed with flying colors.

Designing software that avoids the use of specialized hardware is even more important in the case of malicious software than in normal scenarios. Consider computer viruses, for example. By their very nature they propagate from machine to machine, some of which may lack the needed specialized hardware and all of which are hostile environments to the virus. Such programs clearly cannot assume the presence of specialized hardware random number generators.

3.2 Entropy Extraction via Hashing

It is not an uncommon practice to collect randomness from entropy sources to produce a byte stream and then hash this byte stream to derive a “random” stream of bits. This heuristic is most likely based on the premise that since the outputs of cryptographic hash functions look random, they are random. When hash functions are used as such, they are being used as entropy extractors³.

Consider the SHA-1 cryptographic hash function, for example [211]. SHA-1 takes as input a variable length byte stream and outputs a 160-bit hash value. SHA-1 is based directly on the MD4 algorithm [242]. MD4 is a customized hash function designed with the explicit purpose of hashing with optimized performance in mind. The original MD4 design goals were to:

1. Make finding a collision difficult, taking about 2⁶⁴ operations to do so (collision intractability).
2. Make finding a message yielding a pre-specified hash value difficult, taking about 2¹²⁸ operations to do so (non-invertability).

Despite the fact that finding collisions was supposed to be difficult, a collision in MD4 was in fact found [94]. This demonstrates the danger of relying on primitives that cannot be proven to be correct.

Collision resistance and non-invertability were also the design criteria used in devising SHA [201]. SHA was not designed to output “randomlooking hash values” and it was not designed to “extract truly random bits from inputs with a sufficient amount of entropy.” The fact that it may appear to do so on the surface is immaterial from the standpoint of security. Properties (1) and (2) above were designed to provide sufficient conditions for using a hash function to heuristically protect against existential forgeries in digital signature schemes.

The use of SHA-1 to extract 160 “random” bits from the collected entropy strings is perilous since there is no evidence to suggest that the SHA-1 function does in fact do this. This use of SHA-1 assumes that it is a magic box that can magically extract entropy from the input string and output a truly random 160-bit string. The following quote is from a paper by Juels et al [148]:

Timings of human interaction with a keyboard or mouse are currently the most common source of random seeds for cryptographic applications on PCs. After a sufficient amount of such timing data is gathered, it is generally hashed down to a 128-bit or 160-bit seed. This method relies for its security guarantees on unproven or unprovable assumptions about the entropy generated by human users [97] and the robustness of hash functions as entropy extractors.

The danger of using a complex algorithm to produce strong random numbers in the absence of a theoretical foundation or analysis was noted in RFC 1750 [97]:

Another serious strategy error is to assume that a very complex pseudo-random number generation algorithm will produce strong random numbers when there has been no theory behind or analysis of the algorithm.

There has been no theory or analysis behind SHA-1's ability to extract entropy from its input. The complexity of the SHA-1 algorithm in no way justifies its use as a magic box.

Consider the case in which entropy is taken from two sources. The first source is a weak source derived from user input (e.g., message arrival, mouse inputs, etc.) and potentially guessable inputs such as the system time. The second source is a strong source of entropy such as a hardware RNG. There is strong reason to suspect that the clock input is poor indeed. The following is from RFC 1750 [97]:

Computer clocks, or similar operating system or hardware values, provide significantly fewer real bits of unpredictability than might appear from their specifications.

Suppose that 24 bytes are derived solely from the weak source and 24 bytes are taken directly from the strong source. Finally, suppose that these two sequences are concatenated and fed as input to SHA-1 to produce a 20-byte value. The use of SHA-1 in this fashion could in fact result in a seed that is significantly less random than 24 bytes from the strong entropy source. It is conceivable that SHA-1 mixes this low-quality randomness with the high-quality randomness and outputs bits having a degree of randomness that is somewhere between the two extremes. An extreme, albeit remote, possibility is that SHA-1 will derive virtually all of the resulting entropy from the weak source. Again, since there is no proof regarding SHA-1's true behavior as an entropy extractor, anything seems possible.

3.3 Unbiasing a Biased Coin

The notion of a biased coin is by and large an abstraction used by theorists to articulate the behavior of a source of entropy. A real coin may certainly be biased based on how it was minted. But in the context of computer security, a biased coin is a general term for an entropy source that has a fixed bias towards outputting binary 1's or binary 0's.

As it turns out, the existence of a biased coin is enough to guarantee access to perfectly random bits. For many people, particularly those in the computer security field, the mere mention of perfect anything borders on taboo. Yet, in this case it is safe to say so. The math speaks for itself and the proof of this statement is given in this chapter. The subtlety lies in whether or not a given source of entropy in fact behaves like a biased coin or not.

3.3.1 Von Neumann's Coin Flipping Algorithm

A biased coin is a coin that has a fixed probability of heads, denoted by p_h = 1/2 + δ, where δ is a Real number contained in the interval [-1/2,1/2]. The value δ is referred to as the bias of the coin. Let p_t be the probability of tails. Hence, p_t = 1 − p_h. For example, if a coin comes up heads with probability 51% then δ =1/100. If the coin comes up heads with probability 49% then δ = −1/100.

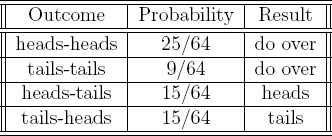
The standard approach to removing bias is to use Neumann's classic unbiasing algorithm [309]. The problem of unbiasing a biased coin is one whose fundamental nature is matched only by its elegant solution. It is instructional to consider the problem using a concrete example. Suppose that we are given a coin that comes up heads with probability 5/8. Neumann's solution is as follows. A series of experiments are performed in which the coin is tossed twice in succession. If in a given experiment the result is heads followed by tails, then the result of the toss is heads and no more experiments are performed. If in a given experiment the result is tails followed by heads, then the final outcome is tails and no more experiments are performed. If in a given experiment the tosses are the same, then another experiment is performed. This is depicted in Table 3.1.

Observe that the probability of heads is the same as the probability of tails. So, given that the two tosses are not the same the answer will be heads with probability 1/2. The answer is therefore always correct when an experiment terminates. An interesting aspect of this algorithm is that the numerical value of the bias is not needed to generate fair coin tosses. The probability that a given experiment will terminate with an answer is 15/64 + 15/64 = 30/64. Although it is possible that this method will never terminate when executed, the chances of this is negligible for a bias of 1/8. Since the algorithm might never halt but always outputs the correct answer when it does halt, it belongs to a class of algorithms known as Las Vegas algorithms. The algorithm is tractable for any bias that is not overwhelmingly close to heads or tails.

The following claim regarding Neumann's algorithm can be proven.

Claim 1 When the input bits to Neumann's algorithm are generated by a biased coin, Neumann's algorithm outputs a heads with probability 1/2.

To see this, consider the case that a value is output in iteration j. Since the two input bits for iteration j are generated by a biased coin it follows that the two flips are independent events. In iteration j, Neumann's algorithm outputs heads with probability (1/2 + δ)(1/2 − δ). It outputs tails with probability (1/2 − δ)(1/2 + δ). It follows from the commutative property of multiplication that these probabilities are equal.

Table 3.1 Unbiasing using Neumann's algorithm

3.3.2 Iterating Neumann's Algorithm

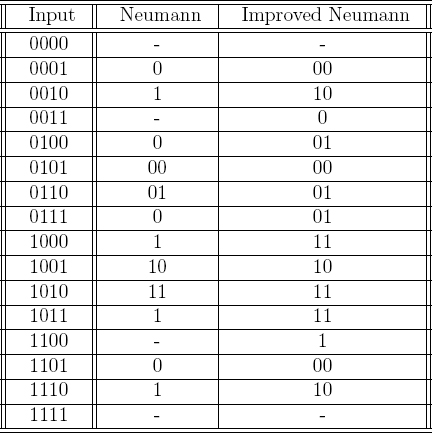
There has been a significant amount of research on improving the efficiency of Neumann's algorithm⁴ [148, 222]. Rather than reiterating one of these algorithms, a simple example of how to slightly improve Neumann's method will be given. In the improvement described in Table 3.2, Neumann's algorithm is modified to accept four bits at a time instead of two. A result of heads is indicated by a binary “1” and a tails is indicated by a binary “0.”

The middle column shows the output when Neumann's algorithm is applied to the input nibble.⁵ For example, if the input is 0001 then the first two zeros causes a rejection, and the 01 causes a zero to be output. The rightmost column shows the output when Neumann's method is generalized to taking 4 bits as input. Observe that in each row the rightmost column has at least as many bits listed as the middle column, and sometimes more so. It follows that this approach has a higher bandwidth than Neumann's algorithm.

To see the utility of this increased bandwidth algorithm, suppose that this improved algorithm is supplied with a very long stream of input bits. We would expect it to produce more perfectly random bits than Neumann's classic algorithm would.

The correctness of the improved algorithm will now be analyzed. Recall from probability theory that if A and B are two events in a uniform probability space, the conditional probability of A given B is defined as follows.

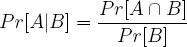
The following are probabilities of outputting 0 and 1 when one bit is output.

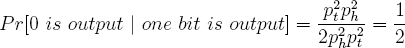
Table 3.2 Improved Neumann Algorithm with 4-bit input

It remains to consider the case that two bits are output. Below, the probability for 00 is derived.

It is straightforward to show that the conditional probability is 1/4 for 01, 10, and 11 as well.

3.3.3 Heuristic Bias Matching

A crucial observation in Neumann's classic algorithm is that the bias must be the same for both flips in a given execution of Neumann's algorithm for the output bit to be unbiased. This suggests that great care should be exercised when applying Neumann's algorithm to a given entropy source.

Neumann's method can be heuristically applied to remove bias in the output of truerand using the following algorithm. (Truerand is discussed in Chapter 2.) In the first step truerand is invoked to obtain the 16 least significant bits of the counter i. Let s₁ denote these 16 bits. Truerand is then invoked again to obtain another set of 16 bits s₂. The least significant bits from each of these two sets are used as a Neumann experiment, then the two penultimate bits are used as a second experiment, and so on. For concreteness, suppose that s₁ and s₂ are as follows:

Experiment 1 results in 10, experiment 2 results in 11, experiment 3 results in 00, and so on. A result of 10 is interpreted as a randomly chosen binary 1 and a result of 01 is interpreted as a randomly chosen binary 0. A result of 00 or 11 is regarded as a failed experiment. Let p_i,j denote the probability that a binary 1 occurs in the j^th bit of the i^th trial, where j = 0, 1,..., 15 and i = 1, 2, 3, 4,.... Consider the following two assumptions:

1. p_i,j = p_i+1,j for i = 1, 3, 5, 7,... and j = 0, 1, 2, ..., 15.
2. for all i there exists a j contained in {0, 1, 2, ..., 15} such that p_i,j is neither overwhelming nor negligible.

Assumption (1) implies that truerand behaves consistently across pairs of invocations, which is necessary for correctness. Assumption (2) implies that in each trial i there is at least one probability p_i,j capable of producing a fair toss⁶. For example, suppose that p_i,15 = 1 for i = 1, 2, 3, .... In this case the random number generator will never output a bit based on bit position j = 15. If for all i, p_i,j = 1 for j = 0, 1, 2, ..., 15 then truerand would not provide any randomness at all.

This approach demonstrates the notion of heuristic bias matching. A series of “random” positive integers are obtained from a timing-sensitive entropy source. The source should not be based on user inputs, and there should be reason to believe that the source behaved in the same basic way to produce each of these numbers. The integers are such that the entropy is arguably concentrated in the least significant bits. The most significant bits may have no entropy at all. Pairs of these integers are obtained from the source. To apply Neumann's algorithm, the least significant bits are run through Neumann's algorithm, then the second least significant bits, and so on. Of course, this is only a heuristic. But, one would expect that the biases may in fact match up this way. If they do, then perfectly random bits will result. To guard against the possibility that the biases do not match up, multiple entropy sources should be used and a general approach such as Santha and Vazirani's algorithm (described in Section 3.4) should be employed to combine the sources.

3.4 Combining Weak Sources of Entropy

Consider a true RNG predicated on the “randomness” derived from keyboard latency. What if the user breaks his or her arm and has to type methodically with one hand?⁷ This may eliminate some if not all the randomness for a time. What if a hardware-based RNG suffers a breakdown, thus rendering the hardware RNG unavailable? Such a solution would then have to rely entirely on other sources of randomness until the failure is rectified.

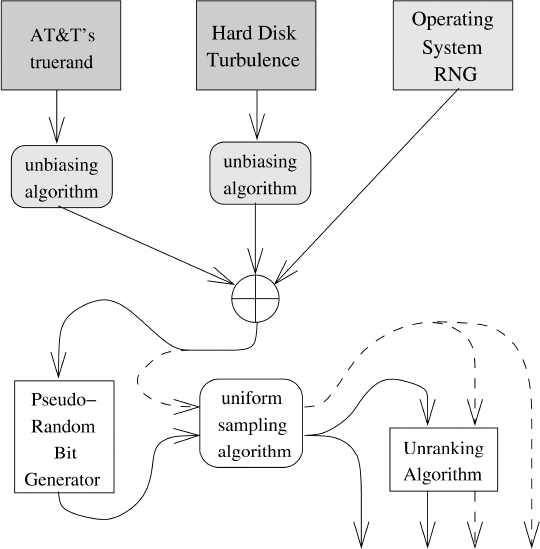
A solid approach to generating pseudorandom bits based on physical randomness is given in Figure 3.1. The two dark gray boxes are separate sources that are believed to provide a measurable amount of true entropy. Each source is treated separately and the output of each source is sent through an unbiasing algorithm as indicated by the light gray boxes. The operating system RNG could, for instance, be the Intel hardware RNG. This RNG uses two free-running oscillators, one that is fast and one that is much slower. A thermal noise source is used to modulate the frequency of the slower clock signal. The slower clock triggers measurements of the faster clock. The drift between the two is used to generate bits, which may be biased [149]. The Intel hardware RNG applies Neumann's algorithm internally to produce an unbiased stream (in theory). This is why the output of the Intel RNG does not go through a light gray box in Figure 3.1.

The three bit streams produced by the three light gray boxes are then bitwise exclusive-or'ed. This is indicated by the ⊕ symbol. Observe that if one of the physical sources of randomness behaves like a biased coin then exactly one of the streams going into ⊕ will be completely random. This is what makes this random number generation method robust. Suppose that all but one of the sources is compromised, either due to device failure or a malicious adversary. As long as one of the streams is truly random, the output of the ⊕ operation will be truly random. If a source were to shut down, then the stream that it would normally contribute to ⊕ can be set to all zeros. This will have a null effect on the bitwise XOR operation.

Figure 3.1 Sound approach to generating and using randomness

In fact, it is sufficient that in the bitwise XOR operation, one bit in each bit position be completely random. This will now be analyzed. Let B_i = b_i,1 b_i,2 . . . b_i,k denote the bit string that is output by Neumann's algorithm when applied to entropy source i. Each string B_i is k bits in length. Since there are three sources in Figure 3.1, it follows that 1 ≤ i ≤ 3. The strings B₁, B₂, and B₃ are bitwise exclusive-or'ed to obtain a k-bit seed S = s₁ s₂ · · · s_k using the following algorithm.

XORTheBitStrings(B₁, B₂, B₃):

1. for j = 1 to k do:

2.           s_i = b_1,j ⊕ b_2,j ⊕ b_3,j

3. output the bit string S = s₁, s₂ · · · s_k

The value S may be used to seed a pseudorandom bit generator.⁸

The following claim can be proven regarding the application of the exclusive-or operation to the streams.

Claim 2 If for all j where 1 ≤ j ≤ k there exists an i [1,3] such that b_i,j is chosen uniformly at random, then S is a truly random k-bit string.

To see this, consider bit position j where 1 ≤ j ≤ k. Without loss of generality, let b_i,j be a bit that is chosen uniformly at random, with 1 ≤ i ≤ 3. Let p_h denote the probability that the three bits in bit position j other than b_i,j exclusive-or to the value heads where heads corresponds to 1. Hence,

The probability that s_j = 1 is 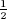p_h + 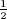(1 − p_h) = 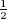. This is the probability that bit b_i,j = 0 and p_h results in heads plus the probability that bit b_ij = 1 and p_h results in tails.

Observe that the perfect randomness in each bit in S is closely related to the security of each plaintext bit in a Vernam ciphertext⁹. The unconditional security of the One-time pad holds regardless of the probability distribution over the message space.

In addition to being provably secure when a biased coin is available, this solution produces quasi-random bits when such a coin is not available, provided that enough sources of weak entropy are used. This follows immediately from the work of Santha and Vazirani [253], who weaken the assumption that a biased coin is available. The pseudorandomness results from the fact that several weakly random bit streams are bitwise exlusive-or'ed with each other. The basic idea may be illustrated using several examples. Consider the two entropy sources in Table 3.3.

Consider the first row in Table 3.3. A final result of heads occurs if source 1 results in heads and source 2 results in tails, or if source 1 results in tails and source 2 results in heads. This is 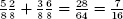. A coinflip that results from the XOR of the bits from the two sources is in every case the same or better than the best flip in either of the two sources.¹⁰

It is important not to misinterpret Figure 3.1. Relying on three sources alone may not always be a good idea. This is especially true if the sources are poor. However, when only a small amount of physical sources is available some form of unbiasing should be performed on each before exclusive-or'ing the resulting bit streams. If only one entropy source is available and the source is known to be reliable then it can be used to form multiple arrays of bytes. These byte arrays can be run through the Santha-Vazirani algorithm to extract quasi-random bits.

The Santha-Vazirani algorithm is a good way to combine weak entropy sources to guarantee that the randomness improves. However, the state of the art in entropy extraction has advanced considerably in recent years. There is a wealth of scientific literature on the subject [207, 266, 267, 296, 297, 298, 299]. Entropy extraction is an area of theoretical computer science unto itself. It has far more applicability than to cryptography alone since truly random numbers are needed to run randomized algorithms such as Quicksort properly. Entropy extraction algorithms have their own set of assumptions, not unlike the factoring assumption, Diffie-Hellman assumption, and so on. It is a subject that has been largely neglected in texts dealing with cryptography. Given the robust nature of modern entropy extraction algorithms, there is little reason not to employ them to arrive at provably random seeds for PRNGs¹¹. Were a company to advertise both the entropy source assumptions and the intractability assumptions that their products relied upon, that company would truly raise the bar in the computer security industry.

It is unfortunate that entropy extractors are largely, if not entirely, ignored by the software industry. They are often dismissed as being too slow or otherwise not necessary. To the contrary, the Santha-Vazirani algorithm is even faster than using most hash functions such as SHA-1 to extract entropy. It simply performs the bitwise XOR operation on collected entropy streams. Also, the speed is in many cases irrelevant. The proper way to generate random bits is to work hard to get a truly random seed and then let the faster pseudorandom number generator do the rest. All that is needed is a truly random seed and perhaps a couple more randomly chosen parameters in order to operate a secure cryptographic pseudorandom number generator properly.

3.5 Pseudorandom Number Generators

Subsection 3.5.1 presents a pseudorandom number generator that has undergone standardization. It does not enjoy provably secure properties, but constitutes a sound heuristic approach to the problem. The approach is ideal for applications that demand a high volume of pseudorandom bits per second. Subsection 3.5.2 covers PRNGs that have provably secure properties under well-accepted intractability assumptions.

3.5.1 Heuristic Pseudorandom Number Generation

The algorithm below is a U.S. Federal Information Processing Standard (FIPS) approved method to pseudorandomly generate keys and initialization vectors for use with DES. It is from the ANSI X9.17 standard [135].

ANSIX917PRBG(s, m, k):

input: a random 64-bit seed s, integer m, and a DES EDE key k

output: m pseudorandom 64-bit strings x₁, x₂, ..., x_m

1. compute I = E_k(D) where D is a 64-bit representation of the date/time in as fine a resolution as possible.

2. for i = 1 to m do:

3.           x_i = E_k(I ⊕ s)

4.           s = E_k(x_i ⊕ I)

5. output (x₁, x₂, ..., x_m)

This approach is a sound way to generate pseudorandom bits provided that DES is replaced by a more modern cipher such as AES. Any programmer that employs this method for pseudorandom bit generation by replacing DES with AES is employing a sound primitive.

3.5.2 PRNGs Based on Reduction Arguments

A definitive source for provably secure techniques regarding pseudorandom number generators and related primitives is Pseudorandomness and Cryptographic Applications by Michael Luby [177]. The definition of a pseudorandom bit generator (PRBG) is given below.

Definition 1 Let k, ℓ be positive integers such that ℓ ≥ k + 1 and ℓ is a specified polynomial function of k. A (k, ℓ)-PRBG is a function from k-bit strings to ℓ-bit strings that can be computed in polynomial time (in k). The input to the PRBG is a k-bit seed s₀ and the output is an ℓ-bit string that is pseudorandom.

A simple and relatively fast (k, ℓ)-PRBG is the Blum-Blum-Shub generator [30]. It uses the parameters p, q, and n. The values p and q be two large distinct primes and n = pq. These two primes must be kept secret. The Blum-Blum-Shub generator is defined as follows. Let s₀ be a quadratic residue modulo n. The pseudorandom bit stream is found by computing z_i for i = 1, 2, 3, ..., ℓ.

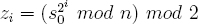
It was originally shown that the output of the Blum-Blum-Shub generator could be -distinguished from ℓ truly random bits if and only if there exists an unbiased Monte Carlo algorithm that solves the quadratic residues problem (see Appendix B.3.5) having an error probability of at most δ, for any δ greater than zero.¹² An even stronger result was shown by Vazirani and Vazirani [307]. They proved that this PRBG is secure under the weaker assumption that factoring is intractable.

The Blum-Blum-Shub PRBG is also regarded as being secure when the log₂(log₂(n)) least significant bits of 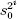mod n are used (instead of just the least significant bit). So, when n is a 768-bit composite, the 9 least significant bits can be used in the pseudorandom bit stream.

Why is this a favorable approach to generating bits pseudorandomly? The answer to that question is simple. Whereas DES, AES, and so forth have only been around for a few decades or less, brilliant mathematicians have been trying to solve the factoring problem for centuries. . . and have yet to publish a solution.

A provably secure pseudorandom number generator (PRNG) will operate in a secure fashion if and only if the following three conditions hold:

1. The secret PRNG parameters must be kept secret. This includes the initial seed (and the primes, as in the case of the Blum-Blum-Shub PRNG, etc.).
2. The parameters for the PRNG must be correct: This means that the seed must be chosen perfectly at random (and the primes in Blum-Blum-Shub must be chosen correctly, etc.).
3. The underlying computational intractability assumption (or assumptions) must hold. In the case of the Blum-Blum-Shub PRNG, this means that factoring must in fact be hard.

If any of the above conditions do not hold then the PRNG may be compromised.

3.6 Uniform Sampling

Often a problem requires that a number be chosen randomly or pseudorandomly from a set that has a number of elements that is not a power of 2. When this is the case random bit generators, be they pseudo or otherwise, cannot be used directly to generate the needed number. What is needed is an algorithm that utilizes the available random bit generator to sample from such sets uniformly at random.

For example, suppose that a computer worm propagates on a local area network by randomly selecting a machine to infect from the set of machines that are adjacent to the current host. If six such machines are connected directly to the host, then such an algorithm will be needed¹³. This problem boils down to using a coin to simulate the rolling of a fair six-sided die. The die roll can be simulated perfectly as follows. The coin is flipped three times to obtain a 3-bit number. This number is uniformly distributed between 0 and 7 inclusive. If the number is between 0 and 5 then the number is output. Otherwise, the three bits are thrown out and this procedure is repeated. Since all 6 faces of the die are equally likely, this method samples {0,1, 2, 3, 4, 5} uniformly at random. Uniform sampling techniques are needed when a random bit generator is available and when elements must be sampled from a set that has a cardinality that is not a power of 2.

This general uniform sampling algorithm is as follows. Let RBG(i) denote a perfectly random bit generator that returns a string consisting of i > 0 truly random bits.

Input: Integer N ≥ 1

Output: R chosen uniformly at random from [0,N-1]

Choose1toNRandomly(N):

1. Let T be the smallest power of 2 such that T ≥ N

2. compute R = RBG(log₂(T))

3. if R < N then output R and halt

4. goto step (2)

The following claim regarding uniform sampling can be proven.

Claim 3 Assuming that the function RBG() returns random bit strings, the function Choose1toNRandomly() outputs R drawn uniformly at random from [0,N-1].

To see this, observe that the strings that are output by RBG are chosen independently at random. Suppose that Choose1toNRandomly halts with R in iteration j. Let p_i,j denote the probability that R = i with 0 ≤ i ≤ N in iteration j. Clearly p_i,j = 1/T. Since step (3) is the only step that outputs a value, and since this value is R it follows that Choose1tnNRandomly outputs R drawn uniformly at random from [0, N − 1].

In a given iteration of Choose1toNRandomly, the value R will be less than N with probability N/T. So, the probability that a given iteration causes a repeat in step (4) is 1 − N/T. Since T is the smallest power of 2 such that T ≥ N, it follows that N/T > 1/2. So, the probability that no answer is found after j iterations is,

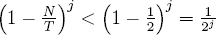
It follows that Choose1toNRandomly is an efficient Las Vegas algorithm. Observe that Choose1toNRandomly will never loop if N is a power of 2. This implies that the algorithm is efficient even when random bit strings are needed. This makes the function ideal for use as a public function in an Application Programming Interface (API). Note that this function is how users obtain random numbers in Figure 3.1. This is indicated by the solid arrow emanating from “uniform sampling algorithm” that terminates at the bottom of the figure. The dotted arrow that leaves the “uniform sampling algorithm” and that terminates at the bottom of the figure indicates that applications have direct access to pseudorandom sampled values.

In OpenSSL [233], the function BN_rand_range() generates a cryptographically strong pseudorandom number rnd in the range 0 ≤ rnd ≤ range. BN_pseudo_rand_range() does the same, but is based on the function BN_pseudo_rand(). The function BN_rand_range() was added¹⁴ in OpenSSL 0.9.6a and the function BN_pseudo_rand_range() was added in OpenSSL 0.9.6c.

int BN_rand_range(BIGNUM *rnd, BIGNUM *range);

int BN_pseudo_rand_range(BIGNUM *rnd, BIGNUM *range);

The functions return 1 on success, 0 on error. The error codes can be obtained by ERR_get_error().

3.7 Random Permutation Generation

Generating random permutations is a fundamental problem in computing. On-line casinos need to generate random permutations over {1, 2, 3,..., 52} to properly shuffle a deck of cards. Computer worms benefit from choosing random permutations over the set of machines on a network to arrive at an unpredictable hit list. This allows worms to attempt to travel from one existing machine to another, rather than simply choosing IP addresses randomly to try to propagate to. This is important since many heuristic antiviral network monitors are effective against stupid worms that ping non-existent Internet addresses. Malicious software is difficult to detect when it looks, smells, tastes, and feels like all the benign software around it.

3.7.1 Shuffling Cards by Repeated Sampling

The following algorithm shuffles a deck of cards in-place and is thereby very memory efficient. Initially, deck[i] = i for i = 1, 2, 3,..., 52.

CardShuffle():

1. for i = 1 to 51 do:

2.       j = number drawn uniformly at random between i and 52 inclusive

3.       card = deck[j]

4.       deck[j] = deck[i]

5.       deck[i] = card

Assuming that a random (or pseudorandom) bit generator is available, step (2) above can be implemented using Neumann's method. For example, when i = 1 a 6-bit number r is generated. If the number is between 0 and 51 inclusive, then we set j = r + 1. Otherwise, we generate another 6 bits and repeat. From Lemma 3 it follows that j will be drawn from the correct probability distribution.

It remains to consider the running time of CardShuffle(). Suppose that a fair coin is available. How many times would one expect to have to flip it to get heads? The answer is 2. Suppose that a biased coin is available that comes up heads with probability 3/4. How many times would one expect to have to flip it to get heads? The answer is 4/3. The expected number of random bits needed to shuffle using CardShuffle() is found by summing the expected number of bits needed in each iteration. The expected number of bits needed per iteration is given below. The number immediately before the colon is i.

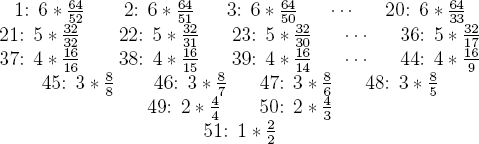
For example, in the first iteration when i = 1, one would expect to have to use 6(64/52) bits to draw the first card in the shuffle. Observe that 6 * 64 = 384 factors out of the top row, 5 * 32 = 160 factors out of the second row, and so on. The top row is equivalent to the following,

The rightmost term is the difference between two Harmonic numbers, namely H₅₂ and H₃₂. The n^th Harmonic number H_n is defined by,

This definition is from Concrete Mathematics by D. Knuth et al [122]. Clearly all Harmonic numbers are rational. The above expression is equivalent to,

After simplifying, the following expression is obtained.

These five Harmonic numbers are given below [111].

The expected number of random bits needed to shuffle a single deck is 355.9 using this method.

3.7.2 Shuffling Cards Using Trotter-Johnson

Algorithms to generate and enumerate permutations fall under the category of algorithmic combinatorics. Ranking and Unranking algorithms allow computer scientists to efficiently store, generate, and use combinatorial objects. Consider the problem of storing a particular permutation of n objects in a computer. If the objects are numbers, for instance, one could simply store them in an array. However, a more efficient way is to establish a bijection between the n! combinatorial objects and the natural numbers from 0 to n! − 1 and subsequently store the natural number that uniquely identifies the object.

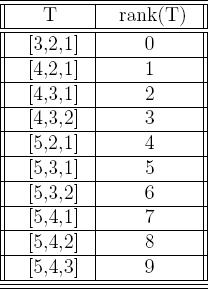
When a Ranking function is supplied with a combinatorial object it returns the object's rank (a natural number that uniquely represents the object). When a rank is given to an Unranking function, it returns the corresponding combinatorial object. An example of such a bijection will go a long way to illustrate this concept. Consider the problem of establishing a bijection between {0, 1, 2,..., 9} and the 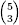subsets of {1, 2, 3, 4, 5} containing three elements. Table 3.4 depicts a co-lex ordering that defines such a bijection.

The Trotter-Johnson algorithm is a minimal-change algorithm for generating the n! permutations. It is a well-known algorithm developed in the early 1960s by Trotter and Johnson [142, 301]. In this algorithm, π is a permutation over {1, 2, 3, ..., n}. The value r is a rank of such a permutation, hence, r {0, 1, 2,..., n! − 1}. Shimon Even and Kreher and Stinson wrote excellent introductory texts on algorithmic combinatorics [98, 163].

Table 3.4 Co-Lex ordering for 3-element subsets

TrotterJohnsonUnrank(r,n):

1. r₂ = 0

2. π[1] = 1

3. for j = 2 to n do:

4.       r₁ =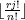

5.       k = r₁ − jr₂

6.       if r₂ is even then

for i = j − 1 down to j − k do:

7.                     π[i + 1] = π[i]

8.                π[j − k] = j

9.     else

10.               for i = j − 1 down to k + 1 do:

11.                   π[i + 1] = π[i]

12.               π[k + 1] = j

13.    r₂ = r₁

14. output π and halt

This algorithm is the natural way to select a particular ordering of the 52 cards in a deck. The actual value of 52! is needed to implement shuffling based on unranking. When expressed in decimal the value of 52! is,

80658175170943878571660636856403766975289505440883277824000000000000

Expressed in hexadecimal, the value of 52! is

2FDE529A3274C649CFEB4B180ADB5CB9602A9E0638AB2000000000000

The abundance of zeros on the right side of these numbers is due to the fact that every other number in 1 * 2 * 3 * 4 * 5 * · · · * 52 is evenly divisible by 2 and every other fifth number is evenly divisible by 5. The number of binary digits needed to express 52! is exactly 226.

Given the above value for 52!, Trotter-Johnson unranking can be used to shuffle as follows. A random 226-bit number r is chosen. If the number is less than 52! then it is supplied to Algorithm 2.18 with n = 52. The algorithm will return the shuffle π. If r ≥ 52! then r is discarded, another 226 bits are chosen randomly, and this process repeats.

Multiprecision libraries such as OpenSSL contain routines for testing if one big number is less than another. To test if x < y the algorithm scans the bits of x from the most significant bits to least significant bits. The algorithm does this with y at the same time. The algorithm makes a determination if and when two bits differ.

Now consider the running time of this approach. Observe that,

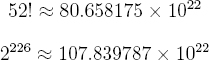
So, one would expect to have to generate a sequence of 226 bits about 1.337 times. It follows that using TrotterJohnsonUnrank, about 302.2 random bits will be needed on average to shuffle a single deck. Since 302.2 < 355.6, it is more efficient to use TrotterJohnsonUnrank to shuffle cards. When 50,000 shuffles are performed we would expect TrotterJohnsonUnrank to use up about 1.8 megabytes of randomness.¹⁵ The iterated approach would use up approximately 2.12 megabytes of randomness. The unranking algorithm helps to pave the way for using PRNGs based on rigorous mathematical foundations that tend to be more computationally demanding than ad hoc constructions.

Finally, if combinatorial objects need to be selected uniformly at random then the output of the uniform sampling algorithm can be used as input to a combinatorial unranking algorithm. This is depicted in Figure 3.1. The rounded box labeled “uniform sampling algorithm” is used to generate a rank r uniformly at random that is supplied to the unranking algorithm.

3.8 Sound Approach to Random Number Generation and Use

The algorithms that were presented for unbiasing coin flips and performing uniform sampling are Las Vegas algorithms. That is, they will always output the correct answer, but strictly speaking there is no guarantee that they will ever halt. Since well-designed functions return error codes anyway, it makes sense to make these algorithms Monte Carlo. To do so, the number of attempts to arrive at an answer can be fixed to, say, 32,000. If they don't arrive at an answer then they halt with failure. Otherwise, they halt at or before 32,000 iterations have passed with the correct answer. This way, the calling function can handle failures gracefully, and we can say something meaningful about the worst-case running time of the algorithm.¹⁶ As of this writing the OpenSSL functions BN_rand_range() and BN_pseudo_rand_range() are still of the Las Vegas type.

Figure 3.1 depicts four output arrows. Two are from the uniform sampling algorithm and two are from the combinatorial unranking algorithm. These give direct access to random and pseudorandomly sampled values as well as random and pseudorandomly generated combinatorial objects. The truly random output of the uniform sampling algorithm gives the calling application access to truly random bits. This call can be used to test the quality of the random seeds that are used to seed the pseudorandom number generator. This may be ascertained by subjecting the bit stream to FIPS-140 statistical tests, among others.¹⁷ The uniform sampling function allows applications to generate coin flips, die rolls, roulette wheel spins, and so on. Finally, the unranking function allows applications to generate random/pseudorandom permutations over sets, random/pseudorandom subsets, and so on. The nice aspect of this API is that at the lowest level, only the uniform sampling algorithm is visible to application programmers. This should help ward off programming errors that result from incorrect sampling.

Developing a design document and documenting code is clearly good software engineering practice. Yet, this seldom ever occurs in practice. Companies are often riddled with deadlines and wind up with off-the-cuff implementations all the time. However, security software should be designed so that third parties can easily verify its correctness. Part of this involves articulating the design and commenting the code, and part of it involves creating a well-designed application programming interface. Adam has seen in a number of consulting engagements no design documents whatsoever, poorly documented code, and to top it all off, random number generation code that is intimately merged with other code that performs such things as socket connections. This hampers efforts to verify the implementation and can be very time-consuming to analyze. Code that performs the functionality described in Figure 3.1 should be implemented in a completely standalone fashion.

3.9 RNGs Are the Beating Heart of System Security

Random number generators constitute the very foundation of secure computing machines. If one were to break or otherwise be able to predict the output of an RNG that is used, it would likely yield unadulterated access to the machine or sensitive data. A random number generator is a prime target for carrying out insider attacks. A Trojan horse that lives in and attacks a random number generator could potentially give the author unfettered access to private keys, symmetric keys, and the like. This is in fact the very heart of kleptographic attacks since it employ cryptotrojans that hide in random number generators and that masquerade as producers of truly random bits.

Military and government agencies would do well to employ the algorithm of Santha and Vazirani to produce seeding material. This will hedge against the threat of insider abuse, a topic that is gaining widespread interest in DARPA and ARDA. Applications that rely on a single source of entropy are paving the way for potentially devastating insider attacks. By exclusive-or'ing the bit streams from multiple sources, this threat is minimized. A malicious software program will also benefit from taking this approach, since it will prevent the program from relying entirely on the random number generator provided by the operating system. It is conceivable that the random numbers produced by the operating system are logged or are otherwise predictable. A computer host is an environment that is hostile to malware and as such malicious software will benefit from taking some entropy directly from available peripherals.

Given that truly random seeds are critical for the operation of INFOSEC devices, one has to wonder why there are no FIPS standards encompassing how they are generated. The ANSI X9.17 standard covers a heuristically sound way to generate pseudorandom bits, but this technique was proposed by the Banking Industry and does not cover how the initial seed is derived. A U.S. government standard that encompasses a sound method for extracting entropy from multiple sources would improve the security of computer software on a very large scale. Neumann's algorithm dates back to the middle of the last century. Formal results on weakening Neumann's assumptions can be traced back to the early 1980s, and research on the subject has continued.

3.10 Cryptovirology Benefits from General Advances

The original Macintosh cryptovirus was a proof-of-concept that had substantial room for improvement. For example, instead of using the outputs of truerand directly, it could have applied Neumann's algorithm or a more advanced entropy extractor to the output of truerand. Ideally, a cryptovirus would also utilize such sources as hard disk turbulence and the RNG that is provided by the underlying operating system. Although the simple extortion attack did not require a large number of random bits, it should have nonetheless applied an entropy extractor to several different sources of entropy. In this section a number of improvements and extensions to the cryptovirus attack are discussed.

3.10.1 Strong Crypto Yields Strong Cryptoviruses

In all likelihood the RSA cipher as originally defined is secure enough to mount the cryptovirus extortion attack. However, improved public key cryptosystems exist. A known drawback to RSA is that each RSA ciphertext c = m^e mod n leaks the Jacobi symbol of m with respect to n [175]. (See Appendix B.2 for an explanation of the Jacobi symbol.) The Jacobi symbol of m with respect to n is either 1 or −1. Since e is odd, it is not hard to see that,

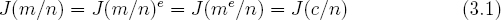
Since the Jacobi symbol must be one of two different values, a single bit of information about m is leaked in every ciphertext. Ideally, no poly-time computable function of the plaintext should be efficiently computable given the ciphertext. In this example the computable function has a certain semantic meaning, namely the Jacobi function. But other efficiently computable functions with semantic meaning may exist. Another drawback to RSA is that it is deterministic. Every time that a particular message m₁ is encrypted in RSA the exact same ciphertext c₁ will result. This means that it is possible to guess the plaintext in a given ciphertext and then verify the guess. For example, suppose c₁ = m^e₁ mod n is known. If m₂ is suspected as being the plaintext it can be encrypted to obtain c₂ = m^e₂ mod n. If c₂ = c₁ then m₂ = m₁. When a user encrypts short messages there is the risk that someone else can guess the plaintext and verify the guess. A heuristic way to prevent adversaries from guessing the plaintext and then verifying is to shrink the message space and include a random bit string in each encryption. This makes each plaintext message map to more than one ciphertext message. However, a provably secure approach is more desirable. In the more general case it should not be possible to select two messages and distinguish between their encryptions.

These observations lead to two notions of security: semantic security and message Indistinguishability, respectively. As it turns out, when the adversary is allowed to be any probabilistic poly-time algorithm these two definitions of security are equivalent. To avoid such vulnerabilities a semantically secure cryptosystem can be used [117]. An encryption algorithm is semantically secure against plaintext attacks if for all probability distributions over the message space, anything that a passive adversary can compute efficiently about the plaintext given the ciphertext can also be efficiently computed without the ciphertext given any historical information about the plaintext.

An efficient public key cryptosystem called Optimal Asymmetric Encryption Padding (OAEP) has been proposed [19] that can be implemented given any trapdoor one-way function such as RSA. Its security was proven within the random oracle model¹⁸ [18]. When a cryptosystem is used that is semantically secure against plaintext attacks to encrypt a symmetric key, no partial information about the symmetric key is revealed in the resulting ciphertext. Such a cryptosystem therefore provides more security than using RSA as originally defined. In computer security, the standard approach is to formalize the capabilities of the adversary in a threat model, develop an algorithm to deal with the possible presence of the adversary, and then prove that the algorithm is secure within that threat model. The bottom line is that a cryptosystem is only guaranteed to be secure within the threat model that it is designed to handle and may well succumb to more powerful adversaries should they exist.¹⁹

Semantic security against plaintext attacks guarantees that an adversary that tries to determine some additional partial information concerning a plaintext given the corresponding ciphertext along with existing partial information cannot do so. However, there exists an even more powerful type of adversary than this. For example, in the case of the cryptovirus extortion attack what has not been considered is a group of victims that is prepared to pay multiple ransoms, that use the virus writer as a decryption oracle, and that choose the public key ciphertexts based on previously decrypted ciphertexts. This amounts to what is called an adaptive chosen-ciphertext attack. This illustrates some of the subtleties in designing secure systems. A cryptosystem that is semantically secure against plaintext attacks is not necessarily semantically secure against adaptive chosen-ciphertext attacks. However, it turns out that OAEP is secure against adaptive chosen-ciphertext attacks.

This reasoning implies that cryptoviruses benefit directly from general advances in cryptology. Even though the original cryptovirus did not use multiple entropy sources and an entropy extractor, and even though it did not use OAEP, it is straightforward to utilize these more advanced techniques to design secure cryptoviruses.

3.10.2 Mix Networks and Cryptovirus Extortion

Arguably, the weakest aspect of the extortion attack from the perspective of the virus writer is obtaining the ransom without getting caught. To this end, it may be best to avoid demanding cash entirely. If the virus writer seeks information alone, then a more attractive alternative is possible. Methods exist that enable two mutually distrusting parties to communicate securely over a network in an anonymous fashion. The basic vehicle for doing so is called a mix network [54]. A mix network forms the basis for anonymous remailing systems and is a fundamental building block for many cryptographic protocols [55, 119, 137, 295]. In a nutshell a mix network is a service that lets users send messages anonymously to other users, and that makes the correlation of output messages with input messages nearly impossible. Mix networks fall into two major catagories: synchronous mixes and asynchronous mixes. In practice asynchronous mixes are ideal for anonymizing e-mail traffic, whereas synchronous mixes are best for randomizing message traffic in batches. It is typically easier to produce formal proofs of security for synchronous mixes than for asynchronous mixes, and as a result synchronous mixes tend to be employed in protocols such as electronic voting. This allows ballots to be cast in a provably anonymous fashion. Asynchronous mixes are arguably easier to deploy on a large scale and rely on a number of heuristic defenses against particular attacks.

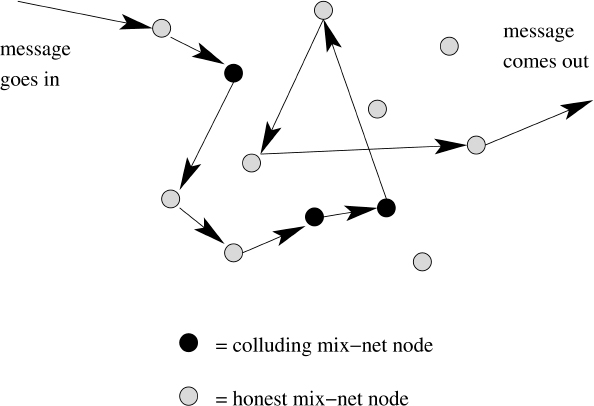
A mix network consists of a collection of N mix net nodes. The basic idea behind an asynchronous mix is to take an incoming message, send it from node to node along a randomly chosen path, and then send it to its final destination. It is necessary to use encryption to prevent correlations based on content as well as to fix the length of each message so that correlations based on size are not possible. This implies that large messages need to be broken down into smaller pieces, and short messages need to be padded out to the requisite length. The fixed sized messages are encrypted using a probabilistic public key cryptosystem. Therefore, even if the same message is sent through the network on more than one occasion it will look different each time with overwhelming probability. Not only are outsiders a threat to mix networks, but insiders are a threat as well. A properly designed mix net is still secure even if a fixed fraction of the nodes are operated by malicious persons that collude in order to track messages. Assuming that a sufficient number of messages go in and out of a given node at any given time it is important that the message go through multiple honest nodes to make the probability of tracing it negligible. A mix network is depicted in Figure 3.2.

Onion routing is a common method for implementing asynchronous mix networks. In an onion routing system, each of the N nodes has a key pair. A user selects a random traversal among the N nodes and successively encrypts in reverse-order the message using the public keys corresponding to the nodes that the message will traverse. In choosing the traversal, the same node can be chosen multiple times and therefore loops are possible in the path that the message takes. The layers of the resulting ciphertext are peeled away by performing decryption as the message travels through the network. By padding with random bytes it is possible to accomplish this in such a way that the length of the transmitted message is always the same.

Figure 3.2 Asynchronous mix network

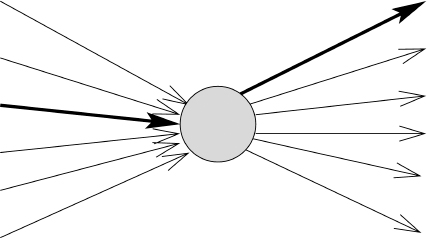
Over time a given mix net node may receive 1,000 incoming messages. These are decrypted, the order of them is mixed, and the resulting messages are sent out. The original packet headers are discarded and the messages are sent in newly constructed packets. This prevents trivial matching based on packet headers. If a message is decrypted entirely then it is sent to the final recipient. This way, a given input message to the node may end up being any of 1,000 different outgoing messages (see Figure 3.3).

It is also possible for a mix node to decrypt a message, determine the next intended recipient, and then re-encrypt the message using the public key of the recipient. When this re-encryption is probabilistic, it makes it more difficult for the original sender to identify his or her own message as it moves through the mix network.

An asynchronous mix network must have a sufficiently large message volume at all times. If only a handful of messages is traveling through the network then correlation is trivial. There are numerous attacks on mix networks that have been described in the literature.²⁰ For example, an active adversary may try to determine the partial path of an unknown message by sandwiching it between messages of the adversaries' own choosing. The object is to fill the queue of messages in the mix with custom-made messages, all except for the one that needs to be traced. The adversary then watches the messages as they leave the node to determine where the sandwiched message goes. The adversary takes note of how many messages each intended recipient receives. This is enough to determine where the sandwiched message went.

Figure 3.3 Mixing in a mix network node

A novel solution to this problem has been proposed [112]. The idea is to regard the mix net nodes as probabilistic algorithms and let them affect the paths that messages take. The way this is accomplished is by flipping coins, and with a certain probability sending a given message on a short, randomly chosen inter-mix detour. When a detour occurs it has the effect of adding a few new layers back onto the message in question. This mechanism has the novel property that even the sender does not know for sure what path his or her message will take within the mix network. The probability that a given message is sent on a detour must be low enough to keep the message volume from growing out of control.

Methods have been devised to not only allow anonymous messages to be sent, but also to allow anonymous replies [112]. In the cryptovirus attack, the virus can instruct the victim to place the victim's email address on a public bulletin board. To avoid embarrassment, the virus can tell the victim to first encrypt the e-mail address using the public key in the virus. The e-mail address can be chosen specifically for dealing with the virus writer and therefore not reveal the identity of the victim. The virus writer periodically scans the board for such ciphertexts, and decrypts them when found. The virus writer then sends the demand anonymously to the victim. Provided that the ransom is information, the victim can include the ransom within the anonymous reply. As long as the ransom itself does not reveal the identity of the victim, the attack preserves the victim's anonymity. A mix network is therefore a powerful building block for carrying out cryptovirus attacks.

To apprehend the virus writer, law enforcement bodies may seek to subpoena the administrators of each node in the mix network. Such a subpoena might call for the current private key and all previous private keys of each of the administrators. If all of the needed private keys and message traffic were obtained, this would allow law enforcement to trace any given message. However, if each mix net node adhered to a de facto mix net protocol standard, generated new key pairs every so often, and deleted all previous private keys and coin tosses, then the subpoena would likely not help law enforcement. Also, if the nodes spanned multiple countries then the tracing effort would be hampered even more due to legal complications.

The fact that mix net nodes traditionally decrypt incoming messages and then re-encrypt them when they are sent out, implies that the individual private keys of each mix net administrator can be used to trace message traffic. A recent method known as universal re-encryption has been proposed as a basis for a provably secure mix network [120]. By using a cryptosystem such as ElGamal that allows re-encryption without first decrypting, it is possible to have the mix net nodes randomize the incoming messages in an oblivious fashion. With respect to the virus attack, this implies that there are no administrator private keys for law enforcement to subpoena. If a re-encryption mix net node does not store the random permutation that it used in a mix operation, then the permutation is effectively lost forever.²¹ This property makes re-encryption mixes very attractive to criminals that need to communicate anonymously.

Various indirect methods exist to achieve financial gain through extortion. For example, a determined attacker may premeditate an extortion attempt by purchasing several shares of a small public company, provided that a substantial number of shares are up for sale. Once the attack is carried out the victim can be forced to purchase a high volume of shares from the small company. This has a tendency to drive the share price up, at which point the attacker can cash out. The obvious drawback to this method is that all of the outstanding shareholders may be regarded as suspects.

3.11 Anonymizing Program Propagation

An important issue that has been glossed over is the anonymity of the actual virus propagation. Strictly speaking, given enough snapshots of the states of machines on a network it is theoretically possible to trace the flow of a virus or worm perfectly. So, an interesting theoretical question is how to design a virus or worm that cannot be traced. Intuitively it would seem that a solution along these lines would make use of some form of mix network.

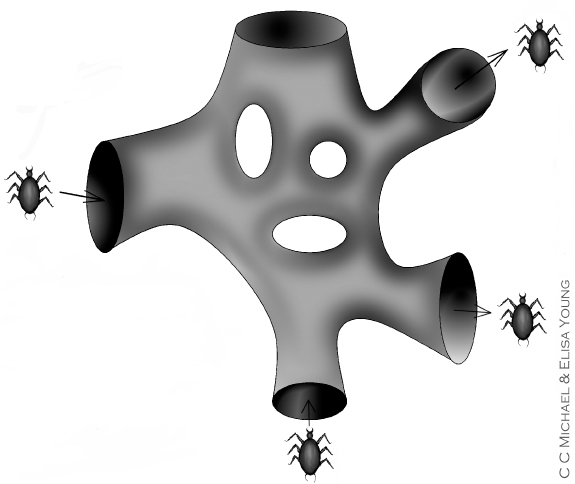
At first sight Figure 3.4 may appear to be quite silly. It looks like an artery or something out of a Dr. Seuss book, but it is quite illustrative of a new concept that will now be introduced. Consider a simple generalization of a mix network in which it is programs that are mixed instead of simply messages. Suppose further that programs can submit themselves to the mix network. In this case a program can choose a destination, jump into the mix, and then reappear at the destination much like the bug does in the figure. This in itself would not be very useful unless the program had a way of gaining control when it arrives at its destination. This could be accomplished by having the client programs for the mix network automatically run the programs that are received from the network.

This system is somewhat similar to the worm that was researched at the Palo Alto Research Center (see Appendix A.1) with one critical difference: a program's starting location cannot be ascertained at all once the program travels through the network.²² A nice feature to have would be a program that submits itself to the mix and that can either choose the destination machine explicitly or let the mix choose the final machine based on its own random coin flips. This latter approach allows programs to literally disappear without a trace from one machine and show up at some random location that the program itself could not have predicted accurately. This aspect would make viruses and worms very happy.

The system can be construed as a distributed operating system in which the processes may optionally be distributed anonymously among many machines. It may at first sight appear to be suicidal for users. In many respects this is in fact the case. However, a virtual machine with a security kernel that verifies the signature on programs before running them can be used to implement execution rights and access control.

Figure 3.4 A mix that mixes programs

The system has some very interesting implications for digital copyright issues. Suppose that the system is based on a mix that enables anonymous messages to be sent along with anonymous replies [112]. Also, suppose that a program is written that uses private information retrieval (see Section 6.2) to search for a particular MP3 song and retrieve it. The program can contain a specific query as well as the database administrator algorithm. The program runs the database administator algorithm on the query and the database of the machine when it arrives.²³ If this program shows up on a machine through the mix, takes an MP3, and then disappears back to where it came from, is the owner of the machine at fault in a legal sense? If the database consists of public domain songs as well as commercial songs then the owner of the machine will never have any way of knowing if a commercial song has ever been taken off the machine or not.

In this respect the system acts like a passive file server since programs can show up out of nowhere, take files, and jump back into the mix. The only overt action that the mix client does that makes file sharing possible is to send control to programs that arrive from the mix. This overt action can be eliminated without hindering public file sharing capabilities. The system can be designed to check for the requisite level of access control, but contain a rather convenient bug that accidentally allows world read permissions to commercial MP3s. Can users be liable for not finding bugs in their software and fixing them? Can companies be liable for selling or distributing buggy software? Should laws be passed to force users not to trust the world? The mix-based distributed operating system just described is hackable by design.²⁴ The cryptographic agent that moves through it is designed to hide what it is doing. This is an example of how cryptography can be maliciously used by software pirates to violate copyright laws.