Allocating Memory Dynamically

The two functions for allocating memory, malloc() and calloc(), have slightly different parameters:

void *malloc( size_t size );

The malloc() function reserves a contiguous memory block whose size in bytes is at least size. When a program obtains a memory block through malloc(), its contents are undetermined.

void *calloc( size_t count, size_t size );

The calloc() function reserves a block of memory whose size in bytes is at least count × size. In other words, the block is large enough to hold an array of count elements, each of which takes up size bytes. Furthermore, calloc() initializes every byte of the memory with the value 0.

Both functions return a pointer to void, also called a typeless pointer. The pointer’s value is the address of the first byte in the memory block allocated, or a null pointer if the memory requested is not available.

When a program assigns the void pointer to a pointer variable of a different type, the compiler implicitly performs the appropriate type conversion. Some programmers prefer to use an explicit type conversion, however.¹ When you access locations in the allocated memory block, the type of the pointer you use determines how the contents of the location are interpreted.

Here are some examples:

#include <stdlib.h>                    // Provides function prototypes.
typedef struct { long key;
                 /* ... more members ... */
               } Record;                // A structure type.

float *myFunc( size_t n )
{
  // Reserve storage for an object of type double.
  double *dPtr = malloc( sizeof(double) );
  if  ( dPtr == NULL )                  // Insufficient memory.
  {
    /* ... Handle the error ... */
    return NULL;
  }
  else                                  // Got the memory: use it.
  {
    *dPtr = 0.07;
    /* ... */
  }

  // Get storage for two objects of type Record.
  Record *rPtr;
  if  ( ( rPtr = malloc( 2 * sizeof(Record) ) == NULL )
  {
    /* ... Handle the insufficient-memory error ... */
    return NULL;
  }
  // Get storage for an array of n elements of type float.
  float *fPtr = malloc( n * sizeof(float) );
  if ( fPtr == NULL )
   {
    /* ... Handle the error ... */
    return NULL;
   }
   /* ... */
   return fPtr;
}

It is often useful to initialize every byte of the allocated memory block to zero, which ensures that not only the members of a structure object have the default value zero but also any padding between the members. In such cases, the calloc() function is preferable to malloc(), although it may be slower, depending on the implementation. The size of the block to be allocated is expressed differently with the calloc() function. We can rewrite the statements in the previous example as follows:

// Get storage for an object of type double.
double *dPtr = calloc( 1, sizeof(double) );

// Get storage for two objects of type Record.
Record *rPtr;
if  ( ( rPtr = calloc( 2, sizeof(Record) ) == NULL )
{  /* ... Handle the insufficient-memory error ... */  }

// Get storage for an array of n elements of type float.
float *fPtr = calloc( n, sizeof(float));

Characteristics of Allocated Memory

A successful memory allocation call yields a pointer to the beginning of a memory block. “The beginning” means that the pointer’s value is equal to the lowest byte address in the block. The allocated block is aligned so that any type of object can be stored at that address.

An allocated memory block stays reserved for your program until you explicitly release it by calling free() or realloc(). In other words, the storage duration of the block extends from its allocation to its release, or to end of the program.

The arrangement of memory blocks allocated by successive calls to malloc(), calloc(), and/or realloc() is unspecified.

It is also unspecified whether a request for a block of size zero results in a null pointer or an ordinary pointer value. In any case, however, there is no way to use a pointer to a block of zero bytes, except perhaps as an argument to realloc() or free().

Resizing and Releasing Memory

When you no longer need a dynamically allocated memory block, you should give it back to the operating system. You can do this by calling the function free(). Alternatively, you can increase or decrease the size of an allocated memory block by calling the function realloc(). The prototypes of these functions are as follows:

void free( void *ptr );

The free() function releases the dynamically allocated memory block that begins at the address in ptr. A null pointer value for the ptr argument is permitted, and such a call has no effect.

void *realloc( void *ptr, size_t size );

The realloc() function releases the memory block addressed by ptr and allocates a new block of size bytes, returning its address. The new block may start at the same address as the old one.

realloc() also preserves the contents of the original memory block—up to the size of whichever block is smaller. If the new block doesn’t begin where the original one did, then realloc() copies the contents to the new memory block. If the new memory block is larger than the original, then the values of the additional bytes are unspecified.

It is permissible to pass a null pointer to realloc() as the argument ptr. If you do, then realloc() behaves similarly to malloc(), and reserves a new memory block of the specified size.

The realloc() function returns a null pointer if it is unable to allocate a memory block of the size requested. In this case, it does not release the original memory block or alter its contents.

The pointer argument that you pass to either of the functions free() and realloc()—if it is not a null pointer—must be the starting address of a dynamically allocated memory block that has not yet been freed. In other words, you may pass these functions only a null pointer or a pointer value obtained from a prior call to malloc(), calloc(), or realloc(). If the pointer argument passed to free() or realloc() has any other value, or if you try to free a memory block that has already been freed, the program’s behavior is undefined.

The memory management functions keep internal records of the size of each allocated memory block. This is why the functions free() and realloc() require only the starting address of the block to be released, and not its size. There is no way to test whether a call to the free() function is successful, because it has no return value.

The function getLine() in Example 12-1 is another variant of the function defined with the same name in Example 9-4. It reads a line of text from standard input and stores it in a dynamically allocated buffer. The maximum length of the line to be stored is one of the function’s parameters. The function releases any memory it doesn’t need. The return value is a pointer to the line read.

// Read a line of text from stdin into a dynamically allocated buffer.
// Replace the newline character with a string terminator.
//
// Arguments:    The maximum line length to read.
// Return value: A pointer to the string read, or
//               NULL if end-of-file was read or if an error occurred.

char *getLine( unsigned int len_max )
{
  char *linePtr = malloc( len_max+1 ); // Reserve storage for "worst case."
  if ( linePtr != NULL )
  {
    // Read a line of text and replace the newline characters with
    // a string terminator:
    int c = EOF;
    unsigned int i = 0;
    while ( i < len_max && ( c = getchar() ) != '\n' && c != EOF )
      linePtr[i++] = (char)c;
    linePtr[i] = '\0';

    if ( c == EOF && i == 0 )      // If end-of-file before any
    {                              // characters were read,
       free( linePtr );            // release the whole buffer.
       linePtr = NULL;
    }
    else                         // Otherwise, release the unused portion.
       linePtr = realloc( linePtr, i+1 );     // i is the string length.
  }
  return linePtr;
}

The following code shows how you might call the getLine() function:

char *line;
if (( line = getLine(128) ) != NULL )   // If we can read a line,
{
  /* ...  */                            // process the line,
  free( line );                         // then release the buffer.
}

An All-Purpose Binary Tree

Dynamic memory management is fundamental to the implementation of dynamic data structures such as linked lists and trees. In Chapter 10, we presented a simple linked list (see Figure 10-1). The advantage of linked lists over arrays is that new elements can be inserted and existing members removed quickly. However, they also have the drawback that you have to search through the list in sequential order to find a specific item.

A binary search tree (BST), on the other hand, makes linked data elements more quickly accessible. The data items must have a key value that can be used to compare and sort them. A binary search tree combines the flexibility of a linked list with the advantage of a sorted array, in which you can find a desired data item using the binary search algorithm.

Characteristics

A binary tree consists of a number of nodes that contain the data to be stored (or pointers to the data), and the following structural characteristics:

• Each node has up to two direct child nodes.

• There is exactly one node, called the root of the tree, that has no parent node. All other nodes have exactly one parent.

• Nodes in a binary tree are placed according to this rule: the value of a node is greater than or equal to the values of any descendant in its left branch, and less than or equal to the value of any descendant in its right branch.

Figure 12-1 illustrates the structure of a binary tree.

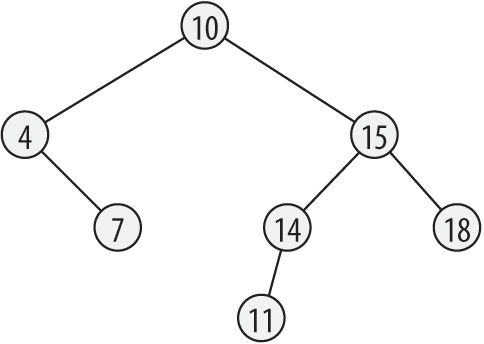
Figure 12-1. A binary tree

A leaf is a node that has no children. Each node of the tree is also considered as the root of a subtree, which consists of the node and all its descendants.

An important property of a binary tree is its height. The height is the length of the longest path from the root to any leaf. A path is a succession of linked nodes that form the connection between a given pair of nodes. The length of a path is the number of nodes in the path, not counting the first node. It follows from these definitions that a tree consisting only of its root node has a height of 0, and the height of the tree in Figure 12-1 is 3.

Implementation

The example that follows is an implementation of the principal functions for a binary search tree, and uses dynamic memory management. This tree is intended to be usable for data of any kind. For this reason, the structure type of the nodes includes a flexible member to store the data, and a member indicating the size of the data:

typedef struct Node { struct Node *left,   // Pointers to the left and
                                  *right;  // right child nodes.
                      size_t size;         // Size of the data payload.
                      char data[];         // The data itself.
                    } Node_t;

The pointers left and right are null pointers if the node has no left or right child.

As the user of our implementation, you must provide two auxiliary functions. The first of these is a function to obtain a key that corresponds to the data value passed to it, and the second compares two keys. The first function has the following type:

    typedef const void *GetKeyFunc_t( const void *dData );

The second function has a type like that of the comparison function used by the standard function bsearch():

    typedef int CmpFunc_t( const void *pKey1, const void *pKey2 );

The arguments passed on calling the comparison function are pointers to the two keys that you want to compare. The function’s return value is less than zero, if the first key is less than the second; or equal to zero, if the two keys are equal; or greater than zero, if the first key is greater than the second. The key may be the same as the data itself. In this case, you need to provide only a comparison function.

Next, we define a structure type to represent a tree. This structure has three members: a pointer to the root of the tree; a pointer to the function to calculate a key, with the type GetKeyFunc_t; and a pointer to the comparison function, with the type CmpFunc_t:

typedef struct { struct Node  *pRoot;     // Pointer to the root.
                 CmpFunc_t    *cmp;       // Compares two keys.
                 GetKeyFunc_t *getKey;    // Converts data into a key
               } BST_t;                   // value.

The pointer pRoot is a null pointer while the tree is empty.

The elementary operations for a binary search tree are performed by functions that insert, find, and delete nodes, and functions to traverse the tree in various ways, performing a programmer-specified operation on each element if desired.

The prototypes of these functions, and the typedef declarations of GetKeyFunc_t, CmpFunc_t, and BST_t, are placed in the header file BSTree.h. To use this binary tree implementation, you must include this header file in the program’s source code.

The function prototypes in BSTree.h are:

BST_t *newBST( CmpFunc_t *cmp, GetKeyFunc_t *getKey );

This function dynamically generates a new object with the type BST_t, and returns a pointer to it.

_Bool BST_insert( BST_t *pBST, const void *pData, size_t size );

BST_insert() dynamically generates a new node, copies the data referenced by pData to the node, and inserts the node in the specified tree.

const void *BST_search( BST_t *pBST, const void *pKey );

The BST_search() function searches the tree and returns a pointer to the data item that matches the key referenced by the pKey argument.

_Bool BST_erase( BST_t *pBST, const void *pKey );

This function deletes the first node whose data contents match the key referenced by pKey.

void BST_clear( BST_t *pBST );

BST_clear() deletes all nodes in the tree, leaving the tree empty.

int BST_inorder( BST_t *pBST, _Bool (*action)( void *pData ));
int BST_rev_inorder( BST_t *pBST, _Bool (*action)( void *pData ));
int BST_preorder( BST_t *pBST, _Bool (*action)( void *pData ));
int BST_postorder( BST_t *pBST, _Bool (*action)( void *pData ));

Each of these functions traverses the tree in a certain order, and calls the function referenced by action to manipulate the data contents of each node. If the action modifies the node’s data, then at least the key value must remain unchanged to preserve the tree’s sorting order.

The function definitions, along with some recursive helper functions, are placed in the source file BSTree.c. The helper functions are declared with the static specifier because they are for internal use only, and not part of the search tree’s “public” interface. The file BSTree.c also contains the definition of the nodes’ structure type. As the programmer, you do not need to deal with the contents of this file, and may be content to use a binary object file compiled for the given system, adding it to the command line when linking the program.

const void *defaultGetKey( const void *pData ) { return pData; }

BST_t *newBST( CmpFunc_t *cmp, GetKeyFunc_t *getKey )
{
  BST_t *pBST = NULL;
  if ( cmp != NULL )
    pBST = malloc( sizeof(BST_t) );
  if ( pBST != NULL )
  {
    pBST->pRoot = NULL;
    pBST->cmp = cmp;
    pBST->getKey = (getKey != NULL) ? getKey : defaultGetKey;
  }
  return pBST;
}

static _Bool insert( BST_t *pBST, Node_t **ppNode, const void *pData,
                     size_t size );

_Bool BST_insert( BST_t *pBST, const void *pData, size_t size )
{
  if ( pBST == NULL || pData == NULL || size == 0 )
    return false;
  return insert( pBST, &(pBST->pRoot), pData, size );
}

static _Bool insert( BST_t *pBST, Node_t **ppNode, const void *pData,
                     size_t size )
{
  Node_t *pNode = *ppNode;      // Pointer to the root node of the
                                // subtree to insert the new node in.
  if ( pNode == NULL )
  {                             // There's a place for a new leaf here.
    pNode = malloc( sizeof(Node_t) + size );
    if ( pNode != NULL )
    {
      pNode->left = pNode->right = NULL;   // Initialize the new node's
                                           // members.
      memcpy( pNode->data, pData, size );
      *ppNode = pNode;                     // Insert the new node.
      return true;
    }
    else
      return false;
  }
  else                              // Continue looking for a place ...
  {
    const void *key1 = pBST->getKey( pData ),
               *key2 = pBST->getKey( pNode->data );
    if ( pBST->cmp( key1, key2 ) < 0 )     // ... in the left subtree,
      return insert( pBST, &(pNode->left), pData, size );
    else                                   // or in the right subtree.
      return insert( pBST, &(pNode->right), pData, size );
  }
}

static const void *search( BST_t *pBST, const Node_t *pNode,
                           const void *pKey );

const void *BST_search( BST_t *pBST, const void *pKey )
{
  if  ( pBST == NULL || pKey == NULL ) return NULL;
  return search( pBST, pBST->pRoot, pKey );  // Start at the root
                                             // of the tree.
}

static const void *search( BST_t *pBST, const Node_t *pNode,
                           const void *pKey )
{
  if ( pNode == NULL )
    return NULL;                               // No subtree to search;
                                               // no match found.
  else
  {                                            // Compare data:
    int cmp_res = pBST->cmp( pKey, pBST->getKey(pNode->data) );

    if ( cmp_res == 0 )                        // Found a match.
      return pNode->data;
    else if ( cmp_res < 0 )                     // Continue the search
      return search( pBST, pNode->left, pKey ); // in the left subtree,
    else
      return search( pBST, pNode->right, pKey ); // or in the right
                                                 // subtree.
  }
}

static Node_t *detachMin( Node_t **ppNode )
{
  Node_t *pNode = *ppNode;            // A pointer to the current node.
  if ( pNode == NULL )
    return NULL;                         // pNode is an empty subtree.
  else if ( pNode->left != NULL )
    return detachMin( &(pNode->left) );  // The minimum is in the left
                                         // subtree.
  else
  {                            // pNode points to the minimum node.
    *ppNode = pNode->right;    // Attach the right child to the parent.
    return pNode;
  }
}

static _Bool erase( BST_t *pBST, Node_t **ppNode, const void *pKey );

_Bool BST_erase( BST_t *pBST, const void *pKey )
{
  if ( pBST == NULL || pKey == NULL ) return false;
  return erase( pBST, &(pBST->pRoot), pKey );     // Start at the root
                                                  // of the tree.
}

static _Bool erase( BST_t *pBST, Node_t **ppNode, const void *pKey )
{
  Node_t *pNode = *ppNode;              // Pointer to the current node.
  if ( pNode == NULL )
    return false;                       // No match found.

                                        // Compare data:
  int cmp_res = pBST->cmp( pKey, pBST->getKey(pNode->data) );

  if ( cmp_res < 0 )                             // Continue the search
    return  erase( pBST, &(pNode->left), pKey);  // in the left subtree,
  else if ( cmp_res > 0 )
    return erase( pBST, &(pNode->right), pKey);  // or in the right
                                                 // subtree.
  else
  {                                 // Found the node to be deleted.
    if ( pNode->left == NULL )      // If no more than one child,
      *ppNode = pNode->right;       // attach the child to the parent.
    else if ( pNode->right == NULL )
      *ppNode = pNode->left;
    else                         // Two children: replace the node with
    {                            // the minimum from the right subtree.
      Node_t *pMin = detachMin( &(pNode->right) );
      *ppNode = pMin;       // Graft it onto the deleted node's parent.
      pMin->left  = pNode->left;  // Graft the deleted node's children.
      pMin->right = pNode->right;
    }
    free( pNode );               // Release the deleted node's storage.
    return true;
  }
}

static void clear( Node_t *pNode );

void BST_clear( BST_t *pBST )
{
  if ( pBST != NULL)
  {
    clear( pBST->pRoot );
    pBST->pRoot = NULL;
  }
}

static void clear( Node_t *pNode )
{
  if ( pNode != NULL )
  {
    clear( pNode->left );
    clear( pNode->right );
    free( pNode );
  }
}

static int inorder( Node_t *pNode, _Bool (*action)(void *pData) );

int BST_inorder( BST_t *pBST, _Bool (*action)(void *pData) )
{
  if  ( pBST == NULL || action ==  NULL )
    return 0;
  else
    return inorder( pBST->pRoot, action );
}

static int inorder( Node_t *pNode, _Bool (*action)(void *pData) )
{
  int count = 0;
  if ( pNode == NULL )
    return 0;

  count = inorder( pNode->left, action );      // L: Traverse the left
                                               // subtree.
  if ( action( pNode->data ))                  // N: Visit the current
    ++count;                                   // node itself.
  count += inorder( pNode-> right, action );   // R: Traverse the right
                                               // subtree.
  return count;
}

sortlines < demo.txt

// This program reads each line of text into a node of a binary tree,
// and then prints the text in sorted order.

#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#include "BSTree.h"               // Prototypes of the BST functions.

#define LEN_MAX 1000              // Maximum length of a line.
char buffer[LEN_MAX];

// Action to perform for each line:
_Bool printStr( void *str ) { return printf( "%s", str ) >= 0; }

int main()
{
  BST_t *pStrTree = newBST( (CmpFunc_t*)strcmp, NULL );
  int n;

  while ( fgets( buffer, LEN_MAX, stdin ) != NULL )   // Read each line.
  {
    size_t len = strlen( buffer );                    // Length incl.
                                                      // newline character.
    if ( !BST_insert( pStrTree, buffer, len+1 ))      // Insert the line in
       break;                                         // the tree.
  }
  if ( !feof(stdin) )
  {                                                   // If unable to read
                                                      // the entire text:
    fprintf( stderr, "sortlines: "
             "Error reading or storing text input.\n" );
    exit( EXIT_FAILURE );
  }
  n = BST_inorder( pStrTree, printStr );              // Print each line,
                                                      // in sorted order.
  fprintf( stderr, "\nsortlines: Printed %d lines.\n", n );

  BST_clear( pStrTree );                              // Discard all nodes.
  return 0;
}