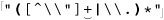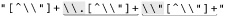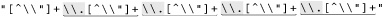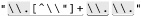Table of Contents for

Mastering Regular Expressions, 3rd Edition

6
Crafting an Efficient Expression

With the regex-directed nature of an NFA engine, as is found in Perl, Java packages, the .NET languages, Python, and PHP (just to name a few; see the table on page 145 for more), subtle changes in an expression can have major effects on what or how it matches. Issues that don’t matter with a DFA engine become paramount. The fine control an NFA engine affords allows you to really craft an expression, although it can sometimes be a source of confusion to the unaware. This chapter helps you learn this art.

At stake are both correctness and efficiency: matching just what you want and no more, and doing it quickly. Chapters 4 and 5 examined correctness; here we’ll look at the efficiency-related issues of NFA engines, and how to make them work to our advantage. (DFA-related issues are mentioned when appropriate, but this chapter is primarily concerned with NFA-based engines.) In a nutshell, the key is to understand the full implications of backtracking, and to learn techniques to avoid it where possible. Armed with the detailed understanding of the processing mechanics, not only will you maximize the speed of matches, you will also be able to write more complex expressions with confidence.

In This Chapter    To arm you well, this chapter first illustrates just how important these issues can be, then prepares you for some of the more advanced techniques presented later by reviewing the basic backtracking described in the previous chapters with a strong emphasis on efficiency and backtracking’s global ramifications. Then we’ll look at some of the common internal optimizations that can have a fairly substantial impact on efficiency, and on how expressions are best written for implementations that employ them. Finally, I bring it all together with some killer techniques to construct lightning-fast NFA regexes.

Tests and Backtracks

The examples we’ll see here illustrate common situations you might meet when using regular expressions. When examining a particular example’s efficiency, I’ll sometimes report the number of individual tests that the regex engine does during the course of a match. For example, in matching ⌈marty⌋ against smarty, there are six individual tests — the initial attempt of ⌈m⌋ against s (which fails), then the matching of ⌈m⌋ against m, ⌈a⌋ against a, and so on. I also often report the number of backtracks (zero in this example, although the implicit backtrack by the regex engine’s transmission to retry the regex at the second character position could be counted as one).

I use these exact numbers not because the precision is important, but rather to be more concrete than words such as “lots,” “few,” “many,” “better,” “not too much,” and so forth. I don’t want to imply that using regular expressions with an NFA is an exercise in counting tests or backtracks; I just want to acquaint you with the relative qualities of the examples.

Another important thing to realize is that these “precise” numbers probably differ from tool to tool. It’s the basic relative performance of the examples that I hope will stay with you. One important variation among tools is the optimizations they might employ. A smart enough implementation completely bypasses the application of a particular regex if it can decide beforehand that the target string cannot possibly match (in cases, for instance, when the string lacks a particular character that the engine knows beforehand must be there for any match to be successful). I discuss these important optimizations in this chapter, but the overall lessons are generally more important than the specific special cases.

Traditional NFA versus POSIX NFA

It’s important to keep in mind the target tool’s engine type, Traditional NFA or POSIX NFA, when analyzing efficiency. As we’ll see in the next section, some concerns matter to one but not the other. Sometimes a change that has no effect on one has a great effect on the other. Again, understanding the basics allows you to judge each situation as it arises.

A Sobering Example

Let’s start with an example that really shows how important a concern backtracking and efficiency can be. On page 198, we came up with ⌈" ( \\ . | [ ^ \\ " ] ) * “ ⌋ to match a quoted string, with internal quotes allowed if escaped. This regex works, but if it’s used with an NFA engine, the alternation applied at each character is very inefficient. With every “normal” (non-escape, non-quote) character in the string, the engine has to test ⌈\\.⌋, fail, and backtrack to finally match with ⌈[^ \\']⌋. If used where efficiency matters, we would certainly like to be able to speed this regex up a bit.

A Simple Change—Placing Your Best Foot Forward

Since the average double-quoted string has more normal characters than escaped ones, one simple change is to swap the order of the alternatives, putting ⌈[^ \\ "]⌋ first and ⌈\\.⌋ second. By placing ⌈[^ \\"]⌋ first, alternation backtracking need be done only when there actually is an escaped item in the string (and once for when the star fails, of course, since all alternatives must fail for the alternation as a whole to stop). Figure 6-1 illustrates this difference visually. The reduction of arrows in the bottom half represents the increased number of times when the first alternative matches. That means less backtracking.

Figure 6-1: Effects of alternative order (Traditional NFA)

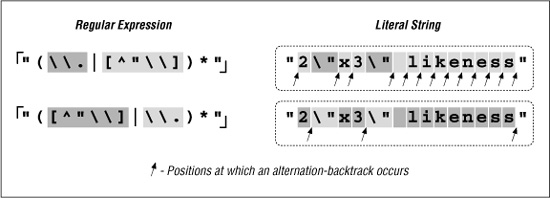
In evaluating this change, consider:

• Does this change benefit a Traditional NFA, POSIX NFA, or both?
• Does this change offer the most benefit when the text matches, when the match fails, or at all times?

  Consider these questions and flip the page to check your answers. Make sure that you have a good grasp of the answers (and reasons) before continuing on to the next section.

Efficiency Versus Correctness

The most important question to ask when making any change for efficiency’s sake is whether the change affects the correctness of a match. Reordering alternatives, as we did earlier, is OK only if the ordering is not relevant to the success of a match. Consider ⌈" ( \\ . | [ ^ " ] ) * "⌋, which is an earlier ( 197) but flawed version of the regex in the previous section. It’s missing the backslash in the negated character class, and so can match data that should not be matched. If the regex is only ever applied to valid data that should be matched, you’d never know of the problem. Thinking that the regex is good and reordering alternatives now to gain more efficiency, we’d be in real trouble. Swapping the alternatives so that ⌈[^ " ]⌋ is first actually ensures that it matches incorrectly every time the target has an escaped quote:

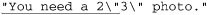
So, be sure that you’re comfortable with the correctness of a match before you worry too much about efficiency.

Advancing Further—Localizing the Greediness

Figure 6-1 makes it clear that in either expression, the star must iterate (or cycle, if you like) for each normal character, entering and leaving the alternation (and the parentheses) over and over. These actions involve overhead, which means extra work—extra work that we’d like to eliminate if possible.

Once while working on a similar expression, I realized that I could optimize it by taking into account that since ⌈[^ \\"]⌋ matches the “normal” (non-quote, non-backslash) case, using ⌈[^ \\"]+ ⌋ instead allows one iteration of (···)* to read as many normal characters as there are in a row. For strings without any escapes, this would be the entire string. This allows a match with almost no backtracking, and also reduces the star iteration to a bare minimum. I was very pleased with myself for making this discovery.

We’ll look at this example in more depth later in this chapter, but a quick look at some statistics clearly shows the benefit. Figure 6-2 looks at this example for a Traditional NFA. In comparison to the original ⌈" ( \\. | [^\\" ])* “⌋ (the top of the upper pair of Figure 6-2), alternation-related backtracks and star iterations are both reduced. The lower pair in Figure 6-2 illustrates that performance is enhanced even further when this change is combined with our previous reordering.

Figure 6-2: Effects of an added plus (Traditional NFA)

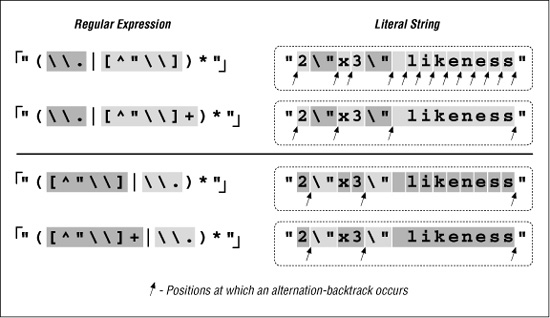
The big gain with the addition of plus is the resulting reduction in the number of alternation backtracks, and, in turn, the number of iterations by the star. The star quantifies a parenthesized subexpression, and each iteration entails some amount of overhead as the parentheses are entered and exited, because the engine needs to keep tabs on what text is matched by the enclosed subexpression. (This is discussed in depth later in this chapter.)

Table 6-1 is similar to the one in the answer block on page 224, but with different expressions and has information about the number of iterations required by star. In each case, the number of individual tests and backtracks increases ever so slightly, but the number of cycles is drastically reduced. This is big savings.

Table 6-1: Match Efficiency for a Traditional NFA

	⌈"( [ ^ \\ "] | \\. )* "
Sample String	tests	b.t.	*-cycles	tests	b.t.	*-cycles
"makudonarudo"	16	2	13	17	3	2
"2\"x3\" likeness"	22	4	15	25	7	6
” very···99 more chars···long”	111	2	108	112	3	2

Reality Check

Yes, I was quite pleased with myself for this discovery. However, as wonderful as this “enhancement” might seem, it is really a disaster waiting to happen. You’ll notice that when extolling its virtues, I didn’t give statistics for a POSIX NFA engine. If I had, you might have been surprised to find the "very•···•long" example requires over three hundred thousand million billion trillion backtracks (for the record, the actual count would be 324,518,553,658,426,726,783,156,020,576,256, or about 325 nonillion). Putting it mildly, that is a LOT of work. This would take well over 50 quintillion years, take or leave a few hundred trillion millennial^†

Quite surprising indeed! So, why does this happen? Briefly, it’s because something in the regex is subject to both an immediate plus and an enclosing star, with nothing to differentiate which is in control of any particular target character. The resulting nondeterminism is the killer. The next section explains a bit more.

“Exponential” matches

Before adding the plus, ⌈[^\\"]⌋ was subject to only the star, and the number of possible ways for the effective ⌈([^ \\"])*⌋ to divvy up the line was limited. It matched one character, then another, and so forth, until each character in the target text had been matched at most one time. It may not have matched everything in the target, but at worst, the number of characters matched was directly proportional to the length of the target string. The possible amount of work rose in step with the length of the target string.

With the new regex’s effective ⌈( [^\\ "] +) *⌋, the number of ways that the plus and star might divvy up the string explodes exponentially. If the target string is makudonarudo, should it be considered 12 iterations of the star, where each internal ⌈[^\\" ] +⌋ matches just one character (as might be shown by 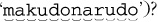Or perhaps one iteration of the star, where the internal ⌈[ ^ \\ " ] +⌋ matches everything 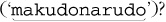Or, perhaps 3 iterations of the star, where the internal ⌈[^\\"]+⌋ matches 5, 3, and 4 characters respectively 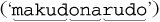. Or perhaps 2, 2, 5, and 3 characters respectively 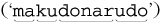. Or, perhaps...

Well, you get the idea — there are a lot of possibilities (4,096 in this 12-character example). For each extra character in the string, the number of possible combinations doubles, and the POSIX NFA must try them all before returning its answer. That’s why these are called “exponential matches.” Another appealing phrase I’ve heard for these types of matches is super-linear.

However called, it means backtracking, and lots of it!^† Twelve characters’ 4,096 combinations doesn’t take long, but 20 characters’ million-plus combinations take more than a few seconds. By 30 characters, the billion-plus combinations take hours, and by 40, it’s well over a year. Obviously, this is not good.

“Ah,” you might think, “but a POSIX NFA is not all that common. I know my tool uses a Traditional NFA, so I’m OK.” Well, the major difference between a POSIX and Traditional NFA is that the latter stops at the first full match. If there is no full match to be had, even a Traditional NFA must test every possible combination before it finds that out. Even in the short “No •\ "match \" •here example from the previous answer block, 8,192 combinations must be tested before the failure can be reported.

When the regex engine crunches away on one of these neverending matches, the tool just seems to “lock up.” The first time I experienced this, I thought I’d discovered a bug in the tool, but now that I understand it, this kind of expression is part of my regular-expression benchmark suite, used to indicate the type of engine a tool implements:

• If one of these regexes is fast even with a non-match, it’s likely a DFA.
• If it’s fast only when there’s a match, it’s a Traditional NFA.
• If it’s slow all the time, it’s a POSIX NFA.

I used “likely” in the first bullet point because NFAs with advanced optimizations can detect and avoid these exponentially-painful neverending matches. (More on this later in this chapter 250.) Also, we’ll see a number of ways to augment or rewrite this expression such that it’s fast for both matches and failures alike.

As the previous list indicates, at least in the absence of certain advanced optimizations, the relative performance of a regex like this can tell you about the type of regex engine. That’s why a form of this regex is used in the “Testing the Engine Type” section in Chapter 4 ( 146).

Certainly, not every little change has the disastrous effects we’ve seen with this example, but unless you know the work going on behind an expression, you will simply never know until you run into the problem. Toward that end, this chapter looks at the efficiency concerns and ramifications of a variety of examples. As with most things, a firm grasp of the underlying basic concepts is essential to an understanding of more advanced ideas, so before looking at ways to get around exponential matches, I’d like to review backtracking in explicit detail.

A Global View of Backtracking

On a local level, backtracking is simply the return to attempt an untried option. That’s simple enough to understand, but the global implications of backtracking are not as easily grasped. In this section, we’ll take an explicit look at the details of backtracking, both during a match and during a non-match, and we’ll try to make some sense out of the patterns we see emerge.

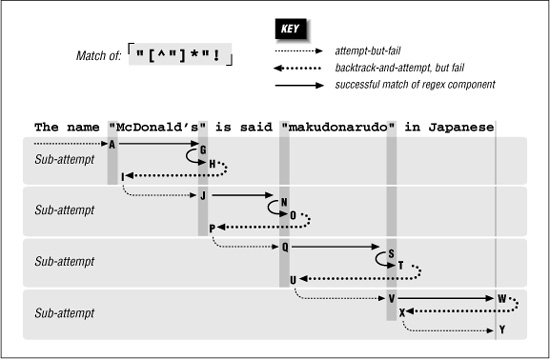
Let’s start by looking closely at some examples from the previous chapters. From page 165, if we apply ⌈". * "⌋ to

The name "McDonald's" is said "makudonarudo" in Japanese we can visualize the matching action as shown in Figure 6-3.

The regex is attempted starting at each string position in turn, but because the initial quote fails immediately, nothing interesting happens until the attempt starting at the location marked A. At this point, the rest of the expression is attempted, but the transmission ( 148) knows that if the attempt turns out to be a dead end, the full regex can still be tried at the next position.

The ⌈. *⌋ then matches to the end of the string, where the dot is unable to match the nothingness at the end of the string and so the star finally stops. None of the 46 characters matched by ⌈. *⌋ is required, so while matching them, the engine accumulated 46 more situations to where it can backtrack if it turns out that it matched too much. Now that ⌈. *⌋ has stopped, the engine backtracks to the last of those saved states, the “try at ” state.

This means that we try to match the closing quote at the end of the string. Well, a quote can match nothingness no better than dot, so this fails too. The engine backtracks again, this time trying to match the closing quote at , which also fails.

Figure 6-3: Successful match of ⌈". * "⌋

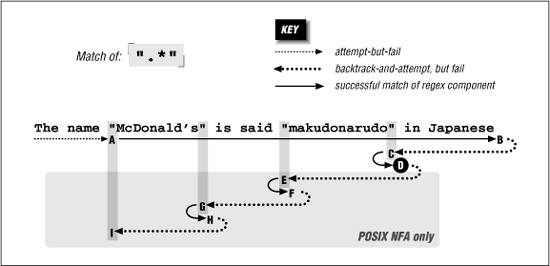
The remembered states accumulated while matching from A to B are tried in reverse (latest first) order as we move from B to C. After trying only about a dozen of them, the state that represents “try at ” is reached, point C. This can match, bringing us to D and an overall match:

If this is a Traditional NFA, the remaining unused states are simply discarded and the successful match is reported.

More Work for a POSIX NFA

For POSIX NFA, the match noted earlier is remembered as “the longest match we’ve seen so far,” but all remaining states must still be explored to see whether they could come up with a longer match. We know this won’t happen in this case, but the regex engine must find that out for itself.

So, the states are tried and immediately discarded except for the remaining two situations where there is a quote in the string available to match the final quote. Thus, the D-E-F and F-G-H are similar to B-C-D, except the matches at F and H are discarded as being shorter than a previously found match at D

By I, the only remaining backtrack is the “bump along and retry” one. However, since the attempt starting at A was able to find a match (three in fact), the POSIX NFA engine is finally done and the match at D is reported.

Work Required During a Non-Match

We still need to look at what happens when there is no match. Let’s look at We know this won’t match our example text, but it comes close on a number of occasions throughout the match attempt. As we’ll see, that results in much more work.

Figure 6-4 illustrates this work. The A-I sequence looks similar to that in Figure 6-3. One difference is that this time it does not match at point D (because the ending exclamation point can’t match). Another difference is that the entire sequence in Figure 6-4 applies to both Traditional and POSIX NFA engines: finding no match, the Traditional NFA must try as many possibilities as the POSIX NFA—all of them.

Figure 6-4: Failing attempt to match ⌈". * " !⌋

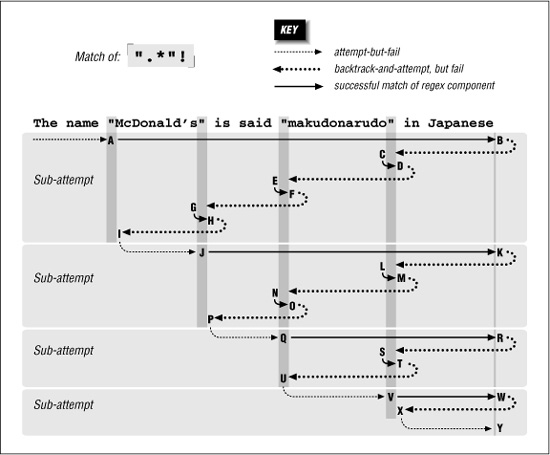
Since there is no match from the overall attempt starting at A and ending at I, the transmission bumps along to retry the match. Attempts eventually starting at points J, Q, and V look promising, but fail similarly to the attempt at A. Finally at Y, there are no more positions for the transmission to try from, so the overall attempt fails. As Figure 6-4 shows, it took a fair amount of work to find this out.

Being More Specific

As a comparison, let’s replace the dot with ⌈[^ " ]⌋. As discussed in the previous chapter, this gives less surprising results because it is more specific, and the end result is that with it, the new regex is more efficient to boot. With ⌈" [^ "] *" !⌋, the ⌈[^" ] *⌋ can’t get past the closing quote, eliminating much matching and subsequent backtracking.

Figure 6-5 shows the failing attempt (compare to Figure 6-4). As you can see, much less backtracking is needed. If the different results suit your needs, the reduced backtracking is a welcome side effect.

Figure 6-5: Failing attempt to match ⌈" [^ "] * "!⌋

Alternation Can Be Expensive

Alternation can be a leading cause of backtracking. As a simple example, let’s use our makudonarudo test string to compare how ⌈U|v|w|x|y|z⌋ and ⌈[uvwxyz]⌋ go about matching. A character class is usually a simple test,^† so ⌈[uvwxyz]⌋ suffers only the bump-along backtracks (34 of them) until we match at:

The name "McDonald's" is said 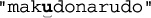in Japanese With ⌈u|v|w|x|y|z⌋, however, six backtracks are required at each starting position, eventually totaling 204 before we achieve the same match. Obviously, not every alternation is replaceable, and even when it is, it’s not necessarily as easily as with this example. In some situations, however, certain techniques that we’ll look at later can greatly reduce the amount of alternation-related backtracking required for a match.

Understanding backtracking is perhaps the most important facet of NFA efficiency, but it’s still only part of the equation. A regex engine’s optimizations can greatly improve efficiency. Later in this chapter, we’ll look in detail at what a regex engine needs to do, and how it can optimize its performance.

Benchmarking

Because this chapter talks a lot about speed and efficiency, and I often mention benchmarks I’ve done, I’d like to mention a few principles of benchmarking. I’ll also show simple ways to benchmark in a few languages.

Basic benchmarking is simply timing how long it takes to do some work. To do the timing, get the system time, do the work, get the system time again, and report the difference between the times as the time it took to do the work. As an example, let’s compare ⌈^(a|b|c|d|e|f|g)+$⌋ with ⌈^ [a-g]+$.⌋ We’ll first look at benchmarking in Perl, but will see it in other languages in a bit. Here’s a simple (but as we’ll see, somewhat lacking) Perl script:

use Time::HiRes 'time'; # So time() gives a high-resolution value.

$StartTime = time();
"abababdedfg" =^~ m/^(a|b|c|d|e|f|g)+$/;
$EndTime = time();
printf("Alternation takes %.3f seconds. \n", $EndTime - $StartTime);

$StartTime = time();
"abababdedfg" =^~ m/^[a-g]+$/;
$EndTime = time();
printf("Character class takes %.3f seconds. \n", $EndTime - $StartTime);

It looks (and is) simple, but there are some important points to keep in mind while constructing a test for benchmarking:

• Time only “interesting” work. Time as much of the “work” as possible, but as little “non-work” as possible. If there is some initialization or other setup that must be done, do it before the starting time is taken. If there’s cleanup, do it after the ending time is taken.
• Do “enough” work. Often, the time it takes to do what you want to test is very short, and a computer’s clock doesn’t have enough granularity to give meaning to the timing.

  When I run the simple Perl test on my system, I get

  Alternation takes 0.000 seconds.
  Character class takes 0.000 seconds.

  which really doesn’t tell me anything other than both are faster than the shortest time that can be measured. So, if something is fast, do it twice, or 10 times, or even 10,000,000 times—whatever is required to make “enough” work. What is “enough” depends on the granularity of the system clock, but most systems now have clocks accurate down to 1/100^th of a second, and in such cases, timing even half a second of work may be sufficient for meaningful results.

• Do the “right” work. Doing a very fast operation ten million times involves the overhead of ten million updates of a counter variable in the block being timed. If possible, it’s best to increase the amount of real work being done in a way that doesn’t increase the overhead work. In our Perl example, the regular expressions are being applied to fairly short strings: if applied to much longer strings, they’d do more “real” work each time.

So, taking these into account, here’s another version:

use Time::HiRes 'time'; # So time() gives a high-resolution value.
$TimesToDo = 1000;                  # Simple setup
$TestString = "abababdedfg" x 1000; # Makes a huge string

$Count = $TimesToDo;
$StartTime = time();
while ($Count-- > 0) {
      $TestString =^~ m/^(a|b|c|d|e|f|g)+$/;
}
$EndTime = time();
printf("Alternation takes %.3f seconds.\n", $EndTime - $StartTime);

$Count = $TimesToDo;
$StartTime = time();
while ($Count-- > 0) {
      $TestString =^~ m/^[a-g]+$/;
}
$EndTime = time();
printf("Character class takes %.3f seconds.\n", $EndTime - $StartTime);

Notice how the $TestString and $Count are initialized before the timing starts? ($TestString is initialized with Perl’s convenient x operator, which replicates the string on its left as many times as the number on its right.) On my system, with Perl 5.8, this prints:

Alternation takes 7.276 seconds.
Character class takes 0.333 seconds.

So, with this test case, one is about 22× faster than the other. The benchmark should be executed a few times, with the fastest times taken, to lessen the impact of sporadic background system activity.

Know What You’re Measuring

It might be interesting to see what happens when the initialization is changed to:

$TimesToDo = 1000000;
$TestString = "abababdedfg";

Now, the test string is 1,000× shorter, but the test is done 1,000× more times. The total number of characters tested and matched by each regex remains the same, so conceptually, one might think that the amount of “work” should also remain the same. However, the results are quite different:

Alternation takes 18.167 seconds.
Character class takes 5.231 seconds.

Both are now much slower than before. This is due to all the extra “non-work” overhead — the update and testing of $Count, and the setup of the regex engine, now each happen 1,000× more than before.

The extra overhead adds almost 5 seconds to the faster test, but more than 10 seconds to the alternation test. Why is the latter affected so much more? It’s mostly due to the extra overhead of the capturing parentheses (which require their own extra processing before and after each test, and doing that 1,000× more adds up).

In any case, the point of this change is to illustrate that the results are strongly inçuenced by how much real work versus non-work overtime is part of the timing.

Benchmarking with PHP

Here’s the benchmark example in PHP, using the pregengine:

$TimesToDo = 1000;

/+ Prepare the test string */
$TestString = "";
for ($i = 0; $i < 1000; $i++)
    $TestString .= "abababdedfg";

/* Do the first test */
$start = gettimeofday();
for ($i = 0; $i < $TimesToDo; $i++)
     pregRmatch('/^(a|b|c|d|e|f|g)+$/', $TestString);
$final = gettimeofday();
$sec = ($final['sec'] + $final['usec']/1000000) -
       ($start['sec'] + $start['usec']/1000000);
printf("Alternation takes %.3f seconds\n", $sec);

/+ And now the second test +/
$start = gettimeofday();
for ($i = 0; $i < $TimesToDo; $i++)
     pregRmatch('/^[a-g]+$/', $TestString);
$final = gettimeofday();
$sec = ($final['sec'] + $final['usec']/1000000) -
       ($start['sec'] + $start['usec']/1000000);
printf("Character class takes %.3f seconds\n", $sec);

On my system, it produces:

Alternation takes 27.404 seconds
Character class takes 0.288 seconds

If, while benchmarking, you get a PHP error about it ônot being safe to rely on the system’s timezone settings,” add the following to the top of your test program:

if (phpversion() >= 5)
   dateRdefaultRtimezoneRset("GMT");

Benchmarking with Java

Benchmarking Java can be a slippery science, for a number of reasons. Let’s first look at a somewhat naive example, and then look at why it’s naive, and at what can be done to make it less so:

import java.util.regex.+;
public class JavaBenchmark {
 public static void main(String [] args)
 {
   Matcher regex1 = Pattern.compile("^(a|b|c|d|e|f|g)+$").matcher("");
   Matcher regex2 = Pattern.compile("^[a-g]+$").matcher("");
   long timesToDo = 1000;

   StringBuffer temp = new StringBuffer();
   for (int i = 1000; i > 0; i--)
           temp.append("abababdedfg");
   String testString = temp.toString();

   // Time first one . . .
   long count = timesToDo;
   long startTime = System.currentTimeMillis();
   while (--count > 0)
         regex1.reset(testString).find();
   double seconds = (System.currentTimeMillis() - startTime)/1000.0;
   System.out.println("Alternation takes " + seconds + " seconds");

   // Time second one . . .
   count = timesToDo;
   startTime = System.currentTimeMillis();
   while (--count > 0)
          regex2.reset(testString).find();
   seconds = (System.currentTimeMillis() - startTime)/1000.0;
   System.out.println("Character class takes " + seconds + " seconds");
  }
}

Notice how the regular expressions are compiled in the initialization part of the program? We want to benchmark the matching speed, not the compile speed.

Speed is dependent upon which virtual machine (VM) is used. Sun standard JRE comes with two virtual machines, a client VM optimized for fast startup, and a server VM optimized for heavy-duty long-haul work.

On my system, running the benchmark on the client VM produces:

Alternation takes 19.318 seconds
Character class takes 1.685 seconds

while the server VM yields:

Alternation takes 12.106 seconds
Character class takes 0.657 seconds

What makes benchmarking slippery, and this example somewhat naive, is that the timing can be highly dependent on how well the automatic pre-execution compiler works, or how the run-time compiler interacts with the code being tested. Some VM have a JIT (Just-In-Time compiler), which compiles code on the fly, just before it’s needed.

Java has what I call a BLTN (Better-Late-Than-Never) compiler, which kicks in during execution, compiling and optimizing heavily-used code on the fly. The nature of a BLTN is that it doesn’t “kick in” until it senses that some code is “hot” (being used a lot). A VM that’s been running for a while, such as in a server environment, will be “warmed up,” while our simple test ensures a “cold” server (nothing yet optimized by the BLTN).

One way to see “warmed up” times is to run the benchmarked parts in a loop:

// Time first one . . .
for (int i = 4; i > 0; i--)
{
    long count = timesToDo;
    long startTime = System.currentTimeMillis();
    while (--count > 0)
          regex1.reset(testString).find();
    double seconds = (System.currentTimeMillis() - startTime)/1000.0;
    System.out.println("Alternation takes " + seconds + " seconds");
}

If the extra loop runs enough times (say, for 10 seconds), the BLTN will have optimized the hot code, leaving the last times reported as representative of a warmed-up system. Testing again with the server VM, these times are indeed a bit faster by about 8 percent and 25 percent:

Alternation takes 11.151 seconds
Character class takes 0.483 seconds

Another issue that makes Java benchmarking slippery is the unpredictable nature of thread scheduling and garbage collection. Again, running the test long enough helps amortize their unpredictable influence.

Benchmarking with VB.NET

Here’s the benchmark example in VB.NET:

Option Explicit On
Option Strict On

Imports System.Text.RegularExpressions

Module Benchmark
Sub Main()
  Dim Regex1 as Regex = New Regex("^(a|b|c|d|e|f|g)+$")
  Dim Regex2 as Regex = New Regex("^[a-g]+$")
  Dim TimesToDo as Integer = 1000
  Dim TestString as String = ""
  Dim I as Integer
  For I = 1 to 1000
     TestString = TestString & "abababdedfg"
  Next

  Dim StartTime as Double = Timer()
  For I = 1 to TimesToDo
     Regex1.Match(TestString)
  Next
  Dim Seconds as Double = Math.Round(Timer() - StartTime, 3)
  Console.WriteLine("Alternation takes " & Seconds & " seconds")

  StartTime = Timer()
  For I = 1 to TimesToDo
     Regex2.Match(TestString)
  Next
  Seconds = Math.Round(Timer() - StartTime, 3)
  Console.WriteLine("Character class takes " & Seconds & " seconds")
End Sub
End Module

On my system, it produces:

Alternation takes 13.311 seconds
Character class takes 1.680 seconds

The .NET Framework allows a regex to be compiled to an even more efficient form, by providing RegexOptions.Compiled as a second argument to each Regex constructor ( 410). Doing that results in:

Alternation takes 5.499 seconds
Character class takes 1.157 seconds

Both tests are faster using the Compiled option, but alternation sees a greater relative benefit (its almost 3× faster when Compiled, but the class version is only about 1.5 × faster), so it seems that alternation benefits from the more efficient compilation relatively more than a character class does.

Benchmarking with Ruby

Here’s the benchmark example in Ruby:

TimesToDo=1000
testString=""
for i in 1..1000
    testString += "abababdedfg"
end

Regex1 = Regexp::new("^(a|b|c|d|e|f|g)+$");
Regex2 = Regexp::new("^[a-g]+$");

startTime = Time.new.toR f
for i in 1..TimesToDo
    Regex1.match(testString)
end
print "Alternation takes %.3f seconds\n" % (Time.new.toRf  -  startTime);

startTime = Time.new.toR f
for i in 1..TimesToDo
    Regex2.match(testString)
end
print "Character class takes %.3f seconds\n" % (Time.new.toRf  -  startTime);

On my system, it produces:

Alternation takes 16.311 seconds
Character class takes 3.479 seconds

Benchmarking with Python

Here’s the benchmark example in Python:

import re
import time
import fpformat

Regex1 = re.compile("^(a|b|c|d|e|f|g)+$")
Regex2 = re.compile("^[a-g]+$")

TimesToDo = 1250;
TestString = ""
for i in range(800):
    TestString += "abababdedfg"

StartTime = time.time()
for i in range(TimesToDo):
   Regex1.search(TestString)
Seconds = time.time() - StartTime
print "Alternation takes " + fpformat.fix(Seconds,3) + " seconds"

StartTime = time.time()
for i in range(TimesToDo):
   Regex2.search(TestString)
Seconds = time.time() - StartTime
print "Character class takes " + fpformat.fix(Seconds,3) + " seconds"

For Python’s regex engine, I had to cut the size of the string a bit because the original causes an internal error (“maximum recursion limit exceeded”) within the regex engine. This is like a pressure release valve, stopping what seems like a neverending match from running too wild.

To compensate, I increased the number of times the test is done by a proportional amount. On my system, the benchmark produces:

Alternation takes 10.3 57 seconds
Character class takes 0.769 seconds

Benchmarking with Tcl

Here’s the benchmark example in Tcl:

set TimesToDo 1000
set TestString ""
for {set i 1000} {$i > 0} {incr i -1} {
    append TestString "abababdedfg"
}

set Count $TimesToDo
set StartTime [clock clicks -milliseconds]
for {} {$Count > 0} {incr Count -1} {
    regexp {^(a|b|c|d|e|f|g)+$} $TestString
}
set EndTime [clock clicks -milliseconds]
set Seconds [expr ($EndTime - $StartTime)/1000.0]
puts [format "Alternation takes %.3f seconds" $Seconds]

set Count $TimesToDo
set StartTime [clock clicks -milliseconds]
for {} {$Count > 0} {incr Count -1} {
    regexp {^[a-g]+$} $TestString
}
set EndTime [clock clicks -milliseconds]
set Seconds [expr ($EndTime - $StartTime)/1000.0]
puts [format "Character class takes %.3f seconds" $Seconds]

On my system, this benchmark produces:

Alternation takes 0.3 62 seconds
Character class takes 0.3 52 seconds

Wow, they’re both about the same speed! Well, recall from the table on page 145 that Tcl has a hybrid NFA/DFA engine, and these regular expressions are exactly the same to a DFA engine. Most of what this chapter talks about simply does not apply to Tcl. See the sidebar on page 243 for more.

Common Optimizations

A smart regex implementation has many ways to optimize how quickly it produces the results you ask of it. Optimizations usually fall into two classes:

• Doing something faster Some types of operations, such as ⌈\d+⌋, are so common that the engine might have special-case handling set up to execute them faster than the general engine mechanics would.
• Avoiding work If the engine can decide that some particular operation is unneeded in producing a correct result, or perhaps that some operation can be applied to less text than originally thought, skipping those operations can result in a time savings. For example, a regex beginning with ⌈\A ⌋ (start-of-line) can match only when started at the beginning of the string, so if no match is found there, the transmission need not bother checking from other positions.

Over the next dozen or so pages, we’ll look at many of the different and ingenious optimizations that I’ve seen. No one language or tool has them all, or even the same mix as another language or tool, and I’m sure that there are plenty of other optimizations that I’ve not yet seen, but this chapter should leave you much more empowered to take advantage of whatever optimizations your tool offers.

No Free Lunch

Optimizations often result in a savings, but not always. There’s a benefit only if the amount of time saved is more than the extra time spent checking to see whether the optimization is applicable in the first place. In fact, if the engine checks to see if an optimization is applicable and the answer is “no,” the overall result is slower because it includes the fruitless check on top of the subsequent normal application of the regex. So, there’s a balance among how much time an optimization takes, how much time it saves, and importantly, how likely it is to be invoked.

Let’s look at an example. The expression ⌈\b\B⌋ (word boundary at the same location as a non-word boundary) can’t possibly match. If an engine were to realize that a regex contained ⌈\b\B⌋ in such a way that it was required for any match, the engine would know that the overall regex could never match, and hence never have to actually apply that regex. Rather, it could always immediately report failure. If applied to long strings, the savings could be substantial.

Yet, no engine that I know of actually uses this optimization. Why not? Well, first of all, it’s not necessarily easy to decide whether it would apply to a particular regex. It’s certainly possible for a regex to have ⌈\b\B⌋ somewhere in it, yet still match, so the engine has to do extra work ahead of time to be absolutely certain. Still, the savings could be truly substantial, so it could be worth doing the extra work if ⌈\b\B⌋ was expected to be common.

But, it’s not common (it’s silly!),^† so even though the savings could be huge in the rare case, the added overhead is not worth slowing down the common case.

Everyone’s Lunch is Different

Keep this in mind when looking at the various kinds of optimizations that this chapter discusses. Even though I’ve tried to pick simple, clean names for each one, it may well be that every engine that implements it does so in a different way. A seemingly innocuous change in a regex can cause it to become substantially faster with one implementation, but substantially slower with another.

The Mechanics of Regex Application

Before looking at how advanced systems optimize their regex performance, and how we can take advantage of those optimizations, it’s important to first understand the basics of regex application. We’ve already covered the details about backtracking, but in this short section, we’ll look at the broader picture.

Here are the main steps taken in applying a regular expression to a target string:

1. Regex Compilation The regex is inspected for errors, and if valid, compiled into an internal form.
2. Transmission Begins The transmission “positions” the engine at the start of the target string.
3. Component Tests The engine works through the regex and the text, moving from component to component in the regex, as described in Chapter 4. We’ve already covered backtracking for NFAs in great detail, but there are a few additional points to mention:

   • With components next to each other, as with the ⌈S⌋, ⌈U⌋, ⌈b⌋, ⌈j⌋, ⌈e⌋. . . , of ⌈Subject⌋, each component is tried in turn, stopping only if one fails.

   • With quantifiers, control jumps between the quantifier (to see whether the quantifier should continue to make additional attempts) and the component quantified (to test whether it matches).

   • There is some overhead when control enters or exits a set of capturing parentheses. The actual text matched by the parentheses must be remembered so that $1 and the like are supported. Since a set of parentheses may be “backtracked out of,” the state of the parentheses is part of the states used for backtracking, so entering and exiting capturing parentheses requires some modification of that state.

4. Finding a Match If a match is found, a Traditional NFA “locks in” the current state and reports overall success. On the other hand, a POSIX NFA merely remembers the possible match if it is the longest seen so far, and continues with any saved states still available. Once no more states are left, the longest match that was seen is the one reported.
5. Transmission Bump-Along If no match is found, the transmission bumps the engine along to the next character in the text, and the engine applies the regex all over again (going back to step 3).
6. Overall Failure If no match is found after having applied the engine at every character in the target string (and after the last character as well), overall failure must be reported.

The next few sections discuss the many ways this work can be reduced by smart implementations, and taken advantage of by smart users.

Pre-Application Optimizations

A good regex engine implementation can reduce the amount of work that needs to be done before the actual application of a regex, and sometimes can even decide quickly beforehand that the regex can never match, thereby avoiding the need to even apply the regex in the first place.

Compile caching

Recall the mini mail program from Chapter 2 ( 57). The skeleton of the main loop, which processes every line of the header, looks like:

while (···)  {
    if ($line =~ m/^\s,$/  )  ···
    if ($line =~ m/^Subject: (.*)/)  ···
    if ($line =~ m/^Date: (.,)/)  ···
    if ($line =~ m/^Reply-To: (\S+)/)···
    if ($line =~ m/^From: (\S+) \(([^()],)\)/)···
      *
      *
      *
}

The first thing that must be done before a regular expression can be used is that it must be inspected for errors, and compiled into an internal form. Once compiled, that internal form can be used in checking many strings, but will it? It would certainly be a waste of time to recompile each regex each time through the loop. Rather, it is much more time efficient (at the cost of some memory) to save, or cache, the internal form after it’s first compiled, and then use that same internal form for each subsequent application during the loop.

The extent to which this can be done depends on the type of regular-expression handling the application offers. As described starting on page 93, the three types of handling are integrated, procedural, and object-oriented.

Compile caching in the integrated approach

An integrated approach, like Perl’s and awk’s, allows compile caching to be done with ease. Internally, each regex is associated with a particular part of the code, and the compiled form can be associated with the code the first time it’s executed, and merely referenced subsequent times. This provides for the maximum optimization of speed at the cost of the memory needed to hold all the cached expressions.

The ability to interpolate variables into the regex operand (that is, use the contents of a variable as part of the regular expression) throws somewhat of a monkey wrench into the caching plan. When variables are interpolated, as with something like m/ ^ Subject: • \Q $DesiredSubject \E\s*$/, the actual regular expression may change from iteration to iteration because it depends on the value in the variable, which can change from iteration to iteration. If it changes every time, the regex must be compiled every time, so nothing can be reused.

Well, the regular expression might change with each iteration, but that doesn’t mean it needs to be recompiled each time. An intermediate optimization is to check the results of the interpolation (the actual value to be used as the regular expression), and recompile only if it’s different from the previous time. If the value actually changes each time, there’s no optimization, as the regex indeed must be recompiled each time. But, if it changes only sporadically, the regular expression need only be checked (but not compiled) most times, yielding a handsome optimization.

Compile caching in the procedural approach

With an integrated approach, regex use is associated with a particular location in a program, so the compiled version of the regex can be cached and used the next time that location in the program is executed. But, with a procedural approach, there is just a general “apply this regex” function that is called as needed. This means that there’s no location in a program with which to associate the compiled form, so the next time the function is called, the regex must be compiled from scratch again. That’s how it works in theory, but in practice, it’s much too inefficient to abandon all attempts at caching. Rather, what’s often done is that a mapping of recently used regex patterns is maintained, linking each pattern to its resulting compiled form.

When the apply-this-regex function is called, it compares the pattern argument with those in the cache of saved regular expressions, and uses the cached version if it’s there. If it’s not, it goes ahead and compiles the regex, saving it to the cache (and perhaps flushing an old one out, if the cache has a size limit). When the cache has become full and a compiled form must be thrown out, it’s usually the least recently used one.

GNU Emacs keeps a cache of up to 20 expressions. Tcl keeps up to 30. PHP keeps more than 4,000. The .NET Framework by default keeps up to only 15 expressions cached, although that can be changed on the fly or even disabled ( 432).

A large cache size can be important because if more regular expressions are used within a loop than the size of the cache, by the time the loop restarts, the first regex will have been flushed from the cache, guaranteeing that every expression will have to be compiled from scratch every time.

Compile caching in the object-oriented approach

The object-oriented approach puts control of when a regex is compiled directly into the programmer’s hands. Compilation of the regex is exposed to the user via object constructors such as New Regex, re.compile, and Pattern.compile (which are from .NET, Python, and java.util.regex, respectively). In the simple examples from Chapter 3 where these are introduced (starting on page 95), the compilation is done just before the regex is actually used, but there’s no reason that they can’t be done earlier (such as sometime before a loop, or even at program initialization) and then used freely as needed. This is done, in the benchmarking examples on pages 235, 237, and 238.

The object-oriented approach also affords the programmer control over when a compiled form is thrown away, via the object’s destructor. Being able to immediately throw away compiled forms that will no longer be needed saves memory.

Pre-check of required character/substring optimization

Searching a string for a particular character (or perhaps some literal substring) is a much “lighter” operation than applying a full NFA regular expression, so some systems do extra analysis of the regex during compilation to determine if there are any characters or substrings that are required to exist in the target for a possible match. Then, before actually applying the regex to a string, the string is quickly checked for the required character or string — if it’s not found, the entire application of the regex can be bypassed.

For example, with ⌈^ Subject: • (.*)⌋, the string 'Subject: •’ is required. A program can look for the entire string, perhaps using the Boyer-Moore search algorithm (which is a fast way to search for literal strings within text — the longer the literal string, the more efficient the search). A program not wishing to implement the Boyer-Moore algorithm can still gain a benefit by picking a required character and just checking every character in the target text. Picking a character less likely to be found in the target (such as picking ‘:’ over 't' from our 'Subject: • ‘ example) is likely to yield better results.

While it’s trivial for a regex engine to realize what part of ⌈^>Subject: • (. *)⌋ is a fixed literal string required for any match, it’s more work to recognize that 'th' is required for any match of ⌈this|that|other⌋, and most don’t do it. It’s not exactly black and white — an implementation not realizing that 'th' is required may well still be able to easily realize that 'h' and 't' are required, so at least do a one-character check.

There is a great variety in how well different applications can recognize required characters and strings. Most are thwarted by the use of alternation. With such systems, using ⌈th(is|at)⌋ can provide an improvement over ⌈this|that⌋. Also, be sure to see the related section “Initial character/class/substring discrimination” on page 247.

Length-cognizance optimization

⌈^ Subject: • (. *)⌋ can match arbitrarily long text, but any match is certainly at least nine characters long. Therefore, the engine need not be started up and applied to strings shorter than that length. Of course, the benefit is more pronounced with a regex with a longer required length, such as ⌈:\d{79 }:⌋ (81 characters in any match).

Also see the length-cognizance transmission optimization on page 247.

Optimizations with the Transmission

If the regex engine can’t decide ahead of time that a particular string can never match, it may still be able to reduce the number of locations that the transmission actually has to apply the regex.

Start of string/line anchor optimization

This optimization recognizes that any regex that begins with ⌈^⌋ can match only when applied where ⌈^⌋ can match, and so need be applied at those locations only.

The comments in the “Pre-check of required character/substring” section on the previous page about the ability of the regex engine to derive just when the optimization is applicable to a regex is also valid here. Any implementation attempting this optimization should be able to recognize that ⌈^(this | that)⌋ can match starting only at locations where ⌈^⌋ can match, but many won’t come to the same realization with ⌈this|^that⌋. In such situations, writing ⌈^(this|that)⌋ or (even better) ⌈^ (?: this|that)⌋ can allow a match to be performed much faster.

Similar optimizations involve ⌈\A⌋, and for repeated matches, ⌈\G⌋.

Implicit-anchor optimization

An engine with this optimization realizes that if a regex begins with ⌈. *⌋ or ⌈. +⌋, and has no global alternation, an implicit ⌈^⌋ can be prepended to the regex. This allows the start of string/line anchor optimization of the previous section to be used, which can provide a lot of savings.

More advanced systems may realize that the same optimization can also be applied when the leading ⌈. *⌋ or ⌈. +⌋ is within parentheses, but care must be taken when the parentheses are capturing. For example, the regex ⌈(.+)X\1⌋ finds locations where a string is repeated on either side of 'X', and an implicit leading ⌈^⌋ causes it to improperly not match ‘’.^†

End of string/line anchor optimization

This optimization recognizes that some regexes ending with ⌈$⌋ or other end anchors ( 129) have matches that start within a certain number of characters from the end of the string. For example, with ⌈regex(es)?$⌋, any match must start no more than eight^† characters from the end of the string, so the transmission can jump directly there, potentially bypassing much of the target string.

Initial character/class/substring discrimination optimization

A more generalized version of the pre-check of required character/string optimization, this optimization uses the same information (that any match by the regex must begin with a specific character or literal substring) to let the transmission use a fast substring check so that it need apply the regex only at appropriate spots in the string. For example ⌈this|that|other⌋ can match only at locations beginning with ⌈[ot]⌋, so having the transmission pre-check each character in the string and applying the regex only at matching positions can afford a huge savings. The longer the substring that can be pre-checked, the fewer “false starts” are likely.

Embedded literal string check optimization

This is almost exactly like the initial string discrimination optimization, but is more advanced in that it works for literal strings embedded a known distance into any match. ⌈\b(perl|java)\.regex\.info\b⌋, for example, has '.regex.info' four characters into any match, so a smart transmission can use a fast Boyer-Moore literal-string check to find '.regex.info', and then actually apply the regex starting four characters before.

In general, this works only when the literal string is embedded a fixed distance into any match. It doesn’t apply to ⌈\b(vb|java) \.regex\.info\b⌋, which does have a literal string, but one that’s embedded either two or four characters into any match. It also doesn’t apply to ⌈\b(\w+)\.regex\.info\b⌋, whose literal string is embedded any number of characters into any match.

Length-cognizance transmission optimization

Directly related to the Length-cognizance optimization on page 245, this optimization allows the transmission to abandon the attempt if it’s gotten too close to the end of the string for a match to be possible.

Optimizations of the Regex Itself

Literal string concatenation optimization

Perhaps the most basic optimization is that ⌈abc⌋ can be treated by the engine as “one part,” rather than the three parts “⌈a⌋ then ⌈b⌋ then ⌈C⌋” If this is done, the one part can be applied by one iteration of the engine mechanics, avoiding the overhead of three separate iterations.

Simple quantifier optimization

Uses of star, plus, and friends that apply to simple items, such as literal characters and character classes, are often optimized such that much of the step-by-step overhead of a normal NFA engine is removed. The main control loop inside a regex engine must be general enough to deal with all the constructs the engine supports. In programming, “general” often means “slow,” so this important optimization makes simple quantifiers like ⌈. *⌋ into one “part” replacing the general engine mechanics of quantifier processing with fast, specialized processing. Thus, the general engine is short-circuited for these tests.

For example, ⌈. *⌋ and ⌈(?:.) *⌋ are logically identical, but for systems with this optimization, the simple ⌈. *⌋ is substantially faster. A few examples: it’s only about 10 percent faster in java.util.regex, but with Ruby and the .NET languages, it’s about two and a half times faster. With Python, it’s about 50 times faster, and with PHP/PCRE, it’s about 150 times faster. Because Perl has the optimization discussed in the next section, both ⌈. *⌋ and ⌈( ?: .) *⌋ are the same speed. (Be sure to see the sidebar on the facing page for more on how to interpret these numbers.)

Needless parentheses elimination

If an implementation can realize that ⌈(?:.) *⌋ is exactly the same as ⌈. *⌋, it opens up the latter to the previous optimization.

Needless character class elimination

A character class with a single character in it is a bit silly because it invokes the processing overhead of a character class, but without any benefits of one. So, a smarter implementation internally converts something like ⌈[ . ]⌋ to ⌈\.⌋.

Character following lazy quantifier optimization

With a lazy quantifier, as in ⌈" (.*?) "⌋, the engine normally must jump between checking what the quantifier controls (the dot) with checking what comes after (⌈"⌋). For this and other reasons, lazy quantifiers are generally much slower than greedy ones, especially for greedy ones that are optimized with the simple quantifier optimization discussed two sections ago. Another factor is that if the lazy quantifier is inside capturing parentheses, control must repeatedly jump in and out of the capturing, which causes additional overhead.

So, this optimization involves the realization that if a literal character follows the lazy quantifier, the lazy quantifier can act like a normal greedy quantifier so long as the engine is not at that literal character. Thus, implementations with this optimization switch to specialized lazy quantifier processing for use in these situations, which quickly checks the target text for the literal character, bypassing the normal “skip this attempt” if the target text is not at that special literal character.

Variations on this optimization might include the ability to pre-check for a class of characters, rather than just a specific literal character (for instance, a pre-check for ⌈[ '" ]⌋ with ⌈[ '" ] (. *?) ["' ]⌋, which is similar to the initial character discrimination optimization discussed on the previous page).

“Excessive” backtracking detection

The problem revealed with the “Reality Check” on page 226 is that certain combinations of quantifiers, such as ⌈(.+) *⌋, can create an exponential amount of backtracking. One simple way to avoid this is to keep a count of the backtracking, and abort the match when there’s “too much.” This is certainly useful in the reality- check situation, but it puts an artificial limit on the amount of text that some regular expressions can be used with.

For example, if the limit is 10,000 backtracks, ⌈. * ?⌋ can never match text longer than 10,000 characters, since each character matched involves a backtrack. Working with these amounts of text is not all that uncommon, particularly when working with, say, web pages, so the limitation is unfortunate.

For different reasons, some implementations have a limit on the size of the backtrack stack (on how many saved states there can be at any one time). For example, Python allows at most 10,000. Like a backtrack limit, it limits the length of text some regular-expressions can work with.

This issue made constructing some of the benchmarks used while researching this book rather difficult. To get the best results, the timed portion of a benchmark should do as much of the target work as possible, so I created huge strings and compared the time it took to execute, say, ⌈"(.*)"⌋, ⌈"(.*)"⌋, ⌈"(.*)?"⌋, and ⌈" ([^" ])* ?"⌋. To keep meaningful results, I had to limit the length of the strings so as not to trip the backtrack-count or stack-size limitations. You can see an example on page 239.

Exponential (a.k.a., super-linear) short-circuiting

A better solution to avoid matching forever on an exponential match is to detect when the match attempt has gone super-linear. You can then make the extra effort to keep track of the position at which each quantifier’s subexpression has been attempted, and short-circuit repeat attempts.

It’s actually fairly easy to detect when a match has gone super-linear. A quantifier should rarely “iterate” (loop) more times than there are characters in the target string. If it does, it’s a good sign that it may be an exponential match. Having been given this clue that matching may go on forever, it’s a more complex issue to detect and eliminate redundant matches, but since the alternative is matching for a very, very long time, it’s probably a good investment.

One negative side effect of detecting a super-linear match and returning a quick failure is that a truly inefficient regex now has its inefficiency mostly hidden. Even with exponential short-circuiting, these matches are much slower than they need to be, but no longer slow enough to be easily detected by a human (instead of finishing long after the sun has gone dormant, it may take ¹/100 of a second — quick to us, but still an eternity in computer time).

Still, the overall benefit is probably worth it. There are many people who don’t care about regex efficiency—they’re scared of regular expressions and just want the thing to work, and don’t care how. (You may have been this way before, but I hope reading this book emboldens you, like the title says, to master the use of regular expressions.)

State-suppression with possessive quantifiers

After something with a normal quantifier has matched, a number of “try the nonmatch option” states have been created (one state per iteration of the quantifier). Possessive quantifiers ( 142) don’t leave those states around. This can be accomplished by removing the extra states after the quantifier has run its course, or, it can be done more efficiently by removing the previous iteration’s state while adding the current iteration’s. (During the matching, one state is always required so that the regex can continue once the quantified item can no longer match.)

The reason the on-the-fly removal is more efficient is because it takes less memory. Applying ⌈. *⌋ leaves one state per character matched, which could consume a vast amount of memory if the string is long.

Small quantifier equivalence

Some people like to write ⌈\d\d\d\d⌋ directly, while some like to use a small quantifier and write ⌈\d{4}.⌋ Is one more efficient than the other? For an NFA, the answer is almost certainly yes, but which is faster depends on the tool. If the tool’s quantifier has been optimized, the ⌈\d{4}⌋ version is likely faster unless the version without the quantifier can somehow be optimized more. Sound a bit confusing? It is.

My tests show that with Perl, Python, PHP/PCRE, and .NET, ⌈\d{4}⌋ is faster by as much as 20 percent. On the other hand, with Ruby and Sun’s Java regex package, ⌈\d\d\d\d⌋ is faster—sometimes several times faster. So, this seems to make it clear that the small quantifier is better for some, but worse for others. But, it can be more complex than that.

Compare ⌈====⌋ with ⌈= {4}.⌋ This is a quite different example because this time, the subject of the repetition is a literal character, and perhaps using ⌈====⌋ directly makes it easier for the regex engine to recognize the literal substring. If it can, the highly effective initial character/substring discrimination optimization ( 247) can kick in, if supported. This is exactly the case for Python and Sun’s Java regex package, for whom the ⌈====⌋ version can be up to 100× faster than ⌈={4}⌋.

More advanced still, Perl, Ruby, and .NET recognize this optimization with either ⌈====⌋ or ⌈ = {4 }⌋, and as such, both are equally fast (and in either case, can be hundreds or thousands of times faster than the ⌈\d\d\d\d⌋ and ⌈\d{4}⌋ counterparts).

Need cognizance

One simple optimization is if the engine realizes that some aspect of the match result isn’t needed (say, the capturing aspect of capturing parentheses), it can eliminate the work to support them. The ability to detect such a thing is very language dependent, but this optimization can be gained as easily as allowing an extra match-time option to disable various high-cost features.

One example of a system that has this optimization is Tcl. Its capturing parentheses don’t actually capture unless you explicitly ask. Conversely, the .NET Framework regular expressions have an option that allows the programmer to indicate that capturing parentheses shouldn’t capture.

Techniques for Faster Expressions

The previous pages list the kinds of optimizations that I’ve seen implemented in Traditional NFA engines. No one program has them all, and whichever ones your favorite program happens to have now, they’re certain to change sometime in the future. But, just understanding the kinds of optimizations that can be done gives you an edge in writing more efficient expressions. Combined with the understanding of how a Traditional NFA engine works, this knowledge can be applied in three powerful ways:

• Write to the optimizations. Compose expressions such that known optimizations (or ones that might be added in the future) can kick in. For example, using ⌈XX*⌋ instead of ⌈X+⌋ can allow a variety of optimizations to more readily kick in, such as the check of a required character or string ( 245), or initial-character discrimination ( 247).
• Mimic the optimizations. There are situations where you know your program doesn’t have a particular optimization, but by mimicking the optimization yourself, you can potentially see a huge savings. As an example that we’ll expand on soon, consider adding ⌈(?=t)⌋ to the start of ⌈this|that⌋, to somewhat mimic the initial-character discrimination ( 247) in systems that don’t already determine from the regex that any match must begin with 't'.
• Lead the engine to a match. Use your knowledge of how a Traditional NFA engine works to lead the engine to a match more quickly. Consider the ⌈this|that⌋ example. Each alternative begins with ⌈th⌋; if the first’s alternative can’t match its ⌈th⌋ the second alternative’s ⌈th⌋ certainly can’t match, so the attempt to do so is wasted. To avert that, you can use ⌈th(?:is|at)⌋ instead. That way, the ⌈th⌋ is tested only once, and the relatively expensive alternation is avoided until it’s actually needed. And as a bonus, the leading raw-text ⌈th⌋ of ⌈th (?: is | at)⌋ is exposed, potentially allowing a number of other optimizations to kick in.

It’s important to realize that efficiency and optimizations can sometimes be touchy. There are a number of issues to keep in mind as you read through the rest of this section:

• Making a change that would seem to be certainly helpful can, in some situations, slow things down because you’ve just untweaked some other optimization that you didn’t know was being applied.
• If you add something to mimic an optimization that you know doesn’t exist, it may well turn out that the work required to process what you added actually takes more time than it saves.
• If you add something to mimic an optimization that you know doesn’t currently exist, it may defeat or duplicate the real optimization if it’s later added when the tool is upgraded.
• Along the same lines, contorting an expression to try to pique one kind of optimization today may prohibit some future, more advantageous optimization from kicking in when the tool is upgraded.
• Contorting an expression for the sake of efficiency may make the expression more difficult to understand and maintain.
• The magnitude of the benefit (or harm) a particular change can have is almost certainly strongly dependent on the data it’s applied to. A change that is beneficial with one set of data may actually be harmful with another type of data.

Let me give a somewhat crazy example: you find ⌈(000 | 999) $⌋ in a Perl script, and decide to turn those capturing parentheses into non-capturing parentheses. This should make things a bit faster, you think, since the overhead of capturing can now be eliminated. But surprise, this small and seemingly beneficial change can slow this regex down by several orders of magnitude (thousands and thousands of times slower). What!? It turns out that a number of factors come together just right in this example to cause the end of string/line anchor optimization ( 246) to be turned off when non-capturing parentheses are used. I don’t want to dissuade you from using non-capturing parentheses with Perl—their use is beneficial in the vast majority of cases—but in this particular case, it’s a disaster.

So, testing and benchmarking with the kind of data you expect to use in practice can help tell you how beneficial or harmful any change will be, but you’ve still got to weigh all the issues for yourself. That being said, I’ll touch on some techniques that can be used toward squeezing out the last bit of efficiency out of an engine.

Common Sense Techniques

Some of the most beneficial things you can do require only common sense.

Avoid recompiling

Compile or define the regular expression as few times as possible. With object-oriented handling ( 95), you have the explicit control to do this. If, for example, you want to apply a regex in a loop, create the regex object outside of the loop, then use it repeatedly inside the loop.

With a procedural approach, as with GNU Emacs and Tcl, try to keep the number of regular expressions used within a loop below the cached threshold of the tool ( 244).

With an integrated approach like Perl, try not to use variable interpolation within a regex inside a loop, because at a minimum, it causes the regex value to be reevaluated at each iteration, even if you know the value never changes. (Perl does, however, provide efficient ways around the problem 348.)

Use non-capturing parentheses

If you don’t use the capturing aspect of capturing parentheses, use non-capturing ⌈(?:···)⌋ parentheses ( 45). Besides the direct savings of not having to capture, there can be residual savings because it can make the state needed for backtracking less complex, and hence faster. It can also open up additional optimizations, such as needless-parentheses elimination ( 248).

Don’t add superfluous parentheses

Use parentheses as you need them, but adding them otherwise can prohibit optimizations from kicking in. Unless you need to know the last character matched by ⌈. *⌋, don’t use ⌈(.) *.⌋ This may seem obvious, but after all, this is the “common sense techniques” section.

Don’t use superfluous character classes

This may seem to be overly obvious as well, but I’ve often seen expressions like ⌈^.* [ : ]⌋ from novice programmers. I’m not sure why one would ever use a class with a single character in it — it incurs the processing overhead of a class without gaining any multi-character matching benefits of a class. I suppose that when the character is a metacharacter, such as ⌈[ . ]⌋ and ⌈[ * ]⌋, it’s probably because the author didn’t know about escaping, as with ⌈\ .⌋ and ⌈\ *⌋. I see this most often with white-space in a free-spacing mode ( 111).

Somewhat related, users of Perl that read the first edition of this book may sometimes write something like ⌈^ [Ff] [Rr] [Oo] [Mm] :⌋ instead of a case-insensitive use of ⌈^ from:⌋. Old versions of Perl were very inefficient with their case-insensitive matching, so I recommended the use of classes like this in some cases. That recommendation has been lifted, as the case-insensitive inefficiency has been fixed for some years now.

Use leading anchors

Except in the most rare cases, any regex that begins with ⌈. *⌋ should probably have ⌈^⌋ or ⌈\A⌋ ( 129) added to the front. If such a regex can’t match when applied at the beginning of the string, it won’t be able to match any better when the bump-along applies it starting at the second character, third character, and so on. Adding the anchor (either explicitly, or auto-added via an optimization 246) allows the common start-of-line anchor optimization to kick in, saving a lot of wasted effort.

Expose Literal Text

Many of the native optimizations we’ve seen in this chapter hinge on the regex engine’s ability to recognize that there is some span of literal text that must be part of any successful match. Some engines are better at figuring this out than others, so here are some hand-optimization techniques that help “expose” literal text, increasing the chances that an engine can recognize more of it, allowing the various literal-text optimizations to kick in.

“Factor out” required components from quantifiers

Using ⌈XX*⌋ instead of ⌈X+⌋ exposes 'x' as being required. The same logic applies to the rewriting of ⌈-{5,7}⌋ as ⌈------{0,2}⌋

“Factor out” required components from the front of alternation

Using ⌈th(?:is | at)⌋ rather than ⌈(? : this | that)⌋ exposes that ⌈th⌋ is required. You can also “factor out” on the right side, when the common text follows the differing text: ⌈(?: optim | standard) ization⌋. As the next section describes, these can be particularly important when what is being factored out includes an anchor.

Expose Anchors

Some of the most fruitful internal regex optimizations are those that take advantage of anchors (like ⌈^⌋, ⌈$⌋, and ⌈\G⌋) that tie the expression to one end of the target string or another. Some engines are not as good as others at understanding when such an optimization can take place, but there are techniques you can use to help.

Expose ^ and \G at the front of expressions

⌈^ (?:abc | 123)⌋ and ⌈^abc | ^123⌋ are logically the same expression, but many more regex engines can apply the Start of string/line anchor optimization ( 246) with the first than the second. So, choosing to write it the first way can make it much more efficient. PCRE (and tools that use it) is efficient with either, but most other NFA tools are much more efficient with the exposed version.

Another difference can be seen by comparing ⌈(^abc)⌋ and ⌈^(abc)⌋. The former doesn’t have many redeeming qualities, as it both “hides” the anchor, and causes the capturing parentheses to be entered before the anchor is even checked, which can be inefficient with some systems. Some systems (PCRE, Perl, the .NET languages) are efficient with either, but others (Ruby and Sun’s Java regex library) recognize the optimization only with the exposed version.

Python doesn’t seem to have the anchor optimization, so these techniques don’t currently matter for it. Of course, most optimizations in this chapter don’t apply to Tcl ( 243).

Expose $ at the end of expressions

This is conceptually very similar to the previous section, where ⌈abc$|123$⌋ and ⌈(?: abc | 123) $⌋ are logically the same expression, but can be treated differently by the optimizers. Currently, there is a difference only for Perl, as only Perl currently has the End of string/line anchor optimization ( 246). The optimization kicks in with ⌈(···|···) $⌋ but not with ⌈(···$ | ···$)⌋.

Lazy Versus Greedy: Be Specific

Usually, the choice between lazy and greedy quantifiers is dictated by the specific needs of the regex. For example, ⌈^ .* :⌋ differs substantially from ⌈^.*?:⌋ in that the former one matches until the final colon, while the latter one matches until the first. But, suppose that you knew that your target data had exactly one colon on it. If that’s the case, the semantics of both are the same (“match until the colon”), so it’s probably smart to pick the one that will run fastest.

It’s not always obvious which is best, but as a rule of thumb when the target strings are long, if you expect the colon to generally be near the start of the string, using the lazy quantifier allows the engine to find the colon sooner. Use the greedy quantifier if you expect the colon to be toward the end of the string. If the data is random, and you have no idea which will be more likely, use a greedy quantifier, as they are generally optimized a bit better than non-greedy quantifier, especially when what follows in the regex disallows the character following lazy quantifier optimization ( 248).

When the strings to be tested are short, it becomes even less clear. When it comes down to it, either way is pretty fast, but if you need every last bit of speed, benchmark against representative data.

A somewhat related issue is in situations where either a lazy quantifier or a negated class can be used (such as ⌈^.*?:⌋ versus ⌈^[^:]*:⌋), which should be used? Again, this is dependent on the data and the language, but with most engines, using a negated class is much more efficient than a lazy quantifier. Perl is an exception, because it has that character following lazy quantifier optimization.

Split Into Multiple Regular Expressions

There are cases where it’s much faster to apply many small regular expressions instead of one large one. For a somewhat contrived example, if you wanted to check a large string to see if it had any of the month names, it would probably be much faster to use separate checks of ⌈January⌋, ⌈February⌋, ⌈March⌋, etc., than to use one ⌋January|February|March|···⌋. With the latter, there’s no literal text known to be required for any match, so an embedded literal string check optimization ( 247) is not possible. With the all-in-one regex, the mechanics of testing each subexpression at each point in the text can be quite slow.

Here’s an interesting situation I ran into at about the same time that I was writing this section. When working with a Perl data-handling module, I realized that I had a bug with my client program that caused it to sent bogus data that looked like ‘HASH(0x80f60ac)’ instead of the actual data. So, I thought I’d augment the module to look for that kind of bogus data and report an error. The straightforward regex for what I wanted is ⌈\b (?: SCALAR|ARRAY|HASH)\(0x[0-9a-fA-F]+\)⌋.

This was a situation where efficiency was extremely important. Would this be fast? Perl has a debugging mode that can tell you about some of the optimizations it uses with any particular regex ( 361), so I checked. I hoped to find that the pre-check of required string optimization ( 245) would kick in, since an advanced enough engine should be able to figure out that ‘(0x' is required in any match. Knowing the data that I’d apply this to would almost never have ‘(0x', I knew that such a pre-check would eliminate virtually every line. Unfortunately, Perl didn’t pick this out, so I was left with a regex that would entail a lot of alternation at every character of every target string. That’s slower than I wanted.

Since I was in the middle of researching and writing about optimizations, I thought hard about how I could rewrite the regex to garner some of the better optimizations. One thought I had was to rewrite it along the form of the somewhat complex . The approach here is that once ⌈\ (0x⌋, has matched, the positive lookbehind (underlined for clarity) makes sure that what came before is allowed, and then checks that what comes after is expected as well. The whole reason to go through these regex gymnastics is to get the regex to lead with non-optional literal text ⌈\ (0x⌋, which allows a lot of good optimizations to kick in. In particular, I’d expect that pre-check of required string optimization to kick in, as well as the initial character/substring discrimination optimization ( 247). I’m sure that these would have made it very fast, but Perl doesn’t allow variable-length lookbehind ( 133), so I was back to square one.

However, I realized that since Perl wasn’t doing the pre-check for ⌈\ (0x⌋ for me, I could just do it myself:

if ($data =^~ m/\(0x/
    and
    $data =^~ m/(?:SCALAR;ARRAY|···|HASH)\(0x[0-9a-fA-F]+\)/)
{
   # warn about bogus data···
}

The check of ⌈\ (0x⌋ eliminates virtually every line, so this leaves the check of the relatively slow full regex for only when the likelihood of a match is high. This created a wonderful balance of efficiency (very high) and readability (very high)^†

Mimic Initial-Character Discrimination

If the initial-character discrimination optimization ( 247) is not done by your implementation, you can mimic it yourself by adding appropriate lookahead ( 133) to the start of the regex. The lookahead can “pre-check” that you’re at an appropriate starting character before you let the rest of the regex match.

For example, for ⌈Jan|Feb|···|Dec⌋, use ⌈(?=[JFMASOND])(?:Jan|Feb| "|Dec). The leading [JFMASOND] represents letters that can begin the month names in English. This must be done with care, though, because the added overhead of the lookahead may overshadow the savings. In this particular example, where the lookahead is pre-checking for many alternatives that are likely to fail, it is beneficial for most systems I’ve tested (Java, Perl, Python, Ruby, .NET languages), none of which apparently are able to derive [JFMASOND] from Jan|Feb|---|Decj themselves.

PHP/PCRE does not apply this optimization by default, but it can with the use of PCRE’s pcre_study (in PHP, the S pattern modifier 478). Tcl, of course, can do it perfectly ( 243).

A behind-the-scenes check of [JFMASOND] by an engine’s native optimization is certainly faster than the same check explicitly added by us to the regex proper. Is there a way we can modify the regex so that the engine will check natively? Well, with many systems, you can by using the horribly contorted:

⌈[JFMASOND](?:(?<=J)an|(?<=F)eb|...|(?<=D)ec)⌋

I don’t expect you to be able to understand that regex at first sight, but taking the time to understand what it does, and how, is a good exercise. The simple class leading the expression can be picked up by most systems’ initial-character discrimination optimization, thereby allowing the transmission itself to effectively pre-check [JFMASOND]. If the target string has few matching characters, the result can be substantially faster than the ⌈Jan|...|Dec⌋ original, or our prepended-look-ahead. But, if the target string has many first-character matches, the extra overhead of all the added lookbehind can actually make things slower. On top of this worry, it’s certainly a much less readable regular expression. But, the exercise is interesting and instructive nevertheless.

Don’t do this with Tcl

The previous example shows how hand tweaking has the potential to really make things worse. The sidebar on page 243 notes that regular expressions in Tcl are mostly immune to the form of the expression, so for the most part attempts to hand optimize are meaningless. Well, here’s an example where it does matter. Adding the explicit ⌈( ?= [JFMASOND] )⌋ pre-check causes Tcl to slow down by a factor of about 100x in my tests.

Don’t do this with PHP

As mentioned earlier, this shouldn’t be done in PHP because you can enable the optimization with PHP’s “study” option, the S pattern modifier. Details are in Chapter 10, starting on page 478.

Use Atomic Grouping and Possessive Quantifiers

There are many cases when atomic grouping ( 139) and possessive quantifiers ( 142) can greatly increase the match speed, even though they don’t change the kind of matches that are possible. For example, if ⌈^[^ : ] + :⌋ can’t match the first time the colon is attempted, it certainly can’t match after backtracking back into the ⌈[^ : ] +⌋, since any character “given up” by that backtracking, by definition, can’t match a colon. The use of atomic grouping ⌈^(?>[^:]+):⌋ or a possessive quantifier ⌈^[^:]++:⌋ causes the states from the plus to be thrown away, or not created in the first place. Since this leaves nothing for the engine to backtrack to, it ensures that it doesn’t backtrack unfruitfully. (The sidebar on page 251 suggests that this can be done automatically by a smart enough engine.)

However, I must stress that misusing either of these constructs can inadvertently change what kind of matches are allowed, so great care must be taken. For example, using them with ⌈^.*:⌋, as with ⌈^(?>.*):⌋, guarantees failure. The entire line is matched by ⌈. *⌋, and this includes any colon that the later ⌈:⌋ needs. The atomic grouping removes the ability for the backtracking required to let ⌈:⌋ match, so failure is guaranteed.

Lead the Engine to a Match

One concept that goes a long way toward more efficient NFA regular expressions is pushing “control” issues as far back in the matching process as possible. One example we’ve seen already is the use of ⌈th(?:is|at)⌋ instead of ⌈this|that⌋. With the latter, the alternation is a top-level control issue, but with the former, the relatively expensive alternation is not considered until ⌈th⌋ has been matched.

The next section, “Unrolling the Loop,” is an advanced form of this, but there are a few simple techniques I can mention here.

Put the most likely alternative first

Throughout the book, we’ve seen a number of situations where the order in which alternatives are presented matters greatly ( 28, 176, 189, 216). In such situations, the correctness of the match take precedence over optimization, but otherwise, if the order doesn’t matter to the correctness, you can gain some efficiency by placing the most-likely alternatives first.

For example, when building a regex to match a hostname ( 205) and listing the final domain parts, some might find it appealing to list them in alphabetical order, as with ⌈(? :aero|biz|com|coop| ···)⌋. However, some of those early in the list are new and not currently popular, so why waste the time to check for them first when you know they will likely fail most of the time? An arrangement with the more popular first, such as ⌈(?:com|edu|org|net| ···)⌋, is likely to lead to a match more quickly, more often.

Of course, this matters only for a Traditional NFA engine, and then, only for when there is a match. With a POSIX NFA, or with a failure, all alternatives must be checked and so the ordering doesn’t matter.

Distribute into the end of alternation

Continuing with a convenient example, compare ⌈(?:com|edu|...| [a-z] [a-z])\b⌋ with ⌈com\b|edu\b|[a-z] [a-z] \b⌋. In the latter, the ⌈\b⌋ after the alternation has been distributed onto the end of each alternative. The possible benefit is that it may allow an alternative that matches, but whose match would have been undone by the ⌈\b⌋ after the alternation, to fail a bit quicker, inside the alternation. This allows the failure to be recognized before the overhead of exiting the alternation is needed.

This is perhaps not the best example to show the value of this technique, since it shows promise only for the specific situation when an alternative is likely to match, but what comes right after is likely to fail. We’ll see a better example of this concept later in this chapter—look for the discussion of $OTHER* on page 280.

This optimization can be dangerous.

One very important concern in applying this hand optimization is that you take care not to defeat more profitable native optimizations. For example, if the “distributed” subexpression is literal text, as with the distribution of the colon from ⌈(?:this|that):)⌋ to ⌈this:|that:⌋, you’re directly conflicting with some of the ideas in the “Expose Literal Text” section ( 255). All things being equal, I think that those optimizations would be much more fruitful, so be careful not to defeat them in favor of this one.

A similar warning applies to distributing a regex-ending ⌈$⌋ on systems that benefit from an exposed end-anchor ( 256). On such systems, ⌈(?:com|edu|...)$⌋ is much faster than the distributed ⌈com$|edu$|...)$⌋. (Among the many systems I tested, only Perl currently supports this.)

Unrolling the Loop

Regardless of what native optimizations a system may support, perhaps the most important gains are to be had by understanding the basics of how the engine works, and writing expressions that help lead the engine to a match. So, now that we’ve reviewed the basics in excruciating detail, let’s step up to the big leagues with a technique I call “unrolling the loop.” It’s effective for speeding up certain common expressions. Using it, for example, to transform the neverending match from near the start of this chapter ( 226) results in an expression that actually finishes a non-match in our lifetime, and as a bonus is faster with a match as well.

The “loop” in the name is the implicit loop imparted by the star in an expression that fits a ⌈(this|that|...)*⌋ pattern. Indeed, our earlier ⌈" (\\. | [^\\"] + ) * "⌋ neverending match fits this pattern. Considering that it takes approximately forever to report a non-match, it’s a good example to try to speed up!

There are two competing roads one can take to arrive at this technique:

1. We can examine which parts of ⌈(\\.|[&\\" ]+)*⌋, actually succeed during a variety of sample matches, leaving a trail of used subexpressions in its wake. We can then reconstruct an efficient expression based upon the patterns we see emerge. The (perhaps far-fetched) mental image I have is that of a big ball, representing a ⌈(···) *⌋ regex, being rolled over some text. The parts inside (...) that are actually used then stick to the text they match, leaving a trail of subexpressions behind like a dirty ball rolling across the carpet.
2. Another approach takes a higher-level look at the construct we want to match. We’ll make an informed assumption about the likely target strings, allowing us to take advantage of what we believe will be the common situation. Using this point of view, we can construct an efficient expression.

Either way, the resulting expressions are identical. I’ll begin from the “unrolling” point of view, and then converge on the same result from the higher-level view.

To keep the examples as uncluttered and as widely usable as possible, I’ll use ⌈(...)⌋ for all parentheses. If ⌈(?:···)⌋ non-capturing parentheses are supported, their use imparts a further efficiency benefit. Later, we’ll also look at using atomic grouping ( 139) and possessive quantifiers ( 142).

Method 1: Building a Regex From Past Experiences

In analyzing ⌈"(\\.|[^\\"]+)*"⌋, it’s instructive to look at some matching strings to see exactly which subexpressions are used during the overall match. For example, with '"hi"', the expression effectively used is just ⌈"[^\\"]+ "⌋. This illustrates that the overall match used the initial ⌈"⌋, one application of the alternative ⌈[^\\"] + ⌋, and the closing ⌈"⌋. With

"he said \'hi there\' and left"

it is 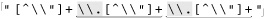. In this example, as well as in Table 6-2, I’ve marked the expressions to make the patterns apparent. It would be nice if we could construct a specific regex for each particular input string. That’s not possible, but we can still identify common patterns to construct a more efficient, yet still general, regular expression.

For the moment, let’s concentrate on the first four examples in Table 6-2. I’ve underlined the portions that refer to “an escaped item, followed by further normal characters.” This is the key point: in each case, the expression between the quotes begins with ⌈[^\\"]+⌋ and is followed by some number of 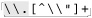sequences. Rephrasing this as a regular expression, we get . This is a specific example of a general pattern that can be used for constructing many useful expressions.

Table 6-2: Unrolling-the-Loop Example Cases

Target String	Effective Expression
"hi there"	"[^\\"]+"
"just one \" here"
"some \"quoted\" things"
"with \"a\" and \"b\"."
"\"ok\"\n"
"empty \"\"

Constructing a general “unrolling-the-loop” pattern

In matching the double-quoted string, the quote itself and the escape are “special” — the quote because it can end the string, and the escape because it means that whatever follows won’t end the string. Everything else, ⌈[^\\"]"⌋, is “normal.” Looking at how these were combined to create , we can see that it fits the general pattern .

Adding in the opening and closing quote, we get . Unfortunately, this won’t match the last two examples in Table 6-2. The problem, essentially, is that our current expression’s two ⌈[^ \ \"] +⌋ require a normal character at the start of the string and after any special character. As the examples show, that’s not always appropriate — the string might start or end with an escaped item, or there might be two escaped items in a row.

We could try changing the two pluses to stars: . Does this have the desired effect? More importantly, does it have any undesirable effects?

As far as desirable effects, it is easy to see that all the examples now match. In fact, even a string such as " \ " \" \"" now matches. This is good. However, we can’t make such a major change without being quite sure there are no undesirable effects. Could anything other than a legal double-quoted string match? Can a legal double-quoted string not match? What about efficiency?

Let’s look at 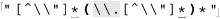carefully. The leading⌈"[^\\"]*⌋ is applied only once and doesn’t seem dangerous: it matches the required opening quote and any normal characters that might follow. No danger there. The subsequent ⌈(\\. [^\\"]*)*⌋ is wrapped by (···)*, so is allowed to match zero times. That means that removing it should still leave a valid expression. Doing so, we get ⌈⌈"[^\\"]*"⌋, which is certainly fine — it represents the common situation where there are no escaped items.

On the other hand, if 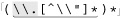matches once, we have an effective . Even if the trailing ⌈[^\\"]*⌋ matches nothing (making it an effective 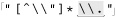, there are no problems. Continuing the analysis in a similar way (if I can remember my high school algebra, it’s “by induction”), we find that there are, indeed, no problems with the proposed changes.

So, that leaves us with the final expression to match a double-quoted string with escaped double quotes inside:

The Real “Unrolling-the-Loop” Pattern

Putting it all together, then, our expression to match a double-quoted string with escaped-items is . This matches and fails on exactly the same strings as the alternation version, but this unrolled version has the benefit of finishing in our lifetime. It is much more efficient, and avoids the neverending- match problem altogether.

The general pattern for unrolling the loop is:

⌈opening normal * (special normal * ) * closing⌋

Avoiding the neverending match

Three extremely important points prevent from becoming a neverending match:

1) The start of special and normal must never intersect.

The special and normal subexpressions must be written such that they can never match at the same point. With our ongoing example, where normal is ⌈[^\\"]⌋ and special is ⌈\\.⌋, it’s clear that they can never begin a match at the same character since the latter one requires a leading backslash, while the former one explicitly disallows a leading backslash.

On the other hand, ⌈\\.⌋ and ⌈[^"]⌋ can both match starting at 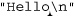, so they are inappropriate as special or normal. If there is a way they can match starting at the same location, it’s not clear which should be used at such a point, and the non-determinism creates a neverending match. The ‘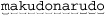’ example illustrates this graphically ( 227). A failing match (or any kind of match attempt with POSIX NFA engines) has to test all these possibilities and permutations. That’s too bad, since the whole reason to re-engineer in the first place was to avoid this.

If we ensure that special and normal can never match at the same point, special acts to checkpoint the nondeterminism that would arise when multiple applications of normal could, by different iterations of the ⌈(···)*⌋ loop, match the same text. If we ensure that special and normal can never match at the same point, there is exactly one “sequence” of specials and normals in which a particular target string matches. Testing this one sequence is much faster than testing a hundred million of them, and thus a neverending match is avoided.

2) Special must not match nothingness.

The second point is that special must always match at least one character if it matches anything at all. If it were able to match without consuming characters, adjacent normal characters would be able to be matched by different iterations of ⌈( special normal * ) *⌋, bringing us right back to the basic (...*)* problem.

For example, choosing a special of ⌈(\\.)*⌋ violates this point. In trying to match the ill-fated 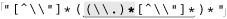against '"Tubby' (which fails), the engine must try every permutation of how multiple ⌈[^\\"] *⌋ might match 'Tubby' before concluding that the match is a failure. Since special can match nothingness, it doesn’t act as the checkpoint it purports to be.

3) Special must be atomic.

Text matched by one application of special must not be able to be matched by multiple applications of special. Consider matching a string of optional Pascal {···} comments and spaces. A regex to match the comment part is ⌈\{[^}]*\}⌋, so the whole (neverending) expression becomes ⌈(\{[^}]*\}|• +) *⌋. With this regex, you might consider special and normal to be:

special	normal
⌈•+⌋	⌈\{[^}]*\}⌋

Plugging this into the 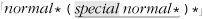pattern we’ve developed, we get: . Now, let’s look at a string:

{comment}•••{another}••

A sequence of multiple spaces could be matched by a single ⌈•+⌋, by many ⌈•+⌋ (each matching a single space), or by various combinations of ⌈•+⌋ matching differing numbers of spaces. This is directly analogous to our 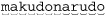problem.

The root of the problem is that special is able to match a smaller amount of text within a larger amount that it could also match, and is able to do so multiple times thanks to (···)*. The nondeterminism opens up the “many ways to match the same text” can of worms.

If there is an overall match, it is likely that only the all-at-once ⌈•+⌋ will happen just once, but if no match is possible (such as might happen if this is used as a subexpression of a larger regex that could possibly fail), the engine must work through each permutation of the effective ⌈(•+)*⌋ to each series of multiple spaces. That takes time, but without any hope for a match. Since special is supposed to act as the checkpoint, there is nothing to check its nondeterminism in this situation.

The solution is to ensure that special can match only a fixed number of spaces. Since it must match at least one, but could match more, we simply choose ⌈•⌋ and let multiple applications of special match multiple spaces via the enclosing ⌈(···) *⌋. This example is useful for discussion, but in real-life use, it’s probably more efficient to swap the normal and special expressions to come up with

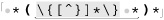
because I would suspect that a Pascal program has more spaces than comments, and it’s more efficient to have normal be the most common case.

General things to look out for

Once you internalize these rules (which might take several readings and some practical experience), you can generalize them into guidelines to help identify regular expressions susceptible to a neverending match. Having multiple levels of quantifiers, such as ⌈(···*) *⌋, is an important warning sign, but many such expressions are perfectly valid. Examples include:

• ⌈(Re:•*) *⌋, to match any number of 'Re:' sequences (such as might be used to clean up a 'Subject:•Re:•Re:•Re:•hey' subject line).
• ⌈(• *\$[0-9]+) *⌋, to match dollar amounts, possibly space-separated.
• ⌈(. * \n)+⌋, to match one or more lines. (Actually, if dot can match a newline, and if there is anything following this subexpression that could cause it to fail, this would become a quintessential neverending match.)

These are OK because each has something to checkpoint the match, keeping a lid on the “many ways to match the same text” can of worms. In the first, it’s ⌈Re:⌋, in the second it’s ⌈\$⌋, and in the third (when dot doesn’t match newline), it’s ⌈\n⌋.

Method 2: A Top-Down View

Recall that I said that there were two paths to the same “unrolling the loop” expression. In this second path, we start by matching only what’s most common in the target, then adding what’s needed to handle the rare cases. Let’s consider what the neverending ⌈( \\. |[^\\"]+)* ⌋, attempts to accomplish and where it will likely be used. Normally, I would think, a quoted string would have more regular characters than escaped items, so ⌈[^\\"]+⌋ does the bulk of the work. The ⌈\\.⌋ is needed only to handle the occasional escaped item. Using alternation to allow either works, but it’s too bad that we need to compromise the efficiency of the whole match for the sake of a few (or more commonly, no) escaped characters.

If we think that ⌈[^\\"]+⌋ will normally match most of the body of the string, we know that once it finishes we can expect either the closing quote or an escaped item. If we have an escape, we want to allow one more character (whatever it might be), and then match more of the bulk with another ⌈[^\\"]+⌋. Every time ⌈[^\\"]+⌋ ends, we are in the same position we were before: expecting either the closing quote or another escape.

Expressing this naturally as a single expression, we arrive at the same expression we had early in Method 1:

Each time the matching reaches the point marked by , we know that we’re expecting either a backslash or a closing quote. If the backslash can match, we take it, the character that follows, and more text until the next “expecting a quote or backslash” point.

As in the previous method, we need to allow for when the initial non-quote segment, or inter-quote segments, are empty. We can do this by changing the two pluses to stars, which results in the same expression as we ended up with on page 264.

Method 3: An Internet Hostname

I promised two methods to arrive at the unrolling-the-loop technique, but I’d like to present something that can be considered a third. It struck me while working with a regex to match a hostname such as www.yahoo.com. A hostname is essentially dot-separated lists of subdomain names, and exactly what’s allowed for one subdomain name is fairly complex to match ( 203), so to keep this example less cluttered, we’ll just use ⌈[a-z]+⌋ to match a subdomain.

If a subdomain is ⌈[a-z]+⌋ and we want a dot-separated list of them, we need to match one subdomain first. After that, further subdomains require a leading period. Expressing this literally, we get: ⌈[a-z]+(\.[a-z]+)*⌋. Now, if I add an underline and some gray, , it sure looks like it almost fits a very familiar pattern, doesn’t it!

To illustrate the similarity, let’s try to map this to our double-quoted string example. If we consider a string to be sequences of our normal ⌈[^\\"]⌋, separated by special ⌈\ \.⌋, all within '"···"', we can plug them into our unrolling-the-loop pattern to form , which is exactly what we had at one point while discussing Method 1. This means that conceptually, we can take the view we used with a hostname — stuff separated by separators — and apply it to double-quoted strings, to give us “sequences of non-escaped stuff separated by escaped items.” This might not seem intuitive, but it yields an interesting path to what we’ve already seen.

The similarity is interesting, but so are the differences. With Method 1, we went on to change the regex to allow empty spans of normal before and after each special, but we don’t want to do that here because a subdomain part cannot be empty. So, even though this example isn’t exactly the same as the previous ones, it’s in the same class, showing that the unrolling technique is powerful and flexible.

There are two differences between this and the subdomain example:

• Domain names don’t have delimiters at their start and end.
• The normal part of a subdomain can never be empty (meaning two periods are not allowed in a row, and can neither start nor end the match). With a double-quoted string, there is no requirement that there be any normal parts at all, even though they are likely, given our assumptions about the data. That’s why we were able to change the 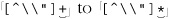. We can’t do that with the subdomain example because special represents a separator, which is required.

Observations

Recapping the double-quoted string example, I see many benefits to our expression, ⌈"[^\\"]*(\\.[^\\"]*)* "⌋, and few pitfalls.

Pitfalls:

• Readability The biggest pitfall is that the original ⌈"([^\\"]|\\.)*"⌋ is probably easier to understand at first glance. We’ve traded a bit of readability for efficiency.
• Maintainability Maintaining 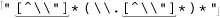might be more difficult, since the two copies of ⌈[^\\"]⌋ must be kept identical across any changes. We’ve traded a bit of maintainability for efficiency.

Benefits:

• Speed The new regex doesn’t buckle under when no match is possible, or when used with a POSIX NFA. By carefully crafting the expression to allow only one way for any particular span of text to be matched, the engine quickly comes to the conclusion that non-matching text indeed does not match.
• More speed The regex “flows” well, a subject taken up in “The Freeflowing Regex” ( 277). In my benchmarks with a Traditional NFA, the unrolled version is consistently faster than the old alternation version. This is true even for successful matches, where the old version did not suffer the lockup problem.

Using Atomic Grouping and Possessive Quantifiers

The problem with our original neverending match regex, ⌈"(\\.|[^\\"]+ )*"⌋, is that it bogs down when there is no match. When there is a match, though, it’s quite fast. It’s quick to find the match because the ⌈[^\\"]+⌋ component is what matches most of the target string (the normal in the previous discussion). Because ⌈[···]+⌋ is usually optimized for speed ( 247), and because this one component handles most of the characters, the overhead of the alternation and the outer ⌈(···) *⌋ quantifier is greatly reduced.

So, the problem with ⌈"(\\.|[^\\"]+ )*"⌋, is that it bogs down on a non-match, backtracking over and over to what we know will always be unfruitful states. We know they’re unfruitful because they’re just testing different permutations of the same thing. (If ⌈abc⌋ doesn’t match 'foo', neither will ⌈abc⌋ or ⌈abc⌋ (or ⌈abc⌋, ⌈abc⌋, or ⌈abc⌋, for that matter). So, if we could throw those states away, this regex would report the non-match quickly.

There are two ways to actually throw away (or otherwise ignore) states: atomic grouping ( 139) and possessive quantifiers ( 142).

Before I get into the elimination of the backtracking, I’d like to swap the order of the alternatives from ⌈"(\\.[^\\"]+)*"⌋ to ⌈"([^\\"]+|\\.)*"⌋, as this places the component matching “normal” text first. As has been noted a few times in the last several chapters, when two or more alternatives can potentially match at the same location, care must be taken when selecting their order, as that order can influence what exactly is matched. But if, as in this case, all alternatives are mutually exclusive (none can match at a point where another can match), the order doesn’t matter from a correctness point of view, so the order can be chosen for clarity or efficiency.

Making a neverending match safe with possessive quantifiers

Our neverending regex ⌈"([^\\"]+|\\.)*"⌋ has two quantifiers. We can make one possessive, the other possessive, or both possessive. Does it matter? Well, most of the backtracking troubles were due to the states left by the⌈[...]+⌋, so making that possessive is my first thought. Doing so yields a regex that’s pretty fast, even when there’s no match. However, making the outer ⌈(···) *⌋ possessive throws away all the states from inside the parentheses, which includes both those of ⌈[···]+⌋ and of the alternation, so if I had to pick one, I’d pick that one.

But I don’t have to pick one because I can make both possessive. Which of the three situations is fastest probably depends a lot on how optimized possessive quantifiers are. Currently, they are supported only by Sun’s Java regex package, so my testing has been limited, but I’ve run all three combinations through tests with it, and found examples where one combination or the other is faster. I would expect the situation where both are possessive could be the fastest, so these results tend to make me believe that Sun hasn’t yet optimized them to their fullest.

Making a neverending match safe with atomic grouping

Looking to add atomic grouping to ⌈"([^\\"]+|\\.)*"⌋, it’s tempting to replace the normal parentheses with atomic ones: ⌈" (?>[^\\"]+ | \\. )* "⌋. It’s important to realize that ⌈(?> ···|···)*]⌋ is very different from the possessive ⌈((···|···)*+⌋ in the previous section when it comes to the states that are thrown away.

The possessive ⌈(··· | ···) * +⌋ leaves no states when it’s done. On the other hand, the atomic grouping in ⌈(?>···|···)*⌋ merely eliminates any states left by each alternative, and by the alternation itself. The star is outside the atomic grouping, so is unaffected by it and still leaves all its “can try skipping this match” states. That means that the individual matches can still be undone via backtracking. We want to eliminate the outer quantifier’s states as well, so we need an outer set of atomic grouping. That’s why ⌈(?> (··· | ···)*)⌋ is needed to mimic the possessive ⌈(··· | ···) *+⌋.

⌈((···|···)*+]⌋ and ⌈(?>···|···)*⌋ are both certainly helpful in solving the neverending match, but which states are thrown away, and when, are different. (For more on the difference between the two, see page 173.)

Short Unrolling Examples

Now that we’ve got the basic idea of unrolling under our belt, let’s look at some examples from earlier in the book, and see how unrolling applies to them.

Unrolling “multi-character” quotes

In Chapter 4 on page 167, we saw this example:

<B>                    #  Match the opening <B>
(                      #  Now, as many of the following as possible . . .
   (?! < /? B>   )     #     If not <B>, and not </B> . . .
   .                   #          . . . any character is okay
)+                     # (now greedy)
</B>                   # <ANNO> . . . until the closing delimiter can match.

With a normal of ⌈[^<]⌋ ! “and a special of ⌈(?!</?B>)<"⌋, here’s the unrolled version:

<B>                 #  Match the opening <B>
  (?> [^<]*   )     #  Now match any "normal" . . .
  (?>               #  Any amount of . . .
      (?! < /?B>  ) #     if not at <B> or </B>,
      <             #     match one "special"
      [^<]*         #     and then any amount of "normal"
   )*               #
</B>                #  And finally the closing </B>

The use of atomic grouping is not required, but does make the expression faster when there’s only a partial match.

Unrolling the continuation-line example

The continuation-line example from the start of the previous chapter ( 186) left off with ⌈^ \w+ = ([^ \n \ \ ] | \ \ . ) *⌋. Well, that certainly looks ripe for unrolling:

^  \w+ =                     #  leading field name and '='
#  Now read (and capture) the value . . .
(
    (?> [^\n\\]+   )         #  "normal"*
    (?> \\. [^\n\\]+   )+    #  ( "special" "normal"* )*
)

As with earlier examples of unrolling, the atomic grouping is not required for this to work, but helps to allow the engine to announce a failure more quickly.

Unrolling the CSV regex

Chapter 5 has a long discussion of CSV processing, which finally worked its way to this snippet, from page 216:

(?:^|,)
(?: # Now, match either a double-quoted field (inside, paired double quotes are allowed) . . .
        "  #  (double-quoted field's opening quote)
         (     (?: [^"]  ;  "" )*        )
        "  # (double-quoted field's closing quote)
  |
    #   . . . or, some non-quote/non-comma text . . .
            (  [^",]* )
)

The text then went on to suggest adding ⌈\G⌋ to the front, just to be sure that the bump-along didn’t get us in trouble as it had throughout the example, and some other efficiency suggestions. Now that we know about unrolling, let’s see where in this example we can apply it.

Well, the part to match a Microsoft CSV string, ⌈( ?: [^"] |"" ) *⌋, certainly looks inviting. In fact, the way it’s presented already has our normal and special picked out for us: ⌈[^"]⌋ and ⌈""⌋. Here’s how it looks with that part unrolled, plugged back into the original Perl snippet to process each field:

while ($line =^~ m{
          \G(?:^|,)
          (?:
             #  Either a double-quoted field (with "" for each ")···
             "  #  field's opening quote
              (  (?> [^"], ) (?> "" [^"]*  )*   )
             "  #  field's closing quote
          #  ..or···
          |
             #  ···  some non-quote/non-comma text....
             (  [^",]*  )
         )
     }gx)
{
  if (defined $2) {
      $field = $2;
  } else {
      $field = $1;
      $field =^~ s/""/"/g;
  }
  print "[$field]"; # print the field, for debugging
  Can work with $field now . . .
}

As with the other examples, the atomic grouping is not required, but may help with efficiency.

Unrolling C Comments

I’d like to give an example of unrolling the loop with a somewhat more complex target. In the C language, comments begin with /*, end with */, and can span across lines, but can’t be nested. (C++, Java, and C# also allow this type of comment.) An expression to match such a comment might be useful in a variety of situations, such as in constructing a filter to remove them. It was when working on this problem that I first came up with my unrolling technique, and the technique has since become a staple in my regex arsenal.

To unroll or to not unroll...

I originally developed the regex that is the subject of this section back in the early 1990s. Prior to that, matching C comments with a regular expression was considered difficult at best, if not impossible, so when I developed something that worked, it became the standard way to match C comments. But, when Perl introduced lazy quantifiers, a much simpler approach became evident: a dot-matches-all application of ⌈/\*.*?\*/⌋.

Had lazy quantifiers been around when I first developed the unrolling technique, I might not have bothered to do so, for the need wouldn’t have been so apparent. Yet, such a solution was still valuable because with that first version of Perl supporting lazy quantifiers, the unrolled version is faster than the lazy-quantifier version by a significant amount (in the variety of tests I’ve done, anywhere from about 50 percent faster, to 3.6× faster).

Yet, with today’s Perl and its different mix of optimizations, those numbers go the other way, with the lazy-quantifier version running anywhere from about 50 percent faster to 5.5× faster. So, with modern versions of Perl, I’d just use ⌈/\*.*?\*/⌋ to match C comments and be done with it.

Does this mean that the unrolling-the-loop technique is no longer useful for matching C comments? Well, if an engine doesn’t support lazy quantifiers, the ability to use the unrolling technique certainly becomes appealing. And not all regex engines have the same mix of optimizations: the unrolling technique is faster with every other language I’ve tested—in my tests, up to 60 times faster! The unrolling technique is definitely useful, so the remainder of this example explores how to apply it to matching C comments.

Since there are no escapes to be recognized within a C comment the way \" must be recognized within a double-quoted string, one might think that this should make things simpler, but actually, it’s much more complex. This is because */, the “ending quote,” is more than one character long. The simple ⌈/\* [^ *] * \ * /⌋ might look good, but that doesn’t match /** some comment here **/ because it has a '*' within. It should be matched, so we need a new approach.

Avoiding regex headaches

You might find that ⌈/ \ * [^ * ] * \ * /⌋ is a bit difficult to read, even with the subtle easy-on-the-eyes spacing I’ve used in typesetting this book. It is unfortunate for our eyes that one of the comment’s delimiting characters, '*', is also a regex metacharacter. The resulting backslashes are enough to give me a headache. To make things more readable during this example, we’ll consider /x···x/, rather than /*···*/, to be our target comment. This superficial cosmetic change allows ⌈/\*[^*]*\*/"⌋ to be written as the more readable ⌈/x [^x]* x/"⌋. As we work through the example and the expression becomes more complex, our eyes will thank us for the reprieve.

A direct approach

In Chapter 5 ( 196), I gave a standard formula for matching delimited text:

1. Match the opening delimiter.
2. Match the main text: really “match anything that is not the ending delimiter.”
3. Match the ending delimiter.

Our pseudo comments, with /x and x/ as our opening and closing delimiters, appear to fit into this pattern. Our difficulties begin when we try to match “anything that is not the ending delimiter.” When the ending delimiter is a single character, we can use a negated character class to match all characters except that delimiter. A character class can’t be used for multi-character subexpressions, but if you have negative lookahead, you can use something like ⌈(?:(?!x/).)*⌋. This is essentially ⌈(anything not x/) +⌋.

Using that, we get ⌈/x(?:(?!x/).)*x/⌋ to match comments. It works perfectly well, but it can be quite slow (in some of my tests, hundreds of times slower than what we’ll develop later in this section). This approach can be useful, but it’s of little use in this particular case because any flavor that supports lookahead almost certainly supports lazy quantifiers, so if efficiency is not an issue, you can just use ⌈/x . * ? x/⌋ and be done with it.

So, continuing with the direct, three-step approach, is there another way to match until the first x/? Two ideas might come to mind. One method is to consider x to be the start of the ending delimiter. That means we’d match anything not x, and allow an x if it is followed by something other than a slash. This makes the “anything that is not the ending delimiter” one of:

• Anything that is not x: ⌈[^x]⌋
• x, so long as not followed by a slash: ⌈x[^/]⌋

This yields ⌈( [^x] | x [^ / ] )*⌋ to match the main text, and ⌈/x ([^ x] | x [^ / ] )* x/⌋ to match the entire pseudo comment. As we’ll see, this doesn’t work.

Another approach is to consider a slash as the ending delimiter, but only if preceded by x. This makes the “anything not the ending delimiter” one of:

• Anything that is not a slash: ⌈[^/]⌋
• A slash, so long as not preceded by x: ⌈[^x]/⌋

This yields ⌈( [^/ ] | [^x] / ) *⌋ to match the main text, and ⌈/x ([^/ ] | [^x] / ) * x/⌋ to match the whole comment.

Unfortunately, it also doesn’t work.

For ⌈/x([^x]| x[^/])* x/⌋, consider the text '/xx•foo•xx/'— after matching ‘foo•’, the first closing x is matched by 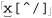which is fine. But then, 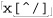matches 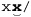, which is the x that should be ending the comment. This opens the door for the next iteration’s ⌈[^x]⌋ to match the slash, thereby errantly matching past the closing x/.

As for ⌈/x ( [^/] | [^x] / )* x/⌋, it can’t match '/x/.•foo•/x/' (the whole of which is a comment and should be matched). In other cases, it can march past the end of a comment that has a slash immediately after its end (in a way similar to the other method). In such a case, the backtracking involved is perhaps a bit confusing, so it should be instructive to understand why ⌈/x( [^/] | [^x]/ )* x/⌋ matches

as it does (an investigation I’ll leave for your free time).

Making it work

Let’s try to fix these regexes. With the first one, where ⌈x[^/]⌋ inadvertently matches the comment-ending , consider . The added plus will, we think, have ⌈x+ [^/]⌋ match a row of x's ending with something other than a slash. Indeed it will, but due to backtracking, that “something other than a slash” can still be x. At first, the greedy ⌈x+⌋ matches that extra x as we want, but backtracking will reclaim an x if needed to secure an overall match. So, it still matches too much of:

The solution comes back to something I’ve said before: say what you mean. If we want “some x, if not followed by a slash” to imply that the non-slash also doesn’t include an x, we should write exactly that: 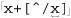. As we want, this stops it from eating ‘’, the final x of a row of x that ends the comment. In fact, it has the added effect of not matching any comment-ending x, so it leaves us at ‘’ to match the ending delimiter. Since the ending delimiter part had been expecting just the one x, it won’t match until we insert 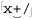to allow this final case.

This leaves us with: ⌈x ( [^x] | x+[^/x]) * x+/⌋ to match our pseudo comments.

Phew!   Somewhat confusing, isn’t it? Real comments (with * instead of x) require ⌈/ \ * ([^ * ] | \ * + [^ / * ]) * \ * + /⌋, which is even more confusing. It’s not easy to read; just remember to keep your wits about you as you carefully parse complex expressions in your mind.

Unrolling the C loop

For efficiency’s sake, let’s look at unrolling this regex. Table 6-3 on the next page shows the expressions we can plug in to our unrolling-the-loop pattern.

Like the subdomain example, the ⌈normal*⌋ is not actually free to match nothingness. With subdomains, it was because the normal part was not allowed to be empty. In this case, it’s due to how we handle the two-character ending delimiter. We ensure that any normal sequence ends with the first character of the ending delimiter, allowing special to pick up the ball only if the following character does not complete the ending.

Table 6-3: Unrolling-the-Loop Components for C Comments

Item	What We Want	Regex
opening	start of comment	/x
normal*	comment text up to, and including, one or more 'x'	[^x]*x+
special	something other than the ending slash (and also not 'x')	[^/x]
closing	trailing slash	/

So, plugging these in to the general unrolling pattern, we get:

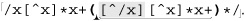
Notice the spot marked with ? The regex engine might work to that spot in two ways (just like the expression on page 267). The first is by progressing to it after the leading ⌈x[^x]*x+⌋. The second is by looping due to the (···)*. Via either path, once we’re at that spot we know we’ve matched x and are at a pivotal point, possibly on the brink of the comment’s end. If the next character is a slash, we’re done. If it’s anything else (but an x, of course), we know the x was a false alarm and we’re back to matching normal stuff, again waiting for the next x. Once we find it, we’re right back on the brink of excitement at the marked spot.

Return to reality

⌈/x[^x]*x+([^/x][^x]*x+)*/⌋ is not quite ready to be used. First, of course, comments are /*···*/ and not /x···x/. This is easily fixed by substituting each x with \* (or, within character classes, each x with *):

⌈/\ * [^ * ] * \ * + ([^/ * ][^ * ] * \ * +) * /⌋

A use-related issue is that comments often span across lines. If the text being matched contains the entire multiline comment, this expression should work. With a strictly line-oriented tool such as egrep, though, there is no way to apply a regex to the full comment. With most utilities mentioned in this book, you can, and this expression might be useful for, say, removing comments.

In practical use, a larger problem arises. This regex understands C comments, but does not understand other important aspects of C syntax. For example, it can falsely match where there is no comment:

We’ll develop this example further, right in the next section.

The Freeflowing Regex

We just spent some time constructing a regex to match a C comment, but left off with the problem of how to stop comment-like items within strings from being matched. Using Perl, we might mistakenly try to remove comments with:

$prog =^~ s{/ \ * [ ^ * ] * \ * + ( ? : [ ^ / * ] [ ^ * ] * \ * + ) * /} { } g ; # remove C comments (and more!)

Text in the variable $prog that is matched by our regex is removed (that is, replaced by nothing). The problem with this is that there’s nothing to stop a match from starting within a string, as in this C snippet:

Here, the underlined portions are what the regex finds, but the bold portions are what we wish to be found. When the engine is searching for a match, it tries to match the expression at each point in the target. Since it is successful only from where a comment begins (or where it looks like one begins), it doesn’t match at most locations, so the transmission bump-along bumps us right into the double-quoted string, whose contents look like the start of a comment. It would be nice if we could tell the regex engine that when it hits a double-quoted string, it should zip right on past it. Well, we can.

A Helping Hand to Guide the Match

Consider:

$COMMENT =  qr{/\+ [^+]+ \++(?:[^/+][^+]+\++)+/};  #  regex to match a comment
$DOUBLE =  qr{"(?:\\.;[^\\"])+"};                  #  regex to match double-quoted string
$text =^~  s/$DOUBLE;$COMMENT//g;

There are two new things here. One is that this time the regex operand, $DOUBLE | $COMMENT, is made up of two variables, each of which is constructed with Perl’s special qr/···/ regex-style “double-quoted string” operator. As discussed at length in Chapter 3 ( 101), one must be careful when using strings that are meant to be interpreted as regular expressions. Perl alleviates this problem by providing the qr/···/ operator, which treats its operand as a regular expression, but doesn’t actually apply it. Rather, it returns a “regex object” value that can later be used to build up a larger regular expression. It’s extremely convenient, as we saw briefly in Chapter 2 (76). Like m/··· / and s/··· /···/, you can pick delimiters to suit your needs ( 71), as we’ve done here using braces.

The other new thing here is the matching of double-quoted strings via the $DOUBLE portion. When the transmission has brought us to a position where the $DOUBLE part can match, it will do so, thereby bypassing the whole string in one fell swoop. It is possible to have both alternatives because they are entirely unambiguous with respect to each other. When applied to a string, as you read from the beginning, any point in the text that you start at is:

• Matchable by the comment part, thereby skipping immediately to the end of the comment, or...
• Matchable by the double-quoted string part, thereby skipping immediately to the end of the string, or...
• Not matchable by either, causing the attempt to fail. This means that the normal bump-along will skip only the one, uninteresting character.

This way, the regex will never be started from within a string or comment, the key to its success. Well, actually, right now it isn’t helpful yet, since it removes the strings as well as the comments, but a slight change puts us back on track.

Consider:

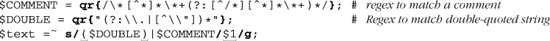
The only differences are that we’ve:

• Added the parentheses to fill $1 if the match is via the string alternative. If the match is via the comment alternative, $1 is left empty.
• Made the replacement value that same $1. The effect is that if a double-quoted string is matched, the replacement is that same double-quoted string — the string is not removed and the substitute becomes an effective no-op (but has the side effect of getting us past the string, which is the reason to add it in the first place). On the other hand, if the comment alternative is the one that matches, the $1 is empty, so the comment is replaced by nothingness just as we want.^†

Finally, we need to take care of single-quoted C constants such as '\t' and the like. This is easy—we simply add another alternative inside the parentheses. If we would like to remove C++/Java/C# style // comments too, that’s as simple as adding ⌈//[^\n]*⌋ as a fourth alternative, outside the parentheses:

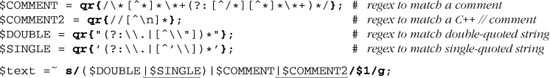
The basic premise is quite slick: when the engine checks the text, it quickly grabs (and if appropriate, removes) these special constructs. On my old (circa 1997!) system, this Perl snippet took about 16.4 seconds to remove all the comments from a 16-megabyte, 500,000-line test file. That’s fast, but we’ll speed it up considerably.

A Well-Guided Regex is a Fast Regex

With just a little hand holding, we can help direct the flow of the regex engine’s attention to match much faster. Let’s consider the long spans of normal C code between the comments and strings. For each such character, the regex engine has to try each of the four alternatives to see whether it’s something that should be gobbled up, and only if all four fail does it bump-along to bypass the character as uninteresting. This is a lot of work that we really don’t need to do.

We know, for example, that for any of the alternatives to have a chance at matching, the lead character must be a slash, a single quote, or a double quote. One of these doesn’t guarantee a match, but not being one does guarantee a non-match. So, rather than letting the engine figure this out the slow and painful way, let’s just tell it directly by adding ⌈[^'" / ]⌋ as an alternative. In fact, any number of such characters in a row can be scooped right up, so let’s use ⌈[^ '"/]+⌋ instead. If you remember the neverending match, you might feel worried about the added plus. Indeed, it could be of great concern if it were within some kind of (···) * loop, but in this stand-alone case it’s quite fine (there’s nothing that follows that could force it to backtrack at all). So, adding:

For reasons that will become apparent after a bit, I’ve put the plus quantifier after $OTHER, rather than part of the contents of $OTHER.

So, I retry my benchmarks, and wow, this one change cuts the time by over 75 percent! We’ve crafted the regex to remove most of the overhead of having to try all the alternatives so often. There are still a few cases where none of the alternatives can match (such as at 'c / 3.14'), and at such times, we’ll have to be content with the bump-along to get us by.

However, we’re not done yet—we can still help the engine flow to a faster match:

• In most cases, the most popular alternative will be ⌈$OTHER⌋, so let’s put that first inside the parentheses. This isn’t an issue for a POSIX NFA engine because it must always check all alternatives anyway, but for a Traditional NFA, which stops once a match has been found, why make it check for relatively rare matches before checking the one we believe will match most often?
• After one of the quoted items matches, it will likely be followed by some $OTHER before another string or a comment is found. If we add ⌈$OTHER*⌋ after each item, we tell the engine that it can immediately flow right into matching $OTHER without bothering with the /g looping.

  This is similar to the unrolling-the-loop technique, which gains much of its speed from the way it leads the regex engine to a match. We use our global knowledge to create the local optimizations that feed the engine just what it needs to work quickly.

  Note that it is very important that this $OTHER, added after each string-matching subexpression, be quantified with star, while the previous $OTHER (the one we moved to the head of the alternation) be quantified by plus. If it’s not clear why, consider what could happen if the appended $OTHER had plus and there were, say, two double-quoted strings right in a row. Also, if the leading $OTHER used star, it would always match!

These changes yield

as the regex, and further cuts the time by an additional five percent.

Let’s step back and think about these last two changes. If we go to the trouble of scooping up $OTHER* after each quoted string, there are only two situations in which the original $OTHER+ (which we moved to be the first alternative) can match: 1) at the very start of the whole s/···/···/g, before any of the quoted strings get a chance to match, and 2) after any comment.

You might be tempted to think “Hey, to take care of point #2, let’s just add $OTHER* after the comments as well!” This would be nice, except everything we want to keep must be inside that first set of parentheses — putting it after the comments would throw out the baby code with the comment bathwater.

So, if the original $OTHER+ is useful primarily only after a comment, do we really want to put it first? I guess that depends on the data—if there are more comments than quoted strings, then yes, placing it first makes sense. Otherwise, I’d place it later. As it turns out with my test data, placing it first yields better results. Placing it later takes away about half the gains we achieved in the last step.

Wrapup

We’re not quite done yet. Don’t forget, each of the quoted-string subexpressions is ripe for unrolling — heck, we spent a long section of this chapter on that very topic. So, as a final change, let’s replace the two string subexpressions with:

$DOUBLE =  qr{"[^\\"]*(?:\\.[^\\"]*)*"} ;
$SINGLE =  qr{'[^'\\]*(?:\\.[^'\\]*)*'} ;

This change yields yet another 15 percent gain. Just a few changes has sped things up from 16.4 seconds to 2.3 seconds—a speedup of over 7×.

This last change also shows how convenient a technique it can be to use variables to build up a regular expression. Individual components, such as $DOUBLE, can be considered in relative isolation, and can be changed without having to wade into the full expression. There are still some overall issues (the counting of capturing parentheses, among others) that must be kept in mind, but it’s a wonderful technique.

One of the features that makes it so convenient in this case is Perl’s qr/··· / operator, which acts like a regex-related type of “string.” Other languages don’t have this exact functionality, but many languages do have string types that are amenable to building regular expressions. See “Strings as Regular Expressions” starting on page 101.

You’ll particularly appreciate the building up of regular expressions this way when you see the raw regex. Here it is, broken across lines to fit the page:

([^"'/]+|"[^\\"]*(?:\\.[^\\"]*)*"[^"'/]*|'[^'\\]*
(?:\\.[^'\\]*)*'[^"'/]*);/\*[^*]*\*+(?:[^/*][^*]*\*+)*/;//[^\n]*

In Summary: Think!

I’d like to end this chapter with a story that illustrates just how much benefit a little thought can go when using NFA regular expressions. Once when using GNU Emacs, I wanted a regex to find certain kinds of contractions such as “don’t,” “I’m,” “we’ll,” and so on, but to ignore other situations where a single quote might be next to a word. I came up with a regex to match a word, ⌈\<\w+⌋, followed by the Emacs equivalent of ⌈' ([tdm] |re|ll|ve)⌋. It worked, but I realized that using ⌈\<\w+⌋ was silly when I needed only \w. You see, if there is a \w immediately before the apostrophe, \w+ is certainly there too, so having the regex check for something we know is there doesn’t add any new information unless I want the exact extent of the match (which I didn’t, I merely wanted to get to the area). Using \w alone made the regex more than 10 times faster.

Yes, a little thought can go a long way. I hope this chapter has given you a little to think about.