We've been given the cause of death using ICD code W75 as accidental suffocation and strangulation in bed. It's not perfectly clear what HQ thinks this data means. However, it has somehow become important. We went to the http://wonder.cdc.gov website to get the summary of cause of death by year.

We wound up with a file that starts out like this:

"Notes"  "Cause of death"  "Cause of death Code"  "Year"  "Year Code"  Deaths  Population  Crude Rate 
  "Accidental suffocation and strangulation in bed"  "W75"  "2000"  "2000"  327  281421906	0.1 
  "Accidental suffocation and strangulation in bed"  "W75"  "2001"  "2001"  456  284968955  0.2 
 … etc. … 

This is a bit painful to process. It's almost—but not quite—in CSV notation. It's true that there aren't many commas, but there are tab characters encoded as \t in Python. These characters are sufficient to make a CSV file, where the tab takes the role of a comma.

We can read this file using Python's csv module with a \t delimiter:

import csv
with open( "Cause of Death by Year.txt" ) as source:
    rdr= csv.DictReader( source, delimiter="\t" )
    for row in rdr:
        if row['Notes'] == "---": break
        print(row)

This snippet will create a csv.DictReader object using the \t delimiter instead of the default value of ,. Once we have a reader that uses \t characters, we can iterate through the rows in the document. Each row will appear as a dictionary. The column title, found in the first row, will be the key for the items in the dictionary.

We used the expression row['Notes'] to get the value from the Notes column of each row. If the notes are equal to ---, this is the beginning of the footnotes for the data. What follows is a great deal of metadata.

The resulting dataset can be summarized easily. First, we'll create a generator function to parse our data:

def deaths():
    with open( "Cause of Death by Year.txt" ) as source:
        rdr= csv.DictReader( source, delimiter="\t" )
        for row in rdr:
            if row['Notes'] == "Total": break
            yield int(row['Year']), int(row['Deaths'])

We replaced the print() function with the yield statement. We also replaced --- with Total to prune the totals off the data. We can compute our own totals. Finally, we converted the year and deaths to integer values so that we can calculate with them.

This function will iterate through the various rows of data producing two-tuples of the year and the number of deaths.

Once we have this generator function, we can collect the summary like this:

year_deaths = list( deaths() )

We get this as a result:

[(2000, 327), (2001, 456), (2002, 509), (2003, 497), 
(2004, 596), (2005, 573), (2006, 661), (2007, 741), 
(2008, 809), (2009, 717), (2010, 684)]

This seems to be the data they're looking for. It gives us more data to work with.

The mean is defined using a daunting formula which looks like 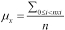. While the formula looks complex, the various parts are first-class built-in functions of Python.

The big sigma 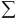is math-speak for the Python sum() function.

Given a list of values, the mean is this:

def mean( values ):
    return sum(values)/len(values)

Our two sets of data are provided as two-tuples with year and amount. We need to reel in the years, stowing away the time for later use. We can use a simple generator function for this. We can use the expression cheese for year, cheese in year_cheese to separate the cheese portion of each two-tuple.

Here's what happens when we use a generator with our mean() function:

>>> mean( cheese for year, cheese in year_cheese )
Traceback (most recent call last):
  File "<stdin>", line 1, in <module>
  File "<stdin>", line 2, in mean
TypeError: object of type 'generator' has no len()

Wait. What?

How can the simple generator not work?

Actually, it does work. It just doesn't do what we assume.

def count( values ):
    return sum( 1 for x in values )

>>> count( cheese for year, cheese in year_cheese )
13

def mean2( values ):
    return sum(values)/count(values)

>>> mean( [cheese for year, cheese in year_cheese] )
32.076153846153844
>>> mean( [death for year, death in year_deaths] )
597.2727272727273

def mean(values):
    """Mean of a sequence (doesn't work with an iterable)"""
    return sum(values)/len(values)

The median value is in the middle of a sorted collection of values. In order to find the median, we need to sort the data.

Here's an easy function to compute the median of a sequence:

def median(values):
    s = sorted(values)
    if len(s) % 2 == 1: # Odd
        return s[len(s)//2]
    else:
        mid= len(s)//2
        return (s[mid-1]+s[mid])/2

This includes the common technique of averaging the two middlemost values when there's an even number of samples.

We used len(s)%2 to determine if the sequence length is odd. In two separate places, we compute len(s)//2; seems like we might be able to simplify things using the divmod() function.

We can use this:

mid, odd = divmod(len(s), 2)

This change removes a little bit of the duplicated code that computes len(s)//2, but is it really more clear?

Two potential issues here are the overheads associated with sorting:

The modal value is the single most popular value in the collection. We can compute this using the Counter class in the collections module.

Here's a mode function:

from collections import Counter
def mode(values):
    c = Counter( values )
    mode_value, count = c.most_common(1)[0]
    return mode_value

The most_common() method of a Counter class returns a sequence of two-tuples. Each tuple has the value and the number of times it occurred. For our purposes, we only wanted the value, so we had to take the first element from the sequence of two-tuples. Then, we had to break the pair down into the value and the counter.

The problem with a demonstration is that our datasets are really small and don't have a proper mode. Here's a contrived example:

>>> mode( [1, 2, 3, 3, 4] )
3

This demonstrates that the mode function works, even though it doesn't make sense for our cheese consumption and death rate data.