The Natural Area Code (NAC) is yet another way to encode geographic position information into a short character string. The whole NAC system can include altitude information along with the surface position. We'll focus on the latitude and longitude conversions for NAC.
See http://www.nacgeo.com/nacsite/documents/nac.asp, for more information
This uses base 30 instead of base 240; we can use most of the alphabets plus some digits to represent a single base 30 digit. This implementation will show a different approach to convert floating-point numbers to an integer approximation. This will combine multiple calculation steps into longer expressions.
NAC uses a 30-character encoding that employs digits and consonants. The string used for encoding and decoding is this:
>>> nac_uppercase= "0123456789BCDFGHJKLMNPQRSTVWXZ"
>>> len(nac_uppercase)
30
>>> nac_uppercase[10]
'B'
>>> nac_uppercase.find('B')
10We can take a longitude (-180 to +180), and add an offset to put it in the range of 0 to 360. If we scale this by (30**4)/360, we'll get a number in the range 0 to 810000. This can be converted to a four-digit base 30 number.
Similarly, we can take a latitude (-90 to +90), and add an offset to put it in the range of 0 to 180. If we scale this by (30**4)/180, similarly, we'll get a number that can be converted to a four-digit base 30 number. The big win here is that we've replaced long strings of base 10 digits with shorter strings of base 30 digits.
The suggested algorithm to encode this is:
def ll_2_nac( lat, lon ):
f_lon= (lon+180)/360
x0 = int( f_lon*30)
x1 = int(( f_lon*30-x0)*30)
x2 = int((( f_lon*30-x0)*30-x1)*30)
x3 = int(.5+(((f_lon*30-x0)*30-x1)*30-x2)*30)
f_lat= (lat+90)/180
y0 = int( f_lat*30 )
y1 = int(( f_lat*30-y0)*30)
y2 = int((( f_lat*30-y0)*30-y1)*30)
y3 = int(0.5+(((f_lat*30-y0)*30-y1)*30-y2)*30)
print( x0, x1, x2, x3, y0, y1, y2, y3 )
return "".join( [
nac_uppercase[x0], nac_uppercase[x1],
nac_uppercase[x2], nac_uppercase[x3],
" ",
nac_uppercase[y0], nac_uppercase[y1],
nac_uppercase[y2], nac_uppercase[y3],
])We've scaled the longitude by adding an offset and dividing it by 360. This creates a number between 0 and 1.0. We can then encode this into base 30 using a large number of multiplications and subtractions. There are a number of ways to optimize this.
Each step follows a similar pattern. We'll step through the longitude calculation. Here's the first character calculation:
>>> lon= -151.3947 >>> f_lon= (lon+180)/360 >>> f_lon 0.07945916666666666 >>> x0 = int(f_lon*30) >>> x0 2
The first step computes f_lon, the fraction of 360 for this longitude (151.3947W). When we multiply f_lon by 30, we get 2.383775. The integer portion, 2, will become the first character. The fraction will be encoded in the remaining three characters.
Here's the next character, based on the first:
>>> x1 = int((f_lon*30-x0)*30) >>> x1 11
The calculation of (f_lon*30-x0) computes the fraction, .383775. We then scale this by 30 to get 11.51325. The integer portion, 11, will become the second character. The fraction will be encoded in the remaining two characters.
At each step, we take all of the previous digits to compute the remaining fractional components. Here are the last two characters:
>>> x2 = int((( f_lon*30-x0)*30-x1)*30) >>> x2 15 >>> x3 = int(0.5+(((f_lon*30-x0)*30-x1)*30-x2)*30) >>> x3 12
Each of these character, takes the difference between the original number (f_lon) and the previously computed digits to get the remaining fraction. The final step involves a lot of multiplication. Previously, in the Creating Maidenhead grid codes section, we showed a variation on this theme that didn't use quite so many multiplication operations.
As an example, we may perform the following:
lat, lon = 43.6508, -151.3947
print( ll_2_nac( lat, lon ) )The output of this is:
2CHD Q87M
This is a pretty tidy summary of a latitude and longitude.
Decoding natural area codes is actually a conversion from a base 30 number to a value between 0 and 810,000. This is then scaled into a proper latitude or longitude value. Although base 30 numbers don't seem simple, the programming is actually pretty succinct. Here's the suggested algorithm:
def nac_2_ll( grid ):
X, Y = grid[:4], grid[5:]
x = [nac_uppercase.find(c) for c in X]
y = [nac_uppercase.find(c) for c in Y]
lon = (x[0]/30+x[1]/30**2+x[2]/30**3+x[3]/30**4)*360-180
lat = (y[0]/30+y[1]/30**2+y[2]/30**3+y[3]/30**4)*180-90
return lat, lonWe've decomposed each part of the nine-character NAC grid code into a longitude substring and a latitude substring. We used a generator function to lookup each character in our nac_uppercase alphabet. This will map each character to a numeric position between 0 and 29.
Once we have the sequence of the four base 30 digits, we can compute a number from the digits. The following expression does the essential work:
(x[0]/30+x[1]/30**2+x[2]/30**3+x[3]/30**4)
The preceding expression is an optimization of the polynomial, 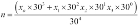 . The Python code simplifies the constants in each term—rather than computing
. The Python code simplifies the constants in each term—rather than computing x[0]*30**3/30**4; this is reduced to x[0]/30.
The intermediate results are scaled by 360 or 180 and offset to get the expected signed values for the final result.
Consider that we evaluate the following:
print( nac_2_ll( "2CHD Q87M" ) )
We get the following as a result:
(43.650888888888886, -151.39466666666667)
This shows how we decode an NAC to recover the latitude and longitude of a position.
