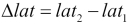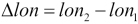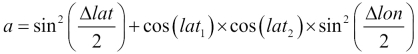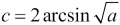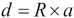How close? What direction?

In order to calculate the distance between two points, we'll need to use some spherical geometry calculations. The problem we will have to overcome is that our charts and maps are flat. But the actual planet is very close to being spherical. While the spherical geometry may be a bit advanced, the programming is pretty simple. It will show us several features of the Python math library.

The distance between two latitude and longitude points on a sphere is defined as follows:

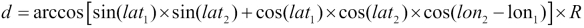
This formula determines the cosine between the two positions; the angle with that cosine is multiplied by the radius of the earth, R, to get the distance along the surface. We can use R = 3,440 NM, R = 3,959 mi, or R = 6,371 km; we get reasonably accurate distances in nautical miles, statute miles, or kilometers.

This formula doesn't work well with small distances. The haversine formula is preferred to compute distances more accurately. Here is some background information http://en.wikipedia.org/wiki/Haversine_formula.

According to the OED, the term "haversine" was coined in 1835 by Prof. James Inman. The term refers to the way the sine function is used.

The haversine calculation is often shown as a sequence of five steps:

The required sine, cosine, and square root portions of this are part of Python's math library. When we look at the definitions of sine and cosine, we see that they work in radians. We'll need to convert our latitude and longitude values from degrees to radians. The rule is simple (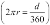 How close? What direction? ), but the math library includes a function, radians(), which will do this for us.

We can look at http://rosettacode.org/wiki/Haversine_formula#Python to learn from the example already there.

We'll use this as the distance between two points:

from math import radians, sin, cos, sqrt, asin

MI= 3959
NM= 3440
KM= 6371

def haversine( point1, point2, R=MI ):
    """Distance between points.
    point1 and point2 are two-tuples of latitude and longitude.
    R is radius, R=MI computes in miles.
    """
    lat_1, lon_1 = point1
    lat_2, lon_2 = point2

    Δ_lat = radians(lat_2 - lat_1)
    Δ_lon = radians(lon_2 - lon_1)
    lat_1 = radians(lat_1)
    lat_2 = radians(lat_2)

    a = sin(Δ_lat/2)**2 + cos(lat_1)*cos(lat_2)*sin(Δ_lon/2)**2
    c = 2*asin(sqrt(a))

    return R * c

We've imported the five functions from the math library that we require for this calculation.

We've defined three constants with the earth's radius in various units. We can plug any of these into our haversine() function as the R parameter to compute distances in different units. These values are approximations, but they'll work to determine how far apart two points are. We can plug in more accurate values if we want more precise answers. Since the earth isn't perfectly spherical, we have to be sure to use mean radius values.

The haversine() function will accept two required positional parameters and an optional parameter. The two positional parameters will be two-tuples of latitude and longitude. We'd like to use a syntax like (36.12, -86.67) to keep the two coordinates bound in a single Python value. The R parameter is optional because we've provided a default value for it. We can use this function to get distances in kilometers instead of in miles: haversine( (36.12, -86.67), (33.94, -118.40), R=KM).

The body of our function breaks down the two-tuples into their component latitude and longitude values. We compute the Δ_lat variable by subtracting and converting the result to radians. Similarly, we compute the Δ_lon variable by subtracting and converting the result to radians. And yes variable names which begin with the Greek Δ character are perfectly valid in Python. After this, we can also convert the other two latitudes to radians. We can then plug these values to other formulae to compute a, c, and finally the distance.

We have a test case based on the example from the Rosetta Code website:

>>> from ch_4_ex_3 import haversine
>>> round(haversine((36.12, -86.67), (33.94, -118.40), R=6372.8), 5)
2887.25995

Note that we rounded the answer to five decimal places. Floating-point numbers are an approximation; it's possible to see some variations between hardware and OS in precisely how floating-point numbers work. By limiting ourselves to five decimal places, we're confident that variations in hardware won't upset the test case.

We can use this haversine() function with our geocode results to compute distances between locations; this will help us find the closest locations.

Combining geocoding and haversine

Between geocoding and the haversine() function, we have the tools to compute the approximate distance between addresses.

Let's take 333 Waterside, Norfolk, Virginia, as our current base of operations. Let's say our informant wants to meet either at 456 Granby or 111 W Tazewell. Which one is closer?

First, we'll need to clean up our geocoding script to make it a usable function. Rather than simply printing a result, we'll need to get the values out of the results dictionary to make a sequence of the two-tuples of the latitude and longitude responses.

Here's what we'll need to add:

    def geocode( address ):
    ...  The previous processing ... 
    loc_dict= [r['geometry']['location'] for r in response['results']]
    loc_pairs= [(l['lat'],l['lng']) for l in loc_dict]
    return loc_pairs

We've used two generator expressions to dismantle the results. The first generator expression took the location information from each alternative in the response['results'] sequence. For geocoding, there should only be one expression, but it's simpler if we pretend we'll get multiple responses.

The second generator expression turned the 'lat' and 'lng' elements of the location dictionary into a two-tuple. Having latitude and longitude two-tuples will play well with our havesine() function.

Here's how we can get three latitude-longitude pairs:

base = geocode( "333 Waterside, Norfolk, VA, 23510" )[0]
loc1 = geocode( "456 Granby St, Norfolk, VA" )[0]
loc2 = geocode( "111 W Tazewell, Norfolk, VA" )[0]

We've applied our geocode() function to get a list of two-tuples and then used [0] to pick the first element from each response list.

Here's how we can report the distances from the base to each location:

print("Base", base)
print("Loc1", loc1, haversine(base, loc1))
print("Loc2", loc2, haversine(base, loc2))

We applied our haversine() function to compute distances. By default, the distances are in miles, not that the units matter to carry out a relative comparison of closer versus further away.

Here are the results:

Base (36.8443027, -76.2910835)
Loc1 (36.8525159, -76.2890381) 0.578671972401055
Loc2 (36.8493341, -76.291527) 0.3485214316218753

We can see that the second location (Loc2), the Tazewell address, is much closer to our base than the Granby street address.

Also, we can see that we need to format these numbers to make them look better. Since we're only working with an approximate mean earth radius in miles, most of those decimal places are just visual noise.

Previous Chapter

Finding out where we are with geocoding services

Next Chapter

Compressing data to make grid codes

Table of Contents for Python for Secret Agents

How close? What direction?

Combining geocoding and haversine

Table of Contents for
Python for Secret Agents