The Python list class can be summarized as a mutable sequence. Mutability means that we can add, change, and remove items (the list can be changed). Sequence means that the items are accessed based on their positions within the list.

The syntax is pleasantly simple; we put the data items in [] and separate the items with ,. We can use any Python object in the sequence.

HQ wants information on per capita consumption of selected cheese varieties. While HQ doesn't reveal much to field agents, we know that they often want to know about natural resources and strategic economic strengths.

We can find cheese consumption data at http://www.ers.usda.gov/datafiles/Dairy_Data/chezcon_1_.xls.

Sadly, the data is in a proprietary spreadsheet format and rather difficult to work with. To automate the data gathering, we would need something like Project Stingray to extract the data from this document. For manual data gathering, we can copy and paste the data.

Here's the data starting in 2000 and extending through 2010; we'll use it to show some simple list processing:

>>> cheese = [29.87, 30.12, 30.60, 30.66, 31.33, 32.62,
...     32.73, 33.50, 32.84, 33.02,]
>>> len(cheese)
10
>>> min(cheese)
29.87
>>> cheese.index( max(cheese) )
7

We created a list object and assigned it to the cheese variable. We used the min() function, which reveals the least value in the 29.87 sequence.

The index() method searches through the sequence for the matching value. We see that the maximum consumption found with the max() function has an index of 7 corresponding to 2007. After that, cheese consumption fell slightly.

Note that we have prefix function notations (min(), max(), len(), and several others). We also have method function notation, cheese.index(), and many others. Python offers a rich variety of notations. There's no fussy adherence to using only method functions.

As a list is mutable, we can append additional values to the list. We can use an cheese.extend() function to extend a given list with an additional list of values:

>>> cheese.extend( [32.92, 33.27, 33.51,] )
>>> cheese
[29.87, 30.12, 30.6, 30.66, 31.33, 32.62, 32.73, 33.5, 32.84, 33.02, 32.92, 33.27, 33.51]

We can also use the + operator to combine two lists.

We can reorder the data so that it's strictly ascending using the following code:

>>> cheese.sort()
>>> cheese
[29.87, 30.12, 30.6, 30.66, 31.33, 32.62, 32.73, 32.84, 32.92, 33.02, 33.27, 33.5, 33.51]

Note that the sort() method doesn't return a value. It mutates the list object itself; it doesn't return a new list. If we try something like sorted_cheese= cheese.sort(), we see that sorted_cheese has a None value. This is a consequence of sort() not returning a value; it mutates the list.

When working with time-series data, this kind of transformation will be confusing because the relationship between year and cheese consumption is lost when we sort the list.

>>> cheese[0]
29.87
>>> cheese[1]
30.12

>>> cheese[-2]
33.5
>>> cheese[-1]
33.51

>>> cheese[:5]
[29.87, 30.12, 30.6, 30.66, 31.33]
>>> cheese[5:]
[32.62, 32.73, 32.84, 32.92, 33.02, 33.27, 33.5, 33.51]

>>> 30.5 in cheese
False
>>> 33.5 in cheese
True

>>> [1, 2, 1] < [1, 2, 2]
True

The Python tuple class can be summarized as an immutable sequence. Immutability means that once created, the tuple cannot be changed. The value of the number 3 is immutable, also: it's always 3. Sequence means that the items are accessed based on their positions within the tuple.

The syntax is pleasantly simple; we might need to put the data items in () and must separate the items with ,. We can use any Python objects in the sequence. The idea is to create an object that looks like a mathematical coordinate: (3, 4).

Tuples are used under the hood at many places within Python. When we use multiple assignments, for example, the right-hand side of the following code creates a tuple and the left-hand side decomposes it:

power, value = 0, 1

The right-hand side created a two-tuple (0, 1). The syntax doesn't require () around the tuple. The left-hand side broke down a two-tuple, assigning the values to two distinct variables.

We generally use tuples for data objects where the number of elements is fixed by the problem domain. We often use tuples for coordinate pairs such as latitude and longitude. We don't need the flexible length that a list offers because the size of a tuple cannot change. What would a three-tuple mean when it's supposed to have just two values, latitude and longitude? A different kind of problem might involve longitude, latitude, and altitude; in this case, we're working with three-tuples. Using two-tuples or three-tuples in these examples is an essential feature of the problem: we won't be mutating objects to add or remove values.

When we looked at HTTP headers in requests and responses, we saw that these are represented as a list of two-tuples, such as ('Content-Type', 'text/html; charset=utf-8'). Each tuple has a header name ('Content-Type') and header value ('text/html; charset=utf-8').

Here's an example of using a two-tuple to include year and cheese consumption:

year_cheese = [(2000, 29.87), (2001, 30.12), (2002, 30.6), (2003, 30.66),
    (2004, 31.33), (2005, 32.62), (2006, 32.73), (2007, 33.5),
    (2008, 32.84), (2009, 33.02), (2010, 32.92), (2011, 33.27),
    (2012, 33.51)]

This list-of-tuple structure allows us to perform a slightly simpler analysis of the data. Here are two examples:

>>> max( year_cheese, key=lambda x:x[1] )
(2012, 33.51)
>>> min( year_cheese, key=lambda x:x[1] )
(2000, 29.87)

We applied the max() function to our list of tuples. The second argument to the max() function is another function—in this case, an anonymous lambda object—that evaluates just the second value in each tuple.

Here are two more examples that show what's happening with the lambda object:

>>> (2007, 33.5)[1]
33.5
>>> (lambda x:x[1])( (2007, 33.5) )
33.5

The (2007, 33.5) two-tuple has the [1] get item operation applied; this will pick the item at position 1, that is, the 33.5 value. The item at position zero is the year 2007.

The (lambda x:x[1]) expression creates an anonymous lambda function. We can then apply this function to the (2007, 33.5) two-tuple. As the x[1] expression picks the item at index position 1, we get the 33.5 value.

We can, if we want, create a fully defined, named function instead of using lambda, as shown in the following code

def by_weight( yr_wt_tuple ):
    year, weight =  yr_wt_tuple
    return weight

A named function has two advantages: it has a name, and it can have multiple lines of code. A lambda function has the advantage of being tiny when the entire function can be reduced to a single expression.

We can use this technique to sort these two-tuples with a function instead of lambda, as shown in the following code snippet:

>>> by_cheese = sorted( year_cheese, key=by_weight )
>>> by_cheese
[(2000, 29.87), (2001, 30.12), (2002, 30.6), (2003, 30.66), (2004, 31.33), (2005, 32.62), (2006, 32.73), (2008, 32.84), (2010, 32.92), (2009, 33.02), (2011, 33.27), (2007, 33.5), (2012, 33.51)]

We used a separate function to create a sorted copy of a sequence. The sorted() function requires an iterable item (the year_cheese list in this case) and a key function; it creates a new list from the old sequence that is sorted into order by the key function. In this case, our key function is the named function, by_weight(). Unlike the list.sort() method, the sorted() function does not modify the original sequence; the new list contains references to the original items.

>>> years = [ item[0] for item in year_cheese ]
>>> years
[2000, 2001, 2002, 2003, 2004, 2005, 2006, 2007, 2008, 2009, 2010, 2011, 2012]

>>> years.index(2005)
5
>>> year_cheese[years.index(2005)]
(2005, 32.62)

A dictionary contains a mapping from keys to values. The Python dictionary class can be summarized as a mutable mapping. Mutability means that we can add, change, and remove items. Mapping means that the values are accessed based on their keys. Order is not preserved in a mapping.

The syntax is pleasantly simple: we put the key-value pairs in {}, separate the key from the value with :, and separate the pairs with ,. The values can be any kind of Python object. The keys, however, suffer from a restriction—they must be immutable objects. As strings and numbers are immutable, they make perfect keys. A tuple is immutable and a good key. A list is mutable though, and can't be used as a key.

When we looked at creating an HTTP form data, in the Getting more RESTful data section, we used a mapping from field name to field value. We got back a response, which was a mapping from keys to values. The response looked like this:

>>> spot_rate= {'currency': 'EUR', 'amount': '361.56'}
>>> spot_rate['currency']
'EUR'
>>> spot_rate['amount']
'361.56'
>>> import decimal
>>> decimal.Decimal(spot_rate['amount'])
Decimal('361.56')

After creating the spot_rate dictionary, we used the dict[key] syntax to get values of two of the keys, currency and amount.

As a dictionary is mutable, we can easily change the values associated with the keys. Here's how we can create and modify a form:

>>> form= {"currency":"EUR"}
>>> form['currency']= "USD"
>>> form
{'currency': 'USD'}

We created the form variable as a small dictionary. We can use this to make one spot-rate query. We then changed the value in the form dictionary. We can use this updated form to make a second spot-rate query.

When getting a value, the key must exist; otherwise, we'll get an exception. As noted earlier, we can also use dict.get(key, default) to get values when a key might not exist in the dictionary. Here are several examples:

>>> spot_rate['currency']
'EUR'
>>> spot_rate['oops']
Traceback (most recent call last):
  File "<stdin>", line 1, in <module>
KeyError: 'oops'
>>> spot_rate.get('amount')
'361.56'
>>> spot_rate.get('oops')
>>> spot_rate.get('oops', '#Missing')
'#Missing'

First, we fetched the value mapped to the currency key. We tried to fetch a value mapped to the oops key. We got a KeyError exception because the oops key isn't in the spot_rate dictionary.

We did the same kinds of things using the get() method. When we executed spot_rate.get('amount'), the key-value pair existed, so the value was returned.

When we executed spot_rate.get('oops'), the key didn't exist; the default return value was None. Python doesn't print None values, so we don't see any obvious result from this. When we executed spot_rate.get('oops', '#Missing'), we provided a return value that is not None, which displayed something visible. The idea is that we can then do things like this to make a series of related queries:

for currency in 'USD', 'EUR', 'UAH':
    form['currency']=  currency
    data= urllib.parse.urlencode( form )
    ...etc...

The for statement includes a tuple of values: 'USD', 'EUR', 'UAH'. We aren't required to put () around the tuple in this particular case because the syntax is unambiguous.

Each value from the literal tuple is used to set the currency value in the form. We can then use the urllib.parse.urlencode() function to build a query string. We might be using this in a urllib.urlopen() function to get a current spot price for bitcoins in that currency.

>>> spot_rate.keys()
dict_keys(['amount', 'currency'])
>>> spot_rate.items()
dict_items([('amount', '361.56'), ('currency', 'EUR')])
>>> spot_rate.values()
dict_values(['361.56', 'EUR'])

>>> rate_as_list= spot_rate.items()
>>> rate_as_list  
dict_items([('amount', '361.56'), ('currency', 'EUR')])

>>> dict(rate_as_list)
{'amount': '361.56', 'currency': 'EUR'}

>>> 'currency' in spot_rate
True
>>> 'USD' in spot_rate
False

'USD' in spot_rate.values()

The data at http://www.coinbase.com/api/v1/currencies/, which was a RESTful request, was a giant list of lists. It started like this:

>>> currencies = [['Afghan Afghani (AFN)', 'AFN'], ['Albanian Lek (ALL)', 'ALL'],  
... ['Algerian Dinar (DZD)', 'DZD'], 
... ]

If we apply the dict() function to this list of lists, we'll build a dictionary. However, this dictionary isn't what we want; the following code is how it looks:

>>> dict(currencies)
{'Afghan Afghani (AFN)': 'AFN', 'Albanian Lek (ALL)': 'ALL', 'Algerian Dinar (DZD)': 'DZD'}

The keys in this dictionary are long country currency (code) strings. The values are the three-letter currency code.

We might want the keys of this as a handy lookup table for a person's reference to track down the proper currency for a given country. We might use something like this:

>>> dict(currencies).keys()
dict_keys(['Afghan Afghani (AFN)', 'Albanian Lek (ALL)', 'Algerian Dinar (DZD)'])

This shows how we can create a dictionary from a list of lists and then extract just the keys() from this dictionary. This is, in a way, an excessive amount of processing for a simple result.

We showed an example of picking up some data using a generator function in the Using a Python tuple section. Here's how we'd apply it to this problem. We'll create a list comprehension using a generator function. The generator, surrounded by [], will lead to a new list object, as shown in the following code:

>>> [name for name, code in currencies]
['Afghan Afghani (AFN)', 'Albanian Lek (ALL)', 'Algerian Dinar (DZD)']

The currencies object is the original list of lists. The real one has 161 items; we're working with a piece of it here to keep the output small.

The generator expression has three clauses. These are subexpressions for targets in source. The [] characters are separate punctuations used to create a list objects from the generated values; they're not part of the generator expression itself. The subexpression is evaluated for each target value. The target variable is assigned to each element from the source iterable object. Each two-tuple from the currencies list is assigned to the name and code target variables. The subexpression is just name. We can use this to build a dictionary from currency to full name:

>>> codes= dict( (code,name) for name,code in currencies )
>>> codes
{'DZD': 'Algerian Dinar (DZD)', 'ALL': 'Albanian Lek (ALL)', 'AFN': 'Afghan Afghani (AFN)'}
>>> codes['AFN']
'Afghan Afghani (AFN)'

We used a generator function to swap the two elements of each item of the currency list. The targets were name and code; the resulting subexpression is the (code,name) two-tuple. We built a dictionary from this; this dictionary maps currency codes to country names.

There are a number of sophisticated mappings that are part of the standard library. Two of these are the defaultdict and Counter mappings. The defaultdict allows us to work more flexibly with keys that don't exist.

Let's look at the word corpus we used to recover a ZIP file password. We can use this word corpus for other purposes. One of the things that can help the crypto department decode messages is knowledge of two-letter sequences (digram or bigram) that occur commonly in the source documents.

What are the most common two-letter digrams in English? We can easily gather this from our dictionary, as shown in the following code:

from collections import defaultdict
corpus_file = "/usr/share/dict/words"
digram_count = defaultdict( int )
with open( corpus_file ) as corpus:
    for line in corpus:
        word= line.lower().strip()
        for position in range(len(word)-1):
            digram= word[position:position+2]
            digram_count[digram] += 1

We need to import the defaultdict class from the collections module because it's not built in. We created an empty defaultdict object, digram_count, using int as the initialization function. The initialization function handles missing keys; we'll look at the details in the following section.

We opened our word corpus. We iterated through each line in corpus. We transformed each line into a word by stripping the trailing spaces and mapping it to lowercase. We used the range() function to generate a sequence of positions from zero to one less than the length of the word (len(word)-1). We can pluck a two-character digram from each word using the word[position:position+2] slice notation.

When we evaluate digram_count[digram], one of two things will happen:

The cool feature of a defaultdict class is that no exception is raised for a missing key value. Instead of raising an exception, the initialization function is used.

This defaultdict(int) class is so common that we can use the Counter class definition for this. We can make two tiny changes to the previous example. The first change is as follows:

from collections import Counter

The second change is as follows:

digram_count= Counter()

The reason for making this change is that Counter classes do some additional things. In particular, we often want to know the most common counts, as shown in the following code:

>>> print( digram_count.most_common( 10 ) )
[('er', 42507), ('in', 33718), ('ti', 31684), ('on', 29811), ('te', 29443), ('an', 28275), ('al', 28178), ('at', 27276), ('ic', 26517), ('en', 25070)]

The most_common() method of a Counter object returns the counts in the descending order. This shows us that er is the most common English-language digram. This information might help the decoders back at HQ.

The Python set class is mutable; we can add, change, and remove items. Items are either present or absent. We don't use positions or keys; we merely add, remove, or test the items. This means that sets have no inherent order.

The syntax is pleasantly simple; we put the data items in {} and separated the items with ,. We can use any immutable Python objects in the set. It's important to note that the items must be immutable—we can include strings, numbers, and tuples. We can't include a list or dictionary in a set.

As the {} characters are used both by dictionaries and sets, it's unclear what the empty pair, {}, means. Is this an empty dictionary or an empty set? It's much more clear if we use dict() to mean an empty dictionary and set() to mean an empty set.

A set is a simple collection of things; it is perhaps the simplest possible collection of things.

In looking at the digrams, we noticed that there were some digrams, including a - character. How many hyphenated words are in the dictionary? This is a simple set processing example:

corpus_file = "/usr/share/dict/words"
hyphenated = set()
with open( corpus_file ) as corpus:
    for line in corpus:
        word= line.lower().strip()
        if '-' in word:
            hyphenated.add(word)

We created an empty set and assigned it to the hyphenated variable. We checked each word in our collection of words to see if the - character is in the collection of characters. If we find the hyphen, we can add this word to our set of hyphenated words.

The word corpus on the author's computer had two hyphenated words. This raises more questions than it answers.

The in operator is essential for working with sets. The comparison operators implement subset and superset comparisons between two sets. The a <= b operation asks if a is a subset of b, mathematically, .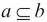

The for statement is the primary tool to iterate through the items in a collection. When working with lists, tuples, or sets, the for statement will pleasantly assure that all values in the collection are assigned to the target variable, one at a time. Something like this works out nicely:

>>> for pounds in cheese:
...     print( pounds )
... 
29.87
etc.
33.51

The for statement assigns each item in the cheese sequence to the target variable. We simply print each value from the collection.

When working with the list-of-tuples structures, we can do something a bit more interesting, as shown in the following code:

>>> for year, pounds in year_cheese:
...     print( year, pounds )
... 
2000 29.87
etc.
2012 33.51

In this example, each two-tuple was decomposed, and the two values were assigned to the target variables, year and pounds.

We can leverage this when transforming a Count object into percentages. Let's look at our digram_count collection:

total= sum( digram_count.values() )
for digram, count in digram_count.items():
    print( "{:2s} {:7d} {:.3%}".format(digram, count, count/total) )

First, we computed the sum of the values in the collection. This is the total number of digrams found in the original corpus. In this example, it was 2,021,337. Different corpora will have different numbers of digrams.

The for statement iterates through the sequence created by digram_count.items(). The items() method produces a sequence of two-tuples with the key and value. We assign these to two target variables: digram and count. We can then produce a nicely formatted table of all 620 digrams, their counts, and their relative frequency.

This is the kind of thing that the folks in the crypto department love.

When we apply the for statement to a dictionary directly, it iterates just over the keys. We could use something like this to iterate through the digram counts:

for digram in digram_count:
    print( digram, digram_count[digram], digram_count[digram]/total )

The target variable, digram, is assigned to each key. We can then use a syntax such as digram_count[digram] to extract the value for this key.

Some of the mathematical operators work with collections. We can use the + and * operators with sequences such as lists and tuples, as shown in the following code:

>>> [2, 3, 5, 7] + [11, 13, 17]
[2, 3, 5, 7, 11, 13, 17]
>>> [2, 3, 5, 7] * 2
[2, 3, 5, 7, 2, 3, 5, 7]
>>> [0]*10
[0, 0, 0, 0, 0, 0, 0, 0, 0, 0]

These examples showed how we can concatenate two lists and multiply a list to create a longer list with multiple copies of the original list. The [0]*10 statement shows a more useful technique to initialize a list to a fixed number of values.

Sets have a number of operators for union (|), intersection (&), difference (-), and symmetric difference (^). Also, the comparison operators are redefined to work as subset or superset comparisons. Here are some examples:

>>> {2, 3, 5, 7} | {5, 7, 11, 13, 17}
{2, 3, 5, 7, 11, 13, 17}
>>> {2, 3, 5, 7} & {5, 7, 11, 13, 17}
{5, 7}
>>> {2, 3, 5, 7} - {5, 7, 11, 13, 17}
{2, 3}
>>> {2, 3, 5, 7} ^ {5, 7, 11, 13, 17}
{2, 3, 11, 13, 17}
>>> {2, 3} <= {2, 5, 7, 3, 11}
True

The union operator, |, combines the two sets. A set means an element only occurs once, so there are no duplicated elements in the union of the sets. The intersection of two sets, &, is the set of common elements in the two sets. The subtraction operator, -, removes elements from the set on the left-hand side. The symmetric difference operator, ^, creates a new set that has elements which are in one or the other set but not both; essentially, it is the same as an exclusive OR.

We showed just one comparison operator, the <= subset operator, between two sets. The other comparison operators perform just as can be expected.